समाकलित बहुभुज: Difference between revisions
(Created page with "{{short description|A convex polytope whose vertices all have integer Cartesian coordinates}} {| class="wikitable" align="right" | 120px | File:Pol...") |
No edit summary |
||
| (11 intermediate revisions by 5 users not shown) | |||
| Line 11: | Line 11: | ||
| [[File:3D chess moves 012.png|120px]] | | [[File:3D chess moves 012.png|120px]] | ||
|- | |- | ||
| [[Cube]] | | [[Cube|घन]] | ||
| [[Cuboctahedron]] | | [[Cuboctahedron|क्यूबोक्टहेड्रॉन]] | ||
| [[Octahedron]] | | [[Octahedron|अष्टफलक]] | ||
| [[Truncated octahedron| | | [[Truncated octahedron|छिन्न अष्टफलक]] | ||
|- | |- | ||
| (±1, ±1, ±1) | | (±1, ±1, ±1) | ||
| Line 21: | Line 21: | ||
| (0, ±1, ±2) | | (0, ±1, ±2) | ||
|- | |- | ||
!colspan="4"| | !colspan="4"| त्रि-आयामों चार पूर्णांक पॉलिटोप | ||
|} | |} | ||
ज्यामिति और | ज्यामिति और बहुभुज संख्यात्मक विज्ञान में, [[उत्तल पॉलीटॉप|पूर्णांकीय बहुभुज]] एक ऐसा अभिन्न बहुभुज होता है जिसके सभी शीर्षों के, कार्तेसीय समन्वयी निर्देशांक होते हैं।{{r|c}} अर्थात, यह एक ऐसा बहुभुज है जो अपनी पूर्णांकीय बिंदुओं के अवमुख समावरक के समान होता है।{{r|m}} पूर्णांकीय बहुभुजों को लैटिस बहुभुज या जेड-बहुभुज भी कहा जाता है। दो- और त्रि-आयामी पूर्णांकीय बहुभुजो के विशेष परिप्रेक्ष्य को क्रमशः पॉलीटोप्स के अतिरिक्त बहुभुज या बहुकोणीय आकृति कहा जा सकता है। | ||
== उदाहरण == | == उदाहरण == | ||
किसी एन-आयामी नियमित [[संकेतन]] को, <math>\mathbb{R}^{n+1}</math> में एक पूर्णांकीय बहुभुज के रूप में प्रस्तुत किया जा सकता है, जहां पूर्णांकीय बिंदुओं का एक आधार एक है और बाकी सभी बिन्दुओ का आधार शून्य हैं। एक और महत्वपूर्ण प्रकार का पूर्णांकीय सिम्प्लेक्स, [[orthoscheme|विषमकोण आयत]], को उन पूर्णांकीय बिंदुओं के अवमुख समावरक द्वारा निर्मित किया जा सकता है, जिनके निर्देशांकों का प्रारंभ कुछ संयुक्त पूर्णांकों के साथ होती है जिसके उपरांत शेष सभी निर्देशांक शून्य होते हैं। <math>\mathbb{R}^n</math> में n-आयामीक [[इकाई घन]] के कोण उन सभी पूर्णांक बिंदुओं से मिलते हैं जिनके निर्देशांक शून्य या एक होतें हैं।एक पर्म्युटाहेड्रन के कोण उस सदिश <math>(1,2,...,n)</math>. पर सभी संभव क्रमचयों को लागू करके प्राप्त किए जाने वाले निर्देशांक होते हैं। लोडे के उच्चतम वास्तविकीकरण में एक असोसिएहेड्रन भी एक पूर्णांक पॉलिटोप और पर्म्युटाहेड्रन का विकर्ण होता है। | |||
== अनुकूलन में == | == अनुकूलन में == | ||
[[रैखिक प्रोग्रामिंग]] और [[गणितीय अनुकूलन]] में संबंधित समस्याओं के संदर्भ में, उत्तल पॉलीटोप्स को | [[रैखिक प्रोग्रामिंग]] और [[गणितीय अनुकूलन]] में संबंधित समस्याओं के संदर्भ में, उत्तल पॉलीटोप्स को प्रायः [[रैखिक असमानता]] की एक प्रणाली द्वारा वर्णित किया जाता है, जो कि उनके बिंदुओं का उपयो करता है। जब एक पॉलीटॉप अभिन्न होता है, तो दी गई असमानताओं की प्रणाली के सापेक्ष [[पूर्णांक प्रोग्रामिंग]] समस्याओं को हल करने के लिए रैखिक प्रोग्रामिंग का उपयोग किया जाता है, जो अन्यथा अत्यधिक कठिन हो सकती है। | ||
संयोजी इष्टतमीकरण समस्याओं से उत्पन्न होने वाले कुछ बहुफलक स्वचालित रूप से अभिन्न हैं। उदाहरण के लिए, यह किसी भी आंशिक रूप से | संयोजी इष्टतमीकरण समस्याओं से उत्पन्न होने वाले कुछ बहुफलक स्वचालित रूप से अभिन्न हैं। उदाहरण के लिए, यह किसी भी आंशिक रूप से समायोजित किए गए समुच्चय के [[ पॉलीटॉप ऑर्डर करें | पॉलीटॉप समायोजन]] के विषय में सत्य है, समुच्चय में तुलनीय तत्वों के अनुरूप निर्देशांक के मध्य युग्मक असमानताओं द्वारा परिभाषित एक पॉलीटोप इन्ही तत्वों द्वारा अनुकूलित होता है।{{r|s}} संयोजी अनुकूलन में एक अन्य प्रसिद्ध पोलीटोप, मिलान पोलीटोप है। स्पष्टतः, हम एकल विधि में विधिकालात्मक रूप से मिलान खोजने का प्रयास करते हैं और इस तकनीक रैखिक प्रोग्रामिंग कहा जाता है। रेखीय प्रोग्रामिंग द्वारा वर्णित पॉलीटोप, प्रति शीर्ष पर वर्णित भुजाओ के योग को द्विदलीय रेखांकन के परिप्रेक्ष्य में अभिन्न बनाता है, अर्थात यह मिलान वाले पॉलीटोप का सटीक वर्णन करता है, जबकि सामान्य रेखांकन के लिए यह गैर-अभिन्न है।<ref>{{Cite book |author=Lovász, László |url=http://worldcat.org/oclc/316569965 |title=मिलान सिद्धांत|date=1986 |publisher=North-Holland |isbn=978-0-444-87916-5 |pages=269–274 |oclc=316569965}}</ref> इसलिए, द्विदलीय रेखांकन में, यह एक वैध [[मिलान (ग्राफ सिद्धांत)|मिलान]] प्राप्त करने के लिए संबंधित रैखिक प्रोग्रामिंग को हल करने के लिए पर्याप्त है। सामान्य रेखांकन के लिए, यद्यपि, मिलान पॉलीटॉप के दो अन्य लक्षण हैं, जिनमें से एक शीर्ष के विषम उपसमुच्चय के लिए ब्लॉसम असमानता का उपयोग करता है और इसलिए वैध मिलान प्राप्त करते हुए पूर्णांक प्रोग्राममिन को एक रेखीय प्रोग्रामिंग में परिवर्तित करने की अनुमति देता है।<ref>{{Cite book |author=Lovász, László |url=http://worldcat.org/oclc/316569965 |title=मिलान सिद्धांत|date=1986 |publisher=North-Holland |isbn=978-0-444-87916-5 |pages=274–281 |oclc=316569965}}</ref> ये विशेषताएँ ब्लॉसम एल्गोरिथम में और अधिक रुचि रखती हैं। एडमंड्स का प्रसिद्ध ब्लॉसम एल्गोरिथम सामान्य आरेख में ऐसे मिलानों को खोजने के लिए उपयोग किया जाता है। | ||
== | == संगणनात्मक जटिलता == | ||
रेखीय असमानताओं द्वारा वर्णित | रेखीय असमानताओं द्वारा वर्णित किसी पॉलीटॉप के लिए, जब पॉलीटॉप गैर-अभिन्न होता है, तो कोई ऐसा शीर्ष ढूंढकर अपनी गैर-अभिन्नता प्रमाणित कर सकता है जिसका निर्देशांक पूर्णांक नहीं हैं। इस तरह के शीर्ष को असमानताओं के एक उपसमुच्चय को निर्दिष्ट करके संयुक्त रूप से वर्णित किया जा सकता है, जब रैखिक समीकरणों की एक प्रणाली में परिवर्तन कर दिया जाता है, तो एक अद्वितीय समाधान होता है, और यह सत्यापित करता है कि यह समाधान बिंदु अन्य सभी असमानताओं का पालन करता है। इसलिए, परीक्षण अभिन्नता, समस्याओं की [[जटिलता वर्ग]] से संबंधित है, जिसके लिए एक नकारात्मक उत्तर सरलता से सिद्ध किया जा सकता है।{{r|dfz}} | ||
== संबंधित | == संबंधित उद्देश्य == | ||
अभिन्न पॉलीटॉप के आयतन और शीर्षों की संख्या सहित कई महत्वपूर्ण गुण, [[एहरहार्ट बहुपद]] द्वारा कूटबद्ध किए गए हैं।{{r|b}} | |||
अभिन्न पॉलीटॉप को प्रमुख रूप से [[टॉरिक किस्म|टॉरिक वरिटीस]] के सिद्धांत में चित्रित किया गया है, जहां वे ध्रुवीकृत प्रक्षेपीय टॉरिक वरिटीस के अंतर्गत अनुरूपित हैं। उदाहरण के लिए, किसी प्रसमुच्चय से संबंधित टोरिक वरिटीस एक [[ प्रक्षेपण स्थान |प्रक्षेपण स्थान]] है। एक इकाई घन से संबंधित टोरिक वरिटीस, परियोजनात्मक रेखा के एन-गुणा उत्पाद का [[सेग्रे एम्बेडिंग|सेग्रे अंत:स्थापन]] है। | |||
उदाहरण के लिए, | |||
[[बीजगणितीय ज्यामिति]] में, | [[बीजगणितीय ज्यामिति]] में, लैटिस पॉलीटोप्स का एक महत्वपूर्ण उदाहरण जिसे [[न्यूटन पॉलीटोप]] भी कहा जाता है, एक [[बहुपद]] के संदर्भ में प्रत्येक चर के घातांक का प्रतिनिधित्व करने वाले वैक्टर के अवमुख समावरक हैं। उदाहरण के लिए, बहुपद <math>xy+2x^2+y^5+4</math> चार पद हैं, <math>xy</math> चरघातांकी सदिश (1,1) के साथ, <math>2x^2</math> चरघातांकी सदिश (2,0) के साथ, <math>y^5</math> चरघातांकी सदिश (0,5) के साथ, और <math>4</math> चरघातांकी सदिश (0,0) के साथ आदि। इसका न्यूटन पॉलीटॉप चार बिंदुओं (1,1), (2,0), (0,5), और (0,0) का अवमुख समावरक है। यह समावरक एक अभिन्न त्रिभुज है जिसमें बिंदु (1,1) त्रिकोण के आंतरिक कोण और अन्य तीन बिंदु इसके शीर्ष के रूप में हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 120: | Line 118: | ||
}} | }} | ||
[[Category:Created On 10/04/2023]] | [[Category:Created On 10/04/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:पॉलीटोप्स]] | |||
Latest revision as of 13:11, 30 October 2023

|

|

|

|

|
|
|

|
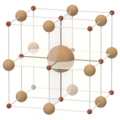
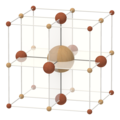
| घन | क्यूबोक्टहेड्रॉन | अष्टफलक | छिन्न अष्टफलक |
| (±1, ±1, ±1) | (0, ±1, ±1) | (0, 0, ±1) | (0, ±1, ±2) |
| त्रि-आयामों चार पूर्णांक पॉलिटोप | |||
|---|---|---|---|
ज्यामिति और बहुभुज संख्यात्मक विज्ञान में, पूर्णांकीय बहुभुज एक ऐसा अभिन्न बहुभुज होता है जिसके सभी शीर्षों के, कार्तेसीय समन्वयी निर्देशांक होते हैं।[1] अर्थात, यह एक ऐसा बहुभुज है जो अपनी पूर्णांकीय बिंदुओं के अवमुख समावरक के समान होता है।[2] पूर्णांकीय बहुभुजों को लैटिस बहुभुज या जेड-बहुभुज भी कहा जाता है। दो- और त्रि-आयामी पूर्णांकीय बहुभुजो के विशेष परिप्रेक्ष्य को क्रमशः पॉलीटोप्स के अतिरिक्त बहुभुज या बहुकोणीय आकृति कहा जा सकता है।
उदाहरण
किसी एन-आयामी नियमित संकेतन को, में एक पूर्णांकीय बहुभुज के रूप में प्रस्तुत किया जा सकता है, जहां पूर्णांकीय बिंदुओं का एक आधार एक है और बाकी सभी बिन्दुओ का आधार शून्य हैं। एक और महत्वपूर्ण प्रकार का पूर्णांकीय सिम्प्लेक्स, विषमकोण आयत, को उन पूर्णांकीय बिंदुओं के अवमुख समावरक द्वारा निर्मित किया जा सकता है, जिनके निर्देशांकों का प्रारंभ कुछ संयुक्त पूर्णांकों के साथ होती है जिसके उपरांत शेष सभी निर्देशांक शून्य होते हैं। में n-आयामीक इकाई घन के कोण उन सभी पूर्णांक बिंदुओं से मिलते हैं जिनके निर्देशांक शून्य या एक होतें हैं।एक पर्म्युटाहेड्रन के कोण उस सदिश . पर सभी संभव क्रमचयों को लागू करके प्राप्त किए जाने वाले निर्देशांक होते हैं। लोडे के उच्चतम वास्तविकीकरण में एक असोसिएहेड्रन भी एक पूर्णांक पॉलिटोप और पर्म्युटाहेड्रन का विकर्ण होता है।
अनुकूलन में
रैखिक प्रोग्रामिंग और गणितीय अनुकूलन में संबंधित समस्याओं के संदर्भ में, उत्तल पॉलीटोप्स को प्रायः रैखिक असमानता की एक प्रणाली द्वारा वर्णित किया जाता है, जो कि उनके बिंदुओं का उपयो करता है। जब एक पॉलीटॉप अभिन्न होता है, तो दी गई असमानताओं की प्रणाली के सापेक्ष पूर्णांक प्रोग्रामिंग समस्याओं को हल करने के लिए रैखिक प्रोग्रामिंग का उपयोग किया जाता है, जो अन्यथा अत्यधिक कठिन हो सकती है।
संयोजी इष्टतमीकरण समस्याओं से उत्पन्न होने वाले कुछ बहुफलक स्वचालित रूप से अभिन्न हैं। उदाहरण के लिए, यह किसी भी आंशिक रूप से समायोजित किए गए समुच्चय के पॉलीटॉप समायोजन के विषय में सत्य है, समुच्चय में तुलनीय तत्वों के अनुरूप निर्देशांक के मध्य युग्मक असमानताओं द्वारा परिभाषित एक पॉलीटोप इन्ही तत्वों द्वारा अनुकूलित होता है।[3] संयोजी अनुकूलन में एक अन्य प्रसिद्ध पोलीटोप, मिलान पोलीटोप है। स्पष्टतः, हम एकल विधि में विधिकालात्मक रूप से मिलान खोजने का प्रयास करते हैं और इस तकनीक रैखिक प्रोग्रामिंग कहा जाता है। रेखीय प्रोग्रामिंग द्वारा वर्णित पॉलीटोप, प्रति शीर्ष पर वर्णित भुजाओ के योग को द्विदलीय रेखांकन के परिप्रेक्ष्य में अभिन्न बनाता है, अर्थात यह मिलान वाले पॉलीटोप का सटीक वर्णन करता है, जबकि सामान्य रेखांकन के लिए यह गैर-अभिन्न है।[4] इसलिए, द्विदलीय रेखांकन में, यह एक वैध मिलान प्राप्त करने के लिए संबंधित रैखिक प्रोग्रामिंग को हल करने के लिए पर्याप्त है। सामान्य रेखांकन के लिए, यद्यपि, मिलान पॉलीटॉप के दो अन्य लक्षण हैं, जिनमें से एक शीर्ष के विषम उपसमुच्चय के लिए ब्लॉसम असमानता का उपयोग करता है और इसलिए वैध मिलान प्राप्त करते हुए पूर्णांक प्रोग्राममिन को एक रेखीय प्रोग्रामिंग में परिवर्तित करने की अनुमति देता है।[5] ये विशेषताएँ ब्लॉसम एल्गोरिथम में और अधिक रुचि रखती हैं। एडमंड्स का प्रसिद्ध ब्लॉसम एल्गोरिथम सामान्य आरेख में ऐसे मिलानों को खोजने के लिए उपयोग किया जाता है।
संगणनात्मक जटिलता
रेखीय असमानताओं द्वारा वर्णित किसी पॉलीटॉप के लिए, जब पॉलीटॉप गैर-अभिन्न होता है, तो कोई ऐसा शीर्ष ढूंढकर अपनी गैर-अभिन्नता प्रमाणित कर सकता है जिसका निर्देशांक पूर्णांक नहीं हैं। इस तरह के शीर्ष को असमानताओं के एक उपसमुच्चय को निर्दिष्ट करके संयुक्त रूप से वर्णित किया जा सकता है, जब रैखिक समीकरणों की एक प्रणाली में परिवर्तन कर दिया जाता है, तो एक अद्वितीय समाधान होता है, और यह सत्यापित करता है कि यह समाधान बिंदु अन्य सभी असमानताओं का पालन करता है। इसलिए, परीक्षण अभिन्नता, समस्याओं की जटिलता वर्ग से संबंधित है, जिसके लिए एक नकारात्मक उत्तर सरलता से सिद्ध किया जा सकता है।[6]
संबंधित उद्देश्य
अभिन्न पॉलीटॉप के आयतन और शीर्षों की संख्या सहित कई महत्वपूर्ण गुण, एहरहार्ट बहुपद द्वारा कूटबद्ध किए गए हैं।[7]
अभिन्न पॉलीटॉप को प्रमुख रूप से टॉरिक वरिटीस के सिद्धांत में चित्रित किया गया है, जहां वे ध्रुवीकृत प्रक्षेपीय टॉरिक वरिटीस के अंतर्गत अनुरूपित हैं। उदाहरण के लिए, किसी प्रसमुच्चय से संबंधित टोरिक वरिटीस एक प्रक्षेपण स्थान है। एक इकाई घन से संबंधित टोरिक वरिटीस, परियोजनात्मक रेखा के एन-गुणा उत्पाद का सेग्रे अंत:स्थापन है।
बीजगणितीय ज्यामिति में, लैटिस पॉलीटोप्स का एक महत्वपूर्ण उदाहरण जिसे न्यूटन पॉलीटोप भी कहा जाता है, एक बहुपद के संदर्भ में प्रत्येक चर के घातांक का प्रतिनिधित्व करने वाले वैक्टर के अवमुख समावरक हैं। उदाहरण के लिए, बहुपद चार पद हैं, चरघातांकी सदिश (1,1) के साथ, चरघातांकी सदिश (2,0) के साथ, चरघातांकी सदिश (0,5) के साथ, और चरघातांकी सदिश (0,0) के साथ आदि। इसका न्यूटन पॉलीटॉप चार बिंदुओं (1,1), (2,0), (0,5), और (0,0) का अवमुख समावरक है। यह समावरक एक अभिन्न त्रिभुज है जिसमें बिंदु (1,1) त्रिकोण के आंतरिक कोण और अन्य तीन बिंदु इसके शीर्ष के रूप में हैं।
यह भी देखें
संदर्भ
- ↑ Cornuéjols, Gérard (2001), Combinatorial Optimization: Packing and Covering, CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 74, Philadelphia, Pennsylvania: Society for Industrial and Applied Mathematics (SIAM), p. 4, doi:10.1137/1.9780898717105, ISBN 0-89871-481-8, MR 1828452
- ↑ Murota, Kazuo (2003), Discrete convex analysis, SIAM Monographs on Discrete Mathematics and Applications, Philadelphia, Pennsylvania: Society for Industrial and Applied Mathematics (SIAM), p. 90, doi:10.1137/1.9780898718508, hdl:2433/149564, ISBN 0-89871-540-7, MR 1997998
- ↑ Stanley, Richard P. (1986), "Two poset polytopes", Discrete & Computational Geometry, 1 (1): 9–23, doi:10.1007/BF02187680, MR 0824105
- ↑ Lovász, László (1986). मिलान सिद्धांत. North-Holland. pp. 269–274. ISBN 978-0-444-87916-5. OCLC 316569965.
- ↑ Lovász, László (1986). मिलान सिद्धांत. North-Holland. pp. 274–281. ISBN 978-0-444-87916-5. OCLC 316569965.
- ↑ Ding, Guoli; Feng, Li; Zang, Wenan (2008), "The complexity of recognizing linear systems with certain integrality properties", Mathematical Programming, Series A, 114 (2): 321–334, doi:10.1007/s10107-007-0103-y, hdl:10722/58972, MR 2393045
- ↑ Barvinok, A. I. (1994), "Computing the Ehrhart polynomial of a convex lattice polytope", Discrete & Computational Geometry, 12 (1): 35–48, doi:10.1007/BF02574364, MR 1280575