एफ़िन लाई बीजगणित

गणित में, एफ़िन लाई बीजगणित अनंत-आयामी लाई बीजगणित है, जो परिमित-आयामी सरल लाई बीजगणित से विहित व्यवहार में निर्मित होता है। एफ़िन लाई बीजगणित को देखते हुए, नीचे वर्णित अनुसार, संबंधित एफ़िन केएसी-मूडी बीजगणित भी बना सकता है। विशुद्ध रूप से गणितीय दृष्टिकोण से, एफ़िन लाई बीजगणित रोचक हैं क्योंकि उनके प्रतिनिधित्व सिद्धांत, परिमित-आयामी अर्ध-सरल लाई बीजगणित के प्रतिनिधित्व सिद्धांत के जैसे, सामान्य केएसी-मूडी बीजगणित की तुलना में अधिक उत्तम समझा जाता है। जैसा कि विक्टर केएसी द्वारा देखा गया है, एफ़िन लाई बीजगणित के निरूपण के लिए वर्ण सूत्र कुछ संयुक्त पहचान, मैकडोनाल्ड पहचान का अर्थ है।

एफ़िन लाई बीजगणित स्ट्रिंग सिद्धांत और द्वि-आयामी अनुरूप क्षेत्र सिद्धांत में महत्वपूर्ण भूमिका निभाते हैं जिस प्रकार से वे निर्मित होते हैं: साधारण लाई बीजगणित से प्रारंभ ${\mathfrak {g}}$, लूप बीजगणित पर विचार करता है, $L{\mathfrak {g}}$, द्वारा गठित ${\mathfrak {g}}$ बिंदुवार कम्यूटेटर के साथ वृत्त (बंद स्ट्रिंग के रूप में व्याख्या) पर मूल्यवान कार्य होता है। द एफ़िन लाई बीजगणित ${\hat {\mathfrak {g}}}$ लूप बीजगणित में अतिरिक्त आयाम जोड़कर और गैर-अल्प प्रकार से कम्यूटेटर को संशोधित करके प्राप्त किया जाता है, जिसे भौतिक विज्ञानी क्वांटम विसंगति कहते हैं (इस स्थिति में, डब्ल्यूजेडडब्ल्यू प्रारूप की विसंगति) और गणितज्ञ केंद्रीय विस्तार है। सामान्यतः यदि σ सरल लाई बीजगणित का ऑटोमोर्फिज्म है ${\mathfrak {g}}$ इसके डायनकिन आरेख, ट्विस्टेड लूप बीजगणित के ऑटोमोर्फिज्म से जुड़ा हुआ है, जो $L_{\sigma }{\mathfrak {g}}$ में सम्मिलित हैं, ${\mathfrak {g}}$ वास्तविक रेखा पर -मूल्यवान कार्य f जो ट्विस्टेड आवधिकता की स्थिति f(x + 2π) = σ f(x) को संतुष्ट करते हैं। उनके केंद्रीय विस्तार त्रुटिहीन रूप से मुड़े हुए चक्कर वाले बीजगणित हैं। स्ट्रिंग सिद्धांत के दृष्टिकोण से एफ़िन लाई बीजगणित के विभिन्न गुणों का अध्ययन करने में सहायता मिलती है, जैसे तथ्य यह है कि उनके प्रतिनिधित्व के पात्र मॉड्यूलर समूह के अंतर्गत आपस में परिवर्तित होते हैं।

सरल लाई बीजगणित से एफ़िन लाई बीजगणित

परिभाषा

यदि ${\mathfrak {g}}$ परिमित-आयामी सरल लाई बीजगणित है, तो संबंधित एफ़िन लाई बीजगणित ${\hat {\mathfrak {g}}}$ लूप बीजगणित के केंद्रीय विस्तार के रूप में ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$ बनाया गया है, आयामी केंद्र के साथ $\mathbb {\mathbb {C} } c$ होता है,

सदिश स्थान के रूप में,

${\widehat {\mathfrak {g}}}={\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]\oplus \mathbb {\mathbb {C} } c,$

जहाँ $\mathbb {\mathbb {C} } [t,t^{-1}]$ अनिश्चित t में लॉरेंट श्रृंखला का जटिल सदिश स्थान है। जिसे लाई ब्रैकेट सूत्र द्वारा परिभाषित किया गया है:

$[a\otimes t^{n}+\alpha c,b\otimes t^{m}+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta _{m+n,0}c$

सभी के लिए $a,b\in {\mathfrak {g}},\alpha ,\beta \in \mathbb {\mathbb {C} }$ और $n,m\in \mathbb {Z}$, जहाँ $[a,b]$ लाई बीजगणित में लाई ब्रैकेट है, ${\mathfrak {g}}$ और $\langle \cdot |\cdot \rangle$ किलिंग रूप है। कार्टन-किलिंग रूप ${\mathfrak {g}}$ है।

परिमित-आयामी अर्ध-सरल लाई बीजगणित के संगत एफ़िन लाई बीजगणित का सीधा योग है जो इसके सरल सारांश के अनुरूप है। परिभाषित एफ़िन लाई बीजगणित की विशिष्ट व्युत्पत्ति है:

$\delta (a\otimes t^{m}+\alpha c)=t{d \over dt}(a\otimes t^{m})$

संबंधित एफ़िन केएसी-मूडी बीजगणित को अतिरिक्त जनरेटर d जोड़कर अर्ध-प्रत्यक्ष उत्पाद के रूप में परिभाषित किया गया है जो [d, A] = δ(A ) को संतुष्ट करता है।

डायकिन आरेखों का निर्माण

प्रत्येक एफ़िन लाई बीजगणित के डायनकिन आरेख में संबंधित सरल लाई बीजगणित और अतिरिक्त नोड होता है, जो काल्पनिक रूट के अतिरिक्त से युग्मित होता है। इस प्रकार के नोड को किसी भी स्थान पर डायनकिन आरेख से जोड़ा नहीं जा सकता है, किन्तु प्रत्येक साधारण लाई बीजगणित के लिए लाई बीजगणित के बाहरी ऑटोमोर्फिज्म समूह की प्रमुखता के समान विभिन्न संभावित अनुलग्नक उपस्थित हैं। विशेष रूप से, इस समूह में सदैव पहचान तत्व होता है, और संबंधित एफ़िन लाई बीजगणित को अनट्विस्टेड एफ़िन लाई बीजगणित कहा जाता है। जब साधारण बीजगणित ऑटोमोर्फिज़्म को स्वीकार करता है जो आंतरिक ऑटोमोर्फिज़्म नहीं हैं, तो कोई अन्य डायनकिन आरेख प्राप्त कर सकता है और ये ट्विस्टेड एफ़िन लाई बीजगणित के अनुरूप होते हैं।

एफ़िन लाई एल्जेब्रस के लिए डाइनकिन डायग्राम

हरे रंग में जोड़े गए नोड्स के साथ विस्तारित (अनट्विस्टेड) ​​एफ़ाइन डाइकिन आरेखों का समूह

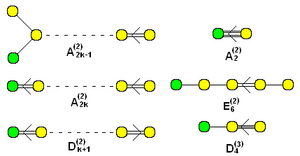"ट्विस्टेड" एफ़िन फॉर्म का नाम (2) या (3) सुपरस्क्रिप्ट के साथ रखा गया है। (k ग्राफ में नोड्स की संख्या है।)

केंद्रीय विस्तार का वर्गीकरण

इसी सरल लाई बीजगणित के डायनकिन आरेख के लिए अतिरिक्त नोड का सम्बन्ध निम्नलिखित निर्माण से युग्मित होता है। एफ़िन लाई बीजगणित सदैव समूह विस्तार के रूप में बनाया जा सकता है, संबंधित सरल लाई बीजगणित के लूप बीजगणित का केंद्रीय विस्तार होता है। यदि कोई इसके अतिरिक्त अर्ध-सरल लाई बीजगणित के साथ प्रारंभ करना चाहता है, तो उसे अर्ध-सरल बीजगणित के सरल घटकों की संख्या के समान तत्वों की संख्या से केंद्रीय रूप से विस्तार करने की आवश्यकता है। भौतिकी में, इसके अतिरिक्त अर्ध-सरल बीजगणित और एबेलियन बीजगणित के प्रत्यक्ष योग $\mathbb {\mathbb {C} } ^{n}$ पर विचार किया जाता है, इस स्थिति में n एबेलियन जनरेटर के लिए और n केंद्रीय तत्वों को जोड़ने की भी आवश्यकता है।

इसी सरल सघन लाई समूह के लूप समूह का दूसरा इंटीग्रल कोहोलॉजी पूर्णांकों के लिए आइसोमोर्फिक है। एकल जनरेटर द्वारा एफ़िन लाई समूह के केंद्रीय विस्तार इस मुक्त लूप समूह पर टोपोलॉजिकल रूप से वृत्त बंडल हैं, जिन्हें दो-श्रेणी द्वारा वर्गीकृत किया जाता है जिसे कंपन के प्रथम चेर्न वर्ग के रूप में जाना जाता है। इसलिए, एफ़िन लाई समूह के केंद्रीय प्रारूप को पैरामीटर के द्वारा वर्गीकृत किया जाता है जिसे भौतिकी साहित्य में स्तर कहा जाता है, जहां यह प्रथम बार दिखाई देता है। एफ़िन सघन समूहों का एकात्मक उच्चतम वजन प्रतिनिधित्व केवल तभी उपस्थित होता है जब k प्राकृतिक संख्या हो। सामान्यतः, यदि कोई अर्ध-सरल बीजगणित पर विचार करता है, तो प्रत्येक साधारण घटक के लिए केंद्रीय शुल्क होता है।

संरचना

कार्टन-वील आधार

जैसा कि परिमित स्थिति में, कार्टन-वेइल आधार का निर्धारण एफ़िन लाई अलजेब्रस की संरचना का निर्धारण करने में महत्वपूर्ण चरण है।

परिमित-आयामी, सरल, जटिल लाई बीजगणित ${\mathfrak {g}}$ को उचित करता है, कार्टन उपबीजगणित के साथ ${\mathfrak {h}}$ और विशेष जड़ प्रणाली $\Delta$ है। अंकन का परिचय $X_{n}=X\otimes t^{n},$ कोई कार्टन-वेइल आधार का विस्तार करने का प्रयास कर सकता है $\{H^{i}\}\cup \{E^{\alpha }|\alpha \in \Delta \}$ के लिए ${\mathfrak {g}}$ एफ़िन लाई बीजगणित के लिए दिया गया है। $\{H_{n}^{i}\}\cup \{c\}\cup \{E_{n}^{\alpha }\}$, के साथ $\{H_{0}^{i}\}\cup \{c\}$ एबेलियन उपबीजगणित बनाता है।

ईगेनवैल्यू $ad(H_{0}^{i})$ और $ad(c)$ पर $E_{n}^{\alpha }$ हैं, $\alpha ^{i}$ और $0$ क्रमशः और स्वतंत्र रूप से $n$ है। इसलिए $\alpha$ इस एबेलियन उपबीजगणित के संबंध में अनंत रूप से पतित है। एबेलियन उपबीजगणित में ऊपर वर्णित व्युत्पत्ति को प्रारम्भ करने से एफ़िन लाई बीजगणित के लिए कार्टन उपबीजगणित में परिवर्तित हो जाता है, ईगेनवैल्यू $(\alpha ^{1},\cdots ,\alpha ^{dim{\mathfrak {h}}},0,n)$ के लिए $E_{n}^{\alpha }$ है।

किलिंग रूप

इसकी अचल संपत्ति का उपयोग करके किलिंग का रूप लगभग प्रत्येक प्रकार से निर्धारित किया जा सकता है। अंकन का उपयोग करना $B$ किलिंग रूप के लिए ${\mathfrak {g}}$ और ${\hat {B}}$ एफिन केएसी-मूडी बीजगणित पर किलिंग रूप के लिए इस प्रकार है,

$${\hat {B}}(X_{n},Y_{m})=B(X,Y)\delta _{n+m,0},$$

$${\hat {B}}(X_{n},c)=0,{\hat {B}}(X_{n},d)=0$$

$${\hat {B}}(c,c)=0,{\hat {B}}(c,d)=1,{\hat {B}}(d,d)=0,$$

जहां केवल अंतिम समीकरण को निश्चरता से स्थिर नहीं किया जाता है और इसके अतिरिक्त सम्मेलन द्वारा चयन किया जाता है। विशेष रूप से, ${\hat {B}}$ का प्रतिबंध $c,d$ तक उपस्थान हस्ताक्षर के साथ बिलिनियर फॉर्म देता है, $(+,-)$

से संबद्ध ऐफिन रूट $E_{n}^{\alpha }$ लिखिए, जैसा ${\hat {\alpha }}=(\alpha ;0;n)$ परिभाषित $\delta =(0,0,1)$, इसे पुनः लिखा जा सकता है:

$${\hat {\alpha }}=\alpha +n\delta .$$

जड़ों का पूर्ण समूह है:

$${\hat {\Delta }}=\{\alpha +n\delta |n\in \mathbb {Z} ,\alpha \in \Delta \}\cup \{n\delta |n\in \mathbb {Z} ,n\neq 0\}.$$

तब $\delta$ असामान्य है क्योंकि इसकी लंबाई शून्य है: $(\delta ,\delta )=0$ जहाँ $(\cdot ,\cdot )$ किलिंग रूप से प्रेरित जड़ों पर द्विरेखीय रूप है।

एफ़िन सरल रूट

एफ़िन बीजगणित के लिए सरल जड़ों का आधार प्राप्त करने के लिए, अतिरिक्त सरल जड़ को जोड़ा जाना चाहिए, और इसके द्वारा दिया गया है:

$$\alpha _{0}=-\theta +\delta$$

जहाँ $\theta$ का उच्चतम मूल ${\mathfrak {g}}$ है, रूट की ऊंचाई की सामान्य धारणा का उपयोग करते हुए। यह विस्तारित कार्टन आव्यूह और विस्तारित डायनकिन आरेखों की परिभाषा की अनुमति देता है।

प्रतिनिधित्व सिद्धांत

एफ़िन लाई बीजगणित के लिए प्रतिनिधित्व सिद्धांत सामान्यतः वर्मा मॉड्यूल का उपयोग करके विकसित किया जाता है। अर्ध-सरल लाई बीजगणित की स्थिति में, ये उच्चतम वजन वाले मॉड्यूल हैं। कोई परिमित-आयामी निरूपण नहीं हैं; यह इस तथ्य से अनुसरण करता है कि परिमित-आयामी वर्मा मॉड्यूल के अशक्त सदिश आवश्यक रूप से शून्य हैं; जबकि एफ़िन लाई बीजगणित के लिए नहीं हैं। सामान्यतः, यह इस प्रकार है क्योंकि किलिंग रूप लोरेंट्ज़ियन $c,\delta$ दिशा में है, इस प्रकार $(z,{\bar {z}})$ स्ट्रिंग पर कभी-कभी लाइटकोन निर्देशांक कहलाते हैं। रेडियल ऑर्डर किए गए वर्तमान बीजगणित उत्पादों को समय-समय पर सामान्य रूप से ऑर्डर करके समझा जा सकता है $z=\exp(\tau +i\sigma )$ साथ $\tau$ स्ट्रिंगविश्व पत्रक के साथ समय जैसी दिशा और $\sigma$ स्थानिक दिशा होती है।

रैंक k का निर्वात प्रतिनिधित्व

अभ्यावेदन अधिक विस्तार से निम्नानुसार निर्मित किए गए हैं।

लाई बीजगणित ${\mathfrak {g}}$ और आधार $\{J^{\rho }\}$ को उचित करता है। तब $\{J_{n}^{\rho }\}=\{J^{\rho }\otimes t^{n}\}$ संबंधित लूप बीजगणित के लिए आधार है, और $\{J_{n}^{\rho }\}\cup \{c\}$ एफ़िन लाई बीजगणित का आधार ${\hat {\mathfrak {g}}}$ है।

रैंक का निर्वात प्रतिनिधित्व $k$, निरूपित $V_{k}({\mathfrak {g}})$ जहाँ $k\in \mathbb {C}$ आधार के साथ जटिल प्रतिनिधित्व है।

$$\{v_{n_{1}\cdots n_{m}}^{\rho _{1}\cdots \rho _{m}}:n_{1}\geq \cdots \geq n_{m}\geq 1,\rho _{1}\leq \cdots \leq \rho _{m}\}\cup \{\Omega \}$$

और क्रिया को परिभाषित करता है ${\hat {\mathfrak {g}}}$ पर $V=V_{k}({\mathfrak {g}})$ द्वारा (के साथ $n>0$)

$$c=k{\text{id}}_{V},\,J_{n}^{\rho }\Omega =0,$$

$$J_{-n}^{\rho }\Omega =v_{n}^{\rho }\,J_{-n}^{\rho }v_{n_{1}\cdots n_{m}}^{\rho _{1}\cdots \rho _{m}}=v_{nn_{1}\cdots n_{m}}^{\rho \rho _{1}\cdots \rho _{m}}.$$

एफिन वर्टेक्स बीजगणित

See also: वर्टेक्स ऑपरेटर बीजगणित उदाहरण: डब्ल्यूजेडडब्ल्यू वैक्यूम मॉड्यूल

वास्तव में निर्वात प्रतिनिधित्व शीर्ष बीजगणित संरचना से सुसज्जित किया जा सकता है, जिस स्थिति में इसे 'रैंक का एफ़िन वर्टेक्स बीजगणित' $k$ कहा जाता है, एफ़िन लाई बीजगणित स्वाभाविक रूप से अंतर के साथ, केएसी-मूडी बीजगणित तक विस्तारित है $d$ अनुवाद ऑपरेटर द्वारा प्रतिनिधित्व किया गया है, शीर्ष बीजगणित में $T$ है।

वेइल समूह और वर्ण

Main article: वेइल-केएसी वर्ण सूत्र

एफ़िन लाई बीजगणित के वेइल समूह को शून्य-मोड बीजगणित (लूप बीजगणित को परिभाषित करने के लिए उपयोग किया जाता है) और कोरूट जाली के वेइल समूह के अर्ध-प्रत्यक्ष उत्पाद के रूप में लिखा जा सकता है।

एफ़िन लाई बीजगणित के बीजगणितीय वर्णों का वेइल वर्ण सूत्र, वेइल-केएसी वर्ण सूत्र के लिए सामान्यीकरण करता है। इनमें से विभिन्न रोचक निर्माण अनुसरण करते हैं। जैकोबी थीटा प्रकार्य के सामान्यीकरण का निर्माण कर सकता है। ये थीटा कार्य मॉड्यूलर समूह के अंतर्गत रूपांतरित होते हैं। अर्ध-सरल लाई बीजगणित की सामान्य भाजक पहचान भी सामान्यीकृत होती है; क्योंकि पात्रों को विकृतियों या उच्चतम वजन के क्यू-एनालॉग के रूप में लिखा जा सकता है, इसने विभिन्न नई संयोजक पहचानों को उत्पन्न किया है, जिसमें डेडेकाइंड और फंक्शन के लिए विभिन्न पूर्व अज्ञात पहचान सम्मिलित हैं। इन सामान्यीकरणों को लैंगलैंड्स कार्यक्रम के व्यावहारिक उदाहरण के रूप में देखा जा सकता है।

अनुप्रयोग

सुगवारा निर्माण के कारण, किसी भी एफ़िन लाई बीजगणित के सार्वभौमिक लिफाफा बीजगणित में विरासोरो बीजगणित उपबीजगणित के रूप में है। यह एफ़िन लाई बीजगणित को डब्ल्यूजेडडब्ल्यू प्रारूप या कोसेट प्रारूप जैसे अनुरूप क्षेत्र सिद्धांतों के समरूपता बीजगणित के रूप में कार्य करने की अनुमति देता है। परिणामस्वरूप, स्ट्रिंग सिद्धांत के वर्ल्डशीट विवरण में एफ़िन लाई बीजगणित भी दिखाई देते हैं।

उदाहरण

हाइजेनबर्ग बीजगणित जनरेटर द्वारा परिभाषित $a_{n},n\in \mathbb {Z}$ रूपांतरण संबंधों को इस प्रकार लिख सकते हैं:

$$[a_{m},a_{n}]=m\delta _{m+n,0}c$$

एफ़िन लाई बीजगणित ${\hat {\mathfrak {u}}}(1)$ के रूप में अनुभूत किया जा सकता है।

संदर्भ

• Fuchs, Jurgen (1992), Affine Lie Algebras and Quantum Groups, Cambridge University Press, ISBN 0-521-48412-X
• Goddard, Peter; Olive, David (1988), Kac-Moody and Virasoro algebras: A Reprint Volume for Physicists, Advanced Series in Mathematical Physics, vol. 3, World Scientific, ISBN 9971-5-0419-7
• Kac, Victor (1990), Infinite dimensional Lie algebras (3 ed.), Cambridge University Press, ISBN 0-521-46693-8
• Kohno, Toshitake (1998), Conformal Field Theory and Topology, American Mathematical Society, ISBN 0-8218-2130-X
• Pressley, Andrew; Segal, Graeme (1986), Loop groups, Oxford University Press, ISBN 0-19-853535-X