उच्चिष्ठ और निम्निष्ठ: Difference between revisions

Latest revision as of 13:24, 1 November 2023

cos(3πx)/x, 0.1≤ x ≤1.1 के लिए स्थानीय और वैश्विक उच्चिष्ठ और निम्निष्ठ

गणितीय विश्लेषण में, किसी फलन (गणित) के उच्चिष्ठ और निम्निष्ठ (अधिकतम और न्यूनतम के संबंधित बहुवचन), सामूहिक रूप से एक्स्ट्रेमा (चरम का बहुवचन) के रूप में जाना जाता है, प्रकार्य का सबसे बड़ा और सबसे छोटा मान है, या तो किसी दिए गए अंतराल के भीतर(गणित)("स्थानीय" या "सापेक्ष" एक्स्ट्रेमा), या किसी प्रकार्य के संपूर्ण कार्यक्षेत्र पर("वैश्विक" या "पूर्ण" एक्स्ट्रेमा)।^[1]^[2]^[3] पियरे डी फर्मेट उन पहले गणितज्ञों में से एक थे जिन्होंने प्रकार्य का उच्चिष्ठ और निम्निष्ठ खोजने के लिए एक सामान्य तकनीक, पर्याप्तता का प्रस्ताव दिया था।

जैसा कि समुच्चय सिद्धांत में परिभाषित किया गया है, एक समुच्चय(गणित) का उच्चिष्ठ और निम्निष्ठ क्रमशः समुच्चय में सबसे बड़ा और सबसे कम तत्व है। असीम अनंत समुच्चय, जैसे कि वास्तविक संख्याओं का समुच्चय, का कोई निम्निष्ठ या उच्चिष्ठ नहीं होता है।

परिभाषा

प्रकार्य X के कार्यक्षेत्र पर परिभाषित एक वास्तविक-मूल्यवान प्रकार्य(गणित) f में 'वैश्विक'(या 'पूर्ण') 'उच्चिष्ठ बिंदु' X पर^∗ है , अगर X में सभी X के लिए f(x^∗) ≥ f(x) है। इसी तरह, प्रकार्य में 'वैश्विक'(या 'पूर्ण') 'निम्निष्ठ बिंदु' X पर^∗ है, अगर X में सभी X के लिए f(x^∗) ≤ f(x) है। उच्चिष्ठ बिंदु पर फलन के मान को फलन का उच्चिष्ठ मान कहते हैं, निरूपित $\max(f(x))$ , और निम्निष्ठ बिंदु पर फलन के मान को फलन का न्यूनतम मान कहा जाता है। प्रतीकात्मक रूप से, इसे इस प्रकार लिखा जा सकता है:

x_{0}\in X

प्रकार्य का वैश्विक उच्चिष्ठ बिंदु

f:X\to \mathbb {R} ,

यदि

(\forall x\in X)\,f(x_{0})\geq f(x)

है।

वैश्विक निम्निष्ठ बिंदु की परिभाषा भी इसी तरह आगे बढ़ती है।

यदि कार्यक्षेत्र X एक मापीय स्थान है, तो f को 'स्थानीय'(या 'सापेक्ष') 'उच्चिष्ठ बिंदु' कहा जाता है बिंदु x पर^∗, यदि कुछ ε > 0 ऐसे उपस्थित है कि, f(x^∗) ≥ f(x) X में सभी X के लिए X^∗ की दूरी ε के भीतर है। इसी तरह, प्रकार्य का X^∗ पर एक स्थानीय निम्निष्ठ बिंदु होता है, अगर f(x^∗) ≤ f(x) सभी x के लिए X में x^∗ की दूरी ε के भीतर है। इसी तरह की परिभाषा का उपयोग तब किया जा सकता है जब X एक स्थलीय स्थान है, क्योंकि अभी दी गई परिभाषा को प्रतिवैस के संदर्भ में फिर से परिभाषित किया जा सकता है। गणितीय रूप से, दी गई परिभाषा इस प्रकार लिखी गई है:

$(X,d_{X})$ को एकमापीय समष्टि मान लीजिए और प्रकार्य को $f:X\to \mathbb {R}$ . फिर $x_{0}\in X$ कार्य का एक स्थानीय उच्चिष्ठ बिंदु है $f$ यदि $(\exists \varepsilon >0)$ ऐसे कि $(\forall x\in X)\,d_{X}(x,x_{0})<\varepsilon \implies f(x_{0})\geq f(x).$

स्थानीय निम्निष्ठ बिंदु की परिभाषा भी इसी तरह आगे बढ़ सकती है।

वैश्विक और स्थानीय दोनों वस्तुस्थिति में, a की निश्चित चरम अवधारणा को परिभाषित किया जा सकता है। उदाहरण के लिए, X^∗ निश्चित वैश्विक अधिकतम बिंदु है। उदाहरण के लिए, x∗ एक सख्त वैश्विक उच्चिष्ठ बिंदु है यदि सभी x में x ≠ x∗ के साथ, हमारे पास f(x∗) > f(x), और x∗ एक सख्त स्थानीय उच्चिष्ठ बिंदु है। यदि वहाँ कुछ ε > 0 ऐसे उपस्थित है कि, X में सभी x के लिए x∗ की दूरी ε के भीतर x ≠ x∗ के साथ है, हमारे पास f(x∗) > f(x) है। ध्यान दें कि एक बिंदु एक सख्त वैश्विक उच्चिष्ठ बिंदु है यदि और केवल यदि यह अद्वितीय वैश्विक उच्चिष्ठ बिंदु है, और इसी तरह निम्निष्ठ बिंदुओं के लिए है।

सघन स्थल कार्यक्षेत्र के साथ एक सतत कार्य वास्तविक-मूल्यवान प्रकार्य में हमेशा उच्चिष्ठ बिंदु और निम्निष्ठ बिंदु होता है। एक महत्वपूर्ण उदाहरण प्रकार्य है जिसका कार्यक्षेत्र वास्तविक संख्याओं का एक बंद और परिबद्ध अंतराल(गणित) है(ऊपर आरेख देखें)।

खोज

वैश्विक उच्चिष्ठ और निम्निष्ठ ढूँढना गणितीय अनुकूलन का लक्ष्य है। यदि कोई प्रकार्य एक बंद अंतराल पर सतत है, तो चरम मूल्य प्रमेय द्वारा वैश्विक उच्चिष्ठ और निम्निष्ठ उपस्थित हैं। इसके अलावा, एक वैश्विक उच्चिष्ठ(या निम्निष्ठ) या तो कार्यक्षेत्र के अभ्यंतर भाग में एक स्थानीय उच्चिष्ठ (या निम्निष्ठ) होना चाहिए, या कार्यक्षेत्र की सीमा पर स्थित होना चाहिए। वैश्विक उच्चिष्ठ(या निम्निष्ठ) खोजने की एक विधि अभ्यंतर में सभी स्थानीय उच्चिष्ठ(या निम्निष्ठ) को देखना है, और सीमा पर बिंदुओं के उच्चिष्ठ (या निम्निष्ठ) को भी देखना है, और सबसे बड़ा(या सबसे छोटा) लेना है।

अवकलनीय प्रकार्य के लिए, फर्मेट के प्रमेय में कहा गया है कि एक कार्यक्षेत्र के अभ्यंतर में स्थानीय एक्स्ट्रेमा महत्वपूर्ण बिंदु(गणित) (या अंक जहां व्युत्पन्न शून्य के बराबर होता है) पर होना चाहिए।^[4] हालांकि, सभी महत्वपूर्ण बिंदु एक्स्ट्रीमा नहीं हैं। पहला व्युत्पन्न परीक्षण, दूसरा व्युत्पन्न परीक्षण, या उच्च-क्रम व्युत्पन्न परीक्षण का उपयोग करके कोई यह भेद कर सकता है कि क्या एक महत्वपूर्ण बिंदु एक स्थानीय उच्चिष्ठ या स्थानीय निम्निष्ठ है, पर्याप्त भिन्नता दी गई है।^[5]

किसी भी प्रकार्य के लिए जिसे टुकड़े के रूप में परिभाषित किया गया है, प्रत्येक टुकड़े के उच्चिष्ठ (या निम्निष्ठ) को अलग-अलग ढूंढकर उच्चिष्ठ(या निम्निष्ठ) पाता है, और फिर यह दृष्टि बोध करता है कि कौन सा सबसे बड़ा (या सबसे छोटा) है।

उदाहरण

वैश्विक उच्चिष्ठ

x \sqrt x

पर होता

x = e

है .

प्रकार्य	उच्चिष्ठ और निम्निष्ठ
x²	x = 0 पर अद्वितीय वैश्विक निम्निष्ठ।
x³	कोई वैश्विक निम्निष्ठ या उच्चिष्ठ नहीं. यद्यपि पहला अवकलज(3x²) x = 0 पर 0 है, यह एक विभक्ति बिंदु है.(दूसरा व्युत्पन्न उस बिंदु पर 0 है।)
${\sqrt[{x}]{x}}$	अद्वितीय वैश्विक उच्चिष्ठ पर x = e.(चित्र को दाईं ओर देखें)।
x^−x	x = 1/e पर सकारात्मक वास्तविक संख्याओं पर अद्वितीय वैश्विक उच्चिष्ठ।
x³/3 − x	पहला अवकलज x2 − 1 और दूसरा अवकलज 2x है। पहले व्युत्पादित को 0 पर अवस्थापन करना और x के लिए हल करना -1 और +1 पर स्थिर अंक देता है। दूसरे अवकलज के चिह्न से, हम देख सकते हैं कि -1 स्थानीय उच्चिष्ठ है और +1 स्थानीय निम्निष्ठ है. इस प्रकार्य का कोई वैश्विक उच्चिष्ठ या निम्निष्ठ नहीं है।
\|x\|	वैश्विक निम्निष्ठ x = 0 पर व्युत्पादित लेकर नहीं पाया जा सकता है, क्योंकि व्युत्पादित x = 0 पर उपस्थित नहीं है।
cos(x)	0, ±2π, ±4π, ... पर अपरिमित रूप से अनेक वैश्विक उच्चिष्ठ और ±π, ±3π, ±5π, .... पर अपरिमित रूप से अनेक वैश्विक निम्निष्ठ।
2 cos(x) − x	अपरिमित रूप से कई स्थानीय उच्चिष्ठ और निम्निष्ठ, लेकिन कोई वैश्विक उच्चिष्ठ या निम्निष्ठ नहीं है।
0.1 ≤ x ≤ 1.1 के साथ cos(3 $π$ x)/x	x = 0.1(एक सीमा) पर वैश्विक उच्चिष्ठ, x = 0.3 के पास एक वैश्विक निम्निष्ठ, x = 0.6 के पास एक स्थानीय उच्चिष्ठ, और x = 1.0 के पास एक स्थानीय निम्निष्ठ।(पृष्ठ के शीर्ष पर चित्र देखें।)
x³ + 3x² − 2x + 1बंद अंतराल(खंड) पर परिभाषित [−4,2]	स्थानीय उच्चिष्ठ x = −1−√15/3, स्थानीय निम्निष्ठ x = −1+√15/3, वैश्विक उच्चिष्ठ x = 2 और वैश्विक निम्निष्ठ x = −4।

एक व्यावहारिक उदाहरण के लिए,[6] एक ऐसी स्थिति मान लें जहां किसी के पास $200$ फीट की बाड़ है और वह एक आयताकार बाड़े के चौकोर फुटमान को उच्चिष्ठ करने की कोशिश कर रहा है, जहां $x$ लंबाई है, $y$ चौड़ाई है, और $xy$ क्षेत्रफल है:

2x+2y=200

2y=200-2x

{\frac {2y}{2}}={\frac {200-2x}{2}}

y=100-x

xy=x(100-x)

के संबंध में व्युत्पन्न $x$ है:

{\begin{aligned}{\frac {d}{dx}}xy&={\frac {d}{dx}}x(100-x)\\&={\frac {d}{dx}}\left(100x-x^{2}\right)\\&=100-2x\end{aligned}}

$0$ के बराबर समुच्चय करके

0=100-2x

2x=100

x=50

प्रकट करता है कि $x=50$ हमारा एकमात्र क्रांतिक बिंदु(गणित) है। अब जिस अंतराल तक $x$ प्रतिबंधित है, उसे निर्धारित करके अंतिम-बिंदुओं को पुनः प्राप्त करें। चूँकि चौड़ाई धनात्मक है, तब $x>0$ , और चूँकि $x=100-y$ , इसका तात्पर्य है कि $x<100$ . महत्वपूर्ण बिंदु $50$ ,, साथ ही समापन बिंदु $0$ और $100$ , को $xy=x(100-x)$ , में प्लग करें, और परिणाम हैं $2500,0,$ तथा $0$ क्रमश।

इसलिए, आयत के साथ प्राप्य सबसे बड़ा क्षेत्र $200$ फीट की बाड़ है।

एक से अधिक चर के कार्य

पीआनो सतह, 19वीं शताब्दी के स्थानीय उच्चिष्ठ के कुछ मानदंडों का प्रति उदाहरण

वैश्विक उच्चिष्ठ शीर्ष पर स्थित बिंदु है

प्रति उदाहरण: लाल बिंदु एक स्थानीय निम्निष्ठ दिखाता है जो वैश्विक निम्निष्ठ नहीं है

एक से अधिक चर वाले कार्यों के लिए समान शर्तें लागू होती हैं। उदाहरण के लिए, दाईं ओर(विस्तारित) आकृति में, स्थानीय उच्चिष्ठ के लिए आवश्यक शर्तें केवल एक चर वाले प्रकार्य के समान होती हैं। Z के रूप में पहला आंशिक व्युत्पादित(उच्चिष्ठ किया जाने वाला चर) उच्चिष्ठ पर शून्य है(चित्र में शीर्ष पर चमकता हुआ बिंदु) दूसरा आंशिक व्युत्पादित नकारात्मक है। काठी बिंदु की संभावना के कारण एक स्थानीय उच्चिष्ठ के लिए शर्तें केवल आवश्यक हैं, पर्याप्त नहीं हैं। उच्चिष्ठ के लिए हल करने के लिए और स्थितियों के उपयोग के लिए, प्रकार्य z को भी अलग-अलग प्रकार्य होना चाहिए। दूसरा आंशिक व्युत्पन्न परीक्षण बिंदु को सापेक्ष उच्चिष्ठ या सापेक्ष निम्निष्ठ के रूप में वर्गीकृत करने में मदद कर सकता है।

इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के कार्यों और एक से अधिक चर के कार्यों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय निम्निष्ठ है, तो यह एक वैश्विक निम्निष्ठ भी है(मध्यवर्ती मूल्य प्रमेय और रोले के प्रमेय का उपयोग करके विरोधाभास द्वारा इसे साबित करें)। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है

f(x,y)=x^{2}+y^{2}(1-x)^{3},\qquad x,y\in \mathbb {R} ,

जिसका एकमात्र महत्वपूर्ण बिंदु(0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय निम्निष्ठ है। हालांकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5।

एक कार्यात्मक की उच्चिष्ठ या निम्निष्ठ

यदि किसी प्रकार्य का कार्यक्षेत्र जिसके लिए एक चरम पाया जाना है, में स्वयं प्रकार्य होते हैं(यानी यदि चरम को एक कार्यात्मक(गणित) के रूप में पाया जाता है), तो चरम विविधताओं के कलन का उपयोग करके पाया जाता है।

समुच्चय के संबंध में

उच्चिष्ठ और निम्निष्ठ को समुच्चय के लिए भी परिभाषित किया जा सकता है। व्यापक रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे इस रूप $\max(S)$ में भी निरूपित किया जाता है। इसके अलावा, यदि S एक आदेशित समुच्चय T का एक उपसमुच्चय है और M S का सबसे बड़ा तत्व है(T द्वारा प्रेरित अनुक्रम के संबंध में), तो M T में S का सर्वोच्च है। इसी तरह के परिणाम कम से कम तत्व, निम्निष्ठ तत्व और अल्प. समुच्चय के लिए उच्चिष्ठ और निम्निष्ठ प्रकार्य का उपयोग डेटाबेस में किया जाता है, और इसकी गणना तेजी से की जा सकती है, क्योंकि एक समुच्चय के उच्चिष्ठ(या निम्निष्ठ) की गणना एक विभाजन की उच्चिष्ठ सीमा से की जा सकती है; औपचारिक रूप से, वे स्व-विघटन योग्य एकत्रीकरण कार्य हैं।

एक सामान्य आंशिक आदेश के मामले में, 'सबसे कम तत्व'(यानी, जो अन्य सभी की तुलना में छोटा है) को 'निम्निष्ठ तत्व'(कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी तरह, आंशिक रूप से अनुक्रम किए गए समुच्चय(पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के भीतर निहित होता है, जबकि पॉसमुच्चय A का 'उच्चिष्ठ तत्व' M A का एक तत्व होता है जैसे कि यदि M ≤ B(A में किसी भी B के लिए), फिर M = B। पोसमुच्चय का कोई भी निम्निष्ठ तत्व या सबसे बड़ा तत्व अद्वितीय है, लेकिन एक पॉसमुच्चय में कई निम्निष्ठ या उच्चिष्ठ तत्व हो सकते हैं। यदि किसी पॉसमुच्चय में एक से अधिक उच्चिष्ठ तत्व हैं, तो ये तत्व परस्पर तुलनीय नहीं होंगे।

कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में उच्चिष्ठ एक निम्निष्ठ तत्व और उच्चिष्ठ एक उच्चिष्ठ तत्व हो सकता है। फिर, आपसी तुलना के कारण, निम्निष्ठ तत्व भी सबसे छोटा तत्व होगा, और उच्चिष्ठ तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी तरह से व्यवस्थित समुच्चय में, हम केवल 'निम्निष्ठ' और 'उच्चिष्ठ' शब्दों का उपयोग कर सकते हैं।

यदि एक श्रृंखला परिमित है, तो इसमें हमेशा उच्चिष्ठ और निम्निष्ठ होगा। यदि एक शृंखला अनंत है, तो उसके लिए उच्चिष्ठ या निम्निष्ठ की आवश्यकता नहीं है। उदाहरण के लिए, प्राकृतिक संख्याओं के समुच्चय का कोई उच्चिष्ठ नहीं है, हालांकि इसमें निम्निष्ठ है। यदि एक अनंत श्रृंखला S परिबद्ध है, तो समुच्चय के संवरण CL(S) में कभी-कभी निम्निष्ठ और उच्चिष्ठ होता है, इस मामले में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय S की 'कम से कम ऊपरी सीमा' कहा जाता है। , क्रमश।

यह भी देखें

उच्चिष्ठ आर्ग
व्युत्पन्न परीक्षण
निम्नतम और उच्चतम
श्रेष्ठ को सीमित करें और हीन को सीमित करें
यांत्रिक संतुलन
मेक्स(गणित)
नमूना उच्चिष्ठ और निम्निष्ठ
पल्याण बिन्दु

संदर्भ

↑ Stewart, James (2008). कैलकुलस: अर्ली ट्रान्सेंडैंटल्स (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.
↑ Larson, Ron; Edwards, Bruce H. (2009). गणना (9th ed.). Brooks/Cole. ISBN 978-0-547-16702-2.
↑ Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). थॉमस कैलकुलस: अर्ली ट्रान्सेंडैंटल्स (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.
↑ Weisstein, Eric W. "न्यूनतम". mathworld.wolfram.com (in English). Retrieved 2020-08-30.
↑ Weisstein, Eric W. से ज्यादा.html "ज्यादा से ज्यादा". mathworld.wolfram.com (in English). Retrieved 2020-08-30. {{cite web}}: Check |url= value (help)

बाहरी संबंध

Thomas Simpson's work on Maxima and Minima at Convergence
Application of Maxima and Minima with sub pages of solved problems
Jolliffe, Arthur Ernest (1911). "Maxima and Minima" . Encyclopædia Britannica (in English). Vol. 17 (11th ed.). pp. 918–920.

[1] Stewart, James (2008). कैलकुलस: अर्ली ट्रान्सेंडैंटल्स (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.

[2] Larson, Ron; Edwards, Bruce H. (2009). गणना (9th ed.). Brooks/Cole. ISBN 978-0-547-16702-2.

[3] Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). थॉमस कैलकुलस: अर्ली ट्रान्सेंडैंटल्स (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.

[4] Weisstein, Eric W. "न्यूनतम". mathworld.wolfram.com (in English). Retrieved 2020-08-30.

[5] Weisstein, Eric W. से ज्यादा.html "ज्यादा से ज्यादा". mathworld.wolfram.com (in English). Retrieved 2020-08-30. {{cite web}}: Check |url= value (help)

[1]

[2]

[3]

[4]

[5]

@@ Line 1: / Line 1: @@
-{{short description|Largest and smallest value taken by a function takes at a given point}}
+[[File:Extrema example original.svg|thumb|cos(3πx)/x, 0.1≤ x ≤1.1 के लिए स्थानीय और वैश्विक उच्चिष्ठ और निम्निष्ठ]][[गणितीय विश्लेषण]] में, किसी फलन (गणित) के उच्चिष्ठ और निम्निष्ठ (अधिकतम और न्यूनतम के संबंधित बहुवचन), सामूहिक रूप से एक्स्ट्रेमा (चरम का बहुवचन) के रूप में जाना जाता है,  प्रकार्य का सबसे बड़ा और सबसे छोटा मान है, या तो किसी दिए गए अंतराल के भीतर(गणित)("स्थानीय" या "सापेक्ष" एक्स्ट्रेमा), या किसी प्रकार्य के संपूर्ण कार्यक्षेत्र पर("वैश्विक" या "पूर्ण" एक्स्ट्रेमा)।<ref>{{cite book | last=Stewart | first=James | author-link=James Stewart (mathematician) | title=कैलकुलस: अर्ली ट्रान्सेंडैंटल्स| publisher=[[Brooks/Cole]] | edition=6th | year=2008 | isbn=978-0-495-01166-8 | url-access=registration | url=https://archive.org/details/calculusearlytra00stew_1 }}</ref><ref>{{cite book | last1=Larson | first1=Ron | author-link=Ron Larson (mathematician)| last2=Edwards | first2=Bruce H. | title=गणना| publisher=[[Brooks/Cole]] | edition=9th | year=2009 | isbn=978-0-547-16702-2}}</ref><ref>{{cite book | last1 = Thomas | first1 = George B. | last2=Weir | first2= Maurice D. | last3=Hass | first3=Joel |author3-link = Joel Hass| author-link=George B. Thomas | title=थॉमस कैलकुलस: अर्ली ट्रान्सेंडैंटल्स| publisher=[[Addison-Wesley]] | year=2010 | edition=12th | isbn=978-0-321-58876-0}}</ref> [[पियरे डी फर्मेट]] उन पहले गणितज्ञों में से एक थे जिन्होंने प्रकार्य का उच्चिष्ठ और निम्निष्ठ खोजने के लिए एक सामान्य तकनीक, [[पर्याप्तता]] का प्रस्ताव दिया था।
-{{For|सांख्यिकी में उपयोग|अधिकतम और न्यूनतम नमूना}}
-{{redirect| चरम मान|सांख्यिकी में अवधारणा|चरम मूल्य सिद्धांत| कलन में अवधारणा|चरम मूल्य प्रमेय}}
-{{redirect-multi|2| अधिकतम| न्यूनतम}}
-[[File:Extrema example original.svg|thumb|cos(3πx)/x, 0.1≤ x ≤1.1 के लिए स्थानीय और वैश्विक दीर्घतम और न्यूनतम]][[गणितीय विश्लेषण]] में, किसी फलन (गणित) के दीर्घतम और न्यूनतम (अधिकतम और न्यूनतम के संबंधित बहुवचन), सामूहिक रूप से एक्स्ट्रेमा (चरम का बहुवचन) के रूप में जाना जाता है,  प्रकार्य का सबसे बड़ा और सबसे छोटा मान है, या तो किसी दिए गए अंतराल के भीतर (गणित) ("स्थानीय" या "सापेक्ष" एक्स्ट्रेमा), या किसी प्रकार्य के संपूर्ण कार्यक्षेत्र पर ("वैश्विक" या "पूर्ण" एक्स्ट्रेमा)।<ref>{{cite book | last=Stewart | first=James | author-link=James Stewart (mathematician) | title=कैलकुलस: अर्ली ट्रान्सेंडैंटल्स| publisher=[[Brooks/Cole]] | edition=6th | year=2008 | isbn=978-0-495-01166-8 | url-access=registration | url=https://archive.org/details/calculusearlytra00stew_1 }}</ref><ref>{{cite book | last1=Larson | first1=Ron | author-link=Ron Larson (mathematician)| last2=Edwards | first2=Bruce H. | title=गणना| publisher=[[Brooks/Cole]] | edition=9th | year=2009 | isbn=978-0-547-16702-2}}</ref><ref>{{cite book | last1 = Thomas | first1 = George B. | last2=Weir | first2= Maurice D. | last3=Hass | first3=Joel |author3-link = Joel Hass| author-link=George B. Thomas | title=थॉमस कैलकुलस: अर्ली ट्रान्सेंडैंटल्स| publisher=[[Addison-Wesley]] | year=2010 | edition=12th | isbn=978-0-321-58876-0}}</ref> [[पियरे डी फर्मेट]] उन पहले गणितज्ञों में से एक थे जिन्होंने प्रकार्य का दीर्घतम और न्यूनतम खोजने के लिए एक सामान्य तकनीक, [[पर्याप्तता]] का प्रस्ताव दिया था।
-जैसा कि समुच्चय सिद्धांत में परिभाषित किया गया है, एक [[सेट (गणित)|समुच्चय (गणित)]] का अधिकतम और न्यूनतम क्रमशः समुच्चय में [[सबसे बड़ा और सबसे कम तत्व]] है। असीम अनंत समुच्चय, जैसे कि [[वास्तविक संख्या]]ओं का समुच्चय, का कोई न्यूनतम या अधिकतम नहीं होता है।
+जैसा कि समुच्चय सिद्धांत में परिभाषित किया गया है, एक [[सेट (गणित)|समुच्चय(गणित)]] का उच्चिष्ठ और निम्निष्ठ क्रमशः समुच्चय में [[सबसे बड़ा और सबसे कम तत्व]] है। असीम अनंत समुच्चय, जैसे कि [[वास्तविक संख्या]]ओं का समुच्चय, का कोई निम्निष्ठ या उच्चिष्ठ नहीं होता है।
 == परिभाषा ==
-प्रकार्य X के कार्यक्षेत्र पर परिभाषित एक वास्तविक-मूल्यवान प्रकार्य  (गणित) f में 'वैश्विक' (या 'पूर्ण') 'अधिकतम बिंदु' X पर<sup>∗</sup> है{{anchor|Global maximum point|Absolute maximum point|Maximum point}} , अगर X में सभी X के लिए {{nowrap|''f''(''x''<sup>∗</sup>) ≥ ''f''(''x'')}} है। इसी तरह, प्रकार्य  में 'वैश्विक' (या 'पूर्ण') 'न्यूनतम बिंदु'  X पर<sup>∗</sup> है{{anchor|Global minimum point|Absolute minimum point|Minimum point}}, अगर X में सभी X के लिए {{nowrap|''f''(''x''<sup>∗</sup>) ≤ ''f''(''x'')}} है। अधिकतम बिंदु पर फलन के मान को फलन का अधिकतम मान कहते हैं, निरूपित <math>\max(f(x))</math>, और न्यूनतम बिंदु पर फलन के मान को फलन का {{visible anchor|न्यूनतम मान}} कहा जाता है। प्रतीकात्मक रूप से, इसे इस प्रकार लिखा जा सकता है:
+प्रकार्य X के कार्यक्षेत्र पर परिभाषित एक वास्तविक-मूल्यवान प्रकार्य(गणित) f में 'वैश्विक'(या 'पूर्ण') 'उच्चिष्ठ बिंदु' X पर<sup>∗</sup> है , अगर X में सभी X के लिए {{nowrap|''f''(''x''<sup>∗</sup>) ≥ ''f''(''x'')}} है। इसी तरह, प्रकार्य  में 'वैश्विक'(या 'पूर्ण') 'निम्निष्ठ बिंदु' X पर<sup>∗</sup> है, अगर X में सभी X के लिए {{nowrap|''f''(''x''<sup>∗</sup>) ≤ ''f''(''x'')}} है। उच्चिष्ठ बिंदु पर फलन के मान को फलन का उच्चिष्ठ मान कहते हैं, निरूपित <math>\max(f(x))</math>, और निम्निष्ठ बिंदु पर फलन के मान को फलन का {{visible anchor|न्यूनतम मान}} कहा जाता है। प्रतीकात्मक रूप से, इसे इस प्रकार लिखा जा सकता है:
-:<math>x_0 \in X</math> प्रकार्य  का वैश्विक अधिकतम बिंदु <math>f:X \to \R,</math> यदि <math>(\forall x \in X)\, f(x_0) \geq f(x)</math> है।
+:<math>x_0 \in X</math> प्रकार्य  का वैश्विक उच्चिष्ठ बिंदु <math>f:X \to \R,</math> यदि <math>(\forall x \in X)\, f(x_0) \geq f(x)</math> है।
-वैश्विक न्यूनतम बिंदु की परिभाषा भी इसी तरह आगे बढ़ती है।
+वैश्विक निम्निष्ठ बिंदु की परिभाषा भी इसी तरह आगे बढ़ती है।
-यदि कार्यक्षेत्र X एक [[मापीय स्थान]] है, तो f को 'स्थानीय' (या 'सापेक्ष') 'अधिकतम बिंदु' कहा जाता है{{anchor|Local maximum point|Relative maximum point}} बिंदु x पर<sup>∗</sup>, यदि कुछ ε > 0 ऐसे मौजूद है कि, {{nowrap|''f''(''x''<sup>∗</sup>) ≥ ''f''(''x'')}} X में सभी X के लिए X<sup>∗</sup> की दूरी ε के भीतर है। इसी तरह, प्रकार्य  का X<sup>∗</sup> पर एक स्थानीय न्यूनतम बिंदु होता है{{anchor|Local minimum point|Relative minimum point}}, अगर f(x<sup>∗</sup>) ≤ f(x) सभी x के लिए X में x<sup>∗</sup> की दूरी ε के भीतर है। इसी तरह की परिभाषा का उपयोग तब किया जा सकता है जब X एक स्थलीय स्थान है, क्योंकि अभी दी गई परिभाषा को प्रतिवैस के संदर्भ में फिर से परिभाषित किया जा सकता है। गणितीय रूप से, दी गई परिभाषा इस प्रकार लिखी गई है:
+यदि कार्यक्षेत्र X एक [[मापीय स्थान]] है, तो f को 'स्थानीय'(या 'सापेक्ष') 'उच्चिष्ठ बिंदु' कहा जाता है बिंदु x पर<sup>∗</sup>, यदि कुछ ε > 0 ऐसे उपस्थित है कि, {{nowrap|''f''(''x''<sup>∗</sup>) ≥ ''f''(''x'')}} X में सभी X के लिए X<sup>∗</sup> की दूरी ε के भीतर है। इसी तरह, प्रकार्य  का X<sup>∗</sup> पर एक स्थानीय निम्निष्ठ बिंदु होता है, अगर f(x<sup>∗</sup>) ≤ f(x) सभी x के लिए X में x<sup>∗</sup> की दूरी ε के भीतर है। इसी तरह की परिभाषा का उपयोग तब किया जा सकता है जब X एक स्थलीय स्थान है, क्योंकि अभी दी गई परिभाषा को प्रतिवैस के संदर्भ में फिर से परिभाषित किया जा सकता है। गणितीय रूप से, दी गई परिभाषा इस प्रकार लिखी गई है:
-<math>(X, d_X)</math> को एकमापीय समष्टि मान लीजिए और प्रकार्य को <math> f:X \to \R</math>. फिर <math>x_0 \in X</math> कार्य का एक स्थानीय अधिकतम बिंदु है <math>f</math> यदि <math> (\exists \varepsilon > 0)</math> ऐसे कि <math>(\forall x \in X)\, d_X(x, x_0)<\varepsilon \implies f(x_0)\geq f(x).</math>
+<math>(X, d_X)</math> को एकमापीय समष्टि मान लीजिए और प्रकार्य को <math> f:X \to \R</math>. फिर <math>x_0 \in X</math> कार्य का एक स्थानीय उच्चिष्ठ बिंदु है <math>f</math> यदि <math> (\exists \varepsilon > 0)</math> ऐसे कि <math>(\forall x \in X)\, d_X(x, x_0)<\varepsilon \implies f(x_0)\geq f(x).</math>
-स्थानीय न्यूनतम बिंदु की परिभाषा भी इसी तरह आगे बढ़ सकती है।
+स्थानीय निम्निष्ठ बिंदु की परिभाषा भी इसी तरह आगे बढ़ सकती है।
-वैश्विक और स्थानीय दोनों वस्तुस्थिति में, a की {{visible anchor| निश्चित चरम}} अवधारणा को परिभाषित किया जा सकता है। उदाहरण के लिए, ''X''<sup>∗</sup> {{visible anchor|निश्चित वैश्विक अधिकतम बिंदु}} है। उदाहरण के लिए, x∗ एक सख्त वैश्विक अधिकतम बिंदु है यदि सभी x में x ≠ x∗ के साथ, हमारे पास f(x∗) > f(x), और x∗ एक सख्त स्थानीय अधिकतम बिंदु है। यदि वहाँ कुछ ε > 0 ऐसे मौजूद है कि, X में सभी x के लिए x∗ की दूरी ε के भीतर x ≠ x∗ के साथ है, हमारे पास f(x∗) > f(x) है। ध्यान दें कि एक बिंदु एक सख्त वैश्विक अधिकतम बिंदु है यदि और केवल यदि यह अद्वितीय वैश्विक अधिकतम बिंदु है, और इसी तरह न्यूनतम बिंदुओं के लिए है।
+वैश्विक और स्थानीय दोनों वस्तुस्थिति में, a की {{visible anchor| निश्चित चरम}} अवधारणा को परिभाषित किया जा सकता है। उदाहरण के लिए, ''X''<sup>∗</sup> {{visible anchor|निश्चित वैश्विक अधिकतम बिंदु}} है। उदाहरण के लिए, x∗ एक सख्त वैश्विक उच्चिष्ठ बिंदु है यदि सभी x में x ≠ x∗ के साथ, हमारे पास f(x∗) > f(x), और x∗ एक सख्त स्थानीय उच्चिष्ठ बिंदु है। यदि वहाँ कुछ ε > 0 ऐसे उपस्थित है कि, X में सभी x के लिए x∗ की दूरी ε के भीतर x ≠ x∗ के साथ है, हमारे पास f(x∗) > f(x) है। ध्यान दें कि एक बिंदु एक सख्त वैश्विक उच्चिष्ठ बिंदु है यदि और केवल यदि यह अद्वितीय वैश्विक उच्चिष्ठ बिंदु है, और इसी तरह निम्निष्ठ बिंदुओं के लिए है।
-[[कॉम्पैक्ट जगह|सघन स्थल]] कार्यक्षेत्र के साथ एक सतत कार्य वास्तविक-मूल्यवान प्रकार्य में हमेशा अधिकतम बिंदु और न्यूनतम बिंदु होता है। एक महत्वपूर्ण उदाहरण प्रकार्य  है जिसका कार्यक्षेत्र वास्तविक संख्याओं का एक बंद और परिबद्ध अंतराल (गणित) है (ऊपर आरेख देखें)।
+[[कॉम्पैक्ट जगह|सघन स्थल]] कार्यक्षेत्र के साथ एक सतत कार्य वास्तविक-मूल्यवान प्रकार्य में हमेशा उच्चिष्ठ बिंदु और निम्निष्ठ बिंदु होता है। एक महत्वपूर्ण उदाहरण प्रकार्य  है जिसका कार्यक्षेत्र वास्तविक संख्याओं का एक बंद और परिबद्ध अंतराल(गणित) है(ऊपर आरेख देखें)।
 == खोज ==
-वैश्विक दीर्घतम और न्यूनतम ढूँढना [[गणितीय अनुकूलन]] का लक्ष्य है। यदि कोई प्रकार्य एक बंद अंतराल पर सतत है, तो [[चरम मूल्य प्रमेय]] द्वारा वैश्विक अधिकतम और निम्निष्ठ मौजूद हैं। इसके अलावा, एक वैश्विक अधिकतम (या न्यूनतम) या तो कार्यक्षेत्र के अभ्यंतर भाग में एक स्थानीय अधिकतम (या न्यूनतम) होना चाहिए, या कार्यक्षेत्र की सीमा पर स्थित होना चाहिए। वैश्विक अधिकतम (या न्यूनतम) खोजने की एक विधि अभ्यंतर में सभी स्थानीय दीर्घतम (या न्यूनतम) को देखना है, और सीमा पर बिंदुओं के दीर्घतम (या न्यूनतम) को भी देखना है, और सबसे बड़ा ( या सबसे छोटा) लेना है।
+वैश्विक उच्चिष्ठ और निम्निष्ठ ढूँढना [[गणितीय अनुकूलन]] का लक्ष्य है। यदि कोई प्रकार्य एक बंद अंतराल पर सतत है, तो [[चरम मूल्य प्रमेय]] द्वारा वैश्विक उच्चिष्ठ और निम्निष्ठ उपस्थित हैं। इसके अलावा, एक वैश्विक उच्चिष्ठ(या निम्निष्ठ) या तो कार्यक्षेत्र के अभ्यंतर भाग में एक स्थानीय उच्चिष्ठ (या निम्निष्ठ) होना चाहिए, या कार्यक्षेत्र की सीमा पर स्थित होना चाहिए। वैश्विक उच्चिष्ठ(या निम्निष्ठ) खोजने की एक विधि अभ्यंतर में सभी स्थानीय उच्चिष्ठ(या निम्निष्ठ) को देखना है, और सीमा पर बिंदुओं के उच्चिष्ठ (या निम्निष्ठ) को भी देखना है, और सबसे बड़ा(या सबसे छोटा) लेना है।
-[[अलग-अलग कार्य|अवकलनीय  प्रकार्य]]  के लिए, फर्मेट के प्रमेय में कहा गया है कि एक कार्यक्षेत्र के अभ्यंतर में स्थानीय एक्स्ट्रेमा [[महत्वपूर्ण बिंदु (गणित)]] (या अंक जहां व्युत्पन्न शून्य के बराबर होता है) पर होना चाहिए।<ref>{{Cite web|last=Weisstein|first=Eric W.|title=न्यूनतम|url=https://mathworld.wolfram.com/न्यूनतम.html|access-date=2020-08-30|website=mathworld.wolfram.com|language=en}}</ref> हालांकि, सभी महत्वपूर्ण बिंदु एक्स्ट्रीमा नहीं हैं। पहला व्युत्पन्न परीक्षण, दूसरा व्युत्पन्न परीक्षण, या उच्च-क्रम व्युत्पन्न परीक्षण का उपयोग करके कोई यह भेद कर सकता है कि क्या एक महत्वपूर्ण बिंदु एक स्थानीय अधिकतम या स्थानीय न्यूनतम है, पर्याप्त भिन्नता दी गई है।<ref>{{Cite web|last=Weisstein|first=Eric W.|title=ज्यादा से ज्यादा|url=https://mathworld.wolfram.com/ज्यादा से ज्यादा.html|access-date=2020-08-30|website=mathworld.wolfram.com|language=en}}</ref>
+[[अलग-अलग कार्य|अवकलनीय  प्रकार्य]]  के लिए, फर्मेट के प्रमेय में कहा गया है कि एक कार्यक्षेत्र के अभ्यंतर में स्थानीय एक्स्ट्रेमा [[महत्वपूर्ण बिंदु (गणित)|महत्वपूर्ण बिंदु(गणित)]] (या अंक जहां व्युत्पन्न शून्य के बराबर होता है) पर होना चाहिए।<ref>{{Cite web|last=Weisstein|first=Eric W.|title=न्यूनतम|url=https://mathworld.wolfram.com/न्यूनतम.html|access-date=2020-08-30|website=mathworld.wolfram.com|language=en}}</ref> हालांकि, सभी महत्वपूर्ण बिंदु एक्स्ट्रीमा नहीं हैं। पहला व्युत्पन्न परीक्षण, दूसरा व्युत्पन्न परीक्षण, या उच्च-क्रम व्युत्पन्न परीक्षण का उपयोग करके कोई यह भेद कर सकता है कि क्या एक महत्वपूर्ण बिंदु एक स्थानीय उच्चिष्ठ या स्थानीय निम्निष्ठ है, पर्याप्त भिन्नता दी गई है।<ref>{{Cite web|last=Weisstein|first=Eric W.|title=ज्यादा से ज्यादा|url=https://mathworld.wolfram.com/ज्यादा से ज्यादा.html|access-date=2020-08-30|website=mathworld.wolfram.com|language=en}}</ref>
-किसी भी प्रकार्य के लिए जिसे टुकड़े के रूप में परिभाषित किया गया है, प्रत्येक टुकड़े के अधिकतम (या न्यूनतम) को अलग-अलग ढूंढकर अधिकतम (या न्यूनतम) पाता है, और फिर यह दृष्टि बोध करता है कि कौन सा सबसे बड़ा (या सबसे छोटा) है।
+किसी भी प्रकार्य के लिए जिसे टुकड़े के रूप में परिभाषित किया गया है, प्रत्येक टुकड़े के उच्चिष्ठ (या निम्निष्ठ) को अलग-अलग ढूंढकर उच्चिष्ठ(या निम्निष्ठ) पाता है, और फिर यह दृष्टि बोध करता है कि कौन सा सबसे बड़ा (या सबसे छोटा) है।
 == उदाहरण ==
-[[Image:xth root of x.svg|thumb|right|वैश्विक अधिकतम {{math|{{sqrt|''x''|''x''}}}} पर होता {{math|''x'' {{=}} ''[[e (mathematical constant)|e]]''}} है .]]
+[[Image:xth root of x.svg|thumb|right|वैश्विक उच्चिष्ठ {{math|{{sqrt|''x''|''x''}}}} पर होता {{math|''x'' {{=}} ''[[e (mathematical constant)|e]]''}} है .]]
 {|class="wikitable"
-!प्रकार्य!!दीर्घतम और न्यूनतम
+!प्रकार्य!!उच्चिष्ठ और निम्निष्ठ
 |-
-| ''x''<sup>2</sup>||''x'' = 0 पर अद्वितीय वैश्विक न्यूनतम।
+| ''x''<sup>2</sup>||''x'' = 0 पर अद्वितीय वैश्विक निम्निष्ठ।
 |-
-| ''x''<sup>3</sup> ||कोई वैश्विक न्यूनतम या अधिकतम नहीं. यद्यपि पहला अवकलज (3''x''<sup>2</sup>) ''x'' = 0 पर 0 है, यह एक [[विभक्ति बिंदु]] है. (दूसरा व्युत्पन्न उस बिंदु पर 0 है।)
+| ''x''<sup>3</sup> ||कोई वैश्विक निम्निष्ठ या उच्चिष्ठ नहीं. यद्यपि पहला अवकलज(3''x''<sup>2</sup>) ''x'' = 0 पर 0 है, यह एक [[विभक्ति बिंदु]] है.(दूसरा व्युत्पन्न उस बिंदु पर 0 है।)
 |-
-| <big><math>\sqrt[x]{x}</math></big> ||अद्वितीय वैश्विक अधिकतम पर ''x'' = ''[[e (mathematical constant)|e]]''. (चित्र को दाईं ओर देखें)।
+| <big><math>\sqrt[x]{x}</math></big> ||अद्वितीय वैश्विक उच्चिष्ठ पर ''x'' = ''[[e (mathematical constant)|e]]''.(चित्र को दाईं ओर देखें)।
 |-
-| ''x''<sup>−''x''</sup> ||x = 1/e पर सकारात्मक वास्तविक संख्याओं पर अद्वितीय वैश्विक अधिकतम।
+| ''x''<sup>−''x''</sup> ||x = 1/e पर सकारात्मक वास्तविक संख्याओं पर अद्वितीय वैश्विक उच्चिष्ठ।
 |-
-| ''x''<sup>3</sup>/3 − ''x'' ||पहला अवकलज x2 − 1 और दूसरा अवकलज 2x है। पहले व्युत्पादित को 0 पर अवस्थापन करना और x के लिए हल करना -1 और +1 पर स्थिर अंक देता है। दूसरे अवकलज के चिह्न से, हम देख सकते हैं कि -1 स्थानीय अधिकतम है और +1 स्थानीय न्यूनतम है. इस प्रकार्य का कोई वैश्विक अधिकतम या न्यूनतम नहीं है।
+| ''x''<sup>3</sup>/3 − ''x'' ||पहला अवकलज x2 − 1 और दूसरा अवकलज 2x है। पहले व्युत्पादित को 0 पर अवस्थापन करना और x के लिए हल करना -1 और +1 पर स्थिर अंक देता है। दूसरे अवकलज के चिह्न से, हम देख सकते हैं कि -1 स्थानीय उच्चिष्ठ है और +1 स्थानीय निम्निष्ठ है. इस प्रकार्य का कोई वैश्विक उच्चिष्ठ या निम्निष्ठ नहीं है।
 |-
-| <nowiki> |</nowiki>''x''<nowiki>|</nowiki> ||वैश्विक न्यूनतम x = 0 पर व्युत्पादित लेकर नहीं पाया जा सकता है, क्योंकि व्युत्पादित x = 0 पर मौजूद नहीं है।
+| <nowiki> |</nowiki>''x''<nowiki>|</nowiki> ||वैश्विक निम्निष्ठ x = 0 पर व्युत्पादित लेकर नहीं पाया जा सकता है, क्योंकि व्युत्पादित x = 0 पर उपस्थित नहीं है।
 |-
 | cos(''x'') ||0, ±2π, ±4π, ... पर अपरिमित रूप से अनेक वैश्विक उच्चिष्ठ और ±π, ±3π, ±5π, .... पर अपरिमित रूप से अनेक वैश्विक निम्निष्ठ।
 |-
-| 2 cos(''x'') − ''x'' ||अपरिमित रूप से कई स्थानीय उच्चिष्ठ और निम्निष्ठ, लेकिन कोई वैश्विक अधिकतम या न्यूनतम नहीं है।
+| 2 cos(''x'') − ''x'' ||अपरिमित रूप से कई स्थानीय उच्चिष्ठ और निम्निष्ठ, लेकिन कोई वैश्विक उच्चिष्ठ या निम्निष्ठ नहीं है।
 |-
-| {{nowrap|0.1 ≤ ''x'' ≤ 1.1}} के साथ cos(3{{pi}}''x'')/''x'' ||x = 0.1 (एक सीमा) पर वैश्विक अधिकतम, x = 0.3 के पास एक वैश्विक न्यूनतम, x = 0.6 के पास एक स्थानीय अधिकतम, और x = 1.0 के पास एक स्थानीय न्यूनतम। (पृष्ठ के शीर्ष पर चित्र देखें।)
+| {{nowrap|0.1 ≤ ''x'' ≤ 1.1}} के साथ cos(3{{pi}}''x'')/''x'' ||x = 0.1(एक सीमा) पर वैश्विक उच्चिष्ठ, x = 0.3 के पास एक वैश्विक निम्निष्ठ, x = 0.6 के पास एक स्थानीय उच्चिष्ठ, और x = 1.0 के पास एक स्थानीय निम्निष्ठ।(पृष्ठ के शीर्ष पर चित्र देखें।)
 |-
-|''x''<sup>3</sup> + 3''x''<sup>2</sup> − 2''x'' + 1बंद अंतराल (खंड) पर परिभाषित [−4,2] || स्थानीय अधिकतम x = −1−√15/3, स्थानीय न्यूनतम x = −1+√15/3, वैश्विक अधिकतम x = 2 और वैश्विक न्यूनतम x = −4।
+|''x''<sup>3</sup> + 3''x''<sup>2</sup> − 2''x'' + 1बंद अंतराल(खंड) पर परिभाषित [−4,2] || स्थानीय उच्चिष्ठ x = −1−√15/3, स्थानीय निम्निष्ठ x = −1+√15/3, वैश्विक उच्चिष्ठ x = 2 और वैश्विक निम्निष्ठ x = −4।
 |}
-एक व्यावहारिक उदाहरण के लिए,[6] एक ऐसी स्थिति मान लें जहां किसी के पास <math>200</math> फीट की बाड़ है और वह एक आयताकार बाड़े के चौकोर फुटमान को अधिकतम करने की कोशिश कर रहा है, जहां <math>x</math> लंबाई है, <math>y</math> चौड़ाई है, और <math>xy</math> क्षेत्रफल है:
+एक व्यावहारिक उदाहरण के लिए,[6] एक ऐसी स्थिति मान लें जहां किसी के पास <math>200</math> फीट की बाड़ है और वह एक आयताकार बाड़े के चौकोर फुटमान को उच्चिष्ठ करने की कोशिश कर रहा है, जहां <math>x</math> लंबाई है, <math>y</math> चौड़ाई है, और <math>xy</math> क्षेत्रफल है:
 :<math> 2x+2y = 200 </math>
@@ Line 71: / Line 67: @@
 :<math>2x=100</math>
 :<math>x=50</math>
-प्रकट करता है कि <math>x=50</math> हमारा एकमात्र क्रांतिक बिंदु (गणित) है। अब जिस अंतराल तक <math>x</math> प्रतिबंधित है, उसे निर्धारित करके अंतिम-बिंदुओं को पुनः प्राप्त करें। चूँकि चौड़ाई धनात्मक है, तब <math>x>0</math>, और चूँकि {{nowrap|<math>x=100-y</math>,}} इसका तात्पर्य है कि {{nowrap|<math>x < 100</math>.}} महत्वपूर्ण बिंदु {{nowrap|<math>50</math>,}}, साथ ही समापन बिंदु <math>0</math> और {{nowrap|<math>100</math>,}} को {{nowrap|<math>xy=x(100-x)</math>,}} में प्लग करें, और परिणाम हैं <math>2500, 0,</math> तथा <math>0</math> क्रमश।
+प्रकट करता है कि <math>x=50</math> हमारा एकमात्र क्रांतिक बिंदु(गणित) है। अब जिस अंतराल तक <math>x</math> प्रतिबंधित है, उसे निर्धारित करके अंतिम-बिंदुओं को पुनः प्राप्त करें। चूँकि चौड़ाई धनात्मक है, तब <math>x>0</math>, और चूँकि {{nowrap|<math>x=100-y</math>,}} इसका तात्पर्य है कि {{nowrap|<math>x < 100</math>.}} महत्वपूर्ण बिंदु {{nowrap|<math>50</math>,}}, साथ ही समापन बिंदु <math>0</math> और {{nowrap|<math>100</math>,}} को {{nowrap|<math>xy=x(100-x)</math>,}} में प्लग करें, और परिणाम हैं <math>2500, 0,</math> तथा <math>0</math> क्रमश।
 इसलिए, आयत के साथ प्राप्य सबसे बड़ा क्षेत्र <math>200</math> फीट की बाड़ है।
@@ Line 77: / Line 73: @@
 == एक से अधिक चर के कार्य ==<!-- This section is linked from [[Indifference curve]] -->
 {{main|दूसरा आंशिक व्युत्पन्न परीक्षण}}
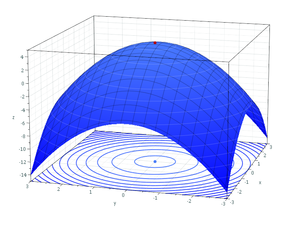
-[[File:Modell einer Peanoschen Fläche -Schilling XLIX, 1-.jpg|thumb|left|पीआनो सतह, 19वीं शताब्दी के स्थानीय दीर्घतम के कुछ मानदंडों का प्रति उदाहरण]][[File:MaximumParaboloid.png|thumb|right|वैश्विक अधिकतम शीर्ष पर स्थित बिंदु है]]
-[[File:MaximumCounterexample.png|thumb|right|प्रति उदाहरण: लाल बिंदु एक स्थानीय न्यूनतम दिखाता है जो वैश्विक न्यूनतम नहीं है]]एक से अधिक चर वाले कार्यों के लिए समान शर्तें लागू होती हैं। उदाहरण के लिए, दाईं ओर (विस्तारित) आकृति में, स्थानीय अधिकतम के लिए आवश्यक शर्तें केवल एक चर वाले प्रकार्य के समान होती हैं। Z के रूप में पहला आंशिक व्युत्पादित (अधिकतम किया जाने वाला चर) अधिकतम पर शून्य है (चित्र में शीर्ष पर चमकता हुआ बिंदु) दूसरा आंशिक व्युत्पादित नकारात्मक है। काठी बिंदु की संभावना के कारण एक स्थानीय अधिकतम के लिए शर्तें केवल आवश्यक हैं, पर्याप्त नहीं हैं। अधिकतम के लिए हल करने के लिए और स्थितियों के उपयोग के लिए, प्रकार्य z को भी अलग-अलग प्रकार्य होना चाहिए। [[दूसरा आंशिक व्युत्पन्न परीक्षण]] बिंदु को सापेक्ष अधिकतम या सापेक्ष न्यूनतम के रूप में वर्गीकृत करने में मदद कर सकता है।
+[[File:Modell einer Peanoschen Fläche -Schilling XLIX, 1-.jpg|thumb|left|पीआनो सतह, 19वीं शताब्दी के स्थानीय उच्चिष्ठ के कुछ मानदंडों का प्रति उदाहरण]][[File:MaximumParaboloid.png|thumb|right|वैश्विक उच्चिष्ठ शीर्ष पर स्थित बिंदु है]]
-इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के कार्यों और एक से अधिक चर के कार्यों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय न्यूनतम है, तो यह एक वैश्विक न्यूनतम भी है ([[मध्यवर्ती मूल्य प्रमेय]] और रोले के प्रमेय का उपयोग करके विरोधाभास द्वारा इसे साबित करें)। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है
+[[File:MaximumCounterexample.png|thumb|right|प्रति उदाहरण: लाल बिंदु एक स्थानीय निम्निष्ठ दिखाता है जो वैश्विक निम्निष्ठ नहीं है]]एक से अधिक चर वाले कार्यों के लिए समान शर्तें लागू होती हैं। उदाहरण के लिए, दाईं ओर(विस्तारित) आकृति में, स्थानीय उच्चिष्ठ के लिए आवश्यक शर्तें केवल एक चर वाले प्रकार्य के समान होती हैं। Z के रूप में पहला आंशिक व्युत्पादित(उच्चिष्ठ किया जाने वाला चर) उच्चिष्ठ पर शून्य है(चित्र में शीर्ष पर चमकता हुआ बिंदु) दूसरा आंशिक व्युत्पादित नकारात्मक है। काठी बिंदु की संभावना के कारण एक स्थानीय उच्चिष्ठ के लिए शर्तें केवल आवश्यक हैं, पर्याप्त नहीं हैं। उच्चिष्ठ के लिए हल करने के लिए और स्थितियों के उपयोग के लिए, प्रकार्य z को भी अलग-अलग प्रकार्य होना चाहिए। [[दूसरा आंशिक व्युत्पन्न परीक्षण]] बिंदु को सापेक्ष उच्चिष्ठ या सापेक्ष निम्निष्ठ के रूप में वर्गीकृत करने में मदद कर सकता है।
+इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के कार्यों और एक से अधिक चर के कार्यों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय निम्निष्ठ है, तो यह एक वैश्विक निम्निष्ठ भी है([[मध्यवर्ती मूल्य प्रमेय]] और रोले के प्रमेय का उपयोग करके विरोधाभास द्वारा इसे साबित करें)। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है
 :<math>f(x,y)= x^2+y^2(1-x)^3,\qquad x,y \in \R,</math>
-जिसका एकमात्र महत्वपूर्ण बिंदु (0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय न्यूनतम है। हालांकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5।
+जिसका एकमात्र महत्वपूर्ण बिंदु(0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय निम्निष्ठ है। हालांकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5।
-=== एक कार्यात्मक की दीर्घतम या न्यूनतम ===
+=== एक कार्यात्मक की उच्चिष्ठ या निम्निष्ठ ===
-यदि किसी प्रकार्य का कार्यक्षेत्र जिसके लिए एक चरम पाया जाना है, में स्वयं प्रकार्य होते हैं (यानी यदि चरम को एक [[कार्यात्मक (गणित)]] के रूप में पाया जाता है), तो चरम विविधताओं के कलन का उपयोग करके पाया जाता है।
+यदि किसी प्रकार्य का कार्यक्षेत्र जिसके लिए एक चरम पाया जाना है, में स्वयं प्रकार्य होते हैं(यानी यदि चरम को एक [[कार्यात्मक (गणित)|कार्यात्मक(गणित)]] के रूप में पाया जाता है), तो चरम विविधताओं के कलन का उपयोग करके पाया जाता है।
 == समुच्चय के संबंध में ==
-दीर्घतम और न्यूनतम को समुच्चय के लिए भी परिभाषित किया जा सकता है। व्यापक रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे इस रूप <math>\max(S)</math> में भी निरूपित किया जाता है। इसके अलावा, यदि S एक आदेशित समुच्चय T का एक उपसमुच्चय है और M S का सबसे बड़ा तत्व है (T द्वारा प्रेरित अनुक्रम के संबंध में), तो M T में S का सर्वोच्च है। इसी तरह के परिणाम [[कम से कम तत्व]], [[न्यूनतम तत्व]] और अल्प. समुच्चय के लिए अधिकतम और न्यूनतम प्रकार्य का उपयोग [[डेटाबेस]] में किया जाता है, और इसकी गणना तेजी से की जा सकती है, क्योंकि एक समुच्चय के अधिकतम (या न्यूनतम) की गणना एक विभाजन की अधिकतम सीमा से की जा सकती है; औपचारिक रूप से, वे स्व-विघटन योग्य एकत्रीकरण कार्य हैं।
+उच्चिष्ठ और निम्निष्ठ को समुच्चय के लिए भी परिभाषित किया जा सकता है। व्यापक रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे इस रूप <math>\max(S)</math> में भी निरूपित किया जाता है। इसके अलावा, यदि S एक आदेशित समुच्चय T का एक उपसमुच्चय है और M S का सबसे बड़ा तत्व है(T द्वारा प्रेरित अनुक्रम के संबंध में), तो M T में S का सर्वोच्च है। इसी तरह के परिणाम [[कम से कम तत्व]], [[न्यूनतम तत्व|निम्निष्ठ तत्व]] और अल्प. समुच्चय के लिए उच्चिष्ठ और निम्निष्ठ प्रकार्य का उपयोग [[डेटाबेस]] में किया जाता है, और इसकी गणना तेजी से की जा सकती है, क्योंकि एक समुच्चय के उच्चिष्ठ(या निम्निष्ठ) की गणना एक विभाजन की उच्चिष्ठ सीमा से की जा सकती है; औपचारिक रूप से, वे स्व-विघटन योग्य एकत्रीकरण कार्य हैं।
-एक सामान्य [[आंशिक आदेश]] के मामले में, '[[सबसे कम]] तत्व' (यानी, जो अन्य सभी की तुलना में छोटा है) को 'न्यूनतम तत्व' (कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी तरह, आंशिक रूप से अनुक्रम किए गए समुच्चय (पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के भीतर निहित होता है, जबकि पॉसमुच्चय A का 'अधिकतम तत्व' M A का एक तत्व होता है जैसे कि यदि M ≤ B (A में किसी भी B के लिए), फिर M = B। पोसमुच्चय का कोई भी न्यूनतम तत्व या सबसे बड़ा तत्व अद्वितीय है, लेकिन एक पॉसमुच्चय में कई न्यूनतम या अधिकतम तत्व हो सकते हैं। यदि किसी पॉसमुच्चय में एक से अधिक अधिकतम तत्व हैं, तो ये तत्व परस्पर तुलनीय नहीं होंगे।
+एक सामान्य [[आंशिक आदेश]] के मामले में, '[[सबसे कम]] तत्व'(यानी, जो अन्य सभी की तुलना में छोटा है) को 'निम्निष्ठ तत्व'(कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी तरह, आंशिक रूप से अनुक्रम किए गए समुच्चय(पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के भीतर निहित होता है, जबकि पॉसमुच्चय A का 'उच्चिष्ठ तत्व' M A का एक तत्व होता है जैसे कि यदि M ≤ B(A में किसी भी B के लिए), फिर M = B। पोसमुच्चय का कोई भी निम्निष्ठ तत्व या सबसे बड़ा तत्व अद्वितीय है, लेकिन एक पॉसमुच्चय में कई निम्निष्ठ या उच्चिष्ठ तत्व हो सकते हैं। यदि किसी पॉसमुच्चय में एक से अधिक उच्चिष्ठ तत्व हैं, तो ये तत्व परस्पर तुलनीय नहीं होंगे।
-कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में अधिकतम एक न्यूनतम तत्व और अधिकतम एक अधिकतम तत्व हो सकता है। फिर, आपसी तुलना के कारण, न्यूनतम तत्व भी सबसे छोटा तत्व होगा, और अधिकतम तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी तरह से व्यवस्थित समुच्चय में, हम केवल 'न्यूनतम' और 'अधिकतम' शब्दों का उपयोग कर सकते हैं।
+कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में उच्चिष्ठ एक निम्निष्ठ तत्व और उच्चिष्ठ एक उच्चिष्ठ तत्व हो सकता है। फिर, आपसी तुलना के कारण, निम्निष्ठ तत्व भी सबसे छोटा तत्व होगा, और उच्चिष्ठ तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी तरह से व्यवस्थित समुच्चय में, हम केवल 'निम्निष्ठ' और 'उच्चिष्ठ' शब्दों का उपयोग कर सकते हैं।
-यदि एक श्रृंखला परिमित है, तो इसमें हमेशा अधिकतम और न्यूनतम होगा। यदि एक शृंखला अनंत है, तो उसके लिए अधिकतम या न्यूनतम की आवश्यकता नहीं है। उदाहरण के लिए, [[प्राकृतिक संख्या]]ओं के समुच्चय का कोई अधिकतम नहीं है, हालांकि इसमें न्यूनतम है। यदि एक अनंत श्रृंखला S परिबद्ध है, तो समुच्चय के [[टोपोलॉजिकल क्लोजर|संवरण]] CL (S) में कभी-कभी न्यूनतम और अधिकतम होता है, इस मामले में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय S की 'कम से कम [[ऊपरी सीमा]]' कहा जाता है। , क्रमश।
+यदि एक श्रृंखला परिमित है, तो इसमें हमेशा उच्चिष्ठ और निम्निष्ठ होगा। यदि एक शृंखला अनंत है, तो उसके लिए उच्चिष्ठ या निम्निष्ठ की आवश्यकता नहीं है। उदाहरण के लिए, [[प्राकृतिक संख्या]]ओं के समुच्चय का कोई उच्चिष्ठ नहीं है, हालांकि इसमें निम्निष्ठ है। यदि एक अनंत श्रृंखला S परिबद्ध है, तो समुच्चय के [[टोपोलॉजिकल क्लोजर|संवरण]] CL(S) में कभी-कभी निम्निष्ठ और उच्चिष्ठ होता है, इस मामले में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय S की 'कम से कम [[ऊपरी सीमा]]' कहा जाता है। , क्रमश।
 == यह भी देखें ==
-* [[आर्ग मैक्स|अधिकतम आर्ग]]
+* [[आर्ग मैक्स|उच्चिष्ठ आर्ग]]
 * [[व्युत्पन्न परीक्षण]]
 *[[निम्नतम और उच्चतम]]
 *श्रेष्ठ को सीमित करें और हीन को सीमित करें
 * [[यांत्रिक संतुलन]]
-*मेक्स (गणित)
+*मेक्स(गणित)
-* [[नमूना अधिकतम और न्यूनतम]]
+* [[नमूना अधिकतम और न्यूनतम|नमूना उच्चिष्ठ और निम्निष्ठ]]
 *पल्याण बिन्दु
 ==संदर्भ==
 {{reflist}}
-*
 ==बाहरी संबंध==
-{{Commons category|Extrema (calculus)}}
-{{Wiktionary|maxima|minima|extremum}}
 *[http://www.maa.org/publications/periodicals/convergence/thomas-simpson-and-maxima-and-minima Thomas Simpson's work on Maxima and Minima] at [https://web.archive.org/web/20070713083148/http://mathdl.maa.org/convergence/1/ Convergence]
 *[http://www.mathalino.com/reviewer/differential-calculus/application-of-maxima-and-minima Application of Maxima and Minima with sub pages of solved problems]
@@ Line 119: / Line 110: @@
 {{Calculus topics}}
-[[Category: कैलकुलस]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
+[[Category:Articles with short description]]
+[[Category:CS1 English-language sources (en)]]
+[[Category:CS1 errors]]
+[[Category:CS1 français-language sources (fr)]]
+[[Category:CS1 maint]]
+[[Category:CS1 Ελληνικά-language sources (el)]]
+[[Category:Citation Style 1 templates|W]]
+[[Category:Collapse templates]]
+[[Category:Created On 25/11/2022]]
+[[Category:Exclude in print]]
+[[Category:Interwiki category linking templates]]
+[[Category:Interwiki link templates]]
+[[Category:Machine Translated Page]]
+[[Category:Missing redirects]]
+[[Category:Navigational boxes| ]]
+[[Category:Navigational boxes without horizontal lists]]
+[[Category:Pages with script errors]]
+[[Category:Short description with empty Wikidata description]]
+[[Category:Sidebars with styles needing conversion]]
+[[Category:Template documentation pages|Documentation/doc]]
+[[Category:Templates based on the Citation/CS1 Lua module]]
+[[Category:Templates generating COinS|Cite web]]
+[[Category:Templates generating microformats]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that are not mobile friendly]]
+[[Category:Templates used by AutoWikiBrowser|Cite web]]
+[[Category:Templates using TemplateData]]
+[[Category:Wikimedia Commons templates]]
+[[Category:Wikipedia articles incorporating a citation from the 1911 Encyclopaedia Britannica with Wikisource reference]]
+[[Category:Wikipedia fully protected templates|Cite web]]
+[[Category:Wikipedia metatemplates]]
+[[Category:कैलकुलस]]
+[[Category:गणितीय अनुकूलन]]
 [[Category:गणितीय विश्लेषण]]
-[[Category: गणितीय अनुकूलन]]
 [[Category:श्रेष्ठतम]]
-[[Category: Machine Translated Page]]
-[[Category:Created On 25/11/2022]]

v t e पथरी
Prealculus	द्विपद प्रमेय अवतल कार्य निरंतर कार्य फैक्टरियल परिमित अंतर मुक्त चर और बाध्य चर एक फ़ंक्शन का ग्राफ रैखिक प्रकार्य रेडियन रोले का प्रमेय सेकंट ढलान स्पर्शरेखा
सीमा	अनिश्चित रूप एक फ़ंक्शन की सीमा एकतरफा सीमा एक अनुक्रम की सीमा सन्निकटन का आदेश ((, Δ)-सीमा की सीमा
अंतर कलन	व्युत्पन्न दूसरा व्युत्पन्न आंशिक व्युत्पन्न अंतर विभेदक ऑपरेटर मतलब मान प्रमेय संकेतन Leibniz का अंकन न्यूटन की संकेतन भेदभाव के नियम रैखिकता शक्ति योग चेन l'hôpital's उत्पाद जनरल लीबनिज़ का नियम भागफल अन्य तकनीकें निहित भेदभाव उलटा कार्य और भेदभाव लॉगरिदमिक व्युत्पन्न संबंधित दरें स्थिर बिंदु पहला व्युत्पन्न परीक्षण दूसरा व्युत्पन्न परीक्षण चरम मूल्य प्रमेय मैक्सिमा और मिनिमा आगे के आवेदन न्यूटन की विधि टेलर का प्रमेय अंतर समीकरण साधारण अंतर समीकरण आंशिक विभेदक समीकरण स्टोचस्टिक डिफरेंशियल इक्वेशन
समाकलन गणित	Antiderivative Arc length Riemann integral Basic properties Constant of integration Fundamental theorem of calculus Differentiating under the integral sign Integration by parts Integration by substitution trigonometric Euler Tangent half-angle substitution Partial fractions in integration Quadratic integral Trapezoidal rule Volumes Washer method Shell method Integral equation Integro-differential equation
वेक्टर कैलकुलस	डेरिवेटिव कर्ल दिशात्मक व्युत्पन्न विचलन ढाल लाप्लासियन बुनियादी प्रमेय लाइन इंटीग्रल ग्रीन स्टोक्स' गॉस '
बहुक्रियाशील पथरी	विचलन प्रमेय ज्यामितीय हेसियन मैट्रिक्स जैकबियन मैट्रिक्स और निर्धारक Lagrange गुणक लाइन इंटीग्रल मैट्रिक्स एकाधिक अभिन्न आंशिक व्युत्पन्न सतह अभिन्न वॉल्यूम इंटीग्रल उन्नत विषय विभेदक रूप बाहरी व्युत्पन्न सामान्यीकृत स्टोक्स 'प्रमेय टेंसर कैलकुलस
अनुक्रम और श्रृंखला	अंकगणित-ज्यामितीय अनुक्रम श्रृंखला के प्रकार वैकल्पिक द्विपद फूरियर ज्यामितीय हार्मोनिक अनंत पावर Maclaurin टेलर दूरबीन अभिसरण के परीक्षण हाबिल अल्टरनेटिंग सीरीज़ Cauchy संघनन प्रत्यक्ष तुलना Dirichlet's अभिन्न सीमा तुलना अनुपात रूट शब्द
विशेष कार्य और संख्या	बर्नौली नंबर ई (गणितीय स्थिरांक) घातांक प्रकार्य प्राकृतिक स्टर्लिंग का अनुमान
कैलकुलस का इतिहास	पर्याप्तता ब्रुक टेलर कॉलिन मैक्लोरिन बीजगणित की सामान्यता गॉटफ्रीड विल्हेम लीबनिज़ Infinitesimal Infinitesimal galulus आइजैक न्यूटन फ्लक्सियन निरंतरता का नियम लियोनहार्ड यूलर प्रवाह की विधि यांत्रिक प्रमेय की विधि
सूचियों	भेदभाव नियम घातीय कार्यों के अभिन्न अंग की सूची हाइपरबोलिक कार्यों के अभिन्न अंग की सूची उलटा हाइपरबोलिक कार्यों के अभिन्न अंग की सूची उलटा त्रिकोणमितीय कार्यों के अभिन्न अंग की सूची तर्कहीन कार्यों के अभिन्न अंग की सूची लघुगणक कार्यों के अभिन्न अंग की सूची तर्कसंगत कार्यों के अभिन्न अंग की सूची त्रिकोणमितीय कार्यों के अभिन्न अंग की सूची सेकंट सेकेंट क्यूबेड सीमाओं की सूची अभिन्न की सूची
विविध विषय	जटिल पथरी समोच्च अभिन्न अंतर ज्यामिति कई गुना वक्रता घटता सतहों का टेंसर यूलर -मेक्लॉरिन फॉर्मूला गेब्रियल का सींग एकीकरण मधुमक्खी प्रमाण है कि 22/7 से अधिक Regiomontanus 'कोण अधिकतमकरण समस्या स्टाइनमेट्ज़ सॉलिड

Anonymous

Search

उच्चिष्ठ और निम्निष्ठ: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 13:24, 1 November 2023

Contents

परिभाषा

खोज

उदाहरण

एक से अधिक चर के कार्य

एक कार्यात्मक की उच्चिष्ठ या निम्निष्ठ

समुच्चय के संबंध में

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

उच्चिष्ठ और निम्निष्ठ: Difference between revisions

Latest revision as of 13:24, 1 November 2023

परिभाषा

खोज

उदाहरण

एक से अधिक चर के कार्य

एक कार्यात्मक की उच्चिष्ठ या निम्निष्ठ

समुच्चय के संबंध में

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories