डेल्टा विभव: Difference between revisions
No edit summary |
m (9 revisions imported from alpha:डेल्टा_विभव) |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Model of an energy potential in quantum mechanics}} | {{Short description|Model of an energy potential in quantum mechanics}} | ||
{{quantum mechanics}} | {{quantum mechanics}} | ||
[[क्वांटम यांत्रिकी]] में '''डेल्टा | [[क्वांटम यांत्रिकी]] में '''डेल्टा विभव''' एक संभावित तरह से गणितीय रूप से [[डिराक डेल्टा फ़ंक्शन|डिराक डेल्टा फलन]] द्वारा वर्णित है - सामान्यीकृत फलन गुणात्मक रूप से, यह ऐसी विभव से मेल खाता है जो प्रत्येक समष्टि शून्य है, जहां यह अनंत मान लेता है। इसका उपयोग उन स्थितियों का अनुकरण करने के लिए किया जा सकता है जहां कण अंतरिक्ष के दो क्षेत्रों में दो क्षेत्रों के मध्य बाधा के साथ घूमने के लिए स्वतंत्र है। उदाहरण के लिए, इलेक्ट्रॉन संवाहक पदार्थ में लगभग स्वतंत्र रूप से घूम सकता है, किन्तु यदि दो संवाहक सतहों को साथ निकट रखा जाता है, तो उनके मध्य का इंटरफ़ेस इलेक्ट्रॉन के लिए बाधा के रूप में कार्य करता है जिसे डेल्टा विभव द्वारा अनुमानित किया जा सकता है। | ||
डेल्टा विभव परिमित क्षमता वाले विभव का [[सीमित मामला (गणित)|सीमित स्थिति (गणित)]] है, जो विभव की चौड़ाई कम करने और | इस प्रकार डेल्टा विभव परिमित क्षमता वाले विभव का [[सीमित मामला (गणित)|सीमित स्थिति (गणित)]] है, जो विभव की चौड़ाई कम करने और विभव बढ़ाने के समय विभव की चौड़ाई और विभव स्थिरांक के उत्पाद को बनाए रखने पर प्राप्त होता है। | ||
यह आलेख, सरलता के लिए, केवल एक-आयामी | यह आलेख, सरलता के लिए, केवल एक-आयामी विभव पर ही विचार करता है, किन्तु विश्लेषण को और अधिक आयामों तक विस्तारित किया जा सकता है। | ||
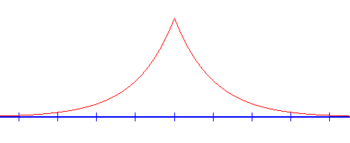
== एकल डेल्टा | == एकल डेल्टा विभव == | ||
[[Image:Deltawell.png|thumb|right]]तरंग फलन के लिए समय-स्वतंत्र श्रोडिंगर समीकरण {{math|''ψ''(''x'')}} अदिश विभव में आयाम में कण का {{math|''V''(''x'')}} है | [[Image:Deltawell.png|thumb|right]]इस प्रकार तरंग फलन के लिए समय-स्वतंत्र श्रोडिंगर समीकरण {{math|''ψ''(''x'')}} अदिश विभव में आयाम में कण का {{math|''V''(''x'')}} है | ||
<math display="block">-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} + V(x) \psi(x) = E \psi(x),</math> | <math display="block">-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} + V(x) \psi(x) = E \psi(x),</math> | ||
जहाँ {{mvar|ħ}} घटा हुआ [[प्लैंक स्थिरांक]] है, और {{mvar|E}} कण की [[ऊर्जा]] है. | जहाँ {{mvar|ħ}} घटा हुआ [[प्लैंक स्थिरांक]] है, और {{mvar|E}} कण की [[ऊर्जा]] है. | ||
डेल्टा | डेल्टा विभव ही विभव है | ||
<math display="block">V(x) = \lambda \delta(x),</math> | <math display="block">V(x) = \lambda \delta(x),</math> | ||
जहाँ {{math|''δ''(''x'')}} डिराक डेल्टा फलन है। | जहाँ {{math|''δ''(''x'')}} डिराक डेल्टा फलन है। | ||
| Line 20: | Line 20: | ||
=== श्रोडिंगर समीकरण को हल करना <ref>{{Cite web|title=क्वांटम यांत्रिकी - डेल्टा क्षमता के साथ तरंग फ़ंक्शन| url=https://physics.stackexchange.com/questions/92240/wave-function-with-a-delta-potential| access-date=2021-03-29| website=Physics Stack Exchange}}</ref> === | === श्रोडिंगर समीकरण को हल करना <ref>{{Cite web|title=क्वांटम यांत्रिकी - डेल्टा क्षमता के साथ तरंग फ़ंक्शन| url=https://physics.stackexchange.com/questions/92240/wave-function-with-a-delta-potential| access-date=2021-03-29| website=Physics Stack Exchange}}</ref> === | ||
विभव अंतरिक्ष को दो भागों ({{math|''x'' < 0}} और {{math|''x'' > 0}}) में विभाजित करता है। इनमें से प्रत्येक भाग में विभव शून्य है, और श्रोडिंगर समीकरण कम हो जाता है | इस प्रकार विभव अंतरिक्ष को दो भागों ({{math|''x'' < 0}} और {{math|''x'' > 0}}) में विभाजित करता है। इनमें से प्रत्येक भाग में विभव शून्य है, और श्रोडिंगर समीकरण कम हो जाता है | ||
<math display="block">\frac{d^2\psi}{dx^2} = -\frac{2mE}{\hbar^2} \psi;</math> यह स्थिर गुणांक वाला एक रैखिक अवकल समीकरण है, जिसके समाधान {{math|''e<sup>ikx</sup>''}} और {{math|''e''<sup>−''ikx''</sup>}} के रैखिक संयोजन हैं, जहां तरंग संख्या {{mvar|k}} ऊर्जा से संबंधित है | <math display="block">\frac{d^2\psi}{dx^2} = -\frac{2mE}{\hbar^2} \psi;</math> यह स्थिर गुणांक वाला एक रैखिक अवकल समीकरण है, जिसके समाधान {{math|''e<sup>ikx</sup>''}} और {{math|''e''<sup>−''ikx''</sup>}} के रैखिक संयोजन हैं, जहां तरंग संख्या {{mvar|k}} ऊर्जा से संबंधित है | ||
<math display="block">k = \frac{\sqrt{2mE}}{\hbar}.</math> सामान्यतः, मूल में डेल्टा | <math display="block">k = \frac{\sqrt{2mE}}{\hbar}.</math> सामान्यतः, मूल में डेल्टा विभव की उपस्थिति के कारण, समाधान के गुणांक दोनों अर्ध-समष्टिों में समान होने की आवश्यकता नहीं है: | ||
<math display="block">\psi(x) = \begin{cases} | <math display="block">\psi(x) = \begin{cases} | ||
\psi_\text{L}(x) = A_\text{r} e^{ikx} + A_\text{l} e^{-ikx}, & \text{ if } x < 0, \\ | \psi_\text{L}(x) = A_\text{r} e^{ikx} + A_\text{l} e^{-ikx}, & \text{ if } x < 0, \\ | ||
| Line 29: | Line 29: | ||
जहां, धनात्मक ऊर्जाओं के स्थिति में (वास्तविक) {{mvar|k}}), {{math|''e<sup>ikx</sup>''}} दाईं ओर यात्रा करने वाली और {{math|''e''<sup>−''ikx''</sup>}} बाईं ओर यात्रा करने वाला प्रत्येक का प्रतिनिधित्व करता है। | जहां, धनात्मक ऊर्जाओं के स्थिति में (वास्तविक) {{mvar|k}}), {{math|''e<sup>ikx</sup>''}} दाईं ओर यात्रा करने वाली और {{math|''e''<sup>−''ikx''</sup>}} बाईं ओर यात्रा करने वाला प्रत्येक का प्रतिनिधित्व करता है। | ||
गुणांकों के मध्य संबंध यह स्थापित करके प्राप्त किया जाता है कि मूल बिंदु पर तरंग फलन निरंतर होते है: | इस प्रकार गुणांकों के मध्य संबंध यह स्थापित करके प्राप्त किया जाता है कि मूल बिंदु पर तरंग फलन निरंतर होते है: | ||
<math display="block">\psi(0) = \psi_L(0) = \psi_R(0) = A_r + A_l = B_r + B_l,</math> | <math display="block">\psi(0) = \psi_L(0) = \psi_R(0) = A_r + A_l = B_r + B_l,</math> | ||
तरंग फलन के व्युत्पन्न का अध्ययन करके दूसरा संबंध पाया जा सकता है। सामान्यतः, हम मूल पर भिन्नता भी प्रयुक्त कर सकते हैं, किन्तु डेल्टा | इस प्रकार तरंग फलन के व्युत्पन्न का अध्ययन करके दूसरा संबंध पाया जा सकता है। सामान्यतः, हम मूल पर भिन्नता भी प्रयुक्त कर सकते हैं, किन्तु डेल्टा विभव के कारण यह संभव नहीं है। चूंकि, यदि हम श्रोडिंगर समीकरण {{math|1=''x'' = 0}} के निकट {{closed-closed|−''ε'', +''ε''}} अंतराल पर एकीकृत करते हैं , : | ||
<math display="block">-\frac{\hbar^2}{2m} \int_{-\varepsilon}^{+\varepsilon} \psi''(x) \,dx + \int_{-\varepsilon}^{+\varepsilon} V(x)\psi(x) \,dx = E \int_{-\varepsilon}^{+\varepsilon} \psi(x) \,dx.</math> | <math display="block">-\frac{\hbar^2}{2m} \int_{-\varepsilon}^{+\varepsilon} \psi''(x) \,dx + \int_{-\varepsilon}^{+\varepsilon} V(x)\psi(x) \,dx = E \int_{-\varepsilon}^{+\varepsilon} \psi(x) \,dx.</math> | ||
जैसी सीमा में {{math|''ε'' → 0}} की सीमा में इस समीकरण का दाहिना पक्ष लुप्त हो जाता है बायां पक्ष बन जाता है | जैसी सीमा में {{math|''ε'' → 0}} की सीमा में इस समीकरण का दाहिना पक्ष लुप्त हो जाता है बायां पक्ष बन जाता है | ||
| Line 45: | Line 45: | ||
=== बाउंड अवस्था (E < 0) === | === बाउंड अवस्था (E < 0) === | ||
[[File:DeltaF-WaveSolution 2.png|right|thumb|350px|डेल्टा फलन | [[File:DeltaF-WaveSolution 2.png|right|thumb|350px|डेल्टा फलन विभव के लिए बाध्य स्थिति तरंग फलन समाधान का आरेख प्रत्येक समष्टि निरंतर है, किन्तु इसके व्युत्पन्न को परिभाषित नहीं किया गया है {{math|1=''x'' = 0}}.]]किसी भी एक आयामी आकर्षक विभव में एक बाउंड अवस्था होगी। इसकी ऊर्जा ज्ञात करने के लिए, ध्यान दें कि {{math|''E'' < 0}} के लिए, {{math|1=''k'' = ''i''{{radic|2''m''{{!}}''E''{{!}}}}/''ħ'' = ''iκ''}} काल्पनिक है, और तरंग फलन जो उपरोक्त गणना में धनात्मक ऊर्जा के लिए दोलन कर रहे थे, अब x के कार्यों में तेजी से वृद्धि या कमी हो रही है। (ऊपर देखें)। यह आवश्यक है कि तरंग फलन अनंत पर विचलन न करें, {{math|1=''A''<sub>r</sub> = ''B''<sub>l</sub> = 0}} के अर्ध शब्द समाप्त हो जाते हैं तरंग फलन तब होता है | ||
<math display="block">\psi(x) = \begin{cases} | <math display="block">\psi(x) = \begin{cases} | ||
\psi_\text{L}(x) = A_\text{l} e^{\kappa x}, & \text{ if } x \le 0, \\ | \psi_\text{L}(x) = A_\text{l} e^{\kappa x}, & \text{ if } x \le 0, \\ | ||
\psi_\text{R}(x) = B_\text{r} e^{-\kappa x}, & \text{ if } x \ge 0. | \psi_\text{R}(x) = B_\text{r} e^{-\kappa x}, & \text{ if } x \ge 0. | ||
\end{cases}</math> | \end{cases}</math> | ||
सीमा नियमो और सामान्यीकरण स्थितियों से, यह इस प्रकार है | इस प्रकार सीमा नियमो और सामान्यीकरण स्थितियों से, यह इस प्रकार है | ||
<math display="block">\begin{cases} | <math display="block">\begin{cases} | ||
A_\text{l} = B_\text{r} = \sqrt{\kappa},\\ | A_\text{l} = B_\text{r} = \sqrt{\kappa},\\ | ||
| Line 62: | Line 62: | ||
=== प्रकीर्णन (''E'' > 0) === | === प्रकीर्णन (''E'' > 0) === | ||
[[Image:Deltapotwell.svg|right|thumb|350px|डेल्टा | [[Image:Deltapotwell.svg|right|thumb|350px|डेल्टा विभव के संचरण ({{mvar|t}}) और प्रतिबिंब ({{mvar|r}}) की संभावना। शक्ति {{math|''E'' > 0}} की इकाइयों में है <math>\frac{m\lambda^2}{2\hbar^2}</math>. धराशायी: मौलिक परिणाम. ठोस रेखा: क्वांटम यांत्रिकी।]]धनात्मक ऊर्जाओं के लिए, कण अर्ध-अंतरिक्ष {{math|''x'' < 0}} या {{math|''x'' > 0}} में स्थानांतरित होने के लिए स्वतंत्र है। यह डेल्टा-फलन विभव पर विस्तृत हुआ हो सकता है। | ||
क्वांटम स्थिति का अध्ययन निम्नलिखित स्थिति में किया जा सकता है: बाईं ओर से बाधा पर एक कण घटना {{math|(''A''<sub>r</sub>)}} यह प्रतिबिंबित ({{math|(''A''<sub>l</sub>)}}) या संचरित ({{math|(''B''<sub>r</sub>)}}) हो सकता है। बाईं ओर से आपतन के लिए परावर्तन और संचरण के आयाम ज्ञात करने के लिए, हम उपरोक्त समीकरण {{math|1=''A''<sub>r</sub> = 1}} (आने वाले कण), {{math|1=''A''<sub>l</sub> = ''r''}} (प्रतिबिंब), {{math|1=''B''<sub>l</sub> = 0}} (दाहिनी ओर से कोई आने वाला कण नहीं) और {{math|1=''B''<sub>r</sub> = ''t''}} रखते हैं। (ट्रांसमिशन), और {{mvar|r}} और {{mvar|t}} के लिए हल करें, संभवतः हमारे निकट {{mvar|t}} में कोई समीकरण न हो परिणाम है | इस प्रकार क्वांटम स्थिति का अध्ययन निम्नलिखित स्थिति में किया जा सकता है: बाईं ओर से बाधा पर एक कण घटना {{math|(''A''<sub>r</sub>)}} यह प्रतिबिंबित ({{math|(''A''<sub>l</sub>)}}) या संचरित ({{math|(''B''<sub>r</sub>)}}) हो सकता है। बाईं ओर से आपतन के लिए परावर्तन और संचरण के आयाम ज्ञात करने के लिए, हम उपरोक्त समीकरण {{math|1=''A''<sub>r</sub> = 1}} (आने वाले कण), {{math|1=''A''<sub>l</sub> = ''r''}} (प्रतिबिंब), {{math|1=''B''<sub>l</sub> = 0}} (दाहिनी ओर से कोई आने वाला कण नहीं) और {{math|1=''B''<sub>r</sub> = ''t''}} रखते हैं। (ट्रांसमिशन), और {{mvar|r}} और {{mvar|t}} के लिए हल करें, संभवतः हमारे निकट {{mvar|t}} में कोई समीकरण न हो परिणाम है | ||
<math display="block">t = \cfrac{1}{1 - \cfrac{m\lambda}{i\hbar^2k}}, \quad r = \cfrac{1}{\cfrac{i\hbar^2 k}{m\lambda} - 1}.</math> | <math display="block">t = \cfrac{1}{1 - \cfrac{m\lambda}{i\hbar^2k}}, \quad r = \cfrac{1}{\cfrac{i\hbar^2 k}{m\lambda} - 1}. </math> | ||
मॉडल की दर्पण [[समरूपता]] के कारण, दाईं ओर से आपतन के आयाम बाईं ओर से समान हैं। परिणाम यह है कि गैर-शून्य संभावना है | इस प्रकार मॉडल की दर्पण [[समरूपता]] के कारण, दाईं ओर से आपतन के आयाम बाईं ओर से समान हैं। परिणाम यह है कि गैर-शून्य संभावना है | ||
<math display="block">R = |r|^2 = \cfrac{1}{1 + \cfrac{\hbar^4 k^2}{m^2\lambda^2}} = \cfrac{1}{1 + \cfrac{2\hbar^2 E}{m \lambda^2}}</math> | <math display="block">R = |r|^2 = \cfrac{1}{1 + \cfrac{\hbar^4 k^2}{m^2\lambda^2}} = \cfrac{1}{1 + \cfrac{2\hbar^2 E}{m \lambda^2}}</math> | ||
कण को प्रतिबिंबित करने के लिए. यह {{mvar|λ}} के चिह्न पर निर्भर नहीं करता है, अर्थात एक अवरोध में कण को विभव के रूप में प्रतिबिंबित करने की समान संभावना होती है। यह मौलिक यांत्रिकी से एक महत्वपूर्ण अंतर है जहां बाधा के लिए प्रतिबिंब संभावना 1 होगी (कण सामान्यतः विपरीत उछलता है) और विभव के लिए 0 (कण बिना किसी बाधा के विभव से निकलता है)। | कण को प्रतिबिंबित करने के लिए. यह {{mvar|λ}} के चिह्न पर निर्भर नहीं करता है, अर्थात एक अवरोध में कण को विभव के रूप में प्रतिबिंबित करने की समान संभावना होती है। यह मौलिक यांत्रिकी से एक महत्वपूर्ण अंतर है जहां बाधा के लिए प्रतिबिंब संभावना 1 होगी (कण सामान्यतः विपरीत उछलता है) और विभव के लिए 0 (कण बिना किसी बाधा के विभव से निकलता है)। | ||
| Line 76: | Line 76: | ||
ऊपर प्रस्तुत गणना पहली बार में अवास्तविक और संभवतः ही उपयोगी लग सकती है। चूंकि, यह विभिन्न वास्तविक जीवन प्रणालियों के लिए उपयुक्त मॉडल सिद्ध हुआ है। | ऊपर प्रस्तुत गणना पहली बार में अवास्तविक और संभवतः ही उपयोगी लग सकती है। चूंकि, यह विभिन्न वास्तविक जीवन प्रणालियों के लिए उपयुक्त मॉडल सिद्ध हुआ है। | ||
ऐसा उदाहरण दो विद्युत चालकता पदार्थो के मध्य इंटरफेस से संबंधित है। अधिकांश पदार्थो में, इलेक्ट्रॉनों की गति अर्ध-मुक्त होती है और इसे प्रभावी द्रव्यमान (ठोस-अवस्था भौतिकी) के साथ उपरोक्त हैमिल्टनियन में गतिज शब्द {{mvar|m}} द्वारा वर्णित किया जा सकता है। अधिकांशतः, ऐसी पदार्थो की सतहें ऑक्साइड परतों से आवरण होती हैं या अन्य कारणों से आदर्श नहीं होती हैं। इस पतली, गैर-संवाहक परत को ऊपर बताए अनुसार समष्टि डेल्टा-फलन | ऐसा उदाहरण दो विद्युत चालकता पदार्थो के मध्य इंटरफेस से संबंधित है। अधिकांश पदार्थो में, इलेक्ट्रॉनों की गति अर्ध-मुक्त होती है और इसे प्रभावी द्रव्यमान (ठोस-अवस्था भौतिकी) के साथ उपरोक्त हैमिल्टनियन में गतिज शब्द {{mvar|m}} द्वारा वर्णित किया जा सकता है। अधिकांशतः, ऐसी पदार्थो की सतहें ऑक्साइड परतों से आवरण होती हैं या अन्य कारणों से आदर्श नहीं होती हैं। इस पतली, गैर-संवाहक परत को ऊपर बताए अनुसार समष्टि डेल्टा-फलन विभव द्वारा मॉडल किया जा सकता है। पुनः इलेक्ट्रॉन पदार्थ से दूसरे पदार्थ तक सुरंग बना सकते हैं, जिससे धारा उत्पन्न होता है। | ||
[[स्कैनिंग टनलिंग माइक्रोस्कोप]] (एसटीएम) का संचालन इस टनलिंग प्रभाव पर निर्भर करता है। उस स्थिति में, बाधा एसटीएम की नोक और अंतर्निहित वस्तु के मध्य वायु के कारण होती है। अवरोध की शक्ति भिन्नता से संबंधित है, दोनों जितना अधिक दूर होंगे, उतना ही सशक्त होगा। इस स्थिति के अधिक सामान्य मॉडल के लिए, [[परिमित संभावित अवरोध (क्यूएम)|परिमित विभव अवरोध (क्यूएम)]] देखें। डेल्टा फलन विभव बाधा बहुत उच्च और संकीर्ण बाधाओं के लिए वहां माने जाने वाले मॉडल का सीमित स्थिति है। | इस प्रकार [[स्कैनिंग टनलिंग माइक्रोस्कोप]] (एसटीएम) का संचालन इस टनलिंग प्रभाव पर निर्भर करता है। उस स्थिति में, बाधा एसटीएम की नोक और अंतर्निहित वस्तु के मध्य वायु के कारण होती है। अवरोध की शक्ति भिन्नता से संबंधित है, दोनों जितना अधिक दूर होंगे, उतना ही सशक्त होगा। इस स्थिति के अधिक सामान्य मॉडल के लिए, [[परिमित संभावित अवरोध (क्यूएम)|परिमित विभव अवरोध (क्यूएम)]] देखें। डेल्टा फलन विभव बाधा बहुत उच्च और संकीर्ण बाधाओं के लिए वहां माने जाने वाले मॉडल का सीमित स्थिति है। | ||
उपरोक्त मॉडल एक-आयामी है जबकि हमारे निकट का समष्टि त्रि-आयामी है। तो, वास्तव में, किसी को श्रोडिंगर समीकरण को तीन आयामों में हल करना चाहिए। दूसरी ओर, विभिन्न प्रणालियाँ केवल समन्वय दिशा में परिवर्तित होती हैं और दूसरों के साथ अनुवादात्मक रूप से अपरिवर्तनीय होती हैं। श्रोडिंगर समीकरण को तब इस प्रकार के तरंग फलन के लिए एन्सैट्ज़ द्वारा यहां विचार किए गए स्थिति में कम किया जा सकता है। | उपरोक्त मॉडल एक-आयामी है जबकि हमारे निकट का समष्टि त्रि-आयामी है। तो, वास्तव में, किसी को श्रोडिंगर समीकरण को तीन आयामों में हल करना चाहिए। दूसरी ओर, विभिन्न प्रणालियाँ केवल समन्वय दिशा में परिवर्तित होती हैं और दूसरों के साथ अनुवादात्मक रूप से अपरिवर्तनीय होती हैं। श्रोडिंगर समीकरण को तब इस प्रकार के तरंग फलन के लिए एन्सैट्ज़ द्वारा यहां विचार किए गए स्थिति में कम किया जा सकता है। | ||
| Line 86: | Line 86: | ||
वैकल्पिक रूप से, कुछ डोमेन डी की सतह पर उपस्थित डेल्टा फलन को सामान्य बनाना संभव है (संकेतक का लाप्लासियन देखें)।<ref name="Lange 2012">{{citation|last=Lange|first=Rutger-Jan|year=2012|title=Potential theory, path integrals and the Laplacian of the indicator|journal=Journal of High Energy Physics|volume=2012 |pages=1–49 | issue=11 |bibcode=2012JHEP...11..032L |doi=10.1007/JHEP11(2012)032|arxiv = 1302.0864 |s2cid=56188533 }}</ref> | वैकल्पिक रूप से, कुछ डोमेन डी की सतह पर उपस्थित डेल्टा फलन को सामान्य बनाना संभव है (संकेतक का लाप्लासियन देखें)।<ref name="Lange 2012">{{citation|last=Lange|first=Rutger-Jan|year=2012|title=Potential theory, path integrals and the Laplacian of the indicator|journal=Journal of High Energy Physics|volume=2012 |pages=1–49 | issue=11 |bibcode=2012JHEP...11..032L |doi=10.1007/JHEP11(2012)032|arxiv = 1302.0864 |s2cid=56188533 }}</ref> | ||
डेल्टा फलन मॉडल वास्तव में डुडले आर. हर्शबैक के समूह द्वारा विकसित आयामी स्केलिंग विधि के अनुसार [[हाइड्रोजन परमाणु]] का आयामी संस्करण है।<ref>[[Dudley R. Herschbach|D.R. Herschbach]], J.S. Avery, and O. Goscinski (eds.), ''Dimensional Scaling in Chemical Physics'', Springer, (1992). [https://www.amazon.com/Dimensional-Scaling-Chemical-Physics-Herschbach/dp/0792320360]</ref> डेल्टा फलन मॉडल डबल-परिमित डिराक डेल्टा फलन मॉडल के साथ विशेष रूप से उपयोगी हो जाता है जो [[हाइड्रोजन अणु आयन]] के एक-आयामी संस्करण का प्रतिनिधित्व करता है, जैसा कि निम्नलिखित अनुभाग में दिखाया गया है। | इस प्रकार डेल्टा फलन मॉडल वास्तव में डुडले आर. हर्शबैक के समूह द्वारा विकसित आयामी स्केलिंग विधि के अनुसार [[हाइड्रोजन परमाणु]] का आयामी संस्करण है।<ref>[[Dudley R. Herschbach|D.R. Herschbach]], J.S. Avery, and O. Goscinski (eds.), ''Dimensional Scaling in Chemical Physics'', Springer, (1992). [https://www.amazon.com/Dimensional-Scaling-Chemical-Physics-Herschbach/dp/0792320360]</ref> डेल्टा फलन मॉडल डबल-परिमित डिराक डेल्टा फलन मॉडल के साथ विशेष रूप से उपयोगी हो जाता है जो [[हाइड्रोजन अणु आयन]] के एक-आयामी संस्करण का प्रतिनिधित्व करता है, जैसा कि निम्नलिखित अनुभाग में दिखाया गया है। | ||
== डबल डेल्टा क्षमता == | == डबल डेल्टा क्षमता == | ||
| Line 111: | Line 111: | ||
जिसके दो समाधान <math>d = d_{\pm}</math> हैं समान आवेशों के स्थिति में (सममित होमोन्यूक्लियर केस), {{math|1=''λ'' = 1}}, और प्सयूडो-द्विघात कम हो जाता है | जिसके दो समाधान <math>d = d_{\pm}</math> हैं समान आवेशों के स्थिति में (सममित होमोन्यूक्लियर केस), {{math|1=''λ'' = 1}}, और प्सयूडो-द्विघात कम हो जाता है | ||
<math display="block">d_\pm = q \left[1 \pm e^{-d_\pm R}\right].</math> | <math display="block">d_\pm = q \left[1 \pm e^{-d_\pm R}\right].</math> | ||
+ स्थिति मध्यबिंदु के बारे में सममित तरंग फलन से मेल खाता है (आरेख में लाल रंग में दिखाया गया है), जहां {{math|1=''A'' = ''B''}}, और आणविक पद चिन्ह कहलाता है। तदनुसार, - स्थिति तरंग फलन है जो मध्यबिंदु के बारे में विरोधी-सममित है, जहां {{math|1=''A'' = −''B''}}, और इसे अनगेरेड कहा जाता है (आरेख में हरे रंग में दिखाया गया है)। वह त्रि-आयामी की दो निम्नतम असतत ऊर्जा अवस्थाओं के अनुमान का प्रतिनिधित्व करते हैं इस प्रकार <chem>H2^+</chem> और इसके विश्लेषण में उपयोगी हैं। सममित आवेशों के स्थिति के लिए ऊर्जा इगेनवलुए के लिए विश्लेषणात्मक समाधान दिए गए हैं<ref>T. C. Scott, J. F. Babb, [[Alexander Dalgarno|A. Dalgarno]] and John D. Morgan III, [http://adsabs.harvard.edu/abs/1993JChPh..99.2841S "The Calculation of Exchange Forces: General Results and Specific Models"], [[Journal of Chemical Physics|J. Chem. Phys.]], 99, pp. 2841–2854, (1993).</ref> | इस प्रकार + स्थिति मध्यबिंदु के बारे में सममित तरंग फलन से मेल खाता है (आरेख में लाल रंग में दिखाया गया है), जहां {{math|1=''A'' = ''B''}}, और आणविक पद चिन्ह कहलाता है। तदनुसार, - स्थिति तरंग फलन है जो मध्यबिंदु के बारे में विरोधी-सममित है, जहां {{math|1=''A'' = −''B''}}, और इसे अनगेरेड कहा जाता है (आरेख में हरे रंग में दिखाया गया है)। इस प्रकार वह त्रि-आयामी की दो निम्नतम असतत ऊर्जा अवस्थाओं के अनुमान का प्रतिनिधित्व करते हैं इस प्रकार <chem>H2^+</chem> और इसके विश्लेषण में उपयोगी हैं। सममित आवेशों के स्थिति के लिए ऊर्जा इगेनवलुए के लिए विश्लेषणात्मक समाधान दिए गए हैं<ref>T. C. Scott, J. F. Babb, [[Alexander Dalgarno|A. Dalgarno]] and John D. Morgan III, [http://adsabs.harvard.edu/abs/1993JChPh..99.2841S "The Calculation of Exchange Forces: General Results and Specific Models"], [[Journal of Chemical Physics|J. Chem. Phys.]], 99, pp. 2841–2854, (1993).</ref> | ||
<math display="block">d_\pm = q + W(\pm q R e^{-q R}) / R,</math> | <math display="block">d_\pm = q + W(\pm q R e^{-q R}) / R,</math> | ||
जहां W मानक लैम्बर्ट W फलन है। ध्यान दें कि सबसे कम ऊर्जा सममित समाधान <math>d_+</math> से | जहां W मानक लैम्बर्ट W फलन है। ध्यान दें कि सबसे कम ऊर्जा सममित समाधान <math>d_+</math> से सम्बंधित है इस प्रकार आवेशों के स्थिति में, और उस स्थिति के लिए त्रि-आयामी आणविक समस्या, समाधान लैम्बर्ट डब्ल्यू फलन के सामान्यीकरण द्वारा दिए जाते हैं (देखें) {{section link|लैम्बर्ट डब्ल्यू फ़ंक्शन|सामान्यीकरण}}). | ||
सबसे रोचक स्थितियों में से एक तब होता है जब qR ≤ 1 होता है, जिसके परिणामस्वरूप <math>d_- = 0</math> होता है, इस प्रकार, किसी के निकट {{math|1=''E'' = 0}} के साथ एक गैर-सामान्य बाध्य स्थिति समाधान होता है। इन विशिष्ट मापदंडों के लिए, विभिन्न रोचक गुण हैं जो घटित होते हैं, उनमें से एक असामान्य प्रभाव यह है कि संचरण गुणांक शून्य ऊर्जा पर एकता है।<ref>{{cite journal | last1=van Dijk | first1=W. | last2=Kiers | first2=K. A. | title=Time delay in simple one‐dimensional systems | journal=American Journal of Physics | publisher=American Association of Physics Teachers (AAPT) | volume=60 | issue=6 | year=1992 | issn=0002-9505 | doi=10.1119/1.16866 | pages=520–527| bibcode=1992AmJPh..60..520V }}</ref> | सबसे रोचक स्थितियों में से एक तब होता है जब qR ≤ 1 होता है, जिसके परिणामस्वरूप <math>d_- = 0</math> होता है, इस प्रकार, किसी के निकट {{math|1=''E'' = 0}} के साथ एक गैर-सामान्य बाध्य स्थिति समाधान होता है। इन विशिष्ट मापदंडों के लिए, विभिन्न रोचक गुण हैं जो घटित होते हैं, उनमें से एक असामान्य प्रभाव यह है कि संचरण गुणांक शून्य ऊर्जा पर एकता है।<ref>{{cite journal | last1=van Dijk | first1=W. | last2=Kiers | first2=K. A. | title=Time delay in simple one‐dimensional systems | journal=American Journal of Physics | publisher=American Association of Physics Teachers (AAPT) | volume=60 | issue=6 | year=1992 | issn=0002-9505 | doi=10.1119/1.16866 | pages=520–527| bibcode=1992AmJPh..60..520V }}</ref> | ||
| Line 146: | Line 146: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 17/11/2023]] | [[Category:Created On 17/11/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 09:30, 1 December 2023
| के बारे में लेखों की एक श्रृंखला का हिस्सा |
| क्वांटम यांत्रिकी |
|---|
क्वांटम यांत्रिकी में डेल्टा विभव एक संभावित तरह से गणितीय रूप से डिराक डेल्टा फलन द्वारा वर्णित है - सामान्यीकृत फलन गुणात्मक रूप से, यह ऐसी विभव से मेल खाता है जो प्रत्येक समष्टि शून्य है, जहां यह अनंत मान लेता है। इसका उपयोग उन स्थितियों का अनुकरण करने के लिए किया जा सकता है जहां कण अंतरिक्ष के दो क्षेत्रों में दो क्षेत्रों के मध्य बाधा के साथ घूमने के लिए स्वतंत्र है। उदाहरण के लिए, इलेक्ट्रॉन संवाहक पदार्थ में लगभग स्वतंत्र रूप से घूम सकता है, किन्तु यदि दो संवाहक सतहों को साथ निकट रखा जाता है, तो उनके मध्य का इंटरफ़ेस इलेक्ट्रॉन के लिए बाधा के रूप में कार्य करता है जिसे डेल्टा विभव द्वारा अनुमानित किया जा सकता है।
इस प्रकार डेल्टा विभव परिमित क्षमता वाले विभव का सीमित स्थिति (गणित) है, जो विभव की चौड़ाई कम करने और विभव बढ़ाने के समय विभव की चौड़ाई और विभव स्थिरांक के उत्पाद को बनाए रखने पर प्राप्त होता है।
यह आलेख, सरलता के लिए, केवल एक-आयामी विभव पर ही विचार करता है, किन्तु विश्लेषण को और अधिक आयामों तक विस्तारित किया जा सकता है।
एकल डेल्टा विभव
इस प्रकार तरंग फलन के लिए समय-स्वतंत्र श्रोडिंगर समीकरण ψ(x) अदिश विभव में आयाम में कण का V(x) है
डेल्टा विभव ही विभव है
यदि λ ऋणात्मक है तो इसे डेल्टा विभव परिमित कहा जाता है, और यदि λ धनात्मक है तो इसे डेल्टा विभव बाधा कहा जाता है। सरलता के लिए डेल्टा को मूल स्थान पर घटित होने के रूप में परिभाषित किया गया है; डेल्टा फलन के तर्क में परिवर्तन से निम्नलिखित में से कोई भी परिणाम नहीं परिवर्तन है।
श्रोडिंगर समीकरण को हल करना [1]
इस प्रकार विभव अंतरिक्ष को दो भागों (x < 0 और x > 0) में विभाजित करता है। इनमें से प्रत्येक भाग में विभव शून्य है, और श्रोडिंगर समीकरण कम हो जाता है
इस प्रकार गुणांकों के मध्य संबंध यह स्थापित करके प्राप्त किया जाता है कि मूल बिंदु पर तरंग फलन निरंतर होते है:
इस अभिव्यक्ति में ψ की परिभाषा को प्रतिस्थापित करने से परिणाम मिलता है
बाउंड अवस्था (E < 0)
किसी भी एक आयामी आकर्षक विभव में एक बाउंड अवस्था होगी। इसकी ऊर्जा ज्ञात करने के लिए, ध्यान दें कि E < 0 के लिए, k = i√2m|E|/ħ = iκ काल्पनिक है, और तरंग फलन जो उपरोक्त गणना में धनात्मक ऊर्जा के लिए दोलन कर रहे थे, अब x के कार्यों में तेजी से वृद्धि या कमी हो रही है। (ऊपर देखें)। यह आवश्यक है कि तरंग फलन अनंत पर विचलन न करें, Ar = Bl = 0 के अर्ध शब्द समाप्त हो जाते हैं तरंग फलन तब होता है
बाउंड अवस्था की ऊर्जा तब होती है
प्रकीर्णन (E > 0)
धनात्मक ऊर्जाओं के लिए, कण अर्ध-अंतरिक्ष x < 0 या x > 0 में स्थानांतरित होने के लिए स्वतंत्र है। यह डेल्टा-फलन विभव पर विस्तृत हुआ हो सकता है।
इस प्रकार क्वांटम स्थिति का अध्ययन निम्नलिखित स्थिति में किया जा सकता है: बाईं ओर से बाधा पर एक कण घटना (Ar) यह प्रतिबिंबित ((Al)) या संचरित ((Br)) हो सकता है। बाईं ओर से आपतन के लिए परावर्तन और संचरण के आयाम ज्ञात करने के लिए, हम उपरोक्त समीकरण Ar = 1 (आने वाले कण), Al = r (प्रतिबिंब), Bl = 0 (दाहिनी ओर से कोई आने वाला कण नहीं) और Br = t रखते हैं। (ट्रांसमिशन), और r और t के लिए हल करें, संभवतः हमारे निकट t में कोई समीकरण न हो परिणाम है
संचरण की संभावना है
टिप्पणियाँ और अनुप्रयोग
ऊपर प्रस्तुत गणना पहली बार में अवास्तविक और संभवतः ही उपयोगी लग सकती है। चूंकि, यह विभिन्न वास्तविक जीवन प्रणालियों के लिए उपयुक्त मॉडल सिद्ध हुआ है।
ऐसा उदाहरण दो विद्युत चालकता पदार्थो के मध्य इंटरफेस से संबंधित है। अधिकांश पदार्थो में, इलेक्ट्रॉनों की गति अर्ध-मुक्त होती है और इसे प्रभावी द्रव्यमान (ठोस-अवस्था भौतिकी) के साथ उपरोक्त हैमिल्टनियन में गतिज शब्द m द्वारा वर्णित किया जा सकता है। अधिकांशतः, ऐसी पदार्थो की सतहें ऑक्साइड परतों से आवरण होती हैं या अन्य कारणों से आदर्श नहीं होती हैं। इस पतली, गैर-संवाहक परत को ऊपर बताए अनुसार समष्टि डेल्टा-फलन विभव द्वारा मॉडल किया जा सकता है। पुनः इलेक्ट्रॉन पदार्थ से दूसरे पदार्थ तक सुरंग बना सकते हैं, जिससे धारा उत्पन्न होता है।
इस प्रकार स्कैनिंग टनलिंग माइक्रोस्कोप (एसटीएम) का संचालन इस टनलिंग प्रभाव पर निर्भर करता है। उस स्थिति में, बाधा एसटीएम की नोक और अंतर्निहित वस्तु के मध्य वायु के कारण होती है। अवरोध की शक्ति भिन्नता से संबंधित है, दोनों जितना अधिक दूर होंगे, उतना ही सशक्त होगा। इस स्थिति के अधिक सामान्य मॉडल के लिए, परिमित विभव अवरोध (क्यूएम) देखें। डेल्टा फलन विभव बाधा बहुत उच्च और संकीर्ण बाधाओं के लिए वहां माने जाने वाले मॉडल का सीमित स्थिति है।
उपरोक्त मॉडल एक-आयामी है जबकि हमारे निकट का समष्टि त्रि-आयामी है। तो, वास्तव में, किसी को श्रोडिंगर समीकरण को तीन आयामों में हल करना चाहिए। दूसरी ओर, विभिन्न प्रणालियाँ केवल समन्वय दिशा में परिवर्तित होती हैं और दूसरों के साथ अनुवादात्मक रूप से अपरिवर्तनीय होती हैं। श्रोडिंगर समीकरण को तब इस प्रकार के तरंग फलन के लिए एन्सैट्ज़ द्वारा यहां विचार किए गए स्थिति में कम किया जा सकता है।
.
वैकल्पिक रूप से, कुछ डोमेन डी की सतह पर उपस्थित डेल्टा फलन को सामान्य बनाना संभव है (संकेतक का लाप्लासियन देखें)।[2]
इस प्रकार डेल्टा फलन मॉडल वास्तव में डुडले आर. हर्शबैक के समूह द्वारा विकसित आयामी स्केलिंग विधि के अनुसार हाइड्रोजन परमाणु का आयामी संस्करण है।[3] डेल्टा फलन मॉडल डबल-परिमित डिराक डेल्टा फलन मॉडल के साथ विशेष रूप से उपयोगी हो जाता है जो हाइड्रोजन अणु आयन के एक-आयामी संस्करण का प्रतिनिधित्व करता है, जैसा कि निम्नलिखित अनुभाग में दिखाया गया है।
डबल डेल्टा क्षमता
डबल-परिमित डिराक डेल्टा फलन संबंधित श्रोडिंगर समीकरण द्वारा डायटोमिक हाइड्रोजन अणु को मॉडल करता है:
सबसे रोचक स्थितियों में से एक तब होता है जब qR ≤ 1 होता है, जिसके परिणामस्वरूप होता है, इस प्रकार, किसी के निकट E = 0 के साथ एक गैर-सामान्य बाध्य स्थिति समाधान होता है। इन विशिष्ट मापदंडों के लिए, विभिन्न रोचक गुण हैं जो घटित होते हैं, उनमें से एक असामान्य प्रभाव यह है कि संचरण गुणांक शून्य ऊर्जा पर एकता है।[5]
यह भी देखें
- मुक्त कण
- डिब्बे में कण
- फाईनिट पोटेंसिअल वेल
- वलय में कण
- वृत्ताकार सममित विभव में कण
- क्वांटम हार्मोनिक ऑसिलेटर
- हाइड्रोजन परमाणु या हाइड्रोजन जैसा परमाणु
- रिंग वेव गाइड
- आयामी जालक में कण (आवधिक क्षमता)
- हाइड्रोजन आणविक आयन
- होल्स्टीन-हेरिंग विधि
- सूचक का लाप्लासियन
- विश्लेषणात्मक समाधानों के साथ क्वांटम-मैकेनिकल प्रणालियों की सूची
संदर्भ
- ↑ "क्वांटम यांत्रिकी - डेल्टा क्षमता के साथ तरंग फ़ंक्शन". Physics Stack Exchange. Retrieved 2021-03-29.
- ↑ Lange, Rutger-Jan (2012), "Potential theory, path integrals and the Laplacian of the indicator", Journal of High Energy Physics, 2012 (11): 1–49, arXiv:1302.0864, Bibcode:2012JHEP...11..032L, doi:10.1007/JHEP11(2012)032, S2CID 56188533
- ↑ D.R. Herschbach, J.S. Avery, and O. Goscinski (eds.), Dimensional Scaling in Chemical Physics, Springer, (1992). [1]
- ↑ T. C. Scott, J. F. Babb, A. Dalgarno and John D. Morgan III, "The Calculation of Exchange Forces: General Results and Specific Models", J. Chem. Phys., 99, pp. 2841–2854, (1993).
- ↑ van Dijk, W.; Kiers, K. A. (1992). "Time delay in simple one‐dimensional systems". American Journal of Physics. American Association of Physics Teachers (AAPT). 60 (6): 520–527. Bibcode:1992AmJPh..60..520V. doi:10.1119/1.16866. ISSN 0002-9505.
- Griffiths, David J. (2005). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. pp. 68–78. ISBN 978-0-13-111892-8.
- For the 3-dimensional case look for the "delta shell potential"; further see K. Gottfried (1966), Quantum Mechanics Volume I: Fundamentals, ch. III, sec. 15.
बाहरी संबंध
 Media related to डेल्टा विभव at Wikimedia Commons
Media related to डेल्टा विभव at Wikimedia Commons