एंडरसन स्थानीयकरण: Difference between revisions
No edit summary |
|||
| Line 9: | Line 9: | ||
मूल एंडरसन टाइट-बाइंडिंग मॉडल में, ''डी''-आयामी जालक Z<sup>d</sup> पर तरंग फलन ''ψ'' का विकास श्रोडिंगर समीकरण द्वारा दिया गया है: | मूल एंडरसन टाइट-बाइंडिंग मॉडल में, ''डी''-आयामी जालक Z<sup>d</sup> पर तरंग फलन ''ψ'' का विकास श्रोडिंगर समीकरण द्वारा दिया गया है: | ||
:<math> i \hbar \frac{d\psi}{dt} = H \psi~, </math> | :<math> i \hbar \frac{d\psi}{dt} = H \psi~, </math> | ||
जहां [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] एच द्वारा दिया गया है<ref name="a58" /> | जहां [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] एच द्वारा दिया गया है<ref name="a58" /> | ||
:<math> H \psi_j = E_j \psi_j + \sum_{k \neq j} V_{jk} \psi_k~, | :<math> H \psi_j = E_j \psi_j + \sum_{k \neq j} V_{jk} \psi_k~, </math> | ||
E<sub>''j''</sub> के साथ यादृच्छिक और स्वतंत्र, और संभावित V(r) अनंत पर r<sup>−3</sup> की तुलना में तेजी से गिर रहा है। उदाहरण के लिए, कोई E<sub>''j''</sub> को [−W, +W] में समान रूप से वितरित कर सकता है, और | E<sub>''j''</sub> के साथ यादृच्छिक और स्वतंत्र, और संभावित V(r) अनंत पर r<sup>−3</sup> की तुलना में तेजी से गिर रहा है। उदाहरण के लिए, कोई E<sub>''j''</sub> को [−W, +W] में समान रूप से वितरित कर सकता है, और | ||
| Line 20: | Line 20: | ||
* यदि d 1 या 2 है और W मनमाना है, या यदि d ≥ 3 और W/ħ पर्याप्त रूप से बड़ा है, तो संभाव्यता वितरण स्थानीयकृत रहता है: | * यदि d 1 या 2 है और W मनमाना है, या यदि d ≥ 3 और W/ħ पर्याप्त रूप से बड़ा है, तो संभाव्यता वितरण स्थानीयकृत रहता है: | ||
::<math> \sum_{n \in \mathbb{Z}^d} |\psi(t,n)|^2 |n| \leq C </math> | ::<math> \sum_{n \in \mathbb{Z}^d} |\psi(t,n)|^2 |n| \leq C </math> | ||
:t में समान रूप से. इस घटना को एंडरसन स्थानीयकरण कहा जाता है। | :t में समान रूप से. इस घटना को एंडरसन स्थानीयकरण कहा जाता है। | ||
| Line 46: | Line 46: | ||
== प्रसार के साथ तुलना == | == प्रसार के साथ तुलना == | ||
इस प्रकार से क्वांटम पूर्वानुमान से असहमत होने के कारण, मानक प्रसार में कोई स्थानीयकरण गुण नहीं होता है। चूंकि, यह पता चला है कि यह अधिकतम एन्ट्रापी के सिद्धांत के सन्निकटन पर आधारित है, जो दर्शाता है कि संभाव्यता वितरण जो ज्ञान की वर्तमान स्थिति का अधिक उचित प्रतिनिधित्व करता है वह अधिक उचित एन्ट्रापी वाला होता है। इस सन्निकटन को [[अधिकतम एन्ट्रापी रैंडम वॉक]] में सुधार किया जाता है, साथ ही असहमति को भी सुधार किया जाता है: यह अपने सशक्त स्थानीयकरण गुणों के साथ पूर्णतः क्वांटम ग्राउंड स्टेट स्थिर संभाव्यता वितरण की ओर ले जाता है।<ref name=prl>[http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.102.160602 Z. Burda, J. Duda, J. M. Luck, and B. Waclaw, ''Localization of the Maximal Entropy Random Walk''], Phys. Rev. Lett., 2009.</ref><ref name=ext>[http://www.fais.uj.edu.pl/documents/41628/d63bc0b7-cb71-4eba-8a5a-d974256fd065 J. Duda, ''Extended Maximal Entropy Random Walk''], PhD Thesis, 2012.</ref> | इस प्रकार से क्वांटम पूर्वानुमान से असहमत होने के कारण, मानक प्रसार में कोई स्थानीयकरण गुण नहीं होता है। चूंकि, यह पता चला है कि यह अधिकतम एन्ट्रापी के सिद्धांत के सन्निकटन पर आधारित है, जो दर्शाता है कि संभाव्यता वितरण जो ज्ञान की वर्तमान स्थिति का अधिक उचित प्रतिनिधित्व करता है वह अधिक उचित एन्ट्रापी वाला होता है। इस सन्निकटन को [[अधिकतम एन्ट्रापी रैंडम वॉक]] में सुधार किया जाता है, साथ ही असहमति को भी सुधार किया जाता है: यह अपने सशक्त स्थानीयकरण गुणों के साथ पूर्णतः क्वांटम ग्राउंड स्टेट स्थिर संभाव्यता वितरण की ओर ले जाता है।<ref name=prl>[http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.102.160602 Z. Burda, J. Duda, J. M. Luck, and B. Waclaw, ''Localization of the Maximal Entropy Random Walk''], Phys. Rev. Lett., 2009.</ref><ref name=ext>[http://www.fais.uj.edu.pl/documents/41628/d63bc0b7-cb71-4eba-8a5a-d974256fd065 J. Duda, ''Extended Maximal Entropy Random Walk''], PhD Thesis, 2012.</ref> | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 95: | Line 94: | ||
*[http://lpmmc.grenoble.cnrs.fr/spip.php?article408 Anderson localization of elastic waves] | *[http://lpmmc.grenoble.cnrs.fr/spip.php?article408 Anderson localization of elastic waves] | ||
*[http://www.opfocus.org/index.php?topic=story&v=1&s=1 Popular scientific article on the first experimental observation of Anderson localization in matter waves] | *[http://www.opfocus.org/index.php?topic=story&v=1&s=1 Popular scientific article on the first experimental observation of Anderson localization in matter waves] | ||
[[Category: मेसोस्कोपिक भौतिकी]] | |||
[[Category: संघनित पदार्थ भौतिकी]] | |||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 18/11/2023]] | [[Category:Created On 18/11/2023]] | ||
Revision as of 12:15, 30 November 2023
संघनित पदार्थ भौतिकी में, एंडरसन स्थानीयकरण (जिसे सशक्त स्थानीयकरण के रूप में भी जाना जाता है)[1] अव्यवस्थित माध्यम में तरंगों के प्रसार की अनुपस्थिति है। इस घटना का नाम अमेरिकी भौतिक विज्ञानी पी. डब्ल्यू. एंडरसन के नाम पर रखा गया है, जिन्होंने सबसे पहले सुझाव दिया था कि एक जालक क्षमता में इलेक्ट्रॉन स्थानीयकरण संभव है, परंतु कि जालक में भौतिक विज्ञान (विकार) में यादृच्छिकता की डिग्री पर्याप्त रूप से बड़ी हो, जैसा कि हो सकता है उदाहरण के लिए अशुद्धियों या क्रिस्टलोग्राफिक दोष वाले अर्धचालक में अनुभव किया जा सकता है।[2]
इस प्रकार से एंडरसन स्थानीयकरण एक सामान्य तरंग घटना है जो की विद्युत चुम्बकीय तरंगों, ध्वनिक तरंगों, क्वांटम तरंगों, स्पिन तरंगों आदि के परिवहन पर प्रयुक्त होती है। इस घटना को अशक्त स्थानीयकरण से अलग किया जाना है, जो एंडरसन स्थानीयकरण का पूर्ववर्ती प्रभाव है (नीचे देखें), और मॉट संक्रमण से, जिसका नाम सर नेविल मॉट के नाम पर रखा गया है, जहां धातु से इन्सुलेशन व्यवहार में संक्रमण विकार के कारण नहीं होता है, किन्तु इलेक्ट्रॉनों के सशक्त पारस्परिक कूलम्ब प्रतिकर्षण के कारण होता है।
परिचय
मूल एंडरसन टाइट-बाइंडिंग मॉडल में, डी-आयामी जालक Zd पर तरंग फलन ψ का विकास श्रोडिंगर समीकरण द्वारा दिया गया है:
जहां हैमिल्टनियन (क्वांटम यांत्रिकी) एच द्वारा दिया गया है[2]
Ej के साथ यादृच्छिक और स्वतंत्र, और संभावित V(r) अनंत पर r−3 की तुलना में तेजी से गिर रहा है। उदाहरण के लिए, कोई Ej को [−W, +W] में समान रूप से वितरित कर सकता है, और
मूल स्थान पर स्थानीयकृत ψ0 से प्रारंभ करके, किसी की रुचि इस तथ्य में है कि संभाव्यता वितरण कितनी तेजी से फैलता है। एंडरसन का विश्लेषण निम्नलिखित दर्शाता है:
- यदि d 1 या 2 है और W मनमाना है, या यदि d ≥ 3 और W/ħ पर्याप्त रूप से बड़ा है, तो संभाव्यता वितरण स्थानीयकृत रहता है:
- t में समान रूप से. इस घटना को एंडरसन स्थानीयकरण कहा जाता है।
- यदि d ≥ 3 और W/ħ छोटा है,
- जहाँ D प्रसार स्थिरांक है।
विश्लेषण
एंडरसन स्थानीयकरण की घटना, विशेष रूप से अशक्त स्थानीयकरण की घटना, बहु-प्रकीर्णन पथों के बीच तरंग हस्तक्षेप में अपनी उत्पत्ति पाती है। सशक्त प्रकीर्णन सीमा में, गंभीर हस्तक्षेप अव्यवस्थित माध्यम के अंदर तरंगों को पूरी तरह से रोक सकता है।
गैर-अंतःक्रियात्मक इलेक्ट्रॉनों के लिए, अब्राहम्स एट अल द्वारा 1979 में अत्यधिक सफल दृष्टिकोण सामने रखा गया था।[3] स्थानीयकरण की यह स्केलिंग परिकल्पना बताती है कि शून्य चुंबकीय क्षेत्र में और स्पिन-ऑर्बिट युग्मन की अनुपस्थिति में तीन आयामों (3 डी) में गैर-अंतःक्रियात्मक इलेक्ट्रॉनों के लिए विकार-प्रेरित धातु-इन्सुलेटर संक्रमण (एमआईटी) उपस्तिथ है। इसके पश्चात बहुत से कार्यों ने विश्लेषणात्मक और संख्यात्मक रूप से इन स्केलिंग तर्कों का समर्थन किया है (ब्रैंडेस एट अल., 2003; आगे की पढ़ाई देखें)। इस प्रकार से 1डी और 2डी में, एक ही परिकल्पना दर्शाती है कि कोई विस्तारित अवस्था नहीं है और इस प्रकार कोई एमआईटी या केवल स्पष्ट एमआईटी नहीं है।[4] चूँकि 2 स्थानीयकरण समस्या का निचला महत्वपूर्ण आयाम है, 2D स्तिथि अर्थ में 3D के समीप है: राज्यों को केवल अशक्त विकार के लिए मामूली रूप से स्थानीयकृत किया जाता है और छोटा स्पिन-ऑर्बिट युग्मन विस्तारित राज्यों के अस्तित्व को जन्म दे सकता है और इस प्रकार एमआईटी. नतीजतन, संभावित-विकार के साथ 2डी प्रणाली की स्थानीयकरण लंबाई अधिक बड़ी हो सकती है जिससे संख्यात्मक दृष्टिकोण में कोई भी सदैव स्थानीयकरण-डेलोकलाइज़ेशन संक्रमण पा सके जब या तो निश्चित विकार के लिए प्रणाली का आकार घट रहा हो या निश्चित प्रणाली आकार के लिए विकार बढ़ रहा हो।
स्थानीयकरण समस्या के अधिकांश संख्यात्मक दृष्टिकोण ऑनसाइट-संभावित विकार के साथ मानक टाइट-बाइंडिंग एंडरसन हैमिल्टनियन (क्वांटम यांत्रिकी) का उपयोग करते हैं। इस प्रकार से स्पष्ट विकर्णीकरण, मल्टीफ्रैक्टल गुणों, स्तर के आँकड़ों और कई अन्य द्वारा प्राप्त भागीदारी संख्याओं के अध्ययन द्वारा इलेक्ट्रॉनिक आइजेनस्टेट्स की विशेषताओं की जांच की जाती है। स्थानांतरण-मैट्रिक्स विधि (टीएमएम) विशेष रूप से उपयोगी है जो स्थानीयकरण लंबाई की सीधी गणना की अनुमति देती है और एक-पैरामीटर स्केलिंग फलन के अस्तित्व के संख्यात्मक प्रमाण द्वारा स्केलिंग परिकल्पना को और अधिक मान्य करती है। किन्तु प्रकाश के एंडरसन स्थानीयकरण को प्रदर्शित करने के लिए मैक्सवेल समीकरणों का प्रत्यक्ष संख्यात्मक समाधान प्रयुक्त किया गया है (कोंटी और फ्रैटालोची, 2008)।
वर्तमान के कार्य से पता चला है कि गैर-इंटरेक्टिंग एंडरसन स्थानीयकृत प्रणाली अशक्त इंटरैक्शन की उपस्थिति में भी कई-निकाय स्थानीयकरण अनेक-निकाय स्थानीयकृत बन सकती है। इस परिणाम को 1D में कठोरता से सिद्ध किया गया है, जबकि विक्षुब्ध करने वाले तर्क दो और तीन आयामों के लिए भी उपस्तिथ हैं।
प्रयोगात्मक साक्ष्य
एंडरसन स्थानीयकरण को विकृत आवधिक क्षमता में देखा जा सकता है जहां प्रकाश का अनुप्रस्थ स्थानीयकरण एक फोटोनिक जालक पर यादृच्छिक उतार-चढ़ाव के कारण होता है। 2डी जालक (श्वार्ट्ज एट अल., 2007) और 1डी जालक (लाहिनी एट अल., 2006) के लिए अनुप्रस्थ स्थानीयकरण की प्रायोगिक प्राप्ति की सूचना दी गई थी। इस प्रकार से प्रकाश के अनुप्रस्थ एंडरसन स्थानीयकरण को ऑप्टिकल फाइबर माध्यम (करबासी एट अल., 2012) और एक जैविक माध्यम (चोई एट अल., 2018) में भी प्रदर्शित किया गया है, और इसका उपयोग फाइबर के माध्यम से छवियों को परिवहन करने के लिए भी किया गया है (करबासी एट अल. ., 2014). इसे 1D अव्यवस्थित ऑप्टिकल क्षमता (बिली एट अल., 2008; रोआटी एट अल., 2008) में बोस-आइंस्टीन कंडेनसेट के स्थानीयकरण द्वारा भी देखा गया है।
इस प्रकार से 3डी में, अवलोकन अधिक दुर्लभ हैं। 3डी अव्यवस्थित माध्यम में लोचदार तरंगों के एंडरसन स्थानीयकरण की सूचना दी गई है (हू एट अल., 2008)। एमआईटी के अवलोकन को परमाणु पदार्थ तरंगों के साथ 3डी मॉडल में रिपोर्ट किया गया है (चाबे एट अल., 2008)। गैर-प्रचारक इलेक्ट्रॉन तरंगों से जुड़े एमआईटी को सेमी-आकार के क्रिस्टल (यिंग एट अल।, 2016) में रिपोर्ट किया गया है। और यादृच्छिक लेजर इस घटना का उपयोग करके काम कर सकते हैं।
किन्तु 3डी में प्रकाश के लिए एंडरसन स्थानीयकरण के अस्तित्व पर वर्षों से विवाद चल रही थी (स्किपेट्रोव एट अल., 2016) और वर्तमान में अनसुलझा है। इस प्रकार से 3डी यादृच्छिक मीडिया में प्रकाश के एंडरसन स्थानीयकरण की रिपोर्ट अवशोषण के प्रतिस्पर्धी/मास्किंग प्रभावों (वाइर्स्मा एट अल., 1997; स्टोर्ज़र एट अल., 2006; शेफ़ोल्ड एट अल., 1999; आगे की पढ़ाई देखें) और/या प्रतिदीप्ति से सम्मिश्र थी। (स्पर्लिंग एट अल., 2016)। वर्तमान के प्रयोग (नाराघी एट अल., 2016; कोबस एट अल., 2023) सैद्धांतिक पूर्वानुमान का समर्थन करते हैं कि प्रकाश की सदिश प्रकृति एंडरसन स्थानीयकरण में संक्रमण को रोकती है (जॉन, 1992; स्किपेट्रोव एट अल., 2019)।
प्रसार के साथ तुलना
इस प्रकार से क्वांटम पूर्वानुमान से असहमत होने के कारण, मानक प्रसार में कोई स्थानीयकरण गुण नहीं होता है। चूंकि, यह पता चला है कि यह अधिकतम एन्ट्रापी के सिद्धांत के सन्निकटन पर आधारित है, जो दर्शाता है कि संभाव्यता वितरण जो ज्ञान की वर्तमान स्थिति का अधिक उचित प्रतिनिधित्व करता है वह अधिक उचित एन्ट्रापी वाला होता है। इस सन्निकटन को अधिकतम एन्ट्रापी रैंडम वॉक में सुधार किया जाता है, साथ ही असहमति को भी सुधार किया जाता है: यह अपने सशक्त स्थानीयकरण गुणों के साथ पूर्णतः क्वांटम ग्राउंड स्टेट स्थिर संभाव्यता वितरण की ओर ले जाता है।[5][6]
यह भी देखें
- ऑब्री-आंद्रे मॉडल
टिप्पणियाँ
- ↑ Teichert, Fabian; Zienert, Andreas; Schuster, Jörg; Schreiber, Michael (2014). "Strong localization in defective carbon nanotubes: a recursive Green's function study". New Journal of Physics. 16 (12): 123026. arXiv:1705.01757. Bibcode:2014NJPh...16l3026T. doi:10.1088/1367-2630/16/12/123026. S2CID 119358293.
- ↑ 2.0 2.1 Anderson, P. W. (1958). "कुछ यादृच्छिक जालकों में प्रसार की अनुपस्थिति". Phys. Rev. 109 (5): 1492–1505. Bibcode:1958PhRv..109.1492A. doi:10.1103/PhysRev.109.1492.
- ↑ Abrahams, E.; Anderson, P.W.; Licciardello, D.C.; Ramakrishnan, T.V. (1979). "Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions". Phys. Rev. Lett. 42 (10): 673–676. Bibcode:1979PhRvL..42..673A. doi:10.1103/PhysRevLett.42.673.
- ↑ Cheremisin, M.V. (March 2017). "The success of Fermi gas model for overall scaling of 2D metal-to-insulator transition data". Solid State Communications (in English). 253: 46–50. arXiv:1603.02326. doi:10.1016/j.ssc.2017.01.027.
- ↑ Z. Burda, J. Duda, J. M. Luck, and B. Waclaw, Localization of the Maximal Entropy Random Walk, Phys. Rev. Lett., 2009.
- ↑ J. Duda, Extended Maximal Entropy Random Walk, PhD Thesis, 2012.
अग्रिम पठन
- Brandes, T. & Kettemann, S. (2003). The Anderson Transition and its Ramifications --- Localisation, Quantum Interference, and Interactions. Lecture Notes in Physics. Berlin: Springer Verlag. ISBN 978-3-642-07398-4.
- Wiersma, Diederik S.; et al. (1997). "Localization of light in a disordered medium". Nature. 390 (6661): 671–673. Bibcode:1997Natur.390..671W. doi:10.1038/37757. S2CID 46723942.
- Störzer, Martin; et al. (2006). "Observation of the critical regime near Anderson localization of light". Phys. Rev. Lett. 96 (6): 063904. arXiv:cond-mat/0511284. Bibcode:2006PhRvL..96f3904S. doi:10.1103/PhysRevLett.96.063904. PMID 16605998. S2CID 12180478.
- Scheffold, Frank; et al. (1999). "Localization or classical diffusion of light?". Nature. 398 (6724): 206–207. Bibcode:1999Natur.398..206S. doi:10.1038/18347. S2CID 4347650.
- Schwartz, T.; et al. (2007). "Transport and Anderson Localization in disordered two-dimensional Photonic Lattices". Nature. 446 (7131): 52–55. Bibcode:2007Natur.446...52S. doi:10.1038/nature05623. PMID 17330037. S2CID 4429992.
- Lahini, Y.; et al. (2008). "Anderson localization and nonlinearity in one dimensional disordered photonic lattices". Physical Review Letters. 100 (1): 013906. arXiv:0704.3788. Bibcode:2008PhRvL.100a3906L. doi:10.1103/PhysRevLett.100.013906. PMID 18232768. S2CID 6376064.
- Karbasi, S.; et al. (2012). "Observation of transverse Anderson localization in an optical fiber". Optics Letters. 37 (12): 2304–6. Bibcode:2012OptL...37.2304K. doi:10.1364/OL.37.002304. PMID 22739889.
- Karbasi, S.; et al. (2014). "Image transport through a disordered optical fibre mediated by transverse Anderson localization". Nature Communications. 5: 3362. arXiv:1307.4160. Bibcode:2014NatCo...5.3362K. doi:10.1038/ncomms4362. PMID 24566557. S2CID 205323503.
- Billy, Juliette; et al. (2008). "Direct observation of Anderson localization of matter waves in a controlled disorder". Nature. 453 (7197): 891–894. arXiv:0804.1621. Bibcode:2008Natur.453..891B. doi:10.1038/nature07000. PMID 18548065. S2CID 4427739.
- Roati, Giacomo; et al. (2008). "Anderson localization of a non-interacting Bose-Einstein condensate". Nature. 453 (7197): 895–898. arXiv:0804.2609. Bibcode:2008Natur.453..895R. doi:10.1038/nature07071. PMID 18548066. S2CID 4388940.
- Ludlam, J. J.; et al. (2005). "Universal features of localized eigenstates in disordered systems". Journal of Physics: Condensed Matter. 17 (30): L321–L327. Bibcode:2005JPCM...17L.321L. doi:10.1088/0953-8984/17/30/L01. S2CID 17243205.
- Conti, C; A. Fratalocchi (2008). "Dynamic light diffusion, three-dimensional Anderson localization and lasing in inverted opals". Nature Physics. 4 (10): 794–798. arXiv:0802.3775. Bibcode:2008NatPh...4..794C. doi:10.1038/nphys1035. S2CID 119115156.
- Hu, Hefei; et al. (2008). "Localization of ultrasound in a three-dimensional elastic network". Nature Physics. 4 (12): 945–948. arXiv:0805.1502. Bibcode:2008NatPh...4..945H. doi:10.1038/nphys1101. S2CID 119097566.
- Chabé, J.; et al. (2008). "Experimental Observation of the Anderson Metal-Insulator Transition with Atomic Matter Waves". Phys. Rev. Lett. 101 (25): 255702. arXiv:0709.4320. Bibcode:2008PhRvL.101y5702C. doi:10.1103/PhysRevLett.101.255702. PMID 19113725. S2CID 773761.
- Ying, Tianping; et al. (2016). "Anderson localization of electrons in single crystals: LixFe7Se8". Science Advances. 2 (2): e1501283. Bibcode:2016SciA....2E1283Y. doi:10.1126/sciadv.1501283. PMC 4788481. PMID 26989781.
- Choi, Seung Ho; et al. (2018). "Anderson light localization in biological nanostructures of native silk". Nature Communications. 9 (1): 452. Bibcode:2018NatCo...9..452C. doi:10.1038/s41467-017-02500-5. PMC 5792459. PMID 29386508.
- Skipetrov, Sergey; et al. (2016). "Red light for Anderson localization". New Journal of Physics. 18 (2): 021001. arXiv:1601.07848. Bibcode:2016NJPh...18b1001S. doi:10.1088/1367-2630/18/2/021001. S2CID 118497908.
बाहरी संबंध
- Fifty years of Anderson localization, Ad Lagendijk, Bart van Tiggelen, and Diederik S. Wiersma, Physics Today 62(8), 24 (2009).
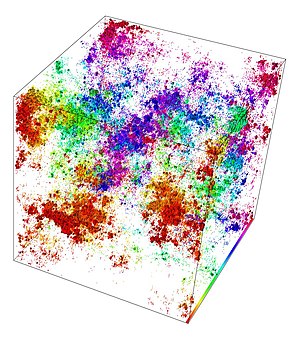
- Example of an electronic eigenstate at the MIT in a system with 1367631 atoms Each cube indicates by its size the probability to find the electron at the given position. The color scale denotes the position of the cubes along the axis into the plane
- Videos of multifractal electronic eigenstates at the MIT
- Anderson localization of elastic waves
- Popular scientific article on the first experimental observation of Anderson localization in matter waves