ऑप्टिकल चरण समष्टि: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Phase space used in quantum optics}} | {{Short description|Phase space used in quantum optics}} | ||
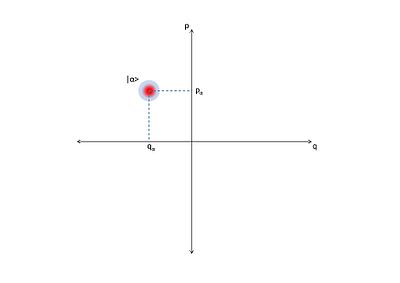
[[File:Optical phase space.jpg|thumb|400px|right|चरण समष्टि में एक सुसंगत अवस्था के वितरण का ऑप्टिकल चरण आरेख।]][[ क्वांटम प्रकाशिकी | क्वांटम | [[File:Optical phase space.jpg|thumb|400px|right|चरण समष्टि में एक सुसंगत अवस्था के वितरण का ऑप्टिकल चरण आरेख।]][[ क्वांटम प्रकाशिकी | क्वांटम ऑप्टिक्स]] में, एक '''ऑप्टिकल [[चरण स्थान|चरण समष्टि]]''' एक चरण समष्टि है जिसमें एक [[ऑप्टिकल प्रणाली]] के सभी क्वांटम अवस्थाओ का वर्णन किया गया है। ऑप्टिकल चरण समष्टि में प्रत्येक बिंदु ''ऑप्टिकल'' प्रणाली की एक अद्वितीय स्थिति से मेल खाता है। ऐसी किसी भी प्रणाली के लिए, संभवतः समय के कार्यों के रूप में, एक दूसरे के विरुद्ध ''चतुर्भुज'' का एक प्लॉट, [[चरण आरेख]] कहलाता है। यदि चतुर्भुज समय के कार्य हैं तो ऑप्टिकल चरण आरेख समय के साथ क्वांटम ऑप्टिकल प्रणाली के विकास को दिखा सकता है। | ||
एक ऑप्टिकल चरण आरेख प्रणाली के गुणों और व्यवहारों में अंतर्दृष्टि दे सकता है जो अन्यथा स्पष्ट नहीं हो सकता है। यह उस प्रणाली के गुणों की ओर संकेत कर सकता है जो किसी ऑप्टिकल प्रणाली का अध्ययन करने वाले व्यक्ति के लिए रुचिकर हो सकता है जिसे अन्यथा निकालना बहुत कठिन होगा। जो कि ऑप्टिकल चरण आरेख का एक अन्य उपयोग यह है कि यह एक ऑप्टिकल प्रणाली की स्थिति के विकास को दर्शाता है। इसका उपयोग किसी भी समय ऑप्टिकल प्रणाली की स्थिति निर्धारित करने के लिए किया जा सकता है। | एक ऑप्टिकल चरण आरेख प्रणाली के गुणों और व्यवहारों में अंतर्दृष्टि दे सकता है जो अन्यथा स्पष्ट नहीं हो सकता है। यह उस प्रणाली के गुणों की ओर संकेत कर सकता है जो किसी ऑप्टिकल प्रणाली का अध्ययन करने वाले व्यक्ति के लिए रुचिकर हो सकता है जिसे अन्यथा निकालना बहुत कठिन होगा। जो कि ऑप्टिकल चरण आरेख का एक अन्य उपयोग यह है कि यह एक ऑप्टिकल प्रणाली की स्थिति के विकास को दर्शाता है। इसका उपयोग किसी भी समय ऑप्टिकल प्रणाली की स्थिति निर्धारित करने के लिए किया जा सकता है। | ||
| Line 6: | Line 6: | ||
==पृष्ठभूमि जानकारी== | ==पृष्ठभूमि जानकारी== | ||
प्रकाश के क्वांटम सिद्धांत पर विचार करते समय, एक मॉडल के रूप में विद्युत चुम्बकीय | प्रकाश के क्वांटम सिद्धांत पर विचार करते समय, एक मॉडल के रूप में विद्युत चुम्बकीय ऑसिलेटर्स का उपयोग करना बहुत समान्य है।<ref name="Measuring the Quantum State of Light">{{cite book|first=Ulf |last=Leonhardt |title=प्रकाश की क्वांटम अवस्था को मापना|pages=18–29| publisher=[[Cambridge University Press]] |location=Cambridge |year=2005 |isbn=0-521-02352-1}}</ref> एक विद्युत चुम्बकीय ऑसिलेटर्स विद्युत क्षेत्र के ऑसिलेटर्स का वर्णन करता है। चूँकि चुंबकीय क्षेत्र विद्युत क्षेत्र के परिवर्तन की दर के समानुपाती होता है, इसलिए यह भी ऑसिलेटर्स करता है। ऐसे ऑसिलेटर्स प्रकाश का वर्णन करते हैं। ऐसे ऑसिलेटर्स से बने प्रणाली को ऑप्टिकल चरण समष्टि द्वारा वर्णित किया जा सकता है। | ||
मान लीजिए कि u(x,t) एक [[वेक्टर फ़ंक्शन]] है जो एक [[सरल हार्मोनिक थरथरानवाला|सरल हार्मोनिक | मान लीजिए कि u(x,t) एक [[वेक्टर फ़ंक्शन]] है जो एक [[सरल हार्मोनिक थरथरानवाला|सरल हार्मोनिक]] ऑसिलेटर्स के [[एकल मोड]] का वर्णन करता है। सरलता के लिए, यह माना जाता है कि यह विद्युत चुम्बकीय ऑसिलेटर्स निर्वात में है। इसका एक उदाहरण समतल तरंग द्वारा दिया गया है | ||
:<math> \mathbf{u}(\mathbf{x},t) = \mathbf{u_{0}}e^{i(\mathbf{k} \cdot \mathbf{x} - \omega t)} </math> | :<math> \mathbf{u}(\mathbf{x},t) = \mathbf{u_{0}}e^{i(\mathbf{k} \cdot \mathbf{x} - \omega t)} </math> | ||
जहां '''u<sub>0</sub>''' ध्रुवीकरण वेक्टर है, जिसमे k तरंग वेक्टर है, <math>\omega </math> आवृत्ति है, और '''A.B''' वेक्टर A और B के बीच डॉट उत्पाद को दर्शाता है। यह एक समतल तरंग के लिए समीकरण है और इस तरह का एक सरल उदाहरण है विद्युत चुम्बकीय | जहां '''u<sub>0</sub>''' ध्रुवीकरण वेक्टर है, जिसमे k तरंग वेक्टर है, <math>\omega </math> आवृत्ति है, और '''A.B''' वेक्टर A और B के बीच डॉट उत्पाद को दर्शाता है। यह एक समतल तरंग के लिए समीकरण है और इस तरह का एक सरल उदाहरण है विद्युत चुम्बकीय ऑसिलेटर्स . जिन ऑसिलेटर्स की जांच की जा रही है वे या तो अंतरिक्ष में मुक्त तरंगें हो सकते हैं या कुछ गुहा में निहित कुछ सामान्य मोड हो सकते हैं। | ||
इलेक्ट्रोमैग्नेटिक | इलेक्ट्रोमैग्नेटिक ऑसिलेटर्स के एक मोड को प्रणाली के शेष भागो से अलग किया जाता है और उसकी जांच की जाती है। ऐसे ऑसिलेटर्स , जब परिमाणित किया जाता है, तो क्वांटम हार्मोनिक ऑसिलेटर्स के गणित द्वारा वर्णित किया जाता है।<ref name="Measuring the Quantum State of Light"/> क्वांटम ऑसिलेटर्स का वर्णन सृजन और विलोपन ऑपरेटरों <math>\hat a^\dagger</math> और <math>\hat a</math>. का उपयोग करके किया गया है। भौतिक मात्राएँ, जैसे विद्युत क्षेत्र की शक्ति, फिर क्वांटम संचालिका बन जाती हैं। | ||
इसका वर्णन करने के लिए उपयोग किए जाने वाले क्वांटम मैकेनिकल | इसका वर्णन करने के लिए उपयोग किए जाने वाले क्वांटम मैकेनिकल संचालिका से किसी भौतिक मात्रा को अलग करने के लिए, संचालिका प्रतीकों के ऊपर एक "टोपी" का उपयोग किया जाता है। इस प्रकार, उदाहरण के लिए, जहां <math>E_i</math> विद्युत क्षेत्र (के एक घटक) का प्रतिनिधित्व कर सकता है, प्रतीक <math>\widehat E_i</math> क्वांटम-मैकेनिकल संचालिका को दर्शाता है जो <math>E_i</math> का वर्णन करता है। इस परिपाटी का उपयोग इस पूरे लेख में किया गया है, किन्तु अधिक उन्नत टेक्स्ट में इसका सामान्य उपयोग नहीं किया जाता है, जो टोपी से बचते हैं, क्योंकि यह केवल पाठ को अव्यवस्थित करता है। | ||
क्वांटम | क्वांटम ऑसिलेटर्स मोड में, भौतिक मात्राओं का प्रतिनिधित्व करने वाले अधिकांश ऑपरेटरों को समान्य रूप से निर्माण और विलोपन ऑपरेटरों के संदर्भ में व्यक्त किया जाता है। इस उदाहरण में, विद्युत क्षेत्र की शक्ति इस प्रकार दी गई है: | ||
:<math>\widehat{E}_{i}=u_{i}^{*}(\mathbf{x},t)\widehat{a}^{\dagger} + u_{i}(\mathbf{x},t)\widehat{a}</math><ref name="Quantum Optics">{{cite book |author1=Scully, Marlan |author2=Zubairy, M. Suhail |title=क्वांटम ऑप्टिक्स|url=https://archive.org/details/quantumoptics00scul |url-access=limited |pages=[https://archive.org/details/quantumoptics00scul/page/n25 5]| publisher=[[Cambridge University Press]] |location=Cambridge |year=1997 |isbn=0-521-43595-1}}</ref> | :<math>\widehat{E}_{i}=u_{i}^{*}(\mathbf{x},t)\widehat{a}^{\dagger} + u_{i}(\mathbf{x},t)\widehat{a}</math><ref name="Quantum Optics">{{cite book |author1=Scully, Marlan |author2=Zubairy, M. Suhail |title=क्वांटम ऑप्टिक्स|url=https://archive.org/details/quantumoptics00scul |url-access=limited |pages=[https://archive.org/details/quantumoptics00scul/page/n25 5]| publisher=[[Cambridge University Press]] |location=Cambridge |year=1997 |isbn=0-521-43595-1}}</ref> | ||
(जहाँ xi, x, स्थिति का एक एकल घटक है)। एक विद्युत चुम्बकीय | (जहाँ xi, x, स्थिति का एक एकल घटक है)। एक विद्युत चुम्बकीय ऑसिलेटर्स के लिए हैमिल्टनियन इस ऑसिलेटर्स के लिए विद्युत चुम्बकीय क्षेत्र की मात्रा निर्धारित करके पाया जाता है और सूत्र इस प्रकार दिया जाता है: | ||
:<math>\widehat{H} = \hbar\omega (\widehat{a}^{\dagger}\widehat{a} + 1/2)</math><ref name="Quantum Optics"/> | :<math>\widehat{H} = \hbar\omega (\widehat{a}^{\dagger}\widehat{a} + 1/2)</math><ref name="Quantum Optics"/> | ||
जहाँ <math>\omega</math> (स्थान-अस्थायी) मोड की आवृत्ति है। सर्वनाश संचालिका बोसोनिक | जहाँ <math>\omega</math> (स्थान-अस्थायी) मोड की आवृत्ति है। सर्वनाश संचालिका बोसोनिक विलोपन संचालिका है और इसलिए यह दिए गए [[विहित रूपान्तरण संबंध]] का पालन करता है: | ||
:<math>[\widehat{a},\widehat{a}^{\dagger}] = 1</math> | :<math>[\widehat{a},\widehat{a}^{\dagger}] = 1</math> | ||
विलोपन संचालिका की मूल अवस्थाओं को [[सुसंगत अवस्थाएँ]] कहा जाता है: | |||
:<math>\widehat{a}|\alpha\rangle = \alpha|\alpha\rangle</math> | :<math>\widehat{a}|\alpha\rangle = \alpha|\alpha\rangle</math> | ||
यह ध्यान रखना महत्वपूर्ण है कि | यह ध्यान रखना महत्वपूर्ण है कि विलोपन संचालिका [[हर्मिटियन]] नहीं है; इसलिए इसके आइजेनवैल्यू <math>\alpha</math> सम्मिश्र हो सकता है. इसके महत्वपूर्ण परिणाम हैं. | ||
अंत में, | अंत में, संचालिका <math> \widehat{N} = \widehat{a}^{\dagger} \widehat{a},</math> द्वारा फोटॉन संख्या दी जाती है, जो दिए गए (स्थानिक-लौकिक) मोड यू में फोटॉनों की संख्या देता है। | ||
==चतुर्भुज== | ==चतुर्भुज== | ||
| Line 54: | Line 54: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
यह स्थिति और गति | यह स्थिति और गति संचालिका के कम्यूटेशन संबंध के समान दिखता है। इस प्रकार, चतुर्भुजों को ऑसिलेटर्स की स्थिति और गति के रूप में सोचना और व्यवहार करना उपयोगी हो सकता है, चूँकि वास्तव में वे स्थानिक-लौकिक मोड के विद्युत क्षेत्र आयाम के इन-फेज और आउट-ऑफ-फेज घटक हैं, या '''u''', और वास्तव में विद्युत चुम्बकीय ऑसिलेटर्स की स्थिति या गति से कोई लेना-देना नहीं है (क्योंकि यह परिभाषित करना कठिन है कि विद्युत चुम्बकीय ऑसिलेटर्स के लिए स्थिति और गति का क्या अर्थ है)।<ref name="Measuring the Quantum State of Light"/> | ||
| Line 69: | Line 69: | ||
===महत्वपूर्ण परिणाम=== | ===महत्वपूर्ण परिणाम=== | ||
निम्नलिखित एक महत्वपूर्ण संबंध है जिसे उपरोक्त से प्राप्त किया जा सकता है जो हमारी व्याख्या को उचित ठहराता है कि चतुर्भुज एक | निम्नलिखित एक महत्वपूर्ण संबंध है जिसे उपरोक्त से प्राप्त किया जा सकता है जो हमारी व्याख्या को उचित ठहराता है कि चतुर्भुज एक सम्मिश्र <math>\alpha</math> के वास्तविक और काल्पनिक भाग हैं (अर्थात विद्युत चुम्बकीय ऑसिलेटर्स के चरण-चरण और आउट-ऑफ-चरण घटक) | ||
:<math> \langle\alpha|\widehat{q}|\alpha\rangle = \frac{1}{2}(\langle\alpha|\widehat{a}^{\dagger}|\alpha\rangle + \langle\alpha|\widehat{a}|\alpha\rangle) = \frac{1}{2}(\alpha^{*}\langle\alpha|\alpha\rangle + \alpha\langle\alpha|\alpha\rangle) </math> | :<math> \langle\alpha|\widehat{q}|\alpha\rangle = \frac{1}{2}(\langle\alpha|\widehat{a}^{\dagger}|\alpha\rangle + \langle\alpha|\widehat{a}|\alpha\rangle) = \frac{1}{2}(\alpha^{*}\langle\alpha|\alpha\rangle + \alpha\langle\alpha|\alpha\rangle) </math> | ||
| Line 90: | Line 90: | ||
:<math>p_{\alpha} = \langle\alpha|\widehat{p}|\alpha\rangle</math>. | :<math>p_{\alpha} = \langle\alpha|\widehat{p}|\alpha\rangle</math>. | ||
ये केवल अपेक्षा के मूल्य हैं <math>\widehat{q}</math> और <math>\widehat{p}</math> | ये केवल अपेक्षा के मूल्य हैं <math>\widehat{q}</math> और <math>\widehat{p}</math> अवस्था के लिए <math>|\alpha\rangle</math>. | ||
ये केवल अवस्था <math>|\alpha\rangle</math> के लिए <math>\widehat{q}</math> और <math>\widehat{p}</math> के अपेक्षित मूल्य हैं। | ये केवल अवस्था <math>|\alpha\rangle</math> के लिए <math>\widehat{q}</math> और <math>\widehat{p}</math> के अपेक्षित मूल्य हैं। | ||
| Line 96: | Line 96: | ||
यह दिखाया जा सकता है कि चतुर्भुज हाइजेनबर्ग के अनिश्चितता सिद्धांत का पालन करते हैं: | यह दिखाया जा सकता है कि चतुर्भुज हाइजेनबर्ग के अनिश्चितता सिद्धांत का पालन करते हैं: | ||
:<math>\Delta q\Delta p \ge 1/2</math><ref name="Measuring the Quantum State of Light"/>(जहाँ <math>\Delta q</math> और <math>\Delta p</math> क्रमशः q और p के वितरण के प्रसरण हैं) | :<math>\Delta q\Delta p \ge 1/2</math><ref name="Measuring the Quantum State of Light"/> (जहाँ <math>\Delta q</math> और <math>\Delta p</math> क्रमशः q और p के वितरण के प्रसरण हैं) | ||
यह असमानता आवश्यक रूप से संतृप्त नहीं होती है और ऐसे अवस्थाओ का एक सामान्य उदाहरण निचोड़ा हुआ सुसंगत अवस्था है। सुसंगत अवस्थाएँ <math>\alpha</math> के आसपास स्थानीयकृत चरण स्थान पर गॉसियन संभाव्यता वितरण हैं। | यह असमानता आवश्यक रूप से संतृप्त नहीं होती है और ऐसे अवस्थाओ का एक सामान्य उदाहरण निचोड़ा हुआ सुसंगत अवस्था है। सुसंगत अवस्थाएँ <math>\alpha</math> के आसपास स्थानीयकृत चरण स्थान पर गॉसियन संभाव्यता वितरण हैं। | ||
| Line 106: | Line 106: | ||
===चरण-स्थानांतरण ऑपरेटर=== | ===चरण-स्थानांतरण ऑपरेटर=== | ||
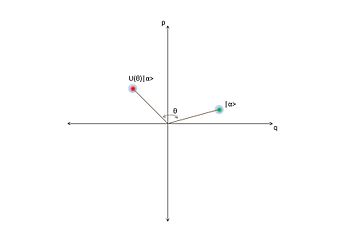
[[File:Rotation operator.jpg|thumb|350px|right|फेज़ स्थानांतरण | [[File:Rotation operator.jpg|thumb|350px|right|फेज़ स्थानांतरण संचालिका एक सुसंगत स्थिति पर कार्य करते हुए इसे <math>\theta</math> चरण समष्टि में एक कोण से घुमाता है]] | ||
चरण-स्थानांतरण संचालिका ऑप्टिकल चरण स्थान में सुसंगत स्थिति को <math>\theta</math> कोण द्वारा घुमाता है। यह संचालिका द्वारा दिया गया है: | |||
चरण-स्थानांतरण | |||
:<math> \widehat{U}(\theta) = e^{-i\theta\widehat{N}} </math> <ref name="Measuring the Quantum State of Light" /> | :<math> \widehat{U}(\theta) = e^{-i\theta\widehat{N}} </math> <ref name="Measuring the Quantum State of Light" /> | ||
| Line 129: | Line 128: | ||
:<math>\widehat{a}(\widehat{U}|\alpha\rangle) = \widehat{U}\widehat{a}e^{-i\theta}|\alpha\rangle </math> | :<math>\widehat{a}(\widehat{U}|\alpha\rangle) = \widehat{U}\widehat{a}e^{-i\theta}|\alpha\rangle </math> | ||
(जो इस तथ्य का उपयोग करके प्राप्त किया जाता है कि चरण-स्थानांतरण | (जो इस तथ्य का उपयोग करके प्राप्त किया जाता है कि चरण-स्थानांतरण संचालिका एकात्मक संचालिका है | ||
:<math> \widehat{a}(\widehat{U}|\alpha\rangle) = \widehat{U} \alpha e^{-i\theta}|\alpha\rangle = \alpha e^{-i\theta}(\widehat{U}|\alpha\rangle) </math> | :<math> \widehat{a}(\widehat{U}|\alpha\rangle) = \widehat{U} \alpha e^{-i\theta}|\alpha\rangle = \alpha e^{-i\theta}(\widehat{U}|\alpha\rangle) </math> | ||
| Line 142: | Line 141: | ||
:<math> (\alpha e^{-i\theta} = 2^{-1/2}[q_{\alpha} \cos(\theta) + p_{\alpha} \sin(\theta)] + i2^{-1/2}[-q_{\alpha} \sin(\theta) + p_{\alpha} \cos(\theta)], \widehat{U}|\alpha\rangle = |\alpha e^{-i\theta}\rangle)</math> | :<math> (\alpha e^{-i\theta} = 2^{-1/2}[q_{\alpha} \cos(\theta) + p_{\alpha} \sin(\theta)] + i2^{-1/2}[-q_{\alpha} \sin(\theta) + p_{\alpha} \cos(\theta)], \widehat{U}|\alpha\rangle = |\alpha e^{-i\theta}\rangle)</math> | ||
जो ईजेनपेयर को व्यक्त करने का एक और विधि है जो सुसंगत अवस्थाओ पर चरण-स्थानांतरण | जो ईजेनपेयर को व्यक्त करने का एक और विधि है जो सुसंगत अवस्थाओ पर चरण-स्थानांतरण संचालिका के प्रभावों को अधिक स्पष्ट रूप से दर्शाता है। | ||
===विस्थापन ऑपरेटर=== | ===विस्थापन ऑपरेटर=== | ||
[[File:Displacement operator.jpg|thumb|350px|right|विस्थापन | [[File:Displacement operator.jpg|thumb|350px|right|विस्थापन संचालिका एक सुसंगत स्थिति पर कार्य करते हुए इसे कुछ मान से <math>\alpha</math> चरण समष्टि में विस्थापित करता है ]]विस्थापन संचालिका एक एकात्मक संचालिका है जो एक सुसंगत अवस्था लेती है और उसे दूसरी सुसंगत अवस्था में बदल देती है। विस्थापन संचालिका द्वारा दिया गया है | ||
:<math>\widehat{D}(\alpha) = e^{\alpha\widehat{a}^{\dagger} - \alpha^{*}\widehat{a}}</math> | :<math>\widehat{D}(\alpha) = e^{\alpha\widehat{a}^{\dagger} - \alpha^{*}\widehat{a}}</math> | ||
| Line 168: | Line 167: | ||
इस प्रकार <math> \widehat{D}(\alpha) | \beta \rangle</math> आइगेनवैल्यू \<math> \alpha + \beta</math> के साथ | इस प्रकार <math> \widehat{D}(\alpha) | \beta \rangle</math> आइगेनवैल्यू \<math> \alpha + \beta</math> के साथ विलोपन संचालिका का एक आइजेनस्टेट है, इसलिए <math> \widehat{D}(\alpha) | \beta \rangle = | \alpha + \beta \rangle</math>। | ||
:<math>\widehat{D}(-\alpha)|\alpha\rangle = |0\rangle</math> | :<math>\widehat{D}(-\alpha)|\alpha\rangle = |0\rangle</math> | ||
| Line 175: | Line 174: | ||
:<math>|\alpha\rangle=\widehat{D}(\alpha)|0\rangle</math>. | :<math>|\alpha\rangle=\widehat{D}(\alpha)|0\rangle</math>. | ||
यह महत्वपूर्ण है क्योंकि यह दर्शाता है कि सभी सुसंगत अवस्थाओं को जमीनी अवस्था के विस्थापन के रूप में प्राप्त किया जा सकता है, जो | यह महत्वपूर्ण है क्योंकि यह दर्शाता है कि सभी सुसंगत अवस्थाओं को जमीनी अवस्था के विस्थापन के रूप में प्राप्त किया जा सकता है, जो ऑप्टिक्स में [[निर्वात अवस्था]] भी है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[अशास्त्रीय प्रकाश|अमौलिक प्रकाश]] | * [[अशास्त्रीय प्रकाश|अमौलिक प्रकाश]] | ||
* [[रोटेशन ऑपरेटर (क्वांटम यांत्रिकी)|घूर्णन | * [[रोटेशन ऑपरेटर (क्वांटम यांत्रिकी)|घूर्णन संचालिका (क्वांटम यांत्रिकी)]] | ||
* क्वांटम हार्मोनिक | * क्वांटम हार्मोनिक ऑसिलेटर्स ` | ||
* [[अर्धसंभाव्यता वितरण]] | * [[अर्धसंभाव्यता वितरण]] | ||
* [[हुसिमी क्यू प्रतिनिधित्व]] | * [[हुसिमी क्यू प्रतिनिधित्व]] | ||
Revision as of 16:44, 30 November 2023
क्वांटम ऑप्टिक्स में, एक ऑप्टिकल चरण समष्टि एक चरण समष्टि है जिसमें एक ऑप्टिकल प्रणाली के सभी क्वांटम अवस्थाओ का वर्णन किया गया है। ऑप्टिकल चरण समष्टि में प्रत्येक बिंदु ऑप्टिकल प्रणाली की एक अद्वितीय स्थिति से मेल खाता है। ऐसी किसी भी प्रणाली के लिए, संभवतः समय के कार्यों के रूप में, एक दूसरे के विरुद्ध चतुर्भुज का एक प्लॉट, चरण आरेख कहलाता है। यदि चतुर्भुज समय के कार्य हैं तो ऑप्टिकल चरण आरेख समय के साथ क्वांटम ऑप्टिकल प्रणाली के विकास को दिखा सकता है।
एक ऑप्टिकल चरण आरेख प्रणाली के गुणों और व्यवहारों में अंतर्दृष्टि दे सकता है जो अन्यथा स्पष्ट नहीं हो सकता है। यह उस प्रणाली के गुणों की ओर संकेत कर सकता है जो किसी ऑप्टिकल प्रणाली का अध्ययन करने वाले व्यक्ति के लिए रुचिकर हो सकता है जिसे अन्यथा निकालना बहुत कठिन होगा। जो कि ऑप्टिकल चरण आरेख का एक अन्य उपयोग यह है कि यह एक ऑप्टिकल प्रणाली की स्थिति के विकास को दर्शाता है। इसका उपयोग किसी भी समय ऑप्टिकल प्रणाली की स्थिति निर्धारित करने के लिए किया जा सकता है।
पृष्ठभूमि जानकारी
प्रकाश के क्वांटम सिद्धांत पर विचार करते समय, एक मॉडल के रूप में विद्युत चुम्बकीय ऑसिलेटर्स का उपयोग करना बहुत समान्य है।[1] एक विद्युत चुम्बकीय ऑसिलेटर्स विद्युत क्षेत्र के ऑसिलेटर्स का वर्णन करता है। चूँकि चुंबकीय क्षेत्र विद्युत क्षेत्र के परिवर्तन की दर के समानुपाती होता है, इसलिए यह भी ऑसिलेटर्स करता है। ऐसे ऑसिलेटर्स प्रकाश का वर्णन करते हैं। ऐसे ऑसिलेटर्स से बने प्रणाली को ऑप्टिकल चरण समष्टि द्वारा वर्णित किया जा सकता है।
मान लीजिए कि u(x,t) एक वेक्टर फ़ंक्शन है जो एक सरल हार्मोनिक ऑसिलेटर्स के एकल मोड का वर्णन करता है। सरलता के लिए, यह माना जाता है कि यह विद्युत चुम्बकीय ऑसिलेटर्स निर्वात में है। इसका एक उदाहरण समतल तरंग द्वारा दिया गया है
जहां u0 ध्रुवीकरण वेक्टर है, जिसमे k तरंग वेक्टर है, आवृत्ति है, और A.B वेक्टर A और B के बीच डॉट उत्पाद को दर्शाता है। यह एक समतल तरंग के लिए समीकरण है और इस तरह का एक सरल उदाहरण है विद्युत चुम्बकीय ऑसिलेटर्स . जिन ऑसिलेटर्स की जांच की जा रही है वे या तो अंतरिक्ष में मुक्त तरंगें हो सकते हैं या कुछ गुहा में निहित कुछ सामान्य मोड हो सकते हैं।
इलेक्ट्रोमैग्नेटिक ऑसिलेटर्स के एक मोड को प्रणाली के शेष भागो से अलग किया जाता है और उसकी जांच की जाती है। ऐसे ऑसिलेटर्स , जब परिमाणित किया जाता है, तो क्वांटम हार्मोनिक ऑसिलेटर्स के गणित द्वारा वर्णित किया जाता है।[1] क्वांटम ऑसिलेटर्स का वर्णन सृजन और विलोपन ऑपरेटरों और . का उपयोग करके किया गया है। भौतिक मात्राएँ, जैसे विद्युत क्षेत्र की शक्ति, फिर क्वांटम संचालिका बन जाती हैं।
इसका वर्णन करने के लिए उपयोग किए जाने वाले क्वांटम मैकेनिकल संचालिका से किसी भौतिक मात्रा को अलग करने के लिए, संचालिका प्रतीकों के ऊपर एक "टोपी" का उपयोग किया जाता है। इस प्रकार, उदाहरण के लिए, जहां विद्युत क्षेत्र (के एक घटक) का प्रतिनिधित्व कर सकता है, प्रतीक क्वांटम-मैकेनिकल संचालिका को दर्शाता है जो का वर्णन करता है। इस परिपाटी का उपयोग इस पूरे लेख में किया गया है, किन्तु अधिक उन्नत टेक्स्ट में इसका सामान्य उपयोग नहीं किया जाता है, जो टोपी से बचते हैं, क्योंकि यह केवल पाठ को अव्यवस्थित करता है।
क्वांटम ऑसिलेटर्स मोड में, भौतिक मात्राओं का प्रतिनिधित्व करने वाले अधिकांश ऑपरेटरों को समान्य रूप से निर्माण और विलोपन ऑपरेटरों के संदर्भ में व्यक्त किया जाता है। इस उदाहरण में, विद्युत क्षेत्र की शक्ति इस प्रकार दी गई है:
(जहाँ xi, x, स्थिति का एक एकल घटक है)। एक विद्युत चुम्बकीय ऑसिलेटर्स के लिए हैमिल्टनियन इस ऑसिलेटर्स के लिए विद्युत चुम्बकीय क्षेत्र की मात्रा निर्धारित करके पाया जाता है और सूत्र इस प्रकार दिया जाता है:
जहाँ (स्थान-अस्थायी) मोड की आवृत्ति है। सर्वनाश संचालिका बोसोनिक विलोपन संचालिका है और इसलिए यह दिए गए विहित रूपान्तरण संबंध का पालन करता है:
विलोपन संचालिका की मूल अवस्थाओं को सुसंगत अवस्थाएँ कहा जाता है:
यह ध्यान रखना महत्वपूर्ण है कि विलोपन संचालिका हर्मिटियन नहीं है; इसलिए इसके आइजेनवैल्यू सम्मिश्र हो सकता है. इसके महत्वपूर्ण परिणाम हैं.
अंत में, संचालिका द्वारा फोटॉन संख्या दी जाती है, जो दिए गए (स्थानिक-लौकिक) मोड यू में फोटॉनों की संख्या देता है।
चतुर्भुज
संचालक (गणित) द्वारा दिया गया है
और
चतुर्भुज कहलाते हैं और वे सम्मिश्र आयाम के वास्तविक और काल्पनिक भागों का प्रतिनिधित्व करते हैं जो द्वारा दर्शाए जाते हैं।[1] दो चतुर्भुजों के बीच कम्यूटेशन संबंध की गणना सरलता से की जा सकती है:
यह स्थिति और गति संचालिका के कम्यूटेशन संबंध के समान दिखता है। इस प्रकार, चतुर्भुजों को ऑसिलेटर्स की स्थिति और गति के रूप में सोचना और व्यवहार करना उपयोगी हो सकता है, चूँकि वास्तव में वे स्थानिक-लौकिक मोड के विद्युत क्षेत्र आयाम के इन-फेज और आउट-ऑफ-फेज घटक हैं, या u, और वास्तव में विद्युत चुम्बकीय ऑसिलेटर्स की स्थिति या गति से कोई लेना-देना नहीं है (क्योंकि यह परिभाषित करना कठिन है कि विद्युत चुम्बकीय ऑसिलेटर्स के लिए स्थिति और गति का क्या अर्थ है)।[1]
चतुर्भुज के गुण
चतुर्भुज ऑपरेटरों के आइजेनस्टेट और चतुर्भुज अवस्थाएँ कहलाती हैं। वे सम्बन्ध को संतुष्ट करते हैं:
- और
- और
- और
क्योंकि ये पूर्ण आधार सेट बनाते हैं।
महत्वपूर्ण परिणाम
निम्नलिखित एक महत्वपूर्ण संबंध है जिसे उपरोक्त से प्राप्त किया जा सकता है जो हमारी व्याख्या को उचित ठहराता है कि चतुर्भुज एक सम्मिश्र के वास्तविक और काल्पनिक भाग हैं (अर्थात विद्युत चुम्बकीय ऑसिलेटर्स के चरण-चरण और आउट-ऑफ-चरण घटक)
निम्नलिखित एक संबंध है जिसका उपयोग उपरोक्त का मूल्यांकन करने में सहायता के लिए किया जा सकता है और इसे निम्न द्वारा दिया गया है:
इससे हमें यह मिलता है:
- उपरोक्त के समान विधि द्वारा।
इस प्रकार, यह केवल चतुर्भुजों की एक रचना है।
सुसंगत अवस्थाओ की एक और बहुत महत्वपूर्ण गुण इस औपचारिकता में बहुत स्पष्ट हो जाती है। एक सुसंगत अवस्था ऑप्टिकल चरण समष्टि में एक बिंदु नहीं है, किन्तु उस पर एक वितरण है। इसके माध्यम से देखा जा सकता है
और
- .
ये केवल अपेक्षा के मूल्य हैं और अवस्था के लिए .
ये केवल अवस्था के लिए और के अपेक्षित मूल्य हैं।
यह दिखाया जा सकता है कि चतुर्भुज हाइजेनबर्ग के अनिश्चितता सिद्धांत का पालन करते हैं:
- [1] (जहाँ और क्रमशः q और p के वितरण के प्रसरण हैं)
यह असमानता आवश्यक रूप से संतृप्त नहीं होती है और ऐसे अवस्थाओ का एक सामान्य उदाहरण निचोड़ा हुआ सुसंगत अवस्था है। सुसंगत अवस्थाएँ के आसपास स्थानीयकृत चरण स्थान पर गॉसियन संभाव्यता वितरण हैं।
चरण समष्टि पर ऑपरेटर
चरण समष्टि के चारों ओर सुसंगत अवस्थाओं को स्थानांतरित करने के लिए ऑपरेटरों को परिभाषित करना संभव है। ये नई सुसंगत अवस्थाएँ उत्पन्न कर सकते हैं और हमें चरण समष्टि के चारों ओर घूमने की अनुमति दे सकते हैं।
चरण-स्थानांतरण ऑपरेटर
चरण-स्थानांतरण संचालिका ऑप्टिकल चरण स्थान में सुसंगत स्थिति को कोण द्वारा घुमाता है। यह संचालिका द्वारा दिया गया है:
महत्वपूर्ण सम्बन्ध
इस प्रकार व्युत्पन्न है:
और इस अंतर समीकरण को हल करने से वांछित परिणाम प्राप्त होता है।
इस प्रकार उपरोक्त के प्रयोग से यह स्पष्ट हो जाता है कि
- ,
या चरण समष्टि में सुसंगत स्थिति पर कोण द्वारा घूर्णन। निम्नलिखित इसे और अधिक स्पष्ट रूप से दर्शाता है:
(जो इस तथ्य का उपयोग करके प्राप्त किया जाता है कि चरण-स्थानांतरण संचालिका एकात्मक संचालिका है
इस प्रकार,
का आइजेनवैल्यू, आइजेनवेक्टर और आइजेनस्पेस है
- .
इससे ये पता चल सकता है
जो ईजेनपेयर को व्यक्त करने का एक और विधि है जो सुसंगत अवस्थाओ पर चरण-स्थानांतरण संचालिका के प्रभावों को अधिक स्पष्ट रूप से दर्शाता है।
विस्थापन ऑपरेटर
विस्थापन संचालिका एक एकात्मक संचालिका है जो एक सुसंगत अवस्था लेती है और उसे दूसरी सुसंगत अवस्था में बदल देती है। विस्थापन संचालिका द्वारा दिया गया है
और इसका नाम एक महत्वपूर्ण संबंध से आया है
- .
वास्तव में, आइए अस्थायी रूप से को वास्तविक से परिचित कराएं और विचार करें कि जब 0 से 1 में परिवर्तित है तो कैसे परिवर्तित है। के संबंध में को अलग करते हुए, हम पाते हैं
जिससे
चूँकि सुसंगत अवस्थाएँ संहार संचालक और किसी संख्या से गुणन संचालक दोनों की मूल अवस्थाएँ हैं, इसलिए यह देखना सरल है कि, वास्तव में, विस्थापन संचालक सुसंगत अवस्थाओं को स्थानांतरित करता है, या, अधिक स्पष्ट रूप से,
वास्तव में, ऊपर प्राप्त संबंध को फिर से के रूप में लिखा जा सकता है
इस प्रकार आइगेनवैल्यू \ के साथ विलोपन संचालिका का एक आइजेनस्टेट है, इसलिए ।
जिससे होता है
- .
यह महत्वपूर्ण है क्योंकि यह दर्शाता है कि सभी सुसंगत अवस्थाओं को जमीनी अवस्था के विस्थापन के रूप में प्राप्त किया जा सकता है, जो ऑप्टिक्स में निर्वात अवस्था भी है।
यह भी देखें
- अमौलिक प्रकाश
- घूर्णन संचालिका (क्वांटम यांत्रिकी)
- क्वांटम हार्मोनिक ऑसिलेटर्स `
- अर्धसंभाव्यता वितरण
- हुसिमी क्यू प्रतिनिधित्व
- निचोड़ा हुआ सुसंगत अवस्था
- विग्नर क्वासिप्रोबेबिलिटी वितरण
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Leonhardt, Ulf (2005). प्रकाश की क्वांटम अवस्था को मापना. Cambridge: Cambridge University Press. pp. 18–29. ISBN 0-521-02352-1.
- ↑ 2.0 2.1 Scully, Marlan; Zubairy, M. Suhail (1997). क्वांटम ऑप्टिक्स. Cambridge: Cambridge University Press. pp. 5. ISBN 0-521-43595-1.