वैरिएशनल बायेसियन विधियाँ: Difference between revisions
(Created page with "{{Short description|Mathematical methods used in Bayesian inference and machine learning}} {{For|the method of approximation in quantum mechanics|Variational method (quantum m...") |
m (1 revision imported from alpha:वैरिएशनल_बायेसियन_विधियाँ) |
||
| (18 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Mathematical methods used in Bayesian inference and machine learning}} | {{Short description|Mathematical methods used in Bayesian inference and machine learning}} | ||
{{For| | {{For|क्वांटम यांत्रिकी में सन्निकटन की विधि|परिवर्तनीय विधि (क्वांटम यांत्रिकी) }}'''वेरिएशनल बायेसियन विधियाँ''' [[बायेसियन अनुमान]] और [[ यंत्र अधिगम |यंत्र अधिगम]] में उत्पन्न होने वाले असाध्य [[ अभिन्न |अभिन्न]] का अनुमान लगाने की विधि का वर्ग है। इनका उपयोग सामान्यतः सम्मिश्र [[सांख्यिकीय मॉडल]] में किया जाता है जिसमें प्रेक्षित वेरिएबल (सामान्यतः डेटा कहा जाता है) | इसके साथ-साथ अज्ञात [[पैरामीटर]] और [[अव्यक्त चर|अव्यक्त]] वेरिएबल होते हैं, तथा यह तीन प्रकार के यादृच्छिक वेरिएबल के मध्य विभिन्न प्रकार के संबंधों के साथ होता है , जैसा कि [[ चित्रमय मॉडल |चित्रमय मॉडल]] द्वारा वर्णित किया जा सकता है। कि बायेसियन अनुमान में विशिष्ट है, पैरामीटर और अव्यक्त वेरिएबल को साथ न देखे गए वेरिएबल के रूप में समूहीकृत किया जाता है। वेरिएशनल बायेसियन विधियाँ मुख्य रूप से दो उद्देश्यों के लिए उपयोग की जाती हैं | | ||
#इन वेरिएबलों का कार्य इन पर सांख्यिकीय अनुमान लगाने के लिए, न देखे गए वेरिएबलों की पूर्व संभावना के लिए विश्लेषणात्मक अनुमान प्रदान करना होता है। | |||
#अवलोकित डेटा की [[सीमांत संभावना]] (जिसे कभी-कभी ''साक्ष्य'' भी कहा जाता है) के लिए निचली सीमा प्राप्त करना है | (अर्थात मॉडल दिए गए डेटा की सीमांत संभावना, बिना देखे गए वेरिएबल पर मर्गिनाल्स पर प्रदर्शन के साथ) होता हैं। इसका उपयोग सामान्यतः [[मॉडल चयन]] करने के लिए किया जाता है, तथा सामान्य विचार यह है कि किसी दिए गए मॉडल के लिए उच्च सीमांत संभावना उस मॉडल द्वारा डेटा के उत्तम फिट को निरुपित करती है और इसलिए अधिक संभावना है कि प्रश्न में मॉडल वह था जिसने डेटा उत्पन्न किया था। ([[बेयस फैक्टर]] लेख भी देखें।) | |||
पूर्व उद्देश्य में (पश्च संभाव्यता का अनुमान लगाने के लिए), वैरिएबल बेयस [[मोंटे कार्लो नमूनाकरण|मोंटे कार्लो प्रतिरूपीकरण]] विधियों का विकल्प है - विशेष रूप से, [[मार्कोव श्रृंखला मोंटे कार्लो]] विधियां जैसे [[गिब्स नमूनाकरण|गिब्स प्रतिरूपीकरण]] - सम्मिश्र संभाव्यता वितरण पर सांख्यिकीय अनुमान के लिए पूर्ण प्रकार से बायेसियन दृष्टिकोण लेने के लिए सीधे या [[नमूना (सांख्यिकी)|प्रतिरूप (सांख्यिकी)]] का विशेष रूप से मूल्यांकन करना कठिन है। जबकि मोंटे कार्लो विधि प्रतिरूपों के समुच्चय का उपयोग करके त्रुटिहीन पोस्टीरियर के लिए संख्यात्मक अनुमान प्रदान करती है, वेरिएबल बेयस पोस्टीरियर के अनुमान के लिए स्थानीय-इष्टतम, त्रुटिहीन विश्लेषणात्मक समाधान प्रदान करता है। | |||
वैरिएशनल बेयस को एक्सपेक्टेशन-मैक्सिमाइजेशन एल्गोरिदम के विस्तार के रूप में देखा जा सकता है। एक्सपेक्टेशन-मैक्सिमाइजेशन (ईएम) एल्गोरिदम प्रत्येक पैरामीटर के एकल सबसे संभावित मूल्य के अधिकतम पोस्टीरियरी अनुमान (एमएपी अनुमान) से लेकर पूर्ण प्रकार से बायेसियन अनुमान तक, जो (एक अनुमान) की गणना करता है। ) मापदंडों और अव्यक्त वेरिएबल का संपूर्ण [[पश्च वितरण]]। ईएम की प्रकार, यह इष्टतम पैरामीटर मानों का समुच्चय ढूंढता है, और इसमें ईएम के समान ही वैकल्पिक संरचना होती है, जो इंटरलॉक्ड (परस्पर निर्भर) समीकरणों के समुच्चय पर आधारित होती है जिसका विश्लेषणात्मक रूप से समाधान नहीं किया जा सकता है। | |||
अनेक अनुप्रयोगों के लिए, वैरिएबल बेयस अधिक गति से गिब्स सैंपलिंग के तुलनीय त्रुटिहीनता के समाधान तैयार करता है। चूँकि, मापदंडों को अद्यतन करने के लिए उपयोग किए जाने वाले समीकरणों के समुच्चय को प्राप्त करने के लिए अधिकांशतः तुलनीय गिब्स प्रतिरूप समीकरणों को प्राप्त करने की तुलना में बड़ी मात्रा में कार्य की आवश्यकता होती है। यह अनेक मॉडलों के लिए भी स्तिथि होती है जो वैचारिक रूप से अधिक सरल हैं, जैसा कि केवल दो मापदंडों और कोई अव्यक्त वेरिएबल के साथ मूलभूत गैर-पदानुक्रमित मॉडल के स्थितियां में नीचे दिखाया गया है। | |||
==गणितीय व्युत्पत्ति== | ==गणितीय व्युत्पत्ति== | ||
| Line 17: | Line 14: | ||
=== समस्या === | === समस्या === | ||
वैरिएबल अनुमान में, कुछ डेटा <math>\mathbf{X}</math> दिए जाने पर न देखे गए वेरिएबल्स <math>\mathbf{Z} = \{Z_1 \dots Z_n\}</math> के समुच्चय पर पश्च वितरण को तथाकथित वेरिएबल डिस्ट्रीब्यूशन, <math>Q(\mathbf{Z}):</math>द्वारा अनुमानित किया जाता है। | |||
: <math>P(\mathbf{Z}\mid \mathbf{X}) \approx Q(\mathbf{Z}).</math> | : <math>P(\mathbf{Z}\mid \mathbf{X}) \approx Q(\mathbf{Z}).</math> | ||
विभाजन <math>Q(\mathbf{Z})</math> <math>P(\mathbf{Z}\mid \mathbf{X})</math> की तुलना में सरल रूप के वितरण के वर्ग से संबंधित होने तक सीमित है (उदाहरण के लिए गॉसियन वितरण का वर्ग ), <math>Q(\mathbf{Z})</math> बनाने के प्रयोजन से चुना गया हैं | यह वास्तविक पश्च भाग के समान, <math>P(\mathbf{Z}\mid \mathbf{X})</math> होता हैं | | |||
समानता (या असमानता) को असमानता | समानता (या असमानता) को असमानता फलन <math>d(Q; P)</math> के संदर्भ में मापा जाता है और इसलिए वितरण <math>Q(\mathbf{Z})</math> का चयन करके अनुमान लगाया जाता है वह <math>d(Q; P)</math> को न्यूनतम करता है | | ||
=== केएल विचलन === | === केएल विचलन === | ||
वैरिएबल बेज़ का सबसे | वैरिएबल बेज़ का सबसे सामान्य प्रकार असमानता फलन की पसंद के रूप में P से Q के कुल्बैक-लीब्लर डाइवर्जेंस (केएल-डाइवर्जेंस) का उपयोग करता है। यह विकल्प इस न्यूनतमकरण को सुव्यवस्थित बनाता है। केएल-विचलन को इस प्रकार परिभाषित किया गया है | ||
:<math>D_{\mathrm{KL}}(Q \parallel P) \triangleq \sum_\mathbf{Z} Q(\mathbf{Z}) \log \frac{Q(\mathbf{Z})}{P(\mathbf{Z}\mid \mathbf{X})}.</math> | :<math>D_{\mathrm{KL}}(Q \parallel P) \triangleq \sum_\mathbf{Z} Q(\mathbf{Z}) \log \frac{Q(\mathbf{Z})}{P(\mathbf{Z}\mid \mathbf{X})}.</math> | ||
ध्यान दें कि Q और P किसी की अपेक्षा से | ध्यान दें कि Q और P किसी की अपेक्षा से विपरीत हैं। विपरीते केएल-विचलन का यह उपयोग अवधारणात्मक रूप से अपेक्षा-अधिकतमकरण एल्गोरिदम के समान होता है। (केएल-डाइवर्जेंस का दूसरे तरीके से उपयोग करने से अपेक्षा प्रसार एल्गोरिदम उत्पन्न होता है।) | ||
=== दुरूहता === | === दुरूहता === | ||
विभिन्न | विभिन्न विधियों का उपयोग सामान्यतः इसका अनुमान लगाने के लिए किया जाता है: | ||
:<math>P(\mathbf Z \mid \mathbf X) = \frac{P(\mathbf X \mid \mathbf Z)P(\mathbf Z)}{P(\mathbf X)} = \frac{P(\mathbf X \mid \mathbf Z)P(\mathbf Z)}{\int_{\mathbf Z} P(\mathbf X,\mathbf Z') \,d\mathbf Z'}</math> | :<math>P(\mathbf Z \mid \mathbf X) = \frac{P(\mathbf X \mid \mathbf Z)P(\mathbf Z)}{P(\mathbf X)} = \frac{P(\mathbf X \mid \mathbf Z)P(\mathbf Z)}{\int_{\mathbf Z} P(\mathbf X,\mathbf Z') \,d\mathbf Z'}</math> | ||
प्रत्येक में <math>P(\mathbf X)</math> की गणना करने के लिए <math>\mathbf Z</math> से अधिक का मर्गिनाल्स पर जाना सामान्यतः कठिन है, क्योंकि, उदाहरण के लिए, <math>\mathbf Z</math> कि खोज समिष्ट संयुक्त रूप से बड़ी होती है। इसलिए, हम <math>Q(\mathbf Z) \approx P(\mathbf Z \mid \mathbf X)</math> का उपयोग करके अनुमान करना चाहते हैं। | |||
=== साक्ष्य निचली सीमा === | === साक्ष्य निचली सीमा === | ||
{{Main| | {{Main|साक्ष्य निचली सीमा }} | ||
मान लें कि <math>P(\mathbf Z \mid \mathbf X) = \frac{P(\mathbf X, \mathbf Z)}{P(\mathbf X)}</math>, उपरोक्त केएल-विचलन को इस प्रकार भी लिखा जा सकता है | मान लें कि <math>P(\mathbf Z \mid \mathbf X) = \frac{P(\mathbf X, \mathbf Z)}{P(\mathbf X)}</math>, उपरोक्त केएल-विचलन को इस प्रकार भी लिखा जा सकता है | | ||
:<math> | :<math> | ||
D_{\mathrm{KL}}(Q \parallel P) | D_{\mathrm{KL}}(Q \parallel P) | ||
= \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log \frac{Q(\mathbf{Z})}{P(\mathbf{Z},\mathbf{X})} + \log P(\mathbf{X}) \right] | = \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log \frac{Q(\mathbf{Z})}{P(\mathbf{Z},\mathbf{X})} + \log P(\mathbf{X}) \right] | ||
= \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] + \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log P(\mathbf{X}) \right] | = \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] + \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log P(\mathbf{X}) \right] | ||
</math> | </math> | ||
क्योंकि <math>P(\mathbf{X})</math> के संबंध में | क्योंकि <math>P(\mathbf{X})</math> के संबंध में स्थिरांक <math>\mathbf Z</math> है और <math>\sum_\mathbf{Z} Q(\mathbf{Z}) = 1</math> क्योंकि <math>Q(\mathbf{Z})</math> वितरण है, जो कि हमारे समीप है | ||
:<math> | :<math> | ||
D_{\mathrm{KL}}(Q \parallel P) = \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] + \log P(\mathbf{X}) | D_{\mathrm{KL}}(Q \parallel P) = \sum_\mathbf{Z} Q(\mathbf{Z}) \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] + \log P(\mathbf{X}) | ||
</math> | </math> | ||
जिसे अपेक्षित मान की परिभाषा के अनुसार (एक असतत यादृच्छिक | जिसे अपेक्षित मान की परिभाषा के अनुसार (एक असतत यादृच्छिक वेरिएबल के लिए) निम्नानुसार लिखा जा सकता है | ||
:<math> | :<math> | ||
| Line 57: | Line 54: | ||
= \mathbb{E}_{\mathbf Q } \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] + \log P(\mathbf{X}) | = \mathbb{E}_{\mathbf Q } \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] + \log P(\mathbf{X}) | ||
</math> | </math> | ||
जिसे पुनर्व्यवस्थित करके बनाया जा सकता है | जिसे पुनर्व्यवस्थित करके बनाया जा सकता है | | ||
:<math> | :<math> | ||
\log P(\mathbf{X}) = | \log P(\mathbf{X}) = | ||
D_{\mathrm{KL}}(Q \parallel P) - \mathbb{E}_{\mathbf Q } \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] = D_{\mathrm{KL}}(Q\parallel P) + \mathcal{L}(Q) | D_{\mathrm{KL}}(Q \parallel P) - \mathbb{E}_{\mathbf Q } \left[ \log Q(\mathbf{Z}) - \log P(\mathbf{Z},\mathbf{X}) \right] = D_{\mathrm{KL}}(Q\parallel P) + \mathcal{L}(Q) | ||
</math> | </math> | ||
लॉग- | चूंकि लॉग-साक्ष्य <math>\log P(\mathbf{X})</math> <math>Q</math> के संबंध में निश्चित किया गया है, अंतिम पद <math>\mathcal{L}(Q)</math> को अधिकतम करने से <math>P</math> से <math>Q</math>. का केएल विचलन कम हो जाता है। <math>Q</math> के उचित विकल्प द्वारा, <math>Q</math>, <math>\mathcal{L}(Q)</math> सुव्यवस्थित हो जाता है इसका कार्य गणना करना और अधिकतम करना होता हैं। इसलिए हमारे समीप पश्च <math>P(\mathbf{Z}\mid \mathbf{X})</math> के लिए विश्लेषणात्मक सन्निकटन और लॉग-साक्ष्य <math>\log P(\mathbf{X})</math> के लिए निचली सीमा <math>\mathcal{L}(Q)</math> दोनों हैं (चूंकि केएल-विचलन गैर-नकारात्मक है)। | ||
निचली सीमा <math>\mathcal{L}(Q)</math> इसे [[थर्मोडायनामिक मुक्त ऊर्जा]] के अनुरूप ( | निचली सीमा <math>\mathcal{L}(Q)</math> इसे [[थर्मोडायनामिक मुक्त ऊर्जा]] के अनुरूप (ऋणात्मक) परिवर्तनशील मुक्त ऊर्जा के रूप में जाना जाता है क्योंकि इसे ऋणात्मक ऊर्जा के रूप में भी व्यक्त किया जा सकता है | यह <math>\operatorname{E}_{Q}[\log P(\mathbf{Z},\mathbf{X})]</math> प्लस <math>Q</math> एन्ट्रॉपी (सूचना सिद्धांत) हैं। शब्द <math>\mathcal{L}(Q)</math> इसे एविडेंस लोअर बाउंड के रूप में भी जाना जाता है, जिसे संक्षेप में एविडेंस लोअर बाउंड के रूप में जाना जाता है, इस बात पर जोर देने के लिए कि यह डेटा के लॉग-एविडेंस पर निचला बाउंड है। | ||
=== प्रमाण === | === प्रमाण === | ||
[[ब्रेगमैन विचलन]] के सामान्यीकृत पायथागॉरियन प्रमेय द्वारा, जिसमें केएल-विचलन | [[ब्रेगमैन विचलन]] के सामान्यीकृत पायथागॉरियन प्रमेय द्वारा, जिसमें केएल-विचलन विशेष स्तिथि होती है, इसमें यह दिखाया जा सकता है कि <ref name=Tran2018>{{cite arXiv|title=सूचना ज्यामिति के माध्यम से कोपुला वेरिएशनल बेज़ अनुमान|first1=Viet Hung|last1=Tran|year=2018|eprint=1803.10998|class=cs.IT}}</ref> <ref name="Martin2014"/> | ||
[[File:Bregman_divergence_Pythagorean.png|right|300px|thumb|ब्रेगमैन विचलन के लिए सामान्यीकृत पाइथागोरस प्रमेय<ref name="Martin2014">{{cite journal |last1=Adamčík |first1=Martin |title=ब्रेगमैन डायवर्जेंस की सूचना ज्यामिति और मल्टी-एक्सपर्ट रीजनिंग में कुछ अनुप्रयोग|journal=Entropy |date=2014 |volume=16 |issue=12 |pages=6338–6381|bibcode=2014Entrp..16.6338A |doi=10.3390/e16126338 |doi-access=free }}</ref>]]:<math> | [[File:Bregman_divergence_Pythagorean.png|right|300px|thumb|ब्रेगमैन विचलन के लिए सामान्यीकृत पाइथागोरस प्रमेय<ref name="Martin2014">{{cite journal |last1=Adamčík |first1=Martin |title=ब्रेगमैन डायवर्जेंस की सूचना ज्यामिति और मल्टी-एक्सपर्ट रीजनिंग में कुछ अनुप्रयोग|journal=Entropy |date=2014 |volume=16 |issue=12 |pages=6338–6381|bibcode=2014Entrp..16.6338A |doi=10.3390/e16126338 |doi-access=free }}</ref>]]:<math> | ||
D_{\mathrm{KL}}(Q\parallel P) \geq D_{\mathrm{KL}}(Q\parallel Q^{*}) + D_{\mathrm{KL}}(Q^{*}\parallel P), \forall Q^{*} \in\mathcal{C} | D_{\mathrm{KL}}(Q\parallel P) \geq D_{\mathrm{KL}}(Q\parallel Q^{*}) + D_{\mathrm{KL}}(Q^{*}\parallel P), \forall Q^{*} \in\mathcal{C} | ||
</math> | </math> | ||
जहाँ <math>\mathcal{C}</math> उत्तल समुच्चय है और समानता जब क्रियान्वित रहती है यदि: | |||
:<math> Q = Q^{*} \triangleq \arg\min_{Q\in\mathcal{C}}D_{\mathrm{KL}}(Q\parallel P). </math> | :<math> Q = Q^{*} \triangleq \arg\min_{Q\in\mathcal{C}}D_{\mathrm{KL}}(Q\parallel P). </math> | ||
इस | इस स्थितियों में, वैश्विक न्यूनतमकर्ता <math>Q^{*}(\mathbf{Z}) = q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)q^{*}(\mathbf{Z}_2) = q^{*}(\mathbf{Z}_2\mid\mathbf{Z}_1)q^{*}(\mathbf{Z}_1),</math> साथ <math>\mathbf{Z}=\{\mathbf{Z_1},\mathbf{Z_2}\},</math> इस प्रकार पाया जा सकता है | <ref name=Tran2018/> | ||
:<math> q^{*}(\mathbf{Z}_2) | :<math> q^{*}(\mathbf{Z}_2) | ||
= \frac{P(\mathbf{X})}{\zeta(\mathbf{X})}\frac{P(\mathbf{Z}_2\mid\mathbf{X})}{\exp(D_{\mathrm{KL}}(q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)\parallel P(\mathbf{Z}_1\mid\mathbf{Z}_2,\mathbf{X})))} | = \frac{P(\mathbf{X})}{\zeta(\mathbf{X})}\frac{P(\mathbf{Z}_2\mid\mathbf{X})}{\exp(D_{\mathrm{KL}}(q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)\parallel P(\mathbf{Z}_1\mid\mathbf{Z}_2,\mathbf{X})))} | ||
= \frac{1}{\zeta(\mathbf{X})}\exp\mathbb{E}_{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\left(\log\frac{P(\mathbf{Z},\mathbf{X})}{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\right),</math> | = \frac{1}{\zeta(\mathbf{X})}\exp\mathbb{E}_{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\left(\log\frac{P(\mathbf{Z},\mathbf{X})}{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\right), </math> | ||
जिसमें सामान्यीकरण स्थिरांक है | जिसमें सामान्यीकरण स्थिरांक है | | ||
:<math>\zeta(\mathbf{X}) | :<math>\zeta(\mathbf{X}) | ||
=P(\mathbf{X})\int_{\mathbf{Z}_2}\frac{P(\mathbf{Z}_2\mid\mathbf{X})}{\exp(D_{\mathrm{KL}}(q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)\parallel P(\mathbf{Z}_1\mid\mathbf{Z}_2,\mathbf{X})))} | =P(\mathbf{X})\int_{\mathbf{Z}_2}\frac{P(\mathbf{Z}_2\mid\mathbf{X})}{\exp(D_{\mathrm{KL}}(q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)\parallel P(\mathbf{Z}_1\mid\mathbf{Z}_2,\mathbf{X})))} | ||
= \int_{\mathbf{Z}_{2}}\exp\mathbb{E}_{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\left(\log\frac{P(\mathbf{Z},\mathbf{X})}{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\right).</math> | = \int_{\mathbf{Z}_{2}}\exp\mathbb{E}_{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\left(\log\frac{P(\mathbf{Z},\mathbf{X})}{q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2)}\right). </math> | ||
शब्द <math>\zeta(\mathbf{X})</math> व्यवहार में इसे | शब्द <math>\zeta(\mathbf{X})</math> व्यवहार में इसे अधिकांशतः मॉडल एविडेंस लोअर बाउंड (ईएलबीओ) कहा जाता है क्योंकि <math>P(\mathbf{X})\geq\zeta(\mathbf{X})=\exp(\mathcal{L}(Q^{*}))</math>,<ref name=Tran2018/> जैसा कि उपर दिखाया गया है। | ||
<math>\mathbf{Z}_1</math>और <math>\mathbf{Z}_2,</math> की भूमिकाओं का परिवर्तन करके हम क्रमशः अनुमानित रूप से <math>q^{*}(\mathbf{Z}_1)</math> और <math>q^{*}(\mathbf{Z}_2)</math> और <math>P(\mathbf{Z}_1\mid\mathbf{X})</math> और <math>P(\mathbf{Z}_2\mid\mathbf{X}),</math> पुनरावर्ती गणना कर सकते हैं | यद्यपि इस पुनरावृत्तीय योजना को नीरस रूप से अभिसरण करने की गारंटी है,<ref name=Tran2018/> एकत्रित <math>Q^{*}</math> का केवल <math>D_{\mathrm{KL}}(Q\parallel P)</math> स्थानीय मिनिमाइज़र होता है| | |||
यदि विवश | यदि विवश समिष्ट <math>\mathcal{C}</math> स्वतंत्र समिष्ट के अंदर ही सीमित है, अर्थात <math>q^{*}(\mathbf{Z}_1\mid\mathbf{Z}_2) = q^{*}(\mathbf{Z_1}),</math>उपरोक्त पुनरावृत्तीय योजना तथाकथित माध्य क्षेत्र सन्निकटन बन जाएगी <math>Q^{*}(\mathbf{Z}) = q^{*}(\mathbf{Z}_1)q^{*}(\mathbf{Z}_2),</math>जैसा कि नीचे दिया गया है। | ||
==माध्य क्षेत्र सन्निकटन== | ==माध्य क्षेत्र सन्निकटन == | ||
परिवर्तनशील वितरण <math>Q(\mathbf{Z})</math> | परिवर्तनशील वितरण <math>Q(\mathbf{Z})</math> सामान्यतः यह माना जाता है कि अव्यक्त वेरिएबल के समुच्चय के कुछ विभाजन पर कारक बनाया जाता है, अर्थात अव्यक्त वेरिएबल के कुछ विभाजन के लिए <math>\mathbf{Z}</math> में <math>\mathbf{Z}_1 \dots \mathbf{Z}_M</math> सम्मिलित होता हैं | | ||
:<math>Q(\mathbf{Z}) = \prod_{i=1}^M q_i(\mathbf{Z}_i\mid \mathbf{X})</math> | :<math>Q(\mathbf{Z}) = \prod_{i=1}^M q_i(\mathbf{Z}_i\mid \mathbf{X})</math> | ||
इसे विविधताओं की गणना (इसलिए नाम वेरिएबल बेयस) का उपयोग करके दिखाया जा सकता है कि सबसे अच्छा वितरण <math>q_j^{*}</math> प्रत्येक कारक के लिए <math>q_j</math> (वितरण के संदर्भ में केएल विचलन को न्यूनतम करना, जैसा कि ऊपर वर्णित है) संतुष्ट करता है | इसे विविधताओं की गणना (इसलिए नाम वेरिएबल बेयस) का उपयोग करके दिखाया जा सकता है कि सबसे अच्छा वितरण <math>q_j^{*}</math> प्रत्येक कारक के लिए <math>q_j</math> (वितरण के संदर्भ में केएल विचलन को न्यूनतम करना, जैसा कि ऊपर वर्णित है) संतुष्ट करता है | | ||
:<math>q_j^{*}(\mathbf{Z}_j\mid \mathbf{X}) = \frac{e^{\operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})]}}{\int e^{\operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})]}\, d\mathbf{Z}_j}</math> | :<math>q_j^{*}(\mathbf{Z}_j\mid \mathbf{X}) = \frac{e^{\operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})]}}{\int e^{\operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})]}\, d\mathbf{Z}_j}</math> | ||
जहाँ <math>\operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})]</math> डेटा और अव्यक्त वेरिएबल की संयुक्त संभावना के लघुगणक का अपेक्षित मूल्य होता है, जिसके संबंध में <math>q^*</math> लिया गया है | जिसके विभाजन में उपस्तिथ सभी वेरिएबल्स पर: लेम्मा 4.1 का संदर्भ लिया जाता हैं | <ref name=Yoon2021>{{Cite journal |last=Lee|first=Se Yoon| title = Gibbs sampler and coordinate ascent variational inference: A set-theoretical review|journal=Communications in Statistics - Theory and Methods|year=2021|pages=1–21|doi=10.1080/03610926.2021.1921214|arxiv=2008.01006|s2cid=220935477}}</ref> यह <math>q_j^{*}(\mathbf{Z}_j\mid \mathbf{X})</math> वितरण की व्युत्पत्ति के लिए किया जाता है | | |||
व्यवहार में, हम सामान्यतः लघुगणक के संदर्भ में कार्य करते हैं, अर्थात: | |||
:<math>\ln q_j^{*}(\mathbf{Z}_j\mid \mathbf{X}) = \operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})] + \text{constant}</math> | |||
उपरोक्त अभिव्यक्ति में स्थिरांक सामान्यीकृत स्थिरांक (उपरोक्त अभिव्यक्ति में प्रत्येक) <math>q_j^{*}</math> से संबंधित है ) और सामान्यतः निरीक्षण द्वारा पुनः स्थापित किया जाता है, क्योंकि अभिव्यक्ति के शेष भागों को सामान्यतः ज्ञात प्रकार के वितरण (जैसे [[गाऊसी वितरण]], [[गामा वितरण]], आदि) के रूप में पहचाना जा सकता है। | |||
अपेक्षाओं के गुणों का प्रयोग, अभिव्यक्ति <math>\operatorname{E}_{q^*_{-j}} [\ln p(\mathbf{Z}, \mathbf{X})]</math> सामान्यतः अव्यक्त वेरिएबल और अपेक्षाओं (और कभी-कभी उच्चतर [[क्षण (गणित)]] जैसे विचरण) पर [[पूर्व वितरण]] के निश्चित [[हाइपरपैरामीटर]] के फलन में सरलीकृत किया जा सकता है, जो कि वर्तमान विभाजन <math>\mathbf{Z}_j</math> में नहीं होता है (अर्थात अव्यक्त वेरिएबल सम्मिलित नहीं हैं) में ) हैं | यह विभाजन में वेरिएबल पर वितरण के मापदंडों और अन्य विभाजन में वेरिएबल की अपेक्षाओं के मध्य परिपत्र निर्भरता बनाता है। यह स्वाभाविक रूप से ईएम (अपेक्षा-अधिकतमकरण एल्गोरिदम) की प्रकार पुनरावृत्त एल्गोरिदम का सुझाव देता है, जिसमें अव्यक्त वेरिएबल की अपेक्षाओं (और संभवतः उच्च क्षणों) को कुछ फैशन में (संभवतःयादृच्छिक रूप से) प्रारंभ किया जाता है, और फिर प्रत्येक वितरण के पैरामीटर होते हैं तथा अपेक्षाओं के वर्तमान मानों का उपयोग करके बारी-बारी से गणना की जाती है, जिसके पश्चात् गणना किए गए मापदंडों के अनुसार नए गणना किए गए वितरण की अपेक्षा उचित रूप से निर्धारित की जाती है। इस प्रकार का एल्गोरिदम अनुक्रम की सीमा की गारंटी देता है। <ref>{{cite book|title=उत्तल अनुकूलन|first1=Stephen P.|last1=Boyd|first2=Lieven|last2=Vandenberghe|year=2004|publisher=Cambridge University Press|isbn=978-0-521-83378-3|url=https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf|access-date=October 15, 2011}}</ref> | |||
दूसरे शब्दों में, वेरिएबल के प्रत्येक विभाजन के लिए, विभाजन के वेरिएबल पर वितरण के लिए अभिव्यक्ति को सरल बनाकर और प्रश्न में वेरिएबल पर वितरण की कार्यात्मक निर्भरता की जांच करके, वितरण का वर्ग सामान्यतः निर्धारित किया जा सकता है (जो इसके स्थान में निर्धारित करता है) स्थिरांक का मान) हैं। वितरण के मापदंडों का सूत्र पूर्व वितरणों के हाइपरपैरामीटर (जो ज्ञात स्थिरांक हैं) के संदर्भ में व्यक्त किया जाता हैं, किन्तु अन्य विभाजनों में वेरिएबल के कार्यों की अपेक्षाओं के संदर्भ में भी व्यक्त किया जाएगा। सामान्यतः इन अपेक्षाओं को स्वयं वेरिएबलों की अपेक्षाओं के कार्यों में सरलीकृत किया जा सकता है ([[अर्थ|अर्थात]] साधन); कभी-कभी वर्गाकार वेरिएबलों की अपेक्षाएं (जो वेरिएबलों के विचरण से संबंधित हो सकती हैं), या उच्च शक्तियों (अर्थात उच्चतर क्षण (गणित)) की अपेक्षाएं भी प्रकट होती हैं। अधिकतर स्थितियों में, अन्य वेरिएबल का वितरण ज्ञात वर्ग से होता हैं, और प्रासंगिक अपेक्षाओं के लिए सूत्रों को देखा जा सकता है। चूँकि, वह सूत्र उन वितरण मापदंडों पर निर्भर करते हैं, जो इसके स्थान में अन्य वेरिएबल के बारे में अपेक्षाओं पर निर्भर करते हैं। इसका परिणाम यह है कि प्रत्येक वेरिएबल के वितरण के मापदंडों के सूत्रों को वेरिएबल के मध्य पारस्परिक, गैर-रेखीय निर्भरता वाले समीकरणों की श्रृंखला के रूप में व्यक्त किया जा सकता है। सामान्यतः, समीकरणों की इस प्रणाली को सीधे समाधान करना संभव नहीं है। चूँकि, जैसा कि ऊपर बताया गया है, निर्भरताएँ सरल पुनरावृत्त एल्गोरिथ्म का सुझाव देती हैं, जो अधिकतर स्थितियों में अभिसरण की गारंटी देता है। उदाहरण से यह प्रक्रिया और स्पष्ट हो जाटी हैं | | |||
दूसरे शब्दों में, | |||
==परिवर्तनात्मक अनुमान के लिए | =='''परिवर्तनात्मक अनुमान के लिए द्वैत सूत्र'''== | ||
[[File:CAVI algorithm explain.jpg|600px|thumb|right|द्वैत सूत्र द्वारा समन्वय आरोहण परिवर्तनीय अनुमान एल्गोरिथ्म का सचित्र चित्रण<ref name=Yoon2021/>]]निम्नलिखित प्रमेय को परिवर्तनशील अनुमान के लिए द्वैत सूत्र के रूप में जाना जाता है।<ref name=Yoon2021/>यह वैरिएबल बेयस विधियों में उपयोग किए जाने वाले वैरिएबल वितरण के कुछ महत्वपूर्ण गुणों की व्याख्या करता है। | [[File:CAVI algorithm explain.jpg|600px|thumb|right|द्वैत सूत्र द्वारा समन्वय आरोहण परिवर्तनीय अनुमान एल्गोरिथ्म का सचित्र चित्रण<ref name=Yoon2021/>]]निम्नलिखित प्रमेय को परिवर्तनशील अनुमान के लिए द्वैत सूत्र के रूप में जाना जाता है। <ref name="Yoon2021" /> यह वैरिएबल बेयस विधियों में उपयोग किए जाने वाले वैरिएबल वितरण के कुछ महत्वपूर्ण गुणों की व्याख्या करता है। | ||
प्रमेय दो [[संभाव्यता स्थान|संभाव्यता]] समिष्ट <math>(\Theta,\mathcal{F},P)</math> और <math>(\Theta,\mathcal{F},Q)</math> के साथ <math>Q \ll P</math> पर विचार करें मान लें कि सामान्य प्रभावी [[संभाव्यता माप]] <math>\lambda</math> होती है जैसे है कि <math>P \ll \lambda</math> और <math>Q \ll \lambda</math>. मान लीजिये कि <math>h</math> <math>(\Theta,\mathcal{F},P)</math> पर किसी भी वास्तविक-मूल्यवान यादृच्छिक वेरिएबल को निरूपित करें जो <math>h \in L_1(P)</math> संतुष्ट करता है | तब निम्नलिखित समानता क्रियान्वित रहती है | | |||
: | |||
:<math> \log E_P[\exp h] = \text{sup}_{Q \ll P} \{ E_Q[h] - D_\text{KL}(Q \parallel P)\}.</math> | :<math> \log E_P[\exp h] = \text{sup}_{Q \ll P} \{ E_Q[h] - D_\text{KL}(Q \parallel P)\}.</math> | ||
इसके | इसके अतिरिक्त, दाहिनी ओर का सर्वोच्च तभी प्राप्त होता है जब वह क्रियान्वित रहता है | ||
:<math> \frac{q(\theta)}{p(\theta)} = \frac{\exp h(\theta)}{E_P[\exp h]},</math> | :<math> \frac{q(\theta)}{p(\theta)} = \frac{\exp h(\theta)}{E_P[\exp h]},</math> | ||
संभाव्यता माप | संभाव्यता माप <math>Q</math> के संबंध में लगभग निश्चित रूप से , जहाँ <math>p(\theta) = dP/d\lambda</math> और <math>q(\theta) = dQ/d\lambda</math> क्रमश <math>\lambda</math> के संबंध में संभाव्यता माप <math>P</math> और <math>Q</math> के रेडॉन-निकोडिम डेरिवेटिव को निरूपित करते है | | ||
==एक | ==एक मूलभूत उदाहरण == | ||
एक सरल गैर-पदानुक्रमित बायेसियन मॉडल पर विचार करें जिसमें स्वतंत्र रूप से वितरित i.i.d. का | एक सरल गैर-पदानुक्रमित बायेसियन मॉडल पर विचार करें जिसमें स्वतंत्र रूप से वितरित i.i.d. का समुच्चय सम्मिलित है। तथा अज्ञात माध्य और विचरण के साथ गॉसियन वितरण से अवलोकन भी सम्मिलित हो सकते हैं। <ref name=bishop>{{Cite book |last=Bishop |first=Christopher M. |chapter=Chapter 10 |title=पैटर्न मान्यता और मशीन प्रवीणता|year=2006 |publisher=Springer |isbn=978-0-387-31073-2 |author-link=Christopher M. Bishop}}</ref> निम्नलिखित में, हम इस मॉडल के माध्यम से वेरिएबल बेयस विधि की कार्यप्रणाली को स्पष्ट करने के लिए विस्तार से कार्य करते हैं। | ||
गणितीय सुविधा के लिए, निम्नलिखित उदाहरण में हम [[परिशुद्धता (सांख्यिकी)]] के संदर्भ में | गणितीय सुविधा के लिए, निम्नलिखित उदाहरण में हम [[परिशुद्धता (सांख्यिकी)]] के संदर्भ में कार्य करते हैं - अर्थात विचरण का व्युत्क्रम हो (या बहुभिन्नरूपी गॉसियन में, सहप्रसरण आव्युह का व्युत्क्रम) - न कि स्वयं विचरण हो । (सैद्धांतिक दृष्टिकोण से, परिशुद्धता और भिन्नता समतुल्य होती हैं क्योंकि दोनों के मध्य वन-से-वन पत्राचार है।) | ||
===गणितीय मॉडल=== | ===गणितीय मॉडल === | ||
हम संयुग्मित पूर्व वितरणों को अज्ञात माध्य | हम संयुग्मित पूर्व वितरणों को अज्ञात माध्य <math>\mu</math> और परिशुद्धता <math>\tau</math> पर रखते हैं अर्थात माध्य भी गाऊसी वितरण का अनुसरण करता है जबकि दूसरे शब्दों में परिशुद्धता गामा वितरण का अनुसरण करती है। | ||
:<math> | :<math> | ||
| Line 134: | Line 133: | ||
N &= \text{number of data points} | N &= \text{number of data points} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
पूर्व वितरणों में हाइपर पैरामीटर <math>\mu_0, \lambda_0, a_0</math> और <math>b_0</math> मान दिए जाते हैं | जिसमे <math>\mu</math> और <math>\tau</math>. के पूर्व में वितरण निश्चित होते हैं, जो पूर्व वितरणों के बारे में अज्ञानता का संकेत देते हैं तथा व्यापक पूर्व वितरण देने के लिए उन्हें लघु धनात्मक संख्याओं पर समुच्चय किया जा सकता है | | |||
हम | हम <math>N</math> डेटा पॉइंट <math>\mathbf{X} = \{x_1, \ldots, x_N\}</math> दे रहे हैं और हमारा लक्ष्य पश्च वितरण <math>q(\mu, \tau)=p(\mu,\tau\mid x_1, \ldots, x_N)</math> का अनुमान लगाना है मापदंडों का <math>\mu</math> और <math>\tau.</math> होता हैं | | ||
===संयुक्त संभावना === | |||
===संयुक्त संभावना=== | सभी वेरिएबलों की संयुक्त प्रायिकता को इस प्रकार पुनः लिखा जा सकता है | ||
सभी | |||
:<math>p(\mathbf{X},\mu,\tau) = p(\mathbf{X}\mid \mu,\tau) p(\mu\mid \tau) p(\tau)</math> | :<math>p(\mathbf{X},\mu,\tau) = p(\mathbf{X}\mid \mu,\tau) p(\mu\mid \tau) p(\tau)</math> | ||
| Line 153: | Line 151: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ | |||
:<math> | :<math> | ||
| Line 164: | Line 162: | ||
===गुणनखंडित सन्निकटन=== | ===गुणनखंडित सन्निकटन=== | ||
यह मान लीजिए <math>q(\mu,\tau) = q(\mu)q(\tau)</math>, अर्थात कि पश्च वितरण <math>\mu</math> और <math>\tau</math> के लिए स्वतंत्र कारकों में विभाजित होता है | इस प्रकार की धारणा वैरिएबल बायेसियन पद्धति को रेखांकित करती है। वास्तविक पश्च वितरण वास्तव में इस प्रकार से कारक नहीं होता है (वास्तव में, इस साधारण स्थितियां में, इसे [[गाऊसी-गामा वितरण]] के रूप में जाना जाता है), और इसलिए हम जो परिणाम प्राप्त करेंगे उसे अनुमान कहा जाता हैं। | |||
===की व्युत्पत्ति {{math|''q''(''μ'')}}=== | ===की व्युत्पत्ति {{math|''q''(''μ'')}}=== | ||
| Line 179: | Line 177: | ||
&= \operatorname{E}_{\tau}\left[\sum_{n=1}^N -\frac{(x_n-\mu)^2\tau}{2}\right] + \operatorname{E}_{\tau}\left[-\frac{(\mu-\mu_0)^2\lambda_0 \tau}{2}\right] + C_3 \\ | &= \operatorname{E}_{\tau}\left[\sum_{n=1}^N -\frac{(x_n-\mu)^2\tau}{2}\right] + \operatorname{E}_{\tau}\left[-\frac{(\mu-\mu_0)^2\lambda_0 \tau}{2}\right] + C_3 \\ | ||
&= - \frac{\operatorname{E}_{\tau}[\tau]}{2} \left\{ \sum_{n=1}^N (x_n-\mu)^2 + \lambda_0(\mu-\mu_0)^2 \right\} + C_3 | &= - \frac{\operatorname{E}_{\tau}[\tau]}{2} \left\{ \sum_{n=1}^N (x_n-\mu)^2 + \lambda_0(\mu-\mu_0)^2 \right\} + C_3 | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
उपरोक्त व्युत्पत्ति में, <math>C</math>, <math>C_2</math> और <math>C_3</math> उन | उपरोक्त व्युत्पत्ति में, <math>C</math>, <math>C_2</math> और <math>C_3</math> उन मानों को संदर्भित करें जो <math>\mu</math> के संबंध में स्थिर होते हैं. ध्यान दें कि शब्द <math>\operatorname{E}_{\tau}[\ln p(\tau)]</math> <math>\mu</math> का कार्य नहीं है और <math>\mu</math> के मूल्य की चिंता किए बिना उसका मूल्य समान होता हैं | इसलिए पंक्ति 3 में हम इसे अंत में स्थिर पद में समाहित कर सकते हैं। हम पंक्ति 7 में भी यही कार्य करते हैं। | ||
अंतिम पंक्ति | अंतिम पंक्ति <math>\mu</math> में बस द्विघात बहुपद है . चूँकि यह <math>q_\mu^*(\mu)</math> का लघुगणक है, हम देख सकते हैं कि <math>q_\mu^*(\mu)</math> स्वयं गाऊसी वितरण है। | ||
एक निश्चित मात्रा में कठिन गणित के साथ (ब्रेसिज़ के अंदर के वर्गों का विस्तार करना, | एक निश्चित मात्रा में कठिन गणित के साथ (ब्रेसिज़ के अंदर के वर्गों का विस्तार करना, <math>\mu</math> और <math>\mu^2</math> से सम्मिलित शब्दों को भिन्न करना और समूहीकृत करना और <math>\mu</math> पर [[वर्ग पूरा करना]] ), हम गाऊसी वितरण के पैरामीटर प्राप्त कर सकते हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 199: | Line 197: | ||
&= -\frac{\operatorname{E}_{\tau}[\tau]}{2} \left\{ (\lambda_0+N)\left(\mu-\frac{\lambda_0\mu_0 + \sum_{n=1}^N x_n}{\lambda_0+N}\right)^2 \right\} + C_5 \\ | &= -\frac{\operatorname{E}_{\tau}[\tau]}{2} \left\{ (\lambda_0+N)\left(\mu-\frac{\lambda_0\mu_0 + \sum_{n=1}^N x_n}{\lambda_0+N}\right)^2 \right\} + C_5 \\ | ||
&= -\frac{1}{2} (\lambda_0+N)\operatorname{E}_{\tau}[\tau] \left(\mu-\frac{\lambda_0\mu_0 + \sum_{n=1}^N x_n}{\lambda_0+N}\right)^2 + C_5 | &= -\frac{1}{2} (\lambda_0+N)\operatorname{E}_{\tau}[\tau] \left(\mu-\frac{\lambda_0\mu_0 + \sum_{n=1}^N x_n}{\lambda_0+N}\right)^2 + C_5 | ||
\end{align}</math> | \end{align} </math> | ||
ध्यान दें कि उपरोक्त सभी चरणों को सामान्य वितरण | ध्यान दें कि उपरोक्त सभी चरणों को सामान्य वितरण या दो द्विघातों के योग के सूत्र का उपयोग करके छोटा किया जा सकता है। | ||
दूसरे शब्दों में: | दूसरे शब्दों में: | ||
| Line 215: | Line 213: | ||
===की व्युत्पत्ति {{math|q(τ)}}=== | ===की व्युत्पत्ति {{math|q(τ)}}=== | ||
की व्युत्पत्ति <math>q_\tau^*(\tau)</math> | उपरोक्त की व्युत्पत्ति <math>q_\tau^*(\tau)</math>के समान है, चूँकि हम संक्षिप्तता के लिए कुछ विवरण छोड़ देते हैं। | ||
:<math> | :<math> | ||
| Line 223: | Line 221: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
दोनों पक्षों को घातांकित करने पर हम यह देख सकते हैं <math>q_\tau^*(\tau)</math> | दोनों पक्षों को घातांकित करने पर हम यह देख सकते हैं कि <math>q_\tau^*(\tau)</math> गामा वितरण है. विशेष रूप से: | ||
:<math> | :<math> | ||
| Line 234: | Line 232: | ||
===पैरामीटर की गणना के लिए एल्गोरिदम=== | ===पैरामीटर की गणना के लिए एल्गोरिदम === | ||
आइए हम | आइए हम पूर्व अनुभागों के निष्कर्षों का पुनर्कथन करें: | ||
:<math> | :<math> | ||
| Line 254: | Line 252: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
प्रत्येक | प्रत्येक स्थितियों में, किसी वेरिएबल पर वितरण के पैरामीटर दूसरे वेरिएबल के संबंध में ली गई अपेक्षाओं पर निर्भर करते हैं। हम गॉसियन और गामा वितरण के क्षणों की अपेक्षाओं के लिए मानक सूत्रों का उपयोग करके अपेक्षाओं का विस्तार कर सकते हैं: | ||
:<math> | :<math> | ||
| Line 264: | Line 262: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
इन सूत्रों को उपरोक्त समीकरणों पर | इन सूत्रों को उपरोक्त समीकरणों पर प्रयुक्त करना अधिकतर स्थितियों में साधारण है, किन्तु समीकरण के लिए <math>b_N</math> अधिक कार्य लेता है: | ||
:<math> | :<math> | ||
| Line 272: | Line 270: | ||
&= b_0 + \frac{1}{2} \left[ (\lambda_0+N)\operatorname{E}_\mu[\mu^2] -2 \left (\lambda_0\mu_0 + \sum_{n=1}^N x_n \right)\operatorname{E}_\mu [\mu] + \left (\sum_{n=1}^N x_n^2 \right ) + \lambda_0\mu_0^2 \right] \\ | &= b_0 + \frac{1}{2} \left[ (\lambda_0+N)\operatorname{E}_\mu[\mu^2] -2 \left (\lambda_0\mu_0 + \sum_{n=1}^N x_n \right)\operatorname{E}_\mu [\mu] + \left (\sum_{n=1}^N x_n^2 \right ) + \lambda_0\mu_0^2 \right] \\ | ||
&= b_0 + \frac{1}{2} \left[ (\lambda_0+N) \left (\lambda_N^{-1} + \mu_N^2 \right ) -2 \left (\lambda_0\mu_0 + \sum_{n=1}^N x_n \right)\mu_N + \left(\sum_{n=1}^N x_n^2 \right) + \lambda_0\mu_0^2 \right] \\ | &= b_0 + \frac{1}{2} \left[ (\lambda_0+N) \left (\lambda_N^{-1} + \mu_N^2 \right ) -2 \left (\lambda_0\mu_0 + \sum_{n=1}^N x_n \right)\mu_N + \left(\sum_{n=1}^N x_n^2 \right) + \lambda_0\mu_0^2 \right] \\ | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
फिर हम पैरामीटर समीकरणों को बिना किसी अपेक्षा के इस प्रकार लिख सकते हैं: | फिर हम पैरामीटर समीकरणों को बिना किसी अपेक्षा के इस प्रकार लिख सकते हैं: | ||
| Line 282: | Line 280: | ||
a_N &= a_0 + \frac{N+1}{2} \\ | a_N &= a_0 + \frac{N+1}{2} \\ | ||
b_N &= b_0 + \frac{1}{2} \left[ (\lambda_0+N) \left (\lambda_N^{-1} + \mu_N^2 \right ) -2 \left (\lambda_0\mu_0 + \sum_{n=1}^N x_n \right )\mu_N + \left (\sum_{n=1}^N x_n^2 \right ) + \lambda_0\mu_0^2 \right] | b_N &= b_0 + \frac{1}{2} \left[ (\lambda_0+N) \left (\lambda_N^{-1} + \mu_N^2 \right ) -2 \left (\lambda_0\mu_0 + \sum_{n=1}^N x_n \right )\mu_N + \left (\sum_{n=1}^N x_n^2 \right ) + \lambda_0\mu_0^2 \right] | ||
\end{align}</math> | \end{align} </math> | ||
ध्यान दें कि | ध्यान दें कि <math>\lambda_N</math>और <math>b_N</math> सूत्रों के मध्य चक्रीय निर्भरताएँ हैं . यह स्वाभाविक रूप से अपेक्षा-अधिकतमकरण ईएम जैसा एल्गोरिदम का सुझाव देता है: | ||
# | #<math>\sum_{n=1}^N x_n</math> और <math>\sum_{n=1}^N x_n^2 </math> गणना करें | <math>\mu_N</math> और <math>a_N </math> गणना करने के लिए इन मानों का उपयोग किया जाता है | | ||
# | #कुछ इच्छानुसार मूल्य के लिए <math>\lambda_N</math> प्रारंभ करें. | ||
# | #<math>b_N</math>की गणना करने के लिए अन्य मापदंडों के ज्ञात मानों के साथ <math>\lambda_N,</math> के वर्तमान मान का उपयोग करें . | ||
#<math>\lambda_N</math> की गणना करने के लिए अन्य मापदंडों के ज्ञात मानों के साथ <math>b_N,</math>के वर्तमान मान का उपयोग करें. | |||
#अंतिम दो चरणों को अभिसरण होने तक दोहराएँ (अर्थात जब तक कि कोई भी मान कुछ | #अंतिम दो चरणों को अभिसरण होने तक दोहराएँ (अर्थात जब तक कि कोई भी मान कुछ लघु राशि से अधिक न बदल जाए)। | ||
फिर हमारे | फिर हमारे समीप पश्च मापदंडों के अनुमानित वितरण के हाइपरपैरामीटर के लिए मान हैं, जिनका उपयोग हम पश्च भाग के किसी भी गुण की गणना करने के लिए कर सकते हैं - उदाहरण के लिए इसका माध्य और विचरण, 95% उच्चतम-घनत्व क्षेत्र (सबसे छोटा अंतराल जिसमें कुल संभावना का 95% सम्मिलित है), आदि। | ||
यह दिखाया जा सकता है कि यह एल्गोरिदम स्थानीय अधिकतम में परिवर्तित होने की गारंटी देता है। | यह दिखाया जा सकता है कि यह एल्गोरिदम स्थानीय अधिकतम में परिवर्तित होने की गारंटी देता है। | ||
यह भी ध्यान दें कि | यह भी ध्यान दें कि पूर्व वितरणों का स्वरूप संबंधित पूर्व वितरणों के समान ही है। हमने यह नहीं माना कि हमने जो एकमात्र धारणा बनाई वह यह थी कि वितरण गुणनखंडित होते हैं, और वितरण का स्वरूप स्वाभाविक रूप से अनुसरण किया जाता है। यह पता चला है (नीचे देखें) कि तथ्य यह है कि पूर्व वितरणों का रूप पूर्व वितरणों के समान है, यह कोई संयोग नहीं है, किंतु सामान्य परिणाम है जब भी पूर्व वितरण [[घातीय परिवार|घातीय वर्ग]] के सदस्य होते हैं, जो कि अधिकांश मानक वितरणों के लिए स्तिथि है . | ||
==आगे की चर्चा== | ==आगे की चर्चा == | ||
===स्टेप-बाय-स्टेप रेसिपी=== | ===स्टेप-बाय-स्टेप रेसिपी=== | ||
उपरोक्त उदाहरण उस विधि को दर्शाता है जिसके द्वारा किसी दिए गए [[बायेसियन नेटवर्क]] में पश्च संभाव्यता घनत्व के लिए वैरिएबल-बायेसियन सन्निकटन प्राप्त किया जाता है: | उपरोक्त उदाहरण उस विधि को दर्शाता है जिसके द्वारा किसी दिए गए [[बायेसियन नेटवर्क]] में पश्च संभाव्यता घनत्व के लिए वैरिएबल-बायेसियन सन्निकटन प्राप्त किया जाता है: | ||
# ग्राफ़िकल मॉडल के साथ नेटवर्क का वर्णन करें, देखे गए | # ग्राफ़िकल मॉडल के साथ नेटवर्क का वर्णन करें, देखे गए वेरिएबल (डेटा) <math>\mathbf{X}</math> और न देखे गए वेरिएबल (पैरामीटर) <math>\boldsymbol\Theta</math> और अव्यक्त वेरिएबल <math>\mathbf{Z}</math>) और उनके [[सशर्त संभाव्यता वितरण]] की पहचान करें। वेरिएशनल बेज़ इसके पश्चात् पश्च संभाव्यता <math>p(\mathbf{Z},\boldsymbol\Theta\mid\mathbf{X})</math> का अनुमान तैयार करेंगे |. सन्निकटन की मूल संपत्ति यह है कि यह गुणनखंडित वितरण है, अर्थात न देखे गए वेरिएबल के असंयुक्त उपसमुच्चय पर दो या दो से अधिक [[सांख्यिकीय स्वतंत्रता]] वितरण का उत्पाद है। | ||
#न देखे गए | #न देखे गए वेरिएबलों को दो या दो से अधिक उपसमूहों में विभाजित करें, जिन पर स्वतंत्र कारक प्राप्त किए जाएंगे। ऐसा करने की कोई सार्वभौमिक प्रक्रिया नहीं है; बहुत अधिक उपसमुच्चय बनाने से खराब सन्निकटन प्राप्त होता है, जबकि बहुत कम उपसमुच्चय बनाने से संपूर्ण परिवर्तनशील बेयस प्रक्रिया कठिन हो जाती है। सामान्यतः, पहला विभाजन पैरामीटर और अव्यक्त वेरिएबल को भिन्न करने के लिए होता है; अधिकांशतः, यह अपने आप में सुगम परिणाम उत्पन्न करने के लिए पर्याप्त होता है। मान लें कि विभाजन <math>\mathbf{Z}_1,\ldots,\mathbf{Z}_M</math> कहा जाता हैं . | ||
#किसी दिए गए विभाजन | #किसी दिए गए विभाजन <math>\mathbf{Z}_j</math> के लिए , मूल समीकरण <math>\ln q_j^{*}(\mathbf{Z}_j\mid \mathbf{X}) = \operatorname{E}_{i \neq j} [\ln p(\mathbf{Z}, \mathbf{X})] + \text{constant}</math> का उपयोग करके सर्वोत्तम अनुमानित वितरण <math>q_j^{*}(\mathbf{Z}_j\mid \mathbf{X})</math> के लिए सूत्र लिखें . | ||
#ग्राफ़िकल मॉडल का उपयोग करके [[संयुक्त संभाव्यता वितरण]] के लिए सूत्र भरें। कोई भी घटक सशर्त वितरण जिसमें | #ग्राफ़िकल मॉडल का उपयोग करके [[संयुक्त संभाव्यता वितरण]] के लिए सूत्र भरें। कोई भी घटक सशर्त वितरण जिसमें <math>\mathbf{Z}_j</math> कोई भी वेरिएबल सम्मिलित नहीं है नजरअंदाज किया जा सकता है; उन्हें स्थिर अवधि में जोड़ दिया जाएगा। | ||
#उपरोक्त उदाहरण का अनुसरण करते हुए सूत्र को सरल बनाएं और अपेक्षा ऑपरेटर | #उपरोक्त उदाहरण का अनुसरण करते हुए सूत्र को सरल बनाएं और अपेक्षा ऑपरेटर प्रयुक्त करें। आदर्श रूप से, इसे वेरिएबल <math>\mathbf{Z}_j</math> के मूलभूत कार्यों की अपेक्षाओं में सरलीकृत नहीं किया जाना चाहिए (जैसे पसमाधाना या दूसरा कच्चा क्षण (गणित), लघुगणक की अपेक्षा, आदि)। वेरिएबल बेयस प्रक्रिया को अच्छी प्रकार से कार्य करने के लिए, इन अपेक्षाओं को सामान्यतः इन वेरिएबल के वितरण के मापदंडों और/या हाइपरपैरामीटर के कार्यों के रूप में विश्लेषणात्मक रूप से व्यक्त किया जाना चाहिए। सभी स्थितियों में, यह अपेक्षा शर्तें वर्तमान विभाजन में वेरिएबल के संबंध में स्थिरांक हैं। | ||
#वर्तमान विभाजन में | #वर्तमान विभाजन में वेरिएबल के संबंध में सूत्र का कार्यात्मक रूप वितरण के प्रकार को निरुपित करता है। विशेष रूप से, सूत्र को घातांकित करने से वितरण की संभाव्यता घनत्व फलन (पीडीएफ) उत्पन्न होती है (या कम से कम, इसके लिए कुछ आनुपातिक, अज्ञात [[सामान्यीकरण स्थिरांक]] के साथ)। समग्र विधि को ट्रैक्टेबल बनाने के लिए उत्पन्न होती है, तथा इस ज्ञात वितरण से संबंधित कार्यात्मक रूप को पहचानना संभव होना चाहिए। सूत्र को ज्ञात वितरण के पीडीएफ से मेल खाने वाले रूप में बदलने के लिए महत्वपूर्ण गणितीय हेरफेर की आवश्यकता हो सकती है। जब यह किया जा सकता है, तब सामान्यीकरण स्थिरांक को परिभाषा द्वारा पुनः स्थापित किया जा सकता है, और ज्ञात वितरण के मापदंडों के लिए समीकरण सूत्र के उचित भागों को निकालकर प्राप्त किया जा सकता है। | ||
#जब सभी अपेक्षाओं को विश्लेषणात्मक रूप से उन | #जब सभी अपेक्षाओं को विश्लेषणात्मक रूप से उन वेरिएबलों के कार्यों से बदला जा सकता है जो वर्तमान विभाजन में नहीं हैं, और पीडीएफ को ऐसे रूप में रखा जाता है जो ज्ञात वितरण के साथ पहचान की अनुमति देता है, तब परिणाम समीकरणों का समुच्चय होता है जो इष्टतम मापदंडों के मानों को अन्य विभाजनों में वेरिएबल के पैरामीटर के कार्यों के रूप में व्यक्त करता है । | ||
#जब इस प्रक्रिया को सभी विभाजनों पर | #जब इस प्रक्रिया को सभी विभाजनों पर प्रयुक्त किया जा सकता है, तब परिणाम सभी मापदंडों के इष्टतम मानों को निर्दिष्ट करने वाले परस्पर जुड़े समीकरणों का समुच्चय होता है। | ||
#फिर | #फिर [[अपेक्षा अधिकतमीकरण]] (ईएम) प्रकार की प्रक्रिया प्रयुक्त की जाती है, प्रत्येक पैरामीटर के लिए प्रारंभिक मान चुना जाता है और चरणों की श्रृंखला के माध्यम से पुनरावृत्ति की जाती है, जहां प्रत्येक चरण में हम समीकरणों के माध्यम से चक्र करते हैं, प्रत्येक पैरामीटर को बारी-बारी से अपडेट करते हैं। यह जुटने की गारंटी है. | ||
===सबसे महत्वपूर्ण बिंदु=== | ===सबसे महत्वपूर्ण बिंदु=== | ||
इसमें | इसमें सम्मिलित सभी गणितीय जोड़-तोड़ों के कारण, बड़ी तस्वीर का ध्यान भटकाना आसान है। महत्वपूर्ण बातें यह हैं: | ||
#वैरिएबल बेयस का विचार डेटा को देखते हुए, न देखे गए | #वैरिएबल बेयस का विचार डेटा को देखते हुए, न देखे गए वेरिएबल (पैरामीटर और अव्यक्त वेरिएबल ) के समुच्चय की पूर्व संभावना के लिए विश्लेषणात्मक सन्निकटन का निर्माण करना है। इसका कारण यह है कि समाधान का रूप अन्य बायेसियन अनुमान विधियों के समान है, जैसे कि गिब्स प्रतिरूपीकरण - अर्थात वितरण जो वेरिएबल के बारे में ज्ञात प्रत्येक चीज का वर्णन करना चाहता है। जैसा कि अन्य बायेसियन विधियों में होता है - किन्तु उदाहरण के विपरीत। अपेक्षा अधिकतमीकरण (ईएम) या अन्य अधिकतम संभावना विधियों में - दोनों प्रकार के अप्राप्य वेरिएबल (अर्थात पैरामीटर और अव्यक्त वेरिएबल ) को समान माना जाता है, अर्थात यादृच्छिक वेरिएबल के रूप में माना जाता है । फिर वेरिएबलों का अनुमान मानक बायेसियन विधियों से प्राप्त किया जा सकता है, जैसे एकल बिंदु अनुमान प्राप्त करने के लिए वितरण के माध्य की गणना करना या [[विश्वसनीय अंतराल]], उच्चतम घनत्व क्षेत्र आदि प्राप्त करना। | ||
# विश्लेषणात्मक सन्निकटन का अर्थ है कि पश्च वितरण के लिए | # विश्लेषणात्मक सन्निकटन का अर्थ है कि पश्च वितरण के लिए सूत्र लिखा जा सकता है। सूत्र में सामान्यतः प्रसिद्ध संभाव्यता वितरण का उत्पाद सम्मिलित होता है, जिनमें से प्रत्येक न देखे गए वेरिएबल के समुच्चय पर कारक होता है (अर्थात, देखे गए डेटा को देखते हुए, यह अन्य वेरिएबल से [[सशर्त रूप से स्वतंत्र]] है)। यह सूत्र वास्तविक पश्च वितरण नहीं है, किंतु इसका अनुमान है; विशेष रूप से, यह सामान्यतः न देखे गए वेरिएबलों के निम्नतम क्षण (गणित) में अधिक निकटता से सहमत होगा, उदाहरण के लिए माध्य और विचरण. | ||
#सभी गणितीय जोड़-तोड़ों का परिणाम है (1) कारकों को बनाने वाले संभाव्यता वितरण की पहचान, और (2) इन वितरणों के मापदंडों के लिए परस्पर निर्भर सूत्र। इन मापदंडों के वास्तविक | #सभी गणितीय जोड़-तोड़ों का परिणाम है (1) कारकों को बनाने वाले संभाव्यता वितरण की पहचान, और (2) इन वितरणों के मापदंडों के लिए परस्पर निर्भर सूत्र। इन मापदंडों के वास्तविक मानों की गणना ईएम की प्रकार वैकल्पिक पुनरावृत्त प्रक्रिया के माध्यम से संख्यात्मक रूप से की जाती है। | ||
===अपेक्षा अधिकतमकरण (ईएम) के साथ तुलना में=== | ===अपेक्षा अधिकतमकरण (ईएम) के साथ तुलना में=== | ||
वेरिएशनल बेयस (वीबी) की तुलना | वेरिएशनल बेयस (वीबी) की तुलना अधिकांशतः अपेक्षा अधिकतमकरण (ईएम) से की जाती है। वास्तविक संख्यात्मक प्रक्रिया अधिक समान है, जिसमें दोनों वैकल्पिक पुनरावृत्त प्रक्रियाएं हैं जो क्रमिक रूप से इष्टतम पैरामीटर मानों पर एकत्रित होती हैं। संबंधित प्रक्रियाओं को प्राप्त करने के प्रारंभिक चरण भी अस्पष्ट रूप से समान हैं, दोनों संभाव्यता घनत्व के सूत्रों के साथ प्रारंभ होते हैं और दोनों में महत्वपूर्ण मात्रा में गणितीय जोड़-तोड़ सम्मिलित होते हैं। | ||
चूँकि, इसमें अनेक अंतर हैं। सबसे महत्वपूर्ण यह है कि गणना क्या की जा रही है। | |||
*ईएम उन यादृच्छिक | *ईएम उन यादृच्छिक वेरिएबलों के पश्च वितरण के बिंदु अनुमानों की गणना करता है जिन्हें मापदंडों के रूप में वर्गीकृत किया जा सकता है, किन्तु केवल अव्यक्त वेरिएबल के वास्तविक पश्च वितरण का अनुमान (कम से कम नरम ईएम में, और अधिकांशतः केवल जब अव्यक्त वेरिएबल भिन्न होते हैं)। गणना किए गए बिंदु अनुमान इन मापदंडों के [[मोड (सांख्यिकी)]] हैं; कोई अन्य जानकारी उपलब्ध नहीं है. | ||
*दूसरी ओर, वीबी सभी | *दूसरी ओर, वीबी सभी वेरिएबल, दोनों मापदंडों और अव्यक्त वेरिएबल के वास्तविक पश्च वितरण के अनुमान की गणना करता है। जब बिंदु अनुमान प्राप्त करने की आवश्यकता होती है, तब सामान्यतः मोड के अतिरिक्त माध्य का उपयोग किया जाता है, जैसा कि बायेसियन अनुमान में सामान्य है। इसके साथ ही, वीबी में गणना किए गए मापदंडों का ईएम के समान महत्व नहीं है। ईएम बेयस नेटवर्क के मापदंडों के इष्टतम मानों की गणना स्वयं करता है। वीबी बेयस नेटवर्क के मापदंडों और अव्यक्त वेरिएबल का अनुमान लगाने के लिए उपयोग किए जाने वाले वितरण के मापदंडों के इष्टतम मानों की गणना करता है। उदाहरण के लिए, विशिष्ट गाऊसी [[मिश्रण मॉडल]] में प्रत्येक मिश्रण घटक के माध्य और विचरण के लिए पैरामीटर होंगे। ईएम सीधे इन मापदंडों के लिए इष्टतम मानों का अनुमान लगाएगा। चूँकि, वीबी पहले इन मापदंडों के अनुसार वितरण को फिट करेगा - सामान्यतः पूर्व वितरण के रूप में, उदाहरण के लिए। [[सामान्य-स्केल व्युत्क्रम गामा वितरण]] - और फिर इस पूर्व वितरण के मापदंडों के लिए मानों की गणना करेगा, अर्थात अनिवार्य रूप से [[हाइपरपैरामीटर]] में गणना की जाती है। इस स्थितियां में, वीबी सामान्य-स्केल व्युत्क्रम गामा वितरण के चार मापदंडों के इष्टतम अनुमानों की गणना करेगा जो घटक के माध्य और विचरण के संयुक्त वितरण का वर्णन करता है। | ||
==एक अधिक सम्मिश्र उदाहरण == | |||
[[File:bayesian-gaussian-mixture-vb.svg|right|300px|thumb|[[ प्लेट संकेतन | प्लेट संकेतन]] का उपयोग करते हुए बायेसियन गॉसियन मिश्रण मॉडल। छोटे वर्ग निश्चित मापदंडों को दर्शाते हैं; बड़े वृत्त यादृच्छिक वेरिएबल दर्शाते हैं। भरी हुई आकृतियाँ ज्ञात मान दर्शाती हैं। संकेत [K] का अर्थ K आकार का सदिश है; [डी,डी] का अर्थ है डी×डी आकार का आव्युह; अकेले K का कारणK परिणामों के साथ [[श्रेणीगत चर|श्रेणीगत]] वेरिएबल है। क्रॉसबार में समाप्त होने वाले z से आने वाली टेढ़ी-मेढ़ी रेखा स्विच को निरुपित करती है - इस वेरिएबल का मान अन्य आने वाले वेरिएबल के लिए चयन करता है, जो संभावित मानों के आकार-K सरणी से उपयोग करने के लिए मान है।]]एक बायेसियन [[गाऊसी मिश्रण मॉडल]] की कल्पना करें जिसका वर्णन इस प्रकार है:<ref name=bishop/> | |||
==एक अधिक | |||
[[File:bayesian-gaussian-mixture-vb.svg|right|300px|thumb|[[ प्लेट संकेतन ]] का उपयोग करते हुए बायेसियन गॉसियन मिश्रण मॉडल। छोटे वर्ग निश्चित मापदंडों को दर्शाते हैं; बड़े वृत्त यादृच्छिक | |||
:<math> | :<math> | ||
| Line 341: | Line 337: | ||
</math> | </math> | ||
टिप्पणी: | टिप्पणी: | ||
* | *सिमडिर()() आयाम का सममित [[डिरिचलेट वितरण]] है <math>K</math>, प्रत्येक घटक के लिए हाइपरपैरामीटर <math>\alpha_0</math> समुच्चय के साथ है. डिरिचलेट वितरण [[श्रेणीबद्ध वितरण]] या [[बहुपद वितरण]] से पहले का संयुग्म है। | ||
*<math>\mathcal{W}()</math> [[विशार्ट वितरण]] है, जो बहुभिन्नरूपी गॉसियन वितरण के लिए | *<math>\mathcal{W}()</math> [[विशार्ट वितरण]] है, जो बहुभिन्नरूपी गॉसियन वितरण के लिए त्रुटिहीन आव्युह (व्युत्क्रम [[परिशुद्धता मैट्रिक्स|परिशुद्धता आव्युह]]) का संयुग्मित पूर्व है। | ||
*मल्टी() एकल अवलोकन पर | *मल्टी() एकल अवलोकन पर बहुपद वितरण है (एक श्रेणीबद्ध वितरण के सामान्तर)। अवस्था समिष्ट वन-के-<math>K</math> प्रतिनिधित्व है, अर्थात, a <math>K</math>-आयामी सदिश जिसमें अवयवों में से 1 है (अवलोकन की पहचान निर्दिष्ट करते हुए) और अन्य सभी अवयव 0 हैं। | ||
*<math>\mathcal{N}()</math> गाऊसी वितरण है, इस | *<math>\mathcal{N}()</math> गाऊसी वितरण है, इस स्थितियां में विशेष रूप से बहुभिन्नरूपी गाऊसी वितरण। | ||
उपरोक्त | उपरोक्त वेरिएबलों की व्याख्या इस प्रकार है:| | ||
*<math>\mathbf{X} = \{\mathbf{x}_1, \dots, \mathbf{x}_N\}</math> | *<math>\mathbf{X} = \{\mathbf{x}_1, \dots, \mathbf{x}_N\}</math> <math>N</math> डेटा बिंदु, का समुच्चय है जिनमें से प्रत्येक बहुभिन्नरूपी गॉसियन वितरण <math>D</math>-आयामी सदिश को वितरित किया जाता है। | ||
*<math>\mathbf{Z} = \{\mathbf{z}_1, \dots, \mathbf{z}_N\}</math> अव्यक्त | *<math>\mathbf{Z} = \{\mathbf{z}_1, \dots, \mathbf{z}_N\}</math> अव्यक्त वेरिएबल का समुच्चय है, प्रति डेटा बिंदु निर्दिष्ट करता है कि संबंधित डेटा बिंदु किस मिश्रण घटक से संबंधित है, जैसा ऊपर वर्णित है। <math>k = 1 \dots K</math> के लिए घटकों <math>z_{nk}</math> के साथ वन-<math>K</math>-सदिश प्रतिनिधित्व का उपयोग करता है | | ||
*<math>\mathbf{\pi}</math> | *<math>\mathbf{\pi}</math> <math>K</math> मिश्रण घटक के लिए मिश्रण अनुपात है . | ||
*<math>\mathbf{\mu}_{i=1 \dots K}</math> और <math>\mathbf{\Lambda}_{i=1 \dots K}</math> प्रत्येक मिश्रण घटक से जुड़े पैरामीटर (माध्य और परिशुद्धता (सांख्यिकी)) निर्दिष्ट | *<math>\mathbf{\mu}_{i=1 \dots K}</math> और <math>\mathbf{\Lambda}_{i=1 \dots K}</math> प्रत्येक मिश्रण घटक से जुड़े पैरामीटर (माध्य और परिशुद्धता (सांख्यिकी)) निर्दिष्ट करते हैं। | ||
*{1} और {2} प्रत्येक मिश्रण घटक से जुड़े पैरामीटर (माध्य और परिशुद्धता) निर्दिष्ट करते हैं। | |||
:<math>p(\mathbf{X},\mathbf{Z},\mathbf{\pi},\mathbf{\mu},\mathbf{\Lambda}) = p(\mathbf{X}\mid \mathbf{Z},\mathbf{\mu},\mathbf{\Lambda}) p(\mathbf{Z}\mid \mathbf{\pi}) p(\mathbf{\pi}) p(\mathbf{\mu}\mid \mathbf{\Lambda}) p(\mathbf{\Lambda})</math> | :<math>p(\mathbf{X},\mathbf{Z},\mathbf{\pi},\mathbf{\mu},\mathbf{\Lambda}) = p(\mathbf{X}\mid \mathbf{Z},\mathbf{\mu},\mathbf{\Lambda}) p(\mathbf{Z}\mid \mathbf{\pi}) p(\mathbf{\pi}) p(\mathbf{\mu}\mid \mathbf{\Lambda}) p(\mathbf{\Lambda})</math> | ||
| Line 364: | Line 359: | ||
p(\mathbf{\mu}\mid \mathbf{\Lambda}) & = \prod_{k=1}^K \mathcal{N}(\mathbf{\mu}_k\mid \mathbf{\mu}_0,(\beta_0 \mathbf{\Lambda}_k)^{-1}) \\ | p(\mathbf{\mu}\mid \mathbf{\Lambda}) & = \prod_{k=1}^K \mathcal{N}(\mathbf{\mu}_k\mid \mathbf{\mu}_0,(\beta_0 \mathbf{\Lambda}_k)^{-1}) \\ | ||
p(\mathbf{\Lambda}) & = \prod_{k=1}^K \mathcal{W}(\mathbf{\Lambda}_k\mid \mathbf{W}_0, \nu_0) | p(\mathbf{\Lambda}) & = \prod_{k=1}^K \mathcal{W}(\mathbf{\Lambda}_k\mid \mathbf{W}_0, \nu_0) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ | |||
:<math> | :<math> | ||
| Line 374: | Line 369: | ||
B(\mathbf{W},\nu) & = |\mathbf{W}|^{-\nu/2} \left\{ 2^{\nu D/2} \pi^{D(D-1)/4} \prod_{i=1}^{D} \Gamma\left(\frac{\nu + 1 - i}{2}\right) \right\}^{-1} \\ | B(\mathbf{W},\nu) & = |\mathbf{W}|^{-\nu/2} \left\{ 2^{\nu D/2} \pi^{D(D-1)/4} \prod_{i=1}^{D} \Gamma\left(\frac{\nu + 1 - i}{2}\right) \right\}^{-1} \\ | ||
D & = \text{dimensionality of each data point} | D & = \text{dimensionality of each data point} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
यह मान लीजिए <math>q(\mathbf{Z},\mathbf{\pi},\mathbf{\mu},\mathbf{\Lambda}) = q(\mathbf{Z})q(\mathbf{\pi},\mathbf{\mu},\mathbf{\Lambda})</math>. | |||
तब | तब | ||
| Line 387: | Line 382: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहां हमने परिभाषित किया है | जहां हमने परिभाषित किया है कि | ||
:<math>\ln \rho_{nk} = \operatorname{E}[\ln \pi_k] + \frac{1}{2} \operatorname{E}[\ln |\mathbf{\Lambda}_k|] - \frac{D}{2} \ln(2\pi) - \frac{1}{2} \operatorname{E}_{\mathbf{\mu}_k,\mathbf{\Lambda}_k} [(\mathbf{x}_n - \mathbf{\mu}_k)^{\rm T} \mathbf{\Lambda}_k (\mathbf{x}_n - \mathbf{\mu}_k)]</math> | :<math>\ln \rho_{nk} = \operatorname{E}[\ln \pi_k] + \frac{1}{2} \operatorname{E}[\ln |\mathbf{\Lambda}_k|] - \frac{D}{2} \ln(2\pi) - \frac{1}{2} \operatorname{E}_{\mathbf{\mu}_k,\mathbf{\Lambda}_k} [(\mathbf{x}_n - \mathbf{\mu}_k)^{\rm T} \mathbf{\Lambda}_k (\mathbf{x}_n - \mathbf{\mu}_k)]</math> | ||
के लिए सूत्र के दोनों पक्षों का घातांक | के लिए सूत्र के दोनों पक्षों का घातांक द्वारा <math>\ln q^*(\mathbf{Z})</math> उत्पन्न | ||
:<math>q^*(\mathbf{Z}) \propto \prod_{n=1}^N \prod_{k=1}^K \rho_{nk}^{z_{nk}}</math> | :<math>q^*(\mathbf{Z}) \propto \prod_{n=1}^N \prod_{k=1}^K \rho_{nk}^{z_{nk}}</math> | ||
इसे सामान्य बनाने की आवश्यकता के | इसे सामान्य बनाने की आवश्यकता के परिणामस्वरूप <math>k</math> के सभी मानों का <math>\rho_{nk}</math> योग 1 हो जाता है जिससे परिणाम मिलता है | ||
:<math>q^*(\mathbf{Z}) = \prod_{n=1}^N \prod_{k=1}^K r_{nk}^{z_{nk}}</math> | :<math>q^*(\mathbf{Z}) = \prod_{n=1}^N \prod_{k=1}^K r_{nk}^{z_{nk}}</math> | ||
जहाँ | |||
:<math>r_{nk} = \frac{\rho_{nk}}{\sum_{j=1}^K \rho_{nj}}</math> | :<math>r_{nk} = \frac{\rho_{nk}}{\sum_{j=1}^K \rho_{nj}}</math> | ||
दूसरे शब्दों में, <math>q^*(\mathbf{Z})</math> एकल-अवलोकन बहुपद वितरण और प्रत्येक व्यक्ति पर कारकों का | दूसरे शब्दों में, <math>q^*(\mathbf{Z})</math> एकल-अवलोकन बहुपद वितरण और प्रत्येक व्यक्ति पर कारकों का उत्पाद है <math>\mathbf{z}_n</math>, जिसे मापदंडों के साथ एकल-अवलोकन बहुपद वितरण के रूप में वितरित किया जाता है <math>r_{nk}</math> के लिए <math>k = 1 \dots K</math>. | ||
इसके | इसके अतिरिक्त, हम उस पर ध्यान देते हैं | ||
:<math>\operatorname{E}[z_{nk}] = r_{nk} \, </math> | :<math>\operatorname{E}[z_{nk}] = r_{nk} \, </math> | ||
जो श्रेणीबद्ध वितरण के लिए | जो श्रेणीबद्ध वितरण के लिए मानक परिणाम है। | ||
अभी, कारक पर विचार करें <math>q(\mathbf{\pi},\mathbf{\mu},\mathbf{\Lambda})</math>, ध्यान दें कि यह स्वचालित रूप से इसमें सम्मिलित होता है <math>q(\mathbf{\pi}) \prod_{k=1}^K q(\mathbf{\mu}_k,\mathbf{\Lambda}_k)</math> हमारे गॉसियन मिश्रण मॉडल को परिभाषित करने वाले ग्राफिकल मॉडल की संरचना के कारण, जो ऊपर निर्दिष्ट है। | |||
तब, | तब, | ||
| Line 419: | Line 414: | ||
:<math>q^*(\mathbf{\pi}) \sim \operatorname{Dir}(\mathbf{\alpha}) \, </math> | :<math>q^*(\mathbf{\pi}) \sim \operatorname{Dir}(\mathbf{\alpha}) \, </math> | ||
जहाँ | |||
:<math>\alpha_k = \alpha_0 + N_k \, </math> | :<math>\alpha_k = \alpha_0 + N_k \, </math> | ||
जहाँ | |||
:<math>N_k = \sum_{n=1}^N r_{nk} \, </math> | :<math>N_k = \sum_{n=1}^N r_{nk} \, </math> | ||
अंततः | |||
:<math>\ln q^*(\mathbf{\mu}_k,\mathbf{\Lambda}_k) = \ln p(\mathbf{\mu}_k,\mathbf{\Lambda}_k) + \sum_{n=1}^N \operatorname{E}[z_{nk}] \ln \mathcal{N}(\mathbf{x}_n\mid \mathbf{\mu}_k,\mathbf{\Lambda}_k^{-1}) + \text{constant}</math> | :<math>\ln q^*(\mathbf{\mu}_k,\mathbf{\Lambda}_k) = \ln p(\mathbf{\mu}_k,\mathbf{\Lambda}_k) + \sum_{n=1}^N \operatorname{E}[z_{nk}] \ln \mathcal{N}(\mathbf{x}_n\mid \mathbf{\mu}_k,\mathbf{\Lambda}_k^{-1}) + \text{constant}</math> | ||
<math>\mathbf{\mu}_k</math> और <math>\mathbf{\Lambda}_k</math> से सम्मिलित नियमों को समूहीकृत करना और पढ़ना , परिणाम [[गाऊसी-विशार्ट वितरण]] द्वारा दिया गया है | |||
:<math>q^*(\mathbf{\mu}_k,\mathbf{\Lambda}_k) = \mathcal{N}(\mathbf{\mu}_k\mid \mathbf{m}_k,(\beta_k \mathbf{\Lambda}_k)^{-1}) \mathcal{W}(\mathbf{\Lambda}_k\mid \mathbf{W}_k,\nu_k)</math> | :<math>q^*(\mathbf{\mu}_k,\mathbf{\Lambda}_k) = \mathcal{N}(\mathbf{\mu}_k\mid \mathbf{m}_k,(\beta_k \mathbf{\Lambda}_k)^{-1}) \mathcal{W}(\mathbf{\Lambda}_k\mid \mathbf{W}_k,\nu_k)</math> | ||
| Line 442: | Line 437: | ||
{\bar{\mathbf{x}}}_k &= \frac{1}{N_k} \sum_{n=1}^N r_{nk} \mathbf{x}_n \\ | {\bar{\mathbf{x}}}_k &= \frac{1}{N_k} \sum_{n=1}^N r_{nk} \mathbf{x}_n \\ | ||
\mathbf{S}_k &= \frac{1}{N_k} \sum_{n=1}^N r_{nk} (\mathbf{x}_n - {\bar{\mathbf{x}}}_k) (\mathbf{x}_n - {\bar{\mathbf{x}}}_k)^{\rm T} | \mathbf{S}_k &= \frac{1}{N_k} \sum_{n=1}^N r_{nk} (\mathbf{x}_n - {\bar{\mathbf{x}}}_k) (\mathbf{x}_n - {\bar{\mathbf{x}}}_k)^{\rm T} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
अंत में, ध्यान दें कि इन कार्यों के लिए | अंत में, ध्यान दें कि इन कार्यों के लिए <math>r_{nk}</math> के मानों की आवश्यकता होती है , जिसका <math>\rho_{nk}</math> उपयोग किया जाता है , जिसके बारी-बारी से <math>\operatorname{E}[\ln \pi_k]</math>, <math>\operatorname{E}[\ln |\mathbf{\Lambda}_k|]</math> और <math>\operatorname{E}_{\mathbf{\mu}_k,\mathbf{\Lambda}_k} [(\mathbf{x}_n - \mathbf{\mu}_k)^{\rm T} \mathbf{\Lambda}_k (\mathbf{x}_n - \mathbf{\mu}_k)]</math> आधार पर परिभाषित किया गया है, अभी जब हमने उन वितरणों को निर्धारित कर लिया है जिन पर यह अपेक्षाएँ ली गई हैं, तब हम उनके लिए सूत्र प्राप्त कर सकते हैं: | ||
:<math> | :<math> | ||
| Line 451: | Line 446: | ||
\ln {\widetilde{\Lambda}}_k &\equiv \operatorname{E}[\ln |\mathbf{\Lambda}_k|] = \sum_{i=1}^D \psi \left(\frac{\nu_k + 1 - i}{2}\right) + D \ln 2 + \ln |\mathbf{W}_k| \\ | \ln {\widetilde{\Lambda}}_k &\equiv \operatorname{E}[\ln |\mathbf{\Lambda}_k|] = \sum_{i=1}^D \psi \left(\frac{\nu_k + 1 - i}{2}\right) + D \ln 2 + \ln |\mathbf{W}_k| \\ | ||
\ln {\widetilde{\pi}}_k &\equiv \operatorname{E}\left[\ln |\pi_k|\right] = \psi(\alpha_k) - \psi\left(\sum_{i=1}^K \alpha_i\right) | \ln {\widetilde{\pi}}_k &\equiv \operatorname{E}\left[\ln |\pi_k|\right] = \psi(\alpha_k) - \psi\left(\sum_{i=1}^K \alpha_i\right) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
इन परिणामों की ओर ले जाते हैं | इन परिणामों की ओर ले जाते हैं | ||
:<math>r_{nk} \propto {\widetilde{\pi}}_k {\widetilde{\Lambda}}_k^{1/2} \exp \left\{ - \frac{D}{2 \beta_k} - \frac{\nu_k}{2} (\mathbf{x}_n - \mathbf{m}_k)^{\rm T} \mathbf{W}_k (\mathbf{x}_n - \mathbf{m}_k) \right\}</math> | :<math>r_{nk} \propto {\widetilde{\pi}}_k {\widetilde{\Lambda}}_k^{1/2} \exp \left\{ - \frac{D}{2 \beta_k} - \frac{\nu_k}{2} (\mathbf{x}_n - \mathbf{m}_k)^{\rm T} \mathbf{W}_k (\mathbf{x}_n - \mathbf{m}_k) \right\}</math> | ||
इन्हें सामान्यीकृत करके आनुपातिक से निरपेक्ष मान में परिवर्तित किया जा सकता है | इन्हें <math>k</math> पर सामान्यीकृत करके आनुपातिक से निरपेक्ष मान में परिवर्तित किया जा सकता है जिससे कि संबंधित मानों का योग 1 हो जाये । | ||
ध्यान दें कि: | ध्यान दें कि: | ||
#पैरामीटर | #पैरामीटर <math>\beta_k</math>, <math>\mathbf{m}_k</math>, <math>\mathbf{W}_k</math> और <math>\nu_k</math> के लिए अद्यतन समीकरण वेरिएबलों का <math>\mathbf{\mu}_k</math> और <math>\mathbf{\Lambda}_k</math> आंकड़ों <math>N_k</math>, <math>{\bar{\mathbf{x}}}_k</math>, और <math>\mathbf{S}_k</math> पर निर्भरकरते है, और यह आँकड़े इसके स्थान में <math>r_{nk}</math> निर्भर करते हैं . | ||
# | #वेरिएबल <math>\mathbf{\pi}</math> के पैरामीटर <math>\alpha_{1 \dots K}</math> के लिए अद्यतन समीकरण का आंकड़ों <math>N_k</math> पर निर्भर करते है, जो इसके स्थान में <math>r_{nk}</math> पर निर्भर करता है . | ||
# | #<math>r_{nk}</math> के लिए अद्यतन समीकरण पर प्रत्यक्ष चक्रीय निर्भरता है <math>\beta_k</math>, <math>\mathbf{m}_k</math>, <math>\mathbf{W}_k</math> और <math>\nu_k</math> साथ ही <math>\mathbf{W}_k</math>, <math>\nu_k</math> और अप्रत्यक्ष चक्रीय निर्भरता भी <math>\alpha_{1 \dots K}</math> द्वारा <math>{\widetilde{\pi}}_k</math> और <math>{\widetilde{\Lambda}}_k</math> पर निर्भर करती है | | ||
यह | यह पुनरावृत्तीय प्रक्रिया का सुझाव देता है जो दो चरणों के मध्य वैकल्पिक होती है: | ||
#एक | #एक E-स्टेप जो अन्य सभी मापदंडों के वर्तमान मानों का उपयोग करके <math>r_{nk}</math> के मूल्य की गणना करता है । | ||
#एक | #एक M-स्टेप जो अन्य सभी मापदंडों के वर्तमान मानों की गणना करने के लिए <math>r_{nk}</math> के वर्तमान मान का उपयोग करता है । | ||
ध्यान दें कि गाऊसी मिश्रण मॉडल के मापदंडों के लिए अधिकतम संभावना या अधिकतम पोस्टीरियरी (एमएपी) समाधान प्राप्त करने के लिए | ध्यान दें कि गाऊसी मिश्रण मॉडल के मापदंडों के लिए अधिकतम संभावना या अधिकतम पोस्टीरियरी (एमएपी) समाधान प्राप्त करने के लिए यहचरण मानक ईएम एल्गोरिथ्म के साथ निकटता से मेल खाते हैं। ज़िम्मेदारियाँ <math>r_{nk}</math> ''E'' चरण में डेटा दिए गए अव्यक्त वेरिएबल की पूर्व संभावना से निकटता <math>p(\mathbf{Z}\mid \mathbf{X})</math> से मेल खाता है, अर्थात। ; सांख्यिकी की गणना <math>N_k</math>, <math>{\bar{\mathbf{x}}}_k</math>, और <math>\mathbf{S}_k</math> डेटा पर संगत सॉफ्ट-काउंट आँकड़ों की गणना से निकटता से मेल खाता है; और पैरामीटर के नए मानों की गणना करने के लिए उन आँकड़ों का उपयोग गाऊसी मिश्रण मॉडल पर सामान्य ईएम में नए पैरामीटर मानों की गणना करने के लिए सॉफ्ट काउंट के उपयोग से निकटता से मेल खाता है। | ||
==घातांकीय-पारिवारिक वितरण== | ==घातांकीय-पारिवारिक वितरण == | ||
ध्यान दें कि | ध्यान दें कि पूर्व उदाहरण में, बार न देखे गए वेरिएबल पर वितरण को मापदंडों पर वितरण और अव्यक्त डेटा पर वितरण में कारक मान लिया गया था, प्रत्येक वेरिएबल के लिए व्युत्पन्न सर्वोत्तम वितरण वेरिएबल पर संबंधित पूर्व वितरण के समान वर्ग में था। यह सामान्य परिणाम है जो घातीय वर्ग से प्राप्त सभी पूर्व वितरणों के लिए सही है। | ||
==यह भी देखें== | ==यह भी देखें == | ||
* [[विविध संदेश भेजना]]: वेरिएशनल बायेसियन अनुमान के लिए | * [[विविध संदेश भेजना]]: वेरिएशनल बायेसियन अनुमान के लिए मॉड्यूलर एल्गोरिदम। | ||
* [[ वैरिएशनल ऑटोएनकोडर ]]: संभाव्य ग्राफिकल मॉडल और वेरिएशनल बायेसियन | * [[ वैरिएशनल ऑटोएनकोडर ]]: संभाव्य ग्राफिकल मॉडल और वेरिएशनल बायेसियन विधियों के वर्गों से संबंधित कृत्रिम तंत्रिका नेटवर्क। | ||
* अपेक्षा-अधिकतमकरण एल्गोरिथ्म: | * अपेक्षा-अधिकतमकरण एल्गोरिथ्म: संबंधित दृष्टिकोण जो परिवर्तनशील बायेसियन अनुमान के विशेष स्थितियां से मेल खाता है। | ||
* [[सामान्यीकृत फ़िल्टरिंग]]: नॉनलाइनियर स्टेट स्पेस मॉडल के लिए | * [[सामान्यीकृत फ़िल्टरिंग]]: नॉनलाइनियर स्टेट स्पेस मॉडल के लिए परिवर्तनीय फ़िल्टरिंग योजना। | ||
* विविधताओं की गणना: गणितीय विश्लेषण का क्षेत्र जो कार्यात्मकताओं को अधिकतम या न्यूनतम करने से संबंधित है। | * विविधताओं की गणना: गणितीय विश्लेषण का क्षेत्र जो कार्यात्मकताओं को अधिकतम या न्यूनतम करने से संबंधित है। | ||
* [[अधिकतम एन्ट्रापी भेदभाव]]: यह | * [[अधिकतम एन्ट्रापी भेदभाव]]: यह परिवर्तनशील अनुमान ढांचा है जो अतिरिक्त बड़े-मार्जिन बाधाओं को प्रस्तुत करने और लेखांकन की अनुमति देता है<ref>Sotirios P. Chatzis, “[http://proceedings.mlr.press/v28/chatzis13.pdf Infinite Markov-Switching Maximum Entropy Discrimination Machines],” Proc. 30th International Conference on Machine Learning (ICML). Journal of Machine Learning Research: Workshop and Conference Proceedings, vol. 28, no. 3, pp. 729–737, June 2013.</ref> | ||
| Line 501: | Line 496: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 07/07/2023]] | [[Category:Created On 07/07/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 22:40, 5 December 2023
वेरिएशनल बायेसियन विधियाँ बायेसियन अनुमान और यंत्र अधिगम में उत्पन्न होने वाले असाध्य अभिन्न का अनुमान लगाने की विधि का वर्ग है। इनका उपयोग सामान्यतः सम्मिश्र सांख्यिकीय मॉडल में किया जाता है जिसमें प्रेक्षित वेरिएबल (सामान्यतः डेटा कहा जाता है) | इसके साथ-साथ अज्ञात पैरामीटर और अव्यक्त वेरिएबल होते हैं, तथा यह तीन प्रकार के यादृच्छिक वेरिएबल के मध्य विभिन्न प्रकार के संबंधों के साथ होता है , जैसा कि चित्रमय मॉडल द्वारा वर्णित किया जा सकता है। कि बायेसियन अनुमान में विशिष्ट है, पैरामीटर और अव्यक्त वेरिएबल को साथ न देखे गए वेरिएबल के रूप में समूहीकृत किया जाता है। वेरिएशनल बायेसियन विधियाँ मुख्य रूप से दो उद्देश्यों के लिए उपयोग की जाती हैं |
- इन वेरिएबलों का कार्य इन पर सांख्यिकीय अनुमान लगाने के लिए, न देखे गए वेरिएबलों की पूर्व संभावना के लिए विश्लेषणात्मक अनुमान प्रदान करना होता है।
- अवलोकित डेटा की सीमांत संभावना (जिसे कभी-कभी साक्ष्य भी कहा जाता है) के लिए निचली सीमा प्राप्त करना है | (अर्थात मॉडल दिए गए डेटा की सीमांत संभावना, बिना देखे गए वेरिएबल पर मर्गिनाल्स पर प्रदर्शन के साथ) होता हैं। इसका उपयोग सामान्यतः मॉडल चयन करने के लिए किया जाता है, तथा सामान्य विचार यह है कि किसी दिए गए मॉडल के लिए उच्च सीमांत संभावना उस मॉडल द्वारा डेटा के उत्तम फिट को निरुपित करती है और इसलिए अधिक संभावना है कि प्रश्न में मॉडल वह था जिसने डेटा उत्पन्न किया था। (बेयस फैक्टर लेख भी देखें।)
पूर्व उद्देश्य में (पश्च संभाव्यता का अनुमान लगाने के लिए), वैरिएबल बेयस मोंटे कार्लो प्रतिरूपीकरण विधियों का विकल्प है - विशेष रूप से, मार्कोव श्रृंखला मोंटे कार्लो विधियां जैसे गिब्स प्रतिरूपीकरण - सम्मिश्र संभाव्यता वितरण पर सांख्यिकीय अनुमान के लिए पूर्ण प्रकार से बायेसियन दृष्टिकोण लेने के लिए सीधे या प्रतिरूप (सांख्यिकी) का विशेष रूप से मूल्यांकन करना कठिन है। जबकि मोंटे कार्लो विधि प्रतिरूपों के समुच्चय का उपयोग करके त्रुटिहीन पोस्टीरियर के लिए संख्यात्मक अनुमान प्रदान करती है, वेरिएबल बेयस पोस्टीरियर के अनुमान के लिए स्थानीय-इष्टतम, त्रुटिहीन विश्लेषणात्मक समाधान प्रदान करता है।
वैरिएशनल बेयस को एक्सपेक्टेशन-मैक्सिमाइजेशन एल्गोरिदम के विस्तार के रूप में देखा जा सकता है। एक्सपेक्टेशन-मैक्सिमाइजेशन (ईएम) एल्गोरिदम प्रत्येक पैरामीटर के एकल सबसे संभावित मूल्य के अधिकतम पोस्टीरियरी अनुमान (एमएपी अनुमान) से लेकर पूर्ण प्रकार से बायेसियन अनुमान तक, जो (एक अनुमान) की गणना करता है। ) मापदंडों और अव्यक्त वेरिएबल का संपूर्ण पश्च वितरण। ईएम की प्रकार, यह इष्टतम पैरामीटर मानों का समुच्चय ढूंढता है, और इसमें ईएम के समान ही वैकल्पिक संरचना होती है, जो इंटरलॉक्ड (परस्पर निर्भर) समीकरणों के समुच्चय पर आधारित होती है जिसका विश्लेषणात्मक रूप से समाधान नहीं किया जा सकता है।
अनेक अनुप्रयोगों के लिए, वैरिएबल बेयस अधिक गति से गिब्स सैंपलिंग के तुलनीय त्रुटिहीनता के समाधान तैयार करता है। चूँकि, मापदंडों को अद्यतन करने के लिए उपयोग किए जाने वाले समीकरणों के समुच्चय को प्राप्त करने के लिए अधिकांशतः तुलनीय गिब्स प्रतिरूप समीकरणों को प्राप्त करने की तुलना में बड़ी मात्रा में कार्य की आवश्यकता होती है। यह अनेक मॉडलों के लिए भी स्तिथि होती है जो वैचारिक रूप से अधिक सरल हैं, जैसा कि केवल दो मापदंडों और कोई अव्यक्त वेरिएबल के साथ मूलभूत गैर-पदानुक्रमित मॉडल के स्थितियां में नीचे दिखाया गया है।
गणितीय व्युत्पत्ति
समस्या
वैरिएबल अनुमान में, कुछ डेटा दिए जाने पर न देखे गए वेरिएबल्स के समुच्चय पर पश्च वितरण को तथाकथित वेरिएबल डिस्ट्रीब्यूशन, द्वारा अनुमानित किया जाता है।
विभाजन की तुलना में सरल रूप के वितरण के वर्ग से संबंधित होने तक सीमित है (उदाहरण के लिए गॉसियन वितरण का वर्ग ), बनाने के प्रयोजन से चुना गया हैं | यह वास्तविक पश्च भाग के समान, होता हैं |
समानता (या असमानता) को असमानता फलन के संदर्भ में मापा जाता है और इसलिए वितरण का चयन करके अनुमान लगाया जाता है वह को न्यूनतम करता है |
केएल विचलन
वैरिएबल बेज़ का सबसे सामान्य प्रकार असमानता फलन की पसंद के रूप में P से Q के कुल्बैक-लीब्लर डाइवर्जेंस (केएल-डाइवर्जेंस) का उपयोग करता है। यह विकल्प इस न्यूनतमकरण को सुव्यवस्थित बनाता है। केएल-विचलन को इस प्रकार परिभाषित किया गया है
ध्यान दें कि Q और P किसी की अपेक्षा से विपरीत हैं। विपरीते केएल-विचलन का यह उपयोग अवधारणात्मक रूप से अपेक्षा-अधिकतमकरण एल्गोरिदम के समान होता है। (केएल-डाइवर्जेंस का दूसरे तरीके से उपयोग करने से अपेक्षा प्रसार एल्गोरिदम उत्पन्न होता है।)
दुरूहता
विभिन्न विधियों का उपयोग सामान्यतः इसका अनुमान लगाने के लिए किया जाता है:
प्रत्येक में की गणना करने के लिए से अधिक का मर्गिनाल्स पर जाना सामान्यतः कठिन है, क्योंकि, उदाहरण के लिए, कि खोज समिष्ट संयुक्त रूप से बड़ी होती है। इसलिए, हम का उपयोग करके अनुमान करना चाहते हैं।
साक्ष्य निचली सीमा
मान लें कि , उपरोक्त केएल-विचलन को इस प्रकार भी लिखा जा सकता है |
क्योंकि के संबंध में स्थिरांक है और क्योंकि वितरण है, जो कि हमारे समीप है
जिसे अपेक्षित मान की परिभाषा के अनुसार (एक असतत यादृच्छिक वेरिएबल के लिए) निम्नानुसार लिखा जा सकता है
जिसे पुनर्व्यवस्थित करके बनाया जा सकता है |
चूंकि लॉग-साक्ष्य के संबंध में निश्चित किया गया है, अंतिम पद को अधिकतम करने से से . का केएल विचलन कम हो जाता है। के उचित विकल्प द्वारा, , सुव्यवस्थित हो जाता है इसका कार्य गणना करना और अधिकतम करना होता हैं। इसलिए हमारे समीप पश्च के लिए विश्लेषणात्मक सन्निकटन और लॉग-साक्ष्य के लिए निचली सीमा दोनों हैं (चूंकि केएल-विचलन गैर-नकारात्मक है)।
निचली सीमा इसे थर्मोडायनामिक मुक्त ऊर्जा के अनुरूप (ऋणात्मक) परिवर्तनशील मुक्त ऊर्जा के रूप में जाना जाता है क्योंकि इसे ऋणात्मक ऊर्जा के रूप में भी व्यक्त किया जा सकता है | यह प्लस एन्ट्रॉपी (सूचना सिद्धांत) हैं। शब्द इसे एविडेंस लोअर बाउंड के रूप में भी जाना जाता है, जिसे संक्षेप में एविडेंस लोअर बाउंड के रूप में जाना जाता है, इस बात पर जोर देने के लिए कि यह डेटा के लॉग-एविडेंस पर निचला बाउंड है।
प्रमाण
ब्रेगमैन विचलन के सामान्यीकृत पायथागॉरियन प्रमेय द्वारा, जिसमें केएल-विचलन विशेष स्तिथि होती है, इसमें यह दिखाया जा सकता है कि [1] [2]

:
जहाँ उत्तल समुच्चय है और समानता जब क्रियान्वित रहती है यदि:
इस स्थितियों में, वैश्विक न्यूनतमकर्ता साथ इस प्रकार पाया जा सकता है | [1]
जिसमें सामान्यीकरण स्थिरांक है |
शब्द व्यवहार में इसे अधिकांशतः मॉडल एविडेंस लोअर बाउंड (ईएलबीओ) कहा जाता है क्योंकि ,[1] जैसा कि उपर दिखाया गया है।
और की भूमिकाओं का परिवर्तन करके हम क्रमशः अनुमानित रूप से और और और पुनरावर्ती गणना कर सकते हैं | यद्यपि इस पुनरावृत्तीय योजना को नीरस रूप से अभिसरण करने की गारंटी है,[1] एकत्रित का केवल स्थानीय मिनिमाइज़र होता है|
यदि विवश समिष्ट स्वतंत्र समिष्ट के अंदर ही सीमित है, अर्थात उपरोक्त पुनरावृत्तीय योजना तथाकथित माध्य क्षेत्र सन्निकटन बन जाएगी जैसा कि नीचे दिया गया है।
माध्य क्षेत्र सन्निकटन
परिवर्तनशील वितरण सामान्यतः यह माना जाता है कि अव्यक्त वेरिएबल के समुच्चय के कुछ विभाजन पर कारक बनाया जाता है, अर्थात अव्यक्त वेरिएबल के कुछ विभाजन के लिए में सम्मिलित होता हैं |
इसे विविधताओं की गणना (इसलिए नाम वेरिएबल बेयस) का उपयोग करके दिखाया जा सकता है कि सबसे अच्छा वितरण प्रत्येक कारक के लिए (वितरण के संदर्भ में केएल विचलन को न्यूनतम करना, जैसा कि ऊपर वर्णित है) संतुष्ट करता है |
जहाँ डेटा और अव्यक्त वेरिएबल की संयुक्त संभावना के लघुगणक का अपेक्षित मूल्य होता है, जिसके संबंध में लिया गया है | जिसके विभाजन में उपस्तिथ सभी वेरिएबल्स पर: लेम्मा 4.1 का संदर्भ लिया जाता हैं | [3] यह वितरण की व्युत्पत्ति के लिए किया जाता है |
व्यवहार में, हम सामान्यतः लघुगणक के संदर्भ में कार्य करते हैं, अर्थात:
उपरोक्त अभिव्यक्ति में स्थिरांक सामान्यीकृत स्थिरांक (उपरोक्त अभिव्यक्ति में प्रत्येक) से संबंधित है ) और सामान्यतः निरीक्षण द्वारा पुनः स्थापित किया जाता है, क्योंकि अभिव्यक्ति के शेष भागों को सामान्यतः ज्ञात प्रकार के वितरण (जैसे गाऊसी वितरण, गामा वितरण, आदि) के रूप में पहचाना जा सकता है।
अपेक्षाओं के गुणों का प्रयोग, अभिव्यक्ति सामान्यतः अव्यक्त वेरिएबल और अपेक्षाओं (और कभी-कभी उच्चतर क्षण (गणित) जैसे विचरण) पर पूर्व वितरण के निश्चित हाइपरपैरामीटर के फलन में सरलीकृत किया जा सकता है, जो कि वर्तमान विभाजन में नहीं होता है (अर्थात अव्यक्त वेरिएबल सम्मिलित नहीं हैं) में ) हैं | यह विभाजन में वेरिएबल पर वितरण के मापदंडों और अन्य विभाजन में वेरिएबल की अपेक्षाओं के मध्य परिपत्र निर्भरता बनाता है। यह स्वाभाविक रूप से ईएम (अपेक्षा-अधिकतमकरण एल्गोरिदम) की प्रकार पुनरावृत्त एल्गोरिदम का सुझाव देता है, जिसमें अव्यक्त वेरिएबल की अपेक्षाओं (और संभवतः उच्च क्षणों) को कुछ फैशन में (संभवतःयादृच्छिक रूप से) प्रारंभ किया जाता है, और फिर प्रत्येक वितरण के पैरामीटर होते हैं तथा अपेक्षाओं के वर्तमान मानों का उपयोग करके बारी-बारी से गणना की जाती है, जिसके पश्चात् गणना किए गए मापदंडों के अनुसार नए गणना किए गए वितरण की अपेक्षा उचित रूप से निर्धारित की जाती है। इस प्रकार का एल्गोरिदम अनुक्रम की सीमा की गारंटी देता है। [4]
दूसरे शब्दों में, वेरिएबल के प्रत्येक विभाजन के लिए, विभाजन के वेरिएबल पर वितरण के लिए अभिव्यक्ति को सरल बनाकर और प्रश्न में वेरिएबल पर वितरण की कार्यात्मक निर्भरता की जांच करके, वितरण का वर्ग सामान्यतः निर्धारित किया जा सकता है (जो इसके स्थान में निर्धारित करता है) स्थिरांक का मान) हैं। वितरण के मापदंडों का सूत्र पूर्व वितरणों के हाइपरपैरामीटर (जो ज्ञात स्थिरांक हैं) के संदर्भ में व्यक्त किया जाता हैं, किन्तु अन्य विभाजनों में वेरिएबल के कार्यों की अपेक्षाओं के संदर्भ में भी व्यक्त किया जाएगा। सामान्यतः इन अपेक्षाओं को स्वयं वेरिएबलों की अपेक्षाओं के कार्यों में सरलीकृत किया जा सकता है (अर्थात साधन); कभी-कभी वर्गाकार वेरिएबलों की अपेक्षाएं (जो वेरिएबलों के विचरण से संबंधित हो सकती हैं), या उच्च शक्तियों (अर्थात उच्चतर क्षण (गणित)) की अपेक्षाएं भी प्रकट होती हैं। अधिकतर स्थितियों में, अन्य वेरिएबल का वितरण ज्ञात वर्ग से होता हैं, और प्रासंगिक अपेक्षाओं के लिए सूत्रों को देखा जा सकता है। चूँकि, वह सूत्र उन वितरण मापदंडों पर निर्भर करते हैं, जो इसके स्थान में अन्य वेरिएबल के बारे में अपेक्षाओं पर निर्भर करते हैं। इसका परिणाम यह है कि प्रत्येक वेरिएबल के वितरण के मापदंडों के सूत्रों को वेरिएबल के मध्य पारस्परिक, गैर-रेखीय निर्भरता वाले समीकरणों की श्रृंखला के रूप में व्यक्त किया जा सकता है। सामान्यतः, समीकरणों की इस प्रणाली को सीधे समाधान करना संभव नहीं है। चूँकि, जैसा कि ऊपर बताया गया है, निर्भरताएँ सरल पुनरावृत्त एल्गोरिथ्म का सुझाव देती हैं, जो अधिकतर स्थितियों में अभिसरण की गारंटी देता है। उदाहरण से यह प्रक्रिया और स्पष्ट हो जाटी हैं |
परिवर्तनात्मक अनुमान के लिए द्वैत सूत्र
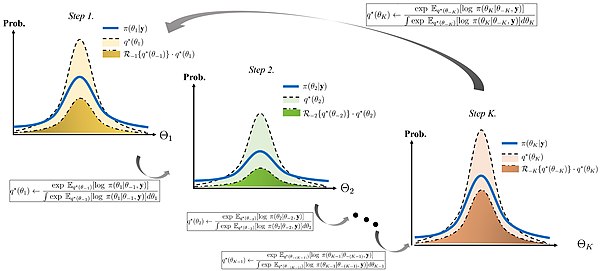
निम्नलिखित प्रमेय को परिवर्तनशील अनुमान के लिए द्वैत सूत्र के रूप में जाना जाता है। [3] यह वैरिएबल बेयस विधियों में उपयोग किए जाने वाले वैरिएबल वितरण के कुछ महत्वपूर्ण गुणों की व्याख्या करता है।
प्रमेय दो संभाव्यता समिष्ट और के साथ पर विचार करें मान लें कि सामान्य प्रभावी संभाव्यता माप होती है जैसे है कि और . मान लीजिये कि पर किसी भी वास्तविक-मूल्यवान यादृच्छिक वेरिएबल को निरूपित करें जो संतुष्ट करता है | तब निम्नलिखित समानता क्रियान्वित रहती है |
इसके अतिरिक्त, दाहिनी ओर का सर्वोच्च तभी प्राप्त होता है जब वह क्रियान्वित रहता है
संभाव्यता माप के संबंध में लगभग निश्चित रूप से , जहाँ और क्रमश के संबंध में संभाव्यता माप और के रेडॉन-निकोडिम डेरिवेटिव को निरूपित करते है |
एक मूलभूत उदाहरण
एक सरल गैर-पदानुक्रमित बायेसियन मॉडल पर विचार करें जिसमें स्वतंत्र रूप से वितरित i.i.d. का समुच्चय सम्मिलित है। तथा अज्ञात माध्य और विचरण के साथ गॉसियन वितरण से अवलोकन भी सम्मिलित हो सकते हैं। [5] निम्नलिखित में, हम इस मॉडल के माध्यम से वेरिएबल बेयस विधि की कार्यप्रणाली को स्पष्ट करने के लिए विस्तार से कार्य करते हैं।
गणितीय सुविधा के लिए, निम्नलिखित उदाहरण में हम परिशुद्धता (सांख्यिकी) के संदर्भ में कार्य करते हैं - अर्थात विचरण का व्युत्क्रम हो (या बहुभिन्नरूपी गॉसियन में, सहप्रसरण आव्युह का व्युत्क्रम) - न कि स्वयं विचरण हो । (सैद्धांतिक दृष्टिकोण से, परिशुद्धता और भिन्नता समतुल्य होती हैं क्योंकि दोनों के मध्य वन-से-वन पत्राचार है।)
गणितीय मॉडल
हम संयुग्मित पूर्व वितरणों को अज्ञात माध्य और परिशुद्धता पर रखते हैं अर्थात माध्य भी गाऊसी वितरण का अनुसरण करता है जबकि दूसरे शब्दों में परिशुद्धता गामा वितरण का अनुसरण करती है।
पूर्व वितरणों में हाइपर पैरामीटर और मान दिए जाते हैं | जिसमे और . के पूर्व में वितरण निश्चित होते हैं, जो पूर्व वितरणों के बारे में अज्ञानता का संकेत देते हैं तथा व्यापक पूर्व वितरण देने के लिए उन्हें लघु धनात्मक संख्याओं पर समुच्चय किया जा सकता है |
हम डेटा पॉइंट दे रहे हैं और हमारा लक्ष्य पश्च वितरण का अनुमान लगाना है मापदंडों का और होता हैं |
संयुक्त संभावना
सभी वेरिएबलों की संयुक्त प्रायिकता को इस प्रकार पुनः लिखा जा सकता है
जहां व्यक्तिगत कारक हैं
जहाँ
गुणनखंडित सन्निकटन
यह मान लीजिए , अर्थात कि पश्च वितरण और के लिए स्वतंत्र कारकों में विभाजित होता है | इस प्रकार की धारणा वैरिएबल बायेसियन पद्धति को रेखांकित करती है। वास्तविक पश्च वितरण वास्तव में इस प्रकार से कारक नहीं होता है (वास्तव में, इस साधारण स्थितियां में, इसे गाऊसी-गामा वितरण के रूप में जाना जाता है), और इसलिए हम जो परिणाम प्राप्त करेंगे उसे अनुमान कहा जाता हैं।
की व्युत्पत्ति q(μ)
तब
उपरोक्त व्युत्पत्ति में, , और उन मानों को संदर्भित करें जो के संबंध में स्थिर होते हैं. ध्यान दें कि शब्द का कार्य नहीं है और के मूल्य की चिंता किए बिना उसका मूल्य समान होता हैं | इसलिए पंक्ति 3 में हम इसे अंत में स्थिर पद में समाहित कर सकते हैं। हम पंक्ति 7 में भी यही कार्य करते हैं।
अंतिम पंक्ति में बस द्विघात बहुपद है . चूँकि यह का लघुगणक है, हम देख सकते हैं कि स्वयं गाऊसी वितरण है।
एक निश्चित मात्रा में कठिन गणित के साथ (ब्रेसिज़ के अंदर के वर्गों का विस्तार करना, और से सम्मिलित शब्दों को भिन्न करना और समूहीकृत करना और पर वर्ग पूरा करना ), हम गाऊसी वितरण के पैरामीटर प्राप्त कर सकते हैं:
ध्यान दें कि उपरोक्त सभी चरणों को सामान्य वितरण या दो द्विघातों के योग के सूत्र का उपयोग करके छोटा किया जा सकता है।
दूसरे शब्दों में:
की व्युत्पत्ति q(τ)
उपरोक्त की व्युत्पत्ति के समान है, चूँकि हम संक्षिप्तता के लिए कुछ विवरण छोड़ देते हैं।
दोनों पक्षों को घातांकित करने पर हम यह देख सकते हैं कि गामा वितरण है. विशेष रूप से:
पैरामीटर की गणना के लिए एल्गोरिदम
आइए हम पूर्व अनुभागों के निष्कर्षों का पुनर्कथन करें:
और
प्रत्येक स्थितियों में, किसी वेरिएबल पर वितरण के पैरामीटर दूसरे वेरिएबल के संबंध में ली गई अपेक्षाओं पर निर्भर करते हैं। हम गॉसियन और गामा वितरण के क्षणों की अपेक्षाओं के लिए मानक सूत्रों का उपयोग करके अपेक्षाओं का विस्तार कर सकते हैं:
इन सूत्रों को उपरोक्त समीकरणों पर प्रयुक्त करना अधिकतर स्थितियों में साधारण है, किन्तु समीकरण के लिए अधिक कार्य लेता है:
फिर हम पैरामीटर समीकरणों को बिना किसी अपेक्षा के इस प्रकार लिख सकते हैं:
ध्यान दें कि और सूत्रों के मध्य चक्रीय निर्भरताएँ हैं . यह स्वाभाविक रूप से अपेक्षा-अधिकतमकरण ईएम जैसा एल्गोरिदम का सुझाव देता है:
- और गणना करें | और गणना करने के लिए इन मानों का उपयोग किया जाता है |
- कुछ इच्छानुसार मूल्य के लिए प्रारंभ करें.
- की गणना करने के लिए अन्य मापदंडों के ज्ञात मानों के साथ के वर्तमान मान का उपयोग करें .
- की गणना करने के लिए अन्य मापदंडों के ज्ञात मानों के साथ के वर्तमान मान का उपयोग करें.
- अंतिम दो चरणों को अभिसरण होने तक दोहराएँ (अर्थात जब तक कि कोई भी मान कुछ लघु राशि से अधिक न बदल जाए)।
फिर हमारे समीप पश्च मापदंडों के अनुमानित वितरण के हाइपरपैरामीटर के लिए मान हैं, जिनका उपयोग हम पश्च भाग के किसी भी गुण की गणना करने के लिए कर सकते हैं - उदाहरण के लिए इसका माध्य और विचरण, 95% उच्चतम-घनत्व क्षेत्र (सबसे छोटा अंतराल जिसमें कुल संभावना का 95% सम्मिलित है), आदि।
यह दिखाया जा सकता है कि यह एल्गोरिदम स्थानीय अधिकतम में परिवर्तित होने की गारंटी देता है।
यह भी ध्यान दें कि पूर्व वितरणों का स्वरूप संबंधित पूर्व वितरणों के समान ही है। हमने यह नहीं माना कि हमने जो एकमात्र धारणा बनाई वह यह थी कि वितरण गुणनखंडित होते हैं, और वितरण का स्वरूप स्वाभाविक रूप से अनुसरण किया जाता है। यह पता चला है (नीचे देखें) कि तथ्य यह है कि पूर्व वितरणों का रूप पूर्व वितरणों के समान है, यह कोई संयोग नहीं है, किंतु सामान्य परिणाम है जब भी पूर्व वितरण घातीय वर्ग के सदस्य होते हैं, जो कि अधिकांश मानक वितरणों के लिए स्तिथि है .
आगे की चर्चा
स्टेप-बाय-स्टेप रेसिपी
उपरोक्त उदाहरण उस विधि को दर्शाता है जिसके द्वारा किसी दिए गए बायेसियन नेटवर्क में पश्च संभाव्यता घनत्व के लिए वैरिएबल-बायेसियन सन्निकटन प्राप्त किया जाता है:
- ग्राफ़िकल मॉडल के साथ नेटवर्क का वर्णन करें, देखे गए वेरिएबल (डेटा) और न देखे गए वेरिएबल (पैरामीटर) और अव्यक्त वेरिएबल ) और उनके सशर्त संभाव्यता वितरण की पहचान करें। वेरिएशनल बेज़ इसके पश्चात् पश्च संभाव्यता का अनुमान तैयार करेंगे |. सन्निकटन की मूल संपत्ति यह है कि यह गुणनखंडित वितरण है, अर्थात न देखे गए वेरिएबल के असंयुक्त उपसमुच्चय पर दो या दो से अधिक सांख्यिकीय स्वतंत्रता वितरण का उत्पाद है।
- न देखे गए वेरिएबलों को दो या दो से अधिक उपसमूहों में विभाजित करें, जिन पर स्वतंत्र कारक प्राप्त किए जाएंगे। ऐसा करने की कोई सार्वभौमिक प्रक्रिया नहीं है; बहुत अधिक उपसमुच्चय बनाने से खराब सन्निकटन प्राप्त होता है, जबकि बहुत कम उपसमुच्चय बनाने से संपूर्ण परिवर्तनशील बेयस प्रक्रिया कठिन हो जाती है। सामान्यतः, पहला विभाजन पैरामीटर और अव्यक्त वेरिएबल को भिन्न करने के लिए होता है; अधिकांशतः, यह अपने आप में सुगम परिणाम उत्पन्न करने के लिए पर्याप्त होता है। मान लें कि विभाजन कहा जाता हैं .
- किसी दिए गए विभाजन के लिए , मूल समीकरण का उपयोग करके सर्वोत्तम अनुमानित वितरण के लिए सूत्र लिखें .
- ग्राफ़िकल मॉडल का उपयोग करके संयुक्त संभाव्यता वितरण के लिए सूत्र भरें। कोई भी घटक सशर्त वितरण जिसमें कोई भी वेरिएबल सम्मिलित नहीं है नजरअंदाज किया जा सकता है; उन्हें स्थिर अवधि में जोड़ दिया जाएगा।
- उपरोक्त उदाहरण का अनुसरण करते हुए सूत्र को सरल बनाएं और अपेक्षा ऑपरेटर प्रयुक्त करें। आदर्श रूप से, इसे वेरिएबल के मूलभूत कार्यों की अपेक्षाओं में सरलीकृत नहीं किया जाना चाहिए (जैसे पसमाधाना या दूसरा कच्चा क्षण (गणित), लघुगणक की अपेक्षा, आदि)। वेरिएबल बेयस प्रक्रिया को अच्छी प्रकार से कार्य करने के लिए, इन अपेक्षाओं को सामान्यतः इन वेरिएबल के वितरण के मापदंडों और/या हाइपरपैरामीटर के कार्यों के रूप में विश्लेषणात्मक रूप से व्यक्त किया जाना चाहिए। सभी स्थितियों में, यह अपेक्षा शर्तें वर्तमान विभाजन में वेरिएबल के संबंध में स्थिरांक हैं।
- वर्तमान विभाजन में वेरिएबल के संबंध में सूत्र का कार्यात्मक रूप वितरण के प्रकार को निरुपित करता है। विशेष रूप से, सूत्र को घातांकित करने से वितरण की संभाव्यता घनत्व फलन (पीडीएफ) उत्पन्न होती है (या कम से कम, इसके लिए कुछ आनुपातिक, अज्ञात सामान्यीकरण स्थिरांक के साथ)। समग्र विधि को ट्रैक्टेबल बनाने के लिए उत्पन्न होती है, तथा इस ज्ञात वितरण से संबंधित कार्यात्मक रूप को पहचानना संभव होना चाहिए। सूत्र को ज्ञात वितरण के पीडीएफ से मेल खाने वाले रूप में बदलने के लिए महत्वपूर्ण गणितीय हेरफेर की आवश्यकता हो सकती है। जब यह किया जा सकता है, तब सामान्यीकरण स्थिरांक को परिभाषा द्वारा पुनः स्थापित किया जा सकता है, और ज्ञात वितरण के मापदंडों के लिए समीकरण सूत्र के उचित भागों को निकालकर प्राप्त किया जा सकता है।
- जब सभी अपेक्षाओं को विश्लेषणात्मक रूप से उन वेरिएबलों के कार्यों से बदला जा सकता है जो वर्तमान विभाजन में नहीं हैं, और पीडीएफ को ऐसे रूप में रखा जाता है जो ज्ञात वितरण के साथ पहचान की अनुमति देता है, तब परिणाम समीकरणों का समुच्चय होता है जो इष्टतम मापदंडों के मानों को अन्य विभाजनों में वेरिएबल के पैरामीटर के कार्यों के रूप में व्यक्त करता है ।
- जब इस प्रक्रिया को सभी विभाजनों पर प्रयुक्त किया जा सकता है, तब परिणाम सभी मापदंडों के इष्टतम मानों को निर्दिष्ट करने वाले परस्पर जुड़े समीकरणों का समुच्चय होता है।
- फिर अपेक्षा अधिकतमीकरण (ईएम) प्रकार की प्रक्रिया प्रयुक्त की जाती है, प्रत्येक पैरामीटर के लिए प्रारंभिक मान चुना जाता है और चरणों की श्रृंखला के माध्यम से पुनरावृत्ति की जाती है, जहां प्रत्येक चरण में हम समीकरणों के माध्यम से चक्र करते हैं, प्रत्येक पैरामीटर को बारी-बारी से अपडेट करते हैं। यह जुटने की गारंटी है.
सबसे महत्वपूर्ण बिंदु
इसमें सम्मिलित सभी गणितीय जोड़-तोड़ों के कारण, बड़ी तस्वीर का ध्यान भटकाना आसान है। महत्वपूर्ण बातें यह हैं:
- वैरिएबल बेयस का विचार डेटा को देखते हुए, न देखे गए वेरिएबल (पैरामीटर और अव्यक्त वेरिएबल ) के समुच्चय की पूर्व संभावना के लिए विश्लेषणात्मक सन्निकटन का निर्माण करना है। इसका कारण यह है कि समाधान का रूप अन्य बायेसियन अनुमान विधियों के समान है, जैसे कि गिब्स प्रतिरूपीकरण - अर्थात वितरण जो वेरिएबल के बारे में ज्ञात प्रत्येक चीज का वर्णन करना चाहता है। जैसा कि अन्य बायेसियन विधियों में होता है - किन्तु उदाहरण के विपरीत। अपेक्षा अधिकतमीकरण (ईएम) या अन्य अधिकतम संभावना विधियों में - दोनों प्रकार के अप्राप्य वेरिएबल (अर्थात पैरामीटर और अव्यक्त वेरिएबल ) को समान माना जाता है, अर्थात यादृच्छिक वेरिएबल के रूप में माना जाता है । फिर वेरिएबलों का अनुमान मानक बायेसियन विधियों से प्राप्त किया जा सकता है, जैसे एकल बिंदु अनुमान प्राप्त करने के लिए वितरण के माध्य की गणना करना या विश्वसनीय अंतराल, उच्चतम घनत्व क्षेत्र आदि प्राप्त करना।
- विश्लेषणात्मक सन्निकटन का अर्थ है कि पश्च वितरण के लिए सूत्र लिखा जा सकता है। सूत्र में सामान्यतः प्रसिद्ध संभाव्यता वितरण का उत्पाद सम्मिलित होता है, जिनमें से प्रत्येक न देखे गए वेरिएबल के समुच्चय पर कारक होता है (अर्थात, देखे गए डेटा को देखते हुए, यह अन्य वेरिएबल से सशर्त रूप से स्वतंत्र है)। यह सूत्र वास्तविक पश्च वितरण नहीं है, किंतु इसका अनुमान है; विशेष रूप से, यह सामान्यतः न देखे गए वेरिएबलों के निम्नतम क्षण (गणित) में अधिक निकटता से सहमत होगा, उदाहरण के लिए माध्य और विचरण.
- सभी गणितीय जोड़-तोड़ों का परिणाम है (1) कारकों को बनाने वाले संभाव्यता वितरण की पहचान, और (2) इन वितरणों के मापदंडों के लिए परस्पर निर्भर सूत्र। इन मापदंडों के वास्तविक मानों की गणना ईएम की प्रकार वैकल्पिक पुनरावृत्त प्रक्रिया के माध्यम से संख्यात्मक रूप से की जाती है।
अपेक्षा अधिकतमकरण (ईएम) के साथ तुलना में
वेरिएशनल बेयस (वीबी) की तुलना अधिकांशतः अपेक्षा अधिकतमकरण (ईएम) से की जाती है। वास्तविक संख्यात्मक प्रक्रिया अधिक समान है, जिसमें दोनों वैकल्पिक पुनरावृत्त प्रक्रियाएं हैं जो क्रमिक रूप से इष्टतम पैरामीटर मानों पर एकत्रित होती हैं। संबंधित प्रक्रियाओं को प्राप्त करने के प्रारंभिक चरण भी अस्पष्ट रूप से समान हैं, दोनों संभाव्यता घनत्व के सूत्रों के साथ प्रारंभ होते हैं और दोनों में महत्वपूर्ण मात्रा में गणितीय जोड़-तोड़ सम्मिलित होते हैं।
चूँकि, इसमें अनेक अंतर हैं। सबसे महत्वपूर्ण यह है कि गणना क्या की जा रही है।
- ईएम उन यादृच्छिक वेरिएबलों के पश्च वितरण के बिंदु अनुमानों की गणना करता है जिन्हें मापदंडों के रूप में वर्गीकृत किया जा सकता है, किन्तु केवल अव्यक्त वेरिएबल के वास्तविक पश्च वितरण का अनुमान (कम से कम नरम ईएम में, और अधिकांशतः केवल जब अव्यक्त वेरिएबल भिन्न होते हैं)। गणना किए गए बिंदु अनुमान इन मापदंडों के मोड (सांख्यिकी) हैं; कोई अन्य जानकारी उपलब्ध नहीं है.
- दूसरी ओर, वीबी सभी वेरिएबल, दोनों मापदंडों और अव्यक्त वेरिएबल के वास्तविक पश्च वितरण के अनुमान की गणना करता है। जब बिंदु अनुमान प्राप्त करने की आवश्यकता होती है, तब सामान्यतः मोड के अतिरिक्त माध्य का उपयोग किया जाता है, जैसा कि बायेसियन अनुमान में सामान्य है। इसके साथ ही, वीबी में गणना किए गए मापदंडों का ईएम के समान महत्व नहीं है। ईएम बेयस नेटवर्क के मापदंडों के इष्टतम मानों की गणना स्वयं करता है। वीबी बेयस नेटवर्क के मापदंडों और अव्यक्त वेरिएबल का अनुमान लगाने के लिए उपयोग किए जाने वाले वितरण के मापदंडों के इष्टतम मानों की गणना करता है। उदाहरण के लिए, विशिष्ट गाऊसी मिश्रण मॉडल में प्रत्येक मिश्रण घटक के माध्य और विचरण के लिए पैरामीटर होंगे। ईएम सीधे इन मापदंडों के लिए इष्टतम मानों का अनुमान लगाएगा। चूँकि, वीबी पहले इन मापदंडों के अनुसार वितरण को फिट करेगा - सामान्यतः पूर्व वितरण के रूप में, उदाहरण के लिए। सामान्य-स्केल व्युत्क्रम गामा वितरण - और फिर इस पूर्व वितरण के मापदंडों के लिए मानों की गणना करेगा, अर्थात अनिवार्य रूप से हाइपरपैरामीटर में गणना की जाती है। इस स्थितियां में, वीबी सामान्य-स्केल व्युत्क्रम गामा वितरण के चार मापदंडों के इष्टतम अनुमानों की गणना करेगा जो घटक के माध्य और विचरण के संयुक्त वितरण का वर्णन करता है।
एक अधिक सम्मिश्र उदाहरण

एक बायेसियन गाऊसी मिश्रण मॉडल की कल्पना करें जिसका वर्णन इस प्रकार है:[5]
टिप्पणी:
- सिमडिर()() आयाम का सममित डिरिचलेट वितरण है , प्रत्येक घटक के लिए हाइपरपैरामीटर समुच्चय के साथ है. डिरिचलेट वितरण श्रेणीबद्ध वितरण या बहुपद वितरण से पहले का संयुग्म है।
- विशार्ट वितरण है, जो बहुभिन्नरूपी गॉसियन वितरण के लिए त्रुटिहीन आव्युह (व्युत्क्रम परिशुद्धता आव्युह) का संयुग्मित पूर्व है।
- मल्टी() एकल अवलोकन पर बहुपद वितरण है (एक श्रेणीबद्ध वितरण के सामान्तर)। अवस्था समिष्ट वन-के- प्रतिनिधित्व है, अर्थात, a -आयामी सदिश जिसमें अवयवों में से 1 है (अवलोकन की पहचान निर्दिष्ट करते हुए) और अन्य सभी अवयव 0 हैं।
- गाऊसी वितरण है, इस स्थितियां में विशेष रूप से बहुभिन्नरूपी गाऊसी वितरण।
उपरोक्त वेरिएबलों की व्याख्या इस प्रकार है:|
- डेटा बिंदु, का समुच्चय है जिनमें से प्रत्येक बहुभिन्नरूपी गॉसियन वितरण -आयामी सदिश को वितरित किया जाता है।
- अव्यक्त वेरिएबल का समुच्चय है, प्रति डेटा बिंदु निर्दिष्ट करता है कि संबंधित डेटा बिंदु किस मिश्रण घटक से संबंधित है, जैसा ऊपर वर्णित है। के लिए घटकों के साथ वन--सदिश प्रतिनिधित्व का उपयोग करता है |
- मिश्रण घटक के लिए मिश्रण अनुपात है .
- और प्रत्येक मिश्रण घटक से जुड़े पैरामीटर (माध्य और परिशुद्धता (सांख्यिकी)) निर्दिष्ट करते हैं।
- {1} और {2} प्रत्येक मिश्रण घटक से जुड़े पैरामीटर (माध्य और परिशुद्धता) निर्दिष्ट करते हैं।
जहां व्यक्तिगत कारक हैं
जहाँ
यह मान लीजिए .
तब
जहां हमने परिभाषित किया है कि
के लिए सूत्र के दोनों पक्षों का घातांक द्वारा उत्पन्न
इसे सामान्य बनाने की आवश्यकता के परिणामस्वरूप के सभी मानों का योग 1 हो जाता है जिससे परिणाम मिलता है
जहाँ
दूसरे शब्दों में, एकल-अवलोकन बहुपद वितरण और प्रत्येक व्यक्ति पर कारकों का उत्पाद है , जिसे मापदंडों के साथ एकल-अवलोकन बहुपद वितरण के रूप में वितरित किया जाता है के लिए .
इसके अतिरिक्त, हम उस पर ध्यान देते हैं
जो श्रेणीबद्ध वितरण के लिए मानक परिणाम है।
अभी, कारक पर विचार करें , ध्यान दें कि यह स्वचालित रूप से इसमें सम्मिलित होता है हमारे गॉसियन मिश्रण मॉडल को परिभाषित करने वाले ग्राफिकल मॉडल की संरचना के कारण, जो ऊपर निर्दिष्ट है।
तब,
दोनों पक्षों का घातांक लेते हुए हम पहचानते हैं डिरिचलेट वितरण के रूप में
जहाँ
जहाँ
अंततः
और से सम्मिलित नियमों को समूहीकृत करना और पढ़ना , परिणाम गाऊसी-विशार्ट वितरण द्वारा दिया गया है
परिभाषाएँ दी गईं
अंत में, ध्यान दें कि इन कार्यों के लिए के मानों की आवश्यकता होती है , जिसका उपयोग किया जाता है , जिसके बारी-बारी से , और आधार पर परिभाषित किया गया है, अभी जब हमने उन वितरणों को निर्धारित कर लिया है जिन पर यह अपेक्षाएँ ली गई हैं, तब हम उनके लिए सूत्र प्राप्त कर सकते हैं:
इन परिणामों की ओर ले जाते हैं
इन्हें पर सामान्यीकृत करके आनुपातिक से निरपेक्ष मान में परिवर्तित किया जा सकता है जिससे कि संबंधित मानों का योग 1 हो जाये ।
ध्यान दें कि:
- पैरामीटर , , और के लिए अद्यतन समीकरण वेरिएबलों का और आंकड़ों , , और पर निर्भरकरते है, और यह आँकड़े इसके स्थान में निर्भर करते हैं .
- वेरिएबल के पैरामीटर के लिए अद्यतन समीकरण का आंकड़ों पर निर्भर करते है, जो इसके स्थान में पर निर्भर करता है .
- के लिए अद्यतन समीकरण पर प्रत्यक्ष चक्रीय निर्भरता है , , और साथ ही , और अप्रत्यक्ष चक्रीय निर्भरता भी द्वारा और पर निर्भर करती है |
यह पुनरावृत्तीय प्रक्रिया का सुझाव देता है जो दो चरणों के मध्य वैकल्पिक होती है:
- एक E-स्टेप जो अन्य सभी मापदंडों के वर्तमान मानों का उपयोग करके के मूल्य की गणना करता है ।
- एक M-स्टेप जो अन्य सभी मापदंडों के वर्तमान मानों की गणना करने के लिए के वर्तमान मान का उपयोग करता है ।
ध्यान दें कि गाऊसी मिश्रण मॉडल के मापदंडों के लिए अधिकतम संभावना या अधिकतम पोस्टीरियरी (एमएपी) समाधान प्राप्त करने के लिए यहचरण मानक ईएम एल्गोरिथ्म के साथ निकटता से मेल खाते हैं। ज़िम्मेदारियाँ E चरण में डेटा दिए गए अव्यक्त वेरिएबल की पूर्व संभावना से निकटता से मेल खाता है, अर्थात। ; सांख्यिकी की गणना , , और डेटा पर संगत सॉफ्ट-काउंट आँकड़ों की गणना से निकटता से मेल खाता है; और पैरामीटर के नए मानों की गणना करने के लिए उन आँकड़ों का उपयोग गाऊसी मिश्रण मॉडल पर सामान्य ईएम में नए पैरामीटर मानों की गणना करने के लिए सॉफ्ट काउंट के उपयोग से निकटता से मेल खाता है।
घातांकीय-पारिवारिक वितरण
ध्यान दें कि पूर्व उदाहरण में, बार न देखे गए वेरिएबल पर वितरण को मापदंडों पर वितरण और अव्यक्त डेटा पर वितरण में कारक मान लिया गया था, प्रत्येक वेरिएबल के लिए व्युत्पन्न सर्वोत्तम वितरण वेरिएबल पर संबंधित पूर्व वितरण के समान वर्ग में था। यह सामान्य परिणाम है जो घातीय वर्ग से प्राप्त सभी पूर्व वितरणों के लिए सही है।
यह भी देखें
- विविध संदेश भेजना: वेरिएशनल बायेसियन अनुमान के लिए मॉड्यूलर एल्गोरिदम।
- वैरिएशनल ऑटोएनकोडर : संभाव्य ग्राफिकल मॉडल और वेरिएशनल बायेसियन विधियों के वर्गों से संबंधित कृत्रिम तंत्रिका नेटवर्क।
- अपेक्षा-अधिकतमकरण एल्गोरिथ्म: संबंधित दृष्टिकोण जो परिवर्तनशील बायेसियन अनुमान के विशेष स्थितियां से मेल खाता है।
- सामान्यीकृत फ़िल्टरिंग: नॉनलाइनियर स्टेट स्पेस मॉडल के लिए परिवर्तनीय फ़िल्टरिंग योजना।
- विविधताओं की गणना: गणितीय विश्लेषण का क्षेत्र जो कार्यात्मकताओं को अधिकतम या न्यूनतम करने से संबंधित है।
- अधिकतम एन्ट्रापी भेदभाव: यह परिवर्तनशील अनुमान ढांचा है जो अतिरिक्त बड़े-मार्जिन बाधाओं को प्रस्तुत करने और लेखांकन की अनुमति देता है[6]
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 Tran, Viet Hung (2018). "सूचना ज्यामिति के माध्यम से कोपुला वेरिएशनल बेज़ अनुमान". arXiv:1803.10998 [cs.IT].
- ↑ 2.0 2.1 Adamčík, Martin (2014). "ब्रेगमैन डायवर्जेंस की सूचना ज्यामिति और मल्टी-एक्सपर्ट रीजनिंग में कुछ अनुप्रयोग". Entropy. 16 (12): 6338–6381. Bibcode:2014Entrp..16.6338A. doi:10.3390/e16126338.
- ↑ 3.0 3.1 3.2 Lee, Se Yoon (2021). "Gibbs sampler and coordinate ascent variational inference: A set-theoretical review". Communications in Statistics - Theory and Methods: 1–21. arXiv:2008.01006. doi:10.1080/03610926.2021.1921214. S2CID 220935477.
- ↑ Boyd, Stephen P.; Vandenberghe, Lieven (2004). उत्तल अनुकूलन (PDF). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 15, 2011.
- ↑ 5.0 5.1 Bishop, Christopher M. (2006). "Chapter 10". पैटर्न मान्यता और मशीन प्रवीणता. Springer. ISBN 978-0-387-31073-2.
- ↑ Sotirios P. Chatzis, “Infinite Markov-Switching Maximum Entropy Discrimination Machines,” Proc. 30th International Conference on Machine Learning (ICML). Journal of Machine Learning Research: Workshop and Conference Proceedings, vol. 28, no. 3, pp. 729–737, June 2013.
बाहरी संबंध
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay provides an introduction to variational methods (p. 422).
- A Tutorial on Variational Bayes. Fox, C. and Roberts, S. 2012. Artificial Intelligence Review, doi:10.1007/s10462-011-9236-8.
- Variational-Bayes Repository A repository of research papers, software, and links related to the use of variational methods for approximate Bayesian learning up to 2003.
- Variational Algorithms for Approximate Bayesian Inference, by M. J. Beal includes comparisons of EM to Variational Bayesian EM and derivations of several models including Variational Bayesian HMMs.
- High-Level Explanation of Variational Inference by Jason Eisner may be worth reading before a more mathematically detailed treatment.
- Copula Variational Bayes inference via information geometry (pdf) by Tran, V.H. 2018. This paper is primarily written for students. Via Bregman divergence, the paper shows that Variational Bayes is simply a generalized Pythagorean projection of true model onto an arbitrarily correlated (copula) distributional space, of which the independent space is merely a special case.