उच्चिष्ठ और निम्निष्ठ

For सांख्यिकी में उपयोग, see अधिकतम और न्यूनतम नमूना.

"चरम मान" redirects here. For सांख्यिकी में अवधारणा, see चरम मूल्य सिद्धांत. For कलन में अवधारणा, see चरम मूल्य प्रमेय.

"अधिकतम" and "न्यूनतम" redirect here. For other uses, see अधिकतम (disambiguation) and न्यूनतम (disambiguation).

cos(3πx)/x, 0.1≤ x ≤1.1 के लिए स्थानीय और वैश्विक दीर्घतम और न्यूनतम

गणितीय विश्लेषण में, किसी फलन(गणित) के दीर्घतम और न्यूनतम(अधिकतम और न्यूनतम के संबंधित बहुवचन), सामूहिक रूप से एक्स्ट्रेमा(चरम का बहुवचन) के रूप में जाना जाता है, प्रकार्य का सबसे बड़ा और सबसे छोटा मान है, या तो किसी दिए गए अंतराल के भीतर(गणित)("स्थानीय" या "सापेक्ष" एक्स्ट्रेमा), या किसी प्रकार्य के संपूर्ण कार्यक्षेत्र पर("वैश्विक" या "पूर्ण" एक्स्ट्रेमा)। पियरे डी फर्मेट उन पहले गणितज्ञों में से एक थे जिन्होंने प्रकार्य का दीर्घतम और न्यूनतम खोजने के लिए एक सामान्य तकनीक, पर्याप्तता का प्रस्ताव दिया था।

जैसा कि समुच्चय सिद्धांत में परिभाषित किया गया है, एक समुच्चय(गणित) का अधिकतम और न्यूनतम क्रमशः समुच्चय में सबसे बड़ा और सबसे कम तत्व है। असीम अनंत समुच्चय, जैसे कि वास्तविक संख्याओं का समुच्चय, का कोई न्यूनतम या अधिकतम नहीं होता है।

परिभाषा

प्रकार्य X के कार्यक्षेत्र पर परिभाषित एक वास्तविक-मूल्यवान प्रकार्य(गणित) f में 'वैश्विक'(या 'पूर्ण') 'अधिकतम बिंदु' X पर^∗ है , अगर X में सभी X के लिए f(x^∗) ≥ f(x) है। इसी तरह, प्रकार्य में 'वैश्विक'(या 'पूर्ण') 'न्यूनतम बिंदु' X पर^∗ है, अगर X में सभी X के लिए f(x^∗) ≤ f(x) है। अधिकतम बिंदु पर फलन के मान को फलन का अधिकतम मान कहते हैं, निरूपित $\max(f(x))$, और न्यूनतम बिंदु पर फलन के मान को फलन का न्यूनतम मान कहा जाता है। प्रतीकात्मक रूप से, इसे इस प्रकार लिखा जा सकता है:

$x_{0}\in X$ प्रकार्य का वैश्विक अधिकतम बिंदु $f:X\to \mathbb {R} ,$ यदि $(\forall x\in X)\,f(x_{0})\geq f(x)$ है।

वैश्विक न्यूनतम बिंदु की परिभाषा भी इसी तरह आगे बढ़ती है।

यदि कार्यक्षेत्र X एक मापीय स्थान है, तो f को 'स्थानीय'(या 'सापेक्ष') 'अधिकतम बिंदु' कहा जाता है बिंदु x पर^∗, यदि कुछ ε > 0 ऐसे मौजूद है कि, f(x^∗) ≥ f(x) X में सभी X के लिए X^∗ की दूरी ε के भीतर है। इसी तरह, प्रकार्य का X^∗ पर एक स्थानीय न्यूनतम बिंदु होता है, अगर f(x^∗) ≤ f(x) सभी x के लिए X में x^∗ की दूरी ε के भीतर है। इसी तरह की परिभाषा का उपयोग तब किया जा सकता है जब X एक स्थलीय स्थान है, क्योंकि अभी दी गई परिभाषा को प्रतिवैस के संदर्भ में फिर से परिभाषित किया जा सकता है। गणितीय रूप से, दी गई परिभाषा इस प्रकार लिखी गई है:

$(X,d_{X})$ को एकमापीय समष्टि मान लीजिए और प्रकार्य को $f:X\to \mathbb {R}$. फिर $x_{0}\in X$ कार्य का एक स्थानीय अधिकतम बिंदु है $f$ यदि $(\exists \varepsilon >0)$ ऐसे कि $(\forall x\in X)\,d_{X}(x,x_{0})<\varepsilon \implies f(x_{0})\geq f(x).$

स्थानीय न्यूनतम बिंदु की परिभाषा भी इसी तरह आगे बढ़ सकती है।

वैश्विक और स्थानीय दोनों वस्तुस्थिति में, a की निश्चित चरम अवधारणा को परिभाषित किया जा सकता है। उदाहरण के लिए, X^∗ निश्चित वैश्विक अधिकतम बिंदु है। उदाहरण के लिए, x∗ एक सख्त वैश्विक अधिकतम बिंदु है यदि सभी x में x ≠ x∗ के साथ, हमारे पास f(x∗) > f(x), और x∗ एक सख्त स्थानीय अधिकतम बिंदु है। यदि वहाँ कुछ ε > 0 ऐसे मौजूद है कि, X में सभी x के लिए x∗ की दूरी ε के भीतर x ≠ x∗ के साथ है, हमारे पास f(x∗) > f(x) है। ध्यान दें कि एक बिंदु एक सख्त वैश्विक अधिकतम बिंदु है यदि और केवल यदि यह अद्वितीय वैश्विक अधिकतम बिंदु है, और इसी तरह न्यूनतम बिंदुओं के लिए है।

सघन स्थल कार्यक्षेत्र के साथ एक सतत कार्य वास्तविक-मूल्यवान प्रकार्य में हमेशा अधिकतम बिंदु और न्यूनतम बिंदु होता है। एक महत्वपूर्ण उदाहरण प्रकार्य है जिसका कार्यक्षेत्र वास्तविक संख्याओं का एक बंद और परिबद्ध अंतराल(गणित) है(ऊपर आरेख देखें)।

खोज

वैश्विक दीर्घतम और न्यूनतम ढूँढना गणितीय अनुकूलन का लक्ष्य है। यदि कोई प्रकार्य एक बंद अंतराल पर सतत है, तो चरम मूल्य प्रमेय द्वारा वैश्विक अधिकतम और निम्निष्ठ मौजूद हैं। इसके अलावा, एक वैश्विक अधिकतम(या न्यूनतम) या तो कार्यक्षेत्र के अभ्यंतर भाग में एक स्थानीय अधिकतम(या न्यूनतम) होना चाहिए, या कार्यक्षेत्र की सीमा पर स्थित होना चाहिए। वैश्विक अधिकतम(या न्यूनतम) खोजने की एक विधि अभ्यंतर में सभी स्थानीय दीर्घतम(या न्यूनतम) को देखना है, और सीमा पर बिंदुओं के दीर्घतम(या न्यूनतम) को भी देखना है, और सबसे बड़ा(या सबसे छोटा) लेना है।

अवकलनीय प्रकार्य के लिए, फर्मेट के प्रमेय में कहा गया है कि एक कार्यक्षेत्र के अभ्यंतर में स्थानीय एक्स्ट्रेमा महत्वपूर्ण बिंदु(गणित)(या अंक जहां व्युत्पन्न शून्य के बराबर होता है) पर होना चाहिए। हालांकि, सभी महत्वपूर्ण बिंदु एक्स्ट्रीमा नहीं हैं। पहला व्युत्पन्न परीक्षण, दूसरा व्युत्पन्न परीक्षण, या उच्च-क्रम व्युत्पन्न परीक्षण का उपयोग करके कोई यह भेद कर सकता है कि क्या एक महत्वपूर्ण बिंदु एक स्थानीय अधिकतम या स्थानीय न्यूनतम है, पर्याप्त भिन्नता दी गई है।

किसी भी प्रकार्य के लिए जिसे टुकड़े के रूप में परिभाषित किया गया है, प्रत्येक टुकड़े के अधिकतम(या न्यूनतम) को अलग-अलग ढूंढकर अधिकतम(या न्यूनतम) पाता है, और फिर यह दृष्टि बोध करता है कि कौन सा सबसे बड़ा(या सबसे छोटा) है।

उदाहरण

वैश्विक अधिकतम ^x√x पर होता x = e है .

प्रकार्य	दीर्घतम और न्यूनतम
x2	x = 0 पर अद्वितीय वैश्विक न्यूनतम।
x3	कोई वैश्विक न्यूनतम या अधिकतम नहीं. यद्यपि पहला अवकलज(3x2) x = 0 पर 0 है, यह एक विभक्ति बिंदु है.(दूसरा व्युत्पन्न उस बिंदु पर 0 है।)
${\sqrt[{x}]{x}}$	अद्वितीय वैश्विक अधिकतम पर x = e.(चित्र को दाईं ओर देखें)।
x−x	x = 1/e पर सकारात्मक वास्तविक संख्याओं पर अद्वितीय वैश्विक अधिकतम।
x3/3 − x	पहला अवकलज x2 − 1 और दूसरा अवकलज 2x है। पहले व्युत्पादित को 0 पर अवस्थापन करना और x के लिए हल करना -1 और +1 पर स्थिर अंक देता है। दूसरे अवकलज के चिह्न से, हम देख सकते हैं कि -1 स्थानीय अधिकतम है और +1 स्थानीय न्यूनतम है. इस प्रकार्य का कोई वैश्विक अधिकतम या न्यूनतम नहीं है।
|x|	वैश्विक न्यूनतम x = 0 पर व्युत्पादित लेकर नहीं पाया जा सकता है, क्योंकि व्युत्पादित x = 0 पर मौजूद नहीं है।
cos(x)	0, ±2π, ±4π, ... पर अपरिमित रूप से अनेक वैश्विक उच्चिष्ठ और ±π, ±3π, ±5π, .... पर अपरिमित रूप से अनेक वैश्विक निम्निष्ठ।
2 cos(x) − x	अपरिमित रूप से कई स्थानीय उच्चिष्ठ और निम्निष्ठ, लेकिन कोई वैश्विक अधिकतम या न्यूनतम नहीं है।
0.1 ≤ x ≤ 1.1 के साथ cos(3πx)/x	x = 0.1(एक सीमा) पर वैश्विक अधिकतम, x = 0.3 के पास एक वैश्विक न्यूनतम, x = 0.6 के पास एक स्थानीय अधिकतम, और x = 1.0 के पास एक स्थानीय न्यूनतम।(पृष्ठ के शीर्ष पर चित्र देखें।)
x3 + 3x2 − 2x + 1बंद अंतराल(खंड) पर परिभाषित [−4,2]	स्थानीय अधिकतम x = −1−√15/3, स्थानीय न्यूनतम x = −1+√15/3, वैश्विक अधिकतम x = 2 और वैश्विक न्यूनतम x = −4।

एक व्यावहारिक उदाहरण के लिए,[6] एक ऐसी स्थिति मान लें जहां किसी के पास $200$ फीट की बाड़ है और वह एक आयताकार बाड़े के चौकोर फुटमान को अधिकतम करने की कोशिश कर रहा है, जहां $x$ लंबाई है, $y$ चौड़ाई है, और $xy$ क्षेत्रफल है:

$2x+2y=200$

$2y=200-2x$

${\frac {2y}{2}}={\frac {200-2x}{2}}$

$y=100-x$

$xy=x(100-x)$

के संबंध में व्युत्पन्न $x$ है:

${\begin{aligned}{\frac {d}{dx}}xy&={\frac {d}{dx}}x(100-x)\\&={\frac {d}{dx}}\left(100x-x^{2}\right)\\&=100-2x\end{aligned}}$

$0$ के बराबर समुच्चय करके

$0=100-2x$

$2x=100$

$x=50$

प्रकट करता है कि $x=50$ हमारा एकमात्र क्रांतिक बिंदु(गणित) है। अब जिस अंतराल तक $x$ प्रतिबंधित है, उसे निर्धारित करके अंतिम-बिंदुओं को पुनः प्राप्त करें। चूँकि चौड़ाई धनात्मक है, तब $x>0$, और चूँकि $x=100-y$, इसका तात्पर्य है कि $x<100$. महत्वपूर्ण बिंदु $50$,, साथ ही समापन बिंदु $0$ और $100$, को $xy=x(100-x)$, में प्लग करें, और परिणाम हैं $2500,0,$ तथा $0$ क्रमश।

इसलिए, आयत के साथ प्राप्य सबसे बड़ा क्षेत्र $200$ फीट की बाड़ है।

एक से अधिक चर के कार्य

Main article: दूसरा आंशिक व्युत्पन्न परीक्षण

पीआनो सतह, 19वीं शताब्दी के स्थानीय दीर्घतम के कुछ मानदंडों का प्रति उदाहरण

वैश्विक अधिकतम शीर्ष पर स्थित बिंदु है

प्रति उदाहरण: लाल बिंदु एक स्थानीय न्यूनतम दिखाता है जो वैश्विक न्यूनतम नहीं है

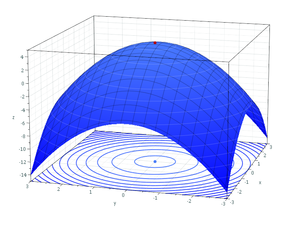
एक से अधिक चर वाले कार्यों के लिए समान शर्तें लागू होती हैं। उदाहरण के लिए, दाईं ओर(विस्तारित) आकृति में, स्थानीय अधिकतम के लिए आवश्यक शर्तें केवल एक चर वाले प्रकार्य के समान होती हैं। Z के रूप में पहला आंशिक व्युत्पादित(अधिकतम किया जाने वाला चर) अधिकतम पर शून्य है(चित्र में शीर्ष पर चमकता हुआ बिंदु) दूसरा आंशिक व्युत्पादित नकारात्मक है। काठी बिंदु की संभावना के कारण एक स्थानीय अधिकतम के लिए शर्तें केवल आवश्यक हैं, पर्याप्त नहीं हैं। अधिकतम के लिए हल करने के लिए और स्थितियों के उपयोग के लिए, प्रकार्य z को भी अलग-अलग प्रकार्य होना चाहिए। दूसरा आंशिक व्युत्पन्न परीक्षण बिंदु को सापेक्ष अधिकतम या सापेक्ष न्यूनतम के रूप में वर्गीकृत करने में मदद कर सकता है।

इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के कार्यों और एक से अधिक चर के कार्यों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय न्यूनतम है, तो यह एक वैश्विक न्यूनतम भी है(मध्यवर्ती मूल्य प्रमेय और रोले के प्रमेय का उपयोग करके विरोधाभास द्वारा इसे साबित करें)। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है

$f(x,y)=x^{2}+y^{2}(1-x)^{3},\qquad x,y\in \mathbb {R} ,$

जिसका एकमात्र महत्वपूर्ण बिंदु(0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय न्यूनतम है। हालांकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5।

एक कार्यात्मक की दीर्घतम या न्यूनतम

यदि किसी प्रकार्य का कार्यक्षेत्र जिसके लिए एक चरम पाया जाना है, में स्वयं प्रकार्य होते हैं(यानी यदि चरम को एक कार्यात्मक(गणित) के रूप में पाया जाता है), तो चरम विविधताओं के कलन का उपयोग करके पाया जाता है।

समुच्चय के संबंध में

दीर्घतम और न्यूनतम को समुच्चय के लिए भी परिभाषित किया जा सकता है। व्यापक रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे इस रूप $\max(S)$ में भी निरूपित किया जाता है। इसके अलावा, यदि S एक आदेशित समुच्चय T का एक उपसमुच्चय है और M S का सबसे बड़ा तत्व है(T द्वारा प्रेरित अनुक्रम के संबंध में), तो M T में S का सर्वोच्च है। इसी तरह के परिणाम कम से कम तत्व, न्यूनतम तत्व और अल्प. समुच्चय के लिए अधिकतम और न्यूनतम प्रकार्य का उपयोग डेटाबेस में किया जाता है, और इसकी गणना तेजी से की जा सकती है, क्योंकि एक समुच्चय के अधिकतम(या न्यूनतम) की गणना एक विभाजन की अधिकतम सीमा से की जा सकती है; औपचारिक रूप से, वे स्व-विघटन योग्य एकत्रीकरण कार्य हैं।

एक सामान्य आंशिक आदेश के मामले में, 'सबसे कम तत्व'(यानी, जो अन्य सभी की तुलना में छोटा है) को 'न्यूनतम तत्व'(कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी तरह, आंशिक रूप से अनुक्रम किए गए समुच्चय(पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के भीतर निहित होता है, जबकि पॉसमुच्चय A का 'अधिकतम तत्व' M A का एक तत्व होता है जैसे कि यदि M ≤ B(A में किसी भी B के लिए), फिर M = B। पोसमुच्चय का कोई भी न्यूनतम तत्व या सबसे बड़ा तत्व अद्वितीय है, लेकिन एक पॉसमुच्चय में कई न्यूनतम या अधिकतम तत्व हो सकते हैं। यदि किसी पॉसमुच्चय में एक से अधिक अधिकतम तत्व हैं, तो ये तत्व परस्पर तुलनीय नहीं होंगे।

कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में अधिकतम एक न्यूनतम तत्व और अधिकतम एक अधिकतम तत्व हो सकता है। फिर, आपसी तुलना के कारण, न्यूनतम तत्व भी सबसे छोटा तत्व होगा, और अधिकतम तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी तरह से व्यवस्थित समुच्चय में, हम केवल 'न्यूनतम' और 'अधिकतम' शब्दों का उपयोग कर सकते हैं।

यदि एक श्रृंखला परिमित है, तो इसमें हमेशा अधिकतम और न्यूनतम होगा। यदि एक शृंखला अनंत है, तो उसके लिए अधिकतम या न्यूनतम की आवश्यकता नहीं है। उदाहरण के लिए, प्राकृतिक संख्याओं के समुच्चय का कोई अधिकतम नहीं है, हालांकि इसमें न्यूनतम है। यदि एक अनंत श्रृंखला S परिबद्ध है, तो समुच्चय के संवरण CL(S) में कभी-कभी न्यूनतम और अधिकतम होता है, इस मामले में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय S की 'कम से कम ऊपरी सीमा' कहा जाता है। , क्रमश।

यह भी देखें

• अधिकतम आर्ग
• व्युत्पन्न परीक्षण
• निम्नतम और उच्चतम
• श्रेष्ठ को सीमित करें और हीन को सीमित करें
• यांत्रिक संतुलन
• मेक्स(गणित)
• नमूना अधिकतम और न्यूनतम
• पल्याण बिन्दु

बाहरी संबंध

• Thomas Simpson's work on Maxima and Minima at Convergence
• Application of Maxima and Minima with sub pages of solved problems
• Jolliffe, Arthur Ernest (1911). "Maxima and Minima" . Encyclopædia Britannica (in English). Vol. 17 (11th ed.). pp. 918–920.