सम्मिश्र लघुगणक: Difference between revisions
No edit summary |
No edit summary |
||
| Line 4: | Line 4: | ||
[[Image:NaturalLogarithmRe.png|200px|thumb|का असली हिस्सा {{math|log(z)}} का [[प्राकृतिक]] लघुगणक है {{math|{{abs|''z''}}}}. किसी फ़ंक्शन का इसका ग्राफ़ इस प्रकार के ग्राफ़ को घुमाकर प्राप्त किया जाता है {{math|ln(''x'')}} z-अक्ष के चारों ओर |{{mvar|z}}-एक्सिस।]]गणित में, एक जटिल लघुगणक गैर-शून्य [[जटिल संख्या|जटिल संख्याओं]] के प्राकृतिक लघुगणक का सामान्यीकरण है। शब्द निम्नलिखित में से एक को संदर्भित करता है, जो दृढ़ता से संबंधित हैं: | [[Image:NaturalLogarithmRe.png|200px|thumb|का असली हिस्सा {{math|log(z)}} का [[प्राकृतिक]] लघुगणक है {{math|{{abs|''z''}}}}. किसी फ़ंक्शन का इसका ग्राफ़ इस प्रकार के ग्राफ़ को घुमाकर प्राप्त किया जाता है {{math|ln(''x'')}} z-अक्ष के चारों ओर |{{mvar|z}}-एक्सिस।]]गणित में, एक जटिल लघुगणक गैर-शून्य [[जटिल संख्या|जटिल संख्याओं]] के प्राकृतिक लघुगणक का सामान्यीकरण है। शब्द निम्नलिखित में से एक को संदर्भित करता है, जो दृढ़ता से संबंधित हैं: | ||
* एक गैर-शून्य जटिल संख्या <math>z</math>, का एक जटिल लघुगणक, जिसे किसी भी सम्मिश्र संख्या के रूप में परिभाषित किया गया है जिसके लिए <math>w</math>, <math>e^w = z</math>.<ref name=Ahlfors>Ahlfors, Section 3.4.</ref><ref name=Sarason>Sarason, Section IV.9.</ref> ऐसी संख्या <math>w | * एक गैर-शून्य जटिल संख्या <math>z</math>, का एक जटिल लघुगणक, जिसे किसी भी सम्मिश्र संख्या के रूप में परिभाषित किया गया है जिसके लिए <math>w</math>, <math>e^w = z</math>.<ref name=Ahlfors>Ahlfors, Section 3.4.</ref><ref name=Sarason>Sarason, Section IV.9.</ref> ऐसी संख्या <math>w | ||
</math> को <math>\log z</math> द्वारा निरूपित किया जाता है.<ref name=Ahlfors/> यदि <math>z</math> के रूप में [[ध्रुवीय रूप]] में <math>z = re^{i\theta}</math> दिया गया है , जहां <math>r</math> तथा <math>\theta</math> के साथ <math>r>0</math> वास्तविक संख्याएँ हैं , तो <math>\ln r + i \theta</math> का एक लघुगणक है <math>z</math>, और <math>z</math> के सभी जटिल लघुगणक <math>\ln r + i\left(\theta + 2\pi k\right)</math> पूर्णांकों के लिए<math>k</math> .<ref name=Ahlfors/><ref name=Sarason/> ये लघुगणक समान रूप से जटिल तल में एक ऊर्ध्वाधर रेखा के साथ स्थित हैं। | </math> को <math>\log z</math> द्वारा निरूपित किया जाता है.<ref name=Ahlfors/> यदि <math>z</math> के रूप में [[ध्रुवीय रूप]] में <math>z = re^{i\theta}</math> दिया गया है , जहां <math>r</math> तथा <math>\theta</math> के साथ <math>r>0</math> वास्तविक संख्याएँ हैं , तो <math>\ln r + i \theta</math> का एक लघुगणक है <math>z</math>, और <math>z</math> के सभी जटिल लघुगणक <math>\ln r + i\left(\theta + 2\pi k\right)</math> पूर्णांकों के लिए <math>k</math> .<ref name=Ahlfors/><ref name=Sarason/> ये लघुगणक समान रूप से जटिल तल में एक ऊर्ध्वाधर रेखा के साथ स्थित हैं। | ||
* एक जटिल-मूल्यवान कार्य <math>\log \colon U \to \mathbb{C}</math>, के कुछ उप-समुच्चय <math>U</math> पर परिभाषित समुच्चय का <math>\mathbb{C}^*</math> गैर-शून्य सम्मिश्र संख्याओं का, संतोषजनक <math>e^{\log z} = z</math> सभी के लिए <math>z</math> में <math>U</math>. इस प्रकार के जटिल वास्तविक लघुगणक कार्य के अनुरूप होते हैं <math>\ln \colon \mathbb{R}_{>0} \to \mathbb{R}</math>, जो वास्तविक चर घातीय फलन का व्युत्क्रम है इसलिए सभी धनात्मक वास्तविक संख्याओं {{mvar|x}} के लिए {{math|''e''<sup>ln ''x''</sup> {{=}} ''x''}} सको संतुष्ट करता है। <math>1/z</math> के एकीकरण द्वारा या [[विश्लेषणात्मक निरंतरता]] की प्रक्रिया द्वारा वास्तविक-मूल्यवान कार्यों को सम्मलित करने वाले स्पष्ट सूत्रों द्वारा जटिल लघुगणक कार्यों का निर्माण किया जा सकता है। | * एक जटिल-मूल्यवान कार्य <math>\log \colon U \to \mathbb{C}</math>, के कुछ उप-समुच्चय <math>U</math> पर परिभाषित समुच्चय का <math>\mathbb{C}^*</math> गैर-शून्य सम्मिश्र संख्याओं का, संतोषजनक <math>e^{\log z} = z</math> सभी के लिए <math>z</math> में <math>U</math>. इस प्रकार के जटिल वास्तविक लघुगणक कार्य के अनुरूप होते हैं <math>\ln \colon \mathbb{R}_{>0} \to \mathbb{R}</math>, जो वास्तविक चर घातीय फलन का व्युत्क्रम है इसलिए सभी धनात्मक वास्तविक संख्याओं {{mvar|x}} के लिए {{math|''e''<sup>ln ''x''</sup> {{=}} ''x''}} सको संतुष्ट करता है। <math>1/z</math> के एकीकरण द्वारा या [[विश्लेषणात्मक निरंतरता]] की प्रक्रिया द्वारा वास्तविक-मूल्यवान कार्यों को सम्मलित करने वाले स्पष्ट सूत्रों द्वारा जटिल लघुगणक कार्यों का निर्माण किया जा सकता है। | ||
| Line 90: | Line 90: | ||
== अनुरूप मानचित्र के रूप में जटिल लघुगणक == | == अनुरूप मानचित्र के रूप में जटिल लघुगणक == | ||
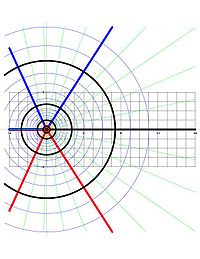
[[Image:Logez02.jpg|200px|right|thumb|जटिल जेड-प्लेन में वृत्त हैं (लॉग जेड) = स्थिर और किरणें (लॉग जेड) = स्थिर।]]कोई भी होलोमॉर्फिक नक्शा <math>f\colon U \to \mathbb{C}</math> | [[Image:Logez02.jpg|200px|right|thumb|जटिल जेड-प्लेन में वृत्त हैं (लॉग जेड) = स्थिर और किरणें (लॉग जेड) = स्थिर।]]कोई भी होलोमॉर्फिक नक्शा <math>f\colon U \to \mathbb{C}</math> संतोषजनक <math>f'(z) \ne 0</math> सभी के लिए <math>z \in U</math> एक अनुरूप मानचित्र है, जिसका अर्थ है कि यदि दो वक्र एक बिंदु <math>U</math> से गुजरते हुए एक कोण बनाते हैं <math>a</math> (इस अर्थ में कि <math>a</math> पर कर्व की [[स्पर्शरेखा]] एक कोण बनाती हैं <math>\alpha</math> तो दो कर्व की छवियां एक ही कोण बनाती हैं <math>f(a)</math>. | ||
की एक शाखा के बाद से<math>\log z</math>होलोमोर्फिक है, और इसके व्युत्पन्न के बाद से<math>\log z</math>कभी 0 नहीं होता, यह एक अनुरूप मानचित्र को परिभाषित करता है। | की एक शाखा के बाद से<math>\log z</math>होलोमोर्फिक है, और इसके व्युत्पन्न के बाद से<math>\log z</math>कभी 0 नहीं होता, यह एक अनुरूप मानचित्र को परिभाषित करता है। | ||
उदाहरण के लिए, प्रमुख शाखा <math>w = \operatorname{Log} z</math>, से मानचित्रण के रूप में देखा गया <math>\ | उदाहरण के लिए, प्रमुख शाखा <math>w = \operatorname{Log} z</math>, से मानचित्रण के रूप में देखा गया I <math>\left| \operatorname{Im}z \right| < \pi</math>, द्वारा परिभाषित क्षैतिज पट्टी के लिए , <math>\mathbb{C}-\mathbb{R}_{\le 0}</math>में निम्नलिखित गुण हैं, जो ध्रुवीय रूप के संदर्भ में सूत्र के प्रत्यक्ष परिणाम हैं: | ||
* वृत्त<ref>Strictly speaking, the point on each circle on the negative real axis should be discarded, or the principal value should be used there.</ref> 0 पर केंद्रित | * जेड-प्लेन में वृत्त<ref>Strictly speaking, the point on each circle on the negative real axis should be discarded, or the principal value should be used there.</ref> को 0 पर केंद्रित करके w-समतल में <math>a - \pi i</math> को <math>a + \pi i</math> से जोड़ने वाले वर्टिकल सेगमेंट में मैप किया जाता है। जहाँ <math>a</math> वृत्त की त्रिज्या का वास्तविक लघुगणक है। | ||
* जेड-प्लेन में 0 से निकलने वाली किरणों को | * जेड-प्लेन में 0 से निकलने वाली किरणों को w-समतल में क्षैतिज रेखाओं से मैप किया जाता है। | ||
ऊपर | ऊपर के प्रकार जेड-प्लेन में प्रत्येक घेरा और किरण समकोण पर मिलते हैं। लॉग के अंतर्गत उनकी छवियां w-समतल में एक ऊर्ध्वाधर खंड और एक क्षैतिज रेखा (क्रमशः) हैं, और ये भी समकोण पर मिलती हैं। यह लॉग की अनुरूप संपत्ति का एक उदाहरण है। | ||
== संबंधित रीमैन सतह == | == संबंधित रीमैन सतह == | ||
Revision as of 23:00, 19 December 2022

गणित में, एक जटिल लघुगणक गैर-शून्य जटिल संख्याओं के प्राकृतिक लघुगणक का सामान्यीकरण है। शब्द निम्नलिखित में से एक को संदर्भित करता है, जो दृढ़ता से संबंधित हैं:
- एक गैर-शून्य जटिल संख्या , का एक जटिल लघुगणक, जिसे किसी भी सम्मिश्र संख्या के रूप में परिभाषित किया गया है जिसके लिए , .[1][2] ऐसी संख्या को द्वारा निरूपित किया जाता है.[1] यदि के रूप में ध्रुवीय रूप में दिया गया है , जहां तथा के साथ वास्तविक संख्याएँ हैं , तो का एक लघुगणक है , और के सभी जटिल लघुगणक पूर्णांकों के लिए .[1][2] ये लघुगणक समान रूप से जटिल तल में एक ऊर्ध्वाधर रेखा के साथ स्थित हैं।
- एक जटिल-मूल्यवान कार्य , के कुछ उप-समुच्चय पर परिभाषित समुच्चय का गैर-शून्य सम्मिश्र संख्याओं का, संतोषजनक सभी के लिए में . इस प्रकार के जटिल वास्तविक लघुगणक कार्य के अनुरूप होते हैं , जो वास्तविक चर घातीय फलन का व्युत्क्रम है इसलिए सभी धनात्मक वास्तविक संख्याओं x के लिए eln x = x सको संतुष्ट करता है। के एकीकरण द्वारा या विश्लेषणात्मक निरंतरता की प्रक्रिया द्वारा वास्तविक-मूल्यवान कार्यों को सम्मलित करने वाले स्पष्ट सूत्रों द्वारा जटिल लघुगणक कार्यों का निर्माण किया जा सकता है।
सभी पर परिभाषित कोई निरंतर जटिल लघुगणक फ़ंक्शन नहीं है। इससे निपटने के उपायों में शाखा बिंदु, संबंधित रीमैन सतह, और जटिल घातीय फलन के आंशिक व्युत्क्रम सम्मलित हैं। मुख्य मान एक विशेष जटिल लघुगणक फ़ंक्शन को परिभाषित करता है जो ऋणात्मक वास्तविक अक्ष को छोड़कर निरंतर है; ऋणात्मक वास्तविक संख्याओं के साथ जटिल तल पर और 0 को हटा दिया गया I यह (वास्तविक) प्राकृतिक लघुगणक की विश्लेषणात्मक निरंतरता है।
जटिल चर घातांकी फलन को उलटने में समस्या
किसी फलन का व्युत्क्रम होने के लिए, उसे भिन्न-भिन्न मानों को भिन्न-भिन्न मानों में मैप करना चाहिए, यह एकैकी होना चाहिए। लेकिन जटिल घातीय कार्य एकैकी नहीं है, क्योंकि किसी भी सम्मिश्र संख्या और पूर्णांक , के लिए, क्योंकि को में जोड़ने से वामावर्त .तो अंक
एक लंबवत रेखा के साथ समान दूरी पर, सभी को घातीय फ़ंक्शन द्वारा समान संख्या में मैप किया जाता है। इसका अर्थ यह है कि घातीय फलन का मानक अर्थों में व्युत्क्रम फलन नहीं होता है।[3][4] इस समस्या के दो समाधान हैं।
एक है घातीय फ़ंक्शन के डोमेन को एक ऐसे क्षेत्र तक सीमित करना है जिसमें के पूर्णांक गुणक से भिन्न कोई भी दो संख्याएं सम्मलित नहीं हैं। यह स्वाभाविक रूप से , की शाखाओं की परिभाषा की ओर ले जाता है, जो कुछ ऐसे कार्य हैं जो अपने डोमेन में प्रत्येक संख्या के एक लघुगणक को एकल करते हैं। यह पर के प्रतिबंध के व्युत्क्रम के रूप में परिभाषा के समान है। अंतराल के लिए असीम रूप से कई वास्तविक संख्याएं हैं के साथ, लेकिन एक मनमाने ढंग से एक को चुनता है .
अनिश्चितता को समाधान करने का एक अन्य उपाय लघुगणक को एक ऐसे कार्य के रूप में देखना है जिसका डोमेन जटिल समतल में एक क्षेत्र नहीं है, लेकिन एक रीमैन सतह है जो छिद्रित जटिल विमान को अनंत-से-1 उपाय से कवर करता है।
शाखाओं का यह लाभ है कि उनका मूल्यांकन जटिल संख्याओं पर किया जा सकता है। दूसरी ओर, रीमैन सतह पर कार्य सुरुचिपूर्ण है क्योंकि यह लघुगणक की सभी शाखाओं को एक साथ संकुलित करता है और इसकी परिभाषा के हिस्से के रूप में मनमाना विकल्प की आवश्यकता नहीं होती है।
मूल मूल्य
परिभाषा
प्रत्येक अशून्य सम्मिश्र संख्या के लिए , मुख्य मूल्य वह लघुगणक है जिसका काल्पनिक भाग अंतराल में स्थित है .[2] अपरिभाषित छोड़ दिया गया है क्योंकि वहाँ कोई सम्मिश्र संख्या नहीं है संतुष्टि देने वाला .[1]
जब संकेतन निर्दिष्ट किए बिना किसी विशेष लघुगणक के प्रकट होता है, तो सामान्यतः यह मान लेना सबसे अच्छा होता है कि मुख्य मान अभीष्ट है। विशेष रूप से, यह z के वास्तविक मान के अनुरूप एक मान देता है, z एक धनात्मक वास्तविक संख्या है।
जब अंकन बिना किसी विशेष लघुगणक के प्रकट होता है, तो आमतौर पर यह मान लेना सबसे अच्छा होता है कि मुख्य मूल्य अभीष्ट है। विशेष रूप से, यह के वास्तविक मूल्य के अनुरूप मान देता है जब एक धनात्मक वास्तविक संख्या है। संकेतन में पूंजीकरण का उपयोग कुछ लेखकों द्वारा के अन्य लघुगणकों से मुख्य मान को अलग करने के लिए किया जाता है। [2]
मुख्य मूल्य की गणना
एक अशून्य सम्मिश्र संख्या का ध्रुवीय रूप है , जहां का निरपेक्ष मान है , तथा इसका तर्क है (जटिल विश्लेषण)। निरपेक्ष मूल्य वास्तविक और सकारात्मक है। तर्क को 2π के एक पूर्णांक गुणक के योग तक परिभाषित किया गया है . इसका मुख्य मूल्य वह मान है जो अंतराल से संबंधित है, जिसे atan2 के रूप में व्यक्त किया जाता है,
यह जटिल लघुगणक के प्रमुख मूल्य के लिए निम्न सूत्र की ओर जाता है:
उदाहरण के लिए, , तथा .
प्रतिलोम फलन के रूप में मुख्य मान
का वर्णन करने का एक अन्य उपाय जटिल घातीय फलन के प्रतिबंध के व्युत्क्रम के रूप में है। जैसा कि पिछले अनुभाग में बताया गया है। क्षैतिज पट्टी जिसमें सम्मिश्र संख्याएँ होती हैं, जैसे कि एक ऐसे क्षेत्र का एक उदाहरण है जिसमें के एक पूर्णांक गुणक से भिन्न किन्हीं भी दो संख्याओं का अंतर नहीं है, इसलिए का व्युत्क्रम है। इसलिए घातीय फलन मैप का प्रतिबंध जटिल समतल और इस प्रतिबंध का विलोम है . नीचे अनुरूप मानचित्रण अनुभाग इस मानचित्र के ज्यामितीय गुणों को और अधिक विस्तार से समझाता है।
गुण
ln से संतुष्ट सभी सर्वसमिकाएँ सम्मिश्र संख्याओं तक विस्तारित नहीं होतीं हैं। यह सच है कि सभी के लिए (इसका अर्थ यही है का लघुगणक होना), लेकिन पहचान पट्टी के बाहर के लिए विफल रहता है I इस कारण से कोई हमेशा को एक पहचान के दोनों पक्षों पर लागू नहीं कर सकता है। निकालने के लिए। साथ ही,असफल हो सकता है: दोनों पक्ष [1]उदाहरण के लिए,
लेकिन
फलन प्रत्येक ऋणात्मक वास्तविक संख्या पर असंतत है, लेकिन अन्य सभी में निरंतर है I विच्छिन्नता की व्याख्या करने के लिए, विचार करें कि का क्या होता है जब एक ऋणात्मक वास्तविक संख्या तक पहुँचता हैI यदि ऊपर से तक पहुंचता है, तो , की ओर बढ़ता है,जो कि है I लेकिन यदि नीचे से, तक पहुंचता है, तो तक पहुंचता है। इसलिए द्वारा कूदता है द्वारा नकारात्मक वास्तविक अक्ष को पार करता है, और इसी प्रकार , द्वारा कूदता हैI
जटिल लघुगणक की शाखाएँ
क्या प्रत्येक अशून्य सम्मिश्र संख्या का लघुगणक चुनने का कोई भिन्न उपाय है जिससे कि एक ऐसा फलन बनाया जा सके जो सभी पर निरंतर है ? उत्तर न है। इसका कारण जानने के लिए के रूप में , से बढ़कर यूनिट सर्कल I यदि निरंतर है, तो ऐसा है , लेकिन बाद वाला दो लघुगणकों का अंतर है, इसलिए यह असतत समुच्चय में मान लेता है इसलिए यह स्थिर है। विशेष रूप से, जो विरोधाभासी है, , ,.
सम्मिश्र संख्याओं पर परिभाषित एक सतत लघुगणक प्राप्त करने के लिए, इसलिए यह आवश्यक है कि डोमेन को एक छोटे उपसमुच्चय तक सीमित कर दिया जाए। क्योंकि लक्ष्यों में से एक कार्य को व्युत्पन्न करने में सक्षम होना है, यह मान लेना उचित है कि कार्य अपने डोमेन के प्रत्येक बिंदु के पड़ोस पर परिभाषित किया गया है; दूसरे शब्दों में, एक खुला समुच्चय होना चाहिए। इसके अतिरिक्त साथ ही यह मानना भी उचित है (संयुक्तता ) विभिन्न घटकों पर फलन मान एक दूसरे से असंबंधित हो सकते हैं। यह सब निम्नलिखित परिभाषा को प्रेरित करता है:
- की 'शाखा' एक सतत कार्य है एक जुड़े हुए खुले उपसमुच्चय पर परिभाषित जटिल तल का इस प्रकार है कि प्रत्येक के लिए का लघुगणक है में .[2]
उदाहरण के लिए, मुख्य मूल्य खुले समुच्चय पर एक शाखा को परिभाषित करता है जहां यह निरंतर है, जो कि समुच्चय है जटिल तल से 0 और सभी नकारात्मक वास्तविक संख्याओं को हटाकर प्राप्त किया गया।
एक अन्य उदाहरण: मर्केटर श्रृंखला
के लिए ,समान रूप से स्थानीय रूप से अभिसरण करता है, इसलिए समुच्चय करना की एक शाखा को परिभाषित करता है त्रिज्या 1 की खुली डिस्क 1 पर केंद्रित है। वास्तव में, यह केवल का प्रतिबंध है जैसा कि अंतर को भिन्न करके 1 पर मूल्यों की तुलना करके दिखाया जा सकता है।
एक बार एक शाखा तय हो जाने के बाद,यदि कोई भ्रम नहीं हो सकता है,तो इसे निरूपित किया जा सकता है I भिन्न -भिन्न शाखाएँ किसी विशेष जटिल संख्या के लघुगणक के लिए भिन्न -भिन्न मान दे सकती हैं, चूंकि, के क्रम में एक शाखा को पहले से तय किया जाना चाहिए (या फिर मुख्य शाखा को समझा जाना चाहिए) एक सटीक स्पष्ट अर्थ रखने के लिए।
शाखा कटना
इकाई घेरा को सम्मलित करने वाला उपरोक्त तर्क यह दिखाने के लिए सामान्यीकृत करता है कि की कोई भी शाखा एक खुले समुच्चय पर सम्मलित नहीं है जिसमें एक बंद वक्र है जो 0 के आसपास घुमावदार संख्या है। एक कहता है कि ' का शाखा बिंदु 0 पर है। 0 के आसपास घुमावदार बंद वक्रों से बचने के लिए, सामान्यतः किसी दिशा में 0 (सम्मिलित) से अनंत तक जाने वाले जटिल तल में किरण या वक्र के पूरक के रूप में चुना जाता है। इस स्थिति में, वक्र को शाखा कट के रूप में जाना जाता है। उदाहरण के लिए, मुख्य शाखा में ऋणात्मक वास्तविक अक्ष के साथ एक शाखा कटी हुई है।
यदि फलन को शाखा कट के एक बिंदु पर परिभाषित होने के लिए विस्तारित किया जाता है, यह अनिवार्य रूप से वहाँ बंद हो जाएगा; सर्वोत्तम रूप से यह "एक ओर" निरंतर होगा, जैसे एक ऋणात्मक वास्तविक संख्या पर।
जटिल लघुगणक का व्युत्पन्न
प्रत्येक शाखा का एक खुले समुच्चय पर घातीय फलन के प्रतिबंध का व्युत्क्रम है, अर्थात् छवि के लिए प्रतिबंध . चूँकि चरघातांकी फलन होलोमॉर्फिक है (अर्थात् जटिल अवकलनीय) अविच्छिन्न अवकलज के साथ, व्युत्क्रम फलन प्रमेय का जटिल अनुरूप लागू होता है। यह दिखाता है कि और होलोमॉर्फिक है, प्रत्येक के लिए में .[2]इसे सिद्ध करने का एक और उपाय है, कॉची-रीमैन समीकरणों की जांच करना है।[2]
एकीकरण के माध्यम से शाखाओं का निर्माण
फलन वास्तविक में सूत्र द्वारा बनाया जा सकता है
जटिल लघुगणक के लिए अनुरूप विकसित करने में, एक अतिरिक्त जटिलता है: जटिल अभिन्न की परिभाषा के लिए पथ की पसंद की आवश्यकता होती है। सौभाग्य से, यदि एकीकृत होलोमोर्फिक है, तो अभिन्न का मान पथ को विकृत करके होमोटॉपी (अंतिम बिंदुओं को स्थिर रखते हुए) से अपरिवर्तित होता है, और एक सरल रूप से जुड़े क्षेत्र में (बिना छेद वाला क्षेत्र), से के अंदर का कोई भी रास्ता लगातार के अंदर किसी अन्य में विकृत हो सकता है। यह सब निम्नलिखित की ओर जाता है
अनुरूप मानचित्र के रूप में जटिल लघुगणक
कोई भी होलोमॉर्फिक नक्शा संतोषजनक सभी के लिए एक अनुरूप मानचित्र है, जिसका अर्थ है कि यदि दो वक्र एक बिंदु से गुजरते हुए एक कोण बनाते हैं (इस अर्थ में कि पर कर्व की स्पर्शरेखा एक कोण बनाती हैं तो दो कर्व की छवियां एक ही कोण बनाती हैं .
की एक शाखा के बाद सेहोलोमोर्फिक है, और इसके व्युत्पन्न के बाद सेकभी 0 नहीं होता, यह एक अनुरूप मानचित्र को परिभाषित करता है।
उदाहरण के लिए, प्रमुख शाखा , से मानचित्रण के रूप में देखा गया I , द्वारा परिभाषित क्षैतिज पट्टी के लिए , में निम्नलिखित गुण हैं, जो ध्रुवीय रूप के संदर्भ में सूत्र के प्रत्यक्ष परिणाम हैं:
- जेड-प्लेन में वृत्त[6] को 0 पर केंद्रित करके w-समतल में को से जोड़ने वाले वर्टिकल सेगमेंट में मैप किया जाता है। जहाँ वृत्त की त्रिज्या का वास्तविक लघुगणक है।
- जेड-प्लेन में 0 से निकलने वाली किरणों को w-समतल में क्षैतिज रेखाओं से मैप किया जाता है।
ऊपर के प्रकार जेड-प्लेन में प्रत्येक घेरा और किरण समकोण पर मिलते हैं। लॉग के अंतर्गत उनकी छवियां w-समतल में एक ऊर्ध्वाधर खंड और एक क्षैतिज रेखा (क्रमशः) हैं, और ये भी समकोण पर मिलती हैं। यह लॉग की अनुरूप संपत्ति का एक उदाहरण है।
संबंधित रीमैन सतह
निर्माण
की विभिन्न शाखाएँएक सतत कार्य देने के लिए चिपकाया नहीं जा सकता क्योंकि दो शाखाएँ उस बिंदु पर भिन्न मान दे सकती हैं जहाँ दोनों परिभाषित हैं। तुलना करें, उदाहरण के लिए, प्रमुख शाखा पर काल्पनिक भाग के साथ में और शाखा पर जिसका काल्पनिक हिस्सा में निहित है . ये ऊपरी आधे तल पर सहमत हैं, लेकिन निचले आधे तल पर नहीं। तो यह इन शाखाओं के डोमेन को केवल ऊपरी आधे विमान की प्रतियों के साथ गोंद करने के लिए समझ में आता है। परिणामी सरेस से जोड़ा हुआ डोमेन जुड़ा हुआ है, लेकिन इसमें निचले आधे विमान की दो प्रतियां हैं। उन दो प्रतियों को एक पार्किंग गैरेज के दो स्तरों के रूप में देखा जा सकता है, और कोई इसे प्राप्त कर सकता है निचले आधे तल का स्तर ऊपर तक निचले आधे विमान के स्तर पर जाकर रेडियंस चारों ओर वामावर्त 0, पहले सकारात्मक वास्तविक अक्ष को पार करना (के स्तर) ऊपरी आधे विमान की साझा प्रति में और फिर नकारात्मक वास्तविक अक्ष को पार करना (के स्तर) में निचले आधे विमान का स्तर।
कोई काल्पनिक भाग के साथ शाखाओं को चिपकाकर जारी रख सकता है में , में , और इसी तरह, और दूसरी दिशा में, काल्पनिक भाग वाली शाखाएँ में , में , और इसी तरह। अंतिम परिणाम एक जुड़ा हुआ सतह है जिसे ऊपर और नीचे दोनों तरफ फैले असीम रूप से कई स्तरों के साथ एक उत्साही पार्किंग गैरेज के रूप में देखा जा सकता है। यह रीमैन सतह है से संबंधित.[7] एक बिंदु पर जोड़ी के रूप में सोचा जा सकता है कहाँ पे के तर्क का संभावित मान है. इस तरह, R में एम्बेड किया जा सकता है .
रीमैन सतह पर लघुगणक फ़ंक्शन
क्योंकि शाखाओं के डोमेन केवल खुले सेटों के साथ चिपके हुए थे जहां उनके मान सहमत थे, शाखाएं एक अच्छी तरह से परिभाषित कार्य देने के लिए गोंद करती हैं .[8] यह प्रत्येक बिंदु को मैप करता है परप्रति . मूल शाखा के विस्तार की यह प्रक्रिया संगत होलोमोर्फिक कार्यों को ग्लूइंग द्वारा विश्लेषणात्मक निरंतरता के रूप में जाना जाता है।
से एक प्रक्षेपण मानचित्र हैनीचे जो सर्पिल को चपटा करता है, भेज रहा है प्रति. किसी के लिए , अगर कोई सभी बिंदुओं को लेता है कासीधे ऊपर लेटा हुआऔर मूल्यांकन करता है'इन सभी बिंदुओं पर, के सभी लघुगणक प्राप्त होते हैं.
की सभी शाखाओं को चिपकाना
केवल ऊपर चुनी गई शाखाओं को चिपकाने के बजाय, कोई भी सभी शाखाओं से शुरू कर सकता है, और साथ ही शाखाओं की हर जोड़ी को गोंद दें तथा के सबसे बड़े खुले उपसमुच्चय के साथ जिस परतथासहमत होना। यह वही रीमैन सतह देता है और समारोह 'पहले जैसा। यह दृष्टिकोण, हालांकि कल्पना करने के लिए थोड़ा कठिन है, इसमें अधिक स्वाभाविक है कि इसमें किसी विशेष शाखा का चयन करने की आवश्यकता नहीं है।
यदि का खुला उपसमुच्चय हैअपनी छवि के लिए विशेष रूप से प्रोजेक्ट करनामें , फिर का प्रतिबंधप्रति की एक शाखा से मेल खाता है ' पर परिभाषित. की हर शाखा'इस प्रकार उत्पन्न होता है।
एक सार्वभौमिक आवरण के रूप में रीमैन सतह
प्रक्षेपण मानचित्र एहसासके आवरण स्थान के रूप में . वास्तव में, यह एक गैलोइस है जो डेक परिवर्तन ग्रुप आइसोमोर्फिक के साथ कवर करता है , होमियोमोर्फिज्म भेजने से उत्पन्न होता है प्रति .
एक जटिल कई गुना के रूप में,के साथ biholomorphic है के जरिए. (उलटा नक्शा भेजता हैप्रति।) यह दर्शाता है किबस जुड़ा हुआ है, इसलिएका सार्वभौम आवरण है .
अनुप्रयोग
- घातांक को परिभाषित करने के लिए जटिल लघुगणक की आवश्यकता है # जटिल संख्याओं की घातें जिनमें आधार एक जटिल संख्या है। अर्थात्, अगरतथाके साथ जटिल संख्याएँ हैं, कोई परिभाषित करने के लिए मुख्य मूल्य का उपयोग कर सकता है. कोई भी बदल सकता हैके अन्य लघुगणकों द्वाराके अन्य मान प्राप्त करने के लिए, फार्म के कारकों से भिन्न.[1][9] भावाभिव्यक्तियदि और केवल यदि का एकल मान हैएक पूर्णांक है।[1]* क्योंकि त्रिकोणमितीय कार्यों को तर्कसंगत कार्यों के रूप में व्यक्त किया जा सकता है, व्युत्क्रम त्रिकोणमितीय फलन#लॉगरिदमिक रूपों को जटिल लघुगणक के संदर्भ में व्यक्त किया जा सकता है।
- मैपिंग के बाद सेपर केंद्रित हलकों को रूपांतरित करता है 0 वर्टिकल स्ट्रेट लाइन सेगमेंट में, यह एनुलस (गणित) से जुड़े इंजीनियरिंग अनुप्रयोगों में उपयोगी है।[citation needed]
सामान्यीकरण
अन्य आधारों के लघुगणक
जैसे वास्तविक संख्याओं के लिए, सम्मिश्र संख्याओं के लिए परिभाषित किया जा सकता हैतथा: एकमात्र चेतावनी के साथ कि इसका मान परिभाषित लॉग की शाखा की पसंद पर निर्भर करता हैतथा(साथ '). उदाहरण के लिए, प्रिंसिपल वैल्यू का उपयोग करके देता है
होलोमोर्फिक कार्यों के लघुगणक
यदि f एक जुड़े हुए खुले उपसमुच्चय पर एक होलोमोर्फिक फ़ंक्शन हैका , फिर की एक शाखा पर एक सतत कार्य हैपरऐसा है किसभी के लिएमें. ऐसा समारोहके साथ अनिवार्य रूप से होलोमोर्फिक हैसभी के लिएमें.
यदिका एक साधारण रूप से जुड़ा हुआ खुला उपसमुच्चय है , तथा ' पर कहीं नहीं लुप्त होनेवाला होलोमॉर्फिक फलन है, फिर ' की एक शाखा पर परिभाषितमें एक प्रारंभिक बिंदु चुनकर बनाया जा सकता है, एक लघुगणक चुननाका, और परिभाषित करना
प्रत्येक के लिएमें.[2]
टिप्पणियाँ
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Ahlfors, Section 3.4.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Sarason, Section IV.9.
- ↑ Conway, p. 39.
- ↑ Another interpretation of this is that the "inverse" of the complex exponential function is a multivalued function taking each nonzero complex number z to the set of all logarithms of z.
- ↑ Lang, p. 121.
- ↑ Strictly speaking, the point on each circle on the negative real axis should be discarded, or the principal value should be used there.
- ↑ Ahlfors, Section 4.3.
- ↑ The notations R and logR are not universally used.
- ↑ Kreyszig, p. 640.
संदर्भ
- Ahlfors, Lars V. (1966). Complex Analysis (2nd ed.). McGraw-Hill.
- Conway, John B. (1978). Functions of One Complex Variable (2nd ed.). Springer. ISBN 9780387903286.
- Kreyszig, Erwin (2011). Advanced Engineering Mathematics (10th ed.). Berlin: Wiley. ISBN 9780470458365.
- Lang, Serge (1993). Complex Analysis (3rd ed.). Springer-Verlag. ISBN 9783642592737.
- Moretti, Gino (1964). Functions of a Complex Variable. Prentice-Hall.
- Sarason, Donald (2007). Complex Function Theory (2nd ed.). American Mathematical Society. ISBN 9780821886229.
- Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis (Fourth ed.). Cambridge University Press.