आण्विक कक्षक: Difference between revisions
m (→अवलोकन-) |
mNo edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Wave-like behavior of an electron in a molecule}} | {{Short description|Wave-like behavior of an electron in a molecule}} | ||
{{See also|Molecular orbital theory|Molecular orbital diagram}} | {{See also|Molecular orbital theory|Molecular orbital diagram}} | ||
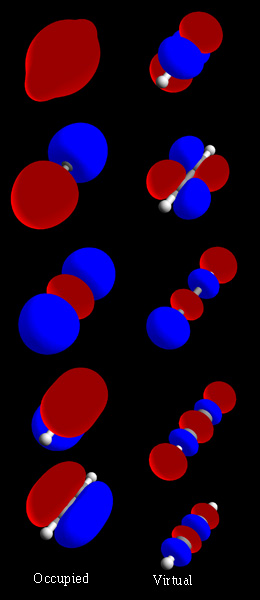
[[File:Orbitals acetylene.jpg|right|thumb|पूर्ण [[एसिटिलीन]] (H -C≡C-H) आणविक | [[File:Orbitals acetylene.jpg|right|thumb|पूर्ण [[एसिटिलीन]] (H -C≡C-H) आणविक कक्षा सेट। बायां स्तंभ एमओ को दिखाता है जो शीर्ष पर सबसे कम ऊर्जा वाले कक्षीय के साथ जमीनी स्थिति में व्याप्त हैं। कुछ एमओ में दिखाई देने वाली सफेद और भूरी रेखाएं नाभिक से गुजरने वाली आणविक धुरी है। कक्षीय तरंग कार्य लाल क्षेत्रों में धनावेशित और नीले रंग में ऋणावेशित होते हैं। दायां स्तम्भ आभासी एमओ को दिखाता है जो जमीनी अवस्था में खाली हैं, लेकिन उत्तेजित अवस्थाओं में व्याप्त हो सकते हैं।]][[रसायन विज्ञान]] में, आणविक कक्षा एक गणितीय कार्य है जो एक [[अणु]] में एक इलेक्ट्रॉन के स्थान और तरंग-समान व्यवहार का वर्णन करता है। इस फलन का उपयोग रासायनिक और भौतिक गुणों की गणना करने के लिए किया जा सकता है, जैसे कि किसी विशिष्ट क्षेत्र में इलेक्ट्रॉन के पाए जाने की संभावना के रूप में। परमाणु कक्षा और आणविक कक्षा शब्द 1932 में रॉबर्ट एस मुल्लिकेन द्वारा एक-इलेक्ट्रॉन ऑर्बिटल वेव विवरण कार्यों का मतलब समझाने के लिए पेश किया गया था। प्रारंभिक स्तर पर, इनका उपयोग अंतरिक्ष के उस क्षेत्र का वर्णन करने के लिए किया जाता है जिसमें फलन का एक महत्वपूर्ण आयाम होता है। | ||
एक एकल [[परमाणु]] में, कक्षीय इलेक्ट्रॉनों का स्थान परमाणु कक्षाओं द्वारा निर्धारित किया जाता है। जब कई परमाणु रासायनिक रूप से एक अणु में संयोजित होते हैं, तो इलेक्ट्रॉनों के स्थान अणु द्वारा पूर्ण रूप से निर्धारित किए जाते हैं, इसलिए परमाणु कक्षाएँ आणविक कक्षाएँ बनाने के लिए संयोजित होती हैं। घटक परमाणुओं से इलेक्ट्रॉन आणविक कक्षाओं में प्रवेश करते हैं। गणितीय रूप से, आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण का एक अनुमानित समाधान हैं। वे अणु के प्रत्येक परमाणु से परमाणु [[संकर कक्षीय| | एक एकल [[परमाणु]] में, कक्षीय इलेक्ट्रॉनों का स्थान परमाणु कक्षाओं द्वारा निर्धारित किया जाता है। जब कई परमाणु रासायनिक रूप से एक अणु में संयोजित होते हैं, तो इलेक्ट्रॉनों के स्थान, अणु द्वारा पूर्ण रूप से निर्धारित किए जाते हैं, इसलिए परमाणु कक्षाएँ आणविक कक्षाएँ बनाने के लिए संयोजित होती हैं। घटक परमाणुओं से इलेक्ट्रॉन आणविक कक्षाओं में प्रवेश करते हैं। गणितीय रूप से, आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण का एक अनुमानित समाधान हैं। वे अणु के प्रत्येक परमाणु से परमाणु [[संकर कक्षीय|कक्षा]] या [[संकर कक्षीय|संकर कक्षा]] के रैखिक संयोजन या परमाणुओं के समूहों से अन्य आणविक कक्षाओं के संयोजन से निर्मित होते हैं। हार्ट्री-फॉक या स्व-सुसंगत क्षेत्र (एस सी एफ) विधियों का उपयोग करके उनकी मात्रात्मक गणना की जा सकती है। | ||
आण्विक कक्षक तीन प्रकार के होते हैं: आबंधी आण्विक कक्षक जिनकी ऊर्जा | आण्विक कक्षक तीन प्रकार के होते हैं: आबंधी आण्विक कक्षक जिनकी ऊर्जा उन परमाणु कक्षकों की ऊर्जा से कम होती है जो उन्हें बनाते हैं और इस प्रकार उन रासायनिक बंधों को बढ़ावा देते हैं जो अणु को एक साथ बांधे रखते हैं। प्रति-आबंधी आणविक कक्षक जिनकी ऊर्जा उनके घटक परमाणु कक्षकों की ऊर्जा से अधिक होती है, और इसलिए ये अणु के बंध का विरोध करते हैं, और अनाबंधी वाले कक्षकों में उनके घटक परमाणु कक्षकों के समान ऊर्जा होती है और इस प्रकार बंध पर कोई प्रभाव नहीं पड़ता है। | ||
== अवलोकन | == अवलोकन == | ||
एक अणु में उन क्षेत्रों का प्रतिनिधित्व करने के लिए एक आणविक | एक अणु में उन क्षेत्रों का प्रतिनिधित्व करने के लिए एक आणविक कक्षा (एम्ओ) का उपयोग किया जा सकता है जहां उस कक्षा पर कब्जा करने वाले एक इलेक्ट्रॉन के पाए जाने की संभावना है। आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के विद्युत क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण के अनुमानित समाधान हैं। यद्यपि इस समीकरण से सीधे कक्षाओं की गणना करना बहुत ही कठिन है। इसके बदले वे परमाणु कक्षकों के संयोजन से प्राप्त होते हैं, जो एक परमाणु में एक [[ऋणावेशित सूक्ष्म अणु का विन्यास|ऋणावेशित सूक्ष्म अणु के विन्यास के]] स्थान की भविष्यवाणी करते हैं। एक आणविक कक्षा एक अणु के इलेक्ट्रॉनिक विन्यास को उल्लिखत कर सकता है: स्थानिक वितरण और एक (या एक जोड़ी) इलेक्ट्रॉन की ऊर्जा। प्रायः एक आणविक कक्षा को परमाणु कक्षकों के रैखिक संयोजन के रूप में दर्शाया जाता है विशेष रूप से गुणात्मक या बहुत अनुमानित उपयोग में। वे [[आणविक कक्षीय सिद्धांत|आणविक कक्षा सिद्धांत]] के माध्यम से समझे जाने वाले अणुओं में बंध का एक सरल मॉडल प्रदान करने में अमूल्य हैं। संगणनात्मक रसायन शास्त्र में अधिकांश वर्तमान-दिन के तरीके प्रणाली के आणविक कक्षा की गणना से शुरू होते हैं। एक आणविक कक्षा नाभिक द्वारा उत्पन्न विद्युत क्षेत्र में एक इलेक्ट्रॉन के व्यवहार और अन्य इलेक्ट्रॉनों के कुछ औसत वितरण का वर्णन करता है। एक ही कक्षा में दो इलेक्ट्रॉनों के विषय में, [[पाउली सिद्धांत]] की मांग है कि उन इलेक्ट्रॉनों के पास विपरीत चक्रण हो। अनिवार्य रूप से यह एक सही अनुमान,है, और आणविक इलेक्ट्रॉनिक तरंग फलन के अत्यधिक सटीक विवरण में कक्षक नहीं हैं। | ||
आण्विक कक्षक सामान्य रूप से पूरे अणु में विस्थानीकृत होते हैं। इसके अलावा, यदि अणु में बंध तत्व हैं, तो इसके गैर-अपघटित आणविक कक्षक इनमें से किसी भी बंध के संबंध में या तो सममित या विषम हैं। दूसरे शब्दों में, आणविक | आण्विक कक्षक सामान्य रूप से पूरे अणु में विस्थानीकृत होते हैं। इसके अलावा, यदि अणु में बंध तत्व हैं, तो इसके गैर-अपघटित आणविक कक्षक इनमें से किसी भी बंध के संबंध में या तो सममित या विषम हैं। दूसरे शब्दों में, आणविक कक्षा ψ पर सममिति संक्रिया S (उदाहरण के लिए, एक प्रतिबिंब, घूर्णन, या व्युत्क्रमण) के प्रयोग से आणविक कक्षा अपरिवर्तित रहता है या इसके गणितीय चिह्न को उलट देता है उदाहरण के लिए Sψ = ±ψ समतलीय अणुओं में, उदाहरण के लिए, आण्विक तल में परावर्तन के संबंध में आण्विक कक्षक या तो सममित ([[सिग्मा बंधन]]) या प्रतिसममित ( p आबंध) होते हैं। यदि विकृत कक्षीय ऊर्जा वाले अणुओं पर भी विचार किया जाता है, तो एक अधिक सामान्य कथन है कि अणु के [[समरूपता समूह|बंध समूह]] के अलघुकरणीय निरूपण के लिए आणविक कक्षाएँ आधार बनाती हैं।<ref>{{Cite book|url=https://archive.org/details/isbn_9780471510949/page/102|title=समूह सिद्धांत के रासायनिक अनुप्रयोग|last=Cotton|first=F. Albert|date=1990|publisher=Wiley|isbn=0471510947|edition=3rd|location=New York|pages=[https://archive.org/details/isbn_9780471510949/page/102 102]|oclc=19975337|url-access=registration}}</ref> आणविक कक्षकों के बंध गुणों का अर्थ है कि निरूपण जो आणविक कक्षा सिद्धांत की एक अंतर्निहित विशेषता है और यह इसे मूल रूप से रासायनिक संयोजन बंध सिद्धांत से अलग बनाता है, जिसमें [[अनुनाद (रसायन विज्ञान)|अनुनाद]] के लिए बंध को स्थानीयकृत इलेक्ट्रॉन जोड़े के रूप में देखा जाता है। | ||
इन बंध-अनुकूलित | इन बंध-अनुकूलित विहित आणविक कक्षकों के विपरीत, [[स्थानीयकृत आणविक ऑर्बिटल्स|स्थानीयकृत आणविक कक्षकों]] को विहित कक्षकों में कुछ गणितीय परिवर्तनों को लागू करके बनाया जा सकता है। इस दृष्टिकोण का लाभ यह है कि ऑर्बिटल्स एक अणु के "बंध" से अधिक मेल खाते हैं जैसा कि लुईस संरचना द्वारा दर्शाया गया है। एक नुकसान के रूप में, इन स्थानीय कक्षकों के ऊर्जा स्तरों का अब भौतिक अर्थ नहीं रह गया है। (इस लेख के बाकी हिस्सों में चर्चा विहित आणविक कक्षाओं पर केंद्रित होगी। स्थानीयकृत आणविक कक्षाओं पर आगे की चर्चा के लिए, देखें: [[प्राकृतिक बंधन कक्षीय|प्राकृतिक बंध कक्षीय]] और सिग्मा-पाई और समकक्ष-कक्षीय मॉडल।) | ||
==आणविक कक्षकों का निर्माण== | ==आणविक कक्षकों का निर्माण== | ||
आणविक कक्षक परमाणु कक्षक के बीच अनुमत अंतःक्रियाओं से उत्पन्न होते हैं, जिनकी अनुमति दी जाती है, परमाणु कक्षकों का बंध ([[समूह सिद्धांत]] से निर्धारित) एक दूसरे के साथ संगत हैं। परमाणु | आणविक कक्षक परमाणु कक्षक के बीच अनुमत अंतःक्रियाओं से उत्पन्न होते हैं, जिनकी अनुमति दी जाती है, परमाणु कक्षकों का बंध ([[समूह सिद्धांत]] से निर्धारित) एक दूसरे के साथ संगत हैं। परमाणु कक्षा अन्योन्यक्रियाओं की दक्षता दो परमाणु कक्षकों के बीच कक्षीय अतिव्यापन (इस बात का माप है कि दो कक्षक एक दूसरे के साथ रचनात्मक रूप से कितनी अच्छी तरह परस्पर क्रिया करते हैं) से निर्धारित होती है, यदि परमाणु कक्षक ऊर्जा के करीब हों तब ये बहुत महत्वपूर्ण है। अंत में बनने वाले आणविक कक्षकों की संख्या अणु बनाने के लिए संयुक्त किए जा रहे परमाणुओं में परमाणु कक्षकों की संख्या के बराबर होनी चाहिए। | ||
== गुणात्मक चर्चा == | == गुणात्मक चर्चा == | ||
एक सटीक, लेकिन गुणात्मक रूप से उपयोगी, आणविक संरचना की चर्चा के लिए, आणविक कक्षक से परमाणु कक्षक आणविक | एक सटीक, लेकिन गुणात्मक रूप से उपयोगी, आणविक संरचना की चर्चा के लिए, आणविक कक्षक से परमाणु कक्षक आणविक कक्षा विधि के [[रैखिक संयोजन]] से प्राप्त किया जा सकता है। यहाँ, आणविक कक्षक को परमाणु कक्षक के रैखिक संयोजन के रूप में व्यक्त किया जाता है।<ref>{{Cite book|title=रसायन विज्ञान में कक्षीय सहभागिता|last1=Albright|first1=T. A.|last2=Burdett|first2=J. K.|last3=Whangbo|first3=M.-H.|publisher=Wiley|year=2013|isbn=9780471080398|location=Hoboken, N.J.}}</ref> | ||
===परमाणु कक्षकों का रैखिक संयोजन (एल सी ए ओ) | ===परमाणु कक्षकों का रैखिक संयोजन (एल सी ए ओ)=== | ||
{{main|Linear combination of atomic orbitals}} | {{main|Linear combination of atomic orbitals}} | ||
1927 और 1928 में फ्रेडरिक हंड और रॉबर्ट एस मुल्लिकेन द्वारा पहली बार आणविक कक्षाओं की शुरुआत की गई थी।<ref>[[Friedrich Hund]] and Chemistry, [[Werner Kutzelnigg]], on the occasion of Hund's 100th birthday, ''[[Angewandte Chemie International Edition]]'', 35, 573–586, (1996)</ref><ref>[[Robert S. Mulliken]]'s Nobel Lecture, ''[[Science (journal)|Science]]'', 157, no. 3785, 13-24. Available on-line at: [http://nobelprize.org/nobel_prizes/chemistry/laureates/1966/mulliken-lecture.pdf Nobelprize.org]</ref> आणविक कक्षकों के लिए परमाणु कक्षकों या समीपता का रैखिक संयोजन 1929 में सर जॉन लेनार्ड-जोन्स द्वारा प्रस्तुत किया गया था।<ref>{{cite journal| url=https://www.chemteam.info/Chem-History/Lennard-Jones-1929/Lennard-Jones-1929.html |last1=Lennard-Jones |first1=John (Sir) |author1-link=John Lennard-Jones |title=कुछ डायटोमिक अणुओं की इलेक्ट्रॉनिक संरचना|journal=Transactions of the Faraday Society |volume=25 |pages=668–686 |date=1929|doi=10.1039/tf9292500668 |bibcode=1929FaTr...25..668L }}</ref> उनके पेपर ने दिखाया कि परिमाण सिद्धांतों से [[एक अधातु तत्त्व]] और [[ऑक्सीजन]] अणुओं की इलेक्ट्रॉनिक संरचना कैसे प्राप्त की जाए। आणविक | 1927 और 1928 में फ्रेडरिक हंड और रॉबर्ट एस मुल्लिकेन द्वारा पहली बार आणविक कक्षाओं की शुरुआत की गई थी।<ref>[[Friedrich Hund]] and Chemistry, [[Werner Kutzelnigg]], on the occasion of Hund's 100th birthday, ''[[Angewandte Chemie International Edition]]'', 35, 573–586, (1996)</ref><ref>[[Robert S. Mulliken]]'s Nobel Lecture, ''[[Science (journal)|Science]]'', 157, no. 3785, 13-24. Available on-line at: [http://nobelprize.org/nobel_prizes/chemistry/laureates/1966/mulliken-lecture.pdf Nobelprize.org]</ref> आणविक कक्षकों के लिए परमाणु कक्षकों या समीपता का रैखिक संयोजन 1929 में सर जॉन लेनार्ड-जोन्स द्वारा प्रस्तुत किया गया था।<ref>{{cite journal| url=https://www.chemteam.info/Chem-History/Lennard-Jones-1929/Lennard-Jones-1929.html |last1=Lennard-Jones |first1=John (Sir) |author1-link=John Lennard-Jones |title=कुछ डायटोमिक अणुओं की इलेक्ट्रॉनिक संरचना|journal=Transactions of the Faraday Society |volume=25 |pages=668–686 |date=1929|doi=10.1039/tf9292500668 |bibcode=1929FaTr...25..668L }}</ref> उनके पेपर ने दिखाया कि परिमाण सिद्धांतों से [[एक अधातु तत्त्व]] और [[ऑक्सीजन]] अणुओं की इलेक्ट्रॉनिक संरचना कैसे प्राप्त की जाए। आणविक कक्षा सिद्धांत के लिए यह गुणात्मक दृष्टिकोण आधुनिक परमाणु [[क्वांटम रसायन|रसायन]] विज्ञान की शुरुआत का हिस्सा है। परमाणु कक्षकों के रैखिक संयोजन (एल सी ए ओ) का उपयोग आणविक कक्षकों का अनुमान लगाने के लिए किया जा सकता है जो अणु के घटक परमाणुओं के के आपस में जुड़ने से बनते हैं। एक परमाणु कक्षा के समान श्रोडिंगर समीकरण जो एक इलेक्ट्रॉन के व्यवहार का वर्णन करता है एक आणविक कक्षा के लिए भी बनाया जा सकता है। हार्ट्री-फॉक समीकरण जो आणविक श्रोडिंगर समीकरण के स्वतंत्र-कण समीपता के अनुरूप हैं परमाणु कक्षकों के रैखिक संयोजन, या परमाणु तरंग क्रिया के योग और अंतर, हार्ट्री-फॉक विधि का अनुमानित समाधान प्रदान करते हैं।। सरल द्विपरमाणुक अणुओं के लिए, प्राप्त तरंगों को समीकरणों द्वारा गणितीय रूप से दर्शाया जाता है- | ||
:<math>\Psi = c_a \psi_a + c_b \psi_b</math> | :<math>\Psi = c_a \psi_a + c_b \psi_b</math> | ||
| Line 68: | Line 68: | ||
=== जिरेड और अनजिरेड बंध === | === जिरेड और अनजिरेड बंध === | ||
उन अणुओं के लिए जिनमें व्युत्क्रम केंद्र ([[सेंट्रोसममिति]]) होता है , बंध के अतिरिक्त लेबल होते हैं जिन्हें आणविक कक्षकों पर लागू किया जा सकता है। केन्द्रसममित अणुओं में सम्मिलित हैं: | उन अणुओं के लिए जिनमें व्युत्क्रम केंद्र ([[सेंट्रोसममिति]]) होता है, बंध के अतिरिक्त लेबल होते हैं जिन्हें आणविक कक्षकों पर लागू किया जा सकता है। केन्द्रसममित अणुओं में सम्मिलित हैं: | ||
* समनाभिकीय [[होमोन्यूक्लियर अणु|अणु]] ,द्विपरमाणुक X <sub>2</sub> | * समनाभिकीय [[होमोन्यूक्लियर अणु|अणु]] ,द्विपरमाणुक X <sub>2</sub> | ||
* अष्टफलकीय [[ऑक्टाहेड्रल आणविक ज्यामिति|आणविक ज्यामिति]] EX6 | * अष्टफलकीय [[ऑक्टाहेड्रल आणविक ज्यामिति|आणविक ज्यामिति]] EX6 | ||
| Line 75: | Line 75: | ||
* विषम नाभिकीय [[हेटेरोन्यूक्लियर अणु|अणु]] ,द्विपरमाणुक XY | * विषम नाभिकीय [[हेटेरोन्यूक्लियर अणु|अणु]] ,द्विपरमाणुक XY | ||
* चतुष्फलकीय [[टेट्राहेड्रल आणविक ज्यामिति|आणविक ज्यामिति]],EX<sub>4</sub>. | * चतुष्फलकीय [[टेट्राहेड्रल आणविक ज्यामिति|आणविक ज्यामिति]],EX<sub>4</sub>. | ||
यदि अणु में बंध के केंद्र के माध्यम से व्युत्क्रम आणविक कक्षा के लिए समान चरणों में परिणाम देता है, तो | यदि अणु में बंध के केंद्र के माध्यम से व्युत्क्रम आणविक कक्षा के लिए समान चरणों में परिणाम देता है, तो आणविक कक्षा को जर्मन शब्द सम के लिए जिरेड(g) बंध कहा जाता है। यदि अणु में बंध के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षा के लिए एक कला परिवर्तन होता है, तो आणविक कक्षा को जर्मन शब्द विषम के लिए अनजिरेड(u) बंध कहा जाता है। σ-बंध वाले आबंधन आणविक कक्षा के लिए कक्षीय σg (s' s<nowiki>''</nowiki> सममित है), क्योंकि s' – s<nowiki>''</nowiki> का व्युत्क्रम प्रतिसममित है जबकि σ-बंध के साथ एक प्रति-बंधन आणविक कक्षा σ<sub>u</sub> है क्योंकि s' का व्युत्क्रम विषम है। π-बंध वाले बंधन आणविक कक्षा के लिए कक्षीय π<sub>u</sub> है क्योंकि बंध के केंद्र के माध्यम से व्युत्क्रम एक संकेत परिवर्तन उत्पन्न करेगा (दो p परमाणु कक्षाएँ एक दूसरे के साथ कला में हैं, लेकिन दो पालियों में विपरीत संकेत हैं), जबकि π-बंध के साथ एक प्रतिरक्षी आणविक कक्षा π<sub>g</sub> है क्योंकि बंध के केंद्र के माध्यम से व्युत्क्रम एक संकेत परिवर्तन का उत्पादन नहीं करेगा (दो p कक्षक कला द्वारा प्रतिसममित हैं)।<ref name = H&C /> | ||
=== आणविक | === आणविक कक्षा आरेख === | ||
{{main|आणविक कक्षीय आरेख}} | {{main|आणविक कक्षीय आरेख}} | ||
आणविक कक्षा विश्लेषण का गुणात्मक दृष्टिकोण एक अणु में बंध की पारस्परिक क्रिया को देखने के लिए एक आणविक | आणविक कक्षा विश्लेषण का गुणात्मक दृष्टिकोण एक अणु में बंध की पारस्परिक क्रिया को देखने के लिए एक आणविक कक्षा आरेख का उपयोग करता है। इस प्रकार के आरेख में, आणविक कक्षकों को क्षैतिज रेखाओं द्वारा दर्शाया जाता है; एक रेखा जितनी ऊँची होती है, कक्षक की ऊर्जा उतनी ही अधिक होती है, और विकृत कक्षकों को उनके बीच एक स्थान के साथ समान स्तर पर रखा जाता है। फिर आणविक कक्षा में रखे जाने वाले इलेक्ट्रॉनों को पाउली अपवर्जन सिद्धांत और हुण्ड के अधिकतम बहुलता के नियम को ध्यान में रखते हुए एक-एक करके निर्धारित किया जाता है (केवल 2 इलेक्ट्रॉन, विपरीत चक्रण वाले, प्रति कक्षीय; एक पर कई अयुग्मित इलेक्ट्रॉनों को रखें। उन्हें युग्म करना शुरू करने से पहले [[ऊर्जा स्तर]] जितना संभव हो)। अधिक जटिल अणुओं के लिए, तरंग यांत्रिकी दृष्टिकोण संबंध की गुणात्मक समझ में उपयोगिता खो देता है (हालांकि मात्रात्मक दृष्टिकोण के लिए अभी भी आवश्यक है)। | ||
* कक्षकों के एक आधार सेट में वे परमाणु कक्षक सम्मिलित होते हैं जो आणविक कक्षक अंतःक्रिया के लिए उपलब्ध होते हैं, जो बंधन या प्रतिरक्षी हो सकते हैं। | * कक्षकों के एक आधार सेट में वे परमाणु कक्षक सम्मिलित होते हैं जो आणविक कक्षक अंतःक्रिया के लिए उपलब्ध होते हैं, जो बंधन या प्रतिरक्षी हो सकते हैं। | ||
* आणविक कक्षकों की संख्या रैखिक विस्तार या आधार सेट में सम्मिलित परमाणु कक्षकों की संख्या के बराबर है। | * आणविक कक्षकों की संख्या रैखिक विस्तार या आधार सेट में सम्मिलित परमाणु कक्षकों की संख्या के बराबर है। | ||
| Line 86: | Line 86: | ||
* परिमित समूहों के एक विशेष प्रतिनिधित्व सिद्धांत के भीतर समरूपता अनुकूलित परमाणु कक्षक अधिक मिश्रण करते हैं यदि उनके परमाणु ऊर्जा स्तर करीब हैं। | * परिमित समूहों के एक विशेष प्रतिनिधित्व सिद्धांत के भीतर समरूपता अनुकूलित परमाणु कक्षक अधिक मिश्रण करते हैं यदि उनके परमाणु ऊर्जा स्तर करीब हैं। | ||
यथोचित सरल अणु के लिए आणविक | यथोचित सरल अणु के लिए आणविक कक्षा आरेख के निर्माण की सामान्य प्रक्रिया को निम्नानुसार संक्षेपित किया जा सकता है: | ||
1. अणु को एक बिंदु समूह में निर्दिष्ट करें। | 1. अणु को एक बिंदु समूह में निर्दिष्ट करें। | ||
| Line 96: | Line 96: | ||
4. दो टुकड़ों से समान सममिति प्रकार के SALCs को मिलाएं, और N SALCs से N आणविक कक्षाएँ बनाते हैं। | 4. दो टुकड़ों से समान सममिति प्रकार के SALCs को मिलाएं, और N SALCs से N आणविक कक्षाएँ बनाते हैं। | ||
5. मूल कक्षकों के अतिव्यापन और सापेक्ष ऊर्जाओं के आधार पर आणविक कक्षकों की सापेक्ष ऊर्जाओं का अनुमान लगाएं, और आणविक | 5. मूल कक्षकों के अतिव्यापन और सापेक्ष ऊर्जाओं के आधार पर आणविक कक्षकों की सापेक्ष ऊर्जाओं का अनुमान लगाएं, और आणविक कक्षा ऊर्जा स्तर आरेख (कक्षकों की उत्पत्ति दिखाते हुए) पर स्तर बनाएं। | ||
6. व्यावसायिक सॉफ़्टवेयर का उपयोग करके आणविक | 6. व्यावसायिक सॉफ़्टवेयर का उपयोग करके आणविक कक्षा गणना करके इस गुणात्मक क्रम की पुष्टि, सही और संशोधित करें।<ref>{{cite book|last1=Atkins |first1=Peter |display-authors=etal |title=अकार्बनिक रसायन शास्त्र|date=2006|publisher=W.H. Freeman|location=New York|isbn=978-0-7167-4878-6|page=208|edition= 4.}}</ref> | ||
=== आण्विक कक्षकों में आबंधन- === | === आण्विक कक्षकों में आबंधन- === | ||
| Line 116: | Line 116: | ||
== होमो और लुमो- == | == होमो और लुमो- == | ||
{{main|HOMO/LUMO}} | {{main|HOMO/LUMO}} | ||
उच्चतम अधिकृत आणविक | उच्चतम अधिकृत आणविक कक्षा और निम्नतम अनधिकृत आणविक कक्षा को क्रमशः होमो और लुमो के रूप में संदर्भित किया जाता है। होमो और लुमो की ऊर्जाओं के अंतर को होमो लुमो अन्तराल कहा जाता है। यह धारणा प्राय: साहित्य में भ्रम का विषय होती है और इस पर सावधानी से विचार किया जाना चाहिए। इसका मान प्राय: मौलिक अंतर (आयनीकरण क्षमता और इलेक्ट्रॉन संबंध के बीच अंतर) और प्रकाशीय अंतर के बीच स्थित होता है। इसके अलावा होमो लुमो अन्तराल अधिकांश भौतिक [[ऊर्जा अंतराल]] या अभिगमन अन्तराल से संबंधित हो सकता है, जो मुख्य अन्तराल से बहुत छोटा होता है।{{cn|date=June 2022}} | ||
== उदाहरण- == | == उदाहरण- == | ||
| Line 122: | Line 122: | ||
समनाभिकीय द्विपरमाणुक एमओ में आधार ढांचे में प्रत्येक परमाणु कक्षीय से समान योगदान होता है। यह H<sub>2</sub>, He<sub>2</sub> ,Li<sub>2</sub>, के लिए समनाभिकीय द्विपरमाणुक एमओ आरेखों में दिखाया गया है , जिनमें से सभी में सममित कक्षाएँ हैं।<ref name = H&C /> | समनाभिकीय द्विपरमाणुक एमओ में आधार ढांचे में प्रत्येक परमाणु कक्षीय से समान योगदान होता है। यह H<sub>2</sub>, He<sub>2</sub> ,Li<sub>2</sub>, के लिए समनाभिकीय द्विपरमाणुक एमओ आरेखों में दिखाया गया है , जिनमें से सभी में सममित कक्षाएँ हैं।<ref name = H&C /> | ||
== H2 -== | == H2 -== | ||
[[File:H2OrbitalsAnimation.gif|thumb|right|300px|एक अकेले हाइड्रोजन परमाणु (बाएं और दाएं) के परमाणु कक्षीय के लिए इलेक्ट्रॉन तरंग कार्य और H<sub>2</sub> अणु के संबंधित बंधन (नीचे) और प्रतिबंधक (शीर्ष) आणविक कक्षक । तरंग फलन का [[वास्तविक भाग]] नीला वक्र है, और [[काल्पनिक भाग]] लाल वक्र है। लाल बिंदु नाभिक के स्थानों को चिह्नित करते हैं। श्रोडिंगर तरंग समीकरण के अनुसार इलेक्ट्रॉन तरंग फलन दोलन करता है, और कक्षक इसकी खड़ी तरंगें हैं। स्थायी तरंग आवृत्ति कक्षीय की गतिज ऊर्जा के समानुपाती होती है। (यह रूप रेखा त्रि-आयामी प्रणाली के माध्यम से एक आयामी टुकड़ा है।)]]एक सरल एम ओ उदाहरण के रूप में, [[हाइड्रोजन]] Hअणु में इलेक्ट्रॉनों पर विचार करें(आणविक | [[File:H2OrbitalsAnimation.gif|thumb|right|300px|एक अकेले हाइड्रोजन परमाणु (बाएं और दाएं) के परमाणु कक्षीय के लिए इलेक्ट्रॉन तरंग कार्य और H<sub>2</sub> अणु के संबंधित बंधन (नीचे) और प्रतिबंधक (शीर्ष) आणविक कक्षक । तरंग फलन का [[वास्तविक भाग]] नीला वक्र है, और [[काल्पनिक भाग]] लाल वक्र है। लाल बिंदु नाभिक के स्थानों को चिह्नित करते हैं। श्रोडिंगर तरंग समीकरण के अनुसार इलेक्ट्रॉन तरंग फलन दोलन करता है, और कक्षक इसकी खड़ी तरंगें हैं। स्थायी तरंग आवृत्ति कक्षीय की गतिज ऊर्जा के समानुपाती होती है। (यह रूप रेखा त्रि-आयामी प्रणाली के माध्यम से एक आयामी टुकड़ा है।)]]एक सरल एम ओ उदाहरण के रूप में, [[हाइड्रोजन]] Hअणु में इलेक्ट्रॉनों पर विचार करें(आणविक कक्षा आरेख देखें) , दो परमाणुओं के साथ H 'और H चिह्नित किया गया।सबसे कम ऊर्जा वाले परमाणु कक्षक 1s' और 1s अणु की सममिति के अनुसार परिवर्तित नहीं होते हैं। यद्यपि निम्नलिखित समरूपता अनुकूलित परमाणु कक्षक करते हैं: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 142: | Line 142: | ||
जबकि समानाभिकीय द्विपरमाणुक अणुओं के लिए एमओ में प्रत्येक परस्पर क्रिया करने वाले परमाणु कक्षीय से समान योगदान होता है, विषम नाभिकीय द्विपरमाणुक के लिए एमओ में विभिन्न परमाणु कक्षीय योगदान होते हैं। विषमनाभिकीय द्विपरमाणुक में आबंधन या प्रतिआबंधी कक्षक उत्पन्न करने के लिए कक्षीय अन्योन्यक्रिया तब होती है जब परमाणु कक्षकों के बीच पर्याप्त अतिच्छादन होता है जैसा कि उनकी सममिति और कक्षीय ऊर्जाओं में समानता द्वारा निर्धारित होता है।{{cn|date=June 2022}} | जबकि समानाभिकीय द्विपरमाणुक अणुओं के लिए एमओ में प्रत्येक परस्पर क्रिया करने वाले परमाणु कक्षीय से समान योगदान होता है, विषम नाभिकीय द्विपरमाणुक के लिए एमओ में विभिन्न परमाणु कक्षीय योगदान होते हैं। विषमनाभिकीय द्विपरमाणुक में आबंधन या प्रतिआबंधी कक्षक उत्पन्न करने के लिए कक्षीय अन्योन्यक्रिया तब होती है जब परमाणु कक्षकों के बीच पर्याप्त अतिच्छादन होता है जैसा कि उनकी सममिति और कक्षीय ऊर्जाओं में समानता द्वारा निर्धारित होता है।{{cn|date=June 2022}} | ||
==== एच एफ (HF)- ==== | ==== एच एफ (HF)- ==== | ||
[[हाइड्रोजिन फ्लोराइड]] (HF) में H1s और F2s कक्षकों के बीच अतिव्यापन को बंध द्वारा अनुमति दी जाती है लेकिन दो परमाणु कक्षकों के बीच ऊर्जा में अंतर उन्हें आणविक | [[हाइड्रोजिन फ्लोराइड]] (HF) में H1s और F2s कक्षकों के बीच अतिव्यापन को बंध द्वारा अनुमति दी जाती है लेकिन दो परमाणु कक्षकों के बीच ऊर्जा में अंतर उन्हें आणविक कक्षा बनाने के लिए रोकता है। H 1s और F 2p के बीच अतिव्यापन कक्षकों को भी बंध की अनुमति है और इन दो परमाणु कक्षकों में एक सूक्ष्म ऊर्जा विभाजन है। इस प्रकार, वे परस्पर क्रिया करते हैं, जिससे σ और σ*एमओ एस का निर्माण होता है और एक अणु का बंधन क्रम 1 होता है। चूंकि HF एक गैर- केन्द्रसममित अणु है, सममिति लेबल g और u इसके आणविक कक्षकों पर लागू नहीं होते हैं।<ref>Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, {{ISBN|0130-39913-2}}, p. 41-43.</ref> | ||
== मात्रात्मक दृष्टिकोण- == | == मात्रात्मक दृष्टिकोण- == | ||
आणविक ऊर्जा स्तरों के लिए मात्रात्मक मान प्राप्त करने के लिए आणविक कक्षकों की आवश्यकता होती है जो ऐसे हों कि समाकृति अंतःक्रिया(सी आई) विस्तार [[पूर्ण कॉन्फ़िगरेशन इंटरैक्शन|पूर्ण समाकृति]] अंतःक्रिया सीमा की ओर तेजी से परिवर्तित हो। इस तरह के कार्यों को प्राप्त करने का सबसे आसान तरीका हार्ट्री-फॉक विधि है, जो आणविक कक्षकों को [[फॉक ऑपरेटर|फॉक संचालक]] के आइगेन [[eigenfunction|फलन]] के रूप में व्यक्त करता है।सामान्यतः परमाणु नाभिक पर केंद्रित गॉसियन कार्यों के रैखिक संयोजनों के रूप में आणविक कक्षाओं का विस्तार करके इस समस्या को हल करता है (परमाणु कक्षाओं के रैखिक संयोजन आणविक | आणविक ऊर्जा स्तरों के लिए मात्रात्मक मान प्राप्त करने के लिए आणविक कक्षकों की आवश्यकता होती है जो ऐसे हों कि समाकृति अंतःक्रिया(सी आई) विस्तार [[पूर्ण कॉन्फ़िगरेशन इंटरैक्शन|पूर्ण समाकृति]] अंतःक्रिया सीमा की ओर तेजी से परिवर्तित हो। इस तरह के कार्यों को प्राप्त करने का सबसे आसान तरीका हार्ट्री-फॉक विधि है, जो आणविक कक्षकों को [[फॉक ऑपरेटर|फॉक संचालक]] के आइगेन [[eigenfunction|फलन]] के रूप में व्यक्त करता है।सामान्यतः परमाणु नाभिक पर केंद्रित गॉसियन कार्यों के रैखिक संयोजनों के रूप में आणविक कक्षाओं का विस्तार करके इस समस्या को हल करता है (परमाणु कक्षाओं के रैखिक संयोजन आणविक कक्षा विधि और [[आधार सेट (रसायन विज्ञान)|आधार सेट]] देखें)। इन रैखिक संयोजनों के गुणांकों के लिए समीकरण एक सामान्यीकृत आइगेन मूल्य [[eigenvalue|अतिलक्षणिक]] समीकरण है जिसे ' रूथन समीकरण' के रूप में जाना जाता है, जो वास्तव में हार्ट्री-फॉक समीकरण का एक विशेष प्रतिनिधित्व है। ऐसे कई कार्यक्रम हैं जिनमें स्पार्टन (रसायन विज्ञान सॉफ्टवेयर) सहित एमओ की परिमाण,रासायनिक गणना की जा सकती है।सरल खाते प्राय सुझाव देते हैं कि प्रायोगिक आणविक कक्षा ऊर्जा को रासायनिक संयोजन कक्षकों के लिए पराबैंगनी प्रकाशिक इलेक्ट्रॉन [[अल्ट्रा वायलेट फोटोइलेक्ट्रॉन स्पेक्ट्रोस्कोपी|स्पेक्ट्रोस्कोपी]] और अंतर्भाग कक्षकों के लिए [[एक्स - रे फ़ोटोइलैक्ट्रॉन स्पेक्ट्रोस्कोपी|एक्स - किरण प्रकाशिक इलेक्ट्रॉन स्पेक्ट्रोस्कोपी]] के तरीकों से प्राप्त किया जा सकता है। यद्यपि यह गलत है क्योंकि ये प्रयोग अणु के बीच ऊर्जा में अंतर और एक इलेक्ट्रॉन को हटाने के परिणामस्वरूप आयनों में से एक आयनीकरण ऊर्जा को मापते हैं। कोपमन्स प्रमेय द्वारा आयनीकरण ऊर्जा लगभग कक्षीय ऊर्जा से जुड़ी हुई है। जबकि कुछ अणुओं के लिए इन दो मूल्यों के बीच समझौता घनिष्ठ हो सकता है, यह अन्य कारकों में बहुत खराब हो सकता है।{{cn|date=June 2022}} | ||
==टिप्पणियाँ-== | ==टिप्पणियाँ-== | ||
{{notes}} | {{notes}} | ||
Revision as of 15:28, 19 January 2023
रसायन विज्ञान में, आणविक कक्षा एक गणितीय कार्य है जो एक अणु में एक इलेक्ट्रॉन के स्थान और तरंग-समान व्यवहार का वर्णन करता है। इस फलन का उपयोग रासायनिक और भौतिक गुणों की गणना करने के लिए किया जा सकता है, जैसे कि किसी विशिष्ट क्षेत्र में इलेक्ट्रॉन के पाए जाने की संभावना के रूप में। परमाणु कक्षा और आणविक कक्षा शब्द 1932 में रॉबर्ट एस मुल्लिकेन द्वारा एक-इलेक्ट्रॉन ऑर्बिटल वेव विवरण कार्यों का मतलब समझाने के लिए पेश किया गया था। प्रारंभिक स्तर पर, इनका उपयोग अंतरिक्ष के उस क्षेत्र का वर्णन करने के लिए किया जाता है जिसमें फलन का एक महत्वपूर्ण आयाम होता है।
एक एकल परमाणु में, कक्षीय इलेक्ट्रॉनों का स्थान परमाणु कक्षाओं द्वारा निर्धारित किया जाता है। जब कई परमाणु रासायनिक रूप से एक अणु में संयोजित होते हैं, तो इलेक्ट्रॉनों के स्थान, अणु द्वारा पूर्ण रूप से निर्धारित किए जाते हैं, इसलिए परमाणु कक्षाएँ आणविक कक्षाएँ बनाने के लिए संयोजित होती हैं। घटक परमाणुओं से इलेक्ट्रॉन आणविक कक्षाओं में प्रवेश करते हैं। गणितीय रूप से, आणविक कक्षाएँ अणु के परमाणु नाभिक के क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण का एक अनुमानित समाधान हैं। वे अणु के प्रत्येक परमाणु से परमाणु कक्षा या संकर कक्षा के रैखिक संयोजन या परमाणुओं के समूहों से अन्य आणविक कक्षाओं के संयोजन से निर्मित होते हैं। हार्ट्री-फॉक या स्व-सुसंगत क्षेत्र (एस सी एफ) विधियों का उपयोग करके उनकी मात्रात्मक गणना की जा सकती है।
आण्विक कक्षक तीन प्रकार के होते हैं: आबंधी आण्विक कक्षक जिनकी ऊर्जा उन परमाणु कक्षकों की ऊर्जा से कम होती है जो उन्हें बनाते हैं और इस प्रकार उन रासायनिक बंधों को बढ़ावा देते हैं जो अणु को एक साथ बांधे रखते हैं। प्रति-आबंधी आणविक कक्षक जिनकी ऊर्जा उनके घटक परमाणु कक्षकों की ऊर्जा से अधिक होती है, और इसलिए ये अणु के बंध का विरोध करते हैं, और अनाबंधी वाले कक्षकों में उनके घटक परमाणु कक्षकों के समान ऊर्जा होती है और इस प्रकार बंध पर कोई प्रभाव नहीं पड़ता है।
अवलोकन
एक अणु में उन क्षेत्रों का प्रतिनिधित्व करने के लिए एक आणविक कक्षा (एम्ओ) का उपयोग किया जा सकता है जहां उस कक्षा पर कब्जा करने वाले एक इलेक्ट्रॉन के पाए जाने की संभावना है। आणविक कक्षाएँ अणु के परमाणु नाभिक के विद्युत क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण के अनुमानित समाधान हैं। यद्यपि इस समीकरण से सीधे कक्षाओं की गणना करना बहुत ही कठिन है। इसके बदले वे परमाणु कक्षकों के संयोजन से प्राप्त होते हैं, जो एक परमाणु में एक ऋणावेशित सूक्ष्म अणु के विन्यास के स्थान की भविष्यवाणी करते हैं। एक आणविक कक्षा एक अणु के इलेक्ट्रॉनिक विन्यास को उल्लिखत कर सकता है: स्थानिक वितरण और एक (या एक जोड़ी) इलेक्ट्रॉन की ऊर्जा। प्रायः एक आणविक कक्षा को परमाणु कक्षकों के रैखिक संयोजन के रूप में दर्शाया जाता है विशेष रूप से गुणात्मक या बहुत अनुमानित उपयोग में। वे आणविक कक्षा सिद्धांत के माध्यम से समझे जाने वाले अणुओं में बंध का एक सरल मॉडल प्रदान करने में अमूल्य हैं। संगणनात्मक रसायन शास्त्र में अधिकांश वर्तमान-दिन के तरीके प्रणाली के आणविक कक्षा की गणना से शुरू होते हैं। एक आणविक कक्षा नाभिक द्वारा उत्पन्न विद्युत क्षेत्र में एक इलेक्ट्रॉन के व्यवहार और अन्य इलेक्ट्रॉनों के कुछ औसत वितरण का वर्णन करता है। एक ही कक्षा में दो इलेक्ट्रॉनों के विषय में, पाउली सिद्धांत की मांग है कि उन इलेक्ट्रॉनों के पास विपरीत चक्रण हो। अनिवार्य रूप से यह एक सही अनुमान,है, और आणविक इलेक्ट्रॉनिक तरंग फलन के अत्यधिक सटीक विवरण में कक्षक नहीं हैं।
आण्विक कक्षक सामान्य रूप से पूरे अणु में विस्थानीकृत होते हैं। इसके अलावा, यदि अणु में बंध तत्व हैं, तो इसके गैर-अपघटित आणविक कक्षक इनमें से किसी भी बंध के संबंध में या तो सममित या विषम हैं। दूसरे शब्दों में, आणविक कक्षा ψ पर सममिति संक्रिया S (उदाहरण के लिए, एक प्रतिबिंब, घूर्णन, या व्युत्क्रमण) के प्रयोग से आणविक कक्षा अपरिवर्तित रहता है या इसके गणितीय चिह्न को उलट देता है उदाहरण के लिए Sψ = ±ψ समतलीय अणुओं में, उदाहरण के लिए, आण्विक तल में परावर्तन के संबंध में आण्विक कक्षक या तो सममित (सिग्मा बंधन) या प्रतिसममित ( p आबंध) होते हैं। यदि विकृत कक्षीय ऊर्जा वाले अणुओं पर भी विचार किया जाता है, तो एक अधिक सामान्य कथन है कि अणु के बंध समूह के अलघुकरणीय निरूपण के लिए आणविक कक्षाएँ आधार बनाती हैं।[1] आणविक कक्षकों के बंध गुणों का अर्थ है कि निरूपण जो आणविक कक्षा सिद्धांत की एक अंतर्निहित विशेषता है और यह इसे मूल रूप से रासायनिक संयोजन बंध सिद्धांत से अलग बनाता है, जिसमें अनुनाद के लिए बंध को स्थानीयकृत इलेक्ट्रॉन जोड़े के रूप में देखा जाता है।
इन बंध-अनुकूलित विहित आणविक कक्षकों के विपरीत, स्थानीयकृत आणविक कक्षकों को विहित कक्षकों में कुछ गणितीय परिवर्तनों को लागू करके बनाया जा सकता है। इस दृष्टिकोण का लाभ यह है कि ऑर्बिटल्स एक अणु के "बंध" से अधिक मेल खाते हैं जैसा कि लुईस संरचना द्वारा दर्शाया गया है। एक नुकसान के रूप में, इन स्थानीय कक्षकों के ऊर्जा स्तरों का अब भौतिक अर्थ नहीं रह गया है। (इस लेख के बाकी हिस्सों में चर्चा विहित आणविक कक्षाओं पर केंद्रित होगी। स्थानीयकृत आणविक कक्षाओं पर आगे की चर्चा के लिए, देखें: प्राकृतिक बंध कक्षीय और सिग्मा-पाई और समकक्ष-कक्षीय मॉडल।)
आणविक कक्षकों का निर्माण
आणविक कक्षक परमाणु कक्षक के बीच अनुमत अंतःक्रियाओं से उत्पन्न होते हैं, जिनकी अनुमति दी जाती है, परमाणु कक्षकों का बंध (समूह सिद्धांत से निर्धारित) एक दूसरे के साथ संगत हैं। परमाणु कक्षा अन्योन्यक्रियाओं की दक्षता दो परमाणु कक्षकों के बीच कक्षीय अतिव्यापन (इस बात का माप है कि दो कक्षक एक दूसरे के साथ रचनात्मक रूप से कितनी अच्छी तरह परस्पर क्रिया करते हैं) से निर्धारित होती है, यदि परमाणु कक्षक ऊर्जा के करीब हों तब ये बहुत महत्वपूर्ण है। अंत में बनने वाले आणविक कक्षकों की संख्या अणु बनाने के लिए संयुक्त किए जा रहे परमाणुओं में परमाणु कक्षकों की संख्या के बराबर होनी चाहिए।
गुणात्मक चर्चा
एक सटीक, लेकिन गुणात्मक रूप से उपयोगी, आणविक संरचना की चर्चा के लिए, आणविक कक्षक से परमाणु कक्षक आणविक कक्षा विधि के रैखिक संयोजन से प्राप्त किया जा सकता है। यहाँ, आणविक कक्षक को परमाणु कक्षक के रैखिक संयोजन के रूप में व्यक्त किया जाता है।[2]
परमाणु कक्षकों का रैखिक संयोजन (एल सी ए ओ)
1927 और 1928 में फ्रेडरिक हंड और रॉबर्ट एस मुल्लिकेन द्वारा पहली बार आणविक कक्षाओं की शुरुआत की गई थी।[3][4] आणविक कक्षकों के लिए परमाणु कक्षकों या समीपता का रैखिक संयोजन 1929 में सर जॉन लेनार्ड-जोन्स द्वारा प्रस्तुत किया गया था।[5] उनके पेपर ने दिखाया कि परिमाण सिद्धांतों से एक अधातु तत्त्व और ऑक्सीजन अणुओं की इलेक्ट्रॉनिक संरचना कैसे प्राप्त की जाए। आणविक कक्षा सिद्धांत के लिए यह गुणात्मक दृष्टिकोण आधुनिक परमाणु रसायन विज्ञान की शुरुआत का हिस्सा है। परमाणु कक्षकों के रैखिक संयोजन (एल सी ए ओ) का उपयोग आणविक कक्षकों का अनुमान लगाने के लिए किया जा सकता है जो अणु के घटक परमाणुओं के के आपस में जुड़ने से बनते हैं। एक परमाणु कक्षा के समान श्रोडिंगर समीकरण जो एक इलेक्ट्रॉन के व्यवहार का वर्णन करता है एक आणविक कक्षा के लिए भी बनाया जा सकता है। हार्ट्री-फॉक समीकरण जो आणविक श्रोडिंगर समीकरण के स्वतंत्र-कण समीपता के अनुरूप हैं परमाणु कक्षकों के रैखिक संयोजन, या परमाणु तरंग क्रिया के योग और अंतर, हार्ट्री-फॉक विधि का अनुमानित समाधान प्रदान करते हैं।। सरल द्विपरमाणुक अणुओं के लिए, प्राप्त तरंगों को समीकरणों द्वारा गणितीय रूप से दर्शाया जाता है-
जहां तथा आबंधन और प्रतिआबंधन आण्विक कक्षकों के लिए आण्विक तरंग फलन हैं, तथा क्रमशः a और b परमाणुओं की परमाणु तरंग हैं, और तथा समायोज्य गुणांक हैं। व्यक्तिगत परमाणु कक्षकों की ऊर्जा और बंध के आधार पर, ये गुणांक धनावेशित या ऋणावेशित हो सकते हैं। जैसे-जैसे दो परमाणु एक-दूसरे के करीब आते हैं, उनके परमाणु कक्षक उच्च इलेक्ट्रॉन घनत्व वाले क्षेत्रों का उत्पादन करने के लिए अतिव्यापित होते हैं, और इसके परिणामस्वरूप, दो परमाणुओं के बीच आणविक कक्षक बनते हैं। परमाणुओं को धनावेशित नाभिक और बंधन आणविक कक्षाओं में रहने वाले ऋणावेशित इलेक्ट्रॉनों के बीच स्थिर वैद्युत विक्षेप आकर्षण द्वारा एक साथ रखा जाता है।
बंधन , प्रतिआबंधन,और अनाबंधी आणविक कक्षक
जब परमाणु कक्षक परस्पर क्रिया करते हैं, तो परिणामी आणविक कक्षक तीन प्रकार के हो सकते हैं बंधन, प्रतिआबंधन, और अनाबंधी। ।
बंधन आणविक कक्षाएँ:
- परमाणु कक्षक के बीच बंधन अंतःक्रिया, रचनात्मक अंतःक्रिया हैं।
- बंधन आणविक कक्षाएँ उन परमाणु कक्षकों की तुलना में ऊर्जा में कम होते हैं जो उन्हें उत्पन्न करने के लिए गठबंधन करते हैं।
प्रतिआबंधन आणविक कक्षक;
- परमाणु कक्षक के बीच प्रतिआबंधन अंतःक्रिया विनाशकारी (आउट-ऑफ-फेज) अंतःक्रिया हैं, एक नोड (भौतिकी) के साथ जहां दो अन्योन्यकारी परमाणुओं के बीच प्रतिआबंधन कक्षकों की तरंग क्रिया शून्य है।
- प्रतिआबंधन आणविक कक्षक उन परमाणु कक्षकों की तुलना में ऊर्जा में अधिक हैं जो उन्हें उत्पन्न करने के लिए संयोजन करते हैं।
अनाबंधी कक्षक:
- अनाबंधी आणविक कक्षक आपसी बंध की कमी के कारण परमाणु कक्षकों के बीच कोई संपर्क नहीं होने का परिणाम है।
- अनाबंधी आणविक कक्षक में अणु में किसी एक परमाणु के परमाणु कक्षक के समान ऊर्जा होगी।
आणविक कक्षक के लिए सिग्मा और पाई लेबलपरमाणु कक्षकों के बीच परस्पर क्रिया के प्रकार को आणविक-कक्षीय बंध लेबल σ (सिग्मा), π (पाई), δ (डेल्टा), φ(फाई ), γ (गामा) आदि द्वारा वर्गीकृत किया जा सकता है। ये क्रमशः परमाणु कक्षकों s, p, d, f और g के संगत यूनानी अक्षर हैं। संबंधित परमाणुओं के बीच आंतरिक अक्ष वाले नोडल विमानों की संख्या σ लिए शून्य, π के लिए एक, δ के लिए दो, φ के लिए तीन और γ के लिए चार है।
सिग्मा बंध-
σ सिग्मा बंध वाला एक आणविक कक्षक या तो दो परमाणु s-कक्षकों या दो परमाणु pz-कक्षकों की अन्योन्य क्रिया का परिणाम होता है। एक आणविक कक्षक में σ-बंध होगा यदि कक्षीय दो परमाणु केंद्रों, आंतरिक परमाणु अक्ष को जोड़ने वाली धुरी के संबंध में सममित है। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में आणविक कक्षक के घूमने से चरण परिवर्तन नहीं होता है। एक σ*कक्षक, सिग्मा प्रतिआबंधन कक्षक, आंतरिक परमाणु अक्ष के बारे में घुमाए जाने पर भी उसी चरण को बनाए रखता है। σ* कक्षा में एक नोडल तल होता है जो नाभिक और आंतरिक नाभिकीय अक्ष के लंबवत होता है।[6]
π बंध -
π बंध वाला एक आणविक कक्षक या तो दो परमाणु px कक्षकों या p y कक्षकों की परस्पर क्रिया से उत्पन्न होता है । एक आणविक कक्षक में π बंध यदि कक्षीय आंतरिक अक्ष के घूर्णन के संबंध में असममित है, इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में आणविक कक्षक के घूमने से चरण परिवर्तन होगा। यदि परमाणु कक्षीय वास्तविक कक्षकों पर विचार किया जाए तो एक नोडल तल होता है जिसमें आंतरिक अक्ष होता है।
एक π* कक्षक, पाई प्रतिआबंधन कक्षक भी आंतरिक परमाणु अक्ष में घुमाए जाने पर एक चरण परिवर्तन उत्पन्न करेगा। π* कक्षा में नाभिकों के बीच एक दूसरा नोडल तल भी होता है।[6][7][8][9]
δ बंध -
δ बंध वाला एक एमओ दो परमाणु dxy या d x2-y2 कक्षकों की परस्पर क्रिया से उत्पन्न होता है क्योंकि इन आणविक कक्षकों में निम्न-ऊर्जा वाले d परमाणु कक्षक सम्मिलित होते हैं, वे संक्रमण-धातु परिसरों में देखे जाते हैं। एक δ बंध कक्षक में आंतरिक परमाणु अक्ष वाले दो नोडल प्लेन होते हैं, और एक δ* प्रतिआबंधन कक्षक में नाभिक के बीच तीसरा नोडल प्लेन भी होता है।
φ बंध-
सैद्धांतिक रसायनज्ञों ने अनुमान लगाया है कि उच्च-क्रम के बंधन, जैसे कि परमाणु कक्षकों के अतिव्यापन के अनुरूप फाई बंध संभव हैं। एक अणु का कोई ज्ञात उदाहरण नहीं है जिसमें कथित तौर पर फाई बंध सम्मिलित हो।
जिरेड और अनजिरेड बंध
उन अणुओं के लिए जिनमें व्युत्क्रम केंद्र (सेंट्रोसममिति) होता है, बंध के अतिरिक्त लेबल होते हैं जिन्हें आणविक कक्षकों पर लागू किया जा सकता है। केन्द्रसममित अणुओं में सम्मिलित हैं:
- समनाभिकीय अणु ,द्विपरमाणुक X 2
- अष्टफलकीय आणविक ज्यामिति EX6
- वर्ग समतलीय आण्विक ज्यामिति EX4.
गैर-केन्द्रसममित अणुओं में सम्मिलित हैं:
- विषम नाभिकीय अणु ,द्विपरमाणुक XY
- चतुष्फलकीय आणविक ज्यामिति,EX4.
यदि अणु में बंध के केंद्र के माध्यम से व्युत्क्रम आणविक कक्षा के लिए समान चरणों में परिणाम देता है, तो आणविक कक्षा को जर्मन शब्द सम के लिए जिरेड(g) बंध कहा जाता है। यदि अणु में बंध के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षा के लिए एक कला परिवर्तन होता है, तो आणविक कक्षा को जर्मन शब्द विषम के लिए अनजिरेड(u) बंध कहा जाता है। σ-बंध वाले आबंधन आणविक कक्षा के लिए कक्षीय σg (s' s'' सममित है), क्योंकि s' – s'' का व्युत्क्रम प्रतिसममित है जबकि σ-बंध के साथ एक प्रति-बंधन आणविक कक्षा σu है क्योंकि s' का व्युत्क्रम विषम है। π-बंध वाले बंधन आणविक कक्षा के लिए कक्षीय πu है क्योंकि बंध के केंद्र के माध्यम से व्युत्क्रम एक संकेत परिवर्तन उत्पन्न करेगा (दो p परमाणु कक्षाएँ एक दूसरे के साथ कला में हैं, लेकिन दो पालियों में विपरीत संकेत हैं), जबकि π-बंध के साथ एक प्रतिरक्षी आणविक कक्षा πg है क्योंकि बंध के केंद्र के माध्यम से व्युत्क्रम एक संकेत परिवर्तन का उत्पादन नहीं करेगा (दो p कक्षक कला द्वारा प्रतिसममित हैं)।[6]
आणविक कक्षा आरेख
आणविक कक्षा विश्लेषण का गुणात्मक दृष्टिकोण एक अणु में बंध की पारस्परिक क्रिया को देखने के लिए एक आणविक कक्षा आरेख का उपयोग करता है। इस प्रकार के आरेख में, आणविक कक्षकों को क्षैतिज रेखाओं द्वारा दर्शाया जाता है; एक रेखा जितनी ऊँची होती है, कक्षक की ऊर्जा उतनी ही अधिक होती है, और विकृत कक्षकों को उनके बीच एक स्थान के साथ समान स्तर पर रखा जाता है। फिर आणविक कक्षा में रखे जाने वाले इलेक्ट्रॉनों को पाउली अपवर्जन सिद्धांत और हुण्ड के अधिकतम बहुलता के नियम को ध्यान में रखते हुए एक-एक करके निर्धारित किया जाता है (केवल 2 इलेक्ट्रॉन, विपरीत चक्रण वाले, प्रति कक्षीय; एक पर कई अयुग्मित इलेक्ट्रॉनों को रखें। उन्हें युग्म करना शुरू करने से पहले ऊर्जा स्तर जितना संभव हो)। अधिक जटिल अणुओं के लिए, तरंग यांत्रिकी दृष्टिकोण संबंध की गुणात्मक समझ में उपयोगिता खो देता है (हालांकि मात्रात्मक दृष्टिकोण के लिए अभी भी आवश्यक है)।
- कक्षकों के एक आधार सेट में वे परमाणु कक्षक सम्मिलित होते हैं जो आणविक कक्षक अंतःक्रिया के लिए उपलब्ध होते हैं, जो बंधन या प्रतिरक्षी हो सकते हैं।
- आणविक कक्षकों की संख्या रैखिक विस्तार या आधार सेट में सम्मिलित परमाणु कक्षकों की संख्या के बराबर है।
- यदि अणु में कुछ समरूपता है, तो विकृत परमाणु कक्षकों (समान परमाणु ऊर्जा के साथ) को रैखिक संयोजनों (सममिति-अनुकूलित परमाणु कक्षक (SO) कहा जाता है) में समूहीकृत किया जाता है, जो समरूपता समूह के प्रतिनिधित्व से संबंधित होते हैं, इसलिए तरंग कार्य करती है कि समूह का वर्णन करें जिन्हें समरूपता-अनुकूलित रैखिक संयोजन (SALC) के रूप में जाना जाता है।
- एक समूह निरूपण से संबंधित आणविक कक्षकों की संख्या इस निरूपण से संबंधित सममिति-अनुकूलित परमाणु कक्षकों की संख्या के बराबर है।
- परिमित समूहों के एक विशेष प्रतिनिधित्व सिद्धांत के भीतर समरूपता अनुकूलित परमाणु कक्षक अधिक मिश्रण करते हैं यदि उनके परमाणु ऊर्जा स्तर करीब हैं।
यथोचित सरल अणु के लिए आणविक कक्षा आरेख के निर्माण की सामान्य प्रक्रिया को निम्नानुसार संक्षेपित किया जा सकता है:
1. अणु को एक बिंदु समूह में निर्दिष्ट करें।
2. SALCs के आकार को देखें।
3. ऊर्जा के बढ़ते क्रम में प्रत्येक आणविक खंड के SALCs को व्यवस्थित करें, पहले ध्यान दें कि क्या वे s, p, या d कक्षकों से उत्पन्न होते हैं(और उन्हें s <'p <'d क्रम में रखें), और फिर उनकी आंतरिक परमाणु नोड्स की संख्या।
4. दो टुकड़ों से समान सममिति प्रकार के SALCs को मिलाएं, और N SALCs से N आणविक कक्षाएँ बनाते हैं।
5. मूल कक्षकों के अतिव्यापन और सापेक्ष ऊर्जाओं के आधार पर आणविक कक्षकों की सापेक्ष ऊर्जाओं का अनुमान लगाएं, और आणविक कक्षा ऊर्जा स्तर आरेख (कक्षकों की उत्पत्ति दिखाते हुए) पर स्तर बनाएं।
6. व्यावसायिक सॉफ़्टवेयर का उपयोग करके आणविक कक्षा गणना करके इस गुणात्मक क्रम की पुष्टि, सही और संशोधित करें।[10]
आण्विक कक्षकों में आबंधन-
कक्षीय अध: पतन-
आण्विक कक्षकों को विकृत कहा जाता है यदि उनमें समान ऊर्जा हो। उदाहरण के लिए, पहले दस तत्वों के समनाभिकीय द्विपरमाणुक अणुओं में, आण्विक कक्षकों की व्युत्पत्ति px और py परमाणु कक्षकों के परिणामस्वरूप दो विकृत बंधन कक्षक (कम ऊर्जा वाले) और दो विकृत प्रतिरक्षी कक्षक (उच्च ऊर्जा वाले) होते हैं।[11]
आयनिक बंधन-
जब दो परमाणुओं के परमाणु कक्षकों के बीच ऊर्जा अंतर काफी बड़ा होता है, तो एक परमाणु के कक्षक लगभग पूरी तरह से बंधन कक्षकों में योगदान करते हैं, और दूसरे परमाणु के कक्षक लगभग पूरी तरह से प्रतिरक्षी कक्षकों में योगदान करते हैं। इस प्रकार, स्थिति प्रभावी रूप से यह है कि एक परमाणु से दूसरे परमाणु में एक या एक से अधिक इलेक्ट्रॉन स्थानांतरित हो गए हैं। इसे आयनिक बंध कहा जाता है।[citation needed]
बंधन आदेश-
बंधन क्रम, या बंध की संख्या एक अणु के बंधन और प्रतिरक्षी आणविक कक्षाओं में इलेक्ट्रॉनों की संख्या को जोड़कर निर्धारित की जा सकता है।बंधन कक्षक में इलेक्ट्रॉनों की एक जोड़ी एक बंध बनाती है, जबकि एक प्रतिरक्षी कक्षक में इलेक्ट्रॉनों की एक जोड़ी एक बंध को अस्वीकार करती है। उदाहरण के लिए n2 बंधन कक्षकों में आठ इलेक्ट्रॉनों और प्रतिरक्षी कक्षकों में दो इलेक्ट्रॉनों के साथ, तीन का बंध गण होता है, जो त्रिक बंध का गठन करता है।
बंध शक्ति बंध गण के समानुपाती होती है- बंधन की अधिक मात्रा अधिक स्थिर बंध बनाती है और बंध की लंबाई इसके व्युत्क्रमानुपाती होती है एक मजबूत बंध छोटा होता है।
धनात्मक बंधन क्रम वाले अणु की आवश्यकता के लिए दुर्लभ अपवाद हैं। यद्यपि Be2 एमओ विश्लेषण के अनुसार 0 का बंध गण है,[6][12]एक अत्यधिक अस्थिर Be2 अणु का प्रायोगिक साक्ष्य है जिसकी बंधन लंबाई 245 और बंधन ऊर्जा 10किलोजूल /मोल है। [14] [1]
होमो और लुमो-
उच्चतम अधिकृत आणविक कक्षा और निम्नतम अनधिकृत आणविक कक्षा को क्रमशः होमो और लुमो के रूप में संदर्भित किया जाता है। होमो और लुमो की ऊर्जाओं के अंतर को होमो लुमो अन्तराल कहा जाता है। यह धारणा प्राय: साहित्य में भ्रम का विषय होती है और इस पर सावधानी से विचार किया जाना चाहिए। इसका मान प्राय: मौलिक अंतर (आयनीकरण क्षमता और इलेक्ट्रॉन संबंध के बीच अंतर) और प्रकाशीय अंतर के बीच स्थित होता है। इसके अलावा होमो लुमो अन्तराल अधिकांश भौतिक ऊर्जा अंतराल या अभिगमन अन्तराल से संबंधित हो सकता है, जो मुख्य अन्तराल से बहुत छोटा होता है।[citation needed]
उदाहरण-
समनाभिकीय द्विपरमाणुक
समनाभिकीय द्विपरमाणुक एमओ में आधार ढांचे में प्रत्येक परमाणु कक्षीय से समान योगदान होता है। यह H2, He2 ,Li2, के लिए समनाभिकीय द्विपरमाणुक एमओ आरेखों में दिखाया गया है , जिनमें से सभी में सममित कक्षाएँ हैं।[6]
H2 -

एक सरल एम ओ उदाहरण के रूप में, हाइड्रोजन Hअणु में इलेक्ट्रॉनों पर विचार करें(आणविक कक्षा आरेख देखें) , दो परमाणुओं के साथ H 'और H चिह्नित किया गया।सबसे कम ऊर्जा वाले परमाणु कक्षक 1s' और 1s अणु की सममिति के अनुसार परिवर्तित नहीं होते हैं। यद्यपि निम्नलिखित समरूपता अनुकूलित परमाणु कक्षक करते हैं:
| 1s' – 1s" | प्रतिसममित संयोजन: प्रतिबिंब द्वारा अस्वीकृत, अन्य परिचालनों द्वारा अपरिवर्तित |
|---|---|
| 1s' + 1s" | सममित संयोजन: सभी समरूपता संचालन द्वारा अपरिवर्तित |
सममित संयोजन (आबंधी कक्षक कहलाता है) आधार कक्षकों की तुलना में ऊर्जा में कम होता है, और प्रतिसममित संयोजन (प्रतिबंध कक्षक कहा जाता है) उच्च होता है। क्योंकि H2अणु में दो इलेक्ट्रॉन होते हैं, वे दोनों बंधी कक्षक में जा सकते हैं, जिससे प्रणाली दो मुक्त हाइड्रोजन परमाणुओं की तुलना में ऊर्जा में कम (इसलिए अधिक स्थिर) हो जाती है। इसे सहसंयोजक बंधन कहा जाता है।आबंध क्रम आबंधी इलेक्ट्रॉनों की संख्या ऋण प्रतिआबंधन इलेक्ट्रॉनों की संख्या के बराबर है, जो 2 से विभाजित है। इस उदाहरण में आबंधक कक्षक में 2 इलेक्ट्रॉन हैं और प्रतिबंधक कक्षक में कोई नहीं है। बंधन क्रम 1 है और दो हाइड्रोजन परमाणुओं के बीच एक ही बंधन है।[citation needed]
He2 -
दूसरी ओर He' और He2 लेबल वाले परमाणुओं के साथ He2 काल्पनिक अणु पर विचार करें। जैसा कि H2 के साथ सबसे कम ऊर्जा वाले परमाणु कक्षक 1s' और 1s हैं और अणु में बन्ध के अनुसार परिवर्तित नहीं होते हैं, जबकि समरूपता अनुकूलित परमाणु कक्षक करते हैं। समरूपता संयोजन-बंधी कक्षक-आधार कक्षकों की तुलना में ऊर्जा में कम है, और प्रतिसममित संयोजन-प्रति आबंधन कक्षक उच्च है।H2 के विपरीत, दो संयोजी इलेक्ट्रॉनों के साथ, He2 इसकी उदासीन स्थिर अवस्था में चार हैं। दो इलेक्ट्रॉन निम्न-ऊर्जा बंधन कक्षक σg (1s)भरते हैं, जबकि शेष दो उच्च-ऊर्जा प्रति-बंधन कक्षक, σu*(1s). भरते हैं। इस प्रकार अणु के चारों ओर परिणामी इलेक्ट्रॉन घनत्व दो परमाणुओं के बीच बंधन के गठन का समर्थन नहीं करता है; परमाणुओं को एक साथ रखने वाले स्थिर बंधन के बिना, अणु के अस्तित्व की उम्मीद नहीं की जाएगी। इसे देखने का एक अन्य तरीका यह है कि दो बंधन इलेक्ट्रॉन और दो प्रतिरक्षी इलेक्ट्रॉन हैं; इसलिए, बंधन क्रम 0 है और कोई बंधन मौजूद नहीं है (अणु में वांडर वॉल्स क्षमता द्वारा समर्थित एक बाध्य अवस्था है)।[citation needed]
डाइलिथियम Li2 -
डाइलिथियम Li2 दो Li परमाणुओं के 1s और 2s परमाणु कक्षकों (आधार सेट) के अतिव्यापन से बनता है। प्रत्येक Li परमाणु बंधन पारस्परिक क्रिया के लिए तीन इलेक्ट्रॉनों का योगदान देता है, और छह इलेक्ट्रॉन निम्नतम ऊर्जा के तीन एमओ σg(1s), σu*(1s)और σg(2s) को भरते हैं, बंध क्रम के समीकरण का उपयोग करते हुए, यह पाया जाता है कि डाइलिथियम में एक, एक बंध का बंध क्रम होता है।[citation needed]
उत्कृष्ट गैसें-
He2 के एक काल्पनिक अणु को ध्यान में रखते हुए, चूंकि परमाणु कक्षकों का आधार सेट H2 के परीक्षण में समान है, हम पाते हैं कि आबंधन और प्रतिआबंधी दोनों कक्षक भरे हुए हैं, इसलिए युग्म को कोई ऊर्जा लाभ नहीं है। HeH को थोड़ा ऊर्जा लाभ होगा, लेकिन H2 + 2 जितना नहीं , इसलिए अणु बहुत अस्थिर है और हाइड्रोजन और हीलियम में विघटित होने से पहले ही संक्षिप्त रूप से मौजूद है। सामान्य तौर पर, हम पाते हैं कि He जैसे परमाणु जिनके पास पूर्ण ऊर्जा के गोले हैं, शायद ही कभी अन्य परमाणुओं के साथ बंधते हैं। अल्पकालिक वांडरवाल परिसरों को छोड़कर, बहुत कम उत्कृष्ट गैस यौगिक ज्ञात हैं।[citation needed]
विषम नाभिकीय द्विपरमाणुक -
जबकि समानाभिकीय द्विपरमाणुक अणुओं के लिए एमओ में प्रत्येक परस्पर क्रिया करने वाले परमाणु कक्षीय से समान योगदान होता है, विषम नाभिकीय द्विपरमाणुक के लिए एमओ में विभिन्न परमाणु कक्षीय योगदान होते हैं। विषमनाभिकीय द्विपरमाणुक में आबंधन या प्रतिआबंधी कक्षक उत्पन्न करने के लिए कक्षीय अन्योन्यक्रिया तब होती है जब परमाणु कक्षकों के बीच पर्याप्त अतिच्छादन होता है जैसा कि उनकी सममिति और कक्षीय ऊर्जाओं में समानता द्वारा निर्धारित होता है।[citation needed]
एच एफ (HF)-
हाइड्रोजिन फ्लोराइड (HF) में H1s और F2s कक्षकों के बीच अतिव्यापन को बंध द्वारा अनुमति दी जाती है लेकिन दो परमाणु कक्षकों के बीच ऊर्जा में अंतर उन्हें आणविक कक्षा बनाने के लिए रोकता है। H 1s और F 2p के बीच अतिव्यापन कक्षकों को भी बंध की अनुमति है और इन दो परमाणु कक्षकों में एक सूक्ष्म ऊर्जा विभाजन है। इस प्रकार, वे परस्पर क्रिया करते हैं, जिससे σ और σ*एमओ एस का निर्माण होता है और एक अणु का बंधन क्रम 1 होता है। चूंकि HF एक गैर- केन्द्रसममित अणु है, सममिति लेबल g और u इसके आणविक कक्षकों पर लागू नहीं होते हैं।[13]
मात्रात्मक दृष्टिकोण-
आणविक ऊर्जा स्तरों के लिए मात्रात्मक मान प्राप्त करने के लिए आणविक कक्षकों की आवश्यकता होती है जो ऐसे हों कि समाकृति अंतःक्रिया(सी आई) विस्तार पूर्ण समाकृति अंतःक्रिया सीमा की ओर तेजी से परिवर्तित हो। इस तरह के कार्यों को प्राप्त करने का सबसे आसान तरीका हार्ट्री-फॉक विधि है, जो आणविक कक्षकों को फॉक संचालक के आइगेन फलन के रूप में व्यक्त करता है।सामान्यतः परमाणु नाभिक पर केंद्रित गॉसियन कार्यों के रैखिक संयोजनों के रूप में आणविक कक्षाओं का विस्तार करके इस समस्या को हल करता है (परमाणु कक्षाओं के रैखिक संयोजन आणविक कक्षा विधि और आधार सेट देखें)। इन रैखिक संयोजनों के गुणांकों के लिए समीकरण एक सामान्यीकृत आइगेन मूल्य अतिलक्षणिक समीकरण है जिसे ' रूथन समीकरण' के रूप में जाना जाता है, जो वास्तव में हार्ट्री-फॉक समीकरण का एक विशेष प्रतिनिधित्व है। ऐसे कई कार्यक्रम हैं जिनमें स्पार्टन (रसायन विज्ञान सॉफ्टवेयर) सहित एमओ की परिमाण,रासायनिक गणना की जा सकती है।सरल खाते प्राय सुझाव देते हैं कि प्रायोगिक आणविक कक्षा ऊर्जा को रासायनिक संयोजन कक्षकों के लिए पराबैंगनी प्रकाशिक इलेक्ट्रॉन स्पेक्ट्रोस्कोपी और अंतर्भाग कक्षकों के लिए एक्स - किरण प्रकाशिक इलेक्ट्रॉन स्पेक्ट्रोस्कोपी के तरीकों से प्राप्त किया जा सकता है। यद्यपि यह गलत है क्योंकि ये प्रयोग अणु के बीच ऊर्जा में अंतर और एक इलेक्ट्रॉन को हटाने के परिणामस्वरूप आयनों में से एक आयनीकरण ऊर्जा को मापते हैं। कोपमन्स प्रमेय द्वारा आयनीकरण ऊर्जा लगभग कक्षीय ऊर्जा से जुड़ी हुई है। जबकि कुछ अणुओं के लिए इन दो मूल्यों के बीच समझौता घनिष्ठ हो सकता है, यह अन्य कारकों में बहुत खराब हो सकता है।[citation needed]
टिप्पणियाँ-
संदर्भ
- ↑ Cotton, F. Albert (1990). समूह सिद्धांत के रासायनिक अनुप्रयोग (3rd ed.). New York: Wiley. pp. 102. ISBN 0471510947. OCLC 19975337.
- ↑ Albright, T. A.; Burdett, J. K.; Whangbo, M.-H. (2013). रसायन विज्ञान में कक्षीय सहभागिता. Hoboken, N.J.: Wiley. ISBN 9780471080398.
- ↑ Friedrich Hund and Chemistry, Werner Kutzelnigg, on the occasion of Hund's 100th birthday, Angewandte Chemie International Edition, 35, 573–586, (1996)
- ↑ Robert S. Mulliken's Nobel Lecture, Science, 157, no. 3785, 13-24. Available on-line at: Nobelprize.org
- ↑ Lennard-Jones, John (Sir) (1929). "कुछ डायटोमिक अणुओं की इलेक्ट्रॉनिक संरचना". Transactions of the Faraday Society. 25: 668–686. Bibcode:1929FaTr...25..668L. doi:10.1039/tf9292500668.
- ↑ 6.0 6.1 6.2 6.3 6.4 Catherine E. Housecroft, Alan G. Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
- ↑ Peter Atkins; Julio De Paula. Atkins’ Physical Chemistry. Oxford University Press, 8th ed., 2006.
- ↑ Yves Jean; François Volatron. An Introduction to Molecular Orbitals. Oxford University Press, 1993.
- ↑ Michael Munowitz, Principles of Chemistry, Norton & Company, 2000, p. 229-233.
- ↑ Atkins, Peter; et al. (2006). अकार्बनिक रसायन शास्त्र (4. ed.). New York: W.H. Freeman. p. 208. ISBN 978-0-7167-4878-6.
- ↑ Miessler, G.L.; Tarr, Donald A. (2008). अकार्बनिक रसायन शास्त्र. Pearson Education. ISBN 978-81-317-1885-8.
- ↑ Bondybey, V.E. (1984). "Be2 की इलेक्ट्रॉनिक संरचना और बंधन". Chemical Physics Letters. 109 (5): 436–441. Bibcode:1984CPL...109..436B. doi:10.1016/0009-2614(84)80339-5.
- ↑ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, ISBN 0130-39913-2, p. 41-43.