प्रवाह (गणित): Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Motion of particles in a fluid}} | {{short description|Motion of particles in a fluid}} | ||
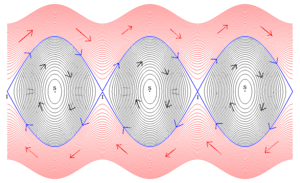
[[File:PenduleEspaceDesPhases.png|thumb| | [[File:PenduleEspaceDesPhases.png|thumb|[[लंगर]] के अंतर समीकरण द्वारा निर्दिष्ट [[चरण स्थान]] में प्रवाह है। क्षैतिज अक्ष पर, पेंडुलम की स्थिति, और ऊर्ध्वाधर पर इसका वेग।]][[गणित]] में, '''प्रवाह''' द्रव में कणों की गति के विचार को औपचारिक रूप देता है। [[अभियांत्रिकी]] और भौतिकी सहित विज्ञान में प्रवाह सर्वव्यापी हैं। साधारण अवकल समीकरणों के अध्ययन के लिए प्रवाह की धारणा आधारभूत है। अनौपचारिक रूप से, प्रवाह को समय के साथ बिंदुओं की निरंतर गति के रूप में देखा जा सकता है। अधिक औपचारिक रूप से, प्रवाह एक [[सेट (गणित)|समुच्चय (गणित)]] पर [[वास्तविक संख्या]]ओं की [[समूह क्रिया (गणित)]] है। | ||
[[सदिश कलन|सदिश]] प्रवाह का विचार, अर्थात, सदिश क्षेत्र द्वारा निर्धारित प्रवाह, अंतर सांस्थिति (टोपोलॉजी), [[रीमैनियन कई गुना|रीमैनियन]] [[ज्यामिति]] और लाई समूहों के क्षेत्रों में होता है। सदिश प्रवाह के विशिष्ट उदाहरणों में जियोडेसिक प्रवाह, हैमिल्टनियन प्रवाह, रिक्की प्रवाह, माध्य वक्रता प्रवाह और एनोसोव प्रवाह | [[सदिश कलन|सदिश]] प्रवाह का विचार, अर्थात, सदिश क्षेत्र द्वारा निर्धारित प्रवाह, अंतर सांस्थिति (टोपोलॉजी), [[रीमैनियन कई गुना|रीमैनियन]] [[ज्यामिति]] और लाई समूहों के क्षेत्रों में होता है। सदिश प्रवाह के विशिष्ट उदाहरणों में जियोडेसिक प्रवाह, हैमिल्टनियन प्रवाह, रिक्की प्रवाह, माध्य वक्रता प्रवाह और एनोसोव प्रवाह सम्मिलित हैं। यादृच्छिक चर और स्टोकेस्टिक प्रक्रियाओं की प्रणालियों के लिए प्रवाह को भी परिभाषित किया जा सकता है, और एर्गोडिक डायनेमिक प्रणाली के अध्ययन में होता है। इनमें से सबसे प्रसिद्ध संभवतया [[बरनौली प्रवाह]] है। | ||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
| Line 13: | Line 13: | ||
& \varphi(\varphi(x,t),s) = \varphi(x,s+t). | & \varphi(\varphi(x,t),s) = \varphi(x,s+t). | ||
\end{align}</math> | \end{align}</math> | ||
यह प्रथागत {{math|''φ<sup>t</sup>''(''x'')}} के बदले में {{math|''φ''(''x'', ''t'')}}, ताकि उपरोक्त समीकरणों को व्यक्त किया जा सके <math>\varphi^0 = \text{Id}</math> ([[पहचान समारोह|तत्समक फलन]]) और <math>\varphi^s \circ \varphi^t = \varphi^{s+t}</math> (समूह नियम) है। फिर, सभी के लिए {{tmath|t \isin \R,}} मानचित्रण {{tmath|\varphi^t: X \to X}} व्युत्क्रम के साथ आक्षेप है {{tmath|\varphi^{-t}: X \to X.}} यह उपरोक्त परिभाषा और वास्तविक | यह प्रथागत {{math|''φ<sup>t</sup>''(''x'')}} के बदले में {{math|''φ''(''x'', ''t'')}}, ताकि उपरोक्त समीकरणों को व्यक्त किया जा सके <math>\varphi^0 = \text{Id}</math> ([[पहचान समारोह|तत्समक फलन]]) और <math>\varphi^s \circ \varphi^t = \varphi^{s+t}</math> (समूह नियम) है। फिर, सभी के लिए {{tmath|t \isin \R,}} मानचित्रण {{tmath|\varphi^t: X \to X}} व्युत्क्रम के साथ आक्षेप है {{tmath|\varphi^{-t}: X \to X.}} यह उपरोक्त परिभाषा और वास्तविक प्राचल से अनुसरण करता है {{mvar|t}} कार्य पुनरावृत्ति के रूप में सामान्यीकृत [[कार्यात्मक शक्ति]] के रूप में लिया जा सकता है। | ||
. | प्रवाह को साधारणतया समुच्चय पर प्रस्तुत [[गणितीय संरचना]]ओं के साथ संगत होने की आवश्यकता होती है {{mvar|X}}. विशेष रूप से, यदि {{mvar|X}} तब एक [[टोपोलॉजिकल स्पेस]] से समविभव है {{mvar|φ}} साधारणतया [[निरंतर कार्य]] करने की आवश्यकता होती है। यदि {{mvar|X}} एक अलग करने योग्य कई गुना से समविभव है, फिर {{mvar|φ}} साधारणतया अलग-अलग फलन की आवश्यकता होती है। इन मामलों में प्रवाह क्रमशः होमोमोर्फिज्म और डिफियोमोर्फिज्म का [[एक-पैरामीटर समूह|एक-प्राचल समूह]] बनाता है। | ||
कुछ स्थितियों में | कुछ स्थितियों में स्थानीय प्रवाहों पर भी विचार किया जा सकता है, जो केवल कुछ उपसमुच्चय में परिभाषित हैं | ||
:<math>\mathrm{dom}(\varphi) = \{ (x,t) \ | \ t\in[a_x,b_x], \ a_x<0<b_x, \ x\in X \} \subset X\times\mathbb R </math> | :<math>\mathrm{dom}(\varphi) = \{ (x,t) \ | \ t\in[a_x,b_x], \ a_x<0<b_x, \ x\in X \} \subset X\times\mathbb R </math> | ||
φ का प्रवाह प्रभावक्षेत्र कहा जाता है। सदिश क्षेत्रों के प्रवाह के मामले में प्रायः ऐसा होता है। | |||
=== वैकल्पिक अंकन === | === वैकल्पिक अंकन === | ||
अभियांत्रिकी, भौतिकी और [[अंतर समीकरण]]ों के अध्ययन सहित कई क्षेत्रों में यह बहुत आम है, एक संकेतन का उपयोग करने के लिए जो प्रवाह को अंतर्निहित बनाता है। इस प्रकार, {{math|''x''(''t'')}} के लिए लिखा गया है {{tmath|\varphi^t(x_0),}} और कोई कह सकता है कि चर {{mvar|x}} समय पर निर्भर करता है {{mvar|t}} और प्रारंभिक स्थिति {{math|1= ''x'' = ''x''<sub>0</sub>}}. उदाहरण नीचे दिए गए हैं। | अभियांत्रिकी, भौतिकी और [[अंतर समीकरण]]ों के अध्ययन सहित कई क्षेत्रों में यह बहुत आम है, एक संकेतन का उपयोग करने के लिए जो प्रवाह को अंतर्निहित बनाता है। इस प्रकार, {{math|''x''(''t'')}} के लिए लिखा गया है {{tmath|\varphi^t(x_0),}} और कोई कह सकता है कि चर {{mvar|x}} समय पर निर्भर करता है {{mvar|t}} और प्रारंभिक स्थिति {{math|1= ''x'' = ''x''<sub>0</sub>}}. उदाहरण नीचे दिए गए हैं। | ||
सदिश क्षेत्र फ्लो कर्व्स के मामले में {{mvar|V}} एक स्मूथ मैनिफोल्ड पर {{mvar|X}}, प्रवाह को प्रायः इस तरह से निरूपित किया जाता है कि इसके जनरेटर को स्पष्ट किया जाता है। उदाहरण के लिए, | |||
:<math>\Phi_V\colon X\times\R\to X; \qquad (x,t)\mapsto\Phi_V^t(x).</math> | :<math>\Phi_V\colon X\times\R\to X; \qquad (x,t)\mapsto\Phi_V^t(x).</math> | ||
== परिक्रमा == | == परिक्रमा == | ||
दिया गया {{mvar|x}} में {{mvar|X}}, समुच्चय <math>\{ \varphi(x,t): t \in \R \}</math> की [[कक्षा (गतिकी)]] कहलाती है {{mvar|x}} अंतर्गत {{mvar|φ}}. अनौपचारिक रूप से, इसे एक कण के प्रक्षेपवक्र के रूप में माना जा सकता है जो प्रारंभ में स्थित था {{mvar|x}}. यदि प्रवाह एक | दिया गया {{mvar|x}} में {{mvar|X}}, समुच्चय <math>\{ \varphi(x,t): t \in \R \}</math> की [[कक्षा (गतिकी)]] कहलाती है {{mvar|x}} अंतर्गत {{mvar|φ}}. अनौपचारिक रूप से, इसे एक कण के प्रक्षेपवक्र के रूप में माना जा सकता है जो प्रारंभ में स्थित था {{mvar|x}}. यदि प्रवाह एक सदिश क्षेत्र द्वारा उत्पन्न होता है, तो इसकी कक्षाएँ इसके [[अभिन्न वक्र]]ों की छवियां होती हैं। | ||
== उदाहरण == | == उदाहरण == | ||
=== बीजगणितीय समीकरण === | === बीजगणितीय समीकरण === | ||
{{tmath|f: \R \to X}} एक समय-निर्भर प्रक्षेपवक्र हो जो एक विशेषण कार्य है, अर्थात, गैर-आवधिक कार्य है। तब एक प्रवाह द्वारा परिभाषित किया जा सकता है | |||
:<math>\varphi(x,t) = f(t + f^{-1}(x)).</math> | :<math>\varphi(x,t) = f(t + f^{-1}(x)).</math> | ||
=== साधारण अंतर समीकरणों की स्वायत्त प्रणाली === | === साधारण अंतर समीकरणों की स्वायत्त प्रणाली === | ||
होने देना {{tmath|\boldsymbol F: \R^n \to \R^n}} एक (समय-स्वतंत्र) | होने देना {{tmath|\boldsymbol F: \R^n \to \R^n}} एक (समय-स्वतंत्र) सदिश क्षेत्र बनें | ||
और {{tmath|\boldsymbol x: \R \to \R^n}} प्रारंभिक मूल्य समस्या का समाधान | और {{tmath|\boldsymbol x: \R \to \R^n}} प्रारंभिक मूल्य समस्या का समाधान | ||
:<math>\dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t)), \qquad \boldsymbol{x}(0)=\boldsymbol{x}_0.</math> | :<math>\dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t)), \qquad \boldsymbol{x}(0)=\boldsymbol{x}_0.</math> | ||
तब <math>\varphi(\boldsymbol x_0,t) = \boldsymbol x(t)</math> | तब <math>\varphi(\boldsymbol x_0,t) = \boldsymbol x(t)</math> सदिश क्षेत्र का प्रवाह है {{mvar|F}}. यह एक अच्छी तरह से परिभाषित स्थानीय प्रवाह है परंतु सदिश क्षेत्र | ||
{{tmath|\boldsymbol F: \R^n \to \R^n}} लिपशिट्ज-निरंतर है। तब {{tmath|\varphi: \R^n \times \R \to \R^n}} लिपशिट्ज-निरंतर भी है जहां भी परिभाषित किया गया है। सामान्य तौर पर यह दिखाना कठिन हो सकता है कि प्रवाह {{mvar|φ}} विश्व स्तर पर परिभाषित है, लेकिन एक साधारण मानदंड यह है कि सदिश क्षेत्र {{mvar|'''F'''}} संक्षिप्त रूप से समर्थित है। | |||
=== समय पर निर्भर साधारण अंतर समीकरण === | === समय पर निर्भर साधारण अंतर समीकरण === | ||
समय-निर्भर | समय-निर्भर सदिश फ़ील्ड के मामले में {{tmath|\boldsymbol F: \R^n \times \R \to \R^n}}, एक दर्शाता है <math>\varphi^{t,t_0}(\boldsymbol x_0) = \boldsymbol{x}(t+t_0),</math> जहाँ {{tmath|\boldsymbol x: \R \to \R^n}} का समाधान है | ||
:<math>\dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t),t), \qquad \boldsymbol{x}(t_0)=\boldsymbol{x}_0.</math> | :<math>\dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t),t), \qquad \boldsymbol{x}(t_0)=\boldsymbol{x}_0.</math> | ||
तब {{tmath|\varphi^{t,t_0}(\boldsymbol x_0)}} का समय-निर्भर प्रवाह है {{mvar|F}}. उपरोक्त परिभाषा के अनुसार यह प्रवाह नहीं है, लेकिन इसके तर्कों को पुनर्व्यवस्थित करके इसे आसानी से एक के रूप में देखा जा सकता है। अर्थात्, मानचित्रण | तब {{tmath|\varphi^{t,t_0}(\boldsymbol x_0)}} का समय-निर्भर प्रवाह है {{mvar|F}}. उपरोक्त परिभाषा के अनुसार यह प्रवाह नहीं है, लेकिन इसके तर्कों को पुनर्व्यवस्थित करके इसे आसानी से एक के रूप में देखा जा सकता है। अर्थात्, मानचित्रण | ||
:<math> \varphi\colon(\R^n\times\R)\times\R \to \R^n\times\R; \qquad | :<math> \varphi\colon(\R^n\times\R)\times\R \to \R^n\times\R; \qquad | ||
\varphi((\boldsymbol{x}_0, t_0), t)=(\varphi^{t,t_0}(\boldsymbol{x}_0),t+t_0)</math> | \varphi((\boldsymbol{x}_0, t_0), t)=(\varphi^{t,t_0}(\boldsymbol{x}_0),t+t_0)</math> | ||
वास्तव में अंतिम चर के लिए समूह | वास्तव में अंतिम चर के लिए समूह नियम को संतुष्ट करता है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\varphi(\varphi((\boldsymbol{x}_0,t_0),t),s) | \varphi(\varphi((\boldsymbol{x}_0,t_0),t),s) | ||
| Line 65: | Line 65: | ||
तब {{math|'''''y'''''(''t'')}} समय-स्वतंत्र प्रारंभिक मूल्य समस्या का समाधान है | तब {{math|'''''y'''''(''t'')}} समय-स्वतंत्र प्रारंभिक मूल्य समस्या का समाधान है | ||
:<math> \dot{\boldsymbol{y}}(s) = \boldsymbol{G}(\boldsymbol{y}(s)), \qquad \boldsymbol{y}(0)=(\boldsymbol{x}_0,t_0)</math> | :<math> \dot{\boldsymbol{y}}(s) = \boldsymbol{G}(\boldsymbol{y}(s)), \qquad \boldsymbol{y}(0)=(\boldsymbol{x}_0,t_0)</math> | ||
यदि और केवल यदि {{math|'''''x'''''(''t'')}} मूल समय-निर्भर प्रारंभिक मूल्य समस्या का समाधान है। इसके अतिरिक्त, फिर मैपिंग {{mvar|φ}} पूर्णतया समय-स्वतंत्र सदिश क्षेत्र का प्रवाह है {{mvar|'''G'''}}. | |||
=== मैनिफोल्ड्स पर सदिश क्षेत्रों का प्रवाह === | |||
टाइम-इंडिपेंडेंट और टाइम-डिपेंडेंट सदिश क्षेत्र के प्रवाह को स्मूथ मैनिफोल्ड्स पर परिभाषित किया गया है, ठीक उसी तरह जैसे वे यूक्लिडियन स्पेस पर परिभाषित हैं। {{tmath|\R^n}} और उनका स्थानीय व्यवहार समान है। हालांकि, एक स्मूथ मैनिफोल्ड की वैश्विक टोपोलॉजिकल संरचना दृढ़ता से प्रकट होती है कि यह किस प्रकार के वैश्विक सदिश क्षेत्रों का समर्थन कर सकता है, और स्मूथ मैनिफोल्ड पर सदिश क्षेत्रों का प्रवाह वास्तव में अंतर टोपोलॉजी में एक महत्वपूर्ण उपकरण है। डायनेमिक प्रणाली में अधिकांश अध्ययन स्मूथ मैनिफोल्ड्स पर किए जाते हैं, जिन्हें अनुप्रयोगों में प्राचल स्पेस के रूप में माना जाता है। | |||
औपचारिक रूप से: <math>\mathcal{M}</math> एक अलग करने योग्य कई गुना हो। होने देना <math>\mathrm{T}_p \mathcal{M}</math> एक बिंदु के [[स्पर्शरेखा स्थान]] को निरूपित करें <math>p \in \mathcal{M}.</math> होने देना <math>\mathrm{T}\mathcal{M}</math> पूर्ण स्पर्शरेखा कई गुना हो; वह है, <math>\mathrm{T}\mathcal{M} = \cup_{p\in\mathcal{M}}\mathrm{T}_p\mathcal{M}.</math> होने देना | |||
<math display="block"> | |||
f : \R\times\mathcal{M} \to \mathrm{T}\mathcal{M} | f : \R\times\mathcal{M} \to \mathrm{T}\mathcal{M} | ||
</ | </math> | ||
< | समय-निर्भर सदिश क्षेत्र है <math>\mathcal{M}</math>; वह है, {{mvar|f}} एक स्मूथ प्रतिचित्रण है जैसे कि प्रत्येक के लिए <math>t\in\R</math> और <math>p\in\mathcal{M}</math>, किसी के पास <math>f(t,p)\in \mathrm{T}_p\mathcal{M};</math> वह है, प्रतिचित्रण <math>x\mapsto f(t,x)</math> प्रत्येक बिंदु को अपने स्वयं के स्पर्शरेखा स्थान के एक तत्व पर मैप करता है। उपयुक्त अंतराल के लिए <math>I\subseteq\R</math> युक्त 0, का प्रवाह {{mvar|f}} एक कार्य है <math>\phi: I\times\mathcal{M} \to \mathcal{M}</math> जो संतुष्ट करता है | ||
\ | |||
<math display="block"> | |||
\begin{align} | |||
\phi(0, x_0) &= x_0&\forall x_0\in\mathcal{M} \\ | \phi(0, x_0) &= x_0&\forall x_0\in\mathcal{M} \\ | ||
\frac{\mathrm{d}}{\mathrm{d}t}\Big|_{t=t_0}\phi(t,x_0) &= f(t_0,\phi(t_0,x_0))&\forall x_0\in\mathcal{M},t_0\in I | \frac{\mathrm{d}}{\mathrm{d}t}\Big|_{t=t_0}\phi(t,x_0) &= f(t_0,\phi(t_0,x_0))&\forall x_0\in\mathcal{M},t_0\in I | ||
\ | \end{align} | ||
</ | </math> | ||
=== उष्मा समीकरण के हल === | === उष्मा समीकरण के हल === | ||
{{math|Ω}} का एक उपप्रभावक्षेत्र (बाध्य या नहीं) हो {{tmath|\R^n}} (साथ {{mvar|n}} पूर्णांक)। द्वारा निरूपित करें {{math|Γ}} इसकी सीमा (स्मूथ मान ली गई)। निम्नलिखित [[ताप समीकरण]] पर विचार करें {{math|Ω × (0, ''T'')}}, के लिए {{math|''T'' > 0}}, | |||
निम्नलिखित [[ताप समीकरण]] पर विचार करें {{math|Ω × (0, ''T'')}}, के लिए {{math|''T'' > 0}}, | |||
:<math> | :<math> | ||
\begin{array}{rcll} | \begin{array}{rcll} | ||
| Line 94: | Line 96: | ||
निम्नलिखित प्रारंभिक सीमा स्थिति के साथ {{math| ''u''(0) {{=}} ''u''<sup>0</sup>}} में {{math|Ω}} . | निम्नलिखित प्रारंभिक सीमा स्थिति के साथ {{math| ''u''(0) {{=}} ''u''<sup>0</sup>}} में {{math|Ω}} . | ||
समीकरण {{math|1=''u'' = 0}} पर {{math|Γ × (0, ''T'')}} सजातीय डिरिचलेट सीमा स्थिति से मेल खाती है। इस समस्या के लिए गणितीय समुच्चयिंग सेमीग्रुप दृष्टिकोण हो सकती है। इस टूल का उपयोग करने के लिए, हम अनबाउंड ऑपरेटर का परिचय देते हैं {{math|Δ<sub>''D''</sub>}} पर परिभाषित <math>L^2(\Omega)</math> इसके | समीकरण {{math|1=''u'' = 0}} पर {{math|Γ × (0, ''T'')}} सजातीय डिरिचलेट सीमा स्थिति से मेल खाती है। इस समस्या के लिए गणितीय समुच्चयिंग सेमीग्रुप दृष्टिकोण हो सकती है। इस टूल का उपयोग करने के लिए, हम अनबाउंड ऑपरेटर का परिचय देते हैं {{math|Δ<sub>''D''</sub>}} पर परिभाषित <math>L^2(\Omega)</math> इसके प्रभावक्षेत्र द्वारा | ||
:<math> D(\Delta_D) = H^2(\Omega) \cap H_0^1(\Omega) </math> (क्लासिकल | :<math> D(\Delta_D) = H^2(\Omega) \cap H_0^1(\Omega) </math> (क्लासिकल सोबोलेव स्पेस पूर्णांक के साथ देखें <math> H^k(\Omega) = W^{k,2}(\Omega)</math> और | ||
:<math>H_0^1(\Omega) = {\overline{C_0^\infty (\Omega)} } ^{H^1(\Omega)}</math> में कॉम्पैक्ट सपोर्ट के साथ असीम रूप से अलग-अलग कार्यों का बंद होना है {{mvar|Ω}} के लिए <math> H^1(\Omega)-</math>मानदंड)। | :<math>H_0^1(\Omega) = {\overline{C_0^\infty (\Omega)} } ^{H^1(\Omega)}</math> में कॉम्पैक्ट सपोर्ट के साथ असीम रूप से अलग-अलग कार्यों का बंद होना है {{mvar|Ω}} के लिए <math> H^1(\Omega)-</math>मानदंड)। | ||
| Line 105: | Line 107: | ||
:<math> | :<math> | ||
\varphi(u^0,t) = \mbox{e}^{t\Delta_D}u^0 ,</math> | \varphi(u^0,t) = \mbox{e}^{t\Delta_D}u^0 ,</math> | ||
जहाँ {{math|exp(''t''Δ<sub>''D''</sub>)}} द्वारा उत्पन्न (विश्लेषणात्मक) अर्धसमूह है {{math|Δ<sub>''D''</sub>}}. | |||
=== तरंग समीकरण के समाधान === | === तरंग समीकरण के समाधान === | ||
{{mvar|Ω}} का एक उपप्रभावक्षेत्र (बाध्य या नहीं) हो {{tmath|\R^n}} (साथ {{mvar|n}} पूर्णांक)। हम द्वारा निरूपित करते हैं {{mvar|Γ}} इसकी सीमा (स्मूथ मान ली गई)। निम्नलिखित [[तरंग समीकरण]] पर विचार करें <math> \Omega \times (0,T) </math> (के लिए {{math|''T'' > 0}}), | |||
निम्नलिखित [[तरंग समीकरण]] पर विचार करें <math> \Omega \times (0,T) </math> (के लिए {{math|''T'' > 0}}), | |||
:<math> | :<math> | ||
\begin{array}{rcll} | \begin{array}{rcll} | ||
| Line 116: | Line 117: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
निम्नलिखित प्रारंभिक स्थिति के साथ {{math| ''u''(0) {{=}} ''u''<sup>1,0</sup>}} में {{math|Ω}} और <math> u_t(0) = u^{2,0} \mbox{ in } \Omega.</math> | निम्नलिखित प्रारंभिक स्थिति के साथ {{math| ''u''(0) {{=}} ''u''<sup>1,0</sup>}} में {{math|Ω}} और <math> u_t(0) = u^{2,0} \mbox{ in } \Omega.</math> उपरोक्त हीट समीकरण के मामले में समान सेमीग्रुप दृष्टिकोण का उपयोग करना हैंl हम निम्नलिखित अनबाउंड ऑपरेटर को निवेदित करके तरंग समीकरण को समय आंशिक अंतर समीकरण में पहले क्रम के रूप में लिखते हैं, | ||
उपरोक्त हीट समीकरण के मामले में समान सेमीग्रुप दृष्टिकोण का उपयोग | |||
:<math> | :<math> | ||
\mathcal{A} = \left(\begin{array}{cc} 0 & Id \\ \Delta_D & 0 \end{array}\right) | \mathcal{A} = \left(\begin{array}{cc} 0 & Id \\ \Delta_D & 0 \end{array}\right) | ||
</math> | </math> | ||
प्रभावक्षेत्र के साथ <math> D(\mathcal{A}) = H^2(\Omega) \cap H_0^1(\Omega) \times H_0^1(\Omega) </math> पर <math> H = H^1_0(\Omega) \times L^2(\Omega)</math> (परिचालक {{math|Δ<sub>''D''</sub>}} पिछले उदाहरण में परिभाषित किया गया है)। | |||
हम कॉलम वैक्टर का परिचय देते हैं | हम कॉलम वैक्टर का परिचय देते हैं | ||
:<math> U = \left(\begin{array}{c} u^1 \\ u^2 \end{array}\right)</math> ( | :<math> U = \left(\begin{array}{c} u^1 \\ u^2 \end{array}\right)</math> (जहाँ <math> u^1 = u</math> और <math> u^2 = u_t</math>) और | ||
:<math> U^0 = \left(\begin{array}{c} u^{1,0} \\ u^{2,0} \end{array} \right).</math> | :<math> U^0 = \left(\begin{array}{c} u^{1,0} \\ u^{2,0} \end{array} \right).</math> | ||
इन धारणाओं से तरंग समीकरण बन जाता है <math> U'(t) = \mathcal{A}U(t) </math> और {{math|1=''U''(0) = ''U''{{sup|0}}}}. | इन धारणाओं से तरंग समीकरण बन जाता है <math> U'(t) = \mathcal{A}U(t) </math> और {{math|1=''U''(0) = ''U''{{sup|0}}}}. | ||
| Line 130: | Line 130: | ||
इस प्रकार, इस समीकरण के अनुरूप प्रवाह है | इस प्रकार, इस समीकरण के अनुरूप प्रवाह है | ||
:<math>\varphi(U^0,t) = \mbox{e}^{t\mathcal{A}}U^0 </math> | :<math>\varphi(U^0,t) = \mbox{e}^{t\mathcal{A}}U^0 </math> | ||
जहाँ <math>\mbox{e}^{t\mathcal{A}}</math> द्वारा उत्पन्न (एकात्मक) अर्धसमूह है <math> \mathcal{A}.</math> | |||
=== बरनौली प्रवाह === | === बरनौली प्रवाह === | ||
एर्गोडिक डायनेमिक | एर्गोडिक डायनेमिक प्रणाली, यानी यादृच्छिकता प्रदर्शित करने वाली प्रणालियाँ, प्रवाह को भी प्रदर्शित करती हैं। इनमें से सबसे प्रसिद्ध संभवतया बरनौली प्रवाह है। [[ऑर्नस्टीन समरूपता प्रमेय]] कहता है कि, किसी दिए गए [[कोलमोगोरोव एन्ट्रापी]] के लिए {{mvar|H}}, एक प्रवाह उपस्थित है {{math|''φ''(''x'', ''t'')}}, बर्नौली प्रवाह कहा जाता है, जैसे समय पर प्रवाह {{math|1=''t'' = 1}}, अर्थात {{math| ''φ''(''x'', 1)}}, [[बरनौली पारी|बरनौली प्रवाह]] है। | ||
इसके | इसके अतिरिक्त, यह प्रवाह अद्वितीय है, समय के निरंतर पुनर्विक्रय तक है। यदि {{math| ''ψ''(''x'', ''t'')}}, उसी एंट्रॉपी के साथ एक और प्रवाह है, फिर {{math|''ψ''(''x'', ''t'') {{=}} ''φ''(''x'', ''t'')}}, कुछ स्थिर के लिए {{mvar|c}}. यहाँ विशिष्टता और समरूपता की धारणा गतिशील प्रणालियों के समरूपतावाद की है। सिनाई के बिलियर्ड्स और एनोसोव प्रवाह सहित कई गतिशील प्रणालियां बर्नौली शिफ्टों के लिए आइसोमॉर्फिक हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 151: | Line 150: | ||
* {{PlanetMath attribution|id=3673|title=Flow}} | * {{PlanetMath attribution|id=3673|title=Flow}} | ||
{{DEFAULTSORT:Flow (Mathematics)}} | |||
{{DEFAULTSORT:Flow (Mathematics)}} | |||
[[Category: Machine Translated Page]] | [[Category:Created On 03/02/2023|Flow (Mathematics)]] | ||
[[Category: | [[Category:Lua-based templates|Flow (Mathematics)]] | ||
[[Category:Machine Translated Page|Flow (Mathematics)]] | |||
[[Category:Pages with script errors|Flow (Mathematics)]] | |||
[[Category:Short description with empty Wikidata description|Flow (Mathematics)]] | |||
[[Category:Templates Vigyan Ready|Flow (Mathematics)]] | |||
[[Category:Templates that add a tracking category|Flow (Mathematics)]] | |||
[[Category:Templates that generate short descriptions|Flow (Mathematics)]] | |||
[[Category:Templates using TemplateData|Flow (Mathematics)]] | |||
[[Category:Wikipedia articles incorporating text from PlanetMath|प्रवाह (गणित)]] | |||
[[Category:गतिशील प्रणाली|Flow (Mathematics)]] | |||
[[Category:समूह क्रियाएं (गणित)|Flow (Mathematics)]] | |||
Latest revision as of 20:05, 8 February 2023
गणित में, प्रवाह द्रव में कणों की गति के विचार को औपचारिक रूप देता है। अभियांत्रिकी और भौतिकी सहित विज्ञान में प्रवाह सर्वव्यापी हैं। साधारण अवकल समीकरणों के अध्ययन के लिए प्रवाह की धारणा आधारभूत है। अनौपचारिक रूप से, प्रवाह को समय के साथ बिंदुओं की निरंतर गति के रूप में देखा जा सकता है। अधिक औपचारिक रूप से, प्रवाह एक समुच्चय (गणित) पर वास्तविक संख्याओं की समूह क्रिया (गणित) है।
सदिश प्रवाह का विचार, अर्थात, सदिश क्षेत्र द्वारा निर्धारित प्रवाह, अंतर सांस्थिति (टोपोलॉजी), रीमैनियन ज्यामिति और लाई समूहों के क्षेत्रों में होता है। सदिश प्रवाह के विशिष्ट उदाहरणों में जियोडेसिक प्रवाह, हैमिल्टनियन प्रवाह, रिक्की प्रवाह, माध्य वक्रता प्रवाह और एनोसोव प्रवाह सम्मिलित हैं। यादृच्छिक चर और स्टोकेस्टिक प्रक्रियाओं की प्रणालियों के लिए प्रवाह को भी परिभाषित किया जा सकता है, और एर्गोडिक डायनेमिक प्रणाली के अध्ययन में होता है। इनमें से सबसे प्रसिद्ध संभवतया बरनौली प्रवाह है।
औपचारिक परिभाषा
समुच्चय X पर प्रवाह X वास्तविक संख्याओं के योगात्मक समूह की एक समूह क्रिया हैI अधिक स्पष्ट रूप से, प्रवाह एक प्रतिचित्रण (मैपिंग_गणित) है
ऐसा कि, सभी के लिए x ∈ X और सभी वास्तविक संख्याएँ s और t,
यह प्रथागत φt(x) के बदले में φ(x, t), ताकि उपरोक्त समीकरणों को व्यक्त किया जा सके (तत्समक फलन) और (समूह नियम) है। फिर, सभी के लिए मानचित्रण व्युत्क्रम के साथ आक्षेप है यह उपरोक्त परिभाषा और वास्तविक प्राचल से अनुसरण करता है t कार्य पुनरावृत्ति के रूप में सामान्यीकृत कार्यात्मक शक्ति के रूप में लिया जा सकता है।
प्रवाह को साधारणतया समुच्चय पर प्रस्तुत गणितीय संरचनाओं के साथ संगत होने की आवश्यकता होती है X. विशेष रूप से, यदि X तब एक टोपोलॉजिकल स्पेस से समविभव है φ साधारणतया निरंतर कार्य करने की आवश्यकता होती है। यदि X एक अलग करने योग्य कई गुना से समविभव है, फिर φ साधारणतया अलग-अलग फलन की आवश्यकता होती है। इन मामलों में प्रवाह क्रमशः होमोमोर्फिज्म और डिफियोमोर्फिज्म का एक-प्राचल समूह बनाता है।
कुछ स्थितियों में स्थानीय प्रवाहों पर भी विचार किया जा सकता है, जो केवल कुछ उपसमुच्चय में परिभाषित हैं
φ का प्रवाह प्रभावक्षेत्र कहा जाता है। सदिश क्षेत्रों के प्रवाह के मामले में प्रायः ऐसा होता है।
वैकल्पिक अंकन
अभियांत्रिकी, भौतिकी और अंतर समीकरणों के अध्ययन सहित कई क्षेत्रों में यह बहुत आम है, एक संकेतन का उपयोग करने के लिए जो प्रवाह को अंतर्निहित बनाता है। इस प्रकार, x(t) के लिए लिखा गया है और कोई कह सकता है कि चर x समय पर निर्भर करता है t और प्रारंभिक स्थिति x = x0. उदाहरण नीचे दिए गए हैं।
सदिश क्षेत्र फ्लो कर्व्स के मामले में V एक स्मूथ मैनिफोल्ड पर X, प्रवाह को प्रायः इस तरह से निरूपित किया जाता है कि इसके जनरेटर को स्पष्ट किया जाता है। उदाहरण के लिए,
परिक्रमा
दिया गया x में X, समुच्चय की कक्षा (गतिकी) कहलाती है x अंतर्गत φ. अनौपचारिक रूप से, इसे एक कण के प्रक्षेपवक्र के रूप में माना जा सकता है जो प्रारंभ में स्थित था x. यदि प्रवाह एक सदिश क्षेत्र द्वारा उत्पन्न होता है, तो इसकी कक्षाएँ इसके अभिन्न वक्रों की छवियां होती हैं।
उदाहरण
बीजगणितीय समीकरण
एक समय-निर्भर प्रक्षेपवक्र हो जो एक विशेषण कार्य है, अर्थात, गैर-आवधिक कार्य है। तब एक प्रवाह द्वारा परिभाषित किया जा सकता है
साधारण अंतर समीकरणों की स्वायत्त प्रणाली
होने देना एक (समय-स्वतंत्र) सदिश क्षेत्र बनें और प्रारंभिक मूल्य समस्या का समाधान
तब सदिश क्षेत्र का प्रवाह है F. यह एक अच्छी तरह से परिभाषित स्थानीय प्रवाह है परंतु सदिश क्षेत्र
लिपशिट्ज-निरंतर है। तब लिपशिट्ज-निरंतर भी है जहां भी परिभाषित किया गया है। सामान्य तौर पर यह दिखाना कठिन हो सकता है कि प्रवाह φ विश्व स्तर पर परिभाषित है, लेकिन एक साधारण मानदंड यह है कि सदिश क्षेत्र F संक्षिप्त रूप से समर्थित है।
समय पर निर्भर साधारण अंतर समीकरण
समय-निर्भर सदिश फ़ील्ड के मामले में , एक दर्शाता है जहाँ का समाधान है
तब का समय-निर्भर प्रवाह है F. उपरोक्त परिभाषा के अनुसार यह प्रवाह नहीं है, लेकिन इसके तर्कों को पुनर्व्यवस्थित करके इसे आसानी से एक के रूप में देखा जा सकता है। अर्थात्, मानचित्रण
वास्तव में अंतिम चर के लिए समूह नियम को संतुष्ट करता है:
निम्नलिखित ट्रिक द्वारा समय-स्वतंत्र लोगों के विशेष मामलों के रूप में सदिश क्षेत्रों के समय-निर्भर प्रवाह को देख सकते हैं। परिभाषित करना
तब y(t) समय-स्वतंत्र प्रारंभिक मूल्य समस्या का समाधान है
यदि और केवल यदि x(t) मूल समय-निर्भर प्रारंभिक मूल्य समस्या का समाधान है। इसके अतिरिक्त, फिर मैपिंग φ पूर्णतया समय-स्वतंत्र सदिश क्षेत्र का प्रवाह है G.
मैनिफोल्ड्स पर सदिश क्षेत्रों का प्रवाह
टाइम-इंडिपेंडेंट और टाइम-डिपेंडेंट सदिश क्षेत्र के प्रवाह को स्मूथ मैनिफोल्ड्स पर परिभाषित किया गया है, ठीक उसी तरह जैसे वे यूक्लिडियन स्पेस पर परिभाषित हैं। और उनका स्थानीय व्यवहार समान है। हालांकि, एक स्मूथ मैनिफोल्ड की वैश्विक टोपोलॉजिकल संरचना दृढ़ता से प्रकट होती है कि यह किस प्रकार के वैश्विक सदिश क्षेत्रों का समर्थन कर सकता है, और स्मूथ मैनिफोल्ड पर सदिश क्षेत्रों का प्रवाह वास्तव में अंतर टोपोलॉजी में एक महत्वपूर्ण उपकरण है। डायनेमिक प्रणाली में अधिकांश अध्ययन स्मूथ मैनिफोल्ड्स पर किए जाते हैं, जिन्हें अनुप्रयोगों में प्राचल स्पेस के रूप में माना जाता है।
औपचारिक रूप से: एक अलग करने योग्य कई गुना हो। होने देना एक बिंदु के स्पर्शरेखा स्थान को निरूपित करें होने देना पूर्ण स्पर्शरेखा कई गुना हो; वह है, होने देना
समय-निर्भर सदिश क्षेत्र है ; वह है, f एक स्मूथ प्रतिचित्रण है जैसे कि प्रत्येक के लिए और , किसी के पास वह है, प्रतिचित्रण प्रत्येक बिंदु को अपने स्वयं के स्पर्शरेखा स्थान के एक तत्व पर मैप करता है। उपयुक्त अंतराल के लिए युक्त 0, का प्रवाह f एक कार्य है जो संतुष्ट करता है
उष्मा समीकरण के हल
Ω का एक उपप्रभावक्षेत्र (बाध्य या नहीं) हो (साथ n पूर्णांक)। द्वारा निरूपित करें Γ इसकी सीमा (स्मूथ मान ली गई)। निम्नलिखित ताप समीकरण पर विचार करें Ω × (0, T), के लिए T > 0,
निम्नलिखित प्रारंभिक सीमा स्थिति के साथ u(0) = u0 में Ω .
समीकरण u = 0 पर Γ × (0, T) सजातीय डिरिचलेट सीमा स्थिति से मेल खाती है। इस समस्या के लिए गणितीय समुच्चयिंग सेमीग्रुप दृष्टिकोण हो सकती है। इस टूल का उपयोग करने के लिए, हम अनबाउंड ऑपरेटर का परिचय देते हैं ΔD पर परिभाषित इसके प्रभावक्षेत्र द्वारा
- (क्लासिकल सोबोलेव स्पेस पूर्णांक के साथ देखें और
- में कॉम्पैक्ट सपोर्ट के साथ असीम रूप से अलग-अलग कार्यों का बंद होना है Ω के लिए मानदंड)।
किसी के लिए , अपने पास
इस संकारक के साथ ऊष्मा समीकरण बन जाता है और u(0) = u0. इस प्रकार, इस समीकरण से संबंधित प्रवाह है (ऊपर नोटेशन देखें)
जहाँ exp(tΔD) द्वारा उत्पन्न (विश्लेषणात्मक) अर्धसमूह है ΔD.
तरंग समीकरण के समाधान
Ω का एक उपप्रभावक्षेत्र (बाध्य या नहीं) हो (साथ n पूर्णांक)। हम द्वारा निरूपित करते हैं Γ इसकी सीमा (स्मूथ मान ली गई)। निम्नलिखित तरंग समीकरण पर विचार करें (के लिए T > 0),
निम्नलिखित प्रारंभिक स्थिति के साथ u(0) = u1,0 में Ω और उपरोक्त हीट समीकरण के मामले में समान सेमीग्रुप दृष्टिकोण का उपयोग करना हैंl हम निम्नलिखित अनबाउंड ऑपरेटर को निवेदित करके तरंग समीकरण को समय आंशिक अंतर समीकरण में पहले क्रम के रूप में लिखते हैं,
प्रभावक्षेत्र के साथ पर (परिचालक ΔD पिछले उदाहरण में परिभाषित किया गया है)।
हम कॉलम वैक्टर का परिचय देते हैं
- (जहाँ और ) और
इन धारणाओं से तरंग समीकरण बन जाता है और U(0) = U0.
इस प्रकार, इस समीकरण के अनुरूप प्रवाह है
जहाँ द्वारा उत्पन्न (एकात्मक) अर्धसमूह है
बरनौली प्रवाह
एर्गोडिक डायनेमिक प्रणाली, यानी यादृच्छिकता प्रदर्शित करने वाली प्रणालियाँ, प्रवाह को भी प्रदर्शित करती हैं। इनमें से सबसे प्रसिद्ध संभवतया बरनौली प्रवाह है। ऑर्नस्टीन समरूपता प्रमेय कहता है कि, किसी दिए गए कोलमोगोरोव एन्ट्रापी के लिए H, एक प्रवाह उपस्थित है φ(x, t), बर्नौली प्रवाह कहा जाता है, जैसे समय पर प्रवाह t = 1, अर्थात φ(x, 1), बरनौली प्रवाह है।
इसके अतिरिक्त, यह प्रवाह अद्वितीय है, समय के निरंतर पुनर्विक्रय तक है। यदि ψ(x, t), उसी एंट्रॉपी के साथ एक और प्रवाह है, फिर ψ(x, t) = φ(x, t), कुछ स्थिर के लिए c. यहाँ विशिष्टता और समरूपता की धारणा गतिशील प्रणालियों के समरूपतावाद की है। सिनाई के बिलियर्ड्स और एनोसोव प्रवाह सहित कई गतिशील प्रणालियां बर्नौली शिफ्टों के लिए आइसोमॉर्फिक हैं।
यह भी देखें
- हाबिल समीकरण
- पुनरावृत्त समारोह
- श्रोडर का समीकरण
- विश्लेषणात्मक कार्यों की अनंत रचनाएँ
संदर्भ
- D.V. Anosov (2001) [1994], "Continuous flow", Encyclopedia of Mathematics, EMS Press
- D.V. Anosov (2001) [1994], "Measureable flow", Encyclopedia of Mathematics, EMS Press
- D.V. Anosov (2001) [1994], "Special flow", Encyclopedia of Mathematics, EMS Press
- This article incorporates material from Flow on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.