आधार (ज्यामिति): Difference between revisions
m (added Category:Vigyan Ready using HotCat) |
No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 14: | Line 14: | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
[[Category:Created On 28/02/2023]] | [[Category:Created On 28/02/2023]] | ||
[[Category:Vigyan Ready]] | [[Category:Lua-based templates]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:आयतन]] | |||
[[Category:क्षेत्र]] | |||
[[Category:त्रिभुज के भाग]] | |||
Latest revision as of 13:09, 24 March 2023
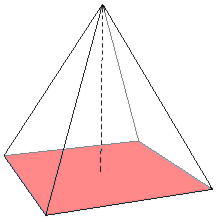
ज्यामिति में, आधार बहुभुज का किनारा (ज्यामिति) या बहुफलक मुख्य रूप से फेस (ज्यामिति) या फलक ज्यामिति होता है, विशेष रूप से इस दिशा में यह लंबवतः उन्मुख होता है जिसमें ऊंचाई को गणना या जिसे "आंकड़ा" माना जाता है इसके द्वारा इसे मापा जाता है ।[1] यह शब्द सामान्यतः त्रिकोण, समांतर चतुर्भुज, ट्रेपेज़ोइड्स, सिलेंडर (ज्यामिति), शंकु (ज्यामिति), पिरामिड (ज्यामिति), समानांतर चतुर्भुज और फलक पर लागू होता है।
क्षेत्र और आयतन गणना में भूमिका
आंकड़ों के क्षेत्रों और मात्राओं की गणना करने के लिए सामान्यतः आधारों (ऊंचाइयों के साथ) का उपयोग किया जाता है। इन प्रक्रियाओं के बारे में बोलते हुए, किसी आकृति के आधार के माप (लंबाई या क्षेत्र) को अधिकांशतः इसका "आधार" कहा जाता है।
इस प्रयोग से समांतर चतुर्भुज का क्षेत्रफल या प्रिज्म (ज्यामिति) या बेलन के आयतन की गणना इसके "आधार" को इसकी ऊंचाई से गुणा करके की जा सकती है, इसी प्रकार त्रिभुजों का क्षेत्रफल और शंकुओं और पिरामिडों का आयतन उनके आधारों और ऊँचाइयों के गुणनफल के अंश हैं। कुछ आकृतियों के दो समानांतर आधार होते हैं (जैसे कि समलम्बाकार और फलक), जिनमें से दोनों का उपयोग आंकड़ों की सीमा की गणना करने के लिए किया जाता है।[2]
त्रिकोणमिति में विस्तारित आधार
त्रिभुज का विस्तारित आधार (विस्तारित भुजा का विशेष स्थिति) वह रेखा (ज्यामिति) है जिसमें आधार होता है। विस्तारित आधार को अधिक त्रिकोण के संदर्भ में महत्वपूर्ण माना जाता हैं: त्रिकोण के शीर्ष (ज्यामिति) से ऊंचाई (त्रिकोण) पर त्रिकोण के बाहर रखा जाता हैं और विस्तारित रूप से विपरीत आधार (किन्तु उचित आधार नहीं) के लंबवत इसे प्रतिच्छेदित किया जाता हैं।
यह भी देखें
संदर्भ
- ↑ Palmer, C.I.; Taylor, D.P. (1918). समतल ज्यामिति. Scott, Foresman & Co. pp. 38, 315, 353.
- ↑ Jacobs, Harold R. (2003). Geometry: Seeing, Doing, Understanding (Third ed.). New York City: W. H. Freeman and Company. p. 281. ISBN 978-0-7167-4361-3.