सर्किट टोपोलॉजी: Difference between revisions
(Created page with "Image:Schematic description of circuit topology.jpg |right|400px|दो बाइनरी संपर्कों के साथ एक श्रृंखला मे...") |
No edit summary |
||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[Image:Schematic description of circuit topology.jpg |right|400px|दो बाइनरी संपर्कों के साथ एक श्रृंखला में सर्किट टोपोलॉजी संबंध।]] | [[Image:Schematic description of circuit topology.jpg |right|400px|दो बाइनरी संपर्कों के साथ एक श्रृंखला में सर्किट टोपोलॉजी संबंध।]] | ||
{{about| | {{about|पॉलिमर की टोपोलॉजी|विद्युत परिपथों की टोपोलॉजी|टोपोलॉजी (विद्युत सर्किट)}} | ||
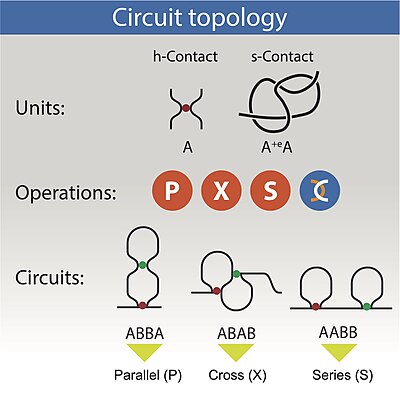
वलित (फोल्डेड) हुए रैखिक बहुलक का परिपथ सांस्थितिकी (सर्किट टोपोलॉजी) इसके इंट्रा-आणविक संपर्कों की व्यवस्था को संदर्भित करता है। इंट्रा-आणविक संपर्क वाले रैखिक[[ पॉलीमर | पॉलीमर]] के उदाहरण[[ न्यूक्लिक अम्ल | न्यूक्लिकअम्ल]] और [[प्रोटीन]] हैं। हाइड्रोजन बॉन्ड, डाइसल्फ़ाइड बॉन्ड और बीटा-बीटा इंटरैक्शन सहित विभिन्न प्रकृति के संपर्कों के निर्माण के माध्यम से प्रोटीन फोल्ड होते हैं।<ref>{{cite journal| doi=10.1016/j.str.2014.06.015 | pmid=25126961 | volume=22 | issue=9 | title=प्रोटीन और न्यूक्लिक एसिड की सर्किट टोपोलॉजी| year=2014 | journal=Structure | pages=1227–1237 | last1 = Mashaghi | first1 = Alireza | last2 = van Wijk | first2 = Roeland J. | last3 = Tans | first3 = Sander J.| doi-access=free }}</ref> जीनोम में संपर्क [[सीटीसीएफ]] और [[ cohesin |कोहसीन]] सहित प्रोटीन पुलों के माध्यम से स्थापित किए जाते हैं और [[गुणसूत्र रचना कैप्चर]] हाय-सी सहित प्रौद्योगिकियों द्वारा मापा जाता है।<ref>Scalvini, B. et al. (2022) ‘Circuit topology analysis of cellular genome reveals signature motifs, conformational heterogeneity, and scaling’, iScience, 25(3), p. 103866.</ref> परिपथ सांस्थितिकी इन भौतिक संपर्कों की टोपोलॉजिकल व्यवस्था को वर्गीकृत करती है, जिन्हें हार्ड संपर्क कहा जाता है। इसके अलावा, जंजीरों को गाँठ (या नरम संपर्कों के गठन) के माध्यम से मोड़ा जा सकता है। सर्किट टोपोलॉजी सॉफ्ट और हार्ड कॉन्टैक्ट्स दोनों को वर्गीकृत करने के लिए एक समान भाषा का उपयोग करती है, और फोल्डेड लीनियर चेन का पूरा विवरण प्रदान करती है। | |||
वलित श्रृंखला का एक सरल उदाहरण दो कठोर संपर्कों वाली एक श्रृंखला है। दो बाइनरी संपर्कों वाली एक श्रृंखला के लिए, तीन व्यवस्थाएँ उपलब्ध हैं: समानांतर (पी), श्रृंखला (एस) और पार (एक्स)। n संपर्कों वाली एक श्रृंखला के लिए, सांस्थितिकी को n द्वारा n मैट्रिक्स द्वारा वर्णित किया जा सकता है जिसमें प्रत्येक तत्व संपर्कों की एक जोड़ी के बीच संबंध को दिखाता है और तीन अवस्थाओं में से एक, पी, एस और एक्स ले सकता है। बहुसंयोजक संपर्क भी हो सकते हैं कई बाइनरी संपर्कों में पूर्ण या अपघटन के माध्यम से वर्गीकृत है। इसी तरह, सर्किट टोपोलॉजी श्रृंखला क्रॉसिंग और टेंगल्स की जोड़ीवार व्यवस्था के वर्गीकरण की अनुमति देती है, इस प्रकार मुड़ी हुई श्रृंखलाओं का एक पूर्ण 3डी विवरण प्रदान करती है। इसके अलावा, कोई जटिल फोल्ड उत्पन्न करने के लिए सॉफ्ट और हार्ड संपर्कों पर सर्किट टोपोलॉजी ऑपरेशंस लागू कर सकता है। | |||
परिपथ सांस्थितिकी (सर्किट टोपोलॉजी) में फोल्डिंग कैनेटीक्स और [[आणविक विकास]] के लिए निहितार्थ हैं और इसे आणविक ओरिगेमी सहित इंजीनियर पॉलिमर पर लागू किया गया है।<ref>Yasuyuki Tezuka and Tetsuo Deguchi, Topological Polymer Chemistry: Concepts and Practices (2022) ISBN 978-981-16-6806-7</ref> परिपथ सांस्थितिकी संपर्क क्रम और आकार के साथ रैखिक पॉलिमर की तह दर के निर्धारक हैं।<ref>{{cite journal | doi =10.1039/C4CP03402C | volume=16 | issue = 41 | title=Circuit topology of self-interacting chains: implications for folding and unfolding dynamics | year=2014 | journal=Phys. Chem. Chem. Phys. | pages=22537–22544 | last1 = Mugler | first1 = Andrew | last2 = Tans | first2 = Sander J. | last3 = Mashaghi | first3 = Alireza| pmid=25228051 | bibcode=2014PCCP...1622537M }}</ref> | |||
== अग्रिम पठन == | == अग्रिम पठन == | ||
* | * बी। स्काल्विनी एट अल।, सेलुलर जीनोम के सर्किट टोपोलॉजी विश्लेषण से सिग्नेचर मोटिफ्स, कन्फॉर्मल हेट्रोजेनिटी और स्केलिंग का पता चलता है। आईसाइंस (2022)। [https://www.sciencedirect.com/science/article/pii/S2589004222001365 link] | ||
* | * बी। स्काल्विनी एट अल।, प्रोटीन फोल्डिंग के टोपोलॉजिकल सिद्धांत। पीसीसीपी (2021)। [https://pubs.rsc.org/en/content/articlelanding/2021/cp/d1cp03390e link] | ||
* | * ए। गोलोवनेव एट अल।, मुड़ी हुई रैखिक श्रृंखलाओं का सामान्यीकृत सर्किट टोपोलॉजी। विज्ञान (2020)। [https://www.cell.com/iscience/fulltext/S2589-0042(20)30684-2 link] | ||
* | * एम. हेदरी एट अल।, पॉलीमर फोल्डिंग रिएक्शन का सर्किट टोपोलॉजी विश्लेषण। एसीएस सेंट्रल साइंस (2020) [https://pubs.acs.org/doi/abs/10.1021/acscentsci.0c00308 link] | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[टोपोलॉजी (रसायन विज्ञान)]] | * [[टोपोलॉजी (रसायन विज्ञान)]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | |||
[[Category:Created On 23/03/2023]] | [[Category:Created On 23/03/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
Latest revision as of 16:35, 27 April 2023
वलित (फोल्डेड) हुए रैखिक बहुलक का परिपथ सांस्थितिकी (सर्किट टोपोलॉजी) इसके इंट्रा-आणविक संपर्कों की व्यवस्था को संदर्भित करता है। इंट्रा-आणविक संपर्क वाले रैखिक पॉलीमर के उदाहरण न्यूक्लिकअम्ल और प्रोटीन हैं। हाइड्रोजन बॉन्ड, डाइसल्फ़ाइड बॉन्ड और बीटा-बीटा इंटरैक्शन सहित विभिन्न प्रकृति के संपर्कों के निर्माण के माध्यम से प्रोटीन फोल्ड होते हैं।[1] जीनोम में संपर्क सीटीसीएफ और कोहसीन सहित प्रोटीन पुलों के माध्यम से स्थापित किए जाते हैं और गुणसूत्र रचना कैप्चर हाय-सी सहित प्रौद्योगिकियों द्वारा मापा जाता है।[2] परिपथ सांस्थितिकी इन भौतिक संपर्कों की टोपोलॉजिकल व्यवस्था को वर्गीकृत करती है, जिन्हें हार्ड संपर्क कहा जाता है। इसके अलावा, जंजीरों को गाँठ (या नरम संपर्कों के गठन) के माध्यम से मोड़ा जा सकता है। सर्किट टोपोलॉजी सॉफ्ट और हार्ड कॉन्टैक्ट्स दोनों को वर्गीकृत करने के लिए एक समान भाषा का उपयोग करती है, और फोल्डेड लीनियर चेन का पूरा विवरण प्रदान करती है।
वलित श्रृंखला का एक सरल उदाहरण दो कठोर संपर्कों वाली एक श्रृंखला है। दो बाइनरी संपर्कों वाली एक श्रृंखला के लिए, तीन व्यवस्थाएँ उपलब्ध हैं: समानांतर (पी), श्रृंखला (एस) और पार (एक्स)। n संपर्कों वाली एक श्रृंखला के लिए, सांस्थितिकी को n द्वारा n मैट्रिक्स द्वारा वर्णित किया जा सकता है जिसमें प्रत्येक तत्व संपर्कों की एक जोड़ी के बीच संबंध को दिखाता है और तीन अवस्थाओं में से एक, पी, एस और एक्स ले सकता है। बहुसंयोजक संपर्क भी हो सकते हैं कई बाइनरी संपर्कों में पूर्ण या अपघटन के माध्यम से वर्गीकृत है। इसी तरह, सर्किट टोपोलॉजी श्रृंखला क्रॉसिंग और टेंगल्स की जोड़ीवार व्यवस्था के वर्गीकरण की अनुमति देती है, इस प्रकार मुड़ी हुई श्रृंखलाओं का एक पूर्ण 3डी विवरण प्रदान करती है। इसके अलावा, कोई जटिल फोल्ड उत्पन्न करने के लिए सॉफ्ट और हार्ड संपर्कों पर सर्किट टोपोलॉजी ऑपरेशंस लागू कर सकता है।
परिपथ सांस्थितिकी (सर्किट टोपोलॉजी) में फोल्डिंग कैनेटीक्स और आणविक विकास के लिए निहितार्थ हैं और इसे आणविक ओरिगेमी सहित इंजीनियर पॉलिमर पर लागू किया गया है।[3] परिपथ सांस्थितिकी संपर्क क्रम और आकार के साथ रैखिक पॉलिमर की तह दर के निर्धारक हैं।[4]
अग्रिम पठन
- बी। स्काल्विनी एट अल।, सेलुलर जीनोम के सर्किट टोपोलॉजी विश्लेषण से सिग्नेचर मोटिफ्स, कन्फॉर्मल हेट्रोजेनिटी और स्केलिंग का पता चलता है। आईसाइंस (2022)। link
- बी। स्काल्विनी एट अल।, प्रोटीन फोल्डिंग के टोपोलॉजिकल सिद्धांत। पीसीसीपी (2021)। link
- ए। गोलोवनेव एट अल।, मुड़ी हुई रैखिक श्रृंखलाओं का सामान्यीकृत सर्किट टोपोलॉजी। विज्ञान (2020)। link
- एम. हेदरी एट अल।, पॉलीमर फोल्डिंग रिएक्शन का सर्किट टोपोलॉजी विश्लेषण। एसीएस सेंट्रल साइंस (2020) link
संदर्भ
- ↑ Mashaghi, Alireza; van Wijk, Roeland J.; Tans, Sander J. (2014). "प्रोटीन और न्यूक्लिक एसिड की सर्किट टोपोलॉजी". Structure. 22 (9): 1227–1237. doi:10.1016/j.str.2014.06.015. PMID 25126961.
- ↑ Scalvini, B. et al. (2022) ‘Circuit topology analysis of cellular genome reveals signature motifs, conformational heterogeneity, and scaling’, iScience, 25(3), p. 103866.
- ↑ Yasuyuki Tezuka and Tetsuo Deguchi, Topological Polymer Chemistry: Concepts and Practices (2022) ISBN 978-981-16-6806-7
- ↑ Mugler, Andrew; Tans, Sander J.; Mashaghi, Alireza (2014). "Circuit topology of self-interacting chains: implications for folding and unfolding dynamics". Phys. Chem. Chem. Phys. 16 (41): 22537–22544. Bibcode:2014PCCP...1622537M. doi:10.1039/C4CP03402C. PMID 25228051.