प्रकाश क्षेत्र: Difference between revisions
mNo edit summary |
No edit summary |
||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Vector function in optics}} | {{Short description|Vector function in optics}} | ||
'''प्रकाश क्षेत्र''' एक सदिश- | '''प्रकाश क्षेत्र''' एक सदिश-कार्य है जो अंतरिक्ष में प्रत्येक बिंदु के माध्यम से प्रत्येक दिशा में बहने वाले प्रकाश की मात्रा का वर्णन करता है। सभी संभावित 'प्रकाश किरणों' का स्थान पंच-आयामी प्लेनोप्टिक कार्य द्वारा दिया जाता है, और प्रत्येक किरण का परिमाण इसकी [[चमक|विकिरण]] द्वारा दिया जाता है। [[माइकल फैराडे]] पहले व्यक्ति थे जिन्होंने प्रस्तावित किया कि प्रकाश को एक क्षेत्र के रूप में व्याख्यायित किया जाना चाहिए, ठीक उसी चुंबकीय क्षेत्र की तरह जिस पर वह काम कर रहे थे।<ref>{{cite journal|last1=Faraday|first1=Michael|date=30 April 2009|title=लिव। किरण-कंपन पर विचार|url=https://www-spof.gsfc.nasa.gov/Education/wfarad1846.html|journal=Philosophical Magazine|series=Series 3|volume=28|issue=188|pages=345–350|doi=10.1080/14786444608645431|archiveurl=https://web.archive.org/web/20130218141803/https://www-spof.gsfc.nasa.gov/Education/wfarad1846.html|archivedate=2013-02-18}}</ref> वाक्यांश प्रकाश क्षेत्र [[एंड्री अलेक्जेंड्रोविच गेर्शुन]] द्वारा त्रि-आयामी अंतरिक्ष में प्रकाश के विकिरणमापी गुणों पर एक प्राचीन 1936 के पेपर में गढ़ा गया था। | ||
प्रकाश क्षेत्र प्रदर्शन के लिए आधुनिक दृष्टिकोण प्रकाशीय तत्वों के सह-प्रारुपण का पता लगाते हैं और उच्च विभेदन, बढ़े हुए वैषम्य, देखने के व्यापक क्षेत्र और अन्य लाभों को प्राप्त करने के लिए संपीडन संगणना करते हैं।<ref>Wetzstein 2012, 2011; Lanman 2011, 2010</ref> | प्रकाश क्षेत्र प्रदर्शन के लिए आधुनिक दृष्टिकोण प्रकाशीय तत्वों के सह-प्रारुपण का पता लगाते हैं और उच्च विभेदन, बढ़े हुए वैषम्य, देखने के लिए व्यापक क्षेत्र और अन्य लाभों को प्राप्त करने के लिए संपीडन संगणना करते हैं।<ref>Wetzstein 2012, 2011; Lanman 2011, 2010</ref> | ||
समान अवधारणाओं को संदर्भित करने के लिए शब्द " | समान अवधारणाओं को संदर्भित करने के लिए शब्द "विकिरण क्षेत्र" का भी उपयोग किया जा सकता है। इस शब्द का प्रयोग आधुनिक शोध में किया जाता है जैसे [[तंत्रिका चमक क्षेत्र|तंत्रिका विकिरण क्षेत्र]]। | ||
== प्लेनोप्टिक कार्य == | == प्लेनोप्टिक कार्य == | ||
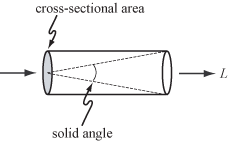
[[Image:Plenoptic-function-a.png|right|frame|एक किरण के साथ रेडियंस L को एक ट्यूब के माध्यम से सभी संभावित सीधी रेखाओं के साथ यात्रा करने वाली प्रकाश की मात्रा के रूप में माना जा सकता है जिसका आकार इसके ठोस कोण और पार-अनुभागीय क्षेत्र द्वारा निर्धारित किया जाता है।]]ज्यामितीय [[प्रकाशिकी]] के लिए - अर्थात, सुसंगतता (भौतिकी) प्रकाश और प्रकाश की तरंग दैर्ध्य से बड़ी वस्तुओं के लिए - प्रकाश का मूल वाहक एक [[किरण (प्रकाशिकी)]] है। किरण के साथ यात्रा करने वाले प्रकाश की मात्रा के लिए माप | [[Image:Plenoptic-function-a.png|right|frame|एक किरण के साथ रेडियंस L को एक ट्यूब के माध्यम से सभी संभावित सीधी रेखाओं के साथ यात्रा करने वाली प्रकाश की मात्रा के रूप में माना जा सकता है जिसका आकार इसके ठोस कोण और पार-अनुभागीय क्षेत्र द्वारा निर्धारित किया जाता है।]]ज्यामितीय [[प्रकाशिकी]] के लिए - अर्थात, सुसंगतता (भौतिकी) प्रकाश और प्रकाश की तरंग दैर्ध्य से बड़ी वस्तुओं के लिए - प्रकाश का मूल वाहक एक [[किरण (प्रकाशिकी)]] है। किरण के साथ यात्रा करने वाले प्रकाश की मात्रा के लिए माप विकिरण है, जिसे L द्वारा निरूपित किया जाता है और {{nobreak|W·sr<sup>−1</sup>·m<sup>−2</sup>}}, में मापा जाता है, यानी [[वाट]] (W) प्रति [[ steradian | स्टरेडियन]] (sr) प्रति वर्ग मीटर (m)<sup>2</sup>). स्टेरेडियन [[ठोस कोण]] का एक माप है, और वर्ग मीटर अंतः-अनुभागीय क्षेत्र के माप के रूप में उपयोग किया जाता है, जैसा कि दाईं ओर दिखाया गया है। | ||
[[Image:Plenoptic function b.svg|left|frame|स्थिति (x, y, z) और दिशा (θ, ϕ) द्वारा त्रि-आयामी अंतरिक्ष अंतरिक्ष में एक किरण को मापना।]]रोशनी की अपरिवर्तनीय व्यवस्था से प्रकाशित त्रि-आयामी अंतरिक्ष के क्षेत्र में ऐसी सभी किरणों के साथ | [[Image:Plenoptic function b.svg|left|frame|स्थिति (x, y, z) और दिशा (θ, ϕ) द्वारा त्रि-आयामी अंतरिक्ष अंतरिक्ष में एक किरण को मापना।]]रोशनी की अपरिवर्तनीय व्यवस्था से प्रकाशित त्रि-आयामी अंतरिक्ष के क्षेत्र में ऐसी सभी किरणों के साथ विकिरण को प्लेनोप्टिक कार्य कहा जाता है।<ref>Adelson 1991</ref> प्लेनोप्टिक रोशनी कार्य एक आदर्श कार्य है जिसका उपयोग [[कंप्यूटर दृष्टि]] और [[कंप्यूटर चित्रलेख]] किसी भी संभावित देखने की स्थिति से दृश्य की छवि को व्यक्त करने के लिए किया जाता है। यह संगणनात्मक रूप से अभ्यास में प्रयोग नहीं किया जाता है, लेकिन दृष्टि और लेखाचित्रीय में अन्य अवधारणाओं को समझने में वैचारिक रूप से उपयोगी है।<ref>Wong 2002</ref> चूंकि अंतरिक्ष में किरणों को तीन निर्देशांक, x, y, और z और दो कोणों θ और ϕ द्वारा प्राचलीकृत किया जा सकता है, जैसा कि बाईं ओर दिखाया गया है, यह एक पांच-आयामी कार्य है, जो कि पांच-आयामी [[कई गुना|बहुमुख]] समतुल्य कार्य एक 3D [[यूक्लिडियन अंतरिक्ष|यूक्लिडियन स्थल]] और 2-गोले का उत्पाद है। | ||
[[Image:Gershun-light-field-fig17.png|right|thumb|175px|विकिरण सदिश को समेटना D<sub>1</sub> और D<sub>2</sub> दो प्रकाश स्रोतों से उत्पन्न I1 और I<sub>2</sub> दिखाए गए परिमाण और दिशा वाले परिणामी वेक्टर D का उत्पादन करता है।<ref>Gershun, fig 17</ref>]]अंतरिक्ष में प्रत्येक बिंदु पर प्रकाश क्षेत्र को सदिशों के एक अनंत संग्रह के रूप में माना जा सकता है, बिंदु पर प्रति दिशा में | [[Image:Gershun-light-field-fig17.png|right|thumb|175px|विकिरण सदिश को समेटना D<sub>1</sub> और D<sub>2</sub> दो प्रकाश स्रोतों से उत्पन्न I1 और I<sub>2</sub> दिखाए गए परिमाण और दिशा वाले परिणामी वेक्टर D का उत्पादन करता है।<ref>Gershun, fig 17</ref>]]अंतरिक्ष में प्रत्येक बिंदु पर प्रकाश क्षेत्र को सदिशों के एक अनंत संग्रह के रूप में माना जा सकता है, एक बिंदु पर प्रति दिशा में, उनकी विकिरण के आनुपातिक लंबाई के साथ। | ||
रोशनी के किसी भी संग्रह पर, या दिशाओं के पूरे क्षेत्र में इन सदिशों को एकीकृत करना, एक एकल अदिश मान उत्पन्न करता है - उस बिंदु पर कुल विकिरण, और परिणामी दिशा। यह आंकड़ा दो प्रकाश स्रोतों की स्थिति में इस गणना को दर्शाता है। कंप्यूटर लेखाचित्रीय में, त्रि-आयामी अंतरिक्ष के इस सदिश | रोशनी के किसी भी संग्रह पर, या दिशाओं के पूरे क्षेत्र में इन सदिशों को एकीकृत करना, एक एकल अदिश मान उत्पन्न करता है - उस बिंदु पर कुल विकिरण, और परिणामी दिशा। यह आंकड़ा दो प्रकाश स्रोतों की स्थिति में इस गणना को दर्शाता है। कंप्यूटर लेखाचित्रीय में, त्रि-आयामी अंतरिक्ष के इस सदिश कार्य को सदिश विकिरण क्षेत्र कहा जाता है।<ref>Arvo, 1994</ref> क्षेत्र में प्रत्येक बिंदु पर सदिश दिशा की व्याख्या उस बिंदु पर रखी गई समतल सतह के अभिविन्यास के रूप में की जा सकती है, जो इसे सबसे अधिक चमकीले रूप से प्रकाशित करती है। | ||
=== उच्च आयामीता === | === उच्च आयामीता === | ||
| Line 19: | Line 19: | ||
== 4D प्रकाश क्षेत्र == | == 4D प्रकाश क्षेत्र == | ||
[[Image:Plenoptic-function-c.png|left|frame|यदि कोई अवरोधक न हो तो किरण के साथ | [[Image:Plenoptic-function-c.png|left|frame|यदि कोई अवरोधक न हो तो किरण के साथ विकिरण स्थिर रहती है।]]एक प्लेनोप्टिक कार्य में, यदि अभिरुचि क्षेत्र में एक [[अवतल बहुभुज|अवतल]] वस्तु होती है, तो वस्तु पर एक बिंदु छोड़ने वाला प्रकाश केवल छोटी दूरी की यात्रा कर सकता है, इससे पहले कि वस्तु पर कोई अन्य बिंदु इसे अवरुद्ध कर दे। कोई व्यावहारिक उपकरण ऐसे क्षेत्र में कार्य को माप नहीं सकता। | ||
हालांकि, वस्तु के अवमुख समावरक के बाहर के स्थानों के लिए (उदाहरण के लिए, | हालांकि, वस्तु के [[अवमुख समावरक]] के बाहर के स्थानों के लिए (उदाहरण के लिए, संकुचन वेष्टन), प्लेनोप्टिक कार्य को कई छवियों को प्रग्रहण करके मापा जा सकता है। इस स्थिति में कार्य में अतिरिक्त जानकारी होती है, क्योंकि किरण के साथ विकिरण इसकी पूरी लंबाई में स्थिर रहती है। अतिरिक्त जानकारी ठीक एक आयाम है, एक चार-आयामी कार्य को छोड़कर जिसे विभिन्न रूप से फोटोनिक क्षेत्र, 4D प्रकाश क्षेत्र या ल्यूमिग्राफ कहा जाता है<ref>Levoy 1996</ref> ।<ref>Gortler 1996</ref> औपचारिक रूप से, क्षेत्र को खाली स्थान में किरणों के साथ विकिरण के रूप में परिभाषित किया गया है। | ||
एक प्रकाश क्षेत्र में किरणों के समुच्चय को विभिन्न प्रकारों से परिचालित किया जा सकता है। सबसे आम दो-तल मानकीकरण है। हालांकि यह मानकीकरण सभी किरणों का प्रतिनिधित्व नहीं कर सकता है, उदाहरण के लिए दो तल के समानांतर किरणें यदि तल एक दूसरे के समानांतर हैं, तो यह | एक प्रकाश क्षेत्र में किरणों के समुच्चय को विभिन्न प्रकारों से परिचालित किया जा सकता है। सबसे आम दो-तल मानकीकरण है। हालांकि यह मानकीकरण सभी किरणों का प्रतिनिधित्व नहीं कर सकता है, उदाहरण के लिए दो तल के समानांतर किरणें यदि तल एक दूसरे के समानांतर हैं, तो यह संदर्श प्रतिबिंब के [[विश्लेषणात्मक ज्यामिति]] से निकटता से संबंधित है। दो-तल प्रकाश क्षेत्र के बारे में सोचने का एक सरल प्रकार ''st'' सतह (और कोई भी वस्तु जो इसके किनारे या उससे आगे हो सकती है) की संदर्श प्रतिबिंबों के संग्रह के रूप में है, प्रत्येक को ''uv'' सतह पर एक पर्यवेक्षक की स्थिति से लिया गया है। एक प्रकाश क्षेत्र को इस तरह परिचालित किया जाता है जिसे कभी-कभी प्रकाश पटिया कहा जाता है। | ||
[[Image:Light-field-parameterizations.png|left|frame| 4D प्रकाश क्षेत्र के कुछ वैकल्पिक मानकीकरण, जो त्रि-आयामी | [[Image:Light-field-parameterizations.png|left|frame| 4D प्रकाश क्षेत्र के कुछ वैकल्पिक मानकीकरण, जो त्रि-आयामी तल के एक खाली क्षेत्र के माध्यम से प्रकाश के प्रवाह का प्रतिनिधित्व करते हैं। बायां: समतल या घुमावदार सतह पर स्थित बिंदु और प्रत्येक बिंदु से निकलने वाली दिशाएं। केंद्र: एक गोले की सतह पर बिंदुओं के जोड़े। दाएं: सामान्य स्थिति में दो तलों पर बिंदुओं के जोड़े (मतलब कोई भी) स्थिति।]] | ||
{{clear}} | {{clear}} | ||
=== ध्वनि अनुरूप === | === ध्वनि अनुरूप === | ||
ध्वनि के लिए 4D प्रकाश क्षेत्र का अनुरूप ध्वनि क्षेत्र या तरंग क्षेत्र है, जैसा कि [[तरंग क्षेत्र संश्लेषण]] में होता है, और संबंधित मानकीकरण किरचॉफ-हेल्महोल्ट्ज़ अभिन्न है, जो बताता है कि, बाधाओं की अनुपस्थिति में, समय के साथ | ध्वनि के लिए 4D प्रकाश क्षेत्र का अनुरूप ध्वनि क्षेत्र या तरंग क्षेत्र है, जैसा कि [[तरंग क्षेत्र संश्लेषण]] में होता है, और संबंधित मानकीकरण [[किरचॉफ-हेल्महोल्ट्ज़ अभिन्न]] है, जो बताता है कि, बाधाओं की अनुपस्थिति में, समय के साथ ध्वनि क्षेत्र एक स्थल पर दबाव द्वारा दिया जाता है। इस प्रकार यह किसी भी समय सूचना के दो आयाम हैं, और समय के साथ, एक 3D क्षेत्र हैै। | ||
प्रकाश की स्पष्ट चार-आयामीता की तुलना में यह द्वि-आयामीता है, क्योंकि प्रकाश किरणों में यात्रा करता है (समय में एक बिंदु पर 0D, समय के साथ 1D), जबकि [[ह्यूजेन्स-फ्रेस्नेल सिद्धांत]] द्वारा, एक ध्वनि [[तरंगाग्र]] को गोलाकार तरंगों के रूप में प्रतिरूपित किया जा सकता है (समय के एक बिंदु पर 2D, समय के साथ 3D): प्रकाश एक ही दिशा में चलता है (सूचना का 2D), जबकि ध्वनि हर दिशा में फैलती है। हालांकि, गैर-निर्वात साधन में प्रकाश यात्रा एक समान प्रकार से बिखर सकती है, और अपरिवर्तनीयता या बिखरने में खो जाने वाली जानकारी पद्धति आयाम के नुकसान स्पष्ट है। | |||
== | == छवि पुनः फ़ोकसन == | ||
क्योंकि प्रकाश क्षेत्र स्थानिक और कोणीय जानकारी प्रदान करता है, हम | क्योंकि प्रकाश क्षेत्र स्थानिक और कोणीय जानकारी प्रदान करता है, हम उद्भासन के बाद फोकल तल की स्थिति को बदल सकते हैं, जिसे प्रायः पुनःफोकसिंग कहा जाता है। पुनःफोकसिंग का सिद्धांत अभिन्न परिवर्तन के माध्यम से एक प्रकाश क्षेत्र से पारंपरिक 2-D तस्वीरें प्राप्त करना है। परिवर्तन एक प्रकाश क्षेत्र को इसके निविष्ट के रूप में लेता है और एक विशिष्ट तल पर केंद्रित एक तस्वीर उत्पन्न करता है। | ||
यह मानते हुए <math>L_{F}(s,t,u,v)</math> एक 4- | यह मानते हुए कि <math>L_{F}(s,t,u,v)</math> एक 4-D प्रकाश क्षेत्र का प्रतिनिधित्व करता है पहले तल जो स्थिति <math>(u,v)</math> से दूसरे तल पर स्थिति <math>(s,t)</math> तक यात्रा करने वाली प्रकाश किरणों को अभिलेखबद्ध करता है, जहाँ <math>F</math> दो तलों के बीच की दूरी है, किसी भी गहराई पर 2-D तस्वीर <math>\alpha F</math> निम्नलिखित अभिन्न परिवर्तन से प्राप्त किया जा सकता है:<ref name="renng">{{Cite journal|last=Ng|first=Ren|date=2005|title=फूरियर टुकड़ा फोटोग्राफी|url=http://dx.doi.org/10.1145/1186822.1073256|journal=ACM SIGGRAPH 2005 Papers on - SIGGRAPH '05|pages=735–744 |location=New York, New York, USA|publisher=ACM Press|doi=10.1145/1186822.1073256|isbn=9781450378253 |s2cid=1806641 }}</ref> | ||
:<math>\mathcal{P}_{\alpha}\left[L_{F}\right](s,t)={1 \over \alpha^2 F^2}\iint L_F(u(1-1/\alpha)+s/\alpha,v(1-1/\alpha)+t/\alpha,u,v)~dudv</math>, | :<math>\mathcal{P}_{\alpha}\left[L_{F}\right](s,t)={1 \over \alpha^2 F^2}\iint L_F(u(1-1/\alpha)+s/\alpha,v(1-1/\alpha)+t/\alpha,u,v)~dudv</math>, | ||
| Line 43: | Line 43: | ||
:<math>\mathcal{P}_{\alpha}\left[L_{F}\right](\boldsymbol{s})=\frac{1}{\alpha^{2} F^{2}} \int L_{F}\left(\boldsymbol{u}\left(1-\frac{1}{\alpha}\right)+\frac{\boldsymbol{s}}{\alpha}, \boldsymbol{u}\right) d \boldsymbol{u}</math>, | :<math>\mathcal{P}_{\alpha}\left[L_{F}\right](\boldsymbol{s})=\frac{1}{\alpha^{2} F^{2}} \int L_{F}\left(\boldsymbol{u}\left(1-\frac{1}{\alpha}\right)+\frac{\boldsymbol{s}}{\alpha}, \boldsymbol{u}\right) d \boldsymbol{u}</math>, | ||
जहाँ <math>\boldsymbol{s}=(s,t)</math>, <math>\boldsymbol{u}=(u,v)</math>, और <math>\mathcal{P}_{\alpha}\left[\cdot\right]</math> छायाचित्रण संचालक है। | |||
व्यवहार में, इस सूत्र का सीधे | व्यवहार में, इस सूत्र का सीधे तरह पर उपयोग नहीं किया जा सकता है क्योंकि प्लेनोप्टिक कैमरा समान्यतः प्रकाश क्षेत्र के असतत प्रतिरूपों को प्रग्रहण करता है <math>L_{F}(s,t,u,v)</math>, और इसलिए गणना करने के लिए पुन: नमूनाकरण (या अंतःप्रक्षेप) की आवश्यकता है <math> L_{F}\left(\boldsymbol{u}\left(1-\frac{1}{\alpha}\right)+\frac{\boldsymbol{s}}{\alpha}, \boldsymbol{u}\right)</math>. एक अन्य समस्या उच्च संगणना जटिलता है। एक <math>N\times N</math> 2-D <math>N\times N\times N\times N</math> 4-D प्रकाश क्षेत्र से तस्वीर की गणना करने के लिए, सूत्र की जटिलता <math>O(N^4)</math>.<ref name="renng" /> है। | ||
=== | === फूरिये अंशअ छायाचित्रण === | ||
संगणना की जटिलता को कम करने का एक | संगणना की जटिलता को कम करने का एक प्रकार [[प्रोजेक्शन-स्लाइस प्रमेय|प्रोजेक्शन-अंशअ प्रमेय]] की अवधारणा को अपनाना है:<ref name="renng" />छायाचित्रण संचालक <math>\mathcal{P}_{\alpha}\left[\cdot\right]</math> को प्रक्षेपण के बाद अपरुपक के रूप में देखा जा सकता है। परिणाम एक प्रकाश क्षेत्र के 4-D फूरियर रूपांतरण के 2-D अंशअ के समानुपाती होना चाहिए। अधिक सटीक रूप से, [[ प्रकाश क्षेत्र माइक्रोस्कोपी ]] से एक पुनःफोकसिंग की गई छवि उत्पन्न की जा सकती है। 2-D अंशअ निकालने, एक व्युत्क्रम 2-D परिवर्तन और प्रवर्धन लागू करके एक प्रकाश क्षेत्र का 4-D फूरिये वर्णक्रम से एक पुनःफोकसिंग की गई छवि उत्पन्न की जा सकती है। कलन-विधि की स्पर्शोन्मुख जटिलता <math>O(N^2 \operatorname{log}N)</math> है | ||
=== असतत फोकल | === असतत फोकल खंड रूपांतरण === | ||
2- | 2-D तस्वीरों की कुशलता से गणना करने का दूसरा प्रकार असतत फोकल खंड रूपांतरण (DFST) को अपनाना है।<ref>{{Cite journal|last1=Nava|first1=F. Pérez|last2=Marichal-Hernández|first2=J.G.|last3=Rodríguez-Ramos|first3=J.M.|date=August 2008|title=असतत फोकल स्टैक रूपांतरण|url=https://ieeexplore.ieee.org/document/7080334|journal=2008 16th European Signal Processing Conference|pages=1–5}}</ref> DFST को पुनःफोकसिंग किए गए 2-D छायाचित्र, या तथाकथित [[फोकस स्टैकिंग|फोकस खंड]] का संग्रह उत्पन्न करने के लिए प्रारुपण किया गया है। इस विधि को तेजी से भिन्नात्मक फूरियर रूपांतरण (FrFT) द्वारा लागू किया जा सकता है। | ||
असतत | असतत छायाचित्रण संचालन <math>\mathcal{P}_{\alpha}\left[\cdot\right]</math> को प्रकाश क्षेत्र के लिए निम्नानुसार परिभाषित किया गया है <math>L_{F}(\boldsymbol {s},\boldsymbol {u})</math> 4-D ग्रिड में प्रतिचयित किया जाता है | ||
<math>\boldsymbol {s} = \Delta s \tilde{\boldsymbol {s}}, \tilde{\boldsymbol {s}}=-\boldsymbol {n}_{\boldsymbol {s}},...,\boldsymbol {n}_{\boldsymbol {s}}</math>, | |||
<math>\boldsymbol {u} = \Delta u \tilde{\boldsymbol {u}}, \tilde{\boldsymbol {u}}=-\boldsymbol {n}_{\boldsymbol {u}},...,\boldsymbol {n}_{\boldsymbol {u}}</math>: | |||
:<math>\mathcal{P}_{q}[L](\boldsymbol{s})= | :<math>\mathcal{P}_{q}[L](\boldsymbol{s})= | ||
| Line 61: | Line 65: | ||
\quad \Delta \boldsymbol{u}=\Delta u\Delta v, | \quad \Delta \boldsymbol{u}=\Delta u\Delta v, | ||
\quad q=\left(1-\frac{1}{\alpha}\right)</math> | \quad q=\left(1-\frac{1}{\alpha}\right)</math> | ||
क्योंकि <math>(\boldsymbol{u} q+\boldsymbol{s}, \boldsymbol{u}) </math> | क्योंकि <math>(\boldsymbol{u} q+\boldsymbol{s}, \boldsymbol{u}) </math> समान्यतः 4-D ग्रिड पर नहीं होता है, DFST गैर-ग्रिड मानों की गणना करने के लिए [[त्रिकोणमितीय अंतःप्रक्षेप]] को अपनाता है। | ||
कलन-विधि में ये चरण होते हैं: | |||
* प्रकाश क्षेत्र को प्रतिरूपित करे <math>L_{F}(\boldsymbol {s},\boldsymbol {u})</math> प्रतिरूपित अवधि के साथ <math>\Delta s</math> और <math>\Delta u</math> और विवेकित प्रकाश क्षेत्र <math>L^d_{F}(\boldsymbol {s},\boldsymbol {u})</math> प्राप्त करें | |||
* खंड <math>L^d_{F}(\boldsymbol {s},\boldsymbol {u})</math> शून्य के साथ जैसे कि संकेतक की लंबाई बिना उपघटन के FrFT के लिए पर्याप्त है। | |||
* हर एक <math>\boldsymbol {u}</math>, के लिए [[असतत फूरियर रूपांतरण]] <math>L^d_{F}(\boldsymbol {s},\boldsymbol {u})</math>, की गणना करें और परिणाम <math>R1</math> प्राप्त करें | |||
* प्रत्येक फोकल लम्बाई <math>\alpha F</math>, के लिए एक भिन्नात्मक फूरियर रूपांतरण की <math>R1</math> की गणना करें, जहां रूपांतरण का क्रम <math>\alpha</math> पर निर्भर करता है और परिणाम <math>R2</math> प्राप्त करें | |||
* <math>R2</math> के व्युत्क्रम असतत फूरियर रूपांतरण की गणना करें | |||
* <math>R2</math> के सीमांत पिक्सेल निकालें ताकि प्रत्येक 2-D तस्वीर का आकार <math>(2{n}_{\boldsymbol {s}}+1) \times (2{n}_{\boldsymbol {s}}+1)</math> हो | |||
== प्रकाश क्षेत्र बनाने के प्रकार == | |||
प्रकाश क्षेत्र प्रकाश के लिए उन्हें परिभाषित करने के लिए कई प्रकारों के साथ एक मौलिक प्रतिनिधित्व है। | |||
कंप्यूटर चित्रमुद्रण में, प्रकाश क्षेत्र समान्यतः या तो एक [[मॉडल की गिनती|प्रतिरूप की गिनती]] को प्रस्तुत करके (कंप्यूटर चित्रमुद्रण) या वास्तविक दृश्य को चित्रित करके निर्मित होते हैं। किसी भी स्थिति में, एक प्रकाश क्षेत्र का निर्माण करने के लिए, दृष्टिकोणों के एक बड़े संग्रह के लिए विचार प्राप्त किए जाने चाहिए। मानकीकरण के आधार पर, यह संग्रह समान्यतः एक रेखा, वृत्त, समतल, गोले या अन्य आकार के कुछ अंश को फैलाता है, हालांकि असंरचित संग्रह संभव हैं।<ref>Buehler 2001</ref> | |||
प्रकाश क्षेत्र | |||
[[प्रकाश क्षेत्र फोटोग्राफी|प्रकाश क्षेत्र छायाचित्रण]] प्रग्रहण करने के लिए उपकरणों में एक गतिमान हाथ से थामे रखे जाने वाला कैमरा या रोबोटिक रूप से नियंत्रित कैमरा समिलित हो सकता है,<ref>Levoy 2002</ref> कैमरों का एक चाप, कैमरों की एक सघन सरणी,<ref>Kanade 1998; Yang 2002; Wilburn 2005</ref> [[लाइट-फील्ड कैमरा]],<ref name="ng">[[Ren Ng|Ng]] 2005 </ref><ref>Georgiev 2006; Marwah 2013</ref> सूक्ष्मदर्शी<ref>Levoy 2006</ref> या अन्य प्रकाशिकी पद्धतियाँ समिलित हो सकते है ।<ref>Bolles 1987</ref> | |||
एक प्रकाश क्षेत्र में कितनी छवियां होनी चाहिए? सबसे बड़ा ज्ञात प्रकाश क्षेत्र (माइकलएंजेलो की [[डॉक्टर चैपल]] की मूर्ति)<ref>{{Cite web|title=माइकलएंजेलो की रात की मूर्ति का प्रकाश क्षेत्र|url=https://accademia.stanford.edu/mich/lightfield-of-night/|access-date=2022-02-08|website=accademia.stanford.edu}}</ref> इसमें 24,000 1.3-मेगापिक्सेल छवियां हैं। गहरे स्तर | एक प्रकाश क्षेत्र में कितनी छवियां होनी चाहिए? सबसे बड़ा ज्ञात प्रकाश क्षेत्र (माइकलएंजेलो की [[डॉक्टर चैपल]] की मूर्ति)है,<ref>{{Cite web|title=माइकलएंजेलो की रात की मूर्ति का प्रकाश क्षेत्र|url=https://accademia.stanford.edu/mich/lightfield-of-night/|access-date=2022-02-08|website=accademia.stanford.edu}}</ref> इसमें 24,000 1.3-मेगापिक्सेल छवियां हैं। यह गहरे स्तर, उत्तर आवेदन पर निर्भर करता है। किसी अपारदर्शी वस्तु को पूरी तरह से प्रग्रहण करने के लिए प्रकाश क्षेत्र अनुवाद के लिए, छवियों को कम से कम आगे और पीछे से लिया जाना चाहिए। कम स्पष्ट रूप से, किसी वस्तु के लिए जो st तल के किनारे स्थित है, बारीक दूरी वाली छवियों को uv तल (ऊपर दिखाए गए दो-प्लेन मानकीकरण में) पर लिया जाना चाहिए। | ||
एक प्रकाश क्षेत्र में छवियों की संख्या और व्यवस्था, और प्रत्येक छवि के विभेदन को एक साथ 4D प्रकाश क्षेत्र का, "प्रतिचयन" कहा जाता है।<ref>Chai (2000)</ref> अधिधारण प्रकाश और प्रतिबिंब के प्रभाव भी रोचक हैं।<ref>Durand (2005)</ref><ref>Ramamoorthi (2006)</ref> | |||
| Line 86: | Line 93: | ||
चयनित अनुप्रयोग: | चयनित अनुप्रयोग: | ||
[[Image:Gershun-light-field-fig24.png|right|thumb|200px| एक अधोमुखी प्रकाश स्रोत (F-F') एक प्रकाश क्षेत्र को प्रेरित करता है जिसका विकिरण सदिश बाहर की ओर वक्र होता है। कलन का उपयोग करते हुए, गेर्शुन बिंदुओं पर गिरने वाले विकिरण की गणना कर सकता है (पी<sub>1</sub>, पी<sub>2</sub>) सतह पर।<ref>Gershun, fig 24</ref>)]] | [[Image:Gershun-light-field-fig24.png|right|thumb|200px| एक अधोमुखी प्रकाश स्रोत (F-F') एक प्रकाश क्षेत्र को प्रेरित करता है जिसका विकिरण सदिश बाहर की ओर वक्र होता है। कलन का उपयोग करते हुए, गेर्शुन बिंदुओं पर गिरने वाले विकिरण की गणना कर सकता है (पी<sub>1</sub>, पी<sub>2</sub>) सतह पर।<ref>Gershun, fig 24</ref>)]] | ||
रोशनी इंजीनियरिंग- प्रकाश क्षेत्र का अध्ययन करने के लिए गेर्शुन का कारण (बंद रूप में) रोशनी के प्रतिरूप को प्राप्त करना था जो इन सतहों के ऊपर स्थित विभिन्न आकृतियों के प्रकाश स्रोतों के कारण सतहों पर देखा जाएगा।<ref>Ashdown 1993</ref> रोशनी इंजीनियरिंग के लिए समर्पित प्रकाशिकी की शाखा अबिम्ब प्रकाशिकी है।<ref>Chaves 2015; Winston 2005</ref> यह व्यापक रूप से प्रवाह रेखाओं (गेर्शुन की फ्लक्स लाइन) और सदिश प्रवाह (गेर्शुन के प्रकाश वेक्टर) की अवधारणा का उपयोग करता है। हालांकि, प्रकाश क्षेत्र (इस स्थिति में प्रकाश किरणों को परिभाषित करने वाली स्थिति और दिशाएं) समान्यतः [[चरण स्थान]] और [[हैमिल्टनियन प्रकाशिकी]] के संदर्भ में वर्णित हैं। | |||
* | * प्रकाश क्षेत्र अनुवाद- किसी दृश्य के 4D प्रकाश क्षेत्र से उपयुक्त 2D अंशअ निकालने से दृश्य के नए दृश्य देखने को मिलते हैं।<ref>Levoy 1996; Gortler 1996</ref> प्रकाश क्षेत्र अनुवाद छवि-आधारित अनुवाद का एक रूप है । | ||
* | * कृत्रिम द्वारक छायाचित्रण - एक प्रकाश क्षेत्र में प्रतिरूपित एक उपयुक्त 4D उपवर्ग को एकीकृत करने से उस दृश्य का अनुमान लगाया जा सकता है जिसे परिमित (यानी, गैर-[[पिनहोल]]) द्वारक वाले कैमरे द्वारा प्रग्रहण किया जाएगा। इस तरह के दृश्य में क्षेत्र की परिमित गहराई होती है। इस एकीकरण को करने से पहले प्रकाश क्षेत्र को अपरुपक विभिन्न फ्रंटो-समानांतर पर ध्यान केंद्रित कर सकता है<ref>Isaksen 2000</ref> <ref>Vaish 2005</ref>। प्रकाश क्षेत्र को प्रग्रहण करने वाले डिजिटल कैमरों द्वारा प्रग्रहण की गई छवियां<ref name="ng" />पुनः ध्यान केन्द्रित किया जा सकता है। | ||
* 3D डिस्प्ले-प्रौद्योगिकी का उपयोग करके एक प्रकाश क्षेत्र प्रस्तुत करना जो प्रत्येक प्रतिरूप को भौतिक स्थान में उपयुक्त किरण के लिए मेल करता है, मूल दृश्य को देखने के लिए एक [[ऑटोस्टेरोस्कोपी]] दृश्य प्रभाव पैदा करता है। ऐसा करने के लिए गैर-डिजिटल तकनीकों में [[ अभिन्न फोटोग्राफी | अभिन्न फोटोग्राफी]] , [[वॉल्यूमेट्रिक डिस्प्ले|आयतनमितीय डिस्प्ले]] और [[ होलोग्रफ़ी | होलोग्रफ़ी]] समिलित हैं; डिजिटल तकनीकों में एक उच्च-विभेदन डिस्प्ले स्क्रीन पर लेंसलेट की एक सरणी रखना, या वीडियो प्रकल्प की एक सरणी का उपयोग करके लेंसलेट की एक सरणी पर काल्पनिक को प्रकल्प करना समिलित है। वीडियो कैमरों की एक सरणी समय-भिन्न प्रकाश क्षेत्र को प्रग्रहण और प्रदर्शित कर सकती है। यह अनिवार्य रूप से एक [[ जेडडी टेलीविजन | जेडडी टेलीविजन]] पद्धति का गठन करता है।<ref>Javidi 2002; Matusik 2004</ref> | |||
* मस्तिष्क इमेजिंग- तंत्रिका गतिविधि को [[जीसीएएमपी|GCAMP]] जैसे प्रतिवर्ती प्रतिदीप्ति मार्करों के साथ आनुवंशिक रूप से संकेतन न्यूरॉन्स द्वारा वैकल्पिक रूप से अभिलेखबद्ध किया जा सकता है जो वास्तविक समय में [[कैल्शियम आयन]] की उपस्थिति का संकेत देते हैं। चूंकि प्रकाश क्षेत्र सूक्ष्मदर्शिकी एक ही फ्रेम में पूर्ण मात्रा की जानकारी को प्रग्रहण करता है, इसलिए वीडियो फ्रैमरेट पर बड़ी मात्रा में उत्तम तरीके से वितरित व्यक्तिगत न्यूरॉन्स में तंत्रिका गतिविधि की निगरानी करना संभव है।<ref>Grosenick, 2009, 2017; Perez, 2015</ref> मस्तिष्क के ऊतकों में प्रकाशिकी विचलन के बाद भी और आयति छवि के पुनर्निर्माण के बिना तंत्रिका गतिविधि का मात्रात्मक माप किया जा सकता है,<ref>Pegard, 2016</ref> और हजारों न्यूरॉन्स में गतिविधि की निगरानी के लिए उपयोग किया जाता है।<ref>Grosenick, 2017</ref> | |||
* सामान्यीकृत दृश्य पुनर्निर्माण (GSR) - यह [[कई छवियों से 3डी पुनर्निर्माण|कई छवियों से 3D पुनर्निर्माण]] की एक विधि है जो एक सामान्यीकृत प्रकाश क्षेत्र का प्रतिनिधित्व करने वाला एक दृश्य प्रतिरूप बनाता है।<ref name="auto">Leffingwell, 2018</ref> प्रकाश क्षेत्र दृश्य में हर बिंदु के माध्यम से हर दिशा में बहने वाले प्रकाश का प्रतिनिधित्व करता है। स्थिति क्षेत्र दृश्य में हर बिंदु पर व्याप्त पदार्थ के प्रकाश संपर्क गुणों का प्रतिनिधित्व करता है। GSR तंत्रिक रेडियंस क्षेत्र (NeRFs), प्लेनॉक्सल्स और उलटा प्रकाश परिवहन का उपयोग करके किया जा सकता है,<ref>Mildenhall, 2020</ref> <ref>Yu & Fridovich-Keil, 2021</ref> ।<ref name="auto" /> | |||
* स्वलिखित त्रिविमचित्र - इमेज उत्पादन और स्वलिखित त्रिविमचित्र के लिए कृत्रिम आकृति का पूर्व विरूपण प्रकाश क्षेत्र के आरंभ उदाहरणों में से एक है।<ref>Halle 1991, 1994</ref> | |||
* रोशनी में घटाव- [[चकाचौंध (दृष्टि)|रोशनी (दृष्टि)]] कैमरा बॉडी के अंदर प्रकाश के कई बिखराव और लेंस प्रकिशिकि के कारण उत्पन्न होती है जो छवि के वैषम्य को कम करती है। जबकि रोशनी का विश्लेषण 2D छवि स्थल में किया गया है,<ref>Talvala 2007</ref> इसे 4D किरण-स्थल घटना के रूप में पहचानना उपयोगी है।<ref name=Raskar>Raskar 2008</ref> एक कैमरे के अंदर किरण-स्थल का सांख्यिकीय विश्लेषण करने से रोशनी की कलाकृतियों को वर्गीकृत करने और हटाने की अनुमति मिलती है। किरण-स्थान में, रोशनी उच्च आवृत्ति शोर के रूप में व्यवहार करती है और इसे बाहरी अस्वीकृति से कम किया जा सकता है। कैमरे के अंदर प्रकाश क्षेत्र को प्रग्रहण करके ऐसा विश्लेषण किया जा सकता है, लेकिन इसके परिणामस्वरूप स्थानिक संकल्प का नुकसान होता है। एक समान और गैर-समान किरण नमूनाकरण का उपयोग छवि संकल्प में महत्वपूर्ण समझौता किए बिना रोशनी को कम करने के लिए किया जा सकता है।<ref name=Raskar/> | |||
| Line 122: | Line 131: | ||
* गेरशुन, ए. (1936). द लाइट फील्ड, मॉस्को, 1936। पी. मून और जी. टिमोचेंको द्वारा गणित और भौतिकी जर्नल में अनुवादित, वॉल्यूम। XVIII, एमआईटी, 1939, पीपी। 51-151। | * गेरशुन, ए. (1936). द लाइट फील्ड, मॉस्को, 1936। पी. मून और जी. टिमोचेंको द्वारा गणित और भौतिकी जर्नल में अनुवादित, वॉल्यूम। XVIII, एमआईटी, 1939, पीपी। 51-151। | ||
* गोर्टलर, एस.जे., ग्रजेसजुक, आर., स्जेलिस्की, आर., कोहेन, एम. (1996)। [http://portal.acm.org/citation.cfm?id=237200 द ल्यूमिग्राफ], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 43-54। | * गोर्टलर, एस.जे., ग्रजेसजुक, आर., स्जेलिस्की, आर., कोहेन, एम. (1996)। [http://portal.acm.org/citation.cfm?id=237200 द ल्यूमिग्राफ], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 43-54। | ||
* लेवॉय, एम., हनराहन, पी. (1996)। [http://graphics.stanford.edu/papers/light/ लाइट फील्ड | * लेवॉय, एम., हनराहन, पी. (1996)। [http://graphics.stanford.edu/papers/light/ लाइट फील्ड अनुवाद], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 31-42। | ||
* मून, पी., स्पेंसर, डी.ई. (1981)। फोटोग्राफिक फील्ड, एमआईटी प्रेस। | * मून, पी., स्पेंसर, डी.ई. (1981)। फोटोग्राफिक फील्ड, एमआईटी प्रेस। | ||
* वोंग, टी.टी., फू, सी.डब्ल्यू., हेंग, पी.ए., लेउंग सी.एस. (2002)। [https://ieeexplore.ieee.org/document/1040963 प्लेनॉप्टिक-रोशनी फंक्शन], IEEE ट्रांस। मल्टीमीडिया, वॉल्यूम। 4, संख्या 3, पीपी। 361-371। | * वोंग, टी.टी., फू, सी.डब्ल्यू., हेंग, पी.ए., लेउंग सी.एस. (2002)। [https://ieeexplore.ieee.org/document/1040963 प्लेनॉप्टिक-रोशनी फंक्शन], IEEE ट्रांस। मल्टीमीडिया, वॉल्यूम। 4, संख्या 3, पीपी। 361-371। | ||
| Line 129: | Line 138: | ||
* जी. वेट्ज़स्टीन, आई. इहर्के, डब्ल्यू. हेड्रिच (2013) [http://www.cs.ubc.ca/labs/imager/tr/2010/TheoryOfPlenopticMultiplexing/PlenopticMultiplexing-IJCV2012.pdf प्लेनोप्टिक मल्टीप्लेक्सिंग और पुनर्निर्माण पर], इंटरनेशनल जर्नल ऑफ कम्प्यूटर विजन (आईजेसीवी), खंड 101, अंक 2, पीपी 384-400। | * जी. वेट्ज़स्टीन, आई. इहर्के, डब्ल्यू. हेड्रिच (2013) [http://www.cs.ubc.ca/labs/imager/tr/2010/TheoryOfPlenopticMultiplexing/PlenopticMultiplexing-IJCV2012.pdf प्लेनोप्टिक मल्टीप्लेक्सिंग और पुनर्निर्माण पर], इंटरनेशनल जर्नल ऑफ कम्प्यूटर विजन (आईजेसीवी), खंड 101, अंक 2, पीपी 384-400। | ||
* राममूर्ति, आर., महाजन, डी., बेलहुमुर, पी. (2006)। [https://web.archive.org/web/20060828222733/http://www1.cs.columbia.edu/~ravir/papers/firstorder/index.html लाइटिंग, शेडिंग और शैडो का पहला क्रम विश्लेषण], एसीएम टॉग। | * राममूर्ति, आर., महाजन, डी., बेलहुमुर, पी. (2006)। [https://web.archive.org/web/20060828222733/http://www1.cs.columbia.edu/~ravir/papers/firstorder/index.html लाइटिंग, शेडिंग और शैडो का पहला क्रम विश्लेषण], एसीएम टॉग। | ||
* ज्विकर, एम., माटुसिक, डब्ल्यू., डूरंड, एफ., फिस्टर, एच. (2006)। [http://people.csail.mit.edu/wojciech/DispAntiAlias/ एंटीअलियासिंग फॉर ऑटोमल्टिस्कोपिक 3डी डिस्प्ले], यूरोग्राफिक्स सिम्पोजियम ऑन | * ज्विकर, एम., माटुसिक, डब्ल्यू., डूरंड, एफ., फिस्टर, एच. (2006)। [http://people.csail.mit.edu/wojciech/DispAntiAlias/ एंटीअलियासिंग फॉर ऑटोमल्टिस्कोपिक 3डी डिस्प्ले], यूरोग्राफिक्स सिम्पोजियम ऑन अनुवाद, 2006। | ||
* एनजी, आर। (2005)। [http://graphics.stanford.edu/papers/fourierphoto/ फूरियर | * एनजी, आर। (2005)। [http://graphics.stanford.edu/papers/fourierphoto/ फूरियर अंशअ फोटोग्राफी], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 735-744। | ||
* डुरंड, एफ., होल्ज़शच, एन., सोलर, सी., चान, ई., सिलियन, एफ.एक्स. (2005)। [http://people.csail.mit.edu/fredo/PUBLI/Fourier/ प्रकाश परिवहन का एक आवृत्ति विश्लेषण], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 1115–1126। | * डुरंड, एफ., होल्ज़शच, एन., सोलर, सी., चान, ई., सिलियन, एफ.एक्स. (2005)। [http://people.csail.mit.edu/fredo/PUBLI/Fourier/ प्रकाश परिवहन का एक आवृत्ति विश्लेषण], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 1115–1126। | ||
* चाई, जे.-एक्स., टोंग, एक्स., चान, एस.-सी., शुम, एच. (2000)। [http://graphics.cs.cmu.edu/projects/plenoptic-sampling/ps_projectpage.htm प्लेनॉप्टिक सैंपलिंग], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी 307–318। | * चाई, जे.-एक्स., टोंग, एक्स., चान, एस.-सी., शुम, एच. (2000)। [http://graphics.cs.cmu.edu/projects/plenoptic-sampling/ps_projectpage.htm प्लेनॉप्टिक सैंपलिंग], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी 307–318। | ||
| Line 138: | Line 147: | ||
=== कैमरा === | === कैमरा === | ||
* मारवाह, के., वेटजस्टीन, जी., बांदो, वाई., रास्कर, आर. (2013)। [http://web.media.mit.edu/~gordonw/CompressiveLightFieldPhotography/ कंप्रेसिव लाइट फ़ील्ड फ़ोटोग्राफ़ी ओवरकंप्लीट डिक्शनरी और ऑप्टिमाइज़्ड प्रोजेक्शन का इस्तेमाल करके ], ग्राफिक्स पर ACM लेनदेन (SIGGRAPH)। | * मारवाह, के., वेटजस्टीन, जी., बांदो, वाई., रास्कर, आर. (2013)। [http://web.media.mit.edu/~gordonw/CompressiveLightFieldPhotography/ कंप्रेसिव लाइट फ़ील्ड फ़ोटोग्राफ़ी ओवरकंप्लीट डिक्शनरी और ऑप्टिमाइज़्ड प्रोजेक्शन का इस्तेमाल करके ], ग्राफिक्स पर ACM लेनदेन (SIGGRAPH)। | ||
* लियांग, सी.के., लिन, टी.एच., वोंग, बी.वाई., लियू, सी., चेन, एच. एच. (2008)। [https://web.archive.org/web/20080513175740/http://mpac.ee.ntu.edu.tw/~chiakai/pap/ प्रोग्रामेबल | * लियांग, सी.के., लिन, टी.एच., वोंग, बी.वाई., लियू, सी., चेन, एच. एच. (2008)। [https://web.archive.org/web/20080513175740/http://mpac.ee.ntu.edu.tw/~chiakai/pap/ प्रोग्रामेबल द्वारक फोटोग्राफी: मल्टीप्लेक्स लाइट फील्ड एक्विजिशन], प्रोक। एसीएम सिग्राफ। | ||
* वीरराघवन, ए., रस्कर, आर., अग्रवाल, ए., मोहन, ए., टंबलिन, जे. (2007)। [http://web.media.mit.edu/~raskar/Mask/ डैपल्ड फ़ोटोग्राफ़ी: हेटेरोडाइन्ड लाइट फ़ील्ड्स और कोडेड अपर्चर रीफ़ोकसिंग के लिए बेहतर कैमरे को मास्क करें], प्रोक. एसीएम सिग्राफ। | * वीरराघवन, ए., रस्कर, आर., अग्रवाल, ए., मोहन, ए., टंबलिन, जे. (2007)। [http://web.media.mit.edu/~raskar/Mask/ डैपल्ड फ़ोटोग्राफ़ी: हेटेरोडाइन्ड लाइट फ़ील्ड्स और कोडेड अपर्चर रीफ़ोकसिंग के लिए बेहतर कैमरे को मास्क करें], प्रोक. एसीएम सिग्राफ। | ||
* जॉर्जिएव, टी., झेंग, सी., नायर, एस., करलेस, बी., सेल्सिन, डी., इंतवाला, सी. (2006)। [http://www.tgeorgiev.net/Spatioangular.pdf इंटीग्रल फ़ोटोग्राफ़ी में अनुपात-कोणीय | * जॉर्जिएव, टी., झेंग, सी., नायर, एस., करलेस, बी., सेल्सिन, डी., इंतवाला, सी. (2006)। [http://www.tgeorgiev.net/Spatioangular.pdf इंटीग्रल फ़ोटोग्राफ़ी में अनुपात-कोणीय विभेदन ट्रेड-ऑफ़], प्रोक। ईजीएसआर 2006। | ||
* कनाडे, टी., सैटो, एच., वेदुला, एस. (1998)। [https://www.cs.cmu.edu/~virtualized-reality/3DRoom/TR.htm 3D रूम: सिंक्रोनाइज्ड मल्टिपल वीडियो स्ट्रीम्स द्वारा डिजिटाइज़िंग टाइम-वैरिंग 3D इवेंट्स ], टेक रिपोर्ट CMU-RI-TR-98- 34, दिसंबर 1998। | * कनाडे, टी., सैटो, एच., वेदुला, एस. (1998)। [https://www.cs.cmu.edu/~virtualized-reality/3DRoom/TR.htm 3D रूम: सिंक्रोनाइज्ड मल्टिपल वीडियो स्ट्रीम्स द्वारा डिजिटाइज़िंग टाइम-वैरिंग 3D इवेंट्स ], टेक रिपोर्ट CMU-RI-TR-98- 34, दिसंबर 1998। | ||
* लेवॉय, एम। (2002)। [http://graphics.stanford.edu/projects/gantry/ स्टैनफोर्ड स्फेरिकल गैन्ट्री]। | * लेवॉय, एम। (2002)। [http://graphics.stanford.edu/projects/gantry/ स्टैनफोर्ड स्फेरिकल गैन्ट्री]। | ||
| Line 146: | Line 155: | ||
* एनजी, आर., लेवॉय, एम., ब्रेडिफ, एम., डुवल, जी., होरोविट्ज़, एम., हनराहन, पी. (2005)। [http://graphics.stanford.edu/papers/lfcamera/ हैंड-हेल्ड प्लेनोप्टिक कैमरा के साथ लाइट फील्ड फोटोग्राफी], स्टैनफोर्ड टेक रिपोर्ट CTSR 2005-02, अप्रैल, 2005। | * एनजी, आर., लेवॉय, एम., ब्रेडिफ, एम., डुवल, जी., होरोविट्ज़, एम., हनराहन, पी. (2005)। [http://graphics.stanford.edu/papers/lfcamera/ हैंड-हेल्ड प्लेनोप्टिक कैमरा के साथ लाइट फील्ड फोटोग्राफी], स्टैनफोर्ड टेक रिपोर्ट CTSR 2005-02, अप्रैल, 2005। | ||
* विलबर्न, बी., जोशी, एन., वैश, वी., तलवाला, ई., एंट्यूनेज़, ई., बार्थ, ए., एडम्स, ए., लेवॉय, एम., होरोविट्ज़, एम. (2005)। [http://graphics.stanford.edu/papers/CameraArray/ बड़े कैमरा एरे का उपयोग करके उच्च प्रदर्शन इमेजिंग], ग्राफिक्स पर ACM लेनदेन (प्रोक. SIGGRAPH), वॉल्यूम। 24, संख्या 3, पीपी। 765–776। | * विलबर्न, बी., जोशी, एन., वैश, वी., तलवाला, ई., एंट्यूनेज़, ई., बार्थ, ए., एडम्स, ए., लेवॉय, एम., होरोविट्ज़, एम. (2005)। [http://graphics.stanford.edu/papers/CameraArray/ बड़े कैमरा एरे का उपयोग करके उच्च प्रदर्शन इमेजिंग], ग्राफिक्स पर ACM लेनदेन (प्रोक. SIGGRAPH), वॉल्यूम। 24, संख्या 3, पीपी। 765–776। | ||
* यांग, जे.सी., एवरेट, एम., ब्यूहलर, सी., मैकमिलन, एल. (2002)। [http://portal.acm.org/citation.cfm?id=581907&dl=ACM&coll=&CFID=15151515&CFTOKEN=6184618 एक रीयल-टाइम डिस्ट्रिब्यूटेड लाइट फील्ड कैमरा], प्रोक। यूरोग्राफिक्स | * यांग, जे.सी., एवरेट, एम., ब्यूहलर, सी., मैकमिलन, एल. (2002)। [http://portal.acm.org/citation.cfm?id=581907&dl=ACM&coll=&CFID=15151515&CFTOKEN=6184618 एक रीयल-टाइम डिस्ट्रिब्यूटेड लाइट फील्ड कैमरा], प्रोक। यूरोग्राफिक्स अनुवाद वर्कशॉप 2002। | ||
* [http://www.cafadis.ull.es CAFADIS कैमरा] | * [http://www.cafadis.ull.es CAFADIS कैमरा] | ||
| Line 170: | Line 179: | ||
* हीड, एफ., वेटजस्टीन, जी., रस्कर, आर., हेड्रिच, डब्ल्यू. (2013) [https://web.archive.org/web/20130703184026/http://adaptiveimagesynthesis.com/ के लिए अनुकूली इमेज सिंथेसिस कंप्रेसिव डिस्प्ले], ग्राफिक्स पर ACM लेनदेन (SIGGRAPH) | * हीड, एफ., वेटजस्टीन, जी., रस्कर, आर., हेड्रिच, डब्ल्यू. (2013) [https://web.archive.org/web/20130703184026/http://adaptiveimagesynthesis.com/ के लिए अनुकूली इमेज सिंथेसिस कंप्रेसिव डिस्प्ले], ग्राफिक्स पर ACM लेनदेन (SIGGRAPH) | ||
* वेटजस्टाइन, जी., रस्कर, आर., हेड्रिच, डब्ल्यू. (2011) [http://www.cs.ubc.ca/labs/imager/tr/2011/LFBOS/index.html हैंड-हेल्ड श्लीरेन फोटोग्राफी विद लाइट फील्ड जांच], कम्प्यूटेशनल फोटोग्राफी पर IEEE अंतर्राष्ट्रीय सम्मेलन (ICCP) | * वेटजस्टाइन, जी., रस्कर, आर., हेड्रिच, डब्ल्यू. (2011) [http://www.cs.ubc.ca/labs/imager/tr/2011/LFBOS/index.html हैंड-हेल्ड श्लीरेन फोटोग्राफी विद लाइट फील्ड जांच], कम्प्यूटेशनल फोटोग्राफी पर IEEE अंतर्राष्ट्रीय सम्मेलन (ICCP) | ||
* पेरेज़, एफ।, मारीचल, जेजी, रोड्रिगेज, जेएम (2008)। [http://www.eurasip.org/Proceedings/Eusipco/Eusipco2008/papers/1569101893.pdf डिस्क्रीट फोकल | * पेरेज़, एफ।, मारीचल, जेजी, रोड्रिगेज, जेएम (2008)। [http://www.eurasip.org/Proceedings/Eusipco/Eusipco2008/papers/1569101893.pdf डिस्क्रीट फोकल खंड ट्रांसफॉर्म], प्रोक। यूसिपको | ||
* रस्कर, आर., अग्रवाल, ए., विल्सन, सी., वीरराघवन, ए. (2008)। [https://web.archive.org/web/20080829185928/http://www.merl.com/people/agrawal/sig08/index.html ग्लेयर अवेयर फोटोग्राफी: कैमरा लेंस के ग्लेयर इफेक्ट को कम करने के लिए 4डी रे सैम्पलिंग], प्रक्रिया। एसीएम सिग्राफ। | * रस्कर, आर., अग्रवाल, ए., विल्सन, सी., वीरराघवन, ए. (2008)। [https://web.archive.org/web/20080829185928/http://www.merl.com/people/agrawal/sig08/index.html ग्लेयर अवेयर फोटोग्राफी: कैमरा लेंस के ग्लेयर इफेक्ट को कम करने के लिए 4डी रे सैम्पलिंग], प्रक्रिया। एसीएम सिग्राफ। | ||
* तलवाला, ई-वी., एडम्स, ए., होरोविट्ज़, एम., लेवॉय, एम. (2007)। [http://graphics.stanford.edu/papers/glare_removal/ वीलिंग ग्लेयर इन हाई डायनामिक रेंज इमेजिंग], प्रोक। एसीएम सिग्राफ। | * तलवाला, ई-वी., एडम्स, ए., होरोविट्ज़, एम., लेवॉय, एम. (2007)। [http://graphics.stanford.edu/papers/glare_removal/ वीलिंग ग्लेयर इन हाई डायनामिक रेंज इमेजिंग], प्रोक। एसीएम सिग्राफ। | ||
* हाले, एम., बेंटन, एस., क्लुग, एम., अंडरकॉफ़्लर, जे. (1991)। [http://www.spl.harvard.edu/~halazar/pubs/ultragram_spie91_preprint.pdf अल्ट्राग्राम: एक सामान्यीकृत होलोग्राफिक स्टीरियोग्राम]{{Dead link|date=February 2020 |bot=InternetArchiveBot |fix-attempted=yes }}, एसपीआईई वॉल्यूम। 1461, प्रैक्टिकल होलोग्राफी वी, एस.ए. बेंटन, एड., पीपी। 142-155। | * हाले, एम., बेंटन, एस., क्लुग, एम., अंडरकॉफ़्लर, जे. (1991)। [http://www.spl.harvard.edu/~halazar/pubs/ultragram_spie91_preprint.pdf अल्ट्राग्राम: एक सामान्यीकृत होलोग्राफिक स्टीरियोग्राम]{{Dead link|date=February 2020 |bot=InternetArchiveBot |fix-attempted=yes }}, एसपीआईई वॉल्यूम। 1461, प्रैक्टिकल होलोग्राफी वी, एस.ए. बेंटन, एड., पीपी। 142-155। | ||
* ज़ोमेट, ए., फेल्डमैन, डी., पेलेग, एस., वीन्सहॉल, डी. (2003)। [http://www2.कंप्यूटर.org/portal/web/csdl/doi/10.1109/TPAMI.2003.1201823 Mosaicing New Views: The Crossed-Slits Projection ], IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), Vol. 25, नंबर 6, जून 2003, पीपी। 741–754। | * ज़ोमेट, ए., फेल्डमैन, डी., पेलेग, एस., वीन्सहॉल, डी. (2003)। [http://www2.कंप्यूटर.org/portal/web/csdl/doi/10.1109/TPAMI.2003.1201823 Mosaicing New Views: The Crossed-Slits Projection ], IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), Vol. 25, नंबर 6, जून 2003, पीपी। 741–754। | ||
* वैश, वी., गर्ग, जी., तलवाला, ई., एंट्यूनेज़, ई., विलबर्न, बी., होरोविट्ज़, एम., लेवॉय, एम. (2005)। [http://portal.acm.org/citation.cfm?id=1099539.1100041&coll=&coll=&dl=GUIDE&CFID=15151515&CFTOKEN=6184618 व्यूइंग ट्रांसफॉर्म के शीयर-वार्प फैक्टराइजेशन का उपयोग कर सिंथेटिक | * वैश, वी., गर्ग, जी., तलवाला, ई., एंट्यूनेज़, ई., विलबर्न, बी., होरोविट्ज़, एम., लेवॉय, एम. (2005)। [http://portal.acm.org/citation.cfm?id=1099539.1100041&coll=&coll=&dl=GUIDE&CFID=15151515&CFTOKEN=6184618 व्यूइंग ट्रांसफॉर्म के शीयर-वार्प फैक्टराइजेशन का उपयोग कर सिंथेटिक द्वारक फोकसिंग], प्रोक। सीवीपीआर 2005 के संयोजन में सुरक्षा और सुरक्षा के लिए उन्नत 3डी इमेजिंग पर कार्यशाला। | ||
*बेडर्ड, एन., शोप, टी., होबरमैन, ए., हरालम, एमए, शेख, एन., कोवासेविक, जे., बलराम, एन., तोसिक, आई. (2016)। [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5231297/ मध्य कान की वीवो इमेजिंग में 3डी के लिए लाइट फील्ड ओटोस्कोप डिजाइन]। बायोमेडिकल ऑप्टिक्स एक्सप्रेस, 8(1), पीपी. 260-272. | *बेडर्ड, एन., शोप, टी., होबरमैन, ए., हरालम, एमए, शेख, एन., कोवासेविक, जे., बलराम, एन., तोसिक, आई. (2016)। [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5231297/ मध्य कान की वीवो इमेजिंग में 3डी के लिए लाइट फील्ड ओटोस्कोप डिजाइन]। बायोमेडिकल ऑप्टिक्स एक्सप्रेस, 8(1), पीपी. 260-272. | ||
*कार्यगिआनी, एस., मार्टिनेलो, एम., स्पिनौलास, एल., फ्रॉसार्ड, पी., टॉसिक, आई. (2018)। [https://ieeexplore.ieee.org/abstract/document/8451719/ लाइट-फील्ड डेटा से ईयरड्रम का ऑटोमेटेड रजिस्ट्रेशन] . इमेज प्रोसेसिंग पर IEEE अंतर्राष्ट्रीय सम्मेलन (ICIP) | *कार्यगिआनी, एस., मार्टिनेलो, एम., स्पिनौलास, एल., फ्रॉसार्ड, पी., टॉसिक, आई. (2018)। [https://ieeexplore.ieee.org/abstract/document/8451719/ लाइट-फील्ड डेटा से ईयरड्रम का ऑटोमेटेड रजिस्ट्रेशन] . इमेज प्रोसेसिंग पर IEEE अंतर्राष्ट्रीय सम्मेलन (ICIP) | ||
* रैडेमाकर, पी., बिशप, जी. (1998)। [http://portal.acm.org/citation.cfm?id=280871&coll=portal&dl=ACM मल्टीपल-सेंटर-ऑफ-प्रोजेक्शन इमेज], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस। | * रैडेमाकर, पी., बिशप, जी. (1998)। [http://portal.acm.org/citation.cfm?id=280871&coll=portal&dl=ACM मल्टीपल-सेंटर-ऑफ-प्रोजेक्शन इमेज], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस। | ||
* इसाकसेन, ए., मैकमिलन, एल., गोर्टलर, एस.जे. (2000)। [http://portal.acm.org/citation.cfm?coll=GUIDE&dl=GUIDE&id=344929 डायनेमिकली रीपैरामीटराइज़्ड लाइट फील्ड्स], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 297–306। | * इसाकसेन, ए., मैकमिलन, एल., गोर्टलर, एस.जे. (2000)। [http://portal.acm.org/citation.cfm?coll=GUIDE&dl=GUIDE&id=344929 डायनेमिकली रीपैरामीटराइज़्ड लाइट फील्ड्स], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 297–306। | ||
* बुहलर, सी., बॉसे, एम., मैकमिलन, एल., गोर्टलर, एस., कोहेन, एम. (2001)। [http://portal.acm.org/citation.cfm?id=383309&dl=ACM&coll=&CFID=15151515&CFTOKEN=6184618 अनस्ट्रक्चर्ड ल्यूमिग्राफ | * बुहलर, सी., बॉसे, एम., मैकमिलन, एल., गोर्टलर, एस., कोहेन, एम. (2001)। [http://portal.acm.org/citation.cfm?id=383309&dl=ACM&coll=&CFID=15151515&CFTOKEN=6184618 अनस्ट्रक्चर्ड ल्यूमिग्राफ अनुवाद], प्रोक। एसीएम सिग्राफ, एसीएम प्रेस। | ||
* एशडाउन, आई. (1993). [http://citeseer.ist.psu.edu/ashdown92nearfield.html नियर-फ़ील्ड फ़ोटोमेट्री: ए न्यू अप्रोच ], जर्नल ऑफ़ द इल्युमिनेटिंग इंजीनियरिंग सोसाइटी, वॉल्यूम। 22, नंबर 1, विंटर, 1993, पीपी. 163–180। | * एशडाउन, आई. (1993). [http://citeseer.ist.psu.edu/ashdown92nearfield.html नियर-फ़ील्ड फ़ोटोमेट्री: ए न्यू अप्रोच ], जर्नल ऑफ़ द इल्युमिनेटिंग इंजीनियरिंग सोसाइटी, वॉल्यूम। 22, नंबर 1, विंटर, 1993, पीपी. 163–180। | ||
* चेव्स, जे. (2015) [https://books.google.com/books?id=e11ECgAAQBAJ नॉनइमेजिंग ऑप्टिक्स का परिचय, दूसरा संस्करण], सीआरसी प्रेस | * चेव्स, जे. (2015) [https://books.google.com/books?id=e11ECgAAQBAJ नॉनइमेजिंग ऑप्टिक्स का परिचय, दूसरा संस्करण], सीआरसी प्रेस | ||
| Line 186: | Line 195: | ||
* पेगार्ड, एन.सी., लियू एच.वाई., एंटिपा, एन., जेरलॉक एम., एडेसनिक, एच., और वालर, एल.. 3डी तंत्रिका गतिविधि रिकॉर्डिंग के लिए कंप्रेसिव लाइट-फील्ड माइक्रोस्कोपी। ऑप्टिका 3, नहीं. 5, पीपी। 517–524 (2016)। | * पेगार्ड, एन.सी., लियू एच.वाई., एंटिपा, एन., जेरलॉक एम., एडेसनिक, एच., और वालर, एल.. 3डी तंत्रिका गतिविधि रिकॉर्डिंग के लिए कंप्रेसिव लाइट-फील्ड माइक्रोस्कोपी। ऑप्टिका 3, नहीं. 5, पीपी। 517–524 (2016)। | ||
* लेफिंगवेल, जे., मेघेर, डी., महमूद, के., एकर्सन, एस. (2018)। [https://arxiv.org/abs/1803.08496v3 सामान्यीकृत दृश्य पुनर्निर्माण। ] arXiv:1803.08496v3 [cs.CV], पीपी। 1-13। | * लेफिंगवेल, जे., मेघेर, डी., महमूद, के., एकर्सन, एस. (2018)। [https://arxiv.org/abs/1803.08496v3 सामान्यीकृत दृश्य पुनर्निर्माण। ] arXiv:1803.08496v3 [cs.CV], पीपी। 1-13। | ||
* मिल्डेनहॉल, बी., श्रीनिवासन, पी.पी., तनिकिक, एम., बैरोन, जे.टी., राममूर्ति, आर., और एनजी, आर. (2020)। [https://doi.org/10.1007/978-3-030-58452-8_24 "NeRF: दृश्य संश्लेषण के लिए तंत्रिका | * मिल्डेनहॉल, बी., श्रीनिवासन, पी.पी., तनिकिक, एम., बैरोन, जे.टी., राममूर्ति, आर., और एनजी, आर. (2020)। [https://doi.org/10.1007/978-3-030-58452-8_24 "NeRF: दृश्य संश्लेषण के लिए तंत्रिका विकिरण क्षेत्रों के रूप में दृश्यों का प्रतिनिधित्व करना।"] कंप्यूटर विजन - ECCV 2020, 405–421। | ||
* यू, ए., फ्रिडोविच-कील, एस., टैनिक, एम., चेन, क्यू., रेचट, बी., कानाज़ावा, ए. (2021)। [https://arxiv.org/abs/2111.11215 प्लेनॉक्सल्स: | * यू, ए., फ्रिडोविच-कील, एस., टैनिक, एम., चेन, क्यू., रेचट, बी., कानाज़ावा, ए. (2021)। [https://arxiv.org/abs/2111.11215 प्लेनॉक्सल्स: तंत्रिक नेटवर्क के बिना रेडियंस फील्ड्स।] आर्क्सिव:2111.11215, पीपी 1-25 | ||
* {{cite journal|last1=Perez|first1=CC|last2=Lauri|first2=A|last3=Symvoulidis|first3=P|last4=Cappetta|first4=M|last5=Erdmann|first5=A|last6=Westmeyer|first6=GG|display-authors=2|title=टर्न-की लाइट फील्ड कैमरा का उपयोग करके जेब्राफिश लार्वा के व्यवहार में कैल्शियम न्यूरोइमेजिंग।|journal=Journal of Biomedical Optics|date=September 2015|volume=20|issue=9|pages=096009|doi=10.1117/1.JBO.20.9.096009|pmid=26358822|bibcode=2015JBO....20i6009C|doi-access=free}} | * {{cite journal|last1=Perez|first1=CC|last2=Lauri|first2=A|last3=Symvoulidis|first3=P|last4=Cappetta|first4=M|last5=Erdmann|first5=A|last6=Westmeyer|first6=GG|display-authors=2|title=टर्न-की लाइट फील्ड कैमरा का उपयोग करके जेब्राफिश लार्वा के व्यवहार में कैल्शियम न्यूरोइमेजिंग।|journal=Journal of Biomedical Optics|date=September 2015|volume=20|issue=9|pages=096009|doi=10.1117/1.JBO.20.9.096009|pmid=26358822|bibcode=2015JBO....20i6009C|doi-access=free}} | ||
*पेरेज़, सी.सी., लॉरी, ए., सिमवॉलिडिस, पी., कैपेटा, एम., एर्डमैन, ए., और वेस्टमेयर, जी.जी. (2015)। टर्न-की लाइट फील्ड कैमरा का उपयोग करके जेब्राफिश लार्वा के व्यवहार में कैल्शियम न्यूरोइमेजिंग। जर्नल ऑफ बायोमेडिकल ऑप्टिक्स, 20(9), 096009-096009। | *पेरेज़, सी.सी., लॉरी, ए., सिमवॉलिडिस, पी., कैपेटा, एम., एर्डमैन, ए., और वेस्टमेयर, जी.जी. (2015)। टर्न-की लाइट फील्ड कैमरा का उपयोग करके जेब्राफिश लार्वा के व्यवहार में कैल्शियम न्यूरोइमेजिंग। जर्नल ऑफ बायोमेडिकल ऑप्टिक्स, 20(9), 096009-096009। | ||
* लियोन, के., गैल्विस, एल., और आर्गुएलो, एच. (2016)। [http://aprendeenlinea.udea.edu.co/revistas/index.php/ingenieria/article/view/24643 मल्टीस्पेक्ट्रल प्रकाश क्षेत्र का पुनर्निर्माण (5डी प्लेनोप्टिक फंक्शन) 2डी अनुमानों से रंगीन कोडेड | * लियोन, के., गैल्विस, एल., और आर्गुएलो, एच. (2016)। [http://aprendeenlinea.udea.edu.co/revistas/index.php/ingenieria/article/view/24643 मल्टीस्पेक्ट्रल प्रकाश क्षेत्र का पुनर्निर्माण (5डी प्लेनोप्टिक फंक्शन) 2डी अनुमानों से रंगीन कोडेड द्वारक के साथ कंप्रेसिव सेंसिंग पर आधारित] रेविस्टा फैकल्टीड डी इंजेनिएरिया यूनिवर्सिडाड डी एंटिओक्विया 80, पीपी। 131। | ||
श्रेणी: प्रकाशिकी | श्रेणी: प्रकाशिकी | ||
श्रेणी:3डी कंप्यूटर ग्राफिक्स | श्रेणी:3डी कंप्यूटर ग्राफिक्स | ||
[[Category:All articles with dead external links]] | |||
[[Category: | [[Category:Articles with dead external links from February 2020]] | ||
[[Category:Articles with permanently dead external links]] | |||
[[Category:Created On 24/03/2023]] | [[Category:Created On 24/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
Latest revision as of 09:21, 16 April 2023
प्रकाश क्षेत्र एक सदिश-कार्य है जो अंतरिक्ष में प्रत्येक बिंदु के माध्यम से प्रत्येक दिशा में बहने वाले प्रकाश की मात्रा का वर्णन करता है। सभी संभावित 'प्रकाश किरणों' का स्थान पंच-आयामी प्लेनोप्टिक कार्य द्वारा दिया जाता है, और प्रत्येक किरण का परिमाण इसकी विकिरण द्वारा दिया जाता है। माइकल फैराडे पहले व्यक्ति थे जिन्होंने प्रस्तावित किया कि प्रकाश को एक क्षेत्र के रूप में व्याख्यायित किया जाना चाहिए, ठीक उसी चुंबकीय क्षेत्र की तरह जिस पर वह काम कर रहे थे।[1] वाक्यांश प्रकाश क्षेत्र एंड्री अलेक्जेंड्रोविच गेर्शुन द्वारा त्रि-आयामी अंतरिक्ष में प्रकाश के विकिरणमापी गुणों पर एक प्राचीन 1936 के पेपर में गढ़ा गया था।
प्रकाश क्षेत्र प्रदर्शन के लिए आधुनिक दृष्टिकोण प्रकाशीय तत्वों के सह-प्रारुपण का पता लगाते हैं और उच्च विभेदन, बढ़े हुए वैषम्य, देखने के लिए व्यापक क्षेत्र और अन्य लाभों को प्राप्त करने के लिए संपीडन संगणना करते हैं।[2]
समान अवधारणाओं को संदर्भित करने के लिए शब्द "विकिरण क्षेत्र" का भी उपयोग किया जा सकता है। इस शब्द का प्रयोग आधुनिक शोध में किया जाता है जैसे तंत्रिका विकिरण क्षेत्र।
प्लेनोप्टिक कार्य
ज्यामितीय प्रकाशिकी के लिए - अर्थात, सुसंगतता (भौतिकी) प्रकाश और प्रकाश की तरंग दैर्ध्य से बड़ी वस्तुओं के लिए - प्रकाश का मूल वाहक एक किरण (प्रकाशिकी) है। किरण के साथ यात्रा करने वाले प्रकाश की मात्रा के लिए माप विकिरण है, जिसे L द्वारा निरूपित किया जाता है और W·sr−1·m−2, में मापा जाता है, यानी वाट (W) प्रति स्टरेडियन (sr) प्रति वर्ग मीटर (m)2). स्टेरेडियन ठोस कोण का एक माप है, और वर्ग मीटर अंतः-अनुभागीय क्षेत्र के माप के रूप में उपयोग किया जाता है, जैसा कि दाईं ओर दिखाया गया है।
रोशनी की अपरिवर्तनीय व्यवस्था से प्रकाशित त्रि-आयामी अंतरिक्ष के क्षेत्र में ऐसी सभी किरणों के साथ विकिरण को प्लेनोप्टिक कार्य कहा जाता है।[3] प्लेनोप्टिक रोशनी कार्य एक आदर्श कार्य है जिसका उपयोग कंप्यूटर दृष्टि और कंप्यूटर चित्रलेख किसी भी संभावित देखने की स्थिति से दृश्य की छवि को व्यक्त करने के लिए किया जाता है। यह संगणनात्मक रूप से अभ्यास में प्रयोग नहीं किया जाता है, लेकिन दृष्टि और लेखाचित्रीय में अन्य अवधारणाओं को समझने में वैचारिक रूप से उपयोगी है।[4] चूंकि अंतरिक्ष में किरणों को तीन निर्देशांक, x, y, और z और दो कोणों θ और ϕ द्वारा प्राचलीकृत किया जा सकता है, जैसा कि बाईं ओर दिखाया गया है, यह एक पांच-आयामी कार्य है, जो कि पांच-आयामी बहुमुख समतुल्य कार्य एक 3D यूक्लिडियन स्थल और 2-गोले का उत्पाद है।
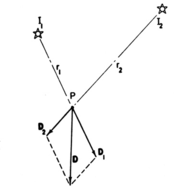
अंतरिक्ष में प्रत्येक बिंदु पर प्रकाश क्षेत्र को सदिशों के एक अनंत संग्रह के रूप में माना जा सकता है, एक बिंदु पर प्रति दिशा में, उनकी विकिरण के आनुपातिक लंबाई के साथ।
रोशनी के किसी भी संग्रह पर, या दिशाओं के पूरे क्षेत्र में इन सदिशों को एकीकृत करना, एक एकल अदिश मान उत्पन्न करता है - उस बिंदु पर कुल विकिरण, और परिणामी दिशा। यह आंकड़ा दो प्रकाश स्रोतों की स्थिति में इस गणना को दर्शाता है। कंप्यूटर लेखाचित्रीय में, त्रि-आयामी अंतरिक्ष के इस सदिश कार्य को सदिश विकिरण क्षेत्र कहा जाता है।[6] क्षेत्र में प्रत्येक बिंदु पर सदिश दिशा की व्याख्या उस बिंदु पर रखी गई समतल सतह के अभिविन्यास के रूप में की जा सकती है, जो इसे सबसे अधिक चमकीले रूप से प्रकाशित करती है।
उच्च आयामीता
समय, तरंग दैर्ध्य, और ध्रुवीकरण (तरंगों) कोण को अतिरिक्त आयामों के रूप में माना जा सकता है, जिसके अनुसार उच्च-आयामी कार्यों को उत्पन्न किया जा सकता है।
4D प्रकाश क्षेत्र
एक प्लेनोप्टिक कार्य में, यदि अभिरुचि क्षेत्र में एक अवतल वस्तु होती है, तो वस्तु पर एक बिंदु छोड़ने वाला प्रकाश केवल छोटी दूरी की यात्रा कर सकता है, इससे पहले कि वस्तु पर कोई अन्य बिंदु इसे अवरुद्ध कर दे। कोई व्यावहारिक उपकरण ऐसे क्षेत्र में कार्य को माप नहीं सकता।
हालांकि, वस्तु के अवमुख समावरक के बाहर के स्थानों के लिए (उदाहरण के लिए, संकुचन वेष्टन), प्लेनोप्टिक कार्य को कई छवियों को प्रग्रहण करके मापा जा सकता है। इस स्थिति में कार्य में अतिरिक्त जानकारी होती है, क्योंकि किरण के साथ विकिरण इसकी पूरी लंबाई में स्थिर रहती है। अतिरिक्त जानकारी ठीक एक आयाम है, एक चार-आयामी कार्य को छोड़कर जिसे विभिन्न रूप से फोटोनिक क्षेत्र, 4D प्रकाश क्षेत्र या ल्यूमिग्राफ कहा जाता है[7] ।[8] औपचारिक रूप से, क्षेत्र को खाली स्थान में किरणों के साथ विकिरण के रूप में परिभाषित किया गया है।
एक प्रकाश क्षेत्र में किरणों के समुच्चय को विभिन्न प्रकारों से परिचालित किया जा सकता है। सबसे आम दो-तल मानकीकरण है। हालांकि यह मानकीकरण सभी किरणों का प्रतिनिधित्व नहीं कर सकता है, उदाहरण के लिए दो तल के समानांतर किरणें यदि तल एक दूसरे के समानांतर हैं, तो यह संदर्श प्रतिबिंब के विश्लेषणात्मक ज्यामिति से निकटता से संबंधित है। दो-तल प्रकाश क्षेत्र के बारे में सोचने का एक सरल प्रकार st सतह (और कोई भी वस्तु जो इसके किनारे या उससे आगे हो सकती है) की संदर्श प्रतिबिंबों के संग्रह के रूप में है, प्रत्येक को uv सतह पर एक पर्यवेक्षक की स्थिति से लिया गया है। एक प्रकाश क्षेत्र को इस तरह परिचालित किया जाता है जिसे कभी-कभी प्रकाश पटिया कहा जाता है।

ध्वनि अनुरूप
ध्वनि के लिए 4D प्रकाश क्षेत्र का अनुरूप ध्वनि क्षेत्र या तरंग क्षेत्र है, जैसा कि तरंग क्षेत्र संश्लेषण में होता है, और संबंधित मानकीकरण किरचॉफ-हेल्महोल्ट्ज़ अभिन्न है, जो बताता है कि, बाधाओं की अनुपस्थिति में, समय के साथ ध्वनि क्षेत्र एक स्थल पर दबाव द्वारा दिया जाता है। इस प्रकार यह किसी भी समय सूचना के दो आयाम हैं, और समय के साथ, एक 3D क्षेत्र हैै।
प्रकाश की स्पष्ट चार-आयामीता की तुलना में यह द्वि-आयामीता है, क्योंकि प्रकाश किरणों में यात्रा करता है (समय में एक बिंदु पर 0D, समय के साथ 1D), जबकि ह्यूजेन्स-फ्रेस्नेल सिद्धांत द्वारा, एक ध्वनि तरंगाग्र को गोलाकार तरंगों के रूप में प्रतिरूपित किया जा सकता है (समय के एक बिंदु पर 2D, समय के साथ 3D): प्रकाश एक ही दिशा में चलता है (सूचना का 2D), जबकि ध्वनि हर दिशा में फैलती है। हालांकि, गैर-निर्वात साधन में प्रकाश यात्रा एक समान प्रकार से बिखर सकती है, और अपरिवर्तनीयता या बिखरने में खो जाने वाली जानकारी पद्धति आयाम के नुकसान स्पष्ट है।
छवि पुनः फ़ोकसन
क्योंकि प्रकाश क्षेत्र स्थानिक और कोणीय जानकारी प्रदान करता है, हम उद्भासन के बाद फोकल तल की स्थिति को बदल सकते हैं, जिसे प्रायः पुनःफोकसिंग कहा जाता है। पुनःफोकसिंग का सिद्धांत अभिन्न परिवर्तन के माध्यम से एक प्रकाश क्षेत्र से पारंपरिक 2-D तस्वीरें प्राप्त करना है। परिवर्तन एक प्रकाश क्षेत्र को इसके निविष्ट के रूप में लेता है और एक विशिष्ट तल पर केंद्रित एक तस्वीर उत्पन्न करता है।
यह मानते हुए कि एक 4-D प्रकाश क्षेत्र का प्रतिनिधित्व करता है पहले तल जो स्थिति से दूसरे तल पर स्थिति तक यात्रा करने वाली प्रकाश किरणों को अभिलेखबद्ध करता है, जहाँ दो तलों के बीच की दूरी है, किसी भी गहराई पर 2-D तस्वीर निम्नलिखित अभिन्न परिवर्तन से प्राप्त किया जा सकता है:[9]
- ,
या अधिक संक्षेप में,
- ,
जहाँ , , और छायाचित्रण संचालक है।
व्यवहार में, इस सूत्र का सीधे तरह पर उपयोग नहीं किया जा सकता है क्योंकि प्लेनोप्टिक कैमरा समान्यतः प्रकाश क्षेत्र के असतत प्रतिरूपों को प्रग्रहण करता है , और इसलिए गणना करने के लिए पुन: नमूनाकरण (या अंतःप्रक्षेप) की आवश्यकता है . एक अन्य समस्या उच्च संगणना जटिलता है। एक 2-D 4-D प्रकाश क्षेत्र से तस्वीर की गणना करने के लिए, सूत्र की जटिलता .[9] है।
फूरिये अंशअ छायाचित्रण
संगणना की जटिलता को कम करने का एक प्रकार प्रोजेक्शन-अंशअ प्रमेय की अवधारणा को अपनाना है:[9]छायाचित्रण संचालक को प्रक्षेपण के बाद अपरुपक के रूप में देखा जा सकता है। परिणाम एक प्रकाश क्षेत्र के 4-D फूरियर रूपांतरण के 2-D अंशअ के समानुपाती होना चाहिए। अधिक सटीक रूप से, प्रकाश क्षेत्र माइक्रोस्कोपी से एक पुनःफोकसिंग की गई छवि उत्पन्न की जा सकती है। 2-D अंशअ निकालने, एक व्युत्क्रम 2-D परिवर्तन और प्रवर्धन लागू करके एक प्रकाश क्षेत्र का 4-D फूरिये वर्णक्रम से एक पुनःफोकसिंग की गई छवि उत्पन्न की जा सकती है। कलन-विधि की स्पर्शोन्मुख जटिलता है
असतत फोकल खंड रूपांतरण
2-D तस्वीरों की कुशलता से गणना करने का दूसरा प्रकार असतत फोकल खंड रूपांतरण (DFST) को अपनाना है।[10] DFST को पुनःफोकसिंग किए गए 2-D छायाचित्र, या तथाकथित फोकस खंड का संग्रह उत्पन्न करने के लिए प्रारुपण किया गया है। इस विधि को तेजी से भिन्नात्मक फूरियर रूपांतरण (FrFT) द्वारा लागू किया जा सकता है।
असतत छायाचित्रण संचालन को प्रकाश क्षेत्र के लिए निम्नानुसार परिभाषित किया गया है 4-D ग्रिड में प्रतिचयित किया जाता है
,
:
क्योंकि समान्यतः 4-D ग्रिड पर नहीं होता है, DFST गैर-ग्रिड मानों की गणना करने के लिए त्रिकोणमितीय अंतःप्रक्षेप को अपनाता है।
कलन-विधि में ये चरण होते हैं:
- प्रकाश क्षेत्र को प्रतिरूपित करे प्रतिरूपित अवधि के साथ और और विवेकित प्रकाश क्षेत्र प्राप्त करें
- खंड शून्य के साथ जैसे कि संकेतक की लंबाई बिना उपघटन के FrFT के लिए पर्याप्त है।
- हर एक , के लिए असतत फूरियर रूपांतरण , की गणना करें और परिणाम प्राप्त करें
- प्रत्येक फोकल लम्बाई , के लिए एक भिन्नात्मक फूरियर रूपांतरण की की गणना करें, जहां रूपांतरण का क्रम पर निर्भर करता है और परिणाम प्राप्त करें
- के व्युत्क्रम असतत फूरियर रूपांतरण की गणना करें
- के सीमांत पिक्सेल निकालें ताकि प्रत्येक 2-D तस्वीर का आकार हो
प्रकाश क्षेत्र बनाने के प्रकार
प्रकाश क्षेत्र प्रकाश के लिए उन्हें परिभाषित करने के लिए कई प्रकारों के साथ एक मौलिक प्रतिनिधित्व है।
कंप्यूटर चित्रमुद्रण में, प्रकाश क्षेत्र समान्यतः या तो एक प्रतिरूप की गिनती को प्रस्तुत करके (कंप्यूटर चित्रमुद्रण) या वास्तविक दृश्य को चित्रित करके निर्मित होते हैं। किसी भी स्थिति में, एक प्रकाश क्षेत्र का निर्माण करने के लिए, दृष्टिकोणों के एक बड़े संग्रह के लिए विचार प्राप्त किए जाने चाहिए। मानकीकरण के आधार पर, यह संग्रह समान्यतः एक रेखा, वृत्त, समतल, गोले या अन्य आकार के कुछ अंश को फैलाता है, हालांकि असंरचित संग्रह संभव हैं।[11]
प्रकाश क्षेत्र छायाचित्रण प्रग्रहण करने के लिए उपकरणों में एक गतिमान हाथ से थामे रखे जाने वाला कैमरा या रोबोटिक रूप से नियंत्रित कैमरा समिलित हो सकता है,[12] कैमरों का एक चाप, कैमरों की एक सघन सरणी,[13] लाइट-फील्ड कैमरा,[14][15] सूक्ष्मदर्शी[16] या अन्य प्रकाशिकी पद्धतियाँ समिलित हो सकते है ।[17]
एक प्रकाश क्षेत्र में कितनी छवियां होनी चाहिए? सबसे बड़ा ज्ञात प्रकाश क्षेत्र (माइकलएंजेलो की डॉक्टर चैपल की मूर्ति)है,[18] इसमें 24,000 1.3-मेगापिक्सेल छवियां हैं। यह गहरे स्तर, उत्तर आवेदन पर निर्भर करता है। किसी अपारदर्शी वस्तु को पूरी तरह से प्रग्रहण करने के लिए प्रकाश क्षेत्र अनुवाद के लिए, छवियों को कम से कम आगे और पीछे से लिया जाना चाहिए। कम स्पष्ट रूप से, किसी वस्तु के लिए जो st तल के किनारे स्थित है, बारीक दूरी वाली छवियों को uv तल (ऊपर दिखाए गए दो-प्लेन मानकीकरण में) पर लिया जाना चाहिए।
एक प्रकाश क्षेत्र में छवियों की संख्या और व्यवस्था, और प्रत्येक छवि के विभेदन को एक साथ 4D प्रकाश क्षेत्र का, "प्रतिचयन" कहा जाता है।[19] अधिधारण प्रकाश और प्रतिबिंब के प्रभाव भी रोचक हैं।[20][21]
अनुप्रयोग
चयनित अनुप्रयोग:

रोशनी इंजीनियरिंग- प्रकाश क्षेत्र का अध्ययन करने के लिए गेर्शुन का कारण (बंद रूप में) रोशनी के प्रतिरूप को प्राप्त करना था जो इन सतहों के ऊपर स्थित विभिन्न आकृतियों के प्रकाश स्रोतों के कारण सतहों पर देखा जाएगा।[23] रोशनी इंजीनियरिंग के लिए समर्पित प्रकाशिकी की शाखा अबिम्ब प्रकाशिकी है।[24] यह व्यापक रूप से प्रवाह रेखाओं (गेर्शुन की फ्लक्स लाइन) और सदिश प्रवाह (गेर्शुन के प्रकाश वेक्टर) की अवधारणा का उपयोग करता है। हालांकि, प्रकाश क्षेत्र (इस स्थिति में प्रकाश किरणों को परिभाषित करने वाली स्थिति और दिशाएं) समान्यतः चरण स्थान और हैमिल्टनियन प्रकाशिकी के संदर्भ में वर्णित हैं।
- प्रकाश क्षेत्र अनुवाद- किसी दृश्य के 4D प्रकाश क्षेत्र से उपयुक्त 2D अंशअ निकालने से दृश्य के नए दृश्य देखने को मिलते हैं।[25] प्रकाश क्षेत्र अनुवाद छवि-आधारित अनुवाद का एक रूप है ।
- कृत्रिम द्वारक छायाचित्रण - एक प्रकाश क्षेत्र में प्रतिरूपित एक उपयुक्त 4D उपवर्ग को एकीकृत करने से उस दृश्य का अनुमान लगाया जा सकता है जिसे परिमित (यानी, गैर-पिनहोल) द्वारक वाले कैमरे द्वारा प्रग्रहण किया जाएगा। इस तरह के दृश्य में क्षेत्र की परिमित गहराई होती है। इस एकीकरण को करने से पहले प्रकाश क्षेत्र को अपरुपक विभिन्न फ्रंटो-समानांतर पर ध्यान केंद्रित कर सकता है[26] [27]। प्रकाश क्षेत्र को प्रग्रहण करने वाले डिजिटल कैमरों द्वारा प्रग्रहण की गई छवियां[14]पुनः ध्यान केन्द्रित किया जा सकता है।
- 3D डिस्प्ले-प्रौद्योगिकी का उपयोग करके एक प्रकाश क्षेत्र प्रस्तुत करना जो प्रत्येक प्रतिरूप को भौतिक स्थान में उपयुक्त किरण के लिए मेल करता है, मूल दृश्य को देखने के लिए एक ऑटोस्टेरोस्कोपी दृश्य प्रभाव पैदा करता है। ऐसा करने के लिए गैर-डिजिटल तकनीकों में अभिन्न फोटोग्राफी , आयतनमितीय डिस्प्ले और होलोग्रफ़ी समिलित हैं; डिजिटल तकनीकों में एक उच्च-विभेदन डिस्प्ले स्क्रीन पर लेंसलेट की एक सरणी रखना, या वीडियो प्रकल्प की एक सरणी का उपयोग करके लेंसलेट की एक सरणी पर काल्पनिक को प्रकल्प करना समिलित है। वीडियो कैमरों की एक सरणी समय-भिन्न प्रकाश क्षेत्र को प्रग्रहण और प्रदर्शित कर सकती है। यह अनिवार्य रूप से एक जेडडी टेलीविजन पद्धति का गठन करता है।[28]
- मस्तिष्क इमेजिंग- तंत्रिका गतिविधि को GCAMP जैसे प्रतिवर्ती प्रतिदीप्ति मार्करों के साथ आनुवंशिक रूप से संकेतन न्यूरॉन्स द्वारा वैकल्पिक रूप से अभिलेखबद्ध किया जा सकता है जो वास्तविक समय में कैल्शियम आयन की उपस्थिति का संकेत देते हैं। चूंकि प्रकाश क्षेत्र सूक्ष्मदर्शिकी एक ही फ्रेम में पूर्ण मात्रा की जानकारी को प्रग्रहण करता है, इसलिए वीडियो फ्रैमरेट पर बड़ी मात्रा में उत्तम तरीके से वितरित व्यक्तिगत न्यूरॉन्स में तंत्रिका गतिविधि की निगरानी करना संभव है।[29] मस्तिष्क के ऊतकों में प्रकाशिकी विचलन के बाद भी और आयति छवि के पुनर्निर्माण के बिना तंत्रिका गतिविधि का मात्रात्मक माप किया जा सकता है,[30] और हजारों न्यूरॉन्स में गतिविधि की निगरानी के लिए उपयोग किया जाता है।[31]
- सामान्यीकृत दृश्य पुनर्निर्माण (GSR) - यह कई छवियों से 3D पुनर्निर्माण की एक विधि है जो एक सामान्यीकृत प्रकाश क्षेत्र का प्रतिनिधित्व करने वाला एक दृश्य प्रतिरूप बनाता है।[32] प्रकाश क्षेत्र दृश्य में हर बिंदु के माध्यम से हर दिशा में बहने वाले प्रकाश का प्रतिनिधित्व करता है। स्थिति क्षेत्र दृश्य में हर बिंदु पर व्याप्त पदार्थ के प्रकाश संपर्क गुणों का प्रतिनिधित्व करता है। GSR तंत्रिक रेडियंस क्षेत्र (NeRFs), प्लेनॉक्सल्स और उलटा प्रकाश परिवहन का उपयोग करके किया जा सकता है,[33] [34] ।[32]
- स्वलिखित त्रिविमचित्र - इमेज उत्पादन और स्वलिखित त्रिविमचित्र के लिए कृत्रिम आकृति का पूर्व विरूपण प्रकाश क्षेत्र के आरंभ उदाहरणों में से एक है।[35]
- रोशनी में घटाव- रोशनी (दृष्टि) कैमरा बॉडी के अंदर प्रकाश के कई बिखराव और लेंस प्रकिशिकि के कारण उत्पन्न होती है जो छवि के वैषम्य को कम करती है। जबकि रोशनी का विश्लेषण 2D छवि स्थल में किया गया है,[36] इसे 4D किरण-स्थल घटना के रूप में पहचानना उपयोगी है।[37] एक कैमरे के अंदर किरण-स्थल का सांख्यिकीय विश्लेषण करने से रोशनी की कलाकृतियों को वर्गीकृत करने और हटाने की अनुमति मिलती है। किरण-स्थान में, रोशनी उच्च आवृत्ति शोर के रूप में व्यवहार करती है और इसे बाहरी अस्वीकृति से कम किया जा सकता है। कैमरे के अंदर प्रकाश क्षेत्र को प्रग्रहण करके ऐसा विश्लेषण किया जा सकता है, लेकिन इसके परिणामस्वरूप स्थानिक संकल्प का नुकसान होता है। एक समान और गैर-समान किरण नमूनाकरण का उपयोग छवि संकल्प में महत्वपूर्ण समझौता किए बिना रोशनी को कम करने के लिए किया जा सकता है।[37]
यह भी देखें
- लाइट-फील्ड कैमरा
- कोण-संवेदनशील पिक्सेल
- लिटरो
- परावर्तन कागज
- रायट्रिक्स
- दोहरी फोटोग्राफी
टिप्पणियाँ
- ↑ Faraday, Michael (30 April 2009). "लिव। किरण-कंपन पर विचार". Philosophical Magazine. Series 3. 28 (188): 345–350. doi:10.1080/14786444608645431. Archived from the original on 2013-02-18.
- ↑ Wetzstein 2012, 2011; Lanman 2011, 2010
- ↑ Adelson 1991
- ↑ Wong 2002
- ↑ Gershun, fig 17
- ↑ Arvo, 1994
- ↑ Levoy 1996
- ↑ Gortler 1996
- ↑ 9.0 9.1 9.2 Ng, Ren (2005). "फूरियर टुकड़ा फोटोग्राफी". ACM SIGGRAPH 2005 Papers on - SIGGRAPH '05. New York, New York, USA: ACM Press: 735–744. doi:10.1145/1186822.1073256. ISBN 9781450378253. S2CID 1806641.
- ↑ Nava, F. Pérez; Marichal-Hernández, J.G.; Rodríguez-Ramos, J.M. (August 2008). "असतत फोकल स्टैक रूपांतरण". 2008 16th European Signal Processing Conference: 1–5.
- ↑ Buehler 2001
- ↑ Levoy 2002
- ↑ Kanade 1998; Yang 2002; Wilburn 2005
- ↑ 14.0 14.1 Ng 2005
- ↑ Georgiev 2006; Marwah 2013
- ↑ Levoy 2006
- ↑ Bolles 1987
- ↑ "माइकलएंजेलो की रात की मूर्ति का प्रकाश क्षेत्र". accademia.stanford.edu. Retrieved 2022-02-08.
- ↑ Chai (2000)
- ↑ Durand (2005)
- ↑ Ramamoorthi (2006)
- ↑ Gershun, fig 24
- ↑ Ashdown 1993
- ↑ Chaves 2015; Winston 2005
- ↑ Levoy 1996; Gortler 1996
- ↑ Isaksen 2000
- ↑ Vaish 2005
- ↑ Javidi 2002; Matusik 2004
- ↑ Grosenick, 2009, 2017; Perez, 2015
- ↑ Pegard, 2016
- ↑ Grosenick, 2017
- ↑ 32.0 32.1 Leffingwell, 2018
- ↑ Mildenhall, 2020
- ↑ Yu & Fridovich-Keil, 2021
- ↑ Halle 1991, 1994
- ↑ Talvala 2007
- ↑ 37.0 37.1 Raskar 2008
संदर्भ
सिद्धांत
- एडल्सन, ई.एच., बर्गन, जे.आर. (1991)। द प्लेनॉप्टिक फंक्शन एंड द एलिमेंट्स ऑफ़ अर्ली विज़न, विजुअल प्रोसेसिंग के कंप्यूटेशन मॉडल में, एम. लैंडी और जे.ए. मूवशोन, एड., एमआईटी प्रेस, कैम्ब्रिज, 1991, पीपी 3-20।
- अरवो, जे। (1994)। आंशिक रूप से बंद पॉलीहेड्रल स्रोतों के लिए विकिरण जैकबियन, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 335-342।
- बोलेस, आर.सी., बेकर, एच.एच., मेरिमोंट, डी.एच. (1987)। एपिपोलर-प्लेन इमेज एनालिसिस: एन अप्रोच टू डिटरमिनिंग स्ट्रक्चर फ्रॉम मोशन, इंटरनेशनल जर्नल ऑफ कंप्यूटर विजन, वॉल्यूम। 1, नंबर 1, 1987, क्लूवर एकेडमिक पब्लिशर्स, पीपी 7-55।
- फैराडे, एम।, रे वाइब्रेशन पर विचार, फिलोसोफिकल मैगज़ीन, S.3, वॉल्यूम XXVIII, N188, मई 1846।
- गेरशुन, ए. (1936). द लाइट फील्ड, मॉस्को, 1936। पी. मून और जी. टिमोचेंको द्वारा गणित और भौतिकी जर्नल में अनुवादित, वॉल्यूम। XVIII, एमआईटी, 1939, पीपी। 51-151।
- गोर्टलर, एस.जे., ग्रजेसजुक, आर., स्जेलिस्की, आर., कोहेन, एम. (1996)। द ल्यूमिग्राफ, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 43-54।
- लेवॉय, एम., हनराहन, पी. (1996)। लाइट फील्ड अनुवाद, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 31-42।
- मून, पी., स्पेंसर, डी.ई. (1981)। फोटोग्राफिक फील्ड, एमआईटी प्रेस।
- वोंग, टी.टी., फू, सी.डब्ल्यू., हेंग, पी.ए., लेउंग सी.एस. (2002)। प्लेनॉप्टिक-रोशनी फंक्शन, IEEE ट्रांस। मल्टीमीडिया, वॉल्यूम। 4, संख्या 3, पीपी। 361-371।
विश्लेषण
- जी. वेट्ज़स्टीन, आई. इहर्के, डब्ल्यू. हेड्रिच (2013) प्लेनोप्टिक मल्टीप्लेक्सिंग और पुनर्निर्माण पर, इंटरनेशनल जर्नल ऑफ कम्प्यूटर विजन (आईजेसीवी), खंड 101, अंक 2, पीपी 384-400।
- राममूर्ति, आर., महाजन, डी., बेलहुमुर, पी. (2006)। लाइटिंग, शेडिंग और शैडो का पहला क्रम विश्लेषण, एसीएम टॉग।
- ज्विकर, एम., माटुसिक, डब्ल्यू., डूरंड, एफ., फिस्टर, एच. (2006)। एंटीअलियासिंग फॉर ऑटोमल्टिस्कोपिक 3डी डिस्प्ले, यूरोग्राफिक्स सिम्पोजियम ऑन अनुवाद, 2006।
- एनजी, आर। (2005)। फूरियर अंशअ फोटोग्राफी, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 735-744।
- डुरंड, एफ., होल्ज़शच, एन., सोलर, सी., चान, ई., सिलियन, एफ.एक्स. (2005)। प्रकाश परिवहन का एक आवृत्ति विश्लेषण, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 1115–1126।
- चाई, जे.-एक्स., टोंग, एक्स., चान, एस.-सी., शुम, एच. (2000)। प्लेनॉप्टिक सैंपलिंग, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी 307–318।
- हाले, एम. (1994) डिस्क्रीट इमेजिंग सिस्टम के रूप में होलोग्राफिक स्टीरियोग्राम[permanent dead link], एसपीआईई प्रोक में। वॉल्यूम। #2176: प्रैक्टिकल होलोग्राफी VIII, एस.ए. बेंटन, एड।, पीपी। 73-84।
- यू, जे., मैकमिलन, एल. (2004)। जनरल लीनियर कैमरा, प्रोक। ECCV 2004, कंप्यूटर विज्ञान में व्याख्यान नोट्स, पीपी। 14-27।
कैमरा
- मारवाह, के., वेटजस्टीन, जी., बांदो, वाई., रास्कर, आर. (2013)। कंप्रेसिव लाइट फ़ील्ड फ़ोटोग्राफ़ी ओवरकंप्लीट डिक्शनरी और ऑप्टिमाइज़्ड प्रोजेक्शन का इस्तेमाल करके , ग्राफिक्स पर ACM लेनदेन (SIGGRAPH)।
- लियांग, सी.के., लिन, टी.एच., वोंग, बी.वाई., लियू, सी., चेन, एच. एच. (2008)। प्रोग्रामेबल द्वारक फोटोग्राफी: मल्टीप्लेक्स लाइट फील्ड एक्विजिशन, प्रोक। एसीएम सिग्राफ।
- वीरराघवन, ए., रस्कर, आर., अग्रवाल, ए., मोहन, ए., टंबलिन, जे. (2007)। डैपल्ड फ़ोटोग्राफ़ी: हेटेरोडाइन्ड लाइट फ़ील्ड्स और कोडेड अपर्चर रीफ़ोकसिंग के लिए बेहतर कैमरे को मास्क करें, प्रोक. एसीएम सिग्राफ।
- जॉर्जिएव, टी., झेंग, सी., नायर, एस., करलेस, बी., सेल्सिन, डी., इंतवाला, सी. (2006)। इंटीग्रल फ़ोटोग्राफ़ी में अनुपात-कोणीय विभेदन ट्रेड-ऑफ़, प्रोक। ईजीएसआर 2006।
- कनाडे, टी., सैटो, एच., वेदुला, एस. (1998)। 3D रूम: सिंक्रोनाइज्ड मल्टिपल वीडियो स्ट्रीम्स द्वारा डिजिटाइज़िंग टाइम-वैरिंग 3D इवेंट्स , टेक रिपोर्ट CMU-RI-TR-98- 34, दिसंबर 1998।
- लेवॉय, एम। (2002)। स्टैनफोर्ड स्फेरिकल गैन्ट्री।
- लेवोय, एम., एनजी, आर., एडम्स, ए., फूटर, एम., होरोविट्ज, एम. (2006)। लाइट फील्ड माइक्रोस्कोपी , ग्राफिक्स पर ACM लेनदेन (प्रोक. SIGGRAPH), वॉल्यूम। 25, नंबर 3।
- एनजी, आर., लेवॉय, एम., ब्रेडिफ, एम., डुवल, जी., होरोविट्ज़, एम., हनराहन, पी. (2005)। हैंड-हेल्ड प्लेनोप्टिक कैमरा के साथ लाइट फील्ड फोटोग्राफी, स्टैनफोर्ड टेक रिपोर्ट CTSR 2005-02, अप्रैल, 2005।
- विलबर्न, बी., जोशी, एन., वैश, वी., तलवाला, ई., एंट्यूनेज़, ई., बार्थ, ए., एडम्स, ए., लेवॉय, एम., होरोविट्ज़, एम. (2005)। बड़े कैमरा एरे का उपयोग करके उच्च प्रदर्शन इमेजिंग, ग्राफिक्स पर ACM लेनदेन (प्रोक. SIGGRAPH), वॉल्यूम। 24, संख्या 3, पीपी। 765–776।
- यांग, जे.सी., एवरेट, एम., ब्यूहलर, सी., मैकमिलन, एल. (2002)। एक रीयल-टाइम डिस्ट्रिब्यूटेड लाइट फील्ड कैमरा, प्रोक। यूरोग्राफिक्स अनुवाद वर्कशॉप 2002।
- CAFADIS कैमरा
प्रदर्शित करता है
- वेटजस्टाइन, जी., लैनमैन, डी., हिर्श, एम., रास्कर, आर. (2012)। टेंसर डिस्प्ले: डायरेक्शनल बैकलाइटिंग के साथ मल्टीलेयर डिस्प्ले का इस्तेमाल करते हुए कंप्रेसिव लाइट फील्ड डिस्प्ले , ग्राफिक्स पर ACM लेनदेन (SIGGRAPH)
- वेटजस्टाइन, जी., लैनमैन, डी., हेड्रिच, डब्ल्यू., रास्कर, आर. (2011)। स्तरित 3D: क्षीणन-आधारित प्रकाश क्षेत्र और उच्च गतिशील रेंज डिस्प्ले के लिए टॉमोग्राफ़िक इमेज सिंथेसिस, ग्राफिक्स पर एसीएम लेनदेन ( सिग्राफ)
- लैनमैन, डी., वेटजस्टीन, जी., हिर्श, एम., हेड्रिच, डब्ल्यू., रस्कर, आर. (2011)। पोलराइज़ेशन फ़ील्ड्स: मल्टी-लेयर LCDs का उपयोग करके डायनामिक लाइट फ़ील्ड डिस्प्ले, ग्राफिक्स पर ACM लेनदेन (SIGGRAPH Asia)
- लैनमैन, डी., हिर्श, एम. किम, वाई., रास्कर, आर. (2010)। HR3D: ड्यूल-स्टैक्ड LCDs हाई-रैंक 3D डिस्प्ले का उपयोग करके सामग्री-अनुकूली लंबन बाधाओं का उपयोग करके चश्मा-मुक्त 3D डिस्प्ले, ACM लेनदेन ग्राफिक्स पर (SIGGRAPH एशिया)
- माटुसिक, डब्ल्यू., फिस्टर, एच. (2004)। 3D TV: रीयल-टाइम अधिग्रहण, ट्रांसमिशन, और डायनामिक दृश्यों के ऑटोस्टेरोस्कोपिक प्रदर्शन के लिए एक स्केलेबल सिस्टम, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस।
- जाविदी, बी., ओकानो, एफ., एड. (2002)। त्रि-आयामी टेलीविजन, वीडियो और डिस्प्ले टेक्नोलॉजी, स्प्रिंगर-वर्लैग।
- क्लुग, एम., बर्नेट, टी., फैनसेलो, ए., हीथ, ए., गार्डनर, के., ओ'कोनेल, एस., न्यूजवैंगर, सी. (2013)। A स्केलेबल, सहयोगी, इंटरएक्टिव लाइट-फील्ड डिस्प्ले सिस्टम , SID सिम्पोज़ियम डाइजेस्ट ऑफ़ टेक्निकल पेपर्स
- फट्टल, डी., पेंग, जेड., ट्रान, टी., वो, एस., फियोरेंटीनो, एम., ब्रुग, जे., ब्यूसोलिल, आर. (2013)। एक चौड़े-कोण, चश्मे से मुक्त त्रि-आयामी डिस्प्ले के लिए एक बहु-दिशात्मक बैकलाइट, नेचर 495, 348–351
अभिलेखागार
- स्टैनफोर्ड लाइट फील्ड आर्काइव
- UCSD/MERL लाइट फील्ड रिपॉजिटरी
- HCI लाइट फील्ड बेंचमार्क
- सिंथेटिक लाइट फील्ड आर्काइव
अनुप्रयोग
- ग्रोसेनिक, एल., एंडरसन, टी., स्मिथ एस.जे. (2009) न्यूरोनल एन्सेंबल्स की विवो इमेजिंग के लिए इलास्टिक सोर्स सेलेक्शन। नैनो से मैक्रो तक, बायोमेडिकल इमेजिंग पर छठा आईईईई अंतर्राष्ट्रीय संगोष्ठी। (2009) 1263-1266।
- ग्रोसेनिक, एल., ब्रोक्सटन, एम., किम, सी.के., लिस्टन, सी., पूले, बी., यांग, एस., एंडलमैन, ए., शार्फ़, ई., कोहेन, एन., यिज़हार, ओ., रामकृष्णन, सी।, गांगुली, एस।, सुपेस, पी।, लेवॉय, एम।, डेसेरोथ, के। (2017) 132688.full.pdf स्तनधारी मस्तिष्क में बड़े ऊतक खंडों में सेलुलर-गतिविधि गतिशीलता की पहचान बायोरेक्सिव 132688; doi: स्तनधारी मस्तिष्क में बड़े ऊतक संस्करणों में सेलुलर-गतिविधि गतिशीलता की पहचान।
- हीड, एफ., वेटजस्टीन, जी., रस्कर, आर., हेड्रिच, डब्ल्यू. (2013) के लिए अनुकूली इमेज सिंथेसिस कंप्रेसिव डिस्प्ले, ग्राफिक्स पर ACM लेनदेन (SIGGRAPH)
- वेटजस्टाइन, जी., रस्कर, आर., हेड्रिच, डब्ल्यू. (2011) हैंड-हेल्ड श्लीरेन फोटोग्राफी विद लाइट फील्ड जांच, कम्प्यूटेशनल फोटोग्राफी पर IEEE अंतर्राष्ट्रीय सम्मेलन (ICCP)
- पेरेज़, एफ।, मारीचल, जेजी, रोड्रिगेज, जेएम (2008)। डिस्क्रीट फोकल खंड ट्रांसफॉर्म, प्रोक। यूसिपको
- रस्कर, आर., अग्रवाल, ए., विल्सन, सी., वीरराघवन, ए. (2008)। ग्लेयर अवेयर फोटोग्राफी: कैमरा लेंस के ग्लेयर इफेक्ट को कम करने के लिए 4डी रे सैम्पलिंग, प्रक्रिया। एसीएम सिग्राफ।
- तलवाला, ई-वी., एडम्स, ए., होरोविट्ज़, एम., लेवॉय, एम. (2007)। वीलिंग ग्लेयर इन हाई डायनामिक रेंज इमेजिंग, प्रोक। एसीएम सिग्राफ।
- हाले, एम., बेंटन, एस., क्लुग, एम., अंडरकॉफ़्लर, जे. (1991)। अल्ट्राग्राम: एक सामान्यीकृत होलोग्राफिक स्टीरियोग्राम[permanent dead link], एसपीआईई वॉल्यूम। 1461, प्रैक्टिकल होलोग्राफी वी, एस.ए. बेंटन, एड., पीपी। 142-155।
- ज़ोमेट, ए., फेल्डमैन, डी., पेलेग, एस., वीन्सहॉल, डी. (2003)। Mosaicing New Views: The Crossed-Slits Projection , IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), Vol. 25, नंबर 6, जून 2003, पीपी। 741–754।
- वैश, वी., गर्ग, जी., तलवाला, ई., एंट्यूनेज़, ई., विलबर्न, बी., होरोविट्ज़, एम., लेवॉय, एम. (2005)। व्यूइंग ट्रांसफॉर्म के शीयर-वार्प फैक्टराइजेशन का उपयोग कर सिंथेटिक द्वारक फोकसिंग, प्रोक। सीवीपीआर 2005 के संयोजन में सुरक्षा और सुरक्षा के लिए उन्नत 3डी इमेजिंग पर कार्यशाला।
- बेडर्ड, एन., शोप, टी., होबरमैन, ए., हरालम, एमए, शेख, एन., कोवासेविक, जे., बलराम, एन., तोसिक, आई. (2016)। मध्य कान की वीवो इमेजिंग में 3डी के लिए लाइट फील्ड ओटोस्कोप डिजाइन। बायोमेडिकल ऑप्टिक्स एक्सप्रेस, 8(1), पीपी. 260-272.
- कार्यगिआनी, एस., मार्टिनेलो, एम., स्पिनौलास, एल., फ्रॉसार्ड, पी., टॉसिक, आई. (2018)। लाइट-फील्ड डेटा से ईयरड्रम का ऑटोमेटेड रजिस्ट्रेशन . इमेज प्रोसेसिंग पर IEEE अंतर्राष्ट्रीय सम्मेलन (ICIP)
- रैडेमाकर, पी., बिशप, जी. (1998)। मल्टीपल-सेंटर-ऑफ-प्रोजेक्शन इमेज, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस।
- इसाकसेन, ए., मैकमिलन, एल., गोर्टलर, एस.जे. (2000)। डायनेमिकली रीपैरामीटराइज़्ड लाइट फील्ड्स, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस, पीपी। 297–306।
- बुहलर, सी., बॉसे, एम., मैकमिलन, एल., गोर्टलर, एस., कोहेन, एम. (2001)। अनस्ट्रक्चर्ड ल्यूमिग्राफ अनुवाद, प्रोक। एसीएम सिग्राफ, एसीएम प्रेस।
- एशडाउन, आई. (1993). नियर-फ़ील्ड फ़ोटोमेट्री: ए न्यू अप्रोच , जर्नल ऑफ़ द इल्युमिनेटिंग इंजीनियरिंग सोसाइटी, वॉल्यूम। 22, नंबर 1, विंटर, 1993, पीपी. 163–180।
- चेव्स, जे. (2015) नॉनइमेजिंग ऑप्टिक्स का परिचय, दूसरा संस्करण, सीआरसी प्रेस
- विंस्टन, आर., मिनानो, जे.सी., बेनिटेज़, पी.जी., शत्ज़, एन., बोर्ट्ज़, जे.सी., (2005) नॉनइमेजिंग ऑप्टिक्स, अकादमिक प्रेस
- पेगार्ड, एन.सी., लियू एच.वाई., एंटिपा, एन., जेरलॉक एम., एडेसनिक, एच., और वालर, एल.. 3डी तंत्रिका गतिविधि रिकॉर्डिंग के लिए कंप्रेसिव लाइट-फील्ड माइक्रोस्कोपी। ऑप्टिका 3, नहीं. 5, पीपी। 517–524 (2016)।
- लेफिंगवेल, जे., मेघेर, डी., महमूद, के., एकर्सन, एस. (2018)। सामान्यीकृत दृश्य पुनर्निर्माण। arXiv:1803.08496v3 [cs.CV], पीपी। 1-13।
- मिल्डेनहॉल, बी., श्रीनिवासन, पी.पी., तनिकिक, एम., बैरोन, जे.टी., राममूर्ति, आर., और एनजी, आर. (2020)। "NeRF: दृश्य संश्लेषण के लिए तंत्रिका विकिरण क्षेत्रों के रूप में दृश्यों का प्रतिनिधित्व करना।" कंप्यूटर विजन - ECCV 2020, 405–421।
- यू, ए., फ्रिडोविच-कील, एस., टैनिक, एम., चेन, क्यू., रेचट, बी., कानाज़ावा, ए. (2021)। प्लेनॉक्सल्स: तंत्रिक नेटवर्क के बिना रेडियंस फील्ड्स। आर्क्सिव:2111.11215, पीपी 1-25
- Perez, CC; Lauri, A; et al. (September 2015). "टर्न-की लाइट फील्ड कैमरा का उपयोग करके जेब्राफिश लार्वा के व्यवहार में कैल्शियम न्यूरोइमेजिंग।". Journal of Biomedical Optics. 20 (9): 096009. Bibcode:2015JBO....20i6009C. doi:10.1117/1.JBO.20.9.096009. PMID 26358822.
- पेरेज़, सी.सी., लॉरी, ए., सिमवॉलिडिस, पी., कैपेटा, एम., एर्डमैन, ए., और वेस्टमेयर, जी.जी. (2015)। टर्न-की लाइट फील्ड कैमरा का उपयोग करके जेब्राफिश लार्वा के व्यवहार में कैल्शियम न्यूरोइमेजिंग। जर्नल ऑफ बायोमेडिकल ऑप्टिक्स, 20(9), 096009-096009।
- लियोन, के., गैल्विस, एल., और आर्गुएलो, एच. (2016)। मल्टीस्पेक्ट्रल प्रकाश क्षेत्र का पुनर्निर्माण (5डी प्लेनोप्टिक फंक्शन) 2डी अनुमानों से रंगीन कोडेड द्वारक के साथ कंप्रेसिव सेंसिंग पर आधारित रेविस्टा फैकल्टीड डी इंजेनिएरिया यूनिवर्सिडाड डी एंटिओक्विया 80, पीपी। 131।
श्रेणी: प्रकाशिकी श्रेणी:3डी कंप्यूटर ग्राफिक्स