संभावित ऊर्जा सतह: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
 
(6 intermediate revisions by 3 users not shown)
Line 4: Line 4:


लैंडस्केप की एनालॉजी का उपयोग करना सहायक होता है, दो स्वतंत्रता की कोटि भौतिकी और रसायन विज्ञान वाली प्रणाली के रूप में होती है, जैसे दो बंध ऊर्जा की तुलना में दो बंध लंबाईयों का काम भूमि पर स्थिति के निर्देशांक के रूप में एनालॉजी होते है।<ref>[http://goldbook.iupac.org/P04780.html Potential-energy (reaction) surface in Compendium of Chemical Terminology, 2nd ed. (the "Gold Book").] Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997)</ref>
लैंडस्केप की एनालॉजी का उपयोग करना सहायक होता है, दो स्वतंत्रता की कोटि भौतिकी और रसायन विज्ञान वाली प्रणाली के रूप में होती है, जैसे दो बंध ऊर्जा की तुलना में दो बंध लंबाईयों का काम भूमि पर स्थिति के निर्देशांक के रूप में एनालॉजी होते है।<ref>[http://goldbook.iupac.org/P04780.html Potential-energy (reaction) surface in Compendium of Chemical Terminology, 2nd ed. (the "Gold Book").] Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997)</ref>
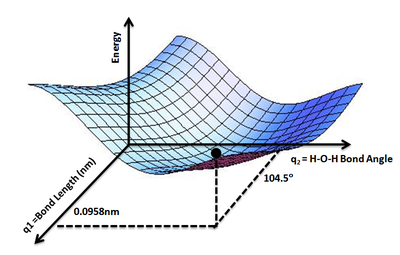
[[File:Potential Energy Surface for Water.png|thumb|400px|right|पानी के अणु के लिए PES: पानी के लिए अनुकूलित आणविक संरचना के अनुरूप न्यूनतम ऊर्जा दिखाता है- 0.0958 एनएम के ओ-एच बांड की लंबाई और 104.5 घात के एच-ओ-एच बांड कोण]]पीईएस अवधारणा [[रसायन विज्ञान]] और भौतिकी जैसे क्षेत्रों में विशेष रूप से इन विषयों की सैद्धांतिक उप-शाखाओं में अनुप्रयोग के रूप में होती है। इसका उपयोग सैद्धांतिक रूप से परमाणुओं से बनी संरचनाओं के गुणों का पता लगाने के लिए किया जा सकता है, उदाहरण के लिए [[अणु]] के न्यूनतम ऊर्जा आकार का पता लगाता है और इस प्रकार [[रासायनिक प्रतिक्रिया]] की प्रतिक्रिया दर की गणना करता है।
[[File:Potential Energy Surface for Water.png|thumb|400px|right|पानी के अणु के लिए पीईएस पानी के लिए अनुकूलित आणविक संरचना के अनुरूप न्यूनतम ऊर्जा दिखाता है- 0.0958 एनएम के O-H बांड की लंबाई और 104.5 घात के H-O-H बांड कोण के रूप में होते है ]]पीईएस अवधारणा [[रसायन विज्ञान]] और भौतिकी जैसे क्षेत्रों में विशेष रूप से इन विषयों की सैद्धांतिक उप-शाखाओं में अनुप्रयोग के रूप में होती है। इसका उपयोग सैद्धांतिक रूप से परमाणुओं से बनी संरचनाओं के गुणों का पता लगाने के लिए किया जा सकता है, उदाहरण के लिए [[अणु]] के न्यूनतम ऊर्जा आकार का पता लगाता है और इस प्रकार [[रासायनिक प्रतिक्रिया]] की प्रतिक्रिया दर की गणना करता है।


== गणितीय परिभाषा और संगणना ==
== गणितीय परिभाषा और संगणना ==


परमाणुओं के एक समूह की ज्यामिति को सदिश {{math| '''r'''}} द्वारा वर्णित किया जा सकता है, जिनके तत्व परमाणु स्थितियों का प्रतिनिधित्व करते हैं। सदिश {{math| '''r'''}} परमाणुओं के [[कार्तीय निर्देशांक|कार्टेशियन निर्देशांक]] का समुच्चय हो सकता है या अंतर-परमाणु दूरियों और कोणों का समुच्चय भी हो सकता है।
परमाणुओं के एक समूह की ज्यामिति को सदिश {{math| '''r'''}} द्वारा वर्णित किया जा सकता है, जिनके तत्व परमाणु स्थितियों का प्रतिनिधित्व करते हैं। सदिश {{math| '''r'''}} परमाणुओं के [[कार्तीय निर्देशांक|कार्टेशियन निर्देशांक]] का समुच्चय हो सकता है या अंतर-परमाणु दूरियों और कोणों का समुच्चय भी हो सकता है।


दिए गए {{math| '''r'''}}, पदों के फलन के रूप में ऊर्जा, {{math| ''E''('''r''')}} सभी ब्याज के लिए सभी के लिए {{math| '''r'''}} का मान है। प्रस्तावना से लैंडस्केप एनालॉजी का उपयोग करते हुए, E ऊर्जा लैंडस्केप की ऊंचाई प्रदान करता है जिससे कि एक संभावित ऊर्जा सतह की अवधारणा उत्पन्न हो सके।
दिए गए {{math| '''r'''}}, पदों के फलन के रूप में ऊर्जा, {{math| ''E''('''r''')}} सभी ब्याज के लिए सभी के लिए {{math| '''r'''}} का मान है। प्रस्तावना से लैंडस्केप एनालॉजी का उपयोग करते हुए, E ऊर्जा लैंडस्केप की ऊंचाई प्रदान करता है जिससे कि एक संभावित ऊर्जा सतह की अवधारणा उत्पन्न हो सके।


परमाणु स्थितियों के एक फलन के रूप में पीईएस का उपयोग करके एक रासायनिक प्रतिक्रिया का अध्ययन करने के लिए ब्याज की प्रत्येक परमाणु व्यवस्था के लिए ऊर्जा की गणना करना आवश्यक होता है। [[ कम्प्यूटेशनल रसायन विज्ञान | अभिकलनात्मक रसायन विज्ञान]] लेख में परमाणुओं की एक विशेष परमाणु व्यवस्था की ऊर्जा की गणना करने की विधि का अच्छी तरह से वर्णन किया जाता है और यहां पर बल के अनुमानों को ढूढ़ने पर जोर दिया जाता है और इस प्रकार {{math| ''E''('''r''')}} ठीक-ठाक ऊर्जा-स्थिति की जानकारी प्राप्त करने के लिए उपयोग किया जाता है।
परमाणु स्थितियों के एक फलन के रूप में पीईएस का उपयोग करके एक रासायनिक प्रतिक्रिया का अध्ययन करने के लिए ब्याज की प्रत्येक परमाणु व्यवस्था के लिए ऊर्जा की गणना करना आवश्यक होता है। [[ कम्प्यूटेशनल रसायन विज्ञान |अभिकलनात्मक रसायन विज्ञान]] लेख में परमाणुओं की एक विशेष परमाणु व्यवस्था की ऊर्जा की गणना करने की विधि का अच्छी तरह से वर्णन किया जाता है और यहां पर बल के अनुमानों को ढूढ़ने पर जोर दिया जाता है और इस प्रकार {{math| ''E''('''r''')}} ठीक-ठाक ऊर्जा-स्थिति की जानकारी प्राप्त करने के लिए उपयोग किया जाता है।


बहुत ही सरल रासायनिक प्रणालियों के लिए अथवा जब अंतर-परमाणु संबंधों के बारे में सरलीकरण करते समय अनुमान लगाया जाता है, तो कभी-कभी परमाणु स्थितियों के फलन के रूप में ऊर्जा की विश्लेषणात्मक रूप से व्युत्पन्न अभिव्यक्ति का उपयोग करना संभव होता है। उदाहरण के लिए तीन H-H. दूरियों के फलन के रूप में H​​+ H<sub>2</sub> प्रणाली के लिए [[फ्रिट्ज लंदन|फ्रिट्ज]] लंदन आइरिंग पोलानी सातो क्षमता के रूप में होना भी एक उदाहरण है।<ref>{{Cite journal | doi = 10.1246/bcsj.28.450| title = संभावित ऊर्जा सतह को चित्रित करने का एक नया तरीका| journal = Bulletin of the Chemical Society of Japan| volume = 28| issue = 7| pages = 450–453| year = 1955| last1 = Sato | first1 = S. | doi-access = free}}{{Cite journal | doi = 10.1063/1.1742043| title = On a New Method of Drawing the Potential Energy Surface| journal = The Journal of Chemical Physics| volume = 23| issue = 3| pages = 592–593| year = 1955|bibcode = 1955JChPh..23..592S | last1 = Sato| first1 = Shin}}</ref><ref>[[Keith J. Laidler]], ''Chemical Kinetics'' (3rd ed., Harper & Row 1987) p.68-70  {{ISBN|0-06-043862-2}}</ref><ref>Steinfeld J.I., Francisco J.S. and Hase W.L. ''Chemical Kinetics and Dynamics'' (2nd ed., Prentice-Hall 1998) p.201-2  {{ISBN|0-13-737123-3}}</ref>  
बहुत ही सरल रासायनिक प्रणालियों के लिए अथवा जब अंतर-परमाणु संबंधों के बारे में सरलीकरण करते समय अनुमान लगाया जाता है, तो कभी-कभी परमाणु स्थितियों के फलन के रूप में ऊर्जा की विश्लेषणात्मक रूप से व्युत्पन्न अभिव्यक्ति का उपयोग करना संभव होता है। उदाहरण के लिए तीन H-H. दूरियों के फलन के रूप में H​​+ H<sub>2</sub> प्रणाली के लिए [[फ्रिट्ज लंदन|फ्रिट्ज]] लंदन आइरिंग पोलानी सातो क्षमता के रूप में होना भी एक उदाहरण है।<ref>{{Cite journal | doi = 10.1246/bcsj.28.450| title = संभावित ऊर्जा सतह को चित्रित करने का एक नया तरीका| journal = Bulletin of the Chemical Society of Japan| volume = 28| issue = 7| pages = 450–453| year = 1955| last1 = Sato | first1 = S. | doi-access = free}}{{Cite journal | doi = 10.1063/1.1742043| title = On a New Method of Drawing the Potential Energy Surface| journal = The Journal of Chemical Physics| volume = 23| issue = 3| pages = 592–593| year = 1955|bibcode = 1955JChPh..23..592S | last1 = Sato| first1 = Shin}}</ref><ref>[[Keith J. Laidler]], ''Chemical Kinetics'' (3rd ed., Harper & Row 1987) p.68-70  {{ISBN|0-06-043862-2}}</ref><ref>Steinfeld J.I., Francisco J.S. and Hase W.L. ''Chemical Kinetics and Dynamics'' (2nd ed., Prentice-Hall 1998) p.201-2  {{ISBN|0-13-737123-3}}</ref>  


अधिक जटिल प्रणालियों के लिए, परमाणुओं की एक विशेष व्यवस्था की ऊर्जा की गणना अधिकांशतः कम्प्यूटेशनल रूप से महत्वपूर्ण होती है, जिससे सतह के बड़े पैमाने पर प्रतिनिधित्व संभव नहीं हो पाता है। इन प्रणालियों के लिए एक संभावित विधि यह है कि पीईएस पर केवल अंकों के घटे हुए समुच्चय की गणना की जाती है और फिर कम्प्यूटेशनल रूप से सस्ते इंटरपोलेशन विधि का उपयोग किया जाता है, उदाहरण के लिए [[ उलटा दूरी भार | शेपर्ड इंटरपोलेशन,]] अंतराल को भरने के लिए उपयोग किया जाता है।<ref>Moving least-squares enhanced Shepard interpolation for the fast marching and string methods, Burger SK1, Liu Y, Sarkar U, Ayers PW, J Chem Phys. 2009 130(2) 024103. doi: 10.1063/1.2996579.</ref>
अधिक जटिल प्रणालियों के लिए, परमाणुओं की एक विशेष व्यवस्था की ऊर्जा की गणना अधिकांशतः कम्प्यूटेशनल रूप से महत्वपूर्ण होती है, जिससे सतह के बड़े पैमाने पर प्रतिनिधित्व संभव नहीं हो पाता है। इन प्रणालियों के लिए एक संभावित विधि यह है कि पीईएस पर केवल अंकों के घटे हुए समुच्चय की गणना की जाती है और फिर कम्प्यूटेशनल रूप से सस्ते इंटरपोलेशन विधि का उपयोग किया जाता है, उदाहरण के लिए [[ उलटा दूरी भार |शेपर्ड इंटरपोलेशन,]] अंतराल को भरने के लिए उपयोग किया जाता है।<ref>Moving least-squares enhanced Shepard interpolation for the fast marching and string methods, Burger SK1, Liu Y, Sarkar U, Ayers PW, J Chem Phys. 2009 130(2) 024103. doi: 10.1063/1.2996579.</ref>
== अनुप्रयोग ==
== अनुप्रयोग ==


Line 24: Line 24:
रासायनिक प्रतिक्रियाओं के लिए संभावित ऊर्जा सतहों को अभिकारकों और उत्पादों के सापेक्ष सक्रिय परिसर में बांड की लंबाई के विस्तार की तुलना करके आकर्षक या प्रतिकारक के रूप में वर्गीकृत किया जा सकता है और इस प्रकार A + B—C → A—B + C की प्रतिक्रिया के लिए, नवनिर्मित A—B बांड के लिए बंधन लंबाई विस्तार को R*<sub>AB</sub> = R<sub>AB</sub> − R<sup>0</sup><sub>AB</sub>, के रूप में परिभाषित किया गया है, जहां R<sub>AB</sub> संक्रमण अवस्था में A-B बंध लंबाई के रूप में होता है और उत्पाद अणु में R<sup>0</sup><sub>AB</sub> के रूप में है इसी प्रकार प्रतिक्रिया में टूटे हुए बंधन के लिए R*<sub>BC</sub> = R<sub>BC</sub> − R<sup>0</sup><sub>BC</sub>, जहां R<sup>0</sup><sub>BC</sub> अभिकारक अणु को संदर्भित करता है।
रासायनिक प्रतिक्रियाओं के लिए संभावित ऊर्जा सतहों को अभिकारकों और उत्पादों के सापेक्ष सक्रिय परिसर में बांड की लंबाई के विस्तार की तुलना करके आकर्षक या प्रतिकारक के रूप में वर्गीकृत किया जा सकता है और इस प्रकार A + B—C → A—B + C की प्रतिक्रिया के लिए, नवनिर्मित A—B बांड के लिए बंधन लंबाई विस्तार को R*<sub>AB</sub> = R<sub>AB</sub> − R<sup>0</sup><sub>AB</sub>, के रूप में परिभाषित किया गया है, जहां R<sub>AB</sub> संक्रमण अवस्था में A-B बंध लंबाई के रूप में होता है और उत्पाद अणु में R<sup>0</sup><sub>AB</sub> के रूप में है इसी प्रकार प्रतिक्रिया में टूटे हुए बंधन के लिए R*<sub>BC</sub> = R<sub>BC</sub> − R<sup>0</sup><sub>BC</sub>, जहां R<sup>0</sup><sub>BC</sub> अभिकारक अणु को संदर्भित करता है।


एक्ज़ोथिर्मिक प्रतिक्रियाओं के लिए, एक पीईएस को आकर्षक या प्रारंभिक-डाउनहिल के रूप में वर्गीकृत किया जाता है यदि R*<sub>AB</sub> > R*<sub>BC</sub> संक्रमण अवस्था तक पहुँच जाए जबकि अभिकारक एक दूसरे के निकट आ रहे हों। तो इस प्रकार संक्रमण अवस्था के बाद, A-B बॉन्ड की लंबाई घटती रहती है, जिससे मुक्त प्रतिक्रिया ऊर्जा का अधिकांश भाग A-B बॉन्ड की [[आणविक कंपन]] ऊर्जा में परिवर्तित हो जाता है। एक उदाहरण हारपून प्रतिक्रिया K + Br<sub>2</sub> → K—Br + Br, जिसमें रिएक्टेंट्स के प्रारंभिक लंबी दूरी के आकर्षण K<sup>+</sup>•••Br<sup>−</sup>•••Br के साथ सक्रिय जटिल की ओर जाता है। विब्रेशनल रासायनिक संदीप्ति से उत्पाद अणुओं की तीव्र उत्साहित जनसंख्या का पता लगाया जा सकता है
एक्ज़ोथिर्मिक प्रतिक्रियाओं के लिए, एक पीईएस को आकर्षक या प्रारंभिक-डाउनहिल के रूप में वर्गीकृत किया जाता है यदि R*<sub>AB</sub> > R*<sub>BC</sub> संक्रमण अवस्था तक पहुँच जाए जबकि अभिकारक एक दूसरे के निकट आ रहे हों। तो इस प्रकार संक्रमण अवस्था के बाद, A-B बॉन्ड की लंबाई घटती रहती है, जिससे मुक्त प्रतिक्रिया ऊर्जा का अधिकांश भाग A-B बॉन्ड की [[आणविक कंपन]] ऊर्जा में परिवर्तित हो जाता है। उदाहरण हारपून प्रतिक्रिया K + Br<sub>2</sub> → K—Br + Br, जिसमें रिएक्टेंट्स के प्रारंभिक लंबी दूरी के आकर्षण K<sup>+</sup>•••Br<sup>−</sup>•••Br के साथ सक्रिय जटिल की ओर जाता है। विब्रेशनल रासायनिक संदीप्ति से उत्पाद अणुओं की तीव्र उत्साहित जनसंख्या का पता लगाया जा सकता है
 
इसके विपरीत प्रतिक्रिया H+ CL2 → HOC + CL के लिए प्रतिकूल या लेट डाउन हिल के रूप में होता है क्योंकि R*<sub>HCl</sub> < R*<sub>ClCl</sub> संक्रमण की अवस्था तक पहुँच जाता है जब उत्पाद भिन्न - भिन्न हो जाते हैं। इस प्रतिक्रिया के लिए जिसमें परमाणु A (यहाँ H) B और C की तुलना में हल्का होता है और इस प्रकार प्रतिक्रिया ऊर्जा मुख्य रूप से उत्पादों की अनुवादिक [[गतिज ऊर्जा]] के रूप में जारी की जाती है। प्रतिक्रिया के लिए जैसे F + H<sub>2</sub> → HF + H जिसमें परमाणु A B और C से भारी है और इसमें मिश्रित ऊर्जा रिलीज है और इस प्रकार कंपन और अनुवाद दोनों ही पीईएस प्रतिकारक है।
 
[[एंडोथर्मिक प्रक्रिया]] के लिए, सतह का प्रकार ऊर्जा के प्रकार को निर्धारित करता है जो प्रतिक्रिया करने में सबसे प्रभावी होता है। एक आकर्षक सतह के साथ प्रतिक्रियाओं को प्रेरित करने के लिए अभिकारकों की ट्रांसलेशनल ऊर्जा सबसे प्रभावी होती है, जबकि एक प्रतिकारक सतह के साथ प्रतिक्रियाओं के लिए कंपन उत्तेजना उच्च आणविक कंपन वी अधिक प्रभावी होती है और इस प्रकार बाद के स्थितियों के उदाहरण के रूप में, प्रतिक्रिया F + HCl(v=1) → Cl + HF की समान कुल ऊर्जा के लिए F + HCl(v=0) → Cl + HF से लगभग पांच गुना तेज है।
 
 
 
 
 
 
 




प्रतिक्रिया एच + सीएल के लिए पीईएस के विपरीत एचसीएल + सीएल प्रतिकूल (या देर से डाउनहिल) है क्योंकि आर और संक्रमण अवस्था तब पहुँच जाती है जब उत्पाद अलग हो रहे होते हैं।इस प्रतिक्रिया के लिए जिसमें परमाणु ए (यहाँ एच) बी और सी की तुलना में हल्का है, प्रतिक्रिया ऊर्जा मुख्य रूप से उत्पादों की अनुवादिक [[गतिज ऊर्जा]] के रूप में जारी की जाती है। एफ + एच जैसी प्रतिक्रिया के लिए एचएफ + एच जिसमें परमाणु ए बी और सी से भारी है, मिश्रित ऊर्जा रिलीज है, कंपन और अनुवाद दोनों, भले ही पीईएस प्रतिकारक है।


[[एंडोथर्मिक प्रक्रिया]] के लिए, सतह का प्रकार ऊर्जा के प्रकार को निर्धारित करता है जो प्रतिक्रिया करने में सबसे प्रभावी होता है। एक आकर्षक सतह के साथ प्रतिक्रियाओं को प्रेरित करने के लिए अभिकारकों की ट्रांसलेशनल ऊर्जा सबसे प्रभावी होती है, जबकि एक प्रतिकारक सतह के साथ प्रतिक्रियाओं के लिए कंपन उत्तेजना (उच्च आणविक कंपन वी) अधिक प्रभावी होती है।बाद के मामले के एक उदाहरण के रूप में, प्रतिक्रिया एफ + एचसीएल (वी = 1) → सीएल + एचएफ एचसीएल की समान कुल ऊर्जा के लिए एफ + एचसीएल (वी = 0) → सीएल + एचएफ से लगभग पांच गुना तेज है।


[[Category:All articles to be merged]]
[[Category:Articles to be merged from February 2023]]
[[Category:Articles with invalid date parameter in template]]
[[Category:Collapse templates]]
[[Category:Created On 18/05/2023]]
[[Category:Machine Translated Page]]
[[Category:Navigational boxes| ]]
[[Category:Navigational boxes without horizontal lists]]
[[Category:Pages with script errors]]
[[Category:Short description with empty Wikidata description]]


== इतिहास ==
== इतिहास ==
रासायनिक प्रतिक्रियाओं के लिए एक संभावित ऊर्जा सतह की अवधारणा पहली बार 1913 में फ्रांसीसी भौतिक विज्ञानी रेने मार्सेलिन द्वारा सुझाई गई थी।<ref name=Lewars>[https://books.google.com/books?id=5gs0v6lEc14C&dq=Lewars+potential+energy+surface+Marcelin&pg=PA21 Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics] Errol G. Lewars, 2nd ed. (Springer 2011) p.21  {{ISBN|978-9048138616}}</ref> एच + एच के लिए एक संभावित ऊर्जा सतह की पहली अर्ध-अनुभवजन्य गणना प्रस्तावित की गई थी<sub>2</sub> 1931 में हेनरी आइरिंग (रसायनज्ञ) और माइकल पोलैनी द्वारा प्रतिक्रिया। 1935 में संक्रमण अवस्था सिद्धांत में [[प्रतिक्रिया दर स्थिर]]ांक की गणना करने के लिए आयरिंग ने संभावित ऊर्जा सतहों का उपयोग किया।
रासायनिक प्रतिक्रियाओं के लिए एक संभावित ऊर्जा सतह की अवधारणा पहली बार 1913 में फ्रांसीसी भौतिक विज्ञानी रेने मार्सेलिन द्वारा सुझाई गई थी।<ref name=Lewars>[https://books.google.com/books?id=5gs0v6lEc14C&dq=Lewars+potential+energy+surface+Marcelin&pg=PA21 Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics] Errol G. Lewars, 2nd ed. (Springer 2011) p.21  {{ISBN|978-9048138616}}</ref> H + H<sub>2</sub> के लिए एक संभावित ऊर्जा सतह की पहली अर्ध-अनुभवजन्य गणना प्रस्तावित की गई थी 1931 में हेनरी आइरिंग (रसायनज्ञ) और माइकल पोलैनी द्वारा प्रतिक्रिया दी गई थी। 1935 में संक्रमण अवस्था सिद्धांत में [[प्रतिक्रिया दर स्थिर|प्रतिक्रिया दर स्थिरांक]] की गणना करने के लिए आयरिंग ने संभावित ऊर्जा सतहों का उपयोग किया था।


== एच + एच<sub>2</sub> द्वि-आयामी पीईएस ==
== H + H<sub>2</sub> द्वि-आयामी पीईएस ==
संभावित ऊर्जा सतहों को आमतौर पर त्रि-आयामी ग्राफ के रूप में दिखाया जाता है, लेकिन उन्हें द्वि-आयामी ग्राफ द्वारा भी प्रदर्शित किया जा सकता है, जिसमें प्रतिक्रिया की प्रगति को आइसोएनर्जेटिक लाइनों के उपयोग से प्लॉट किया जाता है।
संभावित ऊर्जा सतहों को सामान्यतः त्रि-आयामी ग्राफ के रूप में दिखाया जाता है, लेकिन उन्हें द्वि-आयामी ग्राफ द्वारा भी प्रदर्शित किया जा सकता है, जिसमें प्रतिक्रिया की प्रगति को आइसोएनर्जेटिक लाइनों के उपयोग से प्लॉट किया जाता है। संरेख प्रणाली H + H<sub>2</sub> एक सरल प्रतिक्रिया है जो दो-आयामी पीईएस को आसान और समझने योग्य विधि से प्लॉट करने की अनुमति देती है। इस अभिक्रिया में हाइड्रोजन परमाणु (H) डाइहाइड्रोजन अणु (H<sub>2</sub>) अणु से एक परमाणु के साथ एक नया बंध बनाकर अभिक्रिया करता है, जिससे मूल अणु के बंध टूट जाते हैं।। इसे H<sub>a</sub> + H<sub>b</sub>–H<sub>c</sub> → H<sub>a</sub>–H<sub>b</sub> + H<sub>c</sub> से दर्शाया जाता है और इस प्रकार अभिकारकों (H+H₂) से उत्पादों (H-H-H) तक प्रतिक्रिया की प्रगति के साथ ही प्रतिक्रिया में भाग लेने वाली वर्ग की ऊर्जा संबंधित संभावित ऊर्जा सतह में अच्छी तरह से परिभाषित होती है। ऊर्जा रूपरेखा मेंऊर्जा का वर्णन ज्यामितीय चर के एक फलन के रूप में बताया गया है और इस प्रकार किसी भी आयाम में पीईएस समय और तापमान से स्वतंत्र होता है।
संरेख प्रणाली एच + एच<sub>2</sub> एक सरल प्रतिक्रिया है जो एक दो-आयामी पीईएस को आसान और समझने योग्य तरीके से प्लॉट करने की अनुमति देती है।
[[File:H+H2 Potential energy surface.jpg|thumb|403x403px|H+H2 संभावित ऊर्जा सतह]]2-डी पीईएस में हमारे पास विभिन्न प्रासंगिक तत्व के रूप में होते है
इस अभिक्रिया में हाइड्रोजन परमाणु (H) डाइहाइड्रोजन अणु (H<sub>2</sub>) अणु से एक परमाणु के साथ एक नया बंधन बनाकर, जो बदले में मूल अणु के बंधन को तोड़ देता है। इसे H से दर्शाया जाता है<sub>a</sub> + एच<sub>b</sub>-एच<sub>c</sub> → एच<sub>a</sub>-एच<sub>b</sub> + एच<sub>c</sub>. अभिकारकों (H+H₂) से उत्पादों (H-H-H) तक प्रतिक्रिया की प्रगति, साथ ही प्रतिक्रिया में भाग लेने वाली प्रजातियों की ऊर्जा, संबंधित संभावित ऊर्जा सतह में अच्छी तरह से परिभाषित हैं।
* 2-डी प्लॉट न्यूनतम बिंदुओं को दिखाता है जहां हम अभिकारकों, उत्पादों और सैडल बिंदु या संक्रमण अवस्था को पाते हैं।
ऊर्जा प्रोफाइल संभावित ऊर्जा का वर्णन ज्यामितीय चर के एक फलन के रूप में करते हैं (पीईएस किसी भी आयाम में समय और तापमान से स्वतंत्र हैं)।
[[File:H+H2 Potential energy surface.jpg|thumb|403x403px|H+H2 संभावित ऊर्जा सतह]]2-डी पीईएस में हमारे पास विभिन्न प्रासंगिक तत्व हैं:
* 2-डी प्लॉट न्यूनतम बिंदुओं को दिखाता है जहां हम अभिकारकों, उत्पादों और काठी बिंदु या संक्रमण अवस्था को पाते हैं।
* संक्रमण अवस्था अभिक्रिया निर्देशांक में अधिकतम और अभिक्रिया पथ के लम्बवत् निर्देशांक में न्यूनतम होती है।
* संक्रमण अवस्था अभिक्रिया निर्देशांक में अधिकतम और अभिक्रिया पथ के लम्बवत् निर्देशांक में न्यूनतम होती है।
* समय की प्रगति प्रत्येक प्रतिक्रिया में एक प्रक्षेपवक्र का वर्णन करती है। प्रतिक्रिया की स्थितियों के आधार पर प्रक्रिया 2 अक्षों के बीच प्लॉट किए गए उत्पाद निर्माण के लिए अलग-अलग तरीके दिखाएगी।
* समय की प्रगति प्रत्येक प्रतिक्रिया में एक प्रक्षेपवक्र का वर्णन करती है। प्रतिक्रिया की स्थितियों के आधार पर प्रक्रिया 2 अक्षों के बीच प्लॉट किए गए उत्पाद निर्माण के लिए भिन्न - भिन्न विधि के रूप में होती है।


== यह भी देखें ==
== यह भी देखें ==
Line 66: Line 62:


{{Reaction mechanisms}}
{{Reaction mechanisms}}
[[Category: क्वांटम यांत्रिकी]] [[Category: संभावित सिद्धांत]] [[Category: क्वांटम रसायन]]


 
[[Category:All articles to be merged]]
 
[[Category:Articles to be merged from February 2023]]
[[Category: Machine Translated Page]]
[[Category:Articles with invalid date parameter in template]]
[[Category:Collapse templates]]
[[Category:Created On 18/05/2023]]
[[Category:Created On 18/05/2023]]
[[Category:Lua-based templates]]
[[Category:Machine Translated Page]]
[[Category:Navigational boxes| ]]
[[Category:Navigational boxes without horizontal lists]]
[[Category:Pages with script errors]]
[[Category:Short description with empty Wikidata description]]
[[Category:Sidebars with styles needing conversion]]
[[Category:Template documentation pages|Documentation/doc]]
[[Category:Templates Vigyan Ready]]
[[Category:Templates generating microformats]]
[[Category:Templates that add a tracking category]]
[[Category:Templates that are not mobile friendly]]
[[Category:Templates that generate short descriptions]]
[[Category:Templates using TemplateData]]
[[Category:Wikipedia metatemplates]]
[[Category:क्वांटम यांत्रिकी]]
[[Category:क्वांटम रसायन]]
[[Category:संभावित सिद्धांत]]

Latest revision as of 15:22, 15 June 2023

संभावित ऊर्जा सतह (पीईएस) एक भौतिक प्रणाली की ऊर्जा को विशेष रूप से कुछ मापदंडों के संदर्भ में परमाणुओं के संग्रह को वर्णित करता है, सामान्यतया परमाणुओं की स्थिति को दर्शाता है। सतह (गणित) ऊर्जा को एक या अधिक निर्देशांकों के फलन (गणित) के रूप में परिभाषित कर सकता है और इस प्रकार केवल एक निर्देशांक के रूप में होता है ,तो सतह को संभावित ऊर्जा वक्र या ऊर्जा प्रोफाइल के रूप में जाना जाता है और इस प्रकार उदाहरण मोर्स लंबी दूरी की क्षमता के रूप में होता है।

लैंडस्केप की एनालॉजी का उपयोग करना सहायक होता है, दो स्वतंत्रता की कोटि भौतिकी और रसायन विज्ञान वाली प्रणाली के रूप में होती है, जैसे दो बंध ऊर्जा की तुलना में दो बंध लंबाईयों का काम भूमि पर स्थिति के निर्देशांक के रूप में एनालॉजी होते है।[1]

पानी के अणु के लिए पीईएस पानी के लिए अनुकूलित आणविक संरचना के अनुरूप न्यूनतम ऊर्जा दिखाता है- 0.0958 एनएम के O-H बांड की लंबाई और 104.5 घात के H-O-H बांड कोण के रूप में होते है

पीईएस अवधारणा रसायन विज्ञान और भौतिकी जैसे क्षेत्रों में विशेष रूप से इन विषयों की सैद्धांतिक उप-शाखाओं में अनुप्रयोग के रूप में होती है। इसका उपयोग सैद्धांतिक रूप से परमाणुओं से बनी संरचनाओं के गुणों का पता लगाने के लिए किया जा सकता है, उदाहरण के लिए अणु के न्यूनतम ऊर्जा आकार का पता लगाता है और इस प्रकार रासायनिक प्रतिक्रिया की प्रतिक्रिया दर की गणना करता है।

गणितीय परिभाषा और संगणना

परमाणुओं के एक समूह की ज्यामिति को सदिश r द्वारा वर्णित किया जा सकता है, जिनके तत्व परमाणु स्थितियों का प्रतिनिधित्व करते हैं। सदिश r परमाणुओं के कार्टेशियन निर्देशांक का समुच्चय हो सकता है या अंतर-परमाणु दूरियों और कोणों का समुच्चय भी हो सकता है।

दिए गए r, पदों के फलन के रूप में ऊर्जा, E(r) सभी ब्याज के लिए सभी के लिए r का मान है। प्रस्तावना से लैंडस्केप एनालॉजी का उपयोग करते हुए, E ऊर्जा लैंडस्केप की ऊंचाई प्रदान करता है जिससे कि एक संभावित ऊर्जा सतह की अवधारणा उत्पन्न हो सके।

परमाणु स्थितियों के एक फलन के रूप में पीईएस का उपयोग करके एक रासायनिक प्रतिक्रिया का अध्ययन करने के लिए ब्याज की प्रत्येक परमाणु व्यवस्था के लिए ऊर्जा की गणना करना आवश्यक होता है। अभिकलनात्मक रसायन विज्ञान लेख में परमाणुओं की एक विशेष परमाणु व्यवस्था की ऊर्जा की गणना करने की विधि का अच्छी तरह से वर्णन किया जाता है और यहां पर बल के अनुमानों को ढूढ़ने पर जोर दिया जाता है और इस प्रकार E(r) ठीक-ठाक ऊर्जा-स्थिति की जानकारी प्राप्त करने के लिए उपयोग किया जाता है।

बहुत ही सरल रासायनिक प्रणालियों के लिए अथवा जब अंतर-परमाणु संबंधों के बारे में सरलीकरण करते समय अनुमान लगाया जाता है, तो कभी-कभी परमाणु स्थितियों के फलन के रूप में ऊर्जा की विश्लेषणात्मक रूप से व्युत्पन्न अभिव्यक्ति का उपयोग करना संभव होता है। उदाहरण के लिए तीन H-H. दूरियों के फलन के रूप में H​​+ H2 प्रणाली के लिए फ्रिट्ज लंदन आइरिंग पोलानी सातो क्षमता के रूप में होना भी एक उदाहरण है।[2][3][4]

अधिक जटिल प्रणालियों के लिए, परमाणुओं की एक विशेष व्यवस्था की ऊर्जा की गणना अधिकांशतः कम्प्यूटेशनल रूप से महत्वपूर्ण होती है, जिससे सतह के बड़े पैमाने पर प्रतिनिधित्व संभव नहीं हो पाता है। इन प्रणालियों के लिए एक संभावित विधि यह है कि पीईएस पर केवल अंकों के घटे हुए समुच्चय की गणना की जाती है और फिर कम्प्यूटेशनल रूप से सस्ते इंटरपोलेशन विधि का उपयोग किया जाता है, उदाहरण के लिए शेपर्ड इंटरपोलेशन, अंतराल को भरने के लिए उपयोग किया जाता है।[5]

अनुप्रयोग

पीईएस आणविक ज्यामिति और रासायनिक प्रतिक्रिया गतिकी के विश्लेषण में सहायता के लिए एक वैचारिक उपकरण के रूप में होता है। एक बार पीईएस पर आवश्यक बिंदुओं का मूल्यांकन हो जाने के बाद बिंदुओं को स्थिति के संबंध में ऊर्जा के पहले और दूसरे अवकलज के अनुसार वर्गीकृत किया जा सकता है, जो क्रमशः ढाल और वक्रता के रूप में होता है और इस प्रकार स्थिर बिंदु या शून्य ढाल वाले बिंदु का भौतिक अर्थ होता है ऊर्जा मिनिमा भौतिक रूप से स्थिर रासायनिक प्रजातियों के अनुरूप है और अचल बिंदु संक्रमण अवस्थाओं के अनुरूप होता है और इस प्रकार प्रतिक्रिया समन्वय पर उच्चतम ऊर्जा बिंदु एक रासायनिक उत्पाद के रूप में होता है, जो रासायनिक अभिकारक को जोड़ने वाला सबसे कम ऊर्जा मार्ग के रूप में है।

आकर्षक और प्रतिकारक सतहें

रासायनिक प्रतिक्रियाओं के लिए संभावित ऊर्जा सतहों को अभिकारकों और उत्पादों के सापेक्ष सक्रिय परिसर में बांड की लंबाई के विस्तार की तुलना करके आकर्षक या प्रतिकारक के रूप में वर्गीकृत किया जा सकता है और इस प्रकार A + B—C → A—B + C की प्रतिक्रिया के लिए, नवनिर्मित A—B बांड के लिए बंधन लंबाई विस्तार को R*AB = RAB − R0AB, के रूप में परिभाषित किया गया है, जहां RAB संक्रमण अवस्था में A-B बंध लंबाई के रूप में होता है और उत्पाद अणु में R0AB के रूप में है इसी प्रकार प्रतिक्रिया में टूटे हुए बंधन के लिए R*BC = RBC − R0BC, जहां R0BC अभिकारक अणु को संदर्भित करता है।

एक्ज़ोथिर्मिक प्रतिक्रियाओं के लिए, एक पीईएस को आकर्षक या प्रारंभिक-डाउनहिल के रूप में वर्गीकृत किया जाता है यदि R*AB > R*BC संक्रमण अवस्था तक पहुँच जाए जबकि अभिकारक एक दूसरे के निकट आ रहे हों। तो इस प्रकार संक्रमण अवस्था के बाद, A-B बॉन्ड की लंबाई घटती रहती है, जिससे मुक्त प्रतिक्रिया ऊर्जा का अधिकांश भाग A-B बॉन्ड की आणविक कंपन ऊर्जा में परिवर्तित हो जाता है। उदाहरण हारपून प्रतिक्रिया K + Br2 → K—Br + Br, जिसमें रिएक्टेंट्स के प्रारंभिक लंबी दूरी के आकर्षण K+•••Br−•••Br के साथ सक्रिय जटिल की ओर जाता है। विब्रेशनल रासायनिक संदीप्ति से उत्पाद अणुओं की तीव्र उत्साहित जनसंख्या का पता लगाया जा सकता है

इसके विपरीत प्रतिक्रिया H+ CL2 → HOC + CL के लिए प्रतिकूल या लेट डाउन हिल के रूप में होता है क्योंकि R*HCl < R*ClCl संक्रमण की अवस्था तक पहुँच जाता है जब उत्पाद भिन्न - भिन्न हो जाते हैं। इस प्रतिक्रिया के लिए जिसमें परमाणु A (यहाँ H) B और C की तुलना में हल्का होता है और इस प्रकार प्रतिक्रिया ऊर्जा मुख्य रूप से उत्पादों की अनुवादिक गतिज ऊर्जा के रूप में जारी की जाती है। प्रतिक्रिया के लिए जैसे F + H2 → HF + H जिसमें परमाणु A B और C से भारी है और इसमें मिश्रित ऊर्जा रिलीज है और इस प्रकार कंपन और अनुवाद दोनों ही पीईएस प्रतिकारक है।

एंडोथर्मिक प्रक्रिया के लिए, सतह का प्रकार ऊर्जा के प्रकार को निर्धारित करता है जो प्रतिक्रिया करने में सबसे प्रभावी होता है। एक आकर्षक सतह के साथ प्रतिक्रियाओं को प्रेरित करने के लिए अभिकारकों की ट्रांसलेशनल ऊर्जा सबसे प्रभावी होती है, जबकि एक प्रतिकारक सतह के साथ प्रतिक्रियाओं के लिए कंपन उत्तेजना उच्च आणविक कंपन वी अधिक प्रभावी होती है और इस प्रकार बाद के स्थितियों के उदाहरण के रूप में, प्रतिक्रिया F + HCl(v=1) → Cl + HF की समान कुल ऊर्जा के लिए F + HCl(v=0) → Cl + HF से लगभग पांच गुना तेज है।







इतिहास

रासायनिक प्रतिक्रियाओं के लिए एक संभावित ऊर्जा सतह की अवधारणा पहली बार 1913 में फ्रांसीसी भौतिक विज्ञानी रेने मार्सेलिन द्वारा सुझाई गई थी।[6] H + H2 के लिए एक संभावित ऊर्जा सतह की पहली अर्ध-अनुभवजन्य गणना प्रस्तावित की गई थी 1931 में हेनरी आइरिंग (रसायनज्ञ) और माइकल पोलैनी द्वारा प्रतिक्रिया दी गई थी। 1935 में संक्रमण अवस्था सिद्धांत में प्रतिक्रिया दर स्थिरांक की गणना करने के लिए आयरिंग ने संभावित ऊर्जा सतहों का उपयोग किया था।

H + H2 द्वि-आयामी पीईएस

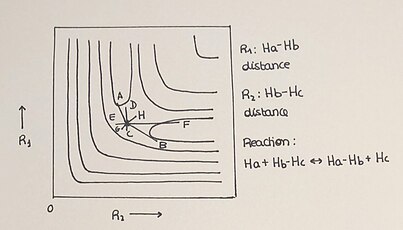
संभावित ऊर्जा सतहों को सामान्यतः त्रि-आयामी ग्राफ के रूप में दिखाया जाता है, लेकिन उन्हें द्वि-आयामी ग्राफ द्वारा भी प्रदर्शित किया जा सकता है, जिसमें प्रतिक्रिया की प्रगति को आइसोएनर्जेटिक लाइनों के उपयोग से प्लॉट किया जाता है। संरेख प्रणाली H + H2 एक सरल प्रतिक्रिया है जो दो-आयामी पीईएस को आसान और समझने योग्य विधि से प्लॉट करने की अनुमति देती है। इस अभिक्रिया में हाइड्रोजन परमाणु (H) डाइहाइड्रोजन अणु (H2) अणु से एक परमाणु के साथ एक नया बंध बनाकर अभिक्रिया करता है, जिससे मूल अणु के बंध टूट जाते हैं।। इसे Ha + Hb–Hc → Ha–Hb + Hc से दर्शाया जाता है और इस प्रकार अभिकारकों (H+H₂) से उत्पादों (H-H-H) तक प्रतिक्रिया की प्रगति के साथ ही प्रतिक्रिया में भाग लेने वाली वर्ग की ऊर्जा संबंधित संभावित ऊर्जा सतह में अच्छी तरह से परिभाषित होती है। ऊर्जा रूपरेखा मेंऊर्जा का वर्णन ज्यामितीय चर के एक फलन के रूप में बताया गया है और इस प्रकार किसी भी आयाम में पीईएस समय और तापमान से स्वतंत्र होता है।

H+H2 संभावित ऊर्जा सतह

2-डी पीईएस में हमारे पास विभिन्न प्रासंगिक तत्व के रूप में होते है

  • 2-डी प्लॉट न्यूनतम बिंदुओं को दिखाता है जहां हम अभिकारकों, उत्पादों और सैडल बिंदु या संक्रमण अवस्था को पाते हैं।
  • संक्रमण अवस्था अभिक्रिया निर्देशांक में अधिकतम और अभिक्रिया पथ के लम्बवत् निर्देशांक में न्यूनतम होती है।
  • समय की प्रगति प्रत्येक प्रतिक्रिया में एक प्रक्षेपवक्र का वर्णन करती है। प्रतिक्रिया की स्थितियों के आधार पर प्रक्रिया 2 अक्षों के बीच प्लॉट किए गए उत्पाद निर्माण के लिए भिन्न - भिन्न विधि के रूप में होती है।

यह भी देखें

संदर्भ

  1. ↑ Potential-energy (reaction) surface in Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997)
  2. ↑ Sato, S. (1955). "संभावित ऊर्जा सतह को चित्रित करने का एक नया तरीका". Bulletin of the Chemical Society of Japan. 28 (7): 450–453. doi:10.1246/bcsj.28.450.Sato, Shin (1955). "On a New Method of Drawing the Potential Energy Surface". The Journal of Chemical Physics. 23 (3): 592–593. Bibcode:1955JChPh..23..592S. doi:10.1063/1.1742043.
  3. ↑ Keith J. Laidler, Chemical Kinetics (3rd ed., Harper & Row 1987) p.68-70 ISBN 0-06-043862-2
  4. ↑ Steinfeld J.I., Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed., Prentice-Hall 1998) p.201-2 ISBN 0-13-737123-3
  5. ↑ Moving least-squares enhanced Shepard interpolation for the fast marching and string methods, Burger SK1, Liu Y, Sarkar U, Ayers PW, J Chem Phys. 2009 130(2) 024103. doi: 10.1063/1.2996579.
  6. ↑ Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics Errol G. Lewars, 2nd ed. (Springer 2011) p.21 ISBN 978-9048138616
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=संभावित_ऊर्जा_सतह&oldid=188082’