आणविक कंपन
आणविक कंपन एक दूसरे के सापेक्ष एक अणु के परमाणुओं की आवधिक कार्य है, जैसे कि अणु के द्रव्यमान का केंद्र अपरिवर्तित रहता है। विशिष्ट कंपन आवृत्तियों की सीमा 1013 हर्ट्ज से कम लेकर लगभग 1014 हर्ट्ज होती है जो लगभग 300 से 3000 सेमी−1 की तरंगों और लगभग 30 से 3 µm माइक्रोन की तरंग दैर्ध्य के अनुरूप होती है।
द्विपरमाणुक अणु A−B के लिए, s−1 में कंपन आवृत्ति द्वारा दी जाती है जहाँ k डाइन/सेमी या एर्ग/सेमी2 में बल स्थिरांक है और μ द्वारा दिया गया घटा हुआ द्रव्यमान है . सेमी−1में कंपन तरंग संख्या -1 है जहाँ c सेमी/सेकेंड में प्रकाश की गति है।
बहुपरमाणुक अणुओं के कंपनों को सामान्य विधाओं के रूप में वर्णित किया जाता है, जो एक दूसरे से स्वतंत्र होती हैं, किन्तु प्रत्येक सामान्य विधा में अणु के विभिन्न भागों के एक साथ कंपन सम्मिलित होते हैं। सामान्यतः , एन परमाणुओं के साथ एक गैर-रैखिक अणु में 3N-6 कंपन मोड होता है, किन्तु एक रैखिक अणु में 3N-5 मोड होते हैं, क्योंकि आणविक अक्ष के बारे में घुमाव नहीं देखा जा सकता है।[1] डायटोमिक अणु में कंपन का एक सामान्य विधि होती है, क्योंकि यह केवल एकल बंधन को फैला या संकुचित कर सकता है।
एक आणविक कंपन उत्तेजित होता है जब अणु ऊर्जा को अवशोषित करता है, ΔE, कंपन की आवृत्ति के अनुरूप, ν, संबंध ΔE = hν के अनुसार, जहां h प्लैंक स्थिरांक है।एक मौलिक कंपन उत्पन्न होता है जब ऊर्जा की एक ऐसी मात्रा अणु द्वारा अपनी जमीनी अवस्था में अवशोषित की जाती है। जब कई क्वांटा अवशोषित होते हैं, तो पहले और संभवतः उच्च अधिस्वर उत्तेजित होते हैं।
पहले सन्निकटन के लिए, एक सामान्य कंपन में गति को एक प्रकार की सरल हार्मोनिक गति के रूप में वर्णित किया जा सकता है। इस सन्निकटन में, कंपन ऊर्जा परमाणु विस्थापन के संबंध में एक द्विघात कार्य (परबोला) है और पहले अधिस्वर में मौलिक की आवृत्ति दोगुनी होती है। वास्तव में, कंपन धार्मिकता है और पहले अधिस्वर में एक आवृत्ति होती है जो मौलिक के दोगुने से थोड़ी कम होती है। उच्च अधिस्वर के उत्तेजना में उत्तरोत्तर कम और कम अतिरिक्त ऊर्जा सम्मिलित होती है और अंततः अणु के पृथक्करण की ओर जाता है, क्योंकि अणु की संभावित ऊर्जा अधिक मोर्स क्षमता या अधिक स्पष्ट रूप से, मोर्स / लंबी दूरी की क्षमता की तरह होती है।
एक अणु की कंपन अवस्थाओं की विभिन्न विधियों से जांच की जा सकती है। अवरक्त स्पेक्ट्रोस्कोपी के माध्यम से सबसे सीधी विधि है, क्योंकि कंपन संक्रमणों को सामान्यतः स्पेक्ट्रम के अवरक्त क्षेत्र से संबंधित ऊर्जा की मात्रा की आवश्यकता होती है। रमन स्पेक्ट्रोस्कोपी, जो सामान्यतः दृश्यमान प्रकाश का उपयोग करती है, का उपयोग सीधे कंपन आवृत्तियों को मापने के लिए भी किया जा सकता है। दो विधि पूरक हैं और दोनों के बीच तुलना उपयोगी संरचनात्मक जानकारी प्रदान कर सकती है जैसे सेंट्रोसममिति के लिए पारस्परिक बहिष्करण के नियम के स्थितियों में है।
कंपन उत्तेजना पराबैंगनी-दृश्य क्षेत्र में इलेक्ट्रॉनिक उत्तेजना के संयोजन के साथ हो सकती है। संयुक्त उत्तेजना को विशेष रूप से गैस अवस्था में अणुओं के लिए इलेक्ट्रॉनिक संक्रमणों के लिए कंपन ठीक संरचना देने वाले वाइब्रोनिक संक्रमण के रूप में जाना जाता है।
एक कंपन और घुमावों का एक साथ उत्तेजना कंपन-रोटेशन स्पेक्ट्रा को जन्म देता है।
कंपन मोड की संख्या
N परमाणुओं वाले एक अणु के लिए सभी N नाभिकों की स्थिति कुल 3N पर निर्भर करता है जिससे अणु में अनुवाद रोटेशन और कंपन सहित 3N स्वतंत्रता की डिग्री हो। अनुवाद द्रव्यमान के केंद्र की गति से मेल खाता है जिसकी स्थिति को 3 कार्टेशियन समन्वय प्रणाली द्वारा वर्णित किया जा सकता है।
एक अरैखिक अणु तीन परस्पर लंबवत अक्षों में से किसी के बारे में घूम सकता है और इसलिए स्वतंत्रता की 3 घूर्णी डिग्री होती है। एक रेखीय आणविक ज्यामिति के लिए, आणविक अक्ष के चारों ओर घूमने में किसी भी परमाणु नाभिक की गति सम्मिलित नहीं होती है, इसलिए स्वतंत्रता की केवल 2 घूर्णी डिग्री होती हैं जो परमाणु निर्देशांक को बदल सकती हैं।[2][3]
एक समतुल्य तर्क यह है कि एक रेखीय अणु के घूर्णन से अंतरिक्ष में आणविक अक्ष की दिशा बदल जाती है, जिसे अक्षांश और देशांतर के अनुरूप 2 निर्देशांकों द्वारा वर्णित किया जा सकता है। एक अरेखीय अणु के लिए, एक अक्ष की दिशा इन दो निर्देशांकों द्वारा वर्णित है, और इस अक्ष के बारे में अणु का उन्मुखीकरण एक तीसरा घूर्णी समन्वय प्रदान करता है।[4]
कंपन मोड की संख्या इसलिए 3N घटा स्वतंत्रता की अनुवाद और घूर्णी डिग्री की संख्या या रैखिक के लिए 3N–5 और गैर-रैखिक अणुओं के लिए 3N-6 है।[2][3][4]
कंपन निर्देशांक
एक सामान्य कंपन का समन्वय अणु में परमाणुओं की स्थिति में परिवर्तन का एक संयोजन है। जब कंपन उत्तेजित होता है तो समन्वय कंपन की आवृत्ति ν आवृत्ति के साथ ज्यावक्रीय रूप से बदलता है|
आंतरिक निर्देशांक
आंतरिक निर्देशांक निम्न प्रकार के होते हैं जिन्हें प्लानर अणु एथिलीन के संदर्भ में चित्रित किया गया है,
- खिंचाव: बंधन की लंबाई में परिवर्तन, जैसे C–H or C–C
- झुकना: दो बंधनों के बीच के कोण में परिवर्तन, जैसे मेथिलीन समूह में HCH कोण
- रॉकिंग: परमाणुओं के एक समूह के बीच कोण में परिवर्तन, जैसे कि मेथिलीन समूह और शेष अणु।
- वैगिंग: परमाणुओं के एक समूह के तल के बीच के कोण में परिवर्तन, जैसे कि मेथिलीन समूह और शेष अणु के माध्यम से एक तल,
- मरोड़ना: परमाणुओं के दो समूहों के तलों के बीच के कोण में परिवर्तन, जैसे कि दो मेथिलीन समूहों के बीच के कोण में परिवर्तन।
- आउट-ऑफ़-प्लेन: C–H बॉन्ड में से किसी एक के बीच के कोण में परिवर्तन और एथिलीन अणु के शेष परमाणुओं द्वारा परिभाषित प्लेन। एक और उदाहरण BF3 में है जब बोरॉन परमाणु तीन फ्लोरीन परमाणुओं के तल के अंदर और बाहर चलता है।
रॉकिंग, वैगिंग या ट्विस्टिंग में सम्मिलित समूहों के भीतर बॉन्ड की लंबाई में बदलाव नहीं होता है। कोण करते हैं। रॉकिंग को वैगिंग से इस तथ्य से अलग किया जाता है कि समूह में परमाणु एक ही विमान में रहते हैं।
एथिलीन में 12 आंतरिक निर्देशांक होते हैं:4 C–H स्ट्रेचिंग,1 C–C स्ट्रेचिंग, 2 H–C–H बेंडिंग, 2 CH2 रॉकिंग, 2 CH2 वैगिंग, 1 ट्विस्टिंग। ध्यान दें कि H-C-C कोणों को आंतरिक निर्देशांक के साथ-साथ H-C-H कोण के रूप में उपयोग नहीं किया जा सकता है क्योंकि प्रत्येक कार्बन परमाणु पर सभी कोण एक ही समय में नहीं बढ़ सकते हैं।
ध्यान दें कि ये निर्देशांक सामान्य मोड के अनुरूप नहीं हैं ( या सामान्य निर्देशांक देखें)। दूसरे शब्दों में, वे विशेष आवृत्तियों या कंपन संक्रमणों के अनुरूप नहीं होते हैं|
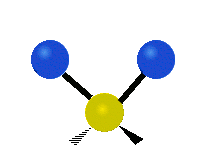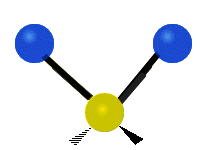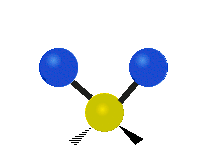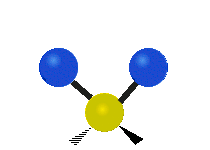
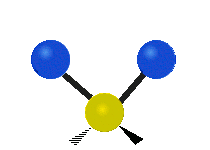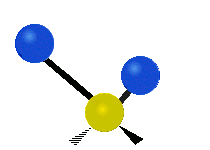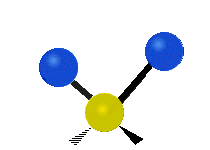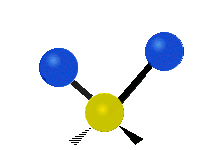
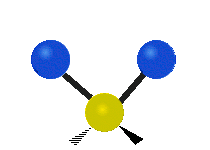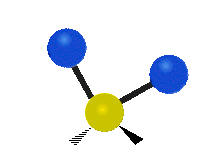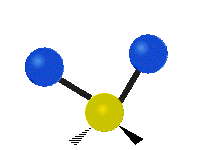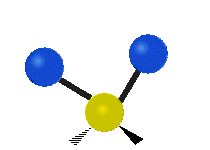
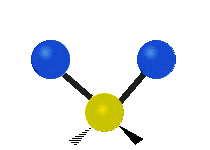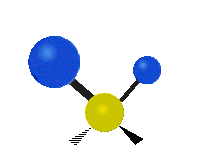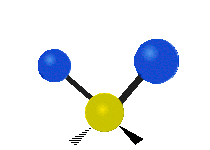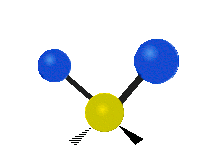
उदाहरण के लिए अणु में मेथिलीन समूह (–CH2–) के कंपन
सामान्यतः कार्बनिक यौगिकों में पाया वाले CH2 समूह के भीतर दो कम द्रव्यमान वाले हाइड्रोजन छह अलग-अलग विधियों से कंपन कर सकते हैं जिन्हें 3 जोड़े मोड के रूप में समूहीकृत किया जा सकता है: 1. सममित और असममित खिंचाव, 2. कैंची, और रॉकिंग, 3. वैगिंग और मरोड़। इन्हें यहां दिखाया गया है:
(ये आंकड़े C परमाणुओं की पुनरावृत्ति का प्रतिनिधित्व नहीं करते हैं, जो कि अणु के समग्र आंदोलनों को संतुलित करने के लिए आवश्यक रूप से उपस्थित हैं, हल्के H परमाणुओं के आंदोलनों की तुलना में बहुत छोटे हैं)।
समरूपता–अनुकूलित निर्देशांक
समरूपता-अनुकूलित निर्देशांक एक प्रोजेक्शन ऑपरेटर को आंतरिक निर्देशांक के एक समूह पर प्रयुक्त करके बनाया जा सकता है।[5] प्रोजेक्शन ऑपरेटर का निर्माण आणविक बिंदु समूह की वर्ण तालिका की सहायता से किया जाता है। उदाहरण के लिए, एथीन अणु के चार (असामान्यीकृत) C-H तनन निर्देशांक निम्न द्वारा दिए गए हैं
जहाँ चार C–H बांडों में से प्रत्येक के खिंचाव के लिए आंतरिक निर्देशांक हैं।
अधिकांश छोटे अणुओं के लिए समरूपता-अनुकूलित निर्देशांक के उदाहरण नाकामोतो में पाए जा सकते हैं।[6]
सामान्य निर्देशांक
सामान्य निर्देशांक, Q के रूप में निरूपित, कंपन के एक सामान्य मोड के संबंध में, उनके संतुलन की स्थिति से दूर परमाणुओं की स्थिति को संदर्भित करता है। प्रत्येक सामान्य मोड को एक सामान्य समन्वय दिया जाता है, और इसलिए सामान्य समन्वय किसी भी समय उस सामान्य मोड के साथ प्रगति को संदर्भित करता है। औपचारिक रूप से, सामान्य मोड एक धर्मनिरपेक्ष निर्धारक को हल करके निर्धारित किए जाते हैं, और फिर सामान्य निर्देशांक (सामान्य मोड पर) को कार्तीय निर्देशांक (परमाणु पदों पर) के योग के रूप में व्यक्त किया जा सकता है। सामान्य मोड आणविक कंपन को नियंत्रित करने वाले आव्यूह को विकर्ण करते हैं, जिससे प्रत्येक सामान्य मोड एक स्वतंत्र आणविक कंपन हो। यदि अणु में समरूपता होती है, तो सामान्य मोड अपने बिंदु समूह के तहत एक अप्रासंगिक प्रतिनिधित्व के रूप में परिवर्तित हो जाते हैं। सामान्य मोड समूह सिद्धांत को प्रयुक्त करने और कार्टेशियन निर्देशांक पर अलघुकरणीय प्रतिनिधित्व प्रस्तुत करके निर्धारित किए जाते हैं। उदाहरण के लिए, जब यह उपचार CO2 पर प्रयुक्त होता है, यह पाया गया है कि C=O खंड स्वतंत्र नहीं हैं, किंतु एक O=C=O सममित खिंचाव और एक O=C=O असममित खिंचाव है:
- सममित खिंचाव: दो सी-ओ खींचने वाले निर्देशांक का योग; दो C-O बंध लंबाई में समान मात्रा में परिवर्तन होता है और कार्बन परमाणु स्थिर रहता है। Q = q1 + q2
- असममित खिंचाव: दो सी-ओ खींचने वाले निर्देशांक का अंतर; एक C–O बंध की लंबाई बढ़ जाती है जबकि दूसरे की घट जाती है।Q = q1 − q2
जब दो या दो से अधिक सामान्य निर्देशांक आणविक बिंदु समूह (बोलचाल की भाषा में, समान समरूपता) के समान अलघुकरणीय प्रतिनिधित्व से संबंधित होते हैं तो मिश्रण होता है और संयोजन के गुणांकों को एक प्राथमिकता निर्धारित नहीं किया जा सकता है। उदाहरण के लिए, रैखिक अणु हाइड्रोजन साइनाइड में, HCN, दो तनन कंपन हैं
- मुख्यतः C–H स्ट्रेचिंग के साथ थोड़ा C–N स्ट्रेचिंग; Q1 = q1 + a q2 (a << 1)
- मुख्य रूप से C-N स्ट्रेचिंग के साथ थोड़ा C-H स्ट्रेचिंग; Q2 = b q1 + q2 (b << 1)
विल्सन जीएफ पद्धति के माध्यम से पूर्ण सामान्य समन्वय विश्लेषण करके गुणांक a और b पाए जाते हैं।[7]
न्यूटोनियन यांत्रिकी
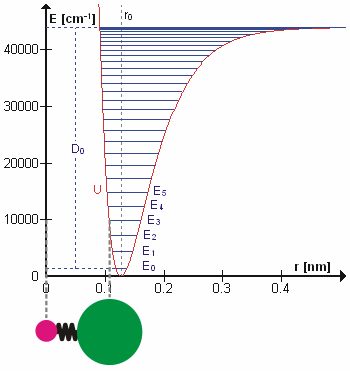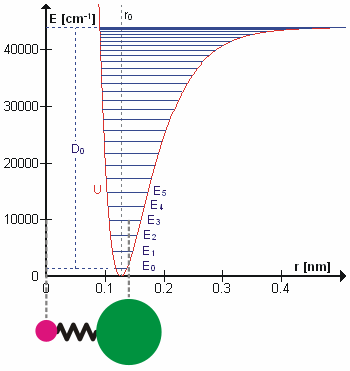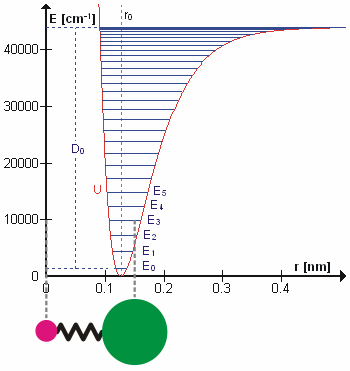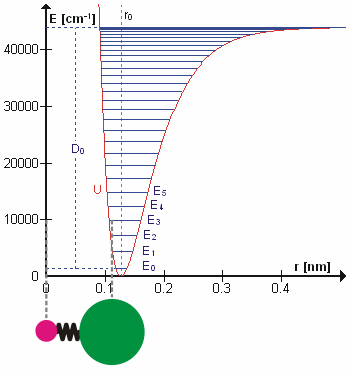
संभवतया सही कंपन आवृत्तियों की गणना करने के लिए न्यूटोनियन यांत्रिकी का उपयोग करके आश्चर्यजनक रूप से आणविक कंपन का इलाज किया जा सकता है। मूल धारणा यह है कि प्रत्येक कंपन का इलाज किया जा सकता है जैसे कि यह वसंत से मेल खाता हो। हार्मोनिक सन्निकटन में वसंत हुक के नियम का पालन करता है: वसंत को विस्तारित करने के लिए आवश्यक बल विस्तार के समानुपाती होता है। आनुपातिकता स्थिरांक को बल स्थिरांक, k के रूप में जाना जाता है। अनहार्मोनिक ऑसिलेटर को अन्यत्र माना जाता है।[8]
न्यूटन के गति के दूसरे नियम के अनुसार यह बल कम द्रव्यमान, μ, गुणा त्वरण के बराबर भी है।
क्वांटम यांत्रिकी
हार्मोनिक सन्निकटन में संभावित ऊर्जा सामान्य निर्देशांक का द्विघात कार्य है। श्रोडिंगर तरंग समीकरण को हल करते हुए, प्रत्येक सामान्य निर्देशांक के लिए ऊर्जा अवस्थाएँ निम्न द्वारा दी गई हैं
ऊर्जा में अंतर जब n (या v) 1 से बदलता है तो बराबर होता है प्लैंक स्थिरांक का उत्पाद और मौलिक यांत्रिकी का उपयोग करके प्राप्त कंपन आवृत्ति। फोटॉन के अवशोषण के कारण स्तर n से स्तर n+1 तक संक्रमण के लिए, फोटॉन की आवृत्ति मौलिक कंपन आवृत्ति (हार्मोनिक ऑसिलेटर सन्निकटन में)के बराबर होती है ।
पहले 5 तरंग कार्यों के ग्राफ के लिए क्वांटम हार्मोनिक ऑसिलेटर देखें, जो कुछ चयन नियमों को तैयार करने की अनुमति देता है। उदाहरण के लिए, एक हार्मोनिक ऑसिलेटर के लिए परिवर्तन की अनुमति तभी दी जाती है जब क्वांटम संख्या n एक से बदलती है,
तीव्रता
एक अवरक्त स्पेक्ट्रम में अवशोषण बैंड की तीव्रता (भौतिकी) सामान्य समन्वय के संबंध में आणविक द्विध्रुवीय क्षण के व्युत्पन्न के समानुपाती होती है।[12] इसी तरह, रमन बैंड की तीव्रता सामान्य समन्वय के संबंध में ध्रुवीकरण के व्युत्पन्न पर निर्भर करती है। उपयोग किए गए लेजर की तरंग दैर्ध्य की चौथी शक्ति पर भी निर्भरता है।
यह भी देखें
- सुसंगत एंटी-स्टोक्स रमन स्पेक्ट्रोस्कोपी (कार्स)
- एकार्ट की स्थिति
- फर्मी अनुनाद
- जीएफ विधि
- धातु कार्बोनिल्स अवरक्त स्पेक्ट्रोस्कोपी के पास
- लेनार्ड-जोन्स क्षमता
- अवरक्त स्पेक्ट्रोस्कोपी के पास
- परमाणु अनुनाद कंपन स्पेक्ट्रोस्कोपी
- अनुनाद रमन स्पेक्ट्रोस्कोपी
- संक्रमण द्विध्रुव क्षण
संदर्भ
- ↑ Landau, L. D.; Lifshitz, E. M. (1976). यांत्रिकी (3rd ed.). Pergamon Press. ISBN 0-08-021022-8.
- ↑ Jump up to: 2.0 2.1 Hollas, J. M. (1996). आधुनिक स्पेक्ट्रोस्कोपी (3rd ed.). John Wiley. p. 77. ISBN 0471965227.
- ↑ Jump up to: 3.0 3.1 Banwell, Colin N.; McCash, Elaine M. (1994). आणविक स्पेक्ट्रोस्कोपी की बुनियादी बातों (4th ed.). McGraw Hill. p. 71. ISBN 0-07-707976-0.
- ↑ Jump up to: 4.0 4.1 Atkins, P. W.; Paula, J. de (2006). भौतिक रसायन (8th ed.). New York: W. H. Freeman. p. 460. ISBN 0716787598.
- ↑ Cotton, F. A. (1971). समूह सिद्धांत के रासायनिक अनुप्रयोग (2nd ed.). New York: Wiley. ISBN 0471175706.
- ↑ Nakamoto, K. (1997). अकार्बनिक और समन्वय यौगिकों के इन्फ्रारेड और रमन स्पेक्ट्रा, भाग ए (5th ed.). New York: Wiley. ISBN 0471163945.
- ↑ Jump up to: 7.0 7.1 Wilson, E. B.; Decius, J. C.; Cross, P. C. (1995) [1955]. आणविक कंपन. New York: Dover. ISBN 048663941X.
- ↑ Califano, S. (1976). कंपन राज्य. New York: Wiley. ISBN 0471129968.
- ↑ Gans, P. (1971). कंपन अणु. New York: Chapman and Hall. ISBN 0412102900.
- ↑ Hollas, J. M. (1996). आधुनिक स्पेक्ट्रोस्कोपी (3rd ed.). John Wiley. p. 21. ISBN 0471965227.
- ↑ Atkins, P. W.; Paula, J. de (2006). भौतिक रसायन (8th ed.). New York: W. H. Freeman. pp. 291 and 453. ISBN 0716787598.
- ↑ Steele, D. (1971). कंपन स्पेक्ट्रोस्कोपी का सिद्धांत. Philadelphia: W. B. Saunders. ISBN 0721685803.
अग्रिम पठन
- Sherwood, P. M. A. (1972). Vibrational Spectroscopy of Solids. Cambridge University Press. ISBN 0521084822.