सुपरलैटिस: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Periodic structure of layers of two or more materials}} | {{Short description|Periodic structure of layers of two or more materials}} | ||
'''सुपरलैटिस''' मुख्य रूप से दो या दो से अधिक पदार्थों की परतों की आवर्ती संरचना है। सामान्यतः एक परत की मोटाई कई [[नैनोमीटर]] हो सकती है। यह निम्न विमीयत संरचना को भी संदर्भित कर सकते है जैसे [[क्वांटम डॉट|क्वांटम बिन्दु]] की सारणी इसका प्रमुख उदाहरण हैं। | |||
== खोज == | == खोज == | ||
[[ सोना |सोना]] -[[ ताँबा | ताँबा]] और [[ दुर्ग |पैलेडियम]]-तांबा प्रणालियों पर उनके विशेष एक्स-किरणें विवर्तन प्रतिरूप के अध्ययन के | [[ सोना |सोना]]-[[ ताँबा |ताँबा]] और [[ दुर्ग |पैलेडियम]]-तांबा प्रणालियों पर उनके विशेष एक्स-किरणें विवर्तन प्रतिरूप के अध्ययन के पश्चात जोहानसन और लिंडे द्वारा 1925 के प्रारम्भ में सुपरलैटिस की खोज की गई थी।<ref>{{cite journal|last1=Johansson|last2=Linde|title=मिश्रित-क्रिस्टल श्रृंखला गोल्ड-कॉपर और पैलेडियम-कॉपर में परमाणु व्यवस्था का एक्स-रे निर्धारण|journal=Annalen der Physik|date=1925|volume=78|issue=21|page=439|doi=10.1002/andp.19253832104|bibcode=1925AnP...383..439J}}</ref> इस प्रकार के क्षेत्रों पर आगे के प्रायोगिक अवलोकन और सैद्धांतिक संशोधन ब्रैडली और जे<ref>{{cite journal|last1=Bradley|last2=Jay|title=लोहा और एल्युमीनियम मिश्र धातुओं में सुपरलैटिस का निर्माण|journal=Proc. R. Soc. A|date=1932|volume=136|issue=829|pages=210–232|doi=10.1098/rspa.1932.0075|bibcode=1932RSPSA.136..210B|doi-access=free}}</ref> गोर्स्की,<ref>{{cite journal|last1=Gorsky|title=CuAu मिश्र धातु में परिवर्तन की एक्स-रे जांच|journal=Z. Phys.|date=1928|volume=50|issue=1–2|pages=64–81|bibcode = 1928ZPhy...50...64G |doi = 10.1007/BF01328593 |s2cid=121876817}}</ref> बोरेलियस,<ref>{{cite journal|last1=Borelius|title=धात्विक मिश्रित चरणों के परिवर्तन का सिद्धांत|journal=Annalen der Physik|date=1934|volume=20|issue=1|page=57|doi=10.1002/andp.19344120105|bibcode=1934AnP...412...57B}}</ref> देहलिंगर और ग्राफ,<ref>{{cite journal|last1=Dehlinger|last2=Graf|title=ठोस धातु चरणों का परिवर्तन I. चतुष्कोणीय सोना-तांबा मिश्र धातु CuAu|journal=Z. Phys. Chem.|date=1934|volume=26|page=343| doi=10.1515/zpch-1934-2631 | s2cid=99550940 }}</ref> ब्रैग और विलियम्स<ref>{{cite journal|last1=Bragg|first1=W.L.|last2=Williams|first2=E.J.|title=मिश्र धातु I में परमाणु व्यवस्था पर थर्मल आंदोलन का प्रभाव|journal=Proc. R. Soc. A|date=1934|volume=145|issue=855|pages=699–730|doi=10.1098/rspa.1934.0132|bibcode=1934RSPSA.145..699B|doi-access=free}}</ref> और बेथे द्वारा किए गए थे।<ref>{{cite journal|last1=Bethe|title=सुपरलैटिस का सांख्यिकीय सिद्धांत|journal=Proc. R. Soc. A|date=1935|volume=150|issue=871|pages=552–575|doi=10.1098/rspa.1935.0122|bibcode=1935RSPSA.150..552B|doi-access=free}}</ref> इस सिद्धांत अव्यवस्थित अवस्था से क्रमित अवस्था में क्रिस्टल जालक में परमाणुओं की व्यवस्था के संक्रमण पर आधारित थे। | ||
== यांत्रिक गुण == | == यांत्रिक गुण == | ||
जे.एस. कोहलर ने सैद्धांतिक रूप से भविष्यवाणी की थी<ref>{{Cite journal | last1 = Koehler | first1 = J. | title = एक मजबूत ठोस डिजाइन करने का प्रयास| doi = 10.1103/PhysRevB.2.547 | journal = Physical Review B | volume = 2 | issue = 2 | pages = 547–551 | year = 1970 |bibcode = 1970PhRvB...2..547K }}</ref> कि उच्च और निम्न प्रत्यास्थ स्थिरांक वाले पदार्थों की वैकल्पिक (नैनो-) परतों का उपयोग करके, अपरूपक प्रतिरोध को 100 गुना तक सुधारा जाता है क्योंकि फ्रैंक-रीड स्रोत [[ अव्यवस्था |अव्यवस्था]] का स्रोत नैनो परतों में काम नहीं कर सकता है। | जे.एस. कोहलर ने सैद्धांतिक रूप से भविष्यवाणी की गयी थी<ref>{{Cite journal | last1 = Koehler | first1 = J. | title = एक मजबूत ठोस डिजाइन करने का प्रयास| doi = 10.1103/PhysRevB.2.547 | journal = Physical Review B | volume = 2 | issue = 2 | pages = 547–551 | year = 1970 |bibcode = 1970PhRvB...2..547K }}</ref> कि उच्च और निम्न प्रत्यास्थ स्थिरांक वाले पदार्थों की वैकल्पिक (नैनो-) परतों का उपयोग करके, अपरूपक प्रतिरोध को 100 गुना तक सुधारा जाता है क्योंकि फ्रैंक-रीड स्रोत [[ अव्यवस्था |अव्यवस्था]] का स्रोत नैनो परतों में काम नहीं कर सकता है। | ||
इस प्रकार | इस प्रकार के सुपरलैटिस पदार्थ की बढ़ी हुई यांत्रिक [[कठोरता|दृढ़ता]] की पुष्टि सबसे पहले 1978 में Al-Cu और Al-Ag पर लेहोक्ज़की द्वारा की गई थी,<ref>{{cite journal|last1=Lehoczky|first1=S. L.|title=पतली परत वाली धातु के लैमिनेट्स में विस्थापन पीढ़ी और गति की मंदता|journal=Acta Metallurgica|date=1973|volume=41|issue=26|page=1814}}</ref> और बाद में कई अन्य लोगों द्वारा की गई,<ref>{{cite journal | last1=Yashar | first1=P. | last2=Barnett | first2=S. A. | last3=Rechner | first3=J. | last4=Sproul | first4=W. D. | title=Structure and mechanical properties of polycrystalline CrN/TiN superlattices | journal=Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films | publisher=American Vacuum Society | volume=16 | issue=5 | year=1998 | issn=0734-2101 | doi=10.1116/1.581439 | pages=2913–2918| bibcode=1998JVSTA..16.2913Y }}</ref> जैसे कि दृढ़ पीवीडी लेपन पर बार्नेट और स्पोर्ल इत्यादि। | ||
== अर्धचालक गुण == | == अर्धचालक गुण == | ||
यदि | यदि सुपरलैटिस अलग-अलग [[ऊर्जा अंतराल]] के साथ दो अर्धचालक पदार्थों से बना है, तो प्रत्येक क्वांटम ठीक रूप से नवीन [[चयन नियम]] स्थापित करते है जो संरचना के माध्यम से आवेशों के प्रवाह की स्थितियों को प्रभावित करते हैं। विकास की दिशा में आवर्ती संरचना बनाने के लिए दो अलग-अलग अर्धचालक पदार्थ एक-दूसरे पर वैकल्पिक रूप से एकत्रित की जाती हैं। [[ लियो इसकी |लियो इसकी]] और [[लैप चमकता है|राफेल त्सू]] द्वारा कृत्रिम सुपरलैटिस के 1970 के प्रस्ताव के पश्चात<ref>{{Cite journal | last1 = Esaki | first1 = L. | last2 = Tsu | first2 = R. | doi = 10.1147/rd.141.0061 | title = सेमीकंडक्टर्स में सुपरलैटिस और नेगेटिव डिफरेंशियल कंडक्टिविटी| journal = IBM Journal of Research and Development | volume = 14 | pages = 61–65 | year = 1970 }}</ref> ऐसे अति सूक्ष्म अर्धचालकों की भौतिकी में प्रगति हुई है, जिन्हें वर्तमान में क्वांटम संरचनाएं कहा जाता है। इस प्रकार क्वांटम परिरोधन की अवधारणा ने पृथक क्वांटम अनुकूल विषम संरचना में क्वांटम आकार के प्रभावों का अवलोकन किया है और इस प्रकार की घटना के माध्यम से सुपरलैटिस से निकटता से संबंधित है। इसलिए इन दो विचारों पर प्रायः एक ही भौतिक आधार पर चर्चा की जाती है, परन्तु प्रत्येक में अलग-अलग भौतिकी होती है, जो विद्युत और प्रकाशिक उपकरणों में अनुप्रयोगों के लिए उपयोगी होती है। | ||
== अर्धचालक | == अर्धचालक सुपरलैटिस प्रकार == | ||
सुपरलैटिस मिनीबैंड संरचनाएं की [[विषमसंधि]] में इसके मुख्य I, II, III प्रकारों पर यह निर्भर करती हैं। प्रथम प्रकार के सुपरलैटिस के लिए यह चालित बैंड के नीचे और संयोजकता उपबैंड के शीर्ष एक ही अर्धचालक परत में बनते हैं। इस प्रकार दूसरे भाग में चालन और संयोजकता उपबैंड वास्तविक और पारस्परिक दोनों स्थानों में कंपित होते हैं, ताकि इलेक्ट्रॉनों और छिद्रों को अलग-अलग परतों में सीमित किया जा सके। इसी प्रकार तीसरे प्रकार के सुपरलैटिस में अर्द्ध धातु पदार्थ सम्मिलित होती है, जैसे एचजीटीई/सीडीटीई इत्यादि। यद्यपि चालन उपबैंड के नीचे और संयोजकता उपबैंड के शीर्ष पर प्रकार तीसरे प्रकार के सुपरलैटिस में एक ही अर्धचालक परत में बनते हैं, जो कि प्रथम प्रकार के सुपरलैटिस के समान है, प्रकार III सुपरलैटिस के बैंड अंतराल को निरंतर अर्धचालक से शून्य बैंड अंतराल के साथ पदार्थ और ऋणात्मक बैंड अंतराल के साथ अर्द्ध धातु में समायोजित किए जा सकते है। | |||
अर्ध आवर्ती सुपरलैटिस के अन्य वर्ग का नाम [[फिबोनाची अनुक्रम]] नाम पर रखा गया है। एक [[फाइबोनैचि]] सुपरलैटिस को विमीय [[quasicrystal|अर्ध क्रिस्टल]] के रूप में देखा जा सकता है, जहां या तो इलेक्ट्रॉन हॉपिंग स्थानांतरण या यथा स्थान ऊर्जा फाइबोनैचि अनुक्रम में व्यवस्थित दो मान लेती है। | |||
== अर्धचालक पदार्थ == | == अर्धचालक पदार्थ == | ||
[[File:GaAs-AlAs SL.JPG|300px|left|thumb|GaAs/AlAs | [[File:GaAs-AlAs SL.JPG|300px|left|thumb|GaAs/AlAs सुपरलैटिस और विकास दिशा (z) के साथ चालन और संयोजकता बैंड की संभावित पार्श्वदृश्य।]]अर्धचालक पदार्थ, जो सुपरलैटिस संरचनाओं को बनाने के लिए उपयोग की जाती है, को तत्व समूहों, IV, III-V और II-VI द्वारा विभाजित किया जा सकता है। जबकि समूह III-V अर्धचालक (विशेष रूप से GaAs/Al<sub>x</sub>Ga<sub>1−x</sub>As) का बड़े पैमाने पर अध्ययन किया गया है, समूह IV विषम संरचना जैसे कि Si<sub>x</sub>Ge<sub>1−x</sub> प्रणाली बड़ी बेमेल के कारण समझना अधिक जटिल है। फिर भी, इन क्वांटम संरचनाओं में उपबैंड संरचनाओं का तनाव संशोधन रुचिपूर्ण है और इसने बहुत ध्यान आकर्षित किया है। | ||
GaAs/AlAs प्रणाली में GaAs और AlAs के बीच स्थिरांक में अंतर और उनके तापीय प्रसार गुणांक का अंतर दोनों ही छोटे हैं। इस प्रकार, [[एपिटैक्सियल ग्रोथ|अधिस्तरी वृद्धि]] तापमान से शीत होने के बाद कक्ष के तापमान पर शेष तनाव को कम किया जा सकता है। GaAs/Al<sub>x</sub>Ga<sub>1−x</sub>As पदार्थ प्रणाली का उपयोग करके पहली रचनात्मक सुपरलैटिस का उपयोग किया जाता हैं। | |||
एक बार जब दो क्रिस्टल संरेखित हो जाते हैं तो [[ग्राफीन]]/[[बोरॉन नाइट्राइड]] प्रणाली अर्धचालक सुपरलैटिस बनाता है। इसके आवेश वाहक कम ऊर्जा अपव्यय के साथ विद्युत क्षेत्र के लंबवत गति करते हैं। एच-बीएन में ग्राफीन के समान [[हेक्सागोनल|षट्कोणीय]] संरचना है। सुपरलैटिस ने [[उलटा समरूपता|प्रतिलोम सममिति]] तोड़ दी है। स्थानीय रूप से, सांस्थितिक धाराएं लागू प्रवाह की तुलना में तुलनीय हैं, जो बड़े घाटी-हॉल कोणों को दर्शाती हैं।<ref>{{Cite journal | doi = 10.1126/science.1254966| title = ग्राफीन सुपरलैटिस में सामयिक धाराओं का पता लगाना| journal = Science| year = 2014| last1 = Gorbachev | first1 = R. V.| last2 = Song | first2 = J. C. W.| last3 = Yu | first3 = G. L.| last4 = Kretinin | first4 = A. V.| last5 = Withers | first5 = F.| last6 = Cao | first6 = Y.| last7 = Mishchenko | first7 = A.| last8 = Grigorieva | first8 = I. V.| last9 = Novoselov | first9 = K. S.| last10 = Levitov | first10 = L. S.| last11 = Geim | first11 = A. K.|arxiv = 1409.0113 |bibcode = 2014Sci...346..448G | volume=346 | issue = 6208| pages=448–451 | pmid=25342798| s2cid = 2795431}}</ref> | |||
===उत्पादन=== | ===उत्पादन=== | ||
विभिन्न तकनीकों का उपयोग करके | विभिन्न तकनीकों का उपयोग करके सुपरलैटिस का उत्पादन किया जा सकता है, परन्तु [[आणविक-बीम एपिटॉक्सी|आणविक-किरण पुंज अधिरोहण]] (एमबीई) और [[स्पटरिंग|कणक्षेपण]] सबसे सामान्य हैं। इन विधियों से, परतों को मात्र कुछ परमाणु रिक्ति की मोटाई के साथ बनाया जा सकता है। सुपरलैटिस निर्दिष्ट करने का एक उदाहरण [{{chem|Fe|20|V|30}}]<sub>20</sub> है। यह 20Å आयरन (Fe) और 30Å वैनेडियम (V) की द्वि-परत को 20 बार दोहराता है, इस प्रकार 1000Å या 100 एनएम की कुल मोटाई का वर्णन करते है। अर्धचालक सुपरलैटिस बनाने के साधन के रूप में एमबीई तकनीक का प्राथमिक महत्व है। एमबीई प्रौद्योगिकी के अतिरिक्त, [[धातु कार्बनिक रासायनिक वाष्प जमाव|धातु कार्बनिक रासायनिक वाष्प निक्षेपण]] (Mo-CVD) ने अतिसंवाहक सुपरलैटिस के विकास में योगदान दिया है, जो कि InGaAsP मिश्र धातुओं जैसे चतुर्धातुक III-V यौगिक अर्धचालकों से बना है। नवीन तकनीकों में अत्युच्च निर्वात (UHV) प्रौद्योगिकियों के साथ गैस स्रोत से निपटने का संयोजन सम्मिलित है जैसे धातु-कार्बनिक अणु स्रोत पदार्थ के रूप में और गैस-स्रोत एमबीई संकर गैसों जैसे कि आर्सिन ({{chem|AsH|3}}) और फॉस्फीन ({{chem|PH|3}}) विकसित किया गया है। | ||
सामान्यतः बोलना एमबीई द्विआधारी प्रणाली में तीन तापमानों का उपयोग करने की विधि है, उदाहरण के लिए, कार्यद्रव तापमान, समूह III के स्रोत पदार्थ तापमान और III-V यौगिकों की स्थिति में समूह V तत्व का उपयोग किया जाता हैं। | |||
उत्पादित | उत्पादित सुपरलैटिस की संरचनात्मक गुणवत्ता को एक्स-किरणें विवर्तन या [[न्यूट्रॉन विवर्तन]] स्पेक्ट्रा के माध्यम से सत्यापित किए जा सकते है जिसमें विशिष्ट उपग्रह शिखर होते हैं। प्रत्यावर्ती परत से जुड़े अन्य प्रभाव हैं: [[विशाल चुंबकत्व]], एक्स-किरणें और न्यूट्रॉन दर्पणों के लिए समस्वरित करने योग्य परावर्तकता, न्यूट्रॉन [[स्पिन ध्रुवीकरण|चक्रण ध्रुवीकरण]], और प्रत्यास्थ और ध्वनिक गुणों में परिवर्तन किया जाता हैं। इसके घटकों की प्रकृति के आधार पर, सुपरलैटिस को चुंबकीय, प्रकाशिक या अर्धचालन कहा जा सकता है। | ||
[[File:Fe20v30.png|300px|right|thumb| | [[File:Fe20v30.png|300px|right|thumb|[Fe<sub>20</sub>V<sub>30</sub>]<sub>20</sub> सुपरलैटिस से एक्स-किरणें और न्यूट्रॉन प्रकीर्णन।]] | ||
== मिनीबैंड संरचना == | == मिनीबैंड संरचना == | ||
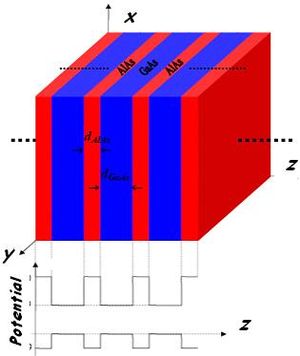
एक | एक आवर्ती सुपरलैटिस की योजनाबद्ध संरचना नीचे दिखाई गई है, जहां a और b संबंधित परत मोटाई a और b (अवधि: <math>d=a+b</math>) के दो अर्धचालक पदार्थ हैं। जब a और b अंतरापरमाणुक अंतरालन की तुलना में बहुत छोटे नहीं होते हैं, तो मूल बल्क अर्धचालक की बैंड संरचना से प्राप्त प्रभावी क्षमता द्वारा इन तीव्रता से बदलती क्षमता को बदलकर पर्याप्त सन्निकटन प्राप्त किया जाता है। व्यक्तिगत परतों में से प्रत्येक में 1D श्रोडिंगर समीकरणों को हल करना प्रत्यक्ष है, जिनके हल <math> \psi</math> वास्तविक या काल्पनिक घातांकों के रैखिक संयोजन हैं। | ||
एक बड़ी बाधा मोटाई के लिए, सुरंग रहित | एक बड़ी बाधा मोटाई के लिए, सुरंग रहित प्रकीर्णन रहित अवस्थाओं के संबंध में सुरंग बनाना दुर्बल प्रक्षोभ है, जो पूर्ण रूप से सीमित हैं। इस स्थिति में प्रकीर्णन संबंध <math> E_z(k_z) </math>, बलोच प्रमेय के आधार पर <math>2 \pi /d </math> से अधिक <math> d=a+b </math> के साथ आवर्ती संबंध, पूर्ण रूप से ज्यावक्रीय है: | ||
:<math>\ E_z(k_z)=\frac{\Delta}{2}(1-\cos(k_z d))</math> | :<math>\ E_z(k_z)=\frac{\Delta}{2}(1-\cos(k_z d))</math> | ||
और प्रभावी | और प्रभावी द्रव्यमान <math> 2\pi /d</math> के लिए संकेत बदलते है: | ||
:<math>\ {m^* = \frac{\hbar^2}{\partial^2 E / \partial k^2}}|_{k=0}</math> | :<math>\ {m^* = \frac{\hbar^2}{\partial^2 E / \partial k^2}}|_{k=0}</math> | ||
मिनीबैंड | मिनीबैंड की स्थिति में, यह ज्यावक्रीय वर्ण अब संरक्षित नहीं है। मिनीबैंड में मात्र उच्च (तरंग सदिश के लिए <math>2 \pi /d</math> के अतिरिक्त) वस्तुतः शीर्ष 'संवेदी' है और प्रभावी द्रव्यमान परिवर्तन संकेत करते है। इस प्रकार मिनीबैंड प्रकीर्णन का आकार मिनीबैंड वाहन को गहनता से प्रभावित करते है और इस प्रकार विस्तृत मिनीबैंड दिए जाने पर यथार्थ प्रकीर्णन संबंध गणना की आवश्यकता होती है। एकल मिनीबैंड वाहन को देखने का प्रतिबन्ध किसी भी प्रक्रिया द्वारा अन्तरमिनिबैंड स्थानांतरण की अनुपस्थिति है। इस प्रकार लागू विद्युत क्षेत्र की उपस्थिति में भी तापीय क्वांटम k<sub>B</sub>T पहले और दूसरे मिनीबैंड के बीच ऊर्जा अंतर <math> E_2-E_1</math> से बहुत छोटा होना चाहिए। | ||
== बलोच | == बलोच अवस्था == | ||
एक आदर्श | एक आदर्श सुपरलैटिस के लिए [[खुद के राज्यों|आईगेन अवस्थाओं]] का पूर्ण समूह समतल तरंगों <math> e^{ i \mathbf{k} \cdot \mathbf{r} }/ 2\pi </math> आश्रित फलन <math>f_k (z)</math> के उत्पादों द्वारा निर्मित किए जा सकते है जो इस प्रकार आईगेनमान समीकरण का प्रयोग होता हैं इस प्रकार हैं- | ||
:<math> \left( E_c(z) - \frac{\partial }{\partial z} \frac{\hbar^2}{2 m_c (z)} \frac{\partial }{\partial z} + \frac {\hbar^2 \mathbf{k} ^2}{2m_c (z)} \right) f_k (z) = E f_k (z) </math> | :<math> \left( E_c(z) - \frac{\partial }{\partial z} \frac{\hbar^2}{2 m_c (z)} \frac{\partial }{\partial z} + \frac {\hbar^2 \mathbf{k} ^2}{2m_c (z)} \right) f_k (z) = E f_k (z) </math> को संतुष्ट करते है। | ||
जैसा <math> E_c (z) </math> और <math> m_c(z) </math> | जैसा कि <math> E_c (z) </math> और <math> m_c(z) </math> सुपरलैटिस अवधि d के साथ आवर्ती फलन हैं, आईगेन अवस्था [[बलोच राज्य|बलोच अवस्था]] <math> f_k (z)= \phi _{q, \mathbf{k}}(z)</math> ऊर्जा <math>E^\nu (q, \mathbf{k})</math> के साथ हैं। K<sup>2</sup> में प्रथम-क्रम [[गड़बड़ी सिद्धांत|प्रक्षोभ सिद्धांत]] के भीतर, ऊर्जा | ||
:<math> E^ \nu (q, \mathbf{k}) \approx E^ \nu(q, \mathbf{0}) + \langle \phi _{q, \mathbf{k}} \mid \frac{\hbar^2 \mathbf{k}^2}{2m_c (z)} \mid \phi _{q, \mathbf{k}} \rangle </math> | :<math> E^ \nu (q, \mathbf{k}) \approx E^ \nu(q, \mathbf{0}) + \langle \phi _{q, \mathbf{k}} \mid \frac{\hbar^2 \mathbf{k}^2}{2m_c (z)} \mid \phi _{q, \mathbf{k}} \rangle </math> प्राप्त होती है। | ||
अब, <math> \phi _{q, \mathbf{0}} (z) </math> | अब, <math> \phi _{q, \mathbf{0}} (z) </math> ठीक रूप से बड़ी संभावना प्रदर्शित करेगा, जिससे कि दूसरे शब्द को | ||
:<math> E_k = \frac{\hbar^2 \mathbf{k}^2}{2m_w} </math> | :<math> E_k = \frac{\hbar^2 \mathbf{k}^2}{2m_w} </math> | ||
द्वारा प्रतिस्थापित करना उचित लगता है जहां <math>m_w</math> क्वांटम कूप का प्रभावी द्रव्यमान है। | |||
== | == वनियर फलन == | ||
परिभाषा के अनुसार बलोच के प्रमेय को | परिभाषा के अनुसार बलोच के प्रमेय को पूर्ण सुपरलैटिस पर निरूपित किया गया है। यदि विद्युत क्षेत्र लागू होते हैं या सुपरलैटिस की परिमित लंबाई के कारण प्रभाव पर विचार किया जाता है तो यह जटिलता प्रदान कर सकता है। इसलिए, आधार अवस्थाओं के विभिन्न समूहों का उपयोग करना प्रायः सहायक होते है जो ठीक स्थानीयकृत होते हैं। इस प्रकार आकर्षक विकल्प एकल क्वांटम कूप के आईगेन अवस्था का उपयोग होगा। फिर इस प्रकार के विकल्प में गंभीर कमी है: संबंधित अवस्था दो अलग-अलग [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] के हल हैं, प्रत्येक दूसरे कूप की उपस्थिति की उपेक्षा करते हैं। इस प्रकार ये अवस्थाएं लांबिक विश्लेषण नहीं हैं, जिससे जटिलताएं उत्पन्न होती हैं। सामान्यतः इस प्रकार युग्मन का अनुमान इस दृष्टिकोण के भीतर हैमिल्टनियन स्थानांतरण द्वारा लगाया जाता है। इन कारणों से, वनियर फलन के समूह का उपयोग करना अधिक सुविधाजनक होता है। | ||
== वानियर-स्टार्क | == वानियर-स्टार्क सोपानी == | ||
विद्युत क्षेत्र F को | विद्युत क्षेत्र F को सुपरलैटिस संरचना में लागू करने से हैमिल्टन को अतिरिक्त अदिश क्षमता eφ(z) = -eFz प्रदर्शित करने का कारण बनता है जो अनुवादकीय अप्रसरण को नष्ट कर देता है। इस स्थिति में, तरंग फलन <math> \Phi_0 (z) </math> और ऊर्जा <math>E_0</math> के साथ आईगेन अवस्था दिया गया है, तो तरंग फलन <math>\Phi_j (z)= \Phi_0 (z-jd) </math> के अनुरूप अवस्थाओं का समूह हैमिल्टनियन के आईगेन अवस्था ऊर्जा ''E<sub>j</sub>'' = ''E''<sub>0</sub> − ''jeFd'' के साथ हैं। ये अवस्था समान रूप से ऊर्जा और वास्तविक स्थान दोनों में हैं और तथाकथित वानियर-स्टार्क सोपानी बनाते हैं। इस प्रकार सामर्थ <math> \Phi_0 (z)</math> अनंत क्रिस्टल के लिए बाध्य नहीं है, जो इस प्रकार निरंतर ऊर्जा वर्णक्रम का तात्पर्य है। फिर इन वानियर-स्टार्क सोपानी के विशिष्ट ऊर्जा वर्णक्रम को प्रयोगात्मक रूप से हल किया जा सकता है। | ||
== | == वाहन == | ||
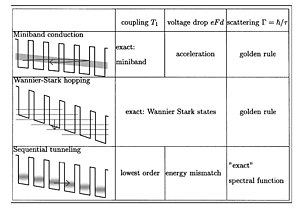
[[File:Sltransport.jpg|300px|right|thumb| | [[File:Sltransport.jpg|300px|right|thumb|सुपरलैटिस वाहन के लिए विभिन्न मानक दृष्टिकोणों का अवलोकन।]]सुपरलैटिस में आवेश वाहकों की गति अलग-अलग परतों में भिन्न होती है: आवेश वाहकों की [[इलेक्ट्रॉन गतिशीलता]] को बढ़ाया जा सकता है, जो उच्च-आवृत्ति वाले उपकरणों के लिए लाभदायक है, और इस प्रकार [[लेज़र|लेज़रों]] में विशिष्ट प्रकाशिक गुणों का उपयोग किया जाता है। | ||
यदि किसी धातु या अर्धचालक जैसे | यदि किसी धातु या अर्धचालक जैसे चालन पर बाहरी पूर्वाग्रह लागू होता है, तो सामान्यतः विद्युत प्रवाह उत्पन्न होता है। इस धारा का परिमाण पदार्थ की बैंड संरचना, प्रकीर्णन प्रक्रम, लागू क्षेत्र का सामर्थ्य और चालन के संतुलन वाहक वितरण द्वारा निर्धारित किए जाते है। | ||
सुपरलैटिस नामक सुपरलैटिस का विशेष स्थिति स्पेसर द्वारा अलग किए गए अतिचालक इकाइयों से बना है। प्रत्येक मिनीबैंड में अतिचालक क्रम पैरामीटर, जिसे अतिचालक अंतराल कहा जाता है, इस प्रकार अलग-अलग मान लेता है, बहु-अंतराल, या द्वि-अंतराल या बहुबैंड अतिसंवाहकता उत्पन्न करते है। | |||
वर्तमान में, फेलिक्स और परेरा ने फाइबोनैचि अनुक्रम के अनुसार ग्राफीन-एचबीएन के आवर्ती <ref>{{cite journal |last1=Felix |first1=Isaac M. |last2=Pereira |first2=Luiz Felipe C. |title=ग्राफीन-एचबीएन सुपरलैटिस रिबन की तापीय चालकता|journal=Scientific Reports |language=en |doi=10.1038/s41598-018-20997-8 |date=9 February 2018|volume=8 |issue=1 |page=2737 |pmid=29426893 |pmc=5807325 |bibcode=2018NatSR...8.2737F }}</ref> और अर्ध आवर्ती<ref>{{cite journal |last1=Felix |first1=Isaac M. |last2=Pereira |first2=Luiz Felipe C. |title=क्वासिपरियोडिक ग्राफीन-एचबीएन सुपरलैटिस रिबन में सुसंगत थर्मल ट्रांसपोर्ट का दमन|url=https://www.sciencedirect.com/science/article/abs/pii/S0008622319313375?dgcid=author |journal=Carbon |pages=335–341 |language=en |doi=10.1016/j.carbon.2019.12.090 |date=30 April 2020|volume=160 |arxiv=2001.03072 |s2cid=210116531 }}</ref><ref>{{cite journal |last1=Felix |first1=Isaac M. |last2=Pereira |first2=Luiz Felipe C. |title=Thermal conductivity of Thue–Morse and double-period quasiperiodic graphene-hBN superlattices |url=https://www.sciencedirect.com/science/article/abs/pii/S0017931021015623 |journal=International Journal of Heat and Mass Transfer |publisher=Elsevier |pages=122464 |language=en |doi=10.1016/j.ijheatmasstransfer.2021.122464 |date=1 May 2022|volume=186 |s2cid=245712349 }}</ref><ref>{{cite web |last1=Félix |first1=Isaac de Macêdo |title=Condução de calor em nanofitas quase-periódicas de grafeno-hBN |url=https://repositorio.ufrn.br/handle/123456789/30749 |language=pt-BR |date=4 August 2020}}</ref> सुपरलैटिस में फ़ोनों द्वारा तापीय वाहन की जांच की। उन्होंने बताया कि अर्ध आवर्ती बढ़ने के साथ सुसंगत तापीय वाहन (फोनन के जैसे-तरंग) के योगदान को निरुद्ध किया गया था। | |||
== अन्य | == अन्य विमीयता == | ||
द्वि- | द्वि- विमीयत इलेक्ट्रॉन गैसों ([[2DEG|2डीईजी]]) के प्रयोगों के लिए सामान्य रूप से उपलब्ध होने के तुरंत बाद, अनुसंधान समूहों ने संरचनाएं बनाने का प्रयास किया<ref>{{Cite journal | last1 = Heitmann | first1 = D. | last2 = Kotthaus | first2 = J. R. P. | doi = 10.1063/1.881355 | title = क्वांटम डॉट एरे की स्पेक्ट्रोस्कोपी| journal = Physics Today | volume = 46 | issue = 6 | pages = 56 | year = 1993 | bibcode = 1993PhT....46f..56H }}</ref> जिसे 2डी कृत्रिम क्रिस्टल कहा जा सकता है। इस प्रकार विषमसंधि अर्थात् z-दिशा के साथ के बीच अंतरापृष्ठ तक सीमित इलेक्ट्रॉनों को एक अतिरिक्त मॉडुलन क्षमता {{as written|''V''(''x'',''y'')}} के अधीन किया जाए। ऊपर वर्णित शास्त्रीय सुपरलैटिस (1डी/3डी, जो कि 3डी बल्क में इलेक्ट्रॉनों का 1डी मॉडुलन है) के विपरीत, यह सामान्यतः विषम संरचना सतह का उपचार करके प्राप्त किए जाते है: एक उपयुक्त प्रतिरूप वाले धातु द्वार या निक्षारण को एकत्रित करना। यदि फर्मी स्तर <math>|V_0|\gg E_f</math> की तुलना में V(x,y) की विमा बड़ी है (उदाहरण के रूप में {{as written|take <math>V(x,y)=-V_0(\cos 2\pi x/a+\cos 2\pi y/a), V_0>0</math>}}), तो सुपरलैटिस में इलेक्ट्रॉनों को वर्ग के साथ परमाणु क्रिस्टल में इलेक्ट्रॉनों के समान व्यवहार करना चाहिए (उदाहरण में, ये परमाणु पदों ({{as written|''na'',''ma''}}) पर स्थित होंगे जहां n,m पूर्णांक हैं)। | ||
अंतर लंबाई और ऊर्जा के पैमाने में है। परमाणु क्रिस्टल के | अंतर लंबाई और ऊर्जा के पैमाने में है। परमाणु क्रिस्टल के स्थिरांक 1Å के क्रम के होते हैं, जबकि सुपरलैटिस (a) कई सैकड़ों या हजारों बड़े होते हैं, जो तकनीकी सीमाओं (जैसे इलेक्ट्रॉन-किरण पुंज लिथोग्राफी का उपयोग विषम संरचना सतह के संरूपण के लिए किए जाते है) द्वारा निर्धारित किए जाते है। इस प्रकार सुपरलैटिस में ऊर्जा समान रूप से छोटी होती है। साधारण क्वांटम-यांत्रिक रूप से सीमित-कण मॉडल का उपयोग करने से <math>E\propto 1/a^2</math> का पता चलता है। यह संबंध मात्र मोटा मार्गदर्शक है और वर्तमान में सामयिक ग्राफीन (एक प्राकृतिक परमाणु क्रिस्टल) और कृत्रिम ग्राफीन (सुपरलैटिस)<ref>{{Cite journal | last1 = Kato | first1 = Y. | last2 = Endo | first2 = A. | last3 = Katsumoto | first3 = S. | last4 = Iye | first4 = Y. | title = हेक्सागोनल लेटरल सुपरलैटिस के मैग्नेटोरेसिस्टेंस में ज्यामितीय अनुनाद| doi = 10.1103/PhysRevB.86.235315 | journal = Physical Review B | volume = 86 | issue = 23 | pages = 235315 | year = 2012 |arxiv = 1208.4480 |bibcode = 2012PhRvB..86w5315K | s2cid = 119289481 }}</ref> के साथ वास्तविक गणना से पता चलता है कि विशेषता बैंड की चौड़ाई क्रमशः 1 eV और 10 meV के क्रम की है। दुर्बल मॉडुलन (<math>|V_0|\ll E_f</math>) की प्रणाली में, अनुरूपता दोलनों या भग्न ऊर्जा स्पेक्ट्रा (हॉफस्टैटर की तितली) जैसी घटनाएं होती हैं। | ||
कृत्रिम द्वि- | कृत्रिम द्वि- विमीयत क्रिस्टल को 2डी/2डी घटना (2डी प्रणाली के 2डी मॉडुलन) के रूप में देखा जा सकता है, और इस प्रकार अन्य संयोजन प्रयोगात्मक रूप से उपलब्ध हैं: क्वांटम तारों की एक सरणी (1डी/2डी) या 3डी/3डी [[फोटोनिक क्रिस्टल]] का प्रयोग होता हैं। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
उच्च विद्युत चालकता को सक्षम करने के लिए पैलेडियम-कॉपर प्रणाली के | उच्च विद्युत चालकता को सक्षम करने के लिए पैलेडियम-कॉपर प्रणाली के सुपरलैटिस का उपयोग उच्च निष्पादन मिश्र धातुओं में किया जाता है, जो कि क्रमित संरचना के पक्ष में है। ठीक यांत्रिक शक्ति और उच्च तापमान स्थिरता के लिए आगे मिश्र धातु तत्व जैसे चांदी, [[ रेनीयाम |रेनीयाम]], [[ रोडियाम |रोडियाम]] और [[दयाता|रूथेनियम]] जोड़े जाते हैं। इस प्रकार [[जांच कार्ड|अन्वेषी कार्ड]] में जांच सुई के लिए इस मिश्र धातु का उपयोग किया जाता है।<ref>{{cite web |title=United States Patent US10385424B2 Palladium-based alloys |url=https://patentimages.storage.googleapis.com/83/53/a1/ecb99f439b0d61/US10385424.pdf |website=google patents |access-date=19 June 2020}}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[III-V सेमीकंडक्टर में Cu-Pt टाइप ऑर्डरिंग|III-V अर्धचालक में Cu-Pt | * [[III-V सेमीकंडक्टर में Cu-Pt टाइप ऑर्डरिंग|III-V अर्धचालक में Cu-Pt प्रकार क्रमण]] | ||
* [[ट्यूब-आधारित नैनोस्ट्रक्चर]] | * [[ट्यूब-आधारित नैनोस्ट्रक्चर|नलिका-आधारित नैनोसंरचनाएं]] | ||
* [[ वानियर समारोह ]] | * [[ वानियर समारोह |वानियर फलन]] | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 110: | Line 105: | ||
*C. Hamaguchi, ''"Basic Semiconductor Physics"'', Springer (2001). {{google books|id=CDF3jNDX_vAC}} {{ISBN|3540416390}} | *C. Hamaguchi, ''"Basic Semiconductor Physics"'', Springer (2001). {{google books|id=CDF3jNDX_vAC}} {{ISBN|3540416390}} | ||
*{{Cite journal | last1 = Wacker | first1 = A. | doi = 10.1016/S0370-1573(01)00029-1 | title = Semiconductor superlattices: A model system for nonlinear transport | journal = Physics Reports | volume = 357 | issue = 1 | pages = 1–7 | year = 2002 |arxiv = cond-mat/0107207 |bibcode = 2002PhR...357....1W | citeseerx = 10.1.1.305.3634 | s2cid = 118885849 }} | *{{Cite journal | last1 = Wacker | first1 = A. | doi = 10.1016/S0370-1573(01)00029-1 | title = Semiconductor superlattices: A model system for nonlinear transport | journal = Physics Reports | volume = 357 | issue = 1 | pages = 1–7 | year = 2002 |arxiv = cond-mat/0107207 |bibcode = 2002PhR...357....1W | citeseerx = 10.1.1.305.3634 | s2cid = 118885849 }} | ||
*{{Cite journal | last1 = Haugan | first1 = H. J. | last2 = Szmulowicz | first2 = F. | last3 = Mahalingam | first3 = K. | last4 = Brown | first4 = G. J. | last5 = Munshi | first5 = S. R. | last6 = Ullrich | first6 = B. | doi = 10.1063/1.2150269 | title = Short-period InAs/GaSb type-II superlattices for mid-infrared detectors | journal = Applied Physics Letters | volume = 87 | issue = 26 | pages = 261106 | year = 2005 |bibcode = 2005ApPhL..87z1106H }} [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TJ6-4FGX82W-3&_user=10&_coverDate=05%2F01%2F2005&_alid=974438730&_rdoc=17&_fmt=high&_orig=search&_cdi=5302&_sort=r&_docanchor=&view=c&_ct=90&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=62d671f26883d898cc218c413592071a]{{dead link|date=March 2019 | *{{Cite journal | last1 = Haugan | first1 = H. J. | last2 = Szmulowicz | first2 = F. | last3 = Mahalingam | first3 = K. | last4 = Brown | first4 = G. J. | last5 = Munshi | first5 = S. R. | last6 = Ullrich | first6 = B. | doi = 10.1063/1.2150269 | title = Short-period InAs/GaSb type-II superlattices for mid-infrared detectors | journal = Applied Physics Letters | volume = 87 | issue = 26 | pages = 261106 | year = 2005 |bibcode = 2005ApPhL..87z1106H }} [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TJ6-4FGX82W-3&_user=10&_coverDate=05%2F01%2F2005&_alid=974438730&_rdoc=17&_fmt=high&_orig=search&_cdi=5302&_sort=r&_docanchor=&view=c&_ct=90&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=62d671f26883d898cc218c413592071a]{{dead link|date=March 2019|bot=medic}} | ||
| Line 116: | Line 111: | ||
*{{Cite journal | last1 = Mendez | first1 = E. E. | last2 = Bastard | first2 = G. R. |author-link2 = Gerald Bastard| doi = 10.1063/1.881353 | title = Wannier-Stark Ladders and Bloch Oscillations in Superlattices | journal = Physics Today | volume = 46 | issue = 6 | pages = 34–42| year = 1993 | bibcode = 1993PhT....46f..34M}} | *{{Cite journal | last1 = Mendez | first1 = E. E. | last2 = Bastard | first2 = G. R. |author-link2 = Gerald Bastard| doi = 10.1063/1.881353 | title = Wannier-Stark Ladders and Bloch Oscillations in Superlattices | journal = Physics Today | volume = 46 | issue = 6 | pages = 34–42| year = 1993 | bibcode = 1993PhT....46f..34M}} | ||
[[Category:All articles with dead external links]] | |||
[[Category: | [[Category:Articles with dead external links from March 2019]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 português do Brasil-language sources (pt-br)]] | |||
[[Category: | |||
[[Category:Created On 11/06/2023]] | [[Category:Created On 11/06/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:संघनित पदार्थ भौतिकी]] | |||
[[Category:स्पिंट्रोनिक्स]] | |||
Latest revision as of 10:19, 21 June 2023
सुपरलैटिस मुख्य रूप से दो या दो से अधिक पदार्थों की परतों की आवर्ती संरचना है। सामान्यतः एक परत की मोटाई कई नैनोमीटर हो सकती है। यह निम्न विमीयत संरचना को भी संदर्भित कर सकते है जैसे क्वांटम बिन्दु की सारणी इसका प्रमुख उदाहरण हैं।
खोज
सोना-ताँबा और पैलेडियम-तांबा प्रणालियों पर उनके विशेष एक्स-किरणें विवर्तन प्रतिरूप के अध्ययन के पश्चात जोहानसन और लिंडे द्वारा 1925 के प्रारम्भ में सुपरलैटिस की खोज की गई थी।[1] इस प्रकार के क्षेत्रों पर आगे के प्रायोगिक अवलोकन और सैद्धांतिक संशोधन ब्रैडली और जे[2] गोर्स्की,[3] बोरेलियस,[4] देहलिंगर और ग्राफ,[5] ब्रैग और विलियम्स[6] और बेथे द्वारा किए गए थे।[7] इस सिद्धांत अव्यवस्थित अवस्था से क्रमित अवस्था में क्रिस्टल जालक में परमाणुओं की व्यवस्था के संक्रमण पर आधारित थे।
यांत्रिक गुण
जे.एस. कोहलर ने सैद्धांतिक रूप से भविष्यवाणी की गयी थी[8] कि उच्च और निम्न प्रत्यास्थ स्थिरांक वाले पदार्थों की वैकल्पिक (नैनो-) परतों का उपयोग करके, अपरूपक प्रतिरोध को 100 गुना तक सुधारा जाता है क्योंकि फ्रैंक-रीड स्रोत अव्यवस्था का स्रोत नैनो परतों में काम नहीं कर सकता है।
इस प्रकार के सुपरलैटिस पदार्थ की बढ़ी हुई यांत्रिक दृढ़ता की पुष्टि सबसे पहले 1978 में Al-Cu और Al-Ag पर लेहोक्ज़की द्वारा की गई थी,[9] और बाद में कई अन्य लोगों द्वारा की गई,[10] जैसे कि दृढ़ पीवीडी लेपन पर बार्नेट और स्पोर्ल इत्यादि।
अर्धचालक गुण
यदि सुपरलैटिस अलग-अलग ऊर्जा अंतराल के साथ दो अर्धचालक पदार्थों से बना है, तो प्रत्येक क्वांटम ठीक रूप से नवीन चयन नियम स्थापित करते है जो संरचना के माध्यम से आवेशों के प्रवाह की स्थितियों को प्रभावित करते हैं। विकास की दिशा में आवर्ती संरचना बनाने के लिए दो अलग-अलग अर्धचालक पदार्थ एक-दूसरे पर वैकल्पिक रूप से एकत्रित की जाती हैं। लियो इसकी और राफेल त्सू द्वारा कृत्रिम सुपरलैटिस के 1970 के प्रस्ताव के पश्चात[11] ऐसे अति सूक्ष्म अर्धचालकों की भौतिकी में प्रगति हुई है, जिन्हें वर्तमान में क्वांटम संरचनाएं कहा जाता है। इस प्रकार क्वांटम परिरोधन की अवधारणा ने पृथक क्वांटम अनुकूल विषम संरचना में क्वांटम आकार के प्रभावों का अवलोकन किया है और इस प्रकार की घटना के माध्यम से सुपरलैटिस से निकटता से संबंधित है। इसलिए इन दो विचारों पर प्रायः एक ही भौतिक आधार पर चर्चा की जाती है, परन्तु प्रत्येक में अलग-अलग भौतिकी होती है, जो विद्युत और प्रकाशिक उपकरणों में अनुप्रयोगों के लिए उपयोगी होती है।
अर्धचालक सुपरलैटिस प्रकार
सुपरलैटिस मिनीबैंड संरचनाएं की विषमसंधि में इसके मुख्य I, II, III प्रकारों पर यह निर्भर करती हैं। प्रथम प्रकार के सुपरलैटिस के लिए यह चालित बैंड के नीचे और संयोजकता उपबैंड के शीर्ष एक ही अर्धचालक परत में बनते हैं। इस प्रकार दूसरे भाग में चालन और संयोजकता उपबैंड वास्तविक और पारस्परिक दोनों स्थानों में कंपित होते हैं, ताकि इलेक्ट्रॉनों और छिद्रों को अलग-अलग परतों में सीमित किया जा सके। इसी प्रकार तीसरे प्रकार के सुपरलैटिस में अर्द्ध धातु पदार्थ सम्मिलित होती है, जैसे एचजीटीई/सीडीटीई इत्यादि। यद्यपि चालन उपबैंड के नीचे और संयोजकता उपबैंड के शीर्ष पर प्रकार तीसरे प्रकार के सुपरलैटिस में एक ही अर्धचालक परत में बनते हैं, जो कि प्रथम प्रकार के सुपरलैटिस के समान है, प्रकार III सुपरलैटिस के बैंड अंतराल को निरंतर अर्धचालक से शून्य बैंड अंतराल के साथ पदार्थ और ऋणात्मक बैंड अंतराल के साथ अर्द्ध धातु में समायोजित किए जा सकते है।
अर्ध आवर्ती सुपरलैटिस के अन्य वर्ग का नाम फिबोनाची अनुक्रम नाम पर रखा गया है। एक फाइबोनैचि सुपरलैटिस को विमीय अर्ध क्रिस्टल के रूप में देखा जा सकता है, जहां या तो इलेक्ट्रॉन हॉपिंग स्थानांतरण या यथा स्थान ऊर्जा फाइबोनैचि अनुक्रम में व्यवस्थित दो मान लेती है।
अर्धचालक पदार्थ
अर्धचालक पदार्थ, जो सुपरलैटिस संरचनाओं को बनाने के लिए उपयोग की जाती है, को तत्व समूहों, IV, III-V और II-VI द्वारा विभाजित किया जा सकता है। जबकि समूह III-V अर्धचालक (विशेष रूप से GaAs/AlxGa1−xAs) का बड़े पैमाने पर अध्ययन किया गया है, समूह IV विषम संरचना जैसे कि SixGe1−x प्रणाली बड़ी बेमेल के कारण समझना अधिक जटिल है। फिर भी, इन क्वांटम संरचनाओं में उपबैंड संरचनाओं का तनाव संशोधन रुचिपूर्ण है और इसने बहुत ध्यान आकर्षित किया है।
GaAs/AlAs प्रणाली में GaAs और AlAs के बीच स्थिरांक में अंतर और उनके तापीय प्रसार गुणांक का अंतर दोनों ही छोटे हैं। इस प्रकार, अधिस्तरी वृद्धि तापमान से शीत होने के बाद कक्ष के तापमान पर शेष तनाव को कम किया जा सकता है। GaAs/AlxGa1−xAs पदार्थ प्रणाली का उपयोग करके पहली रचनात्मक सुपरलैटिस का उपयोग किया जाता हैं।
एक बार जब दो क्रिस्टल संरेखित हो जाते हैं तो ग्राफीन/बोरॉन नाइट्राइड प्रणाली अर्धचालक सुपरलैटिस बनाता है। इसके आवेश वाहक कम ऊर्जा अपव्यय के साथ विद्युत क्षेत्र के लंबवत गति करते हैं। एच-बीएन में ग्राफीन के समान षट्कोणीय संरचना है। सुपरलैटिस ने प्रतिलोम सममिति तोड़ दी है। स्थानीय रूप से, सांस्थितिक धाराएं लागू प्रवाह की तुलना में तुलनीय हैं, जो बड़े घाटी-हॉल कोणों को दर्शाती हैं।[12]
उत्पादन
विभिन्न तकनीकों का उपयोग करके सुपरलैटिस का उत्पादन किया जा सकता है, परन्तु आणविक-किरण पुंज अधिरोहण (एमबीई) और कणक्षेपण सबसे सामान्य हैं। इन विधियों से, परतों को मात्र कुछ परमाणु रिक्ति की मोटाई के साथ बनाया जा सकता है। सुपरलैटिस निर्दिष्ट करने का एक उदाहरण [Fe
20V
30]20 है। यह 20Å आयरन (Fe) और 30Å वैनेडियम (V) की द्वि-परत को 20 बार दोहराता है, इस प्रकार 1000Å या 100 एनएम की कुल मोटाई का वर्णन करते है। अर्धचालक सुपरलैटिस बनाने के साधन के रूप में एमबीई तकनीक का प्राथमिक महत्व है। एमबीई प्रौद्योगिकी के अतिरिक्त, धातु कार्बनिक रासायनिक वाष्प निक्षेपण (Mo-CVD) ने अतिसंवाहक सुपरलैटिस के विकास में योगदान दिया है, जो कि InGaAsP मिश्र धातुओं जैसे चतुर्धातुक III-V यौगिक अर्धचालकों से बना है। नवीन तकनीकों में अत्युच्च निर्वात (UHV) प्रौद्योगिकियों के साथ गैस स्रोत से निपटने का संयोजन सम्मिलित है जैसे धातु-कार्बनिक अणु स्रोत पदार्थ के रूप में और गैस-स्रोत एमबीई संकर गैसों जैसे कि आर्सिन (AsH
3) और फॉस्फीन (PH
3) विकसित किया गया है।
सामान्यतः बोलना एमबीई द्विआधारी प्रणाली में तीन तापमानों का उपयोग करने की विधि है, उदाहरण के लिए, कार्यद्रव तापमान, समूह III के स्रोत पदार्थ तापमान और III-V यौगिकों की स्थिति में समूह V तत्व का उपयोग किया जाता हैं।
उत्पादित सुपरलैटिस की संरचनात्मक गुणवत्ता को एक्स-किरणें विवर्तन या न्यूट्रॉन विवर्तन स्पेक्ट्रा के माध्यम से सत्यापित किए जा सकते है जिसमें विशिष्ट उपग्रह शिखर होते हैं। प्रत्यावर्ती परत से जुड़े अन्य प्रभाव हैं: विशाल चुंबकत्व, एक्स-किरणें और न्यूट्रॉन दर्पणों के लिए समस्वरित करने योग्य परावर्तकता, न्यूट्रॉन चक्रण ध्रुवीकरण, और प्रत्यास्थ और ध्वनिक गुणों में परिवर्तन किया जाता हैं। इसके घटकों की प्रकृति के आधार पर, सुपरलैटिस को चुंबकीय, प्रकाशिक या अर्धचालन कहा जा सकता है।
मिनीबैंड संरचना
एक आवर्ती सुपरलैटिस की योजनाबद्ध संरचना नीचे दिखाई गई है, जहां a और b संबंधित परत मोटाई a और b (अवधि: ) के दो अर्धचालक पदार्थ हैं। जब a और b अंतरापरमाणुक अंतरालन की तुलना में बहुत छोटे नहीं होते हैं, तो मूल बल्क अर्धचालक की बैंड संरचना से प्राप्त प्रभावी क्षमता द्वारा इन तीव्रता से बदलती क्षमता को बदलकर पर्याप्त सन्निकटन प्राप्त किया जाता है। व्यक्तिगत परतों में से प्रत्येक में 1D श्रोडिंगर समीकरणों को हल करना प्रत्यक्ष है, जिनके हल वास्तविक या काल्पनिक घातांकों के रैखिक संयोजन हैं।
एक बड़ी बाधा मोटाई के लिए, सुरंग रहित प्रकीर्णन रहित अवस्थाओं के संबंध में सुरंग बनाना दुर्बल प्रक्षोभ है, जो पूर्ण रूप से सीमित हैं। इस स्थिति में प्रकीर्णन संबंध , बलोच प्रमेय के आधार पर से अधिक के साथ आवर्ती संबंध, पूर्ण रूप से ज्यावक्रीय है:
और प्रभावी द्रव्यमान के लिए संकेत बदलते है:
मिनीबैंड की स्थिति में, यह ज्यावक्रीय वर्ण अब संरक्षित नहीं है। मिनीबैंड में मात्र उच्च (तरंग सदिश के लिए के अतिरिक्त) वस्तुतः शीर्ष 'संवेदी' है और प्रभावी द्रव्यमान परिवर्तन संकेत करते है। इस प्रकार मिनीबैंड प्रकीर्णन का आकार मिनीबैंड वाहन को गहनता से प्रभावित करते है और इस प्रकार विस्तृत मिनीबैंड दिए जाने पर यथार्थ प्रकीर्णन संबंध गणना की आवश्यकता होती है। एकल मिनीबैंड वाहन को देखने का प्रतिबन्ध किसी भी प्रक्रिया द्वारा अन्तरमिनिबैंड स्थानांतरण की अनुपस्थिति है। इस प्रकार लागू विद्युत क्षेत्र की उपस्थिति में भी तापीय क्वांटम kBT पहले और दूसरे मिनीबैंड के बीच ऊर्जा अंतर से बहुत छोटा होना चाहिए।
बलोच अवस्था
एक आदर्श सुपरलैटिस के लिए आईगेन अवस्थाओं का पूर्ण समूह समतल तरंगों आश्रित फलन के उत्पादों द्वारा निर्मित किए जा सकते है जो इस प्रकार आईगेनमान समीकरण का प्रयोग होता हैं इस प्रकार हैं-
- को संतुष्ट करते है।
जैसा कि और सुपरलैटिस अवधि d के साथ आवर्ती फलन हैं, आईगेन अवस्था बलोच अवस्था ऊर्जा के साथ हैं। K2 में प्रथम-क्रम प्रक्षोभ सिद्धांत के भीतर, ऊर्जा
- प्राप्त होती है।
अब, ठीक रूप से बड़ी संभावना प्रदर्शित करेगा, जिससे कि दूसरे शब्द को
द्वारा प्रतिस्थापित करना उचित लगता है जहां क्वांटम कूप का प्रभावी द्रव्यमान है।
वनियर फलन
परिभाषा के अनुसार बलोच के प्रमेय को पूर्ण सुपरलैटिस पर निरूपित किया गया है। यदि विद्युत क्षेत्र लागू होते हैं या सुपरलैटिस की परिमित लंबाई के कारण प्रभाव पर विचार किया जाता है तो यह जटिलता प्रदान कर सकता है। इसलिए, आधार अवस्थाओं के विभिन्न समूहों का उपयोग करना प्रायः सहायक होते है जो ठीक स्थानीयकृत होते हैं। इस प्रकार आकर्षक विकल्प एकल क्वांटम कूप के आईगेन अवस्था का उपयोग होगा। फिर इस प्रकार के विकल्प में गंभीर कमी है: संबंधित अवस्था दो अलग-अलग हैमिल्टनियन (क्वांटम यांत्रिकी) के हल हैं, प्रत्येक दूसरे कूप की उपस्थिति की उपेक्षा करते हैं। इस प्रकार ये अवस्थाएं लांबिक विश्लेषण नहीं हैं, जिससे जटिलताएं उत्पन्न होती हैं। सामान्यतः इस प्रकार युग्मन का अनुमान इस दृष्टिकोण के भीतर हैमिल्टनियन स्थानांतरण द्वारा लगाया जाता है। इन कारणों से, वनियर फलन के समूह का उपयोग करना अधिक सुविधाजनक होता है।
वानियर-स्टार्क सोपानी
विद्युत क्षेत्र F को सुपरलैटिस संरचना में लागू करने से हैमिल्टन को अतिरिक्त अदिश क्षमता eφ(z) = -eFz प्रदर्शित करने का कारण बनता है जो अनुवादकीय अप्रसरण को नष्ट कर देता है। इस स्थिति में, तरंग फलन और ऊर्जा के साथ आईगेन अवस्था दिया गया है, तो तरंग फलन के अनुरूप अवस्थाओं का समूह हैमिल्टनियन के आईगेन अवस्था ऊर्जा Ej = E0 − jeFd के साथ हैं। ये अवस्था समान रूप से ऊर्जा और वास्तविक स्थान दोनों में हैं और तथाकथित वानियर-स्टार्क सोपानी बनाते हैं। इस प्रकार सामर्थ अनंत क्रिस्टल के लिए बाध्य नहीं है, जो इस प्रकार निरंतर ऊर्जा वर्णक्रम का तात्पर्य है। फिर इन वानियर-स्टार्क सोपानी के विशिष्ट ऊर्जा वर्णक्रम को प्रयोगात्मक रूप से हल किया जा सकता है।
वाहन
सुपरलैटिस में आवेश वाहकों की गति अलग-अलग परतों में भिन्न होती है: आवेश वाहकों की इलेक्ट्रॉन गतिशीलता को बढ़ाया जा सकता है, जो उच्च-आवृत्ति वाले उपकरणों के लिए लाभदायक है, और इस प्रकार लेज़रों में विशिष्ट प्रकाशिक गुणों का उपयोग किया जाता है।
यदि किसी धातु या अर्धचालक जैसे चालन पर बाहरी पूर्वाग्रह लागू होता है, तो सामान्यतः विद्युत प्रवाह उत्पन्न होता है। इस धारा का परिमाण पदार्थ की बैंड संरचना, प्रकीर्णन प्रक्रम, लागू क्षेत्र का सामर्थ्य और चालन के संतुलन वाहक वितरण द्वारा निर्धारित किए जाते है।
सुपरलैटिस नामक सुपरलैटिस का विशेष स्थिति स्पेसर द्वारा अलग किए गए अतिचालक इकाइयों से बना है। प्रत्येक मिनीबैंड में अतिचालक क्रम पैरामीटर, जिसे अतिचालक अंतराल कहा जाता है, इस प्रकार अलग-अलग मान लेता है, बहु-अंतराल, या द्वि-अंतराल या बहुबैंड अतिसंवाहकता उत्पन्न करते है।
वर्तमान में, फेलिक्स और परेरा ने फाइबोनैचि अनुक्रम के अनुसार ग्राफीन-एचबीएन के आवर्ती [13] और अर्ध आवर्ती[14][15][16] सुपरलैटिस में फ़ोनों द्वारा तापीय वाहन की जांच की। उन्होंने बताया कि अर्ध आवर्ती बढ़ने के साथ सुसंगत तापीय वाहन (फोनन के जैसे-तरंग) के योगदान को निरुद्ध किया गया था।
अन्य विमीयता
द्वि- विमीयत इलेक्ट्रॉन गैसों (2डीईजी) के प्रयोगों के लिए सामान्य रूप से उपलब्ध होने के तुरंत बाद, अनुसंधान समूहों ने संरचनाएं बनाने का प्रयास किया[17] जिसे 2डी कृत्रिम क्रिस्टल कहा जा सकता है। इस प्रकार विषमसंधि अर्थात् z-दिशा के साथ के बीच अंतरापृष्ठ तक सीमित इलेक्ट्रॉनों को एक अतिरिक्त मॉडुलन क्षमता V(x,y) के अधीन किया जाए। ऊपर वर्णित शास्त्रीय सुपरलैटिस (1डी/3डी, जो कि 3डी बल्क में इलेक्ट्रॉनों का 1डी मॉडुलन है) के विपरीत, यह सामान्यतः विषम संरचना सतह का उपचार करके प्राप्त किए जाते है: एक उपयुक्त प्रतिरूप वाले धातु द्वार या निक्षारण को एकत्रित करना। यदि फर्मी स्तर की तुलना में V(x,y) की विमा बड़ी है (उदाहरण के रूप में take ), तो सुपरलैटिस में इलेक्ट्रॉनों को वर्ग के साथ परमाणु क्रिस्टल में इलेक्ट्रॉनों के समान व्यवहार करना चाहिए (उदाहरण में, ये परमाणु पदों (na,ma) पर स्थित होंगे जहां n,m पूर्णांक हैं)।
अंतर लंबाई और ऊर्जा के पैमाने में है। परमाणु क्रिस्टल के स्थिरांक 1Å के क्रम के होते हैं, जबकि सुपरलैटिस (a) कई सैकड़ों या हजारों बड़े होते हैं, जो तकनीकी सीमाओं (जैसे इलेक्ट्रॉन-किरण पुंज लिथोग्राफी का उपयोग विषम संरचना सतह के संरूपण के लिए किए जाते है) द्वारा निर्धारित किए जाते है। इस प्रकार सुपरलैटिस में ऊर्जा समान रूप से छोटी होती है। साधारण क्वांटम-यांत्रिक रूप से सीमित-कण मॉडल का उपयोग करने से का पता चलता है। यह संबंध मात्र मोटा मार्गदर्शक है और वर्तमान में सामयिक ग्राफीन (एक प्राकृतिक परमाणु क्रिस्टल) और कृत्रिम ग्राफीन (सुपरलैटिस)[18] के साथ वास्तविक गणना से पता चलता है कि विशेषता बैंड की चौड़ाई क्रमशः 1 eV और 10 meV के क्रम की है। दुर्बल मॉडुलन () की प्रणाली में, अनुरूपता दोलनों या भग्न ऊर्जा स्पेक्ट्रा (हॉफस्टैटर की तितली) जैसी घटनाएं होती हैं।
कृत्रिम द्वि- विमीयत क्रिस्टल को 2डी/2डी घटना (2डी प्रणाली के 2डी मॉडुलन) के रूप में देखा जा सकता है, और इस प्रकार अन्य संयोजन प्रयोगात्मक रूप से उपलब्ध हैं: क्वांटम तारों की एक सरणी (1डी/2डी) या 3डी/3डी फोटोनिक क्रिस्टल का प्रयोग होता हैं।
अनुप्रयोग
उच्च विद्युत चालकता को सक्षम करने के लिए पैलेडियम-कॉपर प्रणाली के सुपरलैटिस का उपयोग उच्च निष्पादन मिश्र धातुओं में किया जाता है, जो कि क्रमित संरचना के पक्ष में है। ठीक यांत्रिक शक्ति और उच्च तापमान स्थिरता के लिए आगे मिश्र धातु तत्व जैसे चांदी, रेनीयाम, रोडियाम और रूथेनियम जोड़े जाते हैं। इस प्रकार अन्वेषी कार्ड में जांच सुई के लिए इस मिश्र धातु का उपयोग किया जाता है।[19]
यह भी देखें
संदर्भ
- ↑ Johansson; Linde (1925). "मिश्रित-क्रिस्टल श्रृंखला गोल्ड-कॉपर और पैलेडियम-कॉपर में परमाणु व्यवस्था का एक्स-रे निर्धारण". Annalen der Physik. 78 (21): 439. Bibcode:1925AnP...383..439J. doi:10.1002/andp.19253832104.
- ↑ Bradley; Jay (1932). "लोहा और एल्युमीनियम मिश्र धातुओं में सुपरलैटिस का निर्माण". Proc. R. Soc. A. 136 (829): 210–232. Bibcode:1932RSPSA.136..210B. doi:10.1098/rspa.1932.0075.
- ↑ Gorsky (1928). "CuAu मिश्र धातु में परिवर्तन की एक्स-रे जांच". Z. Phys. 50 (1–2): 64–81. Bibcode:1928ZPhy...50...64G. doi:10.1007/BF01328593. S2CID 121876817.
- ↑ Borelius (1934). "धात्विक मिश्रित चरणों के परिवर्तन का सिद्धांत". Annalen der Physik. 20 (1): 57. Bibcode:1934AnP...412...57B. doi:10.1002/andp.19344120105.
- ↑ Dehlinger; Graf (1934). "ठोस धातु चरणों का परिवर्तन I. चतुष्कोणीय सोना-तांबा मिश्र धातु CuAu". Z. Phys. Chem. 26: 343. doi:10.1515/zpch-1934-2631. S2CID 99550940.
- ↑ Bragg, W.L.; Williams, E.J. (1934). "मिश्र धातु I में परमाणु व्यवस्था पर थर्मल आंदोलन का प्रभाव". Proc. R. Soc. A. 145 (855): 699–730. Bibcode:1934RSPSA.145..699B. doi:10.1098/rspa.1934.0132.
- ↑ Bethe (1935). "सुपरलैटिस का सांख्यिकीय सिद्धांत". Proc. R. Soc. A. 150 (871): 552–575. Bibcode:1935RSPSA.150..552B. doi:10.1098/rspa.1935.0122.
- ↑ Koehler, J. (1970). "एक मजबूत ठोस डिजाइन करने का प्रयास". Physical Review B. 2 (2): 547–551. Bibcode:1970PhRvB...2..547K. doi:10.1103/PhysRevB.2.547.
- ↑ Lehoczky, S. L. (1973). "पतली परत वाली धातु के लैमिनेट्स में विस्थापन पीढ़ी और गति की मंदता". Acta Metallurgica. 41 (26): 1814.
- ↑ Yashar, P.; Barnett, S. A.; Rechner, J.; Sproul, W. D. (1998). "Structure and mechanical properties of polycrystalline CrN/TiN superlattices". Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films. American Vacuum Society. 16 (5): 2913–2918. Bibcode:1998JVSTA..16.2913Y. doi:10.1116/1.581439. ISSN 0734-2101.
- ↑ Esaki, L.; Tsu, R. (1970). "सेमीकंडक्टर्स में सुपरलैटिस और नेगेटिव डिफरेंशियल कंडक्टिविटी". IBM Journal of Research and Development. 14: 61–65. doi:10.1147/rd.141.0061.
- ↑ Gorbachev, R. V.; Song, J. C. W.; Yu, G. L.; Kretinin, A. V.; Withers, F.; Cao, Y.; Mishchenko, A.; Grigorieva, I. V.; Novoselov, K. S.; Levitov, L. S.; Geim, A. K. (2014). "ग्राफीन सुपरलैटिस में सामयिक धाराओं का पता लगाना". Science. 346 (6208): 448–451. arXiv:1409.0113. Bibcode:2014Sci...346..448G. doi:10.1126/science.1254966. PMID 25342798. S2CID 2795431.
- ↑ Felix, Isaac M.; Pereira, Luiz Felipe C. (9 February 2018). "ग्राफीन-एचबीएन सुपरलैटिस रिबन की तापीय चालकता". Scientific Reports (in English). 8 (1): 2737. Bibcode:2018NatSR...8.2737F. doi:10.1038/s41598-018-20997-8. PMC 5807325. PMID 29426893.
- ↑ Felix, Isaac M.; Pereira, Luiz Felipe C. (30 April 2020). "क्वासिपरियोडिक ग्राफीन-एचबीएन सुपरलैटिस रिबन में सुसंगत थर्मल ट्रांसपोर्ट का दमन". Carbon (in English). 160: 335–341. arXiv:2001.03072. doi:10.1016/j.carbon.2019.12.090. S2CID 210116531.
- ↑ Felix, Isaac M.; Pereira, Luiz Felipe C. (1 May 2022). "Thermal conductivity of Thue–Morse and double-period quasiperiodic graphene-hBN superlattices". International Journal of Heat and Mass Transfer (in English). Elsevier. 186: 122464. doi:10.1016/j.ijheatmasstransfer.2021.122464. S2CID 245712349.
- ↑ Félix, Isaac de Macêdo (4 August 2020). "Condução de calor em nanofitas quase-periódicas de grafeno-hBN" (in português do Brasil).
- ↑ Heitmann, D.; Kotthaus, J. R. P. (1993). "क्वांटम डॉट एरे की स्पेक्ट्रोस्कोपी". Physics Today. 46 (6): 56. Bibcode:1993PhT....46f..56H. doi:10.1063/1.881355.
- ↑ Kato, Y.; Endo, A.; Katsumoto, S.; Iye, Y. (2012). "हेक्सागोनल लेटरल सुपरलैटिस के मैग्नेटोरेसिस्टेंस में ज्यामितीय अनुनाद". Physical Review B. 86 (23): 235315. arXiv:1208.4480. Bibcode:2012PhRvB..86w5315K. doi:10.1103/PhysRevB.86.235315. S2CID 119289481.
- ↑ "United States Patent US10385424B2 Palladium-based alloys" (PDF). google patents. Retrieved 19 June 2020.
- H.T. Grahn, "Semiconductor Superlattices", World Scientific (1995). ISBN 978-981-02-2061-7
- Schuller, I. (1980). "New Class of Layered Materials". Physical Review Letters. 44 (24): 1597–1600. Bibcode:1980PhRvL..44.1597S. doi:10.1103/PhysRevLett.44.1597.
- Morten Jagd Christensen, "Epitaxy, Thin Films and Superlattices", Risø National Laboratory, (1997). ISBN 8755022987 सुपरलैटिस at Google Books [1]
- C. Hamaguchi, "Basic Semiconductor Physics", Springer (2001). सुपरलैटिस at Google Books ISBN 3540416390
- Wacker, A. (2002). "Semiconductor superlattices: A model system for nonlinear transport". Physics Reports. 357 (1): 1–7. arXiv:cond-mat/0107207. Bibcode:2002PhR...357....1W. CiteSeerX 10.1.1.305.3634. doi:10.1016/S0370-1573(01)00029-1. S2CID 118885849.
- Haugan, H. J.; Szmulowicz, F.; Mahalingam, K.; Brown, G. J.; Munshi, S. R.; Ullrich, B. (2005). "Short-period InAs/GaSb type-II superlattices for mid-infrared detectors". Applied Physics Letters. 87 (26): 261106. Bibcode:2005ApPhL..87z1106H. doi:10.1063/1.2150269. [2][dead link]
अग्रिम पठन
- Mendez, E. E.; Bastard, G. R. (1993). "Wannier-Stark Ladders and Bloch Oscillations in Superlattices". Physics Today. 46 (6): 34–42. Bibcode:1993PhT....46f..34M. doi:10.1063/1.881353.