प्रकीर्णन मापदंड: Difference between revisions
(Created page with "{{Short description|Values which describe behavior of a linear electric circuit}} {{Use dmy dates|date=January 2020}} बिखरने वाले वाई के म...") |
No edit summary |
||
| (16 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Values which describe behavior of a linear electric circuit}} | {{Short description|Values which describe behavior of a linear electric circuit}} | ||
प्रकीर्णन [[वाई के मानकों|मापदंड]] या एस-मापदंड किसी प्रकीर्णन आव्यूह या एस-आव्यूह के तत्वों को विद्युत संकेतों द्वारा विभिन्न स्थिर समष्टि आवेशों से गुजरने पर रैखिक [[विद्युत नेटवर्क]] के विद्युत व्यवहार का वर्णन करते हैं। | |||
मापदंड,[[ विद्युत अभियन्त्रण | विद्युत अभियन्त्रण]] की कई शाखाओं के लिए उपयोगी हैं, जिनमें [[इलेक्ट्रॉनिक्स इंजीनियरिंग|विद्युत अभियांत्रिकी]], [[संचार प्रणाली]] प्रारूपण और विशेष रूप से [[माइक्रोवेव इंजीनियरिंग|माइक्रोवेव अभियांत्रिकी]] सम्मिलित हैं। | |||
एस-मापदंड, एक समान मापदंड परिवार के सदस्य हैं, जिनके अन्य उदाहरण हैं: Y-मापदंड<ref>Pozar, David M. (2005); ''Microwave Engineering, Third Edition'' (Intl. Ed.); John Wiley & Sons, Inc.; pp. 170–174. {{ISBN|0-471-44878-8}}.</ref>, [[जेड मानकों|Z-मापदंड]], H-मापदंड, T-मापदंड या [[एबीसीडी-पैरामीटर|एबीसीडी-मापदंड]] आदि।<ref>Pozar, David M. (2005) (op. cit.); pp. 170–174.</ref> <ref>Pozar, David M. (2005) (op. cit.); pp. 183–186.</ref><ref>Morton, A. H. (1985); '' Advanced Electrical Engineering''; Pitman Publishing Ltd.; pp. 33–72. {{ISBN|0-273-40172-6}}.</ref> वे इनसे, इस अर्थ में भिन्न हैं कि एस-मापदंड एक रैखिक विद्युत नेटवर्क को चिह्नित करने के लिए विवृत्त या शॉर्ट परिपथ स्थितियों का उपयोग नहीं करते हैं; इसके अतिरिक्त इनमे [[प्रतिबाधा मिलान]] का उपयोग किया जाता है। विवृत्त-परिपथ और शॉर्ट-परिपथ टर्मिनेशन की तुलना में उच्च संकेत आवृत्ती पर इन [[ विद्युत समाप्ति |विद्युत सीमा]] का उपयोग करना अत्यधिक सरल है। साधारण धारणा के विपरीत, 'मात्राओं को शक्ति के संदर्भ में नहीं मापा जाता है'। समकालिक सदिश नेटवर्क विश्लेषक [[ वाल्ट |विभव]] यातायाती तरंग चरण के आंशिकता और [[चरण]] का मापन करते हैं, जो मूल रूप से डिजिटली मोड्यूलेट किए गए ताररहित संकेतों के डीमोडुलेशन के लिए उपयोग किए जाने वाले परिपथ के समान होते हैं। | |||
एस- | विद्युत घटकों (प्रेरक, [[संधारित्र]], प्रतिरोधक ) के नेटवर्क की कई विद्युतीय गुणधर्मों को एस-मापदंड का उपयोग करके व्यक्त किया जा सकता है, जैसे कि [[लाभ (इलेक्ट्रॉनिक्स)|लाभ]], [[ हारकर लौटा |पुनरावृत्ति हानि]], [[ वोल्टेज खड़े लहर अनुपात |वोल्टेज स्टैंडिंग वेव अनुपात]] (वीएसडब्ल्यूआर), [[प्रतिबिंब गुणांक|प्रतिबिंबन संबंधक]] और [[एम्पलीफायर|प्रवर्धक]] स्थिरता आदि। शब्द 'प्रकीर्णन' आरएफ अभियांत्रिकी की तुलना में [[ऑप्टिकल इंजीनियरिंग|प्रकाशीय अभियांत्रिकी]] के लिए अधिक सामान्य है, जब एक विमान की लहर एक बाधा पर घटित होती है या असमान [[ढांकता हुआ|छायांकन]] माध्यम से गुजरती है, तों इस प्रभाव को देखा जा सकता है। एस-मापदंड के संदर्भ में, प्रकीर्णन उस विधि को संदर्भित करता है जिसमें [[ संचरण लाइन |संचरण लाइन]] में एक नेटवर्क के सम्मिलन के कारण संचारण लाइन में [[विद्युत प्रवाह]] और विभव प्रभावित होते हैं। यह [[विद्युत प्रतिबाधा]] से मिलने वाली तरंग के समतुल्य है, जो रेखा के अभिलक्षणिक प्रतिबाधा से भिन्न है। | ||
यद्यपि यह किसी भी [[आवृत्ति]] पर लागू किया जा सकता है, एस-मापदंड अधिकतर[[ आकाशवाणी आवृति | आकाशवाणी आवृति]] और [[माइक्रोवेव]] आवृत्ती पर कार्य करने वाले नेटवर्क के लिए उपयोग किए जाते हैं। सामान्य उपयोग में आने वाले एस-मापदंड - पारंपरिक एस-मापदंड रैखिक मात्राएं हैं। एस-मापदंड माप आवृत्ति के साथ परिवर्तित होते हैं, इसलिए [[विशेषता प्रतिबाधा]] या [[नाममात्र प्रतिबाधा|किंचित प्रतिबाधा]] के अतिरिक्त, किसी भी एस-मापदंड माप के लिए, आवृत्ति को निर्दिष्ट किया जाना चाहिए। | |||
एस-मापदंड सरलता से आव्यूह रूप में प्रदर्शित होते हैं और आव्यूह बीजगणित के नियमों का पालन करते हैं। | |||
== पृष्ठभूमि == | == पृष्ठभूमि == | ||
एस- | एस-मापदंड का पहला प्रकाशित विवरण 1945 में [[विटोल्ड बेलेविच]] की थीसिस में था।<ref>Belevitch, Vitold [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4066784 "Summary of the history of circuit theory"], ''Proceedings of the IRE'', '''vol.50''', iss.5, pp. 848–855, May 1962.<br>Vandewalle, Joos "In memoriam – Vitold Belevitch", ''International Journal of Circuit Theory and Applications'', '''vol.28''', iss.5, pp. 429–430, September/October 2000. {{doi|10.1002/1097-007X(200009/10)28:5<429::AID-CTA121>3.0.CO;2-6}}</ref> बेलेविच द्वारा उपयोग किया जाने वाला नाम पुनर्विभाजन आव्यूह था, और इसने समावेशी तत्व नेटवर्क्स तक सीमित विचार था। प्रकीर्णन आव्यूह शब्द का उपयोग 1947 में भौतिक विज्ञानी और इंजीनियर [[रॉबर्ट हेनरी डिके]] द्वारा किया गया था, जिन्होंने स्वतंत्र रूप से रडार पर युद्धकालीन कार्य के समय इस विचार को विकसित किया था।<ref>Valkenburg, Mac Elwyn Van ''Circuit Theory: Foundations and Classical Contributions'', p.334, Stroudsburg, Pennsylvania: Dowden, Hutchinson & Ross, 1974 {{ISBN|0-87933-084-8}}.</ref><ref>{{cite journal | doi = 10.1063/1.1697561 | volume=18 | issue=10 | title=माइक्रोवेव नेटवर्क के लिए लागू एक कम्प्यूटेशनल विधि| year=1947 | journal=Journal of Applied Physics | pages=873–878 | author=Dicke R. H.| bibcode=1947JAP....18..873D }}</ref>एस-मापदंड और प्रकीर्णन आव्यूह में,प्रकीर्ण तरंगे वे तरंगे होते हैं जिन्हें 'यात्री तरंगे' कहा जाता है। 1960 के दशक में एक अलग प्रकार के एस-मापदंड का परिचय किया गया था। इन्हें "समन्वयक प्रकीर्णन-मापदंड" भी कहा जाता हैं। यह दूसरा प्रकार का एस-मापदंड कानेयुकी कुरोकावा द्वारा प्रसिद्ध हुआ था, जिन्होंने इस नए प्रकीर्ण तरंगों को 'पावर तरंगों' के रूप में संदर्भित किया। इन दो प्रकार के एस-मापदंड में बहुत अलग गुणधर्म होते हैं और इन्हें मिलाने का प्रयास नहीं किया जाना चाहिए। अपने महत्वपूर्ण पेपर में,कुरोकावा ने स्पष्ट रूप से पावर-तरंग एस-मापदंड और पारंपरिक, यात्री-तरंग एस-मापदंड का अंतरीय किया है। इनके एक प्रकार को प्सेडो-यात्री-तरंग एस-मापदंड कहा जाता है। | ||
एस- | |||
एस-मापदंड दृष्टिकोण में, एक विद्युत नेटवर्क को एक 'ब्लैक बॉक्स' के रूप में माना जाता है जिसमें विभिन्न संयुक्त आधारभूत विद्युत परिपथ घटक या संकुचित तत्व सम्मिलित होते हैं, जैसे कि रेजिस्टर, कैपेसिटर, इंडक्टर और ट्रांजिस्टर, जो पोर्ट के माध्यम से अन्य परिपथों के साथ संवाद करते हैं। नेटवर्क को एक वर्गीकरण मायात्रिक संख्याओं का सम्पर्क किया जाता है जिसे इसका एस-मापदंड मायात्रिक कहा जाता है, जो पोर्ट पर लागू किए गए संकेत के प्रतिक्रिया की गणना के लिए उपयोग किया जा सकता है। | |||
एस-मापदंड की परिभाषा के अनुसार, यह समझा जाता है कि एक नेटवर्क में कोई भी घटक हो सकता है, जो संयुक्त छोटे संकेतों के साथ रेखीय रूप से व्यवहार करता है। इसमें एकाधिक संचार प्रणाली के उपयोगी घटक या 'खंड' भी सम्मिलित हो सकते हैं, जैसे प्रवर्धक, क्षीणक, [[इलेक्ट्रॉनिक फिल्टर|विद्युतकीय फिल्टर]], [[दिशात्मक युग्मक]] और [[समानता (संचार)|समानता]] परंतु इन्हें भी रेखीय और परिभाषित शर्तों के अंतर्गत चलाया जाना चाहिए। | |||
एस- | एस-मापदंड द्वारा वर्णित एक विद्युत नेटवर्क में पोर्टो की संख्या हो सकती है। पोर्ट वे बिंदु होते हैं जिन पर विद्युत संकेत या तो नेटवर्क में प्रवेश करते हैं या बाहर निकलते हैं। पोर्ट सामान्यतः सिरो के जोड़े होते हैं जिनकी आवश्यकता होती है कि एक सिरा में विद्युत प्रवाह दूसरे को छोड़कर वर्तमान के बराबर होता है।<ref>Pozar, David M. (2005) (op. cit.); p. 170.</ref><ref>Morton, A. H. (1985) (op. cit.); p. 33.</ref> एस-मापदंड का उपयोग आवृत्तियों पर किया जाता है जहां पोर्ट प्रायः [[समाक्षीय]] या [[वेवगाइड (विद्युत चुंबकत्व)]] संबंध होते हैं। | ||
एन-पोर्ट नेटवर्क का वर्णित करने वाला एस-मापदंड आव्यूह आयाम एन का वर्ग होगा और इसलिए इसमें <math>N^2\,</math> तत्व सम्मिलित होंगे। परीक्षण आवृत्ति पर प्रत्येक तत्व या एस-मापदंड को एक इकाई रहित संयुक्त संख्या द्वारा दर्शाया जाता है जो [[परिमाण (गणित)|परिमाण]] और [[कोण]], अर्थात [[आयाम]] और चरण का प्रतिनिधित्व करता है। सम्मिश्र संख्या या तो [[आयताकार]] रूप में व्यक्त किया जा सकता है या, अधिकांशतः, घूर्णीय रूप में व्यक्त किया जाता है। | |||
एस-मापदंड की परिमाण लीनियर रूप या [[लघुगणकीय पैमाने|लघुगणकीय]] रूप में व्यक्त की जा सकती है। जब लघुगणक रूप में व्यक्त किया जाता है, तो परिमाण" बिन आयामित इकाई" अर्थात [[डेसिबल]] की होती है। एस-मापदंड का कोण अधिकांशतः [[डिग्री (कोण)|डिग्री]] में व्यक्त किया जाता है, परंतु कभी-कभी रेडियन में भी व्यक्त किया जाता है। किसी भी एस-मापदंड को आरेखित रूप में प्रदर्शित किया जा सकता है, जहां एक आवृत्ति के लिए एक बिंदु या आवृत्ति सीमा के लिए एक स्थानक होता है। | |||
एस- | यदि यह केवल एक पोर्ट पर लागू होता है <math>S_{nn}\,</math>, इसे प्रणाली प्रतिबाधा के लिए सामान्यीकृत [[स्मिथ चार्ट]] प्रतिबाधा या प्रवेश पर प्रदर्शित किया जा सकता है। स्मिथ चार्ट के बीच सरल रूपांतरण की अनुमति देता है <math>S_{nn}\,</math> मापदंड, वोल्टेज प्रतिबिंब गुणांक के बराबर और उस पोर्ट पर संबंधित प्रतिबाधा 'देखा'। | ||
एस-मापदंड का एक सेट निर्दिष्ट करते समय निम्नलिखित जानकारी को परिभाषित किया जाना चाहिए: | |||
#आवृत्ति | #आवृत्ति | ||
#नाममात्र विशेषता प्रतिबाधा (अक्सर 50 Ω) | #नाममात्र विशेषता प्रतिबाधा (अक्सर 50 Ω) | ||
| Line 30: | Line 36: | ||
#स्थितियां जो नेटवर्क को प्रभावित कर सकती हैं, जैसे कि तापमान, नियंत्रण वोल्टेज, और बायस करंट, जहां लागू हो। | #स्थितियां जो नेटवर्क को प्रभावित कर सकती हैं, जैसे कि तापमान, नियंत्रण वोल्टेज, और बायस करंट, जहां लागू हो। | ||
== एस- | == एस-मापदंड आव्यूह == | ||
=== एक परिभाषा === | === एक परिभाषा === | ||
एक सामान्य मल्टी-पोर्ट नेटवर्क के लिए, पोर्ट्स को 1 से N तक क्रमांकित किया जाता है, जहाँ N पोर्ट्स की कुल संख्या है। पोर्ट I के लिए, संबंधित एस- | एक सामान्य मल्टी-पोर्ट नेटवर्क के लिए, पोर्ट्स को 1 से N तक क्रमांकित किया जाता है, जहाँ N पोर्ट्स की कुल संख्या है। पोर्ट I के लिए, संबंधित एस-मापदंड परिभाषा घटना और परावर्तित 'शक्ति तरंगों' के संदर्भ में है, <math>a_i\,</math> और <math>b_i\,</math> क्रमश। | ||
कुरोकावा<ref>Kurokawa, K., "Power Waves and the Scattering Matrix", IEEE Trans. Micr. Theory & Tech., Mar. 1965, pp. 194–202</ref> प्रत्येक पोर्ट के लिए घटना शक्ति तरंग को परिभाषित करता है | कुरोकावा<ref>Kurokawa, K., "Power Waves and the Scattering Matrix", IEEE Trans. Micr. Theory & Tech., Mar. 1965, pp. 194–202</ref> प्रत्येक पोर्ट के लिए घटना शक्ति तरंग को परिभाषित करता है | ||
| Line 41: | Line 47: | ||
:<math>b_i = \frac{1}{2}\, k_i (V_i - Z_{i}^{*} I_i)\,</math> | :<math>b_i = \frac{1}{2}\, k_i (V_i - Z_{i}^{*} I_i)\,</math> | ||
जहाँ <math>Z_i\,</math> पोर्ट I के लिए प्रतिबाधा है, <math>Z_i^{*}\,</math> का जटिल संयुग्म है <math>Z_i\,</math>, <math>V_i\,</math> और <math>I_i\,</math> पोर्ट i पर वोल्टेज और करंट के क्रमशः जटिल आयाम हैं, और | |||
:<math>k_i = \left(\sqrt{\left|\real\{Z_{i}\}\right|}\right)^{-1}\,</math> | :<math>k_i = \left(\sqrt{\left|\real\{Z_{i}\}\right|}\right)^{-1}\,</math> | ||
कभी-कभी यह मानना उपयोगी होता है कि संदर्भ प्रतिबाधा सभी | कभी-कभी यह मानना उपयोगी होता है कि संदर्भ प्रतिबाधा सभी पोर्टो के लिए समान है, जिस स्थिति में घटना और परावर्तित तरंगों की परिभाषा को सरल बनाया जा सकता है | ||
:<math>a_i = \frac{1}{2}\, \frac{(V_i + Z_{0} I_i)}{\sqrt{\left|\real\{Z_{0}\}\right|}}\,</math> | :<math>a_i = \frac{1}{2}\, \frac{(V_i + Z_{0} I_i)}{\sqrt{\left|\real\{Z_{0}\}\right|}}\,</math> | ||
| Line 50: | Line 56: | ||
:<math>b_i = \frac{1}{2}\, \frac{(V_i - Z_{0}^{*} I_i)}{\sqrt{\left|\real\{Z_{0}\}\right|}}\,</math> | :<math>b_i = \frac{1}{2}\, \frac{(V_i - Z_{0}^{*} I_i)}{\sqrt{\left|\real\{Z_{0}\}\right|}}\,</math> | ||
ध्यान दें कि जैसा कि स्वयं कुरोकावा ने बताया था, की उपरोक्त परिभाषाएँ <math>a_i</math> और <math>b_i</math> अद्वितीय नहीं हैं। सदिशों a और b के बीच संबंध, जिसके ''i''-वें घटक विद्युत तरंगें हैं <math>a_i</math> और <math>b_i</math> क्रमशः, एस- | ध्यान दें कि जैसा कि स्वयं कुरोकावा ने बताया था, की उपरोक्त परिभाषाएँ <math>a_i</math> और <math>b_i</math> अद्वितीय नहीं हैं। सदिशों a और b के बीच संबंध, जिसके ''i''-वें घटक विद्युत तरंगें हैं <math>a_i</math> और <math>b_i</math> क्रमशः, एस-मापदंड आव्यूह एस का उपयोग करके व्यक्त किया जा सकता है: | ||
:<math>\mathbf{b} = \mathbf{S} \mathbf{a}\,</math> | :<math>\mathbf{b} = \mathbf{S} \mathbf{a}\,</math> | ||
| Line 77: | Line 83: | ||
=== पारस्परिकता === | === पारस्परिकता === | ||
एक नेटवर्क पारस्परिकता प्रमेय | एक नेटवर्क पारस्परिकता प्रमेय होगा यदि यह [[निष्क्रिय घटक]] है और इसमें केवल पारस्परिक तत्व हो जो प्रेषित संकेत को प्रभावित करती है। उदाहरण के लिए, क्षीणकर्ता, केबल, स्प्लिटर्स और कंबाइनर सभी पारस्परिक नेटवर्क हैं और प्रत्येक विषयो में <math>S_{mn} = S_{nm}\,</math>होगा या एस-मापदंड आव्यूह इसके स्थानान्तरण के बराबर होगा। ऐसे नेटवर्क जिनमें संचरण माध्यम में गैर-पारस्परिक तत्व सम्मिलित होती है जैसे कि [[ पूर्वाग्रह (इलेक्ट्रॉनिक्स) |पूर्वाग्रह]] [[फेराइट (चुंबक)]] घटक गैर-पारस्परिक होंगे। एक प्रवर्धक गैर-पारस्परिक नेटवर्क का एक और उदाहरण है। | ||
यद्यपि, 3-पोर्ट नेटवर्क की एक गुण यह है कि वे एक साथ पारस्परिक, हानि-मुक्त और पूरी तरह से मेल नहीं खा सकते हैं।<ref>Pozar, David M. (2005) (op. cit.); p. 173.</ref> {{see also|सम्मेलन आरेख टेलीफोन सम्मेलन परिपथ }} | |||
=== दोषरहित नेटवर्क === | === दोषरहित नेटवर्क === | ||
दोषरहित नेटवर्क वह है जो किसी भी शक्ति का क्षय नहीं करता है, या: <math>\Sigma\left|a_n\right|^2 = \Sigma\left|b_n\right|^2\,</math>. सभी | दोषरहित नेटवर्क वह है जो किसी भी शक्ति का क्षय नहीं करता है, या: <math>\Sigma\left|a_n\right|^2 = \Sigma\left|b_n\right|^2\,</math>. सभी पोर्टो पर घटना शक्तियों का योग सभी पोर्टो पर आउटगोइंग शक्तियों के योग के बराबर है। इसका तात्पर्य है कि एस-मापदंड आव्यूह [[एकात्मक मैट्रिक्स|एकात्मक आव्यूह]] है, अर्थात <math>(S)^H (S) = (I)\,</math>, जहाँ <math>(S)^H\,</math> का संयुग्मी स्थानांतरण है <math>(S)\,</math> और <math>(I)\,</math> पहचान आव्यूह है। | ||
=== [[हानिपूर्ण]] नेटवर्क === | === [[हानिपूर्ण]] नेटवर्क === | ||
एक हानिपूर्ण निष्क्रिय नेटवर्क वह है जिसमें सभी | एक हानिपूर्ण निष्क्रिय नेटवर्क वह है जिसमें सभी पोर्टो पर घटना शक्तियों का योग सभी पोर्टो पर आउटगोइंग शक्तियों के योग से अधिक होता है। इसलिए यह शक्ति का प्रसार करता है: <math>\Sigma\left|a_n\right|^2 \ne \Sigma\left|b_n\right|^2\,</math>. इस प्रकार <math>\Sigma\left|a_n\right|^2 > \Sigma\left|b_n\right|^2\,</math>, और <math>(I) - (S)^H (S)\,</math> [[सकारात्मक-निश्चित मैट्रिक्स|सकारात्मक-निश्चित आव्यूह]] है।<ref>[http://literature.cdn.keysight.com/litweb/pdf/5952-1087.pdf ''S-Parameter Design''; Application Note AN 154; Agilent Technologies; p 7]</ref> | ||
== दो-पोर्ट एस- | == दो-पोर्ट एस-मापदंड == | ||
{{See also| | {{See also|दो-पोर्ट नेटवर्क}} | ||
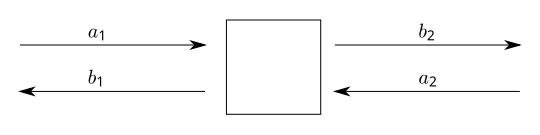
[[File:TwoPortNetworkScatteringAmplitudes.svg|center]]2-पोर्ट नेटवर्क के लिए एस- | [[File:TwoPortNetworkScatteringAmplitudes.svg|center]]2-पोर्ट नेटवर्क के लिए एस-मापदंड आव्यूह संभवतः सबसे आम रूप से उपयोग की जाती है और यह बड़े नेटवर्क के लिए उच्च वर्ग आव्यूह उत्पन्न करने के लिए मूल निर्माण इकाई के रूप में कार्य करती है। [18] इस मामले में, बाहरी ('प्रतिबिंबित') और आंतरिक तरंगों के बीच का संबंध और एस-मापदंड आव्यूह द्वारा दिया जाता है: | ||
:<math>\begin{pmatrix}b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} S_{11} & S_{12} \\ S_{21} & S_{22} \end{pmatrix}\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\,</math>. | :<math>\begin{pmatrix}b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} S_{11} & S_{12} \\ S_{21} & S_{22} \end{pmatrix}\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\,</math>. | ||
| Line 112: | Line 107: | ||
:<math>b_2 = S_{21}a_1 +S_{22}a_2\,</math>. | :<math>b_2 = S_{21}a_1 +S_{22}a_2\,</math>. | ||
प्रत्येक समीकरण नेटवर्क के | प्रत्येक समीकरण नेटवर्क के प्रत्येक पोर्ट, 1 और 2, पर बाहरी और प्रवेशित तरंगों के बीच संबंध को नेटवर्क के व्यक्तिगत एस-मापदंडो <math>S_{11}\,</math>, <math>S_{12}\,</math>, <math>S_{21}\,</math> और <math>S_{22}\,</math>. के माध्यम से देता है। यदि हम पोर्ट 1 पर एक प्रवेशित तरंग (1a_1) को मानते हैं तो इससे पोर्ट 1 या पोर्ट 2 से निकलने वाली तरंगें हो सकती हैं, यद्यपि, अगर, एस-मापदंड की परिभाषा के अनुसार, पोर्ट 2 कोप्रणाली प्रतिबाधा के समान भार में समाप्त किया जाता है (<math>Z_0\,</math>) तब, [[अधिकतम शक्ति प्रमेय]] द्वारा स्थानांतरण सिद्धांत के अनुसार, <math>b_2\,</math> बनाने में पूरी तरह से शोषित हो जाएगी <math>a_2\,</math> शून्य हो जाएगी। इसलिए, प्रवेशित वोल्टेज तरंगों को निर्धारित करते हुए <math>a_1 = V_1^+</math> और <math>a_2 = V_2^+</math> के रूप में परिभाषित करते हैं | ||
:<math>S_{11} = \frac{b_1}{a_1} = \frac{V_1^-}{V_1^+}</math> और <math>S_{21} = \frac{b_2}{a_1} = \frac{V_2^-}{V_1^+}\,</math>. | :<math>S_{11} = \frac{b_1}{a_1} = \frac{V_1^-}{V_1^+}</math> और <math>S_{21} = \frac{b_2}{a_1} = \frac{V_2^-}{V_1^+}\,</math>. | ||
उसी तरह, यदि पोर्ट 1 को प्रणाली आवेश में समाप्त किया जाता है, तो <math>a_1\,</math> शून्य हो जाती है, जिससे वाल्यू 1=0 होती है। | |||
:<math>S_{12} = \frac{b_1}{a_2} = \frac{V_1^-}{V_2^+}\,</math> और <math>S_{22} = \frac{b_2}{a_2} = \frac{V_2^-}{V_2^+}\,</math> | :<math>S_{12} = \frac{b_1}{a_2} = \frac{V_1^-}{V_2^+}\,</math> और <math>S_{22} = \frac{b_2}{a_2} = \frac{V_2^-}{V_2^+}\,</math> | ||
2-पोर्ट एस- | 2-पोर्ट एस-मापदंड में निम्नलिखित सामान्य विवरण हैं: | ||
:<math>S_{11}\,</math> इनपुट पोर्ट वोल्टेज प्रतिबिंब गुणांक है | :<math>S_{11}\,</math> इनपुट पोर्ट वोल्टेज प्रतिबिंब गुणांक है | ||
:<math>S_{12}\,</math> | :<math>S_{12}\,</math> विपरीत वोल्टेज लाभ है | ||
:<math>S_{21}\,</math> आगे वोल्टेज लाभ है | :<math>S_{21}\,</math> आगे वोल्टेज लाभ है | ||
:<math>S_{22}\,</math> आउटपुट पोर्ट वोल्टेज प्रतिबिंब गुणांक है। | :<math>S_{22}\,</math> आउटपुट पोर्ट वोल्टेज प्रतिबिंब गुणांक है। | ||
यदि, प्रत्येक | यदि, प्रत्येक पोर्ट के सापेक्ष वोल्टेज तरंग दिशा को परिभाषित करने के अतिरिक्त उन्हें आगे के रूप में उनकी पूर्ण दिशा द्वारा परिभाषित किया जाता है <math>V^+</math> और उल्टा <math>V^-</math> लहरें तब <math>b_2 = V_2^+</math> और <math>a_1 = V_1^+</math>. एस-मापदंड तब अधिक सहज अर्थ लेते हैं <math>S_{21} = V_2^+/V_1^+</math>जैसे कि आगे वोल्टेज लाभ आगे वोल्टेज के अनुपात द्वारा परिभाषित किया जा रहा है. | ||
इसका उपयोग करके उपरोक्त | इसका उपयोग करके उपरोक्त आव्यूह को और अधिक व्यावहारिक विधियों से विस्तारित किया जा सकता है | ||
:<math>V_1^-= S_{11}V_1^+ +S_{12}V_2^-\,</math> | :<math>V_1^-= S_{11}V_1^+ +S_{12}V_2^-\,</math> | ||
:<math>V_2^+ = S_{21}V_1^+ +S_{22}V_2^-\,</math> | :<math>V_2^+ = S_{21}V_1^+ +S_{22}V_2^-\,</math> | ||
== एस-मापदंड 2-पोर्ट नेटवर्क == | |||
== एस- | रेखीय स्थितियों में कार्यरत एक अधिसूचक अचक्षु एक अनुप्रेषक नेटवर्क का अच्छा उदाहरण है और एक मिलती हुई घटाव कोण एक प्रतिबिंबी नेटवर्क का एक उदाहरण है। निम्नलिखित मामलों में हम मान लेंगे कि प्रवेश और निर्गमन कनेक्शन पोर्ट 1 और 2 को अनुक्रमिक रूप से किए गए हैं जो सबसे सामान्य संवेदना है। सामान्य प्रणाली आवेश, आवृत्ति, और डिवाइस को प्रभावित करने वाले किसी भी अन्य कारक जैसे तापमान आदि को भी निर्दिष्ट किया जाना चाहिए।। | ||
रेखीय | |||
=== जटिल रैखिक लाभ === | === जटिल रैखिक लाभ === | ||
| Line 142: | Line 136: | ||
:<math>G = S_{21} = \frac{b_2}{a_1}\,</math>. | :<math>G = S_{21} = \frac{b_2}{a_1}\,</math>. | ||
यह इनपुट घटना पावर वेव द्वारा विभाजित आउटपुट परावर्तित पावर वेव का रैखिक अनुपात है, सभी मान जटिल मात्रा के रूप में व्यक्त किए जाते हैं। हानिपूर्ण नेटवर्क के लिए यह उप-एकात्मक है, सक्रिय नेटवर्क के लिए <math> |G| > 1</math> . | यह इनपुट घटना पावर वेव द्वारा विभाजित आउटपुट परावर्तित पावर वेव का रैखिक अनुपात है, सभी मान जटिल मात्रा के रूप में व्यक्त किए जाते हैं। हानिपूर्ण नेटवर्क के लिए यह उप-एकात्मक है, सक्रिय नेटवर्क के लिए <math> |G| > 1</math> .यह वोल्टेज लाभ के बराबर तभी होगा जब डिवाइस में समान इनपुट और आउटपुट प्रतिबाधा हो। | ||
यह वोल्टेज लाभ के बराबर तभी होगा जब डिवाइस में समान इनपुट और आउटपुट प्रतिबाधा हो। | |||
=== | === अदिश रैखिक लाभ === | ||
अदिश रैखिक लाभ द्वारा दिया जाता है | |||
:<math>\left|G\right| = \left|S_{21}\right|\,</math>. | :<math>\left|G\right| = \left|S_{21}\right|\,</math>. | ||
यह लाभ | यह आपात संख्या लाभ, यानी आपात ऊर्जा-तरंग से प्रवेश ऊर्जा-तरंग के अनुपात को प्रतिनिधित करता है और इसे पावर लाभ के वर्ग के बराबर होता है। यह एक वास्तविक-मूल्य मात्रा है, जिसमें चरण की जानकारी हटा दी जाती है। | ||
यह एक वास्तविक-मूल्य | |||
=== अदिश लघुगणक लाभ === | === अदिश लघुगणक लाभ === | ||
लाभ (जी) के लिए | लाभ (जी) के लिए अदिश लघुगणकीय अभिव्यक्ति है: | ||
:<math>g = 20\log_{10}\left|S_{21}\right|\,</math> डीबी। | :<math>g = 20\log_{10}\left|S_{21}\right|\,</math> डीबी। | ||
यह | यह अदिश रूपांतरित आपात गुणांक से अधिक प्रयुक्त होता है और सामान्यतः एक सकारात्मक मात्रा को साधारित रूप से एक "गुणांक" के रूप में समझा जाता है, जबकि एक नकारात्मक मात्रा एक "नकारात्मक गुणांक" होती है, जो डीबी में अपने मात्रा के बराबर होती है। उदाहरण के लिए, 100 मेगाहर्ट्ज पर, 10 मीटर लंबी केबल का एक गुणांक -1 डीबी हो सकता है, जो 1 डीबी का हानि के बराबर होता है। | ||
=== सम्मिलन हानि === | === सम्मिलन हानि === | ||
यदि दो मापन पोर्ट एक ही संदर्भ आवेश का उपयोग करते हैं, तो संचालन संख्या के मान के प्रतिक रूप में डेसिबल में व्यक्त बीचवाल (IL) है। इसलिए, यह निम्नलिखित द्वारा दिया जाता है::<ref>Collin, Robert E.; ''Foundations For Microwave Engineering, Second Edition''</ref> | |||
<math>IL = -20\log_{10}\left|S_{21}\right|\,</math> डीबी। | <math>IL = -20\log_{10}\left|S_{21}\right|\,</math> डीबी। | ||
यह | यह मापन के संदर्भ तलों के बीच डिवाइस अंतरीय ्गत परीक्षण (डीयूटी ) के प्रस्तावित करने से उत्पन्न अतिरिक्त हानि है। अतिरिक्त हानि डीयूटी में आंतरिक हानि और/या मिलान में हो सकती है। अतिरिक्त हानि के मामले में, प्रवेश हानि को सकारात्मक परिभाषित किया जाता है। डेसिबल में व्यक्त अवरोध तापमान के उल्टा नकारात्मक होता है और इसे प्रवेश गुण कहा जाता है, जो वैद्यतात्मक लघुगणकीय लाभ के बराबर होता है | ||
=== इनपुट | === इनपुट पुनरावृत्ति हानि === | ||
इनपुट वापसी हानि ({{math|''RL''<sub>in</sub>}}) को एक उपाय के रूप में सोचा जा सकता है कि नेटवर्क का वास्तविक इनपुट प्रतिबाधा नाममात्र प्रणाली प्रतिबाधा मान के कितने | इनपुट वापसी हानि ({{math|''RL''<sub>in</sub>}}) को एक उपाय के रूप में सोचा जा सकता है कि नेटवर्क का वास्तविक इनपुट प्रतिबाधा नाममात्र प्रणाली प्रतिबाधा मान के कितने समीप है। डेसीबल में व्यक्त इनपुट पुनरावृत्ति हानि द्वारा दिया जाता है | ||
:<math>RL_\mathrm{in} = 10\log_{10}\left| \frac{1}{S_{11}^2} \right| = - 20\log_{10} \left| S_{11}\right|\,</math> डीबी। | :<math>RL_\mathrm{in} = 10\log_{10}\left| \frac{1}{S_{11}^2} \right| = - 20\log_{10} \left| S_{11}\right|\,</math> डीबी। | ||
ध्यान दें कि निष्क्रिय दो-पोर्ट नेटवर्क के लिए जिसमें {{math|{{!}}''S<sub>11</sub>''{{!}} ≤ 1}}, यह इस प्रकार है कि | ध्यान दें कि निष्क्रिय दो-पोर्ट नेटवर्क के लिए जिसमें {{math|{{!}}''S<sub>11</sub>''{{!}} ≤ 1}}, यह इस प्रकार है कि पुनरावृत्ति हानि एक गैर-नकारात्मक मात्रा है: {{math|''RL<sub>in</sub>'' ≥ 0}}. यह भी ध्यान दें कि कुछ भ्रामक रूप से, पुनरावृत्ति हानि साइन को कभी-कभी ऊपर परिभाषित मात्रा के नकारात्मक के रूप में उपयोग किया जाता है, परंतु यह उपयोग, हानि की परिभाषा के आधार पर, सख्ती से बोलना गलत है।<ref name=Bird>Trevor S. Bird, [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=5162049 "Definition and Misuse of Return Loss"], ''IEEE Antennas & Propagation Magazine'', '''vol.51''', iss.2, pp.166–167, April 2009.</ref> | ||
=== आउटपुट | === आउटपुट पुनरावृत्ति हानि === | ||
आउटपुट | आउटपुट पुनरावृत्ति हानि ({{math|''RL''<sub>out</sub>}}) को यह सोचा जा सकता है कि यह माप आपात संख्या है जो नेटवर्क की वास्तविक इनपुट आवेशिकता को सामान्य प्रणाली आवेश मान के समीप कितनी समीप प्रस्तुत करती है। इनपुट पुनरावृत्ति हानि को डेसिबल में व्यक्त किया जाता है: | ||
:<math>RL_\mathrm{out} = - 20\log_{10}\left|S_{22}\right|\,</math> डीबी। | :<math>RL_\mathrm{out} = - 20\log_{10}\left|S_{22}\right|\,</math> डीबी। | ||
=== | === विपरीत लाभ और विपरीत वियोजन === | ||
विपरीत लाभ <math>g_\mathrm{rev}\,</math>के लिए अदिश लघुगणकीय अभिव्यक्ति है: | |||
:<math>g_\mathrm{rev} = 20\log_{10}\left|S_{12}\right|\,</math> डीबी। | :<math>g_\mathrm{rev} = 20\log_{10}\left|S_{12}\right|\,</math> डीबी। | ||
प्रायः इसे विपरीतआपाती (<math>I_\mathrm{rev}\,</math>) के रूप में व्यक्त किया जाएगा, जिसके लिए यह विपरीत लाभ <math>g_\mathrm{rev}\,</math>की मानकता के बराबर एक सकारात्मक मात्रा होता है और अभिव्यक्ति इस रूप में होती है | |||
:<math>I_\mathrm{rev} = \left|g_\mathrm{rev}\right| = \left|20\log_{10}\left|S_{12}\right|\right|\,</math> डीबी। | :<math>I_\mathrm{rev} = \left|g_\mathrm{rev}\right| = \left|20\log_{10}\left|S_{12}\right|\right|\,</math> डीबी। | ||
| Line 201: | Line 193: | ||
=== वोल्टेज स्थायी तरंग अनुपात === | === वोल्टेज स्थायी तरंग अनुपात === | ||
एक पोर्ट पर वोल्टेज | एक पोर्ट पर वोल्टेज स्थानिक तरंग अनुपात (वीएसडब्ल्यूआर) को छोटे अक्षर 's' से प्रतिष्ठित किया जाता है, यह पोर्ट मैच का एक समान माप है जो वापसी हानि के समान है, परंतु यह एक अदिश रैखिक मात्रा है, वापसी तरंग के अधिकतम वोल्टेज से वापसी तरंग के न्यूनतम वोल्टेज के अनुपात होता है। इसलिए, यह वोल्टेज प्रतिबिंब संख्या के मान और इस प्रकार इनपुट पोर्ट के लिए <math>S_{11}\,</math>, या आउटपुट पोर्ट के लिए <math>S_{22}\,</math>के मान से संबंधित है। | ||
इनपुट पोर्ट पर, वीएसडब्ल्यूआर (<math>s_\mathrm{in}\,</math>) द्वारा दिया गया है | यहाँ इनपुट पोर्ट पर, वीएसडब्ल्यूआर (<math>s_\mathrm{in}\,</math>) द्वारा दिया गया है | ||
:<math>s_\mathrm{in} = \frac{1+\left|S_{11}\right|}{1-\left|S_{11}\right|}\,</math> | :<math>s_\mathrm{in} = \frac{1+\left|S_{11}\right|}{1-\left|S_{11}\right|}\,</math> | ||
| Line 209: | Line 201: | ||
:<math>s_\mathrm{out} = \frac{1+\left|S_{22}\right|}{1-\left|S_{22}\right|}\,</math> | :<math>s_\mathrm{out} = \frac{1+\left|S_{22}\right|}{1-\left|S_{22}\right|}\,</math> | ||
यह | यह सत्य है जब गुणांक का मान एकाधिकता से अधिक नहीं होता है, जो आमतौर पर मामला होता है। एक एकाधिकता से अधिक मान वाला एक अभिविन्यास, जैसे कि एक टनल डायोड एम्पलिफायर में, इस अभिव्यक्ति के लिए एक नकारात्मक मान देगा। हालांकि, वीएसडब्ल्यूआर, अपनी परिभाषा से,सदैव सकारात्मक होता है। एक बहुपोर्ट के पोर्ट k के लिए एक और सही अभिव्यक्ति है। | ||
:<math>s_k = \frac{1+\left|S_{kk}\right|}{|1-\left|S_{kk}\right||}\,</math> | :<math>s_k = \frac{1+\left|S_{kk}\right|}{|1-\left|S_{kk}\right||}\,</math> | ||
==4-पोर्ट एस- | ==4-पोर्ट एस-मापदंड == | ||
4 पोर्ट एस | 4 पोर्ट एस मापदंड का उपयोग 4 पोर्ट नेटवर्क की विशेषता के लिए किया जाता है। इनमें नेटवर्क के 4 पोर्ट के बीच परावर्तित और आपतित विद्युत तरंगों के बारे में जानकारी शामिल होती है। | ||
:<math>\begin{pmatrix}S_{11} & S_{12} & S_{13} & S_{14} \\ S_{21} & S_{22} & S_{23} & S_{24} \\ S_{31} & S_{32} & S_{33} & S_{34} \\ S_{41} & S_{42} & S_{43} & S_{44} \end{pmatrix} </math> | :<math>\begin{pmatrix}S_{11} & S_{12} & S_{13} & S_{14} \\ S_{21} & S_{22} & S_{23} & S_{24} \\ S_{31} & S_{32} & S_{33} & S_{34} \\ S_{41} & S_{42} & S_{43} & S_{44} \end{pmatrix} </math> | ||
ये आपस में जुड़े हुए ट्रांसमिशन लाइन के जोड़ों का विश्लेषण करने के लिए सामान्यतः उपयोग होते हैं, जिससे यह निर्धारित किया जा सके कि उन्हें दो अलग-अलग संकेत एंडेड सकेत द्वारा प्रेरित किया जाता है या उन पर प्रेरित अंतरीय संकेत के प्रतिबिंबित और घटनायन शक्ति का मापन किया जा सकता है। उच्च गति के अंतरीय संकेत के कई विनिर्देश चैनलों की विशेषताएं 4-पोर्ट एस-पैरामीटर्स के माध्यम से परिभाषित करती हैं, जैसे कि 10-गिगाबिट अटैचमेंट यूनिट इंटरफेस (एक्सएयूआई),सैटा,पीसीआई-एक्स और इन्फिनीबैंड प्रणाली। | |||
===4-पोर्ट मिश्रित-मोड एस- | ===4-पोर्ट मिश्रित-मोड एस-मापदंड === | ||
4-पोर्ट मिश्रित-मोड एस- | 4-पोर्ट मिश्रित-मोड एस-मापदंड सामान्य मोड और अंतरीय प्रोत्साहन संकेतों के लिए नेटवर्क की प्रतिक्रिया के संदर्भ में 4-पोर्ट नेटवर्क की विशेषता बताते हैं। निम्न तालिका 4-पोर्ट मिश्रित-मोड एस-मापदंड प्रदर्शित करती है। | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ 4- | |+ 4-पोर्ट मिश्रित-मोड एस-पैरामीटर | ||
|- | |- | ||
|rowspan="3" colspan="3"| | |rowspan="3" colspan="3"| | ||
!colspan="4" style="text-align:center;"| | !colspan="4" style="text-align:center;"|उद्दीपन | ||
|- | |- | ||
!colspan="2" style="text-align:center;"| | !colspan="2" style="text-align:center;"|अवकल | ||
!colspan="2" style="text-align:center;"| | !colspan="2" style="text-align:center;"|सामान्य मोड | ||
|- | |- | ||
! Port 1 | ! Port 1 | ||
| Line 237: | Line 229: | ||
! Port 2 | ! Port 2 | ||
|- | |- | ||
!rowspan="4"| | !rowspan="4"|प्रतिक्रिया | ||
! | ! colspan="2" |अवकल | ||
| SDD11 | | SDD11 | ||
| SDD12 | | SDD12 | ||
| Line 245: | Line 236: | ||
| SDC12 | | SDC12 | ||
|- | |- | ||
! | |||
! Port 2 | ! Port 2 | ||
| SDD21 | | SDD21 | ||
| Line 251: | Line 243: | ||
| SDC22 | | SDC22 | ||
|- | |- | ||
! | ! colspan="2" |सामान्य मोड | ||
| SCD11 | | SCD11 | ||
| SCD12 | | SCD12 | ||
| Line 258: | Line 249: | ||
| SCC12 | | SCC12 | ||
|- | |- | ||
! | |||
! Port 2 | ! Port 2 | ||
| SCD21 | | SCD21 | ||
| Line 264: | Line 256: | ||
| SCC22 | | SCC22 | ||
|} | |} | ||
SXYab मापदंड नोटेशन का प्रारूप ध्यान दें, जहां "S" स्कैटरिंग मापदंड या एस-मापदंड को दर्शाता है, "X" प्रतिक्रिया मोड होता है, "Y" प्रेरण मोड होता है, "a" प्रतिक्रिया (आउटपुट) पोर्ट होता है और "b" प्रेरण (इनपुट) पोर्ट होता है। यह स्कैटरिंग पैरामीटर्स के लिए प्रामाणिक नामकरण है। | |||
पहले चतुर्भुज को परीक्षण के | पहले चतुर्भुज को परीक्षण के अंतर्गत डिवाइस के अंतरीय उत्तेजना और अंतरीय प्रतिक्रिया विशेषताओं का वर्णन करने वाले ऊपरी बाएं 4 मापदंड के रूप में परिभाषित किया गया है। यह अधिकांश हाई-स्पीड अंतरीय इंटरकनेक्ट्स के लिए ऑपरेशन का वास्तविक तरीका है और यह क्वाड्रंट है जिस पर सबसे अधिक ध्यान दिया जाता है। इसमें इनपुट अंतरीय पुनरावृत्ति हानि (एसडीडी11), इनपुट अंतरीय इंसर्शन लॉस (एसडीडी21), आउटपुट आंतरिक पुनरावृत्ति हानि (एसडीडी22) और आउटपुट अंतरीय हानि (एसडीडी12) सम्मिलित हैं। अंतरीय संकेत प्रोसेसिंग के कुछ लाभ हैं; | ||
* कम विद्युत चुम्बकीय हस्तक्षेप संवेदनशीलता | * कम विद्युत चुम्बकीय हस्तक्षेप संवेदनशीलता | ||
* संतुलित | * संतुलित अंतरीय परिपथ से विद्युत चुम्बकीय विकिरण में कमी | ||
* यहां तक कि ऑर्डर | * यहां तक कि ऑर्डर अंतरीय विरूपण उत्पाद सामान्य मोड संकेत में बदल जाते हैं | ||
* | * संकेत -एंडेड के सापेक्ष वोल्टेज स्तर में दो वृद्धि का कारक | ||
* | * सामान्य मोड आपूर्ति और भूमि के शोर के प्रतिरोध और डिफरेंशियल सिग्नल पर भूमि शोर का कूट लेखन अस्वीकार है। | ||
दूसरा और तीसरा चतुर्भुज क्रमशः ऊपरी दाएँ और निचले बाएँ 4 | दूसरा और तीसरा चतुर्भुज क्रमशः ऊपरी दाएँ और निचले बाएँ 4 मापदंड हैं। इन्हें क्रॉस-मोड क्वाड्रंट भी कहा जाता है। ऐसा इसलिए है क्योंकि वे परीक्षण के अंतर्गत डिवाइस में होने वाले किसी भी मोड रूपांतरण को पूरी तरह से चिह्नित करते हैं, चाहे वह कॉमन-टू-अंतरीय एसडीकैब रूपांतरण (इच्छित अंतरीय संकेत एसडीडी ट्रांसमिशन एप्लिकेशन के लिए ईएमआई संवेदनशीलता) या अंतरीय -टू-कॉमन एससीडीएबी रूपांतरण हो। गीगाबिट डेटा थ्रूपुट के लिए इंटरकनेक्ट के डिज़ाइन को अनुकूलित करने का प्रयास करते समय मोड रूपांतरण को समझना बहुत सहायक होता है। | ||
चौथा चतुर्भुज निचला दायां 4 | चौथा चतुर्भुज निचला दायां 4 मापदंड है और परीक्षण के अंतर्गत डिवाइस के माध्यम से प्रचार करने वाले सामान्य-मोड संकेत एससीसीएबी की प्रदर्शन विशेषताओं का वर्णन करता है। ठीक से प्रारूप किए गए एसडीडीएबी अंतरीय डिवाइस के लिए न्यूनतम सामान्य-मोड आउटपुट एससीसीएबी होना चाहिए। यद्यपि, चौथा चतुर्थांश सामान्य-मोड प्रतिक्रिया डेटा सामान्य-मोड संचरण प्रतिक्रिया का एक उपाय है और नेटवर्क सामान्य-मोड अस्वीकृति को निर्धारित करने के लिए अंतरीय संचरण प्रतिक्रिया के अनुपात में उपयोग किया जाता है। यह कॉमन मोड अस्वीकारअंतरीय संकेत प्रोसेसिंग का एक महत्वपूर्ण लाभ है और इसे कुछ अंतरीय परिपथ कार्यान्वयन में घटाकर एक किया जा सकता है।<ref>[https://web.archive.org/web/20110717081041/http://www.designcon.com/media/2005/Euro/5-TA3--John_DAmbrosia.pdf ''Backplane Channels and Correlation Between Their Frequency and Time Domain Performance''].</ref><ref>{{cite journal |author1=Bockelman, DE |author2=Eisenstadt, WR |title=Combined differential and common-mode scattering parameters: theory and simulation |journal=IEEE Transactions |volume=43 |issue=7 |date=July 1995 |pages=1530–1539 |doi=10.1109/22.392911}}</ref> | ||
== एस- | == प्रवर्धक प्रारूप में एस-मापदंड == | ||
एक प्रवर्धक में विपरीत वियोजन मापदंड <math>S_{12}\,</math> इसके इनपुट से आउटपुट तक वापसी से प्रतिक्रिया के स्तर को निर्धारित करता है और इसलिए उसकी स्थिरता पर प्रभाव डालता हैसाथ ही, आगे की गुणवत्ता <math>S_{21}\,</math> के साथ इनपुट और आउटपुट पोर्ट से पूर्णतः अलग होने वाले एक ऐंप्लीफायर में अविशीष्ट स्केलर लॉग मैग्नीचर वियोजन होगा या<math>S_{12}\,</math> शून्य होगा। का रेखीय मात्रा शून्य होगा। ऐसे एक प्रवर्धक को अनवर्ती कहा जाता है। हालांकि, अधिकांश व्यावहारिक प्रवर्धक में कुछ निर्दिष्ट वियोजन होगी, जिसके कारण इनपुट पर 'देखा जाने वाला' प्रतिबिंब प्रतिरोधक आउटपुट पर जुड़े लोड के कुछ हद तक प्रभावित हो सकता है। <math>\left|S_{12}\right|\,</math> की सबसे छोटी मान्यता वाले एक प्रवर्धक को आमतौर पर एक बफर प्रवर्धक कहा जाता है। | |||
यदि एक वास्तविक प्रवर्धक की आउटपुट पोर्ट को एक विचित्र समायोजन संकेतक, <math>\Gamma_{L}\,</math>. वाले किसी भी लोड से जोड़ा जाता है। तो इनपुट पोर्ट पर देखे जाने वाले वास्तविक प्रतिबिंब संकेतक <math>\Gamma_\mathrm{in}\,</math> इसका निम्नानुसार होगा | |||
:<math>\Gamma_\mathrm{in} = S_{11} + \frac{S_{12}S_{21}\Gamma_L}{1-S_{22}\Gamma_L}\,</math>. | :<math>\Gamma_\mathrm{in} = S_{11} + \frac{S_{12}S_{21}\Gamma_L}{1-S_{22}\Gamma_L}\,</math>. | ||
अगर | अगर प्रवर्धक एकतरफा है तो <math>S_{12} = 0\,</math> और <math>\Gamma_\mathrm{in} = S_{11}\,</math> या, इसे दूसरे तरीके से रखने के लिए, आउटपुट लोडिंग का इनपुट पर कोई प्रभाव नहीं पड़ता है। | ||
एक समान संपत्ति विपरीत दिशा में | एक समान संपत्ति विपरीत दिशा में उपस्थित है, इस विषय में यदि <math>\Gamma_\mathrm{out}\,</math> आउटपुट पोर्ट पर देखा जाने वाला प्रतिबिंब गुणांक है और <math>\Gamma_{s}\,</math> इनपुट पोर्ट से जुड़े स्रोत का प्रतिबिंब गुणांक है। | ||
:<math>\Gamma_{out} = S_{22} + \frac{S_{12}S_{21}\Gamma_s}{1-S_{11}\Gamma_s}\,</math> | :<math>\Gamma_{out} = S_{22} + \frac{S_{12}S_{21}\Gamma_s}{1-S_{11}\Gamma_s}\,</math> | ||
=== एक | === एक प्रवर्धक के लिए बिना शर्त स्थिर होने के लिए पोर्ट लोडिंग की स्थिति === | ||
एक | एक प्रवर्धक निःशर्त रूप से स्थिर होता है यदि किसी भी संकेतक या स्रोत को कनेक्ट करने से अस्थिरता नहीं होती है। यह शर्त उत्पन्न होती है अगर स्रोत, लोड और प्रवर्धक के इनपुट और आउटपुट पोर्टों के प्रतिबिंब संकेतकों के मात्राएँ समकालिक रूप से एक से कम हों। एक महत्वपूर्ण आवश्यकता जो अक्सर ध्यान में नहीं रखी जाती है, यह है कि प्रवर्धक एक रेखीय नेटवर्क होना चाहिए जिसमें दाहिने हाथ के समीकरण नहीं होते हैं। अस्थिरता प्रवर्धक के गेन फ्रीक्वेंसी प्रतिसाधन या चरम स्थिति में विक्षोभ के कारण गंभीर दिक्कत पैदा कर सकती है। इच्छित फ्रीक्वेंसी पर निःशर्त रूप से स्थिर होने के लिए, एक प्रवर्धक को निम्नलिखित 4 समीकरणों को समकालिक रूप से पूरा करना चाहिए::<ref>Gonzalez, Guillermo (op. cit.); pp 217–222</ref> | ||
:<math>\left|\Gamma_s\right| < 1\,</math> | :<math>\left|\Gamma_s\right| < 1\,</math> | ||
:<math>\left|\Gamma_L\right| < 1\,</math> | :<math>\left|\Gamma_L\right| < 1\,</math> | ||
:<math>\left|\Gamma_\mathrm{in}\right| < 1\,</math> | :<math>\left|\Gamma_\mathrm{in}\right| < 1\,</math> | ||
:<math>\left|\Gamma_\mathrm{out}\right| < 1\,</math> | :<math>\left|\Gamma_\mathrm{out}\right| < 1\,</math> | ||
जब इन मूल्यों में से प्रत्येक एकता के बराबर होता है, तो सीमा की स्थिति को (जटिल) प्रतिबिंब गुणांक का प्रतिनिधित्व करने वाले ध्रुवीय आरेख पर खींचे गए एक चक्र द्वारा दर्शाया जा सकता है, एक इनपुट पोर्ट के लिए और दूसरा आउटपुट पोर्ट के लिए। | जब इन मूल्यों में से प्रत्येक एकता के बराबर होता है, तो सीमा की स्थिति को (जटिल) प्रतिबिंब गुणांक का प्रतिनिधित्व करने वाले ध्रुवीय आरेख पर खींचे गए एक चक्र द्वारा दर्शाया जा सकता है, एक इनपुट पोर्ट के लिए और दूसरा आउटपुट पोर्ट के लिए। प्रायः इन्हें स्मिथ चार्ट्स के रूप में स्केल किया जाएगा। प्रत्येक मामले में सर्कल केंद्र और संबंधित त्रिज्या के निर्देशांक निम्नलिखित समीकरणों द्वारा दिए गए हैं: | ||
====<math>\Gamma_{L}</math> के लिए मान <math>|\Gamma_\text{in}| = 1</math> (आउटपुट | ====<math>\Gamma_{L}</math> के लिए मान <math>|\Gamma_\text{in}| = 1</math> (आउटपुट स्थिरता चक्र) ==== | ||
RADIUS <math>r_L = \left| \frac{S_{12}S_{21}}{\left|S_{22}\right|^2 - \left|\Delta\right|^2} \right|.</math> | RADIUS <math>r_L = \left| \frac{S_{12}S_{21}}{\left|S_{22}\right|^2 - \left|\Delta\right|^2} \right|.</math> | ||
केंद्र <math>c_L = \frac{(S_{22} - \Delta S_{11}^*)^*}{\left|S_{22}\right|^2 - \left|\Delta\right|^2}.</math> | केंद्र <math>c_L = \frac{(S_{22} - \Delta S_{11}^*)^*}{\left|S_{22}\right|^2 - \left|\Delta\right|^2}.</math> | ||
| Line 312: | Line 304: | ||
और सुपरस्क्रिप्ट तारा (*) एक जटिल संयुग्म को इंगित करता है। | और सुपरस्क्रिप्ट तारा (*) एक जटिल संयुग्म को इंगित करता है। | ||
इनमें से प्रत्येक मान यूनिटी के बराबर होने के लिए सीमा शर्त को एक परिपथ पर दर्शाया जा सकता है, जो प्रतिबिंब संकेतक को प्रतिष्ठित करने वाले दोनों पोर्टों के लिए दर्शाया जाएगा। प्रायः इन्हें स्मिथ चार्ट के रूप में स्केल किया जाता है। प्रत्येक मामले में, वृत्त के केंद्र और संबंधित त्रिज्या के संबंध में निम्नलिखित समीकरणों द्वारा निर्दिष्ट किए जाते हैं: | |||
: <math>K = \frac{1 - |S_{11}|^2 - |S_{22}|^2 + |\Delta|^2}{2 |S_{12} S_{21}|}.</math> | : <math>K = \frac{1 - |S_{11}|^2 - |S_{22}|^2 + |\Delta|^2}{2 |S_{12} S_{21}|}.</math> | ||
| Line 318: | Line 310: | ||
=== | === प्रकीर्णन स्थानान्तरण मापदंड === | ||
प्रकीर्णन ट्रांसफर मापदंड या 2-पोर्ट नेटवर्क के टी-मापदंड टी-मापदंड आव्यूह द्वारा व्यक्त किए जाते हैं और संबंधित एस-मापदंड आव्यूह से निकटता से संबंधित होते हैं। यद्यपि, एस मापदंड के विपरीत प्रणाली में टी मापदंड को मापने के लिए कोई सरल भौतिक साधन नहीं है, जिसे कभी-कभी यूला तरंगों के रूप में संदर्भित किया जाता है। टी-मापदंड आव्यूह घटना से संबंधित है और निम्नानुसार प्रत्येक पोर्ट पर सामान्यीकृत तरंगें परिलक्षित होती हैं: | |||
:<math>\begin{pmatrix}b_1 \\ a_1 \end{pmatrix} = \begin{pmatrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{pmatrix}\begin{pmatrix} a_2 \\ b_2 \end{pmatrix}\, </math> | :<math>\begin{pmatrix}b_1 \\ a_1 \end{pmatrix} = \begin{pmatrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{pmatrix}\begin{pmatrix} a_2 \\ b_2 \end{pmatrix}\, </math> | ||
यद्यपि, उन्हें निम्नानुसार परिभाषित किया जा सकता है: | |||
:<math>\begin{pmatrix}a_1 \\ b_1 \end{pmatrix} = \begin{pmatrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{pmatrix}\begin{pmatrix} b_2 \\ a_2 \end{pmatrix}\, </math> | :<math>\begin{pmatrix}a_1 \\ b_1 \end{pmatrix} = \begin{pmatrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{pmatrix}\begin{pmatrix} b_2 \\ a_2 \end{pmatrix}\, </math> | ||
मैटलैबमें आरएफ टूलबॉक्स ऐड-ऑन<ref>{{cite web | |||
| url = http://www.mathworks.com/access/helpdesk/help/toolbox/rf/index.html?/access/helpdesk/help/toolbox/rf/s2t.html | | url = http://www.mathworks.com/access/helpdesk/help/toolbox/rf/index.html?/access/helpdesk/help/toolbox/rf/s2t.html | ||
| title = RF Toolbox documentation | | title = RF Toolbox documentation | ||
}}</ref> और कई किताबें | }}</ref> और कई किताबें इस अंतिम परिभाषा का प्रयोग करें, इसलिए सावधानी आवश्यक है। इस लेख में "S से T तक" और "T से S तक" अनुच्छेद पहली परिभाषा पर आधारित हैं। दूसरी परिभाषा में अनुकूलन आसान है दूसरी परिभाषा के लिए अनुकूलन तुच्छ है (इंटरचेंजिंग टी<small>11</small> टी के लिए<small>22</small>, और टी<small>12</small> टी के लिए<small>21</small>). | ||
एस-मापदंड की तुलना में टी-मापदंड का लाभ यह है कि संदर्भ प्रतिबाधा प्रदान करना विशुद्ध रूप से, वास्तविक या जटिल संयुग्म है, T-पैरामीटरों की तुलना में एस-पैरामीटरों के लाभ यह हैं कि संदर्भ आवश्यकियों के केवल वास्तविक या सम्पूर्ण संयोजक होने की व्यवस्था करते हैं, तो इन्हें सीधे तरीके से उपयोग किया जा सकता है उनका उपयोग 2 या अधिक 2-पोर्ट नेटवर्क को कैस्केडिंग के प्रभाव को आसानी से निर्धारित करने के लिए किया जा सकता है, बस संबंधित व्यक्तिगत टी को गुणा करके मापदंड आव्यूह यदि टी-मापदंड कहते हैं कि तीन अलग-अलग 2-पोर्ट नेटवर्क 1, 2 और 3 हैं <math>\begin{pmatrix}T_1\end{pmatrix}\,</math>, <math>\begin{pmatrix}T_2\end{pmatrix}\,</math> और <math>\begin{pmatrix}T_3\end{pmatrix}\,</math> क्रमशः तीनों नेटवर्क के कैस्केड के लिए टी-मापदंड आव्यूह (<math>\begin{pmatrix}T_T\end{pmatrix}\,</math>) क्रम में क्रम द्वारा दिया गया है: | |||
एस- | |||
:<math>\begin{pmatrix}T_T\end{pmatrix} = \begin{pmatrix}T_1\end{pmatrix}\begin{pmatrix}T_2\end{pmatrix}\begin{pmatrix}T_3\end{pmatrix}\,</math> | :<math>\begin{pmatrix}T_T\end{pmatrix} = \begin{pmatrix}T_1\end{pmatrix}\begin{pmatrix}T_2\end{pmatrix}\begin{pmatrix}T_3\end{pmatrix}\,</math> | ||
ध्यान दें कि आव्यूह गुणन क्रमविनिमेय नहीं है, इसलिए क्रम महत्वपूर्ण है। एस- | ध्यान दें कि आव्यूह गुणन क्रमविनिमेय नहीं है, इसलिए क्रम महत्वपूर्ण है। एस-मापदंड के साथ, टी-मापदंड जटिल मान हैं और दो प्रकारों के बीच सीधा रूपांतरण होता है। यद्यपि कैस्केडेड टी-मापदंड व्यक्तिगत टी-मापदंड का एक सरल आव्यूह गुणन है, प्रत्येक नेटवर्क के एस-मापदंड के लिए संबंधित टी-मापदंड में रूपांतरण और कैस्केड टी-मापदंड का समतुल्य कैस्केड एस-मापदंड में रूपांतरण, जो आमतौर पर आवश्यक होते हैं, तुच्छ नहीं होते हैं। यद्यपि एक बार ऑपरेशन पूरा हो जाने के बाद, दोनों दिशाओं में सभी पोर्टो के बीच जटिल फुल वेव इंटरैक्शन को ध्यान में रखा जाएगा। निम्नलिखित समीकरण 2-पोर्ट नेटवर्क के लिए एस और टी मापदंड के बीच रूपांतरण प्रदान करेंगे।<ref>[http://cp.literature.agilent.com/litweb/pdf/5952-1087.pdf ''S-Parameter Design''; Application Note AN 154; Agilent Technologies; p 14]</ref>: | ||
:<math>T_{11} = \frac{-\det \begin{pmatrix}S\end{pmatrix}}{S_{21}}\,</math> | :<math>T_{11} = \frac{-\det \begin{pmatrix}S\end{pmatrix}}{S_{21}}\,</math> | ||
| Line 347: | Line 330: | ||
:<math>T_{21} = \frac{-S_{22}}{S_{21}}\,</math> | :<math>T_{21} = \frac{-S_{22}}{S_{21}}\,</math> | ||
:<math>T_{22} = \frac{1}{S_{21}}\,</math> | :<math>T_{22} = \frac{1}{S_{21}}\,</math> | ||
जहाँ <math>\det \begin{pmatrix}S\end{pmatrix}\,</math> आव्यूह के निर्धारक को इंगित करता है <math>\begin{pmatrix}S\end{pmatrix}</math>, | |||
:<math>\det \begin{pmatrix}S\end{pmatrix}\ = S_{11} \cdot S_{22} - S_{12} \cdot S_{21}</math>. | :<math>\det \begin{pmatrix}S\end{pmatrix}\ = S_{11} \cdot S_{22} - S_{12} \cdot S_{21}</math>. | ||
| Line 356: | Line 339: | ||
:<math>S_{21} = \frac{1}{T_{22}}\,</math> | :<math>S_{21} = \frac{1}{T_{22}}\,</math> | ||
:<math>S_{22} = \frac{-T_{21}}{T_{22}}\,</math> | :<math>S_{22} = \frac{-T_{21}}{T_{22}}\,</math> | ||
जहाँ <math>\det \begin{pmatrix}T\end{pmatrix}\,</math> आव्यूह के निर्धारक को इंगित करता है <math>\begin{pmatrix}T\end{pmatrix}\,</math>. | |||
:<math>\det \begin{pmatrix}T\end{pmatrix}\ = T_{11}.T_{22}-T_{12}.T_{21},</math> | :<math>\det \begin{pmatrix}T\end{pmatrix}\ = T_{11}.T_{22}-T_{12}.T_{21},</math> | ||
==1-पोर्ट एस- | ==1-पोर्ट एस-मापदंड == | ||
1-पोर्ट नेटवर्क के लिए एस-पैरामीटर | एक 1-पोर्ट नेटवर्क के लिए एस-पैरामीटर एक सरल 1 × 1 आव्यूह के रूप में दिया जाता है <math>(s_{nn})\,</math> यहां n आवंटित पोर्ट नंबर होता है। एस-पैरामीटर परिभाषा के अनुसार रेखांकन के साथ मेल खाने के लिए इसे साधारणतः किसी प्रकार का पैसिव लोड होता है। एक एंटीना एक सामान्य एक-पोर्ट नेटवर्क है जिसके लिए <math>s_{11}</math> के छोटे मान इसका संकेत करते हैं कि एंटीना ऊर्जा को या तो छोड़ेगी या ऊर्जा को संगृहीत करेगी। | ||
असमान पोर्टों के लिए उच्चतर क्रम के एस-मापदंड (<math>S_{mn}\,</math>), जहां <math>m \ne \; n\,</math>की तरह 2-पोर्ट नेटवर्क के लिए प्राप्त किए जा सकते हैं, इसके लिए पोर्टों के जोड़ों को एक-दूसरे के साथ मिलाकर विचार करना होगा, प्रत्येक मामले में सुनिश्चित करेंगे कि बचे हुए (अप्रयोगित) पोर्टप्रणाली की आपेक्षिक विपणनयां वाले आवेशिता से लोड होते हैं। इस तरीके से प्रत्येक अप्रयुक्त पोर्ट के लिए प्रवेश ऊर्जा शून्य हो जाती है, जिससे 2-पोर्ट मामले के लिए प्राप्त व्यक्तियों के समान अभिव्यक्तियां प्राप्त होती हैं। केवल एकल पोर्टों के संबंधित S-पैरामीटर <math>S_{mn}\,</math> के लिए प्रणाली आपेक्षित विपणनयां वाले बचे हुए पोर्टों को आवेशित करना आवश्यक होता है, जिससे इन व्यापारों की प्रवेश ऊर्जा शून्य हो जाती है, केवल उस पोर्ट के लिए उन्नति के लिए जिस पर विचार किया जा रहा है। सामान्यतः इसलिए हमारे पास निम्नलिखित होता है: | |||
(<math>S_{mn} = \frac{b_m}{a_n}\,</math> | |||
और | और | ||
:<math>S_{mm} = \frac{b_m}{a_m}\,</math> | :<math>S_{mm} = \frac{b_m}{a_m}\,</math> | ||
उदाहरण के लिए, एक 3-पोर्ट नेटवर्क जैसे 2-वे | उदाहरण के लिए, एक 3-पोर्ट नेटवर्क जैसे 2-वे विभाजक में निम्नलिखित एस-मापदंड परिभाषाएँ होंगी | ||
:<math>\begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix}S_{11} & S_{12} & S_{13} \\ S_{21} & S_{22} & S_{23} \\ S_{31} & S_{32} & S_{33} \end{pmatrix}\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\,</math> | :<math>\begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix}S_{11} & S_{12} & S_{13} \\ S_{21} & S_{22} & S_{23} \\ S_{31} & S_{32} & S_{33} \end{pmatrix}\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\,</math> | ||
साथ | साथ | ||
| Line 377: | Line 358: | ||
:<math>S_{21} = \frac{b_2}{a_1} = \frac{V_2^-}{V_1^+}\,</math> ; <math>S_{22} = \frac{b_2}{a_2} = \frac{V_2^-}{V_2^+}\,</math> ; <math>S_{23} = \frac{b_2}{a_3} = \frac{V_2^-}{V_3^+}\,</math> | :<math>S_{21} = \frac{b_2}{a_1} = \frac{V_2^-}{V_1^+}\,</math> ; <math>S_{22} = \frac{b_2}{a_2} = \frac{V_2^-}{V_2^+}\,</math> ; <math>S_{23} = \frac{b_2}{a_3} = \frac{V_2^-}{V_3^+}\,</math> | ||
:<math>S_{31} = \frac{b_3}{a_1} = \frac{V_3^-}{V_1^+}\,</math> ; <math>S_{32} = \frac{b_3}{a_2} = \frac{V_3^-}{V_2^+}\,</math> ; <math>S_{33} = \frac{b_3}{a_3} = \frac{V_3^-}{V_3^+}\,</math> | :<math>S_{31} = \frac{b_3}{a_1} = \frac{V_3^-}{V_1^+}\,</math> ; <math>S_{32} = \frac{b_3}{a_2} = \frac{V_3^-}{V_2^+}\,</math> ; <math>S_{33} = \frac{b_3}{a_3} = \frac{V_3^-}{V_3^+}\,</math> | ||
जहाँ <math>S_{mn}</math> पोर्ट n पर घटना तरंग द्वारा प्रेरित पोर्ट m पर आउटगोइंग वेव को संदर्भित करता है। | |||
== एस- | == ==एस-मापदंड का मापन == | ||
एस- | एस-मापदंड को सामान्यतः एक [[ नेटवर्क विश्लेषक (विद्युत) | नेटवर्क विश्लेषक]] वीएनए) से मापा जाता है। | ||
=== मापा और सही एस- | === मापा और सही एस-मापदंड डेटा का आउटपुट स्वरूप === | ||
एस- | एस-मापदंड परीक्षण डेटा कई वैकल्पिक स्वरूपों में प्रदान किया जा सकता है, उदाहरण के लिए: सूची, ग्राफिकल ([[स्मिथ चार्ट]] या [[ जटिल विमान |जटिल विमान]] )। | ||
=== सूची प्रारूप === | === सूची प्रारूप === | ||
सूची प्रारूप में | सूची प्रारूप में मापित और सुधारित एस-मापदंड तालिका फ्रीक्वेंसी के विरुद्ध सारणीबद्ध किए जाते हैं। सबसे सामान्य तालिका प्रारूप को मापदंडया एसएनपी के रूप में जाना जाता है, जहां N पोर्ट की संख्या होती है। इस जानकारी को संबंधित पाठ फ़ाइल में संग्रहीत किया जाता है जिसका फ़ाइल नाम एक्सटेंशन '.s2p' होता है। निम्नलिखित उदाहरण में दिखाया गया है कि एक उपकरण के लिए प्राप्त पूर्ण 2-पोर्ट S-पैरामीटर डेटा के लिए एक: | ||
! शुक्र 21 जुलाई, 14:28:50 2005 को बनाया गया | ! शुक्र 21 जुलाई, 14:28:50 2005 को बनाया गया | ||
| Line 397: | Line 378: | ||
54 -16.6 109.3 10.6 187.8 -38.1 9.6 -15.3 71.4 | 54 -16.6 109.3 10.6 187.8 -38.1 9.6 -15.3 71.4 | ||
विस्मयादिबोधक चिह्न से | विस्मयादिबोधक चिह्न से प्रारंभ होने वाली पंक्तियों में केवल टिप्पणियाँ होती हैं। हैश प्रतीक के साथ प्रारंभ होने वाली पंक्ति को संकेत करती है कि इस स्थिति में आवृत्तियाँ मेगाहर्ट्ज़ में, S-मापदंड सूचीबद्ध हैं (S), परिमाण डीबी लॉग परिमाण (डीबी) में हैं और प्रणाली प्रतिबाधा 50 ओम (R 50) है। डेटा के 9 कॉलम हैं। इस मामले में कॉलम 1 मेगाहर्ट्ज़ में परीक्षण आवृत्ति है। कॉलम 2, 4, 6 और 8 के परिमाण हैं <math>S_{11}\,</math>, <math>S_{21}\,</math>, <math>S_{12}\,</math> और <math>S_{22}\,</math> क्रमशः डीबी में। कॉलम 3, 5, 7 और 9 के कोण हैं <math>S_{11}\,</math>, <math>S_{21}\,</math>, <math>S_{12}\,</math> और <math>S_{22}\,</math> क्रमशः डिग्री में। | ||
=== ग्राफिकल (स्मिथ चार्ट) === | === ग्राफिकल (स्मिथ चार्ट) === | ||
किसी भी 2-पोर्ट एस- | किसी भी 2-पोर्ट एस-मापदंड को स्मिथ चार्ट पर ध्रुवीय निर्देशांक का उपयोग करके प्रदर्शित किया जा सकता है, परंतु सबसे सार्थक होगा <math>S_{11}\,</math> और <math>S_{22}\,</math> चूँकि इनमें से किसी को भीप्रणाली इम्पीडेंस के लिए उपयुक्त विशेषता स्मिथ चार्ट इम्पीडेंस (या प्रवेश) स्केलिंग का उपयोग करके सीधे समकक्ष सामान्यीकृत प्रतिबाधा (या प्रवेश) में परिवर्तित किया जा सकता है। | ||
=== ग्राफिकल (ध्रुवीय आरेख) === | === ग्राफिकल (ध्रुवीय आरेख) === | ||
किसी भी 2-पोर्ट एस- | किसी भी 2-पोर्ट एस-मापदंड को ध्रुवीय निर्देशांक का उपयोग करके ध्रुवीय आरेख पर प्रदर्शित किया जा सकता है। | ||
या तो ग्राफिकल प्रारूप में एक विशेष परीक्षण आवृत्ति पर प्रत्येक एस- | या तो ग्राफिकल प्रारूप में एक विशेष परीक्षण आवृत्ति पर प्रत्येक एस-मापदंड को डॉट के रूप में प्रदर्शित किया जाता है। यदि माप कई आवृत्तियों में एक स्वीप है तो प्रत्येक के लिए एक डॉट दिखाई देगा। | ||
=== एक-पोर्ट नेटवर्क के एस- | === एक-पोर्ट नेटवर्क के एस-मापदंड को मापना === | ||
केवल एक पोर्ट वाले नेटवर्क के लिए एस- | केवल एक पोर्ट वाले नेटवर्क के लिए एस-मापदंड आव्यूह के रूप में केवल एक तत्व का प्रतिनिधित्व किया जाएगा <math>S_{nn}\,</math>, जहां n पोर्ट को आवंटित संख्या है। अधिकांश वीएनए समय बचाने के लिए एक पोर्ट माप के लिए एक सरल एक-पोर्ट अंशांकन क्षमता प्रदान करते हैं यदि वह सब आवश्यक है। | ||
=== 2 से अधिक | === 2 से अधिक पोर्टो वाले नेटवर्क के एस-मापदंड को मापना === | ||
दो से अधिक | दो से अधिक पोर्टो वाले नेटवर्क के एस-मापदंड के एक साथ माप के लिए प्रारूप किए गए वीएनए संभव हैं, परंतु जल्दी ही निषेधात्मक रूप से जटिल और महंगे हो जाते हैं। सामान्यतः उनकी खरीद उचित नहीं होती है क्योंकि अतिरिक्त माप के साथ मानक 2-पोर्ट कैलिब्रेटेड वीएनए का उपयोग करके प्राप्त परिणामों की सही व्याख्या के बाद आवश्यक माप प्राप्त किया जा सकता है। आवश्यक एस-मापदंड आव्यूह को चरणों में क्रमिक दो पोर्ट मापों से इकट्ठा किया जा सकता है, एक समय में दो पोर्ट, प्रत्येक अवसर पर अप्रयुक्त पोर्ट्स कोप्रणाली प्रतिबाधा के बराबर उच्च गुणवत्ता भार में समाप्त किया जा सकता है। इस दृष्टिकोण का एक जोखिम यह है कि लोड का पुनरावृत्ति हानि या वीएसडब्ल्यूआर स्वयं को उपयुक्त रूप से निर्दिष्ट किया जाना चाहिए, जितना संभव हो उतना करीब 50 ओम, या जो भी नाममात्र प्रणाली प्रतिबाधा है। कई पोर्टो वाले नेटवर्क के लिए लागत के आधार पर भार के वीएसडब्ल्यूआर को अपर्याप्त रूप से निर्दिष्ट करने का प्रलोभन हो सकता है। लोड का सबसे अयोग्य स्वीकार्य वीएसडब्ल्यूआर क्या होगा, यह निर्धारित करने के लिए कुछ विश्लेषण आवश्यक होगा। | ||
यह मानते हुए कि अतिरिक्त भार को पर्याप्त रूप से निर्दिष्ट किया गया है, यदि आवश्यक हो, तो दो या अधिक एस- | यह मानते हुए कि अतिरिक्त भार को पर्याप्त रूप से निर्दिष्ट किया गया है, यदि आवश्यक हो, तो दो या अधिक एस-मापदंड सबस्क्रिप्ट को वीएनए से संबंधित उन लोगों से संशोधित किया जाता है जो परीक्षण के अंतर्गत नेटवर्क से संबंधित हैं । उदाहरण के लिए, यदि DUT में 5 पोर्ट हैं और एक दो वीएनए पोर्ट 1 से डीयूटी पोर्ट 3 और वीएनए पोर्ट 2 से डीयूटी पोर्ट 5 से जुड़ा है, तो मापा गया वीएनए परिणाम (<math>S_{11}\,</math>, <math>S_{12}\,</math>, <math>S_{21}\,</math> और <math>S_{22}\,</math>) के बराबर होगा <math>S_{33}\,</math>, <math>S_{35}\,</math>, <math>S_{53}\,</math> और <math>S_{55}\,</math> क्रमशः, यह मानते हुए कि डीयूटी पोर्ट 1, 2 और 4 को पर्याप्त 50 ओम भार में समाप्त कर दिया गया था। यह आवश्यक 25 एस-मापदंड में से 4 प्रदान करेगा। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[प्रवेश पैरामीटर]] | * [[प्रवेश पैरामीटर|प्रवेश मापदंड]] | ||
* [[प्रतिबाधा पैरामीटर]] | * [[प्रतिबाधा पैरामीटर|प्रतिबाधा मापदंड]] | ||
* [[दो-पोर्ट नेटवर्क]] | * [[दो-पोर्ट नेटवर्क]] | ||
*[[एक्स-मानकों]], S- | *[[एक्स-मानकों]], S-मापदंड का एक गैर-रैखिक सुपरसेट | ||
* बेलेविच की प्रमेय | * बेलेविच की प्रमेय | ||
| Line 436: | Line 417: | ||
*C. W. Davidson, "Transmission Lines for Communications with CAD Programs", Second Edition, Macmillan Education Ltd.; {{ISBN|0-333-47398-1}} | *C. W. Davidson, "Transmission Lines for Communications with CAD Programs", Second Edition, Macmillan Education Ltd.; {{ISBN|0-333-47398-1}} | ||
{{DEFAULTSORT:Scattering Parameters}} | {{DEFAULTSORT:Scattering Parameters}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Scattering Parameters]] | ||
[[Category:Created On 11/06/2023]] | [[Category:Created On 11/06/2023|Scattering Parameters]] | ||
[[Category:Lua-based templates|Scattering Parameters]] | |||
[[Category:Machine Translated Page|Scattering Parameters]] | |||
[[Category:Pages with script errors|Scattering Parameters]] | |||
[[Category:Templates Vigyan Ready|Scattering Parameters]] | |||
[[Category:Templates that add a tracking category|Scattering Parameters]] | |||
[[Category:Templates that generate short descriptions|Scattering Parameters]] | |||
[[Category:Templates using TemplateData|Scattering Parameters]] | |||
[[Category:दो-पोर्ट नेटवर्क|Scattering Parameters]] | |||
[[Category:विद्युत पैरामीटर|Scattering Parameters]] | |||
[[Category:स्थानांतरण कार्य|Scattering Parameters]] | |||
Latest revision as of 20:14, 19 June 2023
प्रकीर्णन मापदंड या एस-मापदंड किसी प्रकीर्णन आव्यूह या एस-आव्यूह के तत्वों को विद्युत संकेतों द्वारा विभिन्न स्थिर समष्टि आवेशों से गुजरने पर रैखिक विद्युत नेटवर्क के विद्युत व्यवहार का वर्णन करते हैं।
मापदंड, विद्युत अभियन्त्रण की कई शाखाओं के लिए उपयोगी हैं, जिनमें विद्युत अभियांत्रिकी, संचार प्रणाली प्रारूपण और विशेष रूप से माइक्रोवेव अभियांत्रिकी सम्मिलित हैं।
एस-मापदंड, एक समान मापदंड परिवार के सदस्य हैं, जिनके अन्य उदाहरण हैं: Y-मापदंड[1], Z-मापदंड, H-मापदंड, T-मापदंड या एबीसीडी-मापदंड आदि।[2] [3][4] वे इनसे, इस अर्थ में भिन्न हैं कि एस-मापदंड एक रैखिक विद्युत नेटवर्क को चिह्नित करने के लिए विवृत्त या शॉर्ट परिपथ स्थितियों का उपयोग नहीं करते हैं; इसके अतिरिक्त इनमे प्रतिबाधा मिलान का उपयोग किया जाता है। विवृत्त-परिपथ और शॉर्ट-परिपथ टर्मिनेशन की तुलना में उच्च संकेत आवृत्ती पर इन विद्युत सीमा का उपयोग करना अत्यधिक सरल है। साधारण धारणा के विपरीत, 'मात्राओं को शक्ति के संदर्भ में नहीं मापा जाता है'। समकालिक सदिश नेटवर्क विश्लेषक विभव यातायाती तरंग चरण के आंशिकता और चरण का मापन करते हैं, जो मूल रूप से डिजिटली मोड्यूलेट किए गए ताररहित संकेतों के डीमोडुलेशन के लिए उपयोग किए जाने वाले परिपथ के समान होते हैं।
विद्युत घटकों (प्रेरक, संधारित्र, प्रतिरोधक ) के नेटवर्क की कई विद्युतीय गुणधर्मों को एस-मापदंड का उपयोग करके व्यक्त किया जा सकता है, जैसे कि लाभ, पुनरावृत्ति हानि, वोल्टेज स्टैंडिंग वेव अनुपात (वीएसडब्ल्यूआर), प्रतिबिंबन संबंधक और प्रवर्धक स्थिरता आदि। शब्द 'प्रकीर्णन' आरएफ अभियांत्रिकी की तुलना में प्रकाशीय अभियांत्रिकी के लिए अधिक सामान्य है, जब एक विमान की लहर एक बाधा पर घटित होती है या असमान छायांकन माध्यम से गुजरती है, तों इस प्रभाव को देखा जा सकता है। एस-मापदंड के संदर्भ में, प्रकीर्णन उस विधि को संदर्भित करता है जिसमें संचरण लाइन में एक नेटवर्क के सम्मिलन के कारण संचारण लाइन में विद्युत प्रवाह और विभव प्रभावित होते हैं। यह विद्युत प्रतिबाधा से मिलने वाली तरंग के समतुल्य है, जो रेखा के अभिलक्षणिक प्रतिबाधा से भिन्न है।
यद्यपि यह किसी भी आवृत्ति पर लागू किया जा सकता है, एस-मापदंड अधिकतर आकाशवाणी आवृति और माइक्रोवेव आवृत्ती पर कार्य करने वाले नेटवर्क के लिए उपयोग किए जाते हैं। सामान्य उपयोग में आने वाले एस-मापदंड - पारंपरिक एस-मापदंड रैखिक मात्राएं हैं। एस-मापदंड माप आवृत्ति के साथ परिवर्तित होते हैं, इसलिए विशेषता प्रतिबाधा या किंचित प्रतिबाधा के अतिरिक्त, किसी भी एस-मापदंड माप के लिए, आवृत्ति को निर्दिष्ट किया जाना चाहिए।
एस-मापदंड सरलता से आव्यूह रूप में प्रदर्शित होते हैं और आव्यूह बीजगणित के नियमों का पालन करते हैं।
पृष्ठभूमि
एस-मापदंड का पहला प्रकाशित विवरण 1945 में विटोल्ड बेलेविच की थीसिस में था।[5] बेलेविच द्वारा उपयोग किया जाने वाला नाम पुनर्विभाजन आव्यूह था, और इसने समावेशी तत्व नेटवर्क्स तक सीमित विचार था। प्रकीर्णन आव्यूह शब्द का उपयोग 1947 में भौतिक विज्ञानी और इंजीनियर रॉबर्ट हेनरी डिके द्वारा किया गया था, जिन्होंने स्वतंत्र रूप से रडार पर युद्धकालीन कार्य के समय इस विचार को विकसित किया था।[6][7]एस-मापदंड और प्रकीर्णन आव्यूह में,प्रकीर्ण तरंगे वे तरंगे होते हैं जिन्हें 'यात्री तरंगे' कहा जाता है। 1960 के दशक में एक अलग प्रकार के एस-मापदंड का परिचय किया गया था। इन्हें "समन्वयक प्रकीर्णन-मापदंड" भी कहा जाता हैं। यह दूसरा प्रकार का एस-मापदंड कानेयुकी कुरोकावा द्वारा प्रसिद्ध हुआ था, जिन्होंने इस नए प्रकीर्ण तरंगों को 'पावर तरंगों' के रूप में संदर्भित किया। इन दो प्रकार के एस-मापदंड में बहुत अलग गुणधर्म होते हैं और इन्हें मिलाने का प्रयास नहीं किया जाना चाहिए। अपने महत्वपूर्ण पेपर में,कुरोकावा ने स्पष्ट रूप से पावर-तरंग एस-मापदंड और पारंपरिक, यात्री-तरंग एस-मापदंड का अंतरीय किया है। इनके एक प्रकार को प्सेडो-यात्री-तरंग एस-मापदंड कहा जाता है।
एस-मापदंड दृष्टिकोण में, एक विद्युत नेटवर्क को एक 'ब्लैक बॉक्स' के रूप में माना जाता है जिसमें विभिन्न संयुक्त आधारभूत विद्युत परिपथ घटक या संकुचित तत्व सम्मिलित होते हैं, जैसे कि रेजिस्टर, कैपेसिटर, इंडक्टर और ट्रांजिस्टर, जो पोर्ट के माध्यम से अन्य परिपथों के साथ संवाद करते हैं। नेटवर्क को एक वर्गीकरण मायात्रिक संख्याओं का सम्पर्क किया जाता है जिसे इसका एस-मापदंड मायात्रिक कहा जाता है, जो पोर्ट पर लागू किए गए संकेत के प्रतिक्रिया की गणना के लिए उपयोग किया जा सकता है।
एस-मापदंड की परिभाषा के अनुसार, यह समझा जाता है कि एक नेटवर्क में कोई भी घटक हो सकता है, जो संयुक्त छोटे संकेतों के साथ रेखीय रूप से व्यवहार करता है। इसमें एकाधिक संचार प्रणाली के उपयोगी घटक या 'खंड' भी सम्मिलित हो सकते हैं, जैसे प्रवर्धक, क्षीणक, विद्युतकीय फिल्टर, दिशात्मक युग्मक और समानता परंतु इन्हें भी रेखीय और परिभाषित शर्तों के अंतर्गत चलाया जाना चाहिए।
एस-मापदंड द्वारा वर्णित एक विद्युत नेटवर्क में पोर्टो की संख्या हो सकती है। पोर्ट वे बिंदु होते हैं जिन पर विद्युत संकेत या तो नेटवर्क में प्रवेश करते हैं या बाहर निकलते हैं। पोर्ट सामान्यतः सिरो के जोड़े होते हैं जिनकी आवश्यकता होती है कि एक सिरा में विद्युत प्रवाह दूसरे को छोड़कर वर्तमान के बराबर होता है।[8][9] एस-मापदंड का उपयोग आवृत्तियों पर किया जाता है जहां पोर्ट प्रायः समाक्षीय या वेवगाइड (विद्युत चुंबकत्व) संबंध होते हैं।
एन-पोर्ट नेटवर्क का वर्णित करने वाला एस-मापदंड आव्यूह आयाम एन का वर्ग होगा और इसलिए इसमें तत्व सम्मिलित होंगे। परीक्षण आवृत्ति पर प्रत्येक तत्व या एस-मापदंड को एक इकाई रहित संयुक्त संख्या द्वारा दर्शाया जाता है जो परिमाण और कोण, अर्थात आयाम और चरण का प्रतिनिधित्व करता है। सम्मिश्र संख्या या तो आयताकार रूप में व्यक्त किया जा सकता है या, अधिकांशतः, घूर्णीय रूप में व्यक्त किया जाता है।
एस-मापदंड की परिमाण लीनियर रूप या लघुगणकीय रूप में व्यक्त की जा सकती है। जब लघुगणक रूप में व्यक्त किया जाता है, तो परिमाण" बिन आयामित इकाई" अर्थात डेसिबल की होती है। एस-मापदंड का कोण अधिकांशतः डिग्री में व्यक्त किया जाता है, परंतु कभी-कभी रेडियन में भी व्यक्त किया जाता है। किसी भी एस-मापदंड को आरेखित रूप में प्रदर्शित किया जा सकता है, जहां एक आवृत्ति के लिए एक बिंदु या आवृत्ति सीमा के लिए एक स्थानक होता है।
यदि यह केवल एक पोर्ट पर लागू होता है , इसे प्रणाली प्रतिबाधा के लिए सामान्यीकृत स्मिथ चार्ट प्रतिबाधा या प्रवेश पर प्रदर्शित किया जा सकता है। स्मिथ चार्ट के बीच सरल रूपांतरण की अनुमति देता है मापदंड, वोल्टेज प्रतिबिंब गुणांक के बराबर और उस पोर्ट पर संबंधित प्रतिबाधा 'देखा'।
एस-मापदंड का एक सेट निर्दिष्ट करते समय निम्नलिखित जानकारी को परिभाषित किया जाना चाहिए:
- आवृत्ति
- नाममात्र विशेषता प्रतिबाधा (अक्सर 50 Ω)
- पोर्ट नंबर का आवंटन
- स्थितियां जो नेटवर्क को प्रभावित कर सकती हैं, जैसे कि तापमान, नियंत्रण वोल्टेज, और बायस करंट, जहां लागू हो।
एस-मापदंड आव्यूह
एक परिभाषा
एक सामान्य मल्टी-पोर्ट नेटवर्क के लिए, पोर्ट्स को 1 से N तक क्रमांकित किया जाता है, जहाँ N पोर्ट्स की कुल संख्या है। पोर्ट I के लिए, संबंधित एस-मापदंड परिभाषा घटना और परावर्तित 'शक्ति तरंगों' के संदर्भ में है, और क्रमश।
कुरोकावा[10] प्रत्येक पोर्ट के लिए घटना शक्ति तरंग को परिभाषित करता है
और प्रत्येक पोर्ट के लिए परावर्तित तरंग को इस रूप में परिभाषित किया गया है
जहाँ पोर्ट I के लिए प्रतिबाधा है, का जटिल संयुग्म है , और पोर्ट i पर वोल्टेज और करंट के क्रमशः जटिल आयाम हैं, और
कभी-कभी यह मानना उपयोगी होता है कि संदर्भ प्रतिबाधा सभी पोर्टो के लिए समान है, जिस स्थिति में घटना और परावर्तित तरंगों की परिभाषा को सरल बनाया जा सकता है
और
ध्यान दें कि जैसा कि स्वयं कुरोकावा ने बताया था, की उपरोक्त परिभाषाएँ और अद्वितीय नहीं हैं। सदिशों a और b के बीच संबंध, जिसके i-वें घटक विद्युत तरंगें हैं और क्रमशः, एस-मापदंड आव्यूह एस का उपयोग करके व्यक्त किया जा सकता है:
या स्पष्ट घटकों का उपयोग करना:
पारस्परिकता
एक नेटवर्क पारस्परिकता प्रमेय होगा यदि यह निष्क्रिय घटक है और इसमें केवल पारस्परिक तत्व हो जो प्रेषित संकेत को प्रभावित करती है। उदाहरण के लिए, क्षीणकर्ता, केबल, स्प्लिटर्स और कंबाइनर सभी पारस्परिक नेटवर्क हैं और प्रत्येक विषयो में होगा या एस-मापदंड आव्यूह इसके स्थानान्तरण के बराबर होगा। ऐसे नेटवर्क जिनमें संचरण माध्यम में गैर-पारस्परिक तत्व सम्मिलित होती है जैसे कि पूर्वाग्रह फेराइट (चुंबक) घटक गैर-पारस्परिक होंगे। एक प्रवर्धक गैर-पारस्परिक नेटवर्क का एक और उदाहरण है।
यद्यपि, 3-पोर्ट नेटवर्क की एक गुण यह है कि वे एक साथ पारस्परिक, हानि-मुक्त और पूरी तरह से मेल नहीं खा सकते हैं।[11]
दोषरहित नेटवर्क
दोषरहित नेटवर्क वह है जो किसी भी शक्ति का क्षय नहीं करता है, या: . सभी पोर्टो पर घटना शक्तियों का योग सभी पोर्टो पर आउटगोइंग शक्तियों के योग के बराबर है। इसका तात्पर्य है कि एस-मापदंड आव्यूह एकात्मक आव्यूह है, अर्थात , जहाँ का संयुग्मी स्थानांतरण है और पहचान आव्यूह है।
हानिपूर्ण नेटवर्क
एक हानिपूर्ण निष्क्रिय नेटवर्क वह है जिसमें सभी पोर्टो पर घटना शक्तियों का योग सभी पोर्टो पर आउटगोइंग शक्तियों के योग से अधिक होता है। इसलिए यह शक्ति का प्रसार करता है: . इस प्रकार , और सकारात्मक-निश्चित आव्यूह है।[12]
दो-पोर्ट एस-मापदंड
2-पोर्ट नेटवर्क के लिए एस-मापदंड आव्यूह संभवतः सबसे आम रूप से उपयोग की जाती है और यह बड़े नेटवर्क के लिए उच्च वर्ग आव्यूह उत्पन्न करने के लिए मूल निर्माण इकाई के रूप में कार्य करती है। [18] इस मामले में, बाहरी ('प्रतिबिंबित') और आंतरिक तरंगों के बीच का संबंध और एस-मापदंड आव्यूह द्वारा दिया जाता है:
- .
आव्यूहों को समीकरणों में विस्तारित करने पर प्राप्त होता है:
और
- .
प्रत्येक समीकरण नेटवर्क के प्रत्येक पोर्ट, 1 और 2, पर बाहरी और प्रवेशित तरंगों के बीच संबंध को नेटवर्क के व्यक्तिगत एस-मापदंडो , , और . के माध्यम से देता है। यदि हम पोर्ट 1 पर एक प्रवेशित तरंग (1a_1) को मानते हैं तो इससे पोर्ट 1 या पोर्ट 2 से निकलने वाली तरंगें हो सकती हैं, यद्यपि, अगर, एस-मापदंड की परिभाषा के अनुसार, पोर्ट 2 कोप्रणाली प्रतिबाधा के समान भार में समाप्त किया जाता है () तब, अधिकतम शक्ति प्रमेय द्वारा स्थानांतरण सिद्धांत के अनुसार, बनाने में पूरी तरह से शोषित हो जाएगी शून्य हो जाएगी। इसलिए, प्रवेशित वोल्टेज तरंगों को निर्धारित करते हुए और के रूप में परिभाषित करते हैं
- और .
उसी तरह, यदि पोर्ट 1 को प्रणाली आवेश में समाप्त किया जाता है, तो शून्य हो जाती है, जिससे वाल्यू 1=0 होती है।
- और
2-पोर्ट एस-मापदंड में निम्नलिखित सामान्य विवरण हैं:
- इनपुट पोर्ट वोल्टेज प्रतिबिंब गुणांक है
- विपरीत वोल्टेज लाभ है
- आगे वोल्टेज लाभ है
- आउटपुट पोर्ट वोल्टेज प्रतिबिंब गुणांक है।
यदि, प्रत्येक पोर्ट के सापेक्ष वोल्टेज तरंग दिशा को परिभाषित करने के अतिरिक्त उन्हें आगे के रूप में उनकी पूर्ण दिशा द्वारा परिभाषित किया जाता है और उल्टा लहरें तब और . एस-मापदंड तब अधिक सहज अर्थ लेते हैं जैसे कि आगे वोल्टेज लाभ आगे वोल्टेज के अनुपात द्वारा परिभाषित किया जा रहा है.
इसका उपयोग करके उपरोक्त आव्यूह को और अधिक व्यावहारिक विधियों से विस्तारित किया जा सकता है
एस-मापदंड 2-पोर्ट नेटवर्क
रेखीय स्थितियों में कार्यरत एक अधिसूचक अचक्षु एक अनुप्रेषक नेटवर्क का अच्छा उदाहरण है और एक मिलती हुई घटाव कोण एक प्रतिबिंबी नेटवर्क का एक उदाहरण है। निम्नलिखित मामलों में हम मान लेंगे कि प्रवेश और निर्गमन कनेक्शन पोर्ट 1 और 2 को अनुक्रमिक रूप से किए गए हैं जो सबसे सामान्य संवेदना है। सामान्य प्रणाली आवेश, आवृत्ति, और डिवाइस को प्रभावित करने वाले किसी भी अन्य कारक जैसे तापमान आदि को भी निर्दिष्ट किया जाना चाहिए।।
जटिल रैखिक लाभ
जटिल रैखिक लाभ जी द्वारा दिया जाता है
- .
यह इनपुट घटना पावर वेव द्वारा विभाजित आउटपुट परावर्तित पावर वेव का रैखिक अनुपात है, सभी मान जटिल मात्रा के रूप में व्यक्त किए जाते हैं। हानिपूर्ण नेटवर्क के लिए यह उप-एकात्मक है, सक्रिय नेटवर्क के लिए .यह वोल्टेज लाभ के बराबर तभी होगा जब डिवाइस में समान इनपुट और आउटपुट प्रतिबाधा हो।
अदिश रैखिक लाभ
अदिश रैखिक लाभ द्वारा दिया जाता है
- .
यह आपात संख्या लाभ, यानी आपात ऊर्जा-तरंग से प्रवेश ऊर्जा-तरंग के अनुपात को प्रतिनिधित करता है और इसे पावर लाभ के वर्ग के बराबर होता है। यह एक वास्तविक-मूल्य मात्रा है, जिसमें चरण की जानकारी हटा दी जाती है।
अदिश लघुगणक लाभ
लाभ (जी) के लिए अदिश लघुगणकीय अभिव्यक्ति है:
- डीबी।
यह अदिश रूपांतरित आपात गुणांक से अधिक प्रयुक्त होता है और सामान्यतः एक सकारात्मक मात्रा को साधारित रूप से एक "गुणांक" के रूप में समझा जाता है, जबकि एक नकारात्मक मात्रा एक "नकारात्मक गुणांक" होती है, जो डीबी में अपने मात्रा के बराबर होती है। उदाहरण के लिए, 100 मेगाहर्ट्ज पर, 10 मीटर लंबी केबल का एक गुणांक -1 डीबी हो सकता है, जो 1 डीबी का हानि के बराबर होता है।
सम्मिलन हानि
यदि दो मापन पोर्ट एक ही संदर्भ आवेश का उपयोग करते हैं, तो संचालन संख्या के मान के प्रतिक रूप में डेसिबल में व्यक्त बीचवाल (IL) है। इसलिए, यह निम्नलिखित द्वारा दिया जाता है::[13]
डीबी।
यह मापन के संदर्भ तलों के बीच डिवाइस अंतरीय ्गत परीक्षण (डीयूटी ) के प्रस्तावित करने से उत्पन्न अतिरिक्त हानि है। अतिरिक्त हानि डीयूटी में आंतरिक हानि और/या मिलान में हो सकती है। अतिरिक्त हानि के मामले में, प्रवेश हानि को सकारात्मक परिभाषित किया जाता है। डेसिबल में व्यक्त अवरोध तापमान के उल्टा नकारात्मक होता है और इसे प्रवेश गुण कहा जाता है, जो वैद्यतात्मक लघुगणकीय लाभ के बराबर होता है
इनपुट पुनरावृत्ति हानि
इनपुट वापसी हानि (RLin) को एक उपाय के रूप में सोचा जा सकता है कि नेटवर्क का वास्तविक इनपुट प्रतिबाधा नाममात्र प्रणाली प्रतिबाधा मान के कितने समीप है। डेसीबल में व्यक्त इनपुट पुनरावृत्ति हानि द्वारा दिया जाता है
- डीबी।
ध्यान दें कि निष्क्रिय दो-पोर्ट नेटवर्क के लिए जिसमें |S11| ≤ 1, यह इस प्रकार है कि पुनरावृत्ति हानि एक गैर-नकारात्मक मात्रा है: RLin ≥ 0. यह भी ध्यान दें कि कुछ भ्रामक रूप से, पुनरावृत्ति हानि साइन को कभी-कभी ऊपर परिभाषित मात्रा के नकारात्मक के रूप में उपयोग किया जाता है, परंतु यह उपयोग, हानि की परिभाषा के आधार पर, सख्ती से बोलना गलत है।[14]
आउटपुट पुनरावृत्ति हानि
आउटपुट पुनरावृत्ति हानि (RLout) को यह सोचा जा सकता है कि यह माप आपात संख्या है जो नेटवर्क की वास्तविक इनपुट आवेशिकता को सामान्य प्रणाली आवेश मान के समीप कितनी समीप प्रस्तुत करती है। इनपुट पुनरावृत्ति हानि को डेसिबल में व्यक्त किया जाता है:
- डीबी।
विपरीत लाभ और विपरीत वियोजन
विपरीत लाभ के लिए अदिश लघुगणकीय अभिव्यक्ति है:
- डीबी।
प्रायः इसे विपरीतआपाती () के रूप में व्यक्त किया जाएगा, जिसके लिए यह विपरीत लाभ की मानकता के बराबर एक सकारात्मक मात्रा होता है और अभिव्यक्ति इस रूप में होती है
- डीबी।
प्रतिबिंब गुणांक
इनपुट पोर्ट पर प्रतिबिंब गुणांक () या आउटपुट पोर्ट पर () के समकक्ष हैं और क्रमशः, इसलिए
- और .
जैसा और जटिल मात्राएँ हैं, इसलिए हैं और .
प्रतिबिंब गुणांक जटिल मात्राएं हैं और ध्रुवीय आरेखों या स्मिथ चार्ट्स पर रेखांकन का प्रतिनिधित्व किया जा सकता है
प्रतिबिंब गुणांक लेख भी देखें।
वोल्टेज स्थायी तरंग अनुपात
एक पोर्ट पर वोल्टेज स्थानिक तरंग अनुपात (वीएसडब्ल्यूआर) को छोटे अक्षर 's' से प्रतिष्ठित किया जाता है, यह पोर्ट मैच का एक समान माप है जो वापसी हानि के समान है, परंतु यह एक अदिश रैखिक मात्रा है, वापसी तरंग के अधिकतम वोल्टेज से वापसी तरंग के न्यूनतम वोल्टेज के अनुपात होता है। इसलिए, यह वोल्टेज प्रतिबिंब संख्या के मान और इस प्रकार इनपुट पोर्ट के लिए , या आउटपुट पोर्ट के लिए के मान से संबंधित है।
यहाँ इनपुट पोर्ट पर, वीएसडब्ल्यूआर () द्वारा दिया गया है
आउटपुट पोर्ट पर, वीएसडब्ल्यूआर () द्वारा दिया गया है
यह सत्य है जब गुणांक का मान एकाधिकता से अधिक नहीं होता है, जो आमतौर पर मामला होता है। एक एकाधिकता से अधिक मान वाला एक अभिविन्यास, जैसे कि एक टनल डायोड एम्पलिफायर में, इस अभिव्यक्ति के लिए एक नकारात्मक मान देगा। हालांकि, वीएसडब्ल्यूआर, अपनी परिभाषा से,सदैव सकारात्मक होता है। एक बहुपोर्ट के पोर्ट k के लिए एक और सही अभिव्यक्ति है।
4-पोर्ट एस-मापदंड
4 पोर्ट एस मापदंड का उपयोग 4 पोर्ट नेटवर्क की विशेषता के लिए किया जाता है। इनमें नेटवर्क के 4 पोर्ट के बीच परावर्तित और आपतित विद्युत तरंगों के बारे में जानकारी शामिल होती है।
ये आपस में जुड़े हुए ट्रांसमिशन लाइन के जोड़ों का विश्लेषण करने के लिए सामान्यतः उपयोग होते हैं, जिससे यह निर्धारित किया जा सके कि उन्हें दो अलग-अलग संकेत एंडेड सकेत द्वारा प्रेरित किया जाता है या उन पर प्रेरित अंतरीय संकेत के प्रतिबिंबित और घटनायन शक्ति का मापन किया जा सकता है। उच्च गति के अंतरीय संकेत के कई विनिर्देश चैनलों की विशेषताएं 4-पोर्ट एस-पैरामीटर्स के माध्यम से परिभाषित करती हैं, जैसे कि 10-गिगाबिट अटैचमेंट यूनिट इंटरफेस (एक्सएयूआई),सैटा,पीसीआई-एक्स और इन्फिनीबैंड प्रणाली।
4-पोर्ट मिश्रित-मोड एस-मापदंड
4-पोर्ट मिश्रित-मोड एस-मापदंड सामान्य मोड और अंतरीय प्रोत्साहन संकेतों के लिए नेटवर्क की प्रतिक्रिया के संदर्भ में 4-पोर्ट नेटवर्क की विशेषता बताते हैं। निम्न तालिका 4-पोर्ट मिश्रित-मोड एस-मापदंड प्रदर्शित करती है।
| उद्दीपन | ||||||
|---|---|---|---|---|---|---|
| अवकल | सामान्य मोड | |||||
| Port 1 | Port 2 | Port 1 | Port 2 | |||
| प्रतिक्रिया | अवकल | SDD11 | SDD12 | SDC11 | SDC12 | |
| Port 2 | SDD21 | SDD22 | SDC21 | SDC22 | ||
| सामान्य मोड | SCD11 | SCD12 | SCC11 | SCC12 | ||
| Port 2 | SCD21 | SCD22 | SCC21 | SCC22 | ||
SXYab मापदंड नोटेशन का प्रारूप ध्यान दें, जहां "S" स्कैटरिंग मापदंड या एस-मापदंड को दर्शाता है, "X" प्रतिक्रिया मोड होता है, "Y" प्रेरण मोड होता है, "a" प्रतिक्रिया (आउटपुट) पोर्ट होता है और "b" प्रेरण (इनपुट) पोर्ट होता है। यह स्कैटरिंग पैरामीटर्स के लिए प्रामाणिक नामकरण है।
पहले चतुर्भुज को परीक्षण के अंतर्गत डिवाइस के अंतरीय उत्तेजना और अंतरीय प्रतिक्रिया विशेषताओं का वर्णन करने वाले ऊपरी बाएं 4 मापदंड के रूप में परिभाषित किया गया है। यह अधिकांश हाई-स्पीड अंतरीय इंटरकनेक्ट्स के लिए ऑपरेशन का वास्तविक तरीका है और यह क्वाड्रंट है जिस पर सबसे अधिक ध्यान दिया जाता है। इसमें इनपुट अंतरीय पुनरावृत्ति हानि (एसडीडी11), इनपुट अंतरीय इंसर्शन लॉस (एसडीडी21), आउटपुट आंतरिक पुनरावृत्ति हानि (एसडीडी22) और आउटपुट अंतरीय हानि (एसडीडी12) सम्मिलित हैं। अंतरीय संकेत प्रोसेसिंग के कुछ लाभ हैं;
- कम विद्युत चुम्बकीय हस्तक्षेप संवेदनशीलता
- संतुलित अंतरीय परिपथ से विद्युत चुम्बकीय विकिरण में कमी
- यहां तक कि ऑर्डर अंतरीय विरूपण उत्पाद सामान्य मोड संकेत में बदल जाते हैं
- संकेत -एंडेड के सापेक्ष वोल्टेज स्तर में दो वृद्धि का कारक
- सामान्य मोड आपूर्ति और भूमि के शोर के प्रतिरोध और डिफरेंशियल सिग्नल पर भूमि शोर का कूट लेखन अस्वीकार है।
दूसरा और तीसरा चतुर्भुज क्रमशः ऊपरी दाएँ और निचले बाएँ 4 मापदंड हैं। इन्हें क्रॉस-मोड क्वाड्रंट भी कहा जाता है। ऐसा इसलिए है क्योंकि वे परीक्षण के अंतर्गत डिवाइस में होने वाले किसी भी मोड रूपांतरण को पूरी तरह से चिह्नित करते हैं, चाहे वह कॉमन-टू-अंतरीय एसडीकैब रूपांतरण (इच्छित अंतरीय संकेत एसडीडी ट्रांसमिशन एप्लिकेशन के लिए ईएमआई संवेदनशीलता) या अंतरीय -टू-कॉमन एससीडीएबी रूपांतरण हो। गीगाबिट डेटा थ्रूपुट के लिए इंटरकनेक्ट के डिज़ाइन को अनुकूलित करने का प्रयास करते समय मोड रूपांतरण को समझना बहुत सहायक होता है।
चौथा चतुर्भुज निचला दायां 4 मापदंड है और परीक्षण के अंतर्गत डिवाइस के माध्यम से प्रचार करने वाले सामान्य-मोड संकेत एससीसीएबी की प्रदर्शन विशेषताओं का वर्णन करता है। ठीक से प्रारूप किए गए एसडीडीएबी अंतरीय डिवाइस के लिए न्यूनतम सामान्य-मोड आउटपुट एससीसीएबी होना चाहिए। यद्यपि, चौथा चतुर्थांश सामान्य-मोड प्रतिक्रिया डेटा सामान्य-मोड संचरण प्रतिक्रिया का एक उपाय है और नेटवर्क सामान्य-मोड अस्वीकृति को निर्धारित करने के लिए अंतरीय संचरण प्रतिक्रिया के अनुपात में उपयोग किया जाता है। यह कॉमन मोड अस्वीकारअंतरीय संकेत प्रोसेसिंग का एक महत्वपूर्ण लाभ है और इसे कुछ अंतरीय परिपथ कार्यान्वयन में घटाकर एक किया जा सकता है।[15][16]
प्रवर्धक प्रारूप में एस-मापदंड
एक प्रवर्धक में विपरीत वियोजन मापदंड इसके इनपुट से आउटपुट तक वापसी से प्रतिक्रिया के स्तर को निर्धारित करता है और इसलिए उसकी स्थिरता पर प्रभाव डालता हैसाथ ही, आगे की गुणवत्ता के साथ इनपुट और आउटपुट पोर्ट से पूर्णतः अलग होने वाले एक ऐंप्लीफायर में अविशीष्ट स्केलर लॉग मैग्नीचर वियोजन होगा या शून्य होगा। का रेखीय मात्रा शून्य होगा। ऐसे एक प्रवर्धक को अनवर्ती कहा जाता है। हालांकि, अधिकांश व्यावहारिक प्रवर्धक में कुछ निर्दिष्ट वियोजन होगी, जिसके कारण इनपुट पर 'देखा जाने वाला' प्रतिबिंब प्रतिरोधक आउटपुट पर जुड़े लोड के कुछ हद तक प्रभावित हो सकता है। की सबसे छोटी मान्यता वाले एक प्रवर्धक को आमतौर पर एक बफर प्रवर्धक कहा जाता है।
यदि एक वास्तविक प्रवर्धक की आउटपुट पोर्ट को एक विचित्र समायोजन संकेतक, . वाले किसी भी लोड से जोड़ा जाता है। तो इनपुट पोर्ट पर देखे जाने वाले वास्तविक प्रतिबिंब संकेतक इसका निम्नानुसार होगा
- .
अगर प्रवर्धक एकतरफा है तो और या, इसे दूसरे तरीके से रखने के लिए, आउटपुट लोडिंग का इनपुट पर कोई प्रभाव नहीं पड़ता है।
एक समान संपत्ति विपरीत दिशा में उपस्थित है, इस विषय में यदि आउटपुट पोर्ट पर देखा जाने वाला प्रतिबिंब गुणांक है और इनपुट पोर्ट से जुड़े स्रोत का प्रतिबिंब गुणांक है।
एक प्रवर्धक के लिए बिना शर्त स्थिर होने के लिए पोर्ट लोडिंग की स्थिति
एक प्रवर्धक निःशर्त रूप से स्थिर होता है यदि किसी भी संकेतक या स्रोत को कनेक्ट करने से अस्थिरता नहीं होती है। यह शर्त उत्पन्न होती है अगर स्रोत, लोड और प्रवर्धक के इनपुट और आउटपुट पोर्टों के प्रतिबिंब संकेतकों के मात्राएँ समकालिक रूप से एक से कम हों। एक महत्वपूर्ण आवश्यकता जो अक्सर ध्यान में नहीं रखी जाती है, यह है कि प्रवर्धक एक रेखीय नेटवर्क होना चाहिए जिसमें दाहिने हाथ के समीकरण नहीं होते हैं। अस्थिरता प्रवर्धक के गेन फ्रीक्वेंसी प्रतिसाधन या चरम स्थिति में विक्षोभ के कारण गंभीर दिक्कत पैदा कर सकती है। इच्छित फ्रीक्वेंसी पर निःशर्त रूप से स्थिर होने के लिए, एक प्रवर्धक को निम्नलिखित 4 समीकरणों को समकालिक रूप से पूरा करना चाहिए::[17]
जब इन मूल्यों में से प्रत्येक एकता के बराबर होता है, तो सीमा की स्थिति को (जटिल) प्रतिबिंब गुणांक का प्रतिनिधित्व करने वाले ध्रुवीय आरेख पर खींचे गए एक चक्र द्वारा दर्शाया जा सकता है, एक इनपुट पोर्ट के लिए और दूसरा आउटपुट पोर्ट के लिए। प्रायः इन्हें स्मिथ चार्ट्स के रूप में स्केल किया जाएगा। प्रत्येक मामले में सर्कल केंद्र और संबंधित त्रिज्या के निर्देशांक निम्नलिखित समीकरणों द्वारा दिए गए हैं:
के लिए मान (आउटपुट स्थिरता चक्र)
RADIUS केंद्र
के लिए मान (इनपुट स्थिरता चक्र)
RADIUS केंद्र दोनों ही मामलों में
और सुपरस्क्रिप्ट तारा (*) एक जटिल संयुग्म को इंगित करता है।
इनमें से प्रत्येक मान यूनिटी के बराबर होने के लिए सीमा शर्त को एक परिपथ पर दर्शाया जा सकता है, जो प्रतिबिंब संकेतक को प्रतिष्ठित करने वाले दोनों पोर्टों के लिए दर्शाया जाएगा। प्रायः इन्हें स्मिथ चार्ट के रूप में स्केल किया जाता है। प्रत्येक मामले में, वृत्त के केंद्र और संबंधित त्रिज्या के संबंध में निम्नलिखित समीकरणों द्वारा निर्दिष्ट किए जाते हैं:
बिना शर्त स्थिरता की स्थिति तब प्राप्त होती है जब और
प्रकीर्णन स्थानान्तरण मापदंड
प्रकीर्णन ट्रांसफर मापदंड या 2-पोर्ट नेटवर्क के टी-मापदंड टी-मापदंड आव्यूह द्वारा व्यक्त किए जाते हैं और संबंधित एस-मापदंड आव्यूह से निकटता से संबंधित होते हैं। यद्यपि, एस मापदंड के विपरीत प्रणाली में टी मापदंड को मापने के लिए कोई सरल भौतिक साधन नहीं है, जिसे कभी-कभी यूला तरंगों के रूप में संदर्भित किया जाता है। टी-मापदंड आव्यूह घटना से संबंधित है और निम्नानुसार प्रत्येक पोर्ट पर सामान्यीकृत तरंगें परिलक्षित होती हैं:
यद्यपि, उन्हें निम्नानुसार परिभाषित किया जा सकता है:
मैटलैबमें आरएफ टूलबॉक्स ऐड-ऑन[18] और कई किताबें इस अंतिम परिभाषा का प्रयोग करें, इसलिए सावधानी आवश्यक है। इस लेख में "S से T तक" और "T से S तक" अनुच्छेद पहली परिभाषा पर आधारित हैं। दूसरी परिभाषा में अनुकूलन आसान है दूसरी परिभाषा के लिए अनुकूलन तुच्छ है (इंटरचेंजिंग टी11 टी के लिए22, और टी12 टी के लिए21). एस-मापदंड की तुलना में टी-मापदंड का लाभ यह है कि संदर्भ प्रतिबाधा प्रदान करना विशुद्ध रूप से, वास्तविक या जटिल संयुग्म है, T-पैरामीटरों की तुलना में एस-पैरामीटरों के लाभ यह हैं कि संदर्भ आवश्यकियों के केवल वास्तविक या सम्पूर्ण संयोजक होने की व्यवस्था करते हैं, तो इन्हें सीधे तरीके से उपयोग किया जा सकता है उनका उपयोग 2 या अधिक 2-पोर्ट नेटवर्क को कैस्केडिंग के प्रभाव को आसानी से निर्धारित करने के लिए किया जा सकता है, बस संबंधित व्यक्तिगत टी को गुणा करके मापदंड आव्यूह यदि टी-मापदंड कहते हैं कि तीन अलग-अलग 2-पोर्ट नेटवर्क 1, 2 और 3 हैं , और क्रमशः तीनों नेटवर्क के कैस्केड के लिए टी-मापदंड आव्यूह () क्रम में क्रम द्वारा दिया गया है:
ध्यान दें कि आव्यूह गुणन क्रमविनिमेय नहीं है, इसलिए क्रम महत्वपूर्ण है। एस-मापदंड के साथ, टी-मापदंड जटिल मान हैं और दो प्रकारों के बीच सीधा रूपांतरण होता है। यद्यपि कैस्केडेड टी-मापदंड व्यक्तिगत टी-मापदंड का एक सरल आव्यूह गुणन है, प्रत्येक नेटवर्क के एस-मापदंड के लिए संबंधित टी-मापदंड में रूपांतरण और कैस्केड टी-मापदंड का समतुल्य कैस्केड एस-मापदंड में रूपांतरण, जो आमतौर पर आवश्यक होते हैं, तुच्छ नहीं होते हैं। यद्यपि एक बार ऑपरेशन पूरा हो जाने के बाद, दोनों दिशाओं में सभी पोर्टो के बीच जटिल फुल वेव इंटरैक्शन को ध्यान में रखा जाएगा। निम्नलिखित समीकरण 2-पोर्ट नेटवर्क के लिए एस और टी मापदंड के बीच रूपांतरण प्रदान करेंगे।[19]:
जहाँ आव्यूह के निर्धारक को इंगित करता है ,
- .
टी से एस
जहाँ आव्यूह के निर्धारक को इंगित करता है .
1-पोर्ट एस-मापदंड
एक 1-पोर्ट नेटवर्क के लिए एस-पैरामीटर एक सरल 1 × 1 आव्यूह के रूप में दिया जाता है यहां n आवंटित पोर्ट नंबर होता है। एस-पैरामीटर परिभाषा के अनुसार रेखांकन के साथ मेल खाने के लिए इसे साधारणतः किसी प्रकार का पैसिव लोड होता है। एक एंटीना एक सामान्य एक-पोर्ट नेटवर्क है जिसके लिए के छोटे मान इसका संकेत करते हैं कि एंटीना ऊर्जा को या तो छोड़ेगी या ऊर्जा को संगृहीत करेगी।
असमान पोर्टों के लिए उच्चतर क्रम के एस-मापदंड (), जहां की तरह 2-पोर्ट नेटवर्क के लिए प्राप्त किए जा सकते हैं, इसके लिए पोर्टों के जोड़ों को एक-दूसरे के साथ मिलाकर विचार करना होगा, प्रत्येक मामले में सुनिश्चित करेंगे कि बचे हुए (अप्रयोगित) पोर्टप्रणाली की आपेक्षिक विपणनयां वाले आवेशिता से लोड होते हैं। इस तरीके से प्रत्येक अप्रयुक्त पोर्ट के लिए प्रवेश ऊर्जा शून्य हो जाती है, जिससे 2-पोर्ट मामले के लिए प्राप्त व्यक्तियों के समान अभिव्यक्तियां प्राप्त होती हैं। केवल एकल पोर्टों के संबंधित S-पैरामीटर के लिए प्रणाली आपेक्षित विपणनयां वाले बचे हुए पोर्टों को आवेशित करना आवश्यक होता है, जिससे इन व्यापारों की प्रवेश ऊर्जा शून्य हो जाती है, केवल उस पोर्ट के लिए उन्नति के लिए जिस पर विचार किया जा रहा है। सामान्यतः इसलिए हमारे पास निम्नलिखित होता है:
( और
उदाहरण के लिए, एक 3-पोर्ट नेटवर्क जैसे 2-वे विभाजक में निम्नलिखित एस-मापदंड परिभाषाएँ होंगी
साथ
- ; ;
- ; ;
- ; ;
जहाँ पोर्ट n पर घटना तरंग द्वारा प्रेरित पोर्ट m पर आउटगोइंग वेव को संदर्भित करता है।
==एस-मापदंड का मापन
एस-मापदंड को सामान्यतः एक नेटवर्क विश्लेषक वीएनए) से मापा जाता है।
मापा और सही एस-मापदंड डेटा का आउटपुट स्वरूप
एस-मापदंड परीक्षण डेटा कई वैकल्पिक स्वरूपों में प्रदान किया जा सकता है, उदाहरण के लिए: सूची, ग्राफिकल (स्मिथ चार्ट या जटिल विमान )।
सूची प्रारूप
सूची प्रारूप में मापित और सुधारित एस-मापदंड तालिका फ्रीक्वेंसी के विरुद्ध सारणीबद्ध किए जाते हैं। सबसे सामान्य तालिका प्रारूप को मापदंडया एसएनपी के रूप में जाना जाता है, जहां N पोर्ट की संख्या होती है। इस जानकारी को संबंधित पाठ फ़ाइल में संग्रहीत किया जाता है जिसका फ़ाइल नाम एक्सटेंशन '.s2p' होता है। निम्नलिखित उदाहरण में दिखाया गया है कि एक उपकरण के लिए प्राप्त पूर्ण 2-पोर्ट S-पैरामीटर डेटा के लिए एक:
! शुक्र 21 जुलाई, 14:28:50 2005 को बनाया गया # एमएचजेड एस डीबी आर 50 ! SP1.SP 50 -15.4 100.2 10.2 173.5 -30.1 9.6 -13.4 57.2 51 -15.8 103.2 10.7 177.4 -33.1 9.6 -12.4 63.4 52 -15.9 105.5 11.2 179.1 -35.7 9.6 -14.4 66.9 53 -16.4 107.0 10.5 183.1 -36.6 9.6 -14.7 70.3 54 -16.6 109.3 10.6 187.8 -38.1 9.6 -15.3 71.4
विस्मयादिबोधक चिह्न से प्रारंभ होने वाली पंक्तियों में केवल टिप्पणियाँ होती हैं। हैश प्रतीक के साथ प्रारंभ होने वाली पंक्ति को संकेत करती है कि इस स्थिति में आवृत्तियाँ मेगाहर्ट्ज़ में, S-मापदंड सूचीबद्ध हैं (S), परिमाण डीबी लॉग परिमाण (डीबी) में हैं और प्रणाली प्रतिबाधा 50 ओम (R 50) है। डेटा के 9 कॉलम हैं। इस मामले में कॉलम 1 मेगाहर्ट्ज़ में परीक्षण आवृत्ति है। कॉलम 2, 4, 6 और 8 के परिमाण हैं , , और क्रमशः डीबी में। कॉलम 3, 5, 7 और 9 के कोण हैं , , और क्रमशः डिग्री में।
ग्राफिकल (स्मिथ चार्ट)
किसी भी 2-पोर्ट एस-मापदंड को स्मिथ चार्ट पर ध्रुवीय निर्देशांक का उपयोग करके प्रदर्शित किया जा सकता है, परंतु सबसे सार्थक होगा और चूँकि इनमें से किसी को भीप्रणाली इम्पीडेंस के लिए उपयुक्त विशेषता स्मिथ चार्ट इम्पीडेंस (या प्रवेश) स्केलिंग का उपयोग करके सीधे समकक्ष सामान्यीकृत प्रतिबाधा (या प्रवेश) में परिवर्तित किया जा सकता है।
ग्राफिकल (ध्रुवीय आरेख)
किसी भी 2-पोर्ट एस-मापदंड को ध्रुवीय निर्देशांक का उपयोग करके ध्रुवीय आरेख पर प्रदर्शित किया जा सकता है।
या तो ग्राफिकल प्रारूप में एक विशेष परीक्षण आवृत्ति पर प्रत्येक एस-मापदंड को डॉट के रूप में प्रदर्शित किया जाता है। यदि माप कई आवृत्तियों में एक स्वीप है तो प्रत्येक के लिए एक डॉट दिखाई देगा।
एक-पोर्ट नेटवर्क के एस-मापदंड को मापना
केवल एक पोर्ट वाले नेटवर्क के लिए एस-मापदंड आव्यूह के रूप में केवल एक तत्व का प्रतिनिधित्व किया जाएगा , जहां n पोर्ट को आवंटित संख्या है। अधिकांश वीएनए समय बचाने के लिए एक पोर्ट माप के लिए एक सरल एक-पोर्ट अंशांकन क्षमता प्रदान करते हैं यदि वह सब आवश्यक है।
2 से अधिक पोर्टो वाले नेटवर्क के एस-मापदंड को मापना
दो से अधिक पोर्टो वाले नेटवर्क के एस-मापदंड के एक साथ माप के लिए प्रारूप किए गए वीएनए संभव हैं, परंतु जल्दी ही निषेधात्मक रूप से जटिल और महंगे हो जाते हैं। सामान्यतः उनकी खरीद उचित नहीं होती है क्योंकि अतिरिक्त माप के साथ मानक 2-पोर्ट कैलिब्रेटेड वीएनए का उपयोग करके प्राप्त परिणामों की सही व्याख्या के बाद आवश्यक माप प्राप्त किया जा सकता है। आवश्यक एस-मापदंड आव्यूह को चरणों में क्रमिक दो पोर्ट मापों से इकट्ठा किया जा सकता है, एक समय में दो पोर्ट, प्रत्येक अवसर पर अप्रयुक्त पोर्ट्स कोप्रणाली प्रतिबाधा के बराबर उच्च गुणवत्ता भार में समाप्त किया जा सकता है। इस दृष्टिकोण का एक जोखिम यह है कि लोड का पुनरावृत्ति हानि या वीएसडब्ल्यूआर स्वयं को उपयुक्त रूप से निर्दिष्ट किया जाना चाहिए, जितना संभव हो उतना करीब 50 ओम, या जो भी नाममात्र प्रणाली प्रतिबाधा है। कई पोर्टो वाले नेटवर्क के लिए लागत के आधार पर भार के वीएसडब्ल्यूआर को अपर्याप्त रूप से निर्दिष्ट करने का प्रलोभन हो सकता है। लोड का सबसे अयोग्य स्वीकार्य वीएसडब्ल्यूआर क्या होगा, यह निर्धारित करने के लिए कुछ विश्लेषण आवश्यक होगा।
यह मानते हुए कि अतिरिक्त भार को पर्याप्त रूप से निर्दिष्ट किया गया है, यदि आवश्यक हो, तो दो या अधिक एस-मापदंड सबस्क्रिप्ट को वीएनए से संबंधित उन लोगों से संशोधित किया जाता है जो परीक्षण के अंतर्गत नेटवर्क से संबंधित हैं । उदाहरण के लिए, यदि DUT में 5 पोर्ट हैं और एक दो वीएनए पोर्ट 1 से डीयूटी पोर्ट 3 और वीएनए पोर्ट 2 से डीयूटी पोर्ट 5 से जुड़ा है, तो मापा गया वीएनए परिणाम (, , और ) के बराबर होगा , , और क्रमशः, यह मानते हुए कि डीयूटी पोर्ट 1, 2 और 4 को पर्याप्त 50 ओम भार में समाप्त कर दिया गया था। यह आवश्यक 25 एस-मापदंड में से 4 प्रदान करेगा।
यह भी देखें
- प्रवेश मापदंड
- प्रतिबाधा मापदंड
- दो-पोर्ट नेटवर्क
- एक्स-मानकों, S-मापदंड का एक गैर-रैखिक सुपरसेट
- बेलेविच की प्रमेय
संदर्भ
- ↑ Pozar, David M. (2005); Microwave Engineering, Third Edition (Intl. Ed.); John Wiley & Sons, Inc.; pp. 170–174. ISBN 0-471-44878-8.
- ↑ Pozar, David M. (2005) (op. cit.); pp. 170–174.
- ↑ Pozar, David M. (2005) (op. cit.); pp. 183–186.
- ↑ Morton, A. H. (1985); Advanced Electrical Engineering; Pitman Publishing Ltd.; pp. 33–72. ISBN 0-273-40172-6.
- ↑ Belevitch, Vitold "Summary of the history of circuit theory", Proceedings of the IRE, vol.50, iss.5, pp. 848–855, May 1962.
Vandewalle, Joos "In memoriam – Vitold Belevitch", International Journal of Circuit Theory and Applications, vol.28, iss.5, pp. 429–430, September/October 2000. doi:10.1002/1097-007X(200009/10)28:5<429::AID-CTA121>3.0.CO;2-6 - ↑ Valkenburg, Mac Elwyn Van Circuit Theory: Foundations and Classical Contributions, p.334, Stroudsburg, Pennsylvania: Dowden, Hutchinson & Ross, 1974 ISBN 0-87933-084-8.
- ↑ Dicke R. H. (1947). "माइक्रोवेव नेटवर्क के लिए लागू एक कम्प्यूटेशनल विधि". Journal of Applied Physics. 18 (10): 873–878. Bibcode:1947JAP....18..873D. doi:10.1063/1.1697561.
- ↑ Pozar, David M. (2005) (op. cit.); p. 170.
- ↑ Morton, A. H. (1985) (op. cit.); p. 33.
- ↑ Kurokawa, K., "Power Waves and the Scattering Matrix", IEEE Trans. Micr. Theory & Tech., Mar. 1965, pp. 194–202
- ↑ Pozar, David M. (2005) (op. cit.); p. 173.
- ↑ S-Parameter Design; Application Note AN 154; Agilent Technologies; p 7
- ↑ Collin, Robert E.; Foundations For Microwave Engineering, Second Edition
- ↑ Trevor S. Bird, "Definition and Misuse of Return Loss", IEEE Antennas & Propagation Magazine, vol.51, iss.2, pp.166–167, April 2009.
- ↑ Backplane Channels and Correlation Between Their Frequency and Time Domain Performance.
- ↑ Bockelman, DE; Eisenstadt, WR (July 1995). "Combined differential and common-mode scattering parameters: theory and simulation". IEEE Transactions. 43 (7): 1530–1539. doi:10.1109/22.392911.
- ↑ Gonzalez, Guillermo (op. cit.); pp 217–222
- ↑ "RF Toolbox documentation".
- ↑ S-Parameter Design; Application Note AN 154; Agilent Technologies; p 14
ग्रन्थसूची
- Guillermo Gonzalez, "Microwave Transistor Amplifiers, Analysis and Design, 2nd. Ed.", Prentice Hall, New Jersey; ISBN 0-13-581646-7
- David M. Pozar, "Microwave Engineering", Third Edition, John Wiley & Sons Inc.; ISBN 0-471-17096-8
- William Eisenstadt, Bob Stengel, and Bruce Thompson, "Microwave Differential Circuit Design using Mixed-Mode S-Parameters", Artech House; ISBN 1-58053-933-5; ISBN 978-1-58053-933-3
- "S-Parameter Design", Application Note AN 154, Keysight Technologies
- "S-Parameter Techniques for Faster, More Accurate Network Design", Application Note AN 95-1, Keysight Technologies, PDF slides plus QuickTime video or scan of Richard W. Anderson's original article
- A. J. Baden Fuller, "An Introduction to Microwave Theory and Techniques, Second Edition, Pergammon International Library; ISBN 0-08-024227-8
- Ramo, Whinnery and Van Duzer, "Fields and Waves in Communications Electronics", John Wiley & Sons; ISBN 0-471-70721-X
- C. W. Davidson, "Transmission Lines for Communications with CAD Programs", Second Edition, Macmillan Education Ltd.; ISBN 0-333-47398-1