आंशिक मोलर गुण: Difference between revisions
mNo edit summary |
No edit summary |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Change in a property of a mixture component with respect to amount}} | {{short description|Change in a property of a mixture component with respect to amount}}[[ऊष्मप्रवैगिकी]] में, एक आंशिक मोलर गुण एक मात्रा है जो निरंतर तापमान और दबाव पर मिश्रण की मोलर संरचना में परिवर्तन के साथ एक विलयन या मिश्रण की व्यापक गुणों की भिन्नता का वर्णन करती है। यह ब्याज के घटक की राशि (मोल्स की संख्या) के संबंध में विस्तृत संपत्ति का आंशिक व्युत्पन्न है। किसी मिश्रण के प्रत्येक विस्तृत गुण का संगत आंशिक मोलर गुण होता है। | ||
[[ऊष्मप्रवैगिकी]] में, एक आंशिक | |||
== परिभाषा == | == परिभाषा == | ||
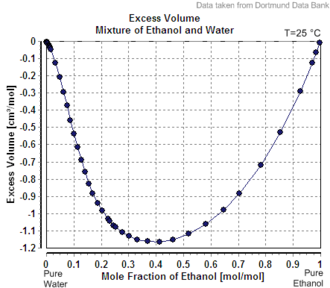
[[File:Excess Volume Mixture of Ethanol and Water.png|thumb|right|मिश्रित होने पर | [[File:Excess Volume Mixture of Ethanol and Water.png|thumb|right|मिश्रित होने पर जल और इथेनॉल में हमेशा ऋणात्मक अतिरिक्त मात्रा होती है, यह दर्शाता है कि शुद्ध होने पर इसकी मोलर की मात्रा की तुलना में मिश्रित होने पर प्रत्येक घटक की आंशिक मोलर मात्रा कम होती है।]]आंशिक मोलर आयतन को मोटे तौर पर उस योगदान के रूप में समझा जाता है जो मिश्रण का एक घटक विलयन के समग्र आयतन में बनाता है। यद्यपि, इसके अलावा भी बहुत कुछ है: | ||
जब 25 °C पर | जब 25 °C पर जल की एक बड़ी मात्रा में एक मोल जल मिलाया जाता है, तो आयतन 18 सेमी3 बढ़ जाता है। इस प्रकार शुद्ध जल का मोलर आयतन 18 cm3 mol<sup>-<sup>1 <big>बताया जाएगा। यद्यपि, शुद्ध इथेनॉल की एक बड़ी मात्रा में एक मोल जल मिलाने से केवल 14 सेमी<sup>3 की मात्रा में वृद्धि होती है। वृद्धि के भिन्न होने का कारण यह है कि जल के अणुओं की एक निश्चित संख्या द्वारा घेरा गया आयतन आसपास के अणुओं की पहचान पर निर्भर करता है। मान14 सेमी<sup>3</big> <sup><sup><big><sup>को इथेनॉल में जल का आंशिक मोलर आयतन कहा जाता है।</big> | ||
सामान्य तौर पर, किसी मिश्रण में पदार्थ X का आंशिक मोलर आयतन, मिश्रण में जोड़े गए X के प्रति मोल आयतन में परिवर्तन होता है। | सामान्य तौर पर, किसी मिश्रण में पदार्थ X का आंशिक मोलर आयतन, मिश्रण में जोड़े गए X के प्रति मोल आयतन में परिवर्तन होता है। | ||
मिश्रण के घटकों के आंशिक | मिश्रण के घटकों के आंशिक मोलर की मात्रा मिश्रण की संरचना के साथ भिन्न होती है, क्योंकि मिश्रण में अणुओं का वातावरण संरचना के साथ बदलता है। यह बदलता हुआ आणविक वातावरण है (और अणुओं के बीच परस्पर क्रियाओं का परिणामी परिवर्तन) जिसके परिणामस्वरूप मिश्रण के ऊष्मप्रवैगिकी गुणों में परिवर्तन होता है क्योंकि इसकी संरचना बदल जाती है। | ||
अगर, द्वारा <math>Z</math>, एक मिश्रण की एक सामान्य व्यापक संपत्ति को दर्शाता है, यह हमेशा सच होगा कि यह [[दबाव]] पर निर्भर करता है (<math>P</math>), [[तापमान]] (<math>T</math>), और मिश्रण के प्रत्येक घटक की मात्रा (मोल | अगर, द्वारा <math>Z</math>, एक मिश्रण की एक सामान्य व्यापक संपत्ति को दर्शाता है, यह हमेशा सच होगा कि यह [[दबाव]] पर निर्भर करता है (<math>P</math>), [[तापमान]] (<math>T</math>), और मिश्रण के प्रत्येक घटक की मात्रा (मोल में मापा गया, N) में मापा जाता है। क्यू घटकों वाले मिश्रण के लिए, इसे इस रूप में व्यक्त किया जाता है | ||
:<math>Z=Z(T,P,n_1,n_2,\cdots,n_q).</math> | :<math>Z=Z(T,P,n_1,n_2,\cdots,n_q).</math> | ||
अब यदि तापमान T और दबाव P को स्थिर रखा जाए, <math>Z=Z(n_1,n_2,\cdots)</math> डिग्री 1 का एक सजातीय कार्य है, क्योंकि मिश्रण में प्रत्येक घटक की मात्रा को दोगुना करने से दोगुनी हो जाएगी <math>Z</math>. अधिक | अब यदि तापमान T और दबाव P को स्थिर रखा जाए, <math>Z=Z(n_1,n_2,\cdots)</math> डिग्री 1 का एक सजातीय कार्य है, क्योंकि मिश्रण में प्रत्येक घटक की मात्रा को दोगुना करने से दोगुनी हो जाएगी <math>Z</math>. अधिक सामान्यतः, किसी के लिए <math>\lambda</math>: | ||
:<math>Z(\lambda n_1,\lambda n_2, \cdots,\lambda n_q)=\lambda Z(n_1,n_2,\cdots,n_q).</math> | :<math>Z(\lambda n_1,\lambda n_2, \cdots,\lambda n_q)=\lambda Z(n_1,n_2,\cdots,n_q).</math> | ||
सजातीय फलन के लिए यूलर की प्रारंभिक प्रमेय, इसका तात्पर्य है<ref>[http://mathworld.wolfram.com/EulersHomogeneousFunctionTheorem.html Wolfram Mathworld: Euler's homogeneous function theorem]</ref> | |||
:<math>Z=\sum _{i=1}^q n_i \bar{Z_i},</math> | :<math>Z=\sum _{i=1}^q n_i \bar{Z_i},</math> | ||
जहाँ <math>\bar{Z_i}</math> आंशिक मोलर है <math>Z</math> घटक का <math>i</math> के रूप में परिभाषित: | |||
:<math>\bar{Z_i}=\left( \frac{\partial Z}{\partial n_i} \right)_{T,P,n_{j\neq i}}.</math> | :<math>\bar{Z_i}=\left( \frac{\partial Z}{\partial n_i} \right)_{T,P,n_{j\neq i}}.</math> | ||
सजातीय फलन के लिए यूलर की दूसरी प्रमेय, <math>\bar{Z_i}</math> डिग्री 0 का एक सजातीय कार्य है ((अर्थात, <math>\bar{Z_i}</math>एक गहन संपत्ति है) जिसका अर्थ है कि किसी के लिए <math>\lambda </math>: | |||
:<math>\bar{Z_i}(\lambda n_1,\lambda n_2,\cdots ,\lambda n_q)=\bar{Z_i}(n_1,n_2,\cdots,n_q).</math> | :<math>\bar{Z_i}(\lambda n_1,\lambda n_2,\cdots ,\lambda n_q)=\bar{Z_i}(n_1,n_2,\cdots,n_q).</math> | ||
विशेष रूप से, लेना <math>\lambda = 1/n_T</math> | विशेष रूप से, लेना <math>\lambda = 1/n_T</math> जहाँ <math>n_T=n_1+n_2+ \cdots </math>, किसी के पास | ||
:<math>\bar{Z_i}(x_1,x_2, \cdots )=\bar{Z_i}(n_1,n_2,\cdots),</math> | :<math>\bar{Z_i}(x_1,x_2, \cdots )=\bar{Z_i}(n_1,n_2,\cdots),</math> | ||
जहाँ <math>x_i=\frac{n_i}{n_T}</math> घटक के मोल अंश के रूप में व्यक्त की जाने वाली सांद्रता है <math>i</math>.चूंकि मोलर अंश संबंध को संतुष्ट करते हैं | |||
चूंकि | |||
:<math>\sum _{i=1}^q x_i = 1,</math> | :<math>\sum _{i=1}^q x_i = 1,</math> | ||
x<sub>i</sub>स्वतंत्र नहीं हैं, और आंशिक मोलर गुण केवल का एक फलन है <math>q-1</math> मोल अंश: | |||
:<math>\bar{Z_i}=\bar{Z_i}(x_1,x_2, \cdots , x_{q-1}).</math> | :<math>\bar{Z_i}=\bar{Z_i}(x_1,x_2, \cdots , x_{q-1}).</math> | ||
इस प्रकार आंशिक मोलर गुण एक गहन संपत्ति है - यह प्रणाली के आकार पर निर्भर नहीं करती है। | |||
आंशिक आयतन आंशिक मोलर आयतन नहीं है। | आंशिक आयतन आंशिक मोलर आयतन नहीं है। | ||
| Line 43: | Line 39: | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
आंशिक | आंशिक मोलर गुण उपयोगी होते हैं क्योंकि रासायनिक मिश्रण प्रायः स्थिर तापमान और दबाव पर बनाए रखा जाता है और इन स्थितियों के तहत, किसी भी व्यापक संपत्ति का मूल्य उसके आंशिक मोलर गुण से प्राप्त किया जा सकता है। वे विशेष रूप से तब उपयोगी होते हैं जब [[शुद्ध पदार्थ|शुद्ध पदार्थों]] की [[विशिष्ट संपत्ति]] (अर्थात शुद्ध पदार्थ के एक मोल के गुण) और मिश्रण के गुणों (जैसे [[मिश्रण की गर्मी]] या [[मिश्रण की एन्ट्रापी]]) पर विचार किया जाता है। परिभाषा के अनुसार, मिश्रण के गुण शुद्ध पदार्थों के गुणों से संबंधित हैं: | ||
:<math>\Delta z^M=z-\sum_i x_iz^*_i.</math> | :<math>\Delta z^M=z-\sum_i x_iz^*_i.</math> | ||
यहाँ <math>*</math> एक शुद्ध पदार्थ को दर्शाता है, <math>M</math> मिश्रण संपत्ति, और <math>z</math> विचाराधीन विशिष्ट संपत्ति के अनुरूप है। आंशिक | यहाँ <math>*</math> एक शुद्ध पदार्थ को दर्शाता है, <math>M</math> मिश्रण संपत्ति, और <math>z</math> विचाराधीन विशिष्ट संपत्ति के अनुरूप है। आंशिक मोलर गुणों की परिभाषा से, | ||
:<math>z=\sum_i x_i \bar{Z_i},</math> | :<math>z=\sum_i x_i \bar{Z_i},</math> | ||
| Line 52: | Line 48: | ||
:<math>\Delta z^M=\sum_i x_i(\bar{Z_i}-z_i^*).</math> | :<math>\Delta z^M=\sum_i x_i(\bar{Z_i}-z_i^*).</math> | ||
तो आंशिक | तो आंशिक मोलर गुणों के ज्ञान से, एकल घटकों से मिश्रण के गुणों के विचलन की गणना की जा सकती है। | ||
== | == ऊष्मप्रवैगिकी क्षमता से संबंध == | ||
आंशिक | आंशिक मोलर गुण व्यापक गुणों के अनुरूप संबंधों को संतुष्ट करते हैं। [[आंतरिक ऊर्जा]] U, [[ तापीय धारिता ]] H, [[हेल्महोल्ट्ज़ मुक्त ऊर्जा]] A, और [[गिब्स मुक्त ऊर्जा]] G के लिए, निम्नलिखित धारण करते हैं: | ||
:<math>\bar{H_i}=\bar{U_i}+P\bar{V_i},</math> | :<math>\bar{H_i}=\bar{U_i}+P\bar{V_i},</math> | ||
:<math>\bar{A_i}=\bar{U_i}-T\bar{S_i},</math> | :<math>\bar{A_i}=\bar{U_i}-T\bar{S_i},</math> | ||
:<math>\bar{G_i}=\bar{H_i}-T\bar{S_i},</math> | :<math>\bar{G_i}=\bar{H_i}-T\bar{S_i},</math> | ||
जहाँ <math>P</math> दबाव है, <math>V</math> [[आयतन]], <math>T</math> तापमान, और <math>S</math> [[एन्ट्रापी]]। | |||
== | == ऊष्मप्रवैगिकी क्षमता का विभेदक रूप == | ||
ऊष्मप्रवैगिकी क्षमता भी संतुष्ट करती है | |||
:<math>dU= TdS-PdV+\sum_i \mu_i dn_i,\,</math> | :<math>dU= TdS-PdV+\sum_i \mu_i dn_i,\,</math> | ||
| Line 71: | Line 67: | ||
:<math>dA=-SdT-PdV+\sum_i \mu_i dn_i,\,</math> | :<math>dA=-SdT-PdV+\sum_i \mu_i dn_i,\,</math> | ||
:<math>dG=-SdT+VdP+\sum_i \mu_i dn_i,\,</math> | :<math>dG=-SdT+VdP+\sum_i \mu_i dn_i,\,</math> | ||
जहाँ <math>\mu_i</math> [[रासायनिक क्षमता]] के रूप में परिभाषित किया गया है (j≠i के साथ निरंतर n<sub>j</sub> के लिए): | |||
:<math>\mu_i=\left( \frac{\partial U}{\partial n_i}\right)_{S,V}=\left( \frac{\partial H}{\partial n_i}\right)_{S,P}=\left( \frac{\partial A}{\partial n_i}\right)_{T,V}=\left( \frac{\partial G}{\partial n_i}\right)_{T,P}.</math> | :<math>\mu_i=\left( \frac{\partial U}{\partial n_i}\right)_{S,V}=\left( \frac{\partial H}{\partial n_i}\right)_{S,P}=\left( \frac{\partial A}{\partial n_i}\right)_{T,V}=\left( \frac{\partial G}{\partial n_i}\right)_{T,P}.</math> | ||
यह अंतिम आंशिक व्युत्पन्न समान है <math>\bar{G_i}</math>, आंशिक | यह अंतिम आंशिक व्युत्पन्न के समान है <math>\bar{G_i}</math>, आंशिक मोलर गिब्स मुक्त ऊर्जा। इसका मतलब है कि आंशिक मोलर गिब्स मुक्त ऊर्जा और रासायनिक क्षमता, ऊष्मप्रवैगिकी और रसायन विज्ञान में सबसे महत्वपूर्ण गुणों में से एक, समान मात्रा में है। समदाब रेखीय प्रक्रिया (स्थिर P) और समतापीय प्रक्रिया (स्थिर T) स्थितियों के तहत, रासायनिक क्षमता का ज्ञान, <math>\mu_i(x_1,x_2,\cdots , x_m)</math>, मिश्रण की हर संपत्ति पैदा करता है क्योंकि वे गिब्स मुक्त ऊर्जा को पूरी तरह से निर्धारित करते हैं। | ||
==आंशिक | ==आंशिक मोलर गुण को मापना== | ||
आंशिक | आंशिक मोलर गुण को मापने के लिए <math>\bar{Z_1}</math> एक द्विआधारी विलयन के रूप में निरूपित शुद्ध घटक के साथ शुरू होता है <math>2</math> और पूरी प्रक्रिया के दौरान तापमान और दबाव को स्थिर रखते हुए, घटक के अतिसूक्ष्म हिस्से को जोड़ें <math>1</math>; माप प्रत्येक जोड़ के बाद <math>Z</math>। ब्याज की रचनाओं का नमूना लेने के बाद प्रायोगिक आंकड़े के लिए [[वक्र फिटिंग|वक्र]] फिट(उपयुक्त) किया जा सकता है। यह प्रकार्य होगा <math>Z(n_1)</math> के सम्बन्ध में विभेद करना <math>n_1</math> दे देंगे <math>\bar{Z_1}</math> <math>\bar{Z_2}</math> तब संबंध से प्राप्त किया जाता है: | ||
के सम्बन्ध में विभेद करना <math>n_1</math> दे देंगे <math>\bar{Z_1}</math> | |||
<math>\bar{Z_2}</math> तब संबंध से प्राप्त किया जाता है: | |||
:<math>Z=\bar{Z_1}n_1+\bar{Z_2}n_2.</math> | :<math>Z=\bar{Z_1}n_1+\bar{Z_2}n_2.</math> | ||
== स्पष्ट मोलर मात्रा से संबंध == | |||
आंशिक मोलर गुणों और स्पष्ट गुणों के बीच संबंध को स्पष्ट मात्रा और मोलिटी की परिभाषा से प्राप्त किया जा सकता है। | |||
== स्पष्ट | |||
आंशिक | |||
:<math>\bar{V_1}={}^\phi\tilde{V}_1 + b \frac{\partial {}^\phi\tilde{V}_1}{\partial b}.</math> | :<math>\bar{V_1}={}^\phi\tilde{V}_1 + b \frac{\partial {}^\phi\tilde{V}_1}{\partial b}.</math> | ||
यह संबंध बहुघटक मिश्रणों के लिए भी लागू होता है, बस इस मामले में सबस्क्रिप्ट i की आवश्यकता होती है। | यह संबंध बहुघटक मिश्रणों के लिए भी लागू होता है, बस इस मामले में उपलेख(सबस्क्रिप्ट) i की आवश्यकता होती है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[स्पष्ट दाढ़ संपत्ति]] | * [[स्पष्ट दाढ़ संपत्ति|स्पष्ट मोलर संपत्ति]] | ||
*[[आदर्श समाधान|आदर्श विलयन]] | *[[आदर्श समाधान|आदर्श विलयन]] | ||
* अतिरिक्त मोलर मात्रा | * अतिरिक्त मोलर मात्रा | ||
* [[आंशिक विशिष्ट मात्रा]] | * [[आंशिक विशिष्ट मात्रा]] | ||
* [[थर्मोडायनामिक गतिविधि]] | * [[थर्मोडायनामिक गतिविधि|ऊष्मप्रवैगिकी गतिविधि]] | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 114: | Line 106: | ||
*Lecture notes from the University of Arizona detailing [https://web.archive.org/web/20070607142802/http://www.chem.arizona.edu/~salzmanr/480a/480ants/mixpmqis/mixpmqis.html mixtures, partial molar quantities, and ideal solutions]<sup>[https://web.archive.org/web/20161104141817/http://cbc.arizona.edu/~salzmanr/480a/480ants/mixpmqis/mixpmqis.html <nowiki>[archive]</nowiki>]</sup> | *Lecture notes from the University of Arizona detailing [https://web.archive.org/web/20070607142802/http://www.chem.arizona.edu/~salzmanr/480a/480ants/mixpmqis/mixpmqis.html mixtures, partial molar quantities, and ideal solutions]<sup>[https://web.archive.org/web/20161104141817/http://cbc.arizona.edu/~salzmanr/480a/480ants/mixpmqis/mixpmqis.html <nowiki>[archive]</nowiki>]</sup> | ||
*[http://www.aim.env.uea.ac.uk/aim/density/density_electrolyte.php On-line calculator for densities and partial molar volumes of aqueous solutions of some common electrolytes and their mixtures, at temperatures up to 323.15 K.] | *[http://www.aim.env.uea.ac.uk/aim/density/density_electrolyte.php On-line calculator for densities and partial molar volumes of aqueous solutions of some common electrolytes and their mixtures, at temperatures up to 323.15 K.] | ||
[[Category:Created On 25/05/2023]] | [[Category:Created On 25/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:थर्मोडायनामिक गुण]] | |||
[[Category:भौतिक रसायन]] | |||
[[Category:रासायनिक ऊष्मप्रवैगिकी]] | |||
Latest revision as of 09:33, 28 June 2023
ऊष्मप्रवैगिकी में, एक आंशिक मोलर गुण एक मात्रा है जो निरंतर तापमान और दबाव पर मिश्रण की मोलर संरचना में परिवर्तन के साथ एक विलयन या मिश्रण की व्यापक गुणों की भिन्नता का वर्णन करती है। यह ब्याज के घटक की राशि (मोल्स की संख्या) के संबंध में विस्तृत संपत्ति का आंशिक व्युत्पन्न है। किसी मिश्रण के प्रत्येक विस्तृत गुण का संगत आंशिक मोलर गुण होता है।
परिभाषा
आंशिक मोलर आयतन को मोटे तौर पर उस योगदान के रूप में समझा जाता है जो मिश्रण का एक घटक विलयन के समग्र आयतन में बनाता है। यद्यपि, इसके अलावा भी बहुत कुछ है:
जब 25 °C पर जल की एक बड़ी मात्रा में एक मोल जल मिलाया जाता है, तो आयतन 18 सेमी3 बढ़ जाता है। इस प्रकार शुद्ध जल का मोलर आयतन 18 cm3 mol-1 बताया जाएगा। यद्यपि, शुद्ध इथेनॉल की एक बड़ी मात्रा में एक मोल जल मिलाने से केवल 14 सेमी3 की मात्रा में वृद्धि होती है। वृद्धि के भिन्न होने का कारण यह है कि जल के अणुओं की एक निश्चित संख्या द्वारा घेरा गया आयतन आसपास के अणुओं की पहचान पर निर्भर करता है। मान14 सेमी3 को इथेनॉल में जल का आंशिक मोलर आयतन कहा जाता है।
सामान्य तौर पर, किसी मिश्रण में पदार्थ X का आंशिक मोलर आयतन, मिश्रण में जोड़े गए X के प्रति मोल आयतन में परिवर्तन होता है।
मिश्रण के घटकों के आंशिक मोलर की मात्रा मिश्रण की संरचना के साथ भिन्न होती है, क्योंकि मिश्रण में अणुओं का वातावरण संरचना के साथ बदलता है। यह बदलता हुआ आणविक वातावरण है (और अणुओं के बीच परस्पर क्रियाओं का परिणामी परिवर्तन) जिसके परिणामस्वरूप मिश्रण के ऊष्मप्रवैगिकी गुणों में परिवर्तन होता है क्योंकि इसकी संरचना बदल जाती है।
अगर, द्वारा , एक मिश्रण की एक सामान्य व्यापक संपत्ति को दर्शाता है, यह हमेशा सच होगा कि यह दबाव पर निर्भर करता है (), तापमान (), और मिश्रण के प्रत्येक घटक की मात्रा (मोल में मापा गया, N) में मापा जाता है। क्यू घटकों वाले मिश्रण के लिए, इसे इस रूप में व्यक्त किया जाता है
अब यदि तापमान T और दबाव P को स्थिर रखा जाए, डिग्री 1 का एक सजातीय कार्य है, क्योंकि मिश्रण में प्रत्येक घटक की मात्रा को दोगुना करने से दोगुनी हो जाएगी . अधिक सामान्यतः, किसी के लिए :
सजातीय फलन के लिए यूलर की प्रारंभिक प्रमेय, इसका तात्पर्य है[1]
जहाँ आंशिक मोलर है घटक का के रूप में परिभाषित:
सजातीय फलन के लिए यूलर की दूसरी प्रमेय, डिग्री 0 का एक सजातीय कार्य है ((अर्थात, एक गहन संपत्ति है) जिसका अर्थ है कि किसी के लिए :
विशेष रूप से, लेना जहाँ , किसी के पास
जहाँ घटक के मोल अंश के रूप में व्यक्त की जाने वाली सांद्रता है .चूंकि मोलर अंश संबंध को संतुष्ट करते हैं
xiस्वतंत्र नहीं हैं, और आंशिक मोलर गुण केवल का एक फलन है मोल अंश:
इस प्रकार आंशिक मोलर गुण एक गहन संपत्ति है - यह प्रणाली के आकार पर निर्भर नहीं करती है।
आंशिक आयतन आंशिक मोलर आयतन नहीं है।
अनुप्रयोग
आंशिक मोलर गुण उपयोगी होते हैं क्योंकि रासायनिक मिश्रण प्रायः स्थिर तापमान और दबाव पर बनाए रखा जाता है और इन स्थितियों के तहत, किसी भी व्यापक संपत्ति का मूल्य उसके आंशिक मोलर गुण से प्राप्त किया जा सकता है। वे विशेष रूप से तब उपयोगी होते हैं जब शुद्ध पदार्थों की विशिष्ट संपत्ति (अर्थात शुद्ध पदार्थ के एक मोल के गुण) और मिश्रण के गुणों (जैसे मिश्रण की गर्मी या मिश्रण की एन्ट्रापी) पर विचार किया जाता है। परिभाषा के अनुसार, मिश्रण के गुण शुद्ध पदार्थों के गुणों से संबंधित हैं:
यहाँ एक शुद्ध पदार्थ को दर्शाता है, मिश्रण संपत्ति, और विचाराधीन विशिष्ट संपत्ति के अनुरूप है। आंशिक मोलर गुणों की परिभाषा से,
प्रतिस्थापन उपज:
तो आंशिक मोलर गुणों के ज्ञान से, एकल घटकों से मिश्रण के गुणों के विचलन की गणना की जा सकती है।
ऊष्मप्रवैगिकी क्षमता से संबंध
आंशिक मोलर गुण व्यापक गुणों के अनुरूप संबंधों को संतुष्ट करते हैं। आंतरिक ऊर्जा U, तापीय धारिता H, हेल्महोल्ट्ज़ मुक्त ऊर्जा A, और गिब्स मुक्त ऊर्जा G के लिए, निम्नलिखित धारण करते हैं:
जहाँ दबाव है, आयतन, तापमान, और एन्ट्रापी।
ऊष्मप्रवैगिकी क्षमता का विभेदक रूप
ऊष्मप्रवैगिकी क्षमता भी संतुष्ट करती है
जहाँ रासायनिक क्षमता के रूप में परिभाषित किया गया है (j≠i के साथ निरंतर nj के लिए):
यह अंतिम आंशिक व्युत्पन्न के समान है , आंशिक मोलर गिब्स मुक्त ऊर्जा। इसका मतलब है कि आंशिक मोलर गिब्स मुक्त ऊर्जा और रासायनिक क्षमता, ऊष्मप्रवैगिकी और रसायन विज्ञान में सबसे महत्वपूर्ण गुणों में से एक, समान मात्रा में है। समदाब रेखीय प्रक्रिया (स्थिर P) और समतापीय प्रक्रिया (स्थिर T) स्थितियों के तहत, रासायनिक क्षमता का ज्ञान, , मिश्रण की हर संपत्ति पैदा करता है क्योंकि वे गिब्स मुक्त ऊर्जा को पूरी तरह से निर्धारित करते हैं।
आंशिक मोलर गुण को मापना
आंशिक मोलर गुण को मापने के लिए एक द्विआधारी विलयन के रूप में निरूपित शुद्ध घटक के साथ शुरू होता है और पूरी प्रक्रिया के दौरान तापमान और दबाव को स्थिर रखते हुए, घटक के अतिसूक्ष्म हिस्से को जोड़ें ; माप प्रत्येक जोड़ के बाद । ब्याज की रचनाओं का नमूना लेने के बाद प्रायोगिक आंकड़े के लिए वक्र फिट(उपयुक्त) किया जा सकता है। यह प्रकार्य होगा के सम्बन्ध में विभेद करना दे देंगे तब संबंध से प्राप्त किया जाता है:
स्पष्ट मोलर मात्रा से संबंध
आंशिक मोलर गुणों और स्पष्ट गुणों के बीच संबंध को स्पष्ट मात्रा और मोलिटी की परिभाषा से प्राप्त किया जा सकता है।
यह संबंध बहुघटक मिश्रणों के लिए भी लागू होता है, बस इस मामले में उपलेख(सबस्क्रिप्ट) i की आवश्यकता होती है।
यह भी देखें
- स्पष्ट मोलर संपत्ति
- आदर्श विलयन
- अतिरिक्त मोलर मात्रा
- आंशिक विशिष्ट मात्रा
- ऊष्मप्रवैगिकी गतिविधि
संदर्भ
अग्रिम पठन
- P. Atkins and J. de Paula, "Atkins' Physical Chemistry" (8th edition, Freeman 2006), chap.5
- T. Engel and P. Reid, "Physical Chemistry" (Pearson Benjamin-Cummings 2006), p. 210
- K.J. Laidler and J.H. Meiser, "Physical Chemistry" (Benjamin-Cummings 1982), p. 184-189
- P. Rock, "Chemical Thermodynamics" (MacMillan 1969), chap.9
- Ira Levine, "Physical Chemistry" (6th edition,McGraw Hill 2009),p.125-128
बाहरी संबंध
- Lecture notes from the University of Arizona detailing mixtures, partial molar quantities, and ideal solutions[archive]
- On-line calculator for densities and partial molar volumes of aqueous solutions of some common electrolytes and their mixtures, at temperatures up to 323.15 K.