भाजक (बीजगणितीय ज्यामिति): Difference between revisions
No edit summary |
No edit summary |
||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Generalizations of codimension-1 subvarieties of algebraic varieties}} | {{short description|Generalizations of codimension-1 subvarieties of algebraic varieties}} | ||
बीजगणितीय ज्यामिति में, '''भाजक''' बीजगणितीय रूपों की कोडिमेशन-1 उप-विविधता का सामान्यीकरण है। दो भिन्न-भिन्न सामान्यीकरण कार्टियर भाजक और वेइल भाजक (डेविड मम्फोर्ड द्वारा पियरे कार्टियर और आंद्रे वेइल के नाम पर) सामान्य उपयोग में हैं। दोनों [[पूर्णांक]] और बीजगणितीय संख्या क्षेत्रों में विभाज्यता की धारणा से प्राप्त हुए हैं। | |||
विश्व स्तर पर, | विश्व स्तर पर, प्रक्षेप्य समिष्ट के प्रत्येक कोडिमेशन-1 उपविविधता को [[सजातीय बहुपद]] के लुप्त होने से परिभाषित किया जाता है; इसके विपरीत, कोडिमेंशन-r आर उपविविधता को केवल r समीकरणों द्वारा परिभाषित करने की आवश्यकता नहीं होती है जब r 1 से अधिक होता है। (अर्थात्, प्रक्षेप्य समिष्ट की प्रत्येक उपविविधता पूर्ण प्रतिच्छेदन नहीं है।) स्थानीय रूप से, सुचारु योजना के प्रत्येक कोडिमेशन-1 उपविविधता को प्रत्येक बिंदु के निकट में समीकरण द्वारा परिभाषित किया जा सकता है। फिर, समान कथन उच्च-संकेतन उप-विविधता के लिए विफल रहता है। इस संपत्ति के परिणामस्वरूप, बीजगणितीय ज्यामिति का अधिकांश भाग इसके कोडिमेशन-1 उप-विविधता और संबंधित [[लाइन बंडल|लाइन बंडलों]] का विश्लेषण करके इच्छानुसार विविधता का अध्ययन करता है। | ||
एकवचन प्रकारों पर, यह संपत्ति भी विफल हो सकती है, और इसलिए किसी को कोडिमेंशन-1 उप-विविधता और प्रकारों के मध्य अंतर करना होगा जिन्हें स्थानीय रूप से समीकरण द्वारा परिभाषित किया जा सकता है। पूर्व वेइल | एकवचन प्रकारों पर, यह संपत्ति भी विफल हो सकती है, और इसलिए किसी को कोडिमेंशन-1 उप-विविधता और प्रकारों के मध्य अंतर करना होगा जिन्हें स्थानीय रूप से समीकरण द्वारा परिभाषित किया जा सकता है। पूर्व वेइल भाजक हैं जबकि पश्चात वाले कार्टियर भाजक हैं। | ||
टोपोलॉजिकल रूप से, वेइल | टोपोलॉजिकल रूप से, वेइल भाजक होमोलॉजी कक्षाओं की भूमिका निभाते हैं, जबकि कार्टियर भाजक[[ सह-समरूपता ]] कक्षाओं का प्रतिनिधित्व करते हैं। सहज विविधता (या अधिक सामान्यतः [[नियमित योजना]]) पर, पोंकारे द्वैत के अनुरूप परिणाम कहता है कि वेइल और कार्टियर भाजक समान हैं। | ||
" | "भाजक" नाम [[रिचर्ड डेडेकाइंड|डेडेकाइंड]] और हेनरिक एम. वेबर के कार्य पर आधारित है, जिन्होंने बीजगणितीय वक्रों के अध्ययन के लिए [[डेडेकाइंड डोमेन]] की प्रासंगिकता दिखाई थी।<ref>Dieudonné (1985), section VI.6.</ref> वक्र पर भाजकों का समूह (सभी भाजकों द्वारा उत्पन्न मुक्त एबेलियन समूह) डेडेकाइंड डोमेन के लिए भिन्नात्मक आदर्शों के समूह से निकटता से संबंधित है। | ||
[[बीजगणितीय चक्र]] भाजक का उच्च कोडिमेंशन सामान्यीकरण है; परिभाषा के अनुसार, वेइल | [[बीजगणितीय चक्र]] भाजक का उच्च कोडिमेंशन सामान्यीकरण है; परिभाषा के अनुसार, वेइल भाजक संहिता 1 का चक्र है। | ||
==[[रीमैन सतह]] पर | ==[[रीमैन सतह]] पर भाजक== | ||
रीमैन सतह 1-आयामी समिष्ट मैनिफोल्ड है, और इसलिए इसके कोडिमेंशन-1 सबमैनिफोल्ड्स का आयाम 0 है।[[ सघन स्थान | सघन]] रीमैन सतह X पर | रीमैन सतह 1-आयामी समिष्ट मैनिफोल्ड है, और इसलिए इसके कोडिमेंशन-1 सबमैनिफोल्ड्स का आयाम 0 है।[[ सघन स्थान | सघन]] रीमैन सतह X पर भाजकों का समूह X के बिंदुओं पर मुक्त एबेलियन समूह है। | ||
समान रूप से, सघन रीमैन सतह X पर | समान रूप से, सघन रीमैन सतह X पर भाजक पूर्णांक गुणांक के साथ X के बिंदुओं का सीमित [[रैखिक संयोजन]] है। X पर भाजक की ''''डिग्री'''<nowiki/>' उसके गुणांकों का योग है। | ||
X पर किसी भी गैर-शून्य [[मेरोमोर्फिक फ़ंक्शन|मेरोमोर्फिक फलन]] f के लिए, कोई X ord<sub>p</sub>(f) में बिंदु p पर f के लुप्त होने के क्रम को परिभाषित कर सकता है। यदि f का ध्रुव p पर है तो यह पूर्णांक, ऋणात्मक है। सघन रीमैन सतह X पर गैर-शून्य मेरोमोर्फिक फलन f के | X पर किसी भी गैर-शून्य [[मेरोमोर्फिक फ़ंक्शन|मेरोमोर्फिक फलन]] f के लिए, कोई X ord<sub>p</sub>(f) में बिंदु p पर f के लुप्त होने के क्रम को परिभाषित कर सकता है। यदि f का ध्रुव p पर है तो यह पूर्णांक, ऋणात्मक है। सघन रीमैन सतह X पर गैर-शून्य मेरोमोर्फिक फलन f के भाजक को इस प्रकार परिभाषित किया गया है: | ||
:<math>(f):=\sum_{p \in X} \operatorname{ord}_p(f) p,</math> | :<math>(f):=\sum_{p \in X} \operatorname{ord}_p(f) p,</math> | ||
जो सीमित राशि है। (f) रूप के भाजक को ' | जो सीमित राशि है। (f) रूप के भाजक को ''''मुख्य भाजक'''<nowiki/>' भी कहा जाता है। चूँकि (fg) = (f) + (g), प्रमुख भाजक का समुच्चय भाजक के समूह का उपसमूह है। दो भाजक जो मुख्य भाजक से भिन्न होते हैं उन्हें ''''रैखिक समतुल्य'''<nowiki/>' कहा जाता है। | ||
सघन रीमैन सतह पर, मुख्य भाजक की डिग्री शून्य होती है; अर्थात्, मेरोमॉर्फिक फलन के शून्यों की संख्या बहुलता के साथ | सघन रीमैन सतह पर, मुख्य भाजक की डिग्री शून्य होती है; अर्थात्, मेरोमॉर्फिक फलन के शून्यों की संख्या बहुलता के साथ गणना किये जाने वाले ध्रुवों की संख्या के समान होती है। परिणामस्वरूप, भाजक के रैखिक तुल्यता वर्गों पर डिग्री उचित प्रकार से परिभाषित होती है। | ||
सघन रीमैन सतह | सघन रीमैन सतह D से संबंधित 'लाइन बंडल के अनुभागों का स्थान' है। D की डिग्री इस सदिश समिष्ट के आयाम के विषय में बहुत कुछ कहती है। उदाहरण के लिए, यदि D की डिग्री ऋणात्मक है, तो इसकी सदिश समष्टि शून्य है (क्योंकि मेरोमोर्फिक फलन में ध्रुवों से अधिक शून्य नहीं हो सकते हैं)। यदि D की धनात्मक डिग्री है, तो H<sup>0</sup>(X, O(mD)) का आयाम m के लिए पर्याप्त रूप से बड़े होने पर रैखिक रूप से बढ़ता है। रीमैन-रोच प्रमेय इन पंक्तियों के साथ अधिक त्रुटिहीन कथन है। दूसरी ओर, निम्न डिग्री के भाजक D के लिए H<sup>0</sup>(X, O(D)) का त्रुटिहीन आयाम सूक्ष्म है, और D की डिग्री द्वारा पूर्ण रूप से निर्धारित नहीं होता है। सघन रीमैन सतह की विशिष्ट विशेषताएं इन आयामों में परिलक्षित होती हैं। | ||
सघन रीमैन सतह पर | सघन रीमैन सतह पर प्रमुख भाजक विहित भाजक है। इसे परिभाषित करने के लिए, सबसे पूर्व उपरोक्त पंक्तियों के साथ गैर-शून्य मेरोमोर्फिक 1-रूप के भाजक को परिभाषित किया जाता है। चूँकि मेरोमोर्फिक [[1-रूप|1-रूपों]] की समिष्ट मेरोमोर्फिक कार्यों के क्षेत्र पर 1-आयामी सदिश समिष्ट है, कोई भी दो गैर-शून्य मेरोमोर्फिक 1-रूप रैखिक रूप से समतुल्य भाजक उत्पन्न करते हैं। इस रैखिक तुल्यता वर्ग में किसी भी भाजक को X, K<sub>''X''</sub> का '[[विहित भाजक]]' कहा जाता है। X के [[जीनस (गणित)|जीनस]] g को विहित भाजक से पढ़ा जा सकता है: अर्थात्, K<sub>''X''</sub> की डिग्री 2g - 2 है। सघन रीमैन सतहों X के मध्य मुख्य ट्राइकोटॉमी यह है कि क्या विहित भाजक में नकारात्मक डिग्री है (इसलिए X में जीनस शून्य है), शून्य डिग्री (जीनस) एक), या धनात्मक डिग्री (जीनस कम से कम 2)। उदाहरण के लिए, यह निर्धारित करता है कि क्या X के निकट धनात्मक [[अनुभागीय वक्रता|वक्रता]], शून्य वक्रता, या नकारात्मक वक्रता वाला काहलर मीट्रिक है। विहित भाजक की डिग्री ऋणात्मक है यदि और केवल X [[रीमैन क्षेत्र]] CP<sup>1</sup> के लिए समरूपी है। | ||
==वेइल | ==वेइल भाजक== | ||
मान लीजिए कि X | मान लीजिए कि X [[अभिन्न योजना|अभिन्न स्थानीय नोथेरियन योजना]] है। X पर ''''अभाज्य भाजक'''<nowiki/>' या ''''अपरिवर्तनीय भाजक'''<nowiki/>' X में कोडिमेशन 1 का अभिन्न विवृत उपयोजना Z है। X पर '''वेइल भाजक''', X के अभाज्य भाजक Z पर औपचारिक योग है: | ||
:<math>\sum_Z n_Z Z,</math> | :<math>\sum_Z n_Z Z,</math> | ||
जहां संग्रह <math>\{Z : n_Z \neq 0\}</math> स्थानीय रूप से सीमित | जहां संग्रह <math>\{Z : n_Z \neq 0\}</math> स्थानीय रूप से सीमित है। यदि X अर्ध-सघन है, तो स्थानीय परिमितता इसके समान है <math>\{Z : n_Z \neq 0\}</math> परिमित होता है। सभी वेइल भाजकों के समूह को {{math|Div(''X'')}} द्वारा दर्शाया गया है। यदि सभी गुणांक गैर-ऋणात्मक हैं तो वेइल भाजक D ''''प्रभावी'''<nowiki/>' है। यदि अंतर {{math|''D'' − ''D′''}} प्रभावी है तो {{math|''D'' ≥ ''D′''}} लिखा जाता है। | ||
उदाहरण के लिए, किसी क्षेत्र के बीजगणितीय वक्र पर | उदाहरण के लिए, किसी क्षेत्र के बीजगणितीय वक्र पर भाजक सीमित रूप से कई विवृत बिंदुओं का औपचारिक योग होता है। {{math|Spec '''Z'''}} पर भाजक पूर्णांक गुणांक के साथ अभाज्य संख्याओं का औपचारिक योग है और इसलिए Q में गैर-शून्य भिन्नात्मक आदर्श से युग्मित होता है। समान लक्षण वर्णन भाजक <math>\operatorname{Spec} \mathcal{O}_K</math> के लिए सत्य है, जहाँ K संख्या क्षेत्र है। | ||
यदि Z ⊂ X | यदि Z ⊂ X अभाज्य भाजक है, तो स्थानीय वलय <math>\mathcal{O}_{X,Z}</math> में [[क्रुल आयाम]] है। यदि <math>f \in \mathcal{O}_{X,Z}</math> गैर-शून्य है, तो ''Z'' के साथ f के लुप्त होने का क्रम, जिसे {{math|ord<sub>''Z''</sub>(''f'')}} लिखा जाता है, [[एक मॉड्यूल की लंबाई|मॉड्यूल की लंबाई]] <math>\mathcal{O}_{X,Z}/(f)</math> है यह लंबाई सीमित है,<ref>{{Citation | title=Stacks Project, Tag 00PF | url=http://stacks.math.columbia.edu/tag/00PF}}.</ref> और यह गुणन के संबंध में योगात्मक है, अर्थात, {{math|1=ord<sub>''Z''</sub>(''fg'') = ord<sub>''Z''</sub>(''f'') + ord<sub>''Z''</sub>(''g'')}} है।<ref>{{Citation | title=Stacks Project, Tag 02MC | url=http://stacks.math.columbia.edu/tag/02MC}}.</ref> यदि k(X) X पर तर्कसंगत कार्यों का क्षेत्र है, तो किसी भी गैर-शून्य {{math|''f'' ∈ ''k''(''X'')}} को भागफल {{math|''g'' / ''h''}} के रूप में लिखा जा सकता है, जहां g और h हैं <math>\mathcal{O}_{X,Z},</math> और f के लुप्त होने के क्रम को {{math|ord<sub>''Z''</sub>(''g'') − ord<sub>''Z''</sub>(''h'')}} के रूप में परिभाषित किया गया है।<ref>{{Citation | title=Stacks Project, Tag 02MD | url=http://stacks.math.columbia.edu/tag/02MD}}.</ref> इस परिभाषा के साथ, लुप्त होने का क्रम फलन {{math|ord<sub>''Z''</sub> : ''k''(''X'')<sup>×</sup> → '''Z'''}} है। यदि X [[सामान्य योजना|सामान्य]] है, तो स्थानीय वलय <math>\mathcal{O}_{X,Z}</math> भिन्न मूल्यांकन वलय और फलन {{math|ord<sub>''Z''</sub>}} संबंधित मूल्यांकन है। X पर गैर-शून्य तर्कसंगत फलन f के लिए, f से जुड़े ''''प्रमुख वेइल भाजक'''<nowiki/>' को वेइल भाजक के रूप में परिभाषित किया गया है: | ||
:<math>\operatorname{div} f = \sum_Z \operatorname{ord}_Z(f) Z.</math> | :<math>\operatorname{div} f = \sum_Z \operatorname{ord}_Z(f) Z.</math> | ||
यह दिखाया जा सकता है कि यह योग स्थानीय रूप से सीमित है और इसलिए यह वास्तव में | यह दिखाया जा सकता है कि यह योग स्थानीय रूप से सीमित है और इसलिए यह वास्तव में वेइल भाजक को परिभाषित करता है। f से जुड़े प्रमुख वेइल भाजक {{math|(''f'')}} को भी नोट किया गया है। यदि f नियमित फलन है, तो इसका प्रमुख वेइल भाजक प्रभावी है, किन्तु सामान्यतः यह सत्य नहीं है। लुप्त होने वाले फलन के क्रम की योज्यता का तात्पर्य यह है: | ||
:<math>\operatorname{div} fg = \operatorname{div} f + \operatorname{div} g.</math> | :<math>\operatorname{div} fg = \operatorname{div} f + \operatorname{div} g.</math> | ||
परिणामस्वरूप {{math|div}} समरूपता है, और विशेष रूप से इसकी छवि सभी वेइल भाजकों के समूह का उपसमूह है। | |||
मान लीजिए कि X | मान लीजिए कि X सामान्य इंटीग्रल नॉथेरियन योजना है। प्रत्येक वेइल भाजक D [[सुसंगत शीफ]] <math>\mathcal{O}_X(D)</math> ''X'' पर निर्धारित करता है। ठोस रूप से इसे तर्कसंगत कार्यों के शीफ के उपशीर्षक के रूप में परिभाषित किया जा सकता है।<ref name="K1.2">Kollár (2013), Notation 1.2.</ref> | ||
:<math>\Gamma(U, \mathcal{O}_X(D)) = \{ f \in k(X) : f = 0 \text{ or } \operatorname{div}(f) + D \ge 0 \text{ on } U \}.</math> | :<math>\Gamma(U, \mathcal{O}_X(D)) = \{ f \in k(X) : f = 0 \text{ or } \operatorname{div}(f) + D \ge 0 \text{ on } U \}.</math> | ||
अर्थात्, | अर्थात्, शून्येतर परिमेय फलन f का भाग है <math>\mathcal{O}_X(D)</math> U से अधिक यदि और केवल किसी अभाज्य भाजक Z के लिए जो U को प्रतिच्छेद करता है, | ||
:<math>\operatorname{ord}_Z(f) \ge -n_Z</math> | :<math>\operatorname{ord}_Z(f) \ge -n_Z</math> | ||
जहां ''n''<sub>Z</sub> D में Z का गुणांक है। यदि D प्रमुख है, इसलिए D परिमेय फलन g का भाजक है, तो समरूपता है: | |||
:<math>\begin{cases} \mathcal{O}(D) \to \mathcal{O}_X \\ f \mapsto fg \end{cases}</math> तब से <math>\operatorname{div}(fg)</math> प्रभावी | :<math>\begin{cases} \mathcal{O}(D) \to \mathcal{O}_X \\ f \mapsto fg \end{cases}</math> | ||
:तब से <math>\operatorname{div}(fg)</math> प्रभावी भाजक <math>fg</math> है और इसलिए X की सामान्यता के कारण नियमित है। इसके विपरीत, यदि <math>\mathcal{O}(D)</math> समरूपी है <math>\mathcal{O}_X</math> के रूप में <math>\mathcal{O}_X</math>-मॉड्यूल, तो D प्रमुख है। इसका तात्पर्य यह है कि D स्थानीय रूप से प्रमुख है यदि और केवल <math>\mathcal{O}(D)</math> विपरीत है; अर्थात लाइन बंडल है। | |||
यदि D | यदि D प्रभावी भाजक है तो <math>\mathcal{O}(-D)</math> से प्रायः उपयोग किया जाने वाला संक्षिप्त त्रुटिहीनअनुक्रम प्राप्त होता है, | ||
:<math>0 \to \mathcal{O}_X(-D) \to \mathcal{O}_X \to \mathcal{O}_D \to 0.</math> | :<math>0 \to \mathcal{O}_X(-D) \to \mathcal{O}_X \to \mathcal{O}_D \to 0.</math> | ||
इस क्रम की शीफ सहसंरचना यह दर्शाती है <math>H^1(X, \mathcal{O}_X(-D))</math> | इस क्रम की शीफ सहसंरचना यह दर्शाती है <math>H^1(X, \mathcal{O}_X(-D))</math> में यह सूचना सम्मिलित है कि क्या D पर नियमित कार्य X पर नियमित कार्य के प्रतिबंध हैं। | ||
इसमें | इसमें समूहों का भी समावेश है: | ||
:<math>0 \to \mathcal{O}_X \to \mathcal{O}_X(D).</math> | :<math>0 \to \mathcal{O}_X \to \mathcal{O}_X(D).</math> | ||
यह | यह विहित तत्व <math>\Gamma(X, \mathcal{O}_X(D))</math> प्रस्तुत करता है, अर्थात्, वैश्विक भाग 1 की छवि है। इसे विहित अनुभाग कहा जाता है और इसे ''s''<sub>D</sub> से दर्शाया जा सकता है। जबकि विहित अनुभाग कहीं लुप्त न होने वाले तर्कसंगत फलन की छवि है, इसकी छवि <math>\mathcal{O}(D)</math> D के साथ लुप्त हो जाता है क्योंकि संक्रमण फलन D के साथ लुप्त हो जाते हैं। जब D सुचारु कार्टियर भाजक होता है, तो उपरोक्त समावेशन के कोकर्नेल की पहचान की जा सकती है; नीचे कार्टियर भाजक देखें। | ||
मान लें कि | मान लें कि X क्षेत्र पर परिमित प्रकार की सामान्य अभिन्न पृथक योजना है। मान लीजिए D वेइल भाजक है। तब <math>\mathcal{O}(D)</math> श्रेणी वन [[रिफ्लेक्सिव शीफ]] है, और तब से <math>\mathcal{O}(D)</math> के उपशीर्षक के रूप में परिभाषित किया गया है। <math>\mathcal{M}_X</math> यह भिन्नात्मक आदर्श शीफ है (नीचे देखें)। इसके विपरीत, प्रत्येक श्रेणी रिफ्लेक्सिव शीफ वेइल भाजक से युग्मित होती है: शीफ को नियमित लोकस तक सीमित किया जा सकता है, जहां यह मुक्त हो जाता है और इसलिए कार्टियर भाजक से युग्मित होता है (पुनः, नीचे देखें), और क्योंकि एकवचन लोकस में कम से कम दो कोडिमेंशन होता है, कार्टियर भाजक का विवृत होना वेइल भाजक है। | ||
== भाजक वर्ग समूह == | == भाजक वर्ग समूह == | ||
वेइल | वेइल भाजक वर्ग समूह Cl(X) सभी प्रमुख वेइल भाजक के उपसमूह द्वारा Div(X) का भागफल है। दो भाजकों को रैखिक रूप से समतुल्य कहा जाता है यदि उनका अंतर प्रमुख है, इसलिए भाजक वर्ग समूह भाजक मॉड्यूलो रैखिक तुल्यता का समूह है। किसी फ़ील्ड पर आयाम ''n'' की विविधता ''X'' के लिए, भाजक वर्ग समूह [[चाउ समूह]] है; अर्थात्, Cl(X) (n−1)-आयामी चक्रों का चाउ समूह CH<sub>''n''−1</sub>(X) है। | ||
मान लीजिए Z, X का | मान लीजिए Z, X का विवृत उपसमुच्चय है। यदि Z, कोड आयाम का अपरिवर्तनीय है, तो Cl(X - Z) Z के वर्ग द्वारा Cl(X) के भागफल समूह के लिए समरूपी है। यदि Z का कोड आयाम X में कम से कम 2 है , तो प्रतिबंध Cl(X) → Cl(X − ''Z'') समरूपता है।<ref>Hartshorne (1977), Proposition II.6.5.</ref> (ये तथ्य चाउ समूहों के स्थानीयकरण अनुक्रम की विशेष स्थिति है।) | ||
सामान्य इंटीग्रल नोथेरियन | सामान्य इंटीग्रल नोथेरियन योजना X पर, दो वेइल भाजक D, E रैखिक रूप से समतुल्य हैं यदि और केवल <math>\mathcal{O}(D)</math> और <math>\mathcal{O}(E)</math> के रूप में समरूपी हैं <math>\mathcal{O}_X</math>-मॉड्यूल X पर रिफ्लेक्सिव शीव्स के समरूपी वर्ग मोनोइड बनाते हैं जिसमें उत्पाद को टेंसर उत्पाद के रिफ्लेक्सिव पतवार के रूप में दिया जाता है। तब <math>D \mapsto \mathcal{O}_X(D)</math> X के वेइल भाजक वर्ग समूह से X पर श्रेणी-वन रिफ्लेक्सिव शीव्स के समरूपी वर्गों के मोनोइड तक मोनोइड समरूपता को परिभाषित करता है। | ||
=== उदाहरण === | === उदाहरण === | ||
* मान लीजिए k | * मान लीजिए k क्षेत्र है, और मान लीजिए n धनात्मक पूर्णांक है। चूँकि बहुपद वलय k[x<sub>1</sub>, ..., x<sub>n</sub>] अद्वितीय गुणनखंडन डोमेन है, एफाइन समिष्ट '''A'''<sup>n</sup> k का भाजक वर्ग समूह शून्य के समानहै।<ref name=H6.2/> चूँकि k से हाइपरप्लेन H के ऊपर प्रक्षेप्य समिष्ट P<sup>n</sup>, A<sup>n</sup> के समरूपी है, इसलिए यह इस प्रकार है कि P<sup>n</sup> का भाजक वर्ग समूह H के वर्ग द्वारा उत्पन्न होता है। वहां से, यह परिक्षण सीधा है कि Cl('P'<sup>n</sup>) वास्तव में H द्वारा उत्पन्न पूर्णांक 'Z' के समरूपी है। सामान्यतः, इसका तात्पर्य है कि P<sup>n</sup> का प्रत्येक कोडिमेशन-1 उप-विविधता को एकल सजातीय बहुपद के लुप्त होने से परिभाषित किया गया है। | ||
* मान लीजिए कि X | * मान लीजिए कि X क्षेत्र k पर बीजगणितीय वक्र है। X में प्रत्येक विवृत बिंदु p में k के कुछ परिमित विस्तार क्षेत्र E के लिए विशिष्ट E का रूप होता है, और p की 'डिग्री' को k के ऊपर E की डिग्री के रूप में परिभाषित किया जाता है। इसे रैखिकता द्वारा विस्तारित करने से X पर भाजक के लिए 'डिग्री' की धारणा मिलती है। यदि X, k पर प्रक्षेप्य वक्र है, तो X पर गैर-शून्य तर्कसंगत फलन f के भाजक की डिग्री शून्य है।<ref>{{Citation | title=Stacks Project, Tag 02RS | url=http://stacks.math.columbia.edu/tag/02RS}}.</ref> परिणामस्वरूप, प्रक्षेप्य वक्र X के लिए, डिग्री समरूपता डिग्री देती है: Cl(X) → 'Z'। | ||
* प्रक्षेप्य रेखा | * क्षेत्र k पर प्रक्षेप्य रेखा P<sup>1</sup> के लिए, डिग्री समरूपता Cl('''P'''<sup>1</sup>) ≅ Z देती है। k-[[तर्कसंगत बिंदु]] के साथ किसी भी सुचारु प्रक्षेप्य वक्र X के लिए, डिग्री समरूपता विशेषण है, और कर्नेल के समूह के लिए समरूपता है - X की [[जैकोबियन किस्म|जैकोबियन प्रकार]] पर k-बिंदु, जो X के जीनस के समान आयाम का [[एबेलियन किस्म|एबेलियन प्रकार]] है। उदाहरण के लिए, यह इस प्रकार है कि समिष्ट [[अण्डाकार वक्र]] का भाजक वर्ग समूह [[बेशुमार|अनंत]] एबेलियन समूह है। | ||
* पिछले उदाहरण को सामान्यीकृत करना: | * पिछले उदाहरण को सामान्यीकृत करना: क्षेत्र k पर किसी भी सहज प्रक्षेप्य विविधता ''X'' के लिए, जैसे कि X में ''k''-तर्कसंगत बिंदु है, भाजक वर्ग समूह Cl('' X'') जुड़े हुए [[समूह योजना]] के ''k''-बिंदुओं के समूह द्वारा सूक्ष्म रूप से उत्पन्न एबेलियन समूह, नेरॉन-सेवेरी समूह का विस्तार <math>\operatorname{Pic}^0_{X/k}</math> है।<ref>Kleiman (2005), Theorems 2.5 and 5.4, Remark 6.19.</ref> विशेषता शून्य के k के लिए, <math>\operatorname{Pic}^0_{X/k}</math> एबेलियन विविधता है, X की [[पिकार्ड किस्म|पिकार्ड विविधता है]]। | ||
* | *R के लिए किसी [[संख्या क्षेत्र]] के पूर्णांकों का वलय, भाजक वर्ग समूह Cl(R) := Cl(Spec R) को R का [[आदर्श वर्ग समूह]] भी कहा जाता है। यह परिमित एबेलियन समूह है। आदर्श वर्ग समूहों को समझना [[बीजगणितीय संख्या सिद्धांत]] का केंद्रीय लक्ष्य है। | ||
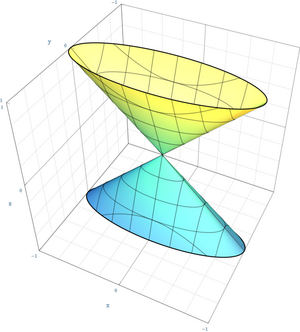
* [[File:Elliptical Cone Quadric.Png|thumb|एफ़िन क्वाड्रिक शंकु xy = z<sup>2</sup> | * [[File:Elliptical Cone Quadric.Png|thumb|एफ़िन क्वाड्रिक शंकु xy = z<sup>2</sup>]]मान लीजिए कि X आयाम 2 का चतुर्भुज शंकु है, जो क्षेत्र के ऊपर एफ़िन 3-समिष्ट में समीकरण xy = z<sup>2</sup> द्वारा परिभाषित है। फिर x = z = 0 द्वारा परिभाषित X में रेखा D मूल बिंदु के निकट X पर प्रमुख नहीं है। ध्यान दें कि D को X पर समीकरण द्वारा समुच्चय के रूप में परिभाषित किया जा सकता है, अर्थात् x = 0; किन्तु X पर फलन x, D के अनुदिश क्रम 2 पर लुप्त हो जाता है, और इसलिए हम केवल यह पाते हैं कि 2D, X पर कार्टियर (जैसा कि नीचे परिभाषित है) है। वास्तव में, भाजक वर्ग समूह Cl(X) चक्रीय समूह 'Z'/2 के लिए समरूपी है। जो D के वर्ग द्वारा उत्पन्न होता है।<ref>Hartshorne (1977), Example II.6.5.2.</ref> | ||
* मान लीजिए कि X आयाम 3 का चतुर्भुज शंकु है, जो | * मान लीजिए कि X आयाम 3 का चतुर्भुज शंकु है, जो क्षेत्र के ऊपर 4-समिष्ट में समीकरण xy = zw द्वारा परिभाषित है। फिर x = z = 0 द्वारा परिभाषित X में समतल D को मूल बिंदु के निकट समीकरण द्वारा, यहां तक कि समुच्चय के रूप में भी, X में परिभाषित नहीं किया जा सकता है। इससे यह निष्कर्ष निकलता है कि D, X पर 'Q-कार्टियर' नहीं है; अर्थात्, D का कोई भी धनात्मक गुणज कार्टियर नहीं है। वास्तव में, भाजक वर्ग समूह Cl(X) D के वर्ग द्वारा उत्पन्न पूर्णांक ''''Z'''' <nowiki/>के समरूपी है।<ref>Hartshorne(1977), Exercise II.6.5.</ref> | ||
'''विहित भाजक''' | '''विहित भाजक''' | ||
मान लीजिए कि X | मान लीजिए कि X आदर्श क्षेत्र में सामान्य प्रकार है। X की सहज समिष्ट U विवृत उपसमुच्चय है जिसके पूरक का कोड आयाम कम से कम 2 है। मान लीजिए कि j: U → X समावेशन मानचित्र है, तो प्रतिबंध समरूपता इस प्रकार है: | ||
:<math>j^*: \operatorname{Cl}(X) \to \operatorname{Cl}(U) = \operatorname{Pic}(U)</math> | :<math>j^*: \operatorname{Cl}(X) \to \operatorname{Cl}(U) = \operatorname{Pic}(U)</math> | ||
समरूपता है, क्योंकि X - U का X में कोड आयाम कम से कम 2 है। उदाहरण के लिए, कोई विहित | समरूपता है, क्योंकि X - U का X में कोड आयाम कम से कम 2 कोडिमेंशन है। उदाहरण के लिए, कोई X के विहित भाजक K<sub>''X''</sub> को परिभाषित करने के लिए इस समरूपता का उपयोग कर सकता है: यह U पर शीर्ष डिग्री के विभेदक रूपों के लाइन बंडल के अनुरूप वेइल भाजक (रैखिक तुल्यता तक) है। समतुल्य रूप से, शीफ <math>\mathcal{O}(K_X)</math> प्रत्यक्ष छवि शीफ <math>j_*\Omega^n_U</math> है, जहाँ n, X का आयाम है। | ||
'उदाहरण': मान लीजिए X = 'P'<sup>n</sup>सजातीय निर्देशांक x | '''<nowiki/>'उदाहरण':''' मान लीजिए X = 'P'<sup>n</sup> सजातीय निर्देशांक x<sub>0</sub>, ...,x<sub>n</sub> के साथ प्रक्षेप्य n-समिष्ट है। माना U = {x<sub>0</sub> ≠ 0} तब U निर्देशांक y<sub>i</sub> = x<sub>i</sub>/x<sub>0</sub> के साथ एफ़िन ''n''-समिष्ट के लिए समरूपी है। मान लीजिए कि: | ||
:<math>\omega = { dy_1 \over y_1 } \wedge \dots \wedge {dy_n \over y_n}.</math> | :<math>\omega = { dy_1 \over y_1 } \wedge \dots \wedge {dy_n \over y_n}.</math> | ||
तब ω | तब ω U पर तर्कसंगत अंतर रूप है; इस प्रकार, यह तर्कसंगत भाग <math>\Omega^n_{\mathbf{P}^n}</math>है। जिसमें Z<sub>i</sub>= {x<sub>i</sub>= 0}, i = 1, ..., n के अनुदिश सरल ध्रुव हैं। भिन्न एफ़िन चार्ट पर स्विच करने से केवल ω का चिह्न परिवर्तित होता है और इसलिए हम देखते हैं कि ω में Z<sub>0</sub> के साथ सरल ध्रुव भी है। इस प्रकार, ω का भाजक है: | ||
:<math>\operatorname{div}(\omega) = -Z_0 - \dots - Z_n</math> | :<math>\operatorname{div}(\omega) = -Z_0 - \dots - Z_n</math> | ||
और इसका | और इसका भाजक वर्ग है: | ||
:<math>K_{\mathbf{P}^n} = [\operatorname{div}(\omega)] = -(n+1) [H]</math> | :<math>K_{\mathbf{P}^n} = [\operatorname{div}(\omega)] = -(n+1) [H]</math> | ||
जहां [ | जहां [H] = [Z<sub>i</sub>], i = 0, ..., n है। ([[यूलर अनुक्रम]] भी देखें।) | ||
==कार्टियर | ==कार्टियर भाजक== | ||
मान लीजिए कि X | मान लीजिए कि X अभिन्न नोथेरियन योजना है। तब X के निकट तर्कसंगत फलनों का समूह <math>\mathcal{M}_X</math> है सभी नियमित फलन तर्कसंगत फलन हैं, जो संक्षिप्त त्रुटिहीन अनुक्रम की ओर ले जाते हैं: | ||
:<math>0 \to \mathcal{O}_X^\times \to \mathcal{M}_X^\times \to \mathcal{M}_X^\times / \mathcal{O}_X^\times \to 0.</math> | :<math>0 \to \mathcal{O}_X^\times \to \mathcal{M}_X^\times \to \mathcal{M}_X^\times / \mathcal{O}_X^\times \to 0.</math> | ||
''X'' पर कार्टियर | ''X'' पर कार्टियर भाजक का वैश्विक भाग है। <math>\mathcal{M}_X^\times / \mathcal{O}_X^\times.</math> <math>\{(U_i, f_i)\},</math> जहाँ <math>\{U_i\}</math> का संवृत आवरण है <math>X, f_i</math> का भाग है <math>\mathcal M_X^\times</math> पर <math>U_i,</math> और <math>f_i=f_j</math> पर <math>U_i \cap U_j</math> के भाग से गुणा तक <math>\mathcal O_X^\times.</math>है। | ||
उपरोक्त | कार्टियर भाजक में शीफ-सैद्धांतिक विवरण भी होता है। भिन्नात्मक आदर्श शीफ उप- है <math>\mathcal O_X</math>-मॉड्यूल का <math>\mathcal{M}_X.</math> भिन्नात्मक आदर्श शीफ़ J 'विपरीत' है यदि, X में प्रत्येक x के लिए, x का संवृत U उपस्थित है जिस पर J से U का प्रतिबंध समान होता है <math>\mathcal{O}_U \cdot f,</math> जहाँ <math>f \in \mathcal{M}_X^{\times}(U)</math> और उत्पाद अंदर ले जाया जाता है <math>\mathcal{M}_X.</math> प्रत्येक कार्टियर भाजक संग्रह के रूप में कार्टियर भाजक के विवरण का उपयोग करके विपरीत भिन्नात्मक आदर्श शीफ <math>\{(U_i, f_i)\},</math> को परिभाषित करता है और इसके विपरीत, व्युत्क्रमणीय भिन्नात्मक आदर्श शीव्स कार्टियर भाजक को परिभाषित करते हैं। यदि कार्टियर भाजक को D निरूपित किया जाता है, तो संबंधित भिन्नात्मक आदर्श शीफ को <math>\mathcal{O}(D)</math> या L(D) निरूपित किया जाता है। | ||
उपरोक्त त्रुटिहीन अनुक्रम के अनुसार, शीफ़ कोहोलॉजी समूहों का त्रुटिहीन अनुक्रम है: | |||
:<math>H^0(X, \mathcal{M}^\times_X) \to H^0(X, \mathcal{M}^\times_X / \mathcal{O}^\times_X) \to H^1(X, \mathcal O^\times_X) = \operatorname{Pic}(X).</math> | :<math>H^0(X, \mathcal{M}^\times_X) \to H^0(X, \mathcal{M}^\times_X / \mathcal{O}^\times_X) \to H^1(X, \mathcal O^\times_X) = \operatorname{Pic}(X).</math> | ||
कार्टियर | कार्टियर भाजक को प्रमुख कहा जाता है यदि यह समरूपता की छवि में <math>H^0(X,\mathcal{M}_X^{\times}) \to H^0(X, \mathcal{M}_X^{\times}/\mathcal{O}_X^{\times})</math> है, अर्थात्, यदि यह X पर परिमेय फलन का भाजक है। दो कार्टियर भाजक 'रैखिक रूप से समतुल्य' हैं यदि उनका अंतर मूलधन है। इंटीग्रल नोथेरियन योजना X पर प्रत्येक लाइन बंडल L कुछ कार्टियर भाजक का वर्ग है। परिणामस्वरूप, उपरोक्त त्रुटिहीन अनुक्रम कार्टियर डिवाइजर्स मॉड्यूलो रैखिक तुल्यता के समूह के साथ अभिन्न नोथेरियन योजना X पर लाइन बंडलों के [[पिकार्ड समूह]] की पहचान करता है। यह सामान्यतः कम नोथेरियन योजनाओं, या नोथेरियन रिंग पर अर्ध-प्रोजेक्टिव योजनाओं के लिए प्रारम्भ होता है,<ref>Grothendieck, EGA IV, Part 4, Proposition 21.3.4, Corollaire 21.3.5.</ref> किन्तु यह सामान्य रूप से विफल हो सकता है (यहां तक कि '''C''' से अधिक उचित योजनाओं के लिए भी), जो पूर्ण व्यापकता में कार्टियर भाजकों की रुचि को अल्प कर देता है।<ref>Lazarsfeld (2004), Example 1.1.6.</ref> | ||
मान लें कि D प्रभावी कार्टियर | |||
मान लें कि D प्रभावी कार्टियर भाजक है। फिर संक्षिप्त त्रुटिहीन क्रम है: | |||
:<math>0 \to \mathcal{O}_X \to \mathcal{O}_X(D) \to \mathcal{O}_D(D) \to 0.</math> | :<math>0 \to \mathcal{O}_X \to \mathcal{O}_X(D) \to \mathcal{O}_D(D) \to 0.</math> | ||
यह क्रम <math>\mathcal{O}(D)</math> स्थानीय रूप से मुफ़्त है, और इसलिए उस अनुक्रम को | यह क्रम <math>\mathcal{O}(D)</math> स्थानीय रूप से मुफ़्त है, और इसलिए उस अनुक्रम को टेंसर किया जा रहा है <math>\mathcal{O}(D)</math> और संक्षिप्त त्रुटिहीन अनुक्रम उत्पन्न करता है। जब D सुचारु हो, <math>O_D(D)</math> X में D का सामान्य बंडल है। | ||
===वेइल भाजक और कार्टियर भाजक की तुलना=== | |||
वेइल भाजक D को 'कार्टियर' कहा जाता है यदि और केवल शीफ <math>\mathcal{O}(D)</math> विपरीत है। जब ऐसा होता है, <math>\mathcal{O}(D)</math> (M<sub>X</sub> में इसके एम्बेडिंग के साथ) कार्टियर भाजक से संबद्ध रेखा बंडल है। अधिक त्रुटिहीन रूप से, यदि <math>\mathcal{O}(D)</math> विपरीत है, तो ऐसा संवृत आवरण {U<sub>i</sub>} उपस्थित है जैसे कि <math>\mathcal{O}(D)</math> प्रत्येक संवृत समुच्चय पर तुच्छ बंडल तक सीमित है। प्रत्येक U<sub>i</sub> के लिए, समरूपता का चयन किया जाता है, <math>\mathcal{O}_{U_i} \to \mathcal{O}(D)|_{U_i}.</math> की छवि <math>1 \in \Gamma(U_i, \mathcal{O}_{U_i}) = \Gamma(U_i, \mathcal{O}_X)</math> इस मानचित्र के अंतर्गत अनुभाग <math>\mathcal{O}(D)</math> है। क्योंकि <math>\mathcal{O}(D)</math> तर्कसंगत फलन के समूह के उपशीर्षक के रूप में परिभाषित किया गया है, 1 की छवि को कुछ तर्कसंगत फलन के साथ पहचाना जा सकता है, संग्रह <math>\{(U_i, f_i)\}</math> तब कार्टियर भाजक है। यह उचित प्रकार से परिभाषित है क्योंकि इसमें सम्मिलित एकमात्र विकल्प कवरिंग और समरूपता के थे, जिनमें से कोई भी कार्टियर भाजक को नहीं परिवर्तित करता है। इस कार्टियर भाजक का उपयोग शीफ का उत्पादन करने के लिए किया जा सकता है, जिसे भेद के लिए हम L(D) नोट करेंगे। <math>\mathcal{O}(D)</math> की समरूपता है संवृत कवर {U<sub>i</sub>} पर कार्य करके L(D) के साथ <math>\mathcal{O}(D)</math> को परिभाषित किया गया है। यह परीक्षण करने के लिए मुख्य तथ्य यह है कि संक्रमण फलन करता है <math>\mathcal{O}(D)</math> और L(D) संगत हैं, और इसका तात्पर्य यह है कि इन सभी फलनों <math>f_i/f_j.</math> का रूप है। | |||
विपरीत दिशा में, कार्टियर भाजक <math>\{(U_i, f_i)\}</math> इंटीग्रल नोथेरियन योजना पर X प्राकृतिक प्रकार से X पर वेइल भाजक निर्धारित करता है <math>\operatorname{div} </math> संवृत समुच्चय U<sub>i</sub> पर फलन f''<sub>i</sub>'' के लिए है। | |||
विपरीत दिशा में, | |||
यदि | यदि; | ||
नोएथेरियन | नोएथेरियन योजना X को 'फैक्टोरियल' कहा जाता है यदि X के सभी स्थानीय वलय [[अद्वितीय गुणनखंडन डोमेन]] हैं।<ref name="K1.2" /> (कुछ लेखक स्थानीय रूप से फैक्टोरियल कहते हैं।) विशेष रूप से, प्रत्येक नियमित योजना तथ्यात्मक होती है।<ref>{{Citation| title=Stacks Project, Tag 0AFW | url=http://stacks.math.columbia.edu/tag/0AFW}}.</ref> फैक्टोरियल योजना X पर, प्रत्येक वेइल भाजक D स्थानीय रूप से प्रमुख है, और इसी प्रकार <math>\mathcal{O}(D)</math> सदैव लाइन बंडल होता है।<ref name="H6.2">Hartshorne (1977), Proposition II.6.2.</ref> चूँकि, सामान्यतः, सामान्य योजना पर वेइल भाजक को स्थानीय रूप से प्रमुख होने की आवश्यकता नहीं होती है; ऊपर चतुर्भुज शंकु के उदाहरण देखें। | ||
===प्रभावी कार्टियर | ===प्रभावी कार्टियर भाजक=== | ||
प्रभावी कार्टियर | प्रभावी कार्टियर भाजक वे होते हैं जो आदर्श शीव्स के अनुरूप होते हैं। वास्तव में, प्रभावी कार्टियर भाजक के सिद्धांत को तर्कसंगत कार्यों के समूह या आंशिक आदर्श समूह के संदर्भ के बिना विकसित किया जा सकता है। | ||
मान लीजिए कि X | मान लीजिए कि X योजना है। X पर ''''प्रभावी कार्टियर भाजक'''<nowiki/>' आदर्श शीफ I है जो विपरीत है और ऐसा है कि X में प्रत्येक बिंदु x के लिए, आधार I<sub>x</sub> प्रमुख है। यह आवश्यक है कि प्रत्येक x के निकट, संवृत एफ़िन उपसमुच्चय {{math|1=''U'' = Spec ''A''}} उपस्थित हो, जैसे कि {{math|1=''U'' ∩ ''D'' = Spec ''A'' / (''f'')}}, जहां f, A में गैर-शून्य भाजक है। दो प्रभावी कार्टियर भाजकों का योग आदर्श शीव्स के गुणन से युग्मित होता है। | ||
प्रभावी कार्टियर | प्रभावी कार्टियर भाजक के परिवारों का उत्तम सिद्धांत है। मान लीजिए {{math|φ : ''X'' → ''S''}} रूपवाद है। X पर ''S'' के लिए [[सापेक्ष प्रभावी कार्टियर विभाजक|सापेक्ष प्रभावी कार्टियर भाजक]] X पर प्रभावी कार्टियर भाजक ''D'' है जो ''S'' पर समतल है। समतलता धारणा के कारण, प्रत्येक के लिए <math>S'\to S,</math> D से पुलबैक <math>X \times_S S'</math> है, और यह पुलबैक प्रभावी कार्टियर भाजक है। विशेष रूप से, यह φ के फाइबर के लिए सत्य है। | ||
==कोडैरा की लेम्मा== | ==कोडैरा की लेम्मा== | ||
(बड़े) कार्टियर | (बड़े) कार्टियर भाजक के मूल परिणाम के रूप में, कोडैरा का लेम्मा नामक परिणाम होता है:<ref>{{cite book |doi=10.2969/msjmemoirs/03501C020|chapter=Chapter 2. Preliminaries |title=न्यूनतम मॉडल कार्यक्रम की नींव|series=Mathematical Society of Japan Memoirs |year=2017 |pages=16–47 |isbn=978-4-86497-045-7 }}</ref><ref>{{harv|Lazarsfeld|2004|p=141|loc=Proposition 2.2.6.}}</ref> | ||
<ref>{{harv|Lazarsfeld|2004|p=141|loc=Proposition 2.2.6.}}</ref> | |||
{{quote| | {{quote|मान लीजिये {{mvar|X}} एक अघुलनशील है [[प्रोजेक्टिव किस्म]] और मान लीजिये {{mvar|D}} बड़ा कार्टियर विभाजक बनाया जाता है {{mvar|X}} और मान लीजिये {{mvar|H}} पर प्रभावी कार्टियर विभाजक बनाया जाता है {{mvar|X}} तब | ||
:<math>H^{0} (X, \mathcal{O}_{X} (mD - H)) \neq 0</math>. | :<math>H^{0} (X, \mathcal{O}_{X} (mD - H)) \neq 0</math>. | ||
सभी के लिए पर्याप्त रूप से बड़ा <math>m \in N (X,D)</math>}} | |||
कोडैरा की प्रमेयिका बड़े भाजक के विषय में कुछ परिणाम देती है। | |||
==कार्यात्मकता== | ==कार्यात्मकता== | ||
मान लीजिए {{math|φ : ''X'' → ''Y''}} अभिन्न स्थानीय नोथेरियन योजनाओं का रूप है। भाजक D को एक योजना से दूसरी योजना में स्थानांतरित करने के लिए φ का उपयोग करना प्रायः—किन्तु सदैव नहीं—संभव होता है। क्या यह संभव है यह इस विषय पर निर्भर करता है कि भाजक वेइल या कार्टियर भाजक है, क्या भाजक को X से Y या इसके विपरीत स्थानांतरित किया जाना है, और φ में कौन से अतिरिक्त गुण हो सकते हैं। | |||
यदि Z, X पर | यदि Z, X पर अभाज्य वेइल भाजक है, तो <math>\overline{\varphi(Z)}</math> Y का विवृत अपरिवर्तनीय उपयोजना है। φ के आधार पर, यह प्राइम वेइल भाजक हो भी सकता है और नहीं भी। उदाहरण के लिए, यदि φ समतल में किसी बिंदु का ब्लो अप है और Z असाधारण भाजक है, तो इसकी छवि वेइल भाजक नहीं है। इसलिए, φ<sub>*</sub>Z को परिभाषित किया गया है <math>\overline{\varphi(Z)}</math> यदि वह उपयोजना अभाज्य भाजक है और अन्यथा उसे शून्य भाजक के रूप में परिभाषित किया गया है। इसे रैखिकता द्वारा विस्तारित करने पर, यह मानते हुए कि X अर्ध-सघन है, जो समरूपता {{math|Div(''X'') → Div(''Y'')}} को परिभाषित करेगा जिसे पुशफॉरवर्ड कहा जाता है। (यदि ''X'' अर्ध-सघन नहीं है, तो पुशफॉरवर्ड स्थानीय रूप से सीमित योग होने में विफल हो सकता है।) यह चाउ समूहों पर पुशफॉरवर्ड की विशेष स्थिति है। | ||
यदि ''Z'' | यदि ''Z'' कार्टियर भाजक है, तो φ पर हल्की परिकल्पना के अंतर्गत, पुलबैक <math>\varphi^*Z</math> है। शीफ़-सैद्धांतिक रूप से, जब कोई पुलबैक मानचित्र <math>\varphi^{-1}\mathcal{M}_Y \to \mathcal{M}_X</math> होता है, तो इस पुलबैक का उपयोग कार्टियर भाजकों के पुलबैक को परिभाषित करने के लिए किया जा सकता है। स्थानीय अनुभागों के संदर्भ में, का पुलबैक <math>\{(U_i, f_i)\}</math> को <math>\{(\varphi ^{-1}(U_i), f_i \circ \varphi)\}</math> द्वारा परिभाषित किया गया है यदि φ प्रभावी है तो पुलबैक को सदैव परिभाषित किया जाता है, किन्तु इसे सामान्य रूप से परिभाषित नहीं किया जा सकता है। उदाहरण के लिए, यदि {{math|1=''X'' = ''Z''}} और φ, Y में Z का समावेश है, फिर φ<sup>*</sup>Z अपरिभाषित है क्योंकि संबंधित स्थानीय अनुभाग प्रत्येक समिष्ट पर शून्य होंगे। (चूँकि, संबंधित लाइन बंडल का पुलबैक परिभाषित है।) | ||
यदि φ समतल है, तो वेइल | यदि φ समतल है, तो वेइल भाजक का पुलबैक परिभाषित किया गया है। इस स्थिति में, Z का पुलबैक {{math|1=φ<sup>*</sup>''Z'' = φ<sup>−1</sup>(''Z'')}} है। φ की समतलता यह सुनिश्चित करती है कि Z की व्युत्क्रम छवि का कोड आयाम बना रहे। यह उन आकृतियों के लिए विफल हो सकता है जो समतल नहीं हैं, उदाहरण के लिए, छोटे संकुचन के लिए है। | ||
==प्रथम चेर्न वर्ग== | ==प्रथम चेर्न वर्ग== | ||
अभिन्न नोथेरियन योजना | अभिन्न नोथेरियन योजना; | ||
:<math> c_1 : \operatorname{Pic}(X) \to \operatorname{Cl}(X),</math> | :<math> c_1 : \operatorname{Pic}(X) \to \operatorname{Cl}(X),</math> | ||
प्रथम चेर्न वर्ग के रूप में जाना जाता है।<ref>For a variety ''X'' over a field, the Chern classes of any vector bundle on ''X'' act by [[cap product]] on the Chow groups of ''X'', and the homomorphism here can be described as ''L'' ↦ c<sub>1</sub>(''L'') ∩ [''X''].</ref><ref>{{harvnb|Eisenbud|Harris|2016|loc=§ 1.4.}}</ref> यदि X सामान्य है तो | प्रथम चेर्न वर्ग के रूप में जाना जाता है।<ref>For a variety ''X'' over a field, the Chern classes of any vector bundle on ''X'' act by [[cap product]] on the Chow groups of ''X'', and the homomorphism here can be described as ''L'' ↦ c<sub>1</sub>(''L'') ∩ [''X''].</ref><ref>{{harvnb|Eisenbud|Harris|2016|loc=§ 1.4.}}</ref> यदि X सामान्य है तो प्रथम चेर्न वर्ग इंजेक्शन है, और यदि X फैक्टोरियल है (जैसा कि ऊपर परिभाषित है) तो यह समरूपता है। विशेष रूप से, कार्टियर भाजक को किसी भी नियमित योजना पर वेइल भाजक के साथ पहचाना जा सकता है, और इसलिए प्रथम चेर्न वर्ग X नियमित के लिए समरूपता है। | ||
स्पष्ट रूप से, प्रथम चेर्न वर्ग को इस प्रकार परिभाषित किया जा सकता है। इंटीग्रल नोथेरियन | स्पष्ट रूप से, प्रथम चेर्न वर्ग को इस प्रकार परिभाषित किया जा सकता है। इंटीग्रल नोथेरियन योजना तब L के प्रथम चेर्न वर्ग को भाजक के रूप में परिभाषित किया जा सकता है। परिमेय भाग s को परिवर्तित करने से यह भाजक रैखिक तुल्यता द्वारा परिवर्तित किया जाता है, क्योंकि (fs) = (f) + (s) गैर-शून्य परिमेय फलन f और L के गैर-शून्य परिमेय भागs के लिए है। इसलिए Cl(X) में तत्व c<sub>1</sub>(L) उचित प्रकार से परिभाषित है। | ||
आयाम n | आयाम n का समिष्ट प्रकार; | ||
:<math>\operatorname{Cl}(X) \to H_{2n-2}^{\operatorname{BM}}(X, \mathbf{Z}).</math> | :<math>\operatorname{Cl}(X) \to H_{2n-2}^{\operatorname{BM}}(X, \mathbf{Z}).</math> | ||
पश्चात वाले समूह को इसकी शास्त्रीय (यूक्लिडियन) टोपोलॉजी के साथ, X के समिष्ट बिंदुओं के X('''C''') का उपयोग करके परिभाषित किया गया है। इसी प्रकार, पिकार्ड समूह टोपोलॉजिकल अर्थ में प्रथम चेर्न वर्ग द्वारा इंटीग्रल कोहोमोलॉजी का मानचित्रण करता है: | |||
:<math>\operatorname{Pic}(X) \to H^2(X, \mathbf{Z}).</math> | :<math>\operatorname{Pic}(X) \to H^2(X, \mathbf{Z}).</math> | ||
दो समरूपताएं | दो समरूपताएं [[क्रमविनिमेय आरेख]] से संबंधित हैं, जहां उचित ऊर्ध्वाधर मानचित्र बोरेल-मूर होमोलॉजी में X के मौलिक वर्ग के साथ कैप उत्पाद है: | ||
:<math> \begin{array}{ccc} | :<math> \begin{array}{ccc} | ||
| Line 176: | Line 179: | ||
\operatorname{Cl}(X) &\longrightarrow & H_{2n-2}^{\operatorname{BM}}(X,\mathbf{Z}) | \operatorname{Cl}(X) &\longrightarrow & H_{2n-2}^{\operatorname{BM}}(X,\mathbf{Z}) | ||
\end{array} </math> | \end{array} </math> | ||
' | 'C ' पर X के लिए, दोनों ऊर्ध्वाधर मानचित्र समरूपता हैं। | ||
==लाइन बंडलों और रैखिक प्रणालियों के वैश्विक भाग == | |||
कार्टियर भाजक प्रभावी होता है यदि इसका स्थानीय परिभाषित फलन f<sub>''i''</sub> नियमित हो (केवल तर्कसंगत फलन नहीं)। उस स्थिति में, कार्टियर भाजक को X में कोडिमेंशन 1 की विवृत उप-योजना के साथ पहचाना जा सकता है, उप-योजना को स्थानीय रूप से f<sub>i</sub> = 0 द्वारा परिभाषित किया गया है। कार्टियर भाजक D प्रभावी भाजक के रैखिक रूप से समतुल्य है यदि और केवल इसकी संबद्ध रेखा बंडल हो <math>\mathcal{O}(D)</math> गैर-शून्य वैश्विक अनुभाग है; तब D, s के शून्य बिंदुपथ के रैखिक रूप से समतुल्य है। | |||
मान लीजिए कि X क्षेत्र k पर प्रक्षेप्य विविधता है। फिर वैश्विक भाग को गुणा करना <math>\mathcal{O}(D)</math> k में शून्येतर अदिश द्वारा इसका शून्य स्थान परिवर्तित नहीं किया जाता है। परिणामस्वरूप, वैश्विक वर्गों H<sup>0</sup>(X, O(D)) के k-सदिश समिष्ट में रेखाओं के प्रक्षेप्य समिष्ट को D के रैखिक रूप से समतुल्य प्रभावी भाजकों के समुच्चय से पहचाना जा सकता है, जिसे D की 'पूर्ण रैखिक प्रणाली' कहा जाता है। इस प्रक्षेप्य समिष्ट के प्रक्षेप्य रैखिक उपसमिष्ट को भाजकों की रैखिक प्रणाली कहा जाता है। | |||
लाइन बंडल के वैश्विक भागों के समिष्ट का अध्ययन करने का कारण किसी दिए गए विविधता से लेकर प्रक्षेप्य समिष्ट तक के संभावित मानचित्रों को समझना है। बीजगणितीय विविधता के वर्गीकरण के लिए यह आवश्यक है। स्पष्ट रूप से, क्षेत्र k पर विविधता X से प्रक्षेप्य समिष्ट P<sup>n</sup> तक रूपवाद, X पर लाइन बंडल L निर्धारित करता है, जो मानक लाइन बंडल का [[पुलबैक बंडल]] <math>\mathcal{O}(1)</math> पर P<sup>n</sup> है। इसके अतिरिक्त, L n+1 अनुभागों के साथ आता है जिनका [[आधार स्थान|आधार समिष्ट]] रिक्त है। रूपवाद X → P<sup>n</sup> निर्धारित करता है।<ref>Hartshorne (1977), Theorem II.7.1.</ref> ये अवलोकन कार्टियर भाजक (या लाइन बंडल) के लिए धनात्मकता की कई धारणाओं को उत्पन्न करते हैं, जैसे कि पर्याप्त भाजक और [[नेफ विभाजक|नेफ भाजक]] है।<ref>{{harv|Lazarsfeld|2004|loc=Chapter 1}}</ref> | |||
क्षेत्र k पर प्रक्षेप्य विविधता X पर भाजक D के लिए, k-सदिश समिष्ट H<sup>0</sup>(X, O(D)) का सीमित आयाम है। रीमैन-रोच प्रमेय इस सदिश समिष्ट के आयाम की गणना करने के लिए मौलिक उपकरण है जब X प्रक्षेप्य वक्र है। क्रमिक सामान्यीकरण, हिरज़ेब्रुच-रीमैन-रोच प्रमेय और ग्रोथेंडिक-रीमैन-रोच प्रमेय, किसी क्षेत्र पर किसी भी आयाम की प्रक्षेप्य विविधता X के लिए H<sup>0</sup>(X, O(D)) के आयाम के विषय में कुछ सूचना देते हैं। | |||
क्योंकि विहित | क्योंकि विहित भाजक आंतरिक रूप से विविधता से जुड़ा होता है, विविधता के वर्गीकरण में महत्वपूर्ण भूमिका K<sub>X</sub> और उसके धनात्मक गुणकों द्वारा दिए गए प्रक्षेप्य समिष्ट के मानचित्रों द्वारा निभाई जाती है। X का कोडैरा आयाम प्रमुख [[द्विवार्षिक ज्यामिति|द्विवार्षिक]] अपरिवर्तनीय है, जो m बढ़ने पर सदिश रिक्त समिष्ट H<sup>0</sup>(X, mK<sub>X</sub>) (अर्थात् H<sup>0</sup>(X, O(mK<sub>X</sub>))) की वृद्धि को मापता है। कोडैरा आयाम सभी n-आयामी विविधता को n+2 वर्गों में विभाजित करता है, जो (सामान्यतः) धनात्मक वक्रता से ऋणात्मक वक्रता की ओर जाते हैं। | ||
== | == Q-भाजक == | ||
माना कि X | माना कि X सामान्य प्रकार है। (वेइल) '<nowiki/>'''Q'''<nowiki/>'-भाजक तर्कसंगत गुणांक के साथ X की इरेड्यूसबल कोडिमेंशन-1 उप-विविधता का सीमित औपचारिक रैखिक संयोजन है। ('<nowiki/>'''R'''<nowiki/>'-भाजक को इसी प्रकार परिभाषित किया गया है।) यदि गुणांक गैर-नकारात्मक हैं तो '<nowiki/>'''Q'''<nowiki/>'-भाजक 'प्रभावी' होता है। यदि mD किसी धनात्मक पूर्णांक m के लिए कार्टियर भाजक है तो '<nowiki/>'''Q'''<nowiki/>'-भाजक D '<nowiki/>'''Q'''-कार्टियर' है। यदि X सुचारू है, तो प्रत्येक ''''Q'''<nowiki/>'-भाजक ''''Q'''<nowiki/>'-कार्टियर है। | ||
यदि, | |||
:<math>D= \sum_j a_j Z_j</math> | :<math>D= \sum_j a_j Z_j</math> | ||
क्यू- | क्यू-भाजक है, तो इसका राउंड-डाउन भाजक है: | ||
:<math>\lfloor D\rfloor = \sum \lfloor a_j \rfloor Z_j,</math> | :<math>\lfloor D\rfloor = \sum \lfloor a_j \rfloor Z_j,</math> | ||
जहाँ <math>\lfloor a \rfloor</math> a से कम या उसके समान सबसे बड़ा पूर्णांक है। शीफ <math>\mathcal{O}(D)</math> को तब <math>\mathcal{O}(\lfloor D\rfloor)</math> के रूप में परिभाषित किया जाता है। | |||
== ग्रोथेंडि-लेफ़्सचेत्ज़ हाइपरप्लेन प्रमेय == | == ग्रोथेंडि-लेफ़्सचेत्ज़ हाइपरप्लेन प्रमेय == | ||
[[लेफ्शेट्ज़ हाइपरप्लेन प्रमेय]] का तात्पर्य है कि कम से कम 4 आयाम की | [[लेफ्शेट्ज़ हाइपरप्लेन प्रमेय]] का तात्पर्य है कि कम से कम 4 आयाम की चिकनी समिष्ट प्रक्षेप्य प्रकार उदाहरण के लिए, यदि Y समिष्ट प्रक्षेप्य में कम से कम 3 आयाम का सहज पूर्ण प्रतिच्छेदन प्रकार है, तो Y का पिकार्ड समूह 'Z' के समरूपी है, जो प्रक्षेप्य समिष्ट पर लाइन बंडल O(1) के प्रतिबंध से उत्पन्न होता है। | ||
[[अलेक्जेंडर ग्रोथेंडिक]] ने लेफ्शेट्ज़ के प्रमेय को कई दिशाओं में सामान्यीकृत किया, जिसमें | [[अलेक्जेंडर ग्रोथेंडिक|ग्रोथेंडिक]] ने लेफ्शेट्ज़ के प्रमेय को कई दिशाओं में सामान्यीकृत किया, जिसमें इच्छानुसार आधार क्षेत्र, एकवचन प्रकार और प्रक्षेपी प्रकारों के अतिरिक्त स्थानीय वलय पर परिणाम सम्मिलित थे। विशेष रूप से, यदि R पूर्ण प्रतिच्छेदन स्थानीय वलय है, जो अधिकतम 3 कोड आयाम में भाज्य है (उदाहरण के लिए, यदि R के गैर-नियमित स्थान का कोड आयाम कम से कम 4 है), तो R अद्वितीय गुणनभागडोमेन है (और इसलिए प्रत्येक Spec(R) पर वेइल भाजक कार्टियर है)।<ref>Grothendieck, SGA 2, Corollaire XI.3.14.</ref> यहां बंधा हुआ आयाम इष्टतम है, जैसा कि ऊपर दिए गए 3-आयामी क्वाड्रिक शंकु के उदाहरण से दिखाया गया है। | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 245: | Line 249: | ||
*{{Citation | author1=The Stacks Project Authors | title=The Stacks Project | url=http://stacks.math.columbia.edu/}} | *{{Citation | author1=The Stacks Project Authors | title=The Stacks Project | url=http://stacks.math.columbia.edu/}} | ||
{{DEFAULTSORT:Divisor (Algebraic Geometry)}} | {{DEFAULTSORT:Divisor (Algebraic Geometry)}} | ||
[[Category: Machine Translated Page]] | [[Category:Created On 10/07/2023|Divisor (Algebraic Geometry)]] | ||
[[Category: | [[Category:Lua-based templates|Divisor (Algebraic Geometry)]] | ||
[[Category:Machine Translated Page|Divisor (Algebraic Geometry)]] | |||
[[Category:Pages with script errors|Divisor (Algebraic Geometry)]] | |||
[[Category:Templates Vigyan Ready|Divisor (Algebraic Geometry)]] | |||
[[Category:Templates that add a tracking category|Divisor (Algebraic Geometry)]] | |||
[[Category:Templates that generate short descriptions|Divisor (Algebraic Geometry)]] | |||
[[Category:Templates using TemplateData|Divisor (Algebraic Geometry)]] | |||
[[Category:भाजक की ज्यामिति|Divisor (Algebraic Geometry)]] | |||
Latest revision as of 11:52, 8 September 2023
बीजगणितीय ज्यामिति में, भाजक बीजगणितीय रूपों की कोडिमेशन-1 उप-विविधता का सामान्यीकरण है। दो भिन्न-भिन्न सामान्यीकरण कार्टियर भाजक और वेइल भाजक (डेविड मम्फोर्ड द्वारा पियरे कार्टियर और आंद्रे वेइल के नाम पर) सामान्य उपयोग में हैं। दोनों पूर्णांक और बीजगणितीय संख्या क्षेत्रों में विभाज्यता की धारणा से प्राप्त हुए हैं।
विश्व स्तर पर, प्रक्षेप्य समिष्ट के प्रत्येक कोडिमेशन-1 उपविविधता को सजातीय बहुपद के लुप्त होने से परिभाषित किया जाता है; इसके विपरीत, कोडिमेंशन-r आर उपविविधता को केवल r समीकरणों द्वारा परिभाषित करने की आवश्यकता नहीं होती है जब r 1 से अधिक होता है। (अर्थात्, प्रक्षेप्य समिष्ट की प्रत्येक उपविविधता पूर्ण प्रतिच्छेदन नहीं है।) स्थानीय रूप से, सुचारु योजना के प्रत्येक कोडिमेशन-1 उपविविधता को प्रत्येक बिंदु के निकट में समीकरण द्वारा परिभाषित किया जा सकता है। फिर, समान कथन उच्च-संकेतन उप-विविधता के लिए विफल रहता है। इस संपत्ति के परिणामस्वरूप, बीजगणितीय ज्यामिति का अधिकांश भाग इसके कोडिमेशन-1 उप-विविधता और संबंधित लाइन बंडलों का विश्लेषण करके इच्छानुसार विविधता का अध्ययन करता है।
एकवचन प्रकारों पर, यह संपत्ति भी विफल हो सकती है, और इसलिए किसी को कोडिमेंशन-1 उप-विविधता और प्रकारों के मध्य अंतर करना होगा जिन्हें स्थानीय रूप से समीकरण द्वारा परिभाषित किया जा सकता है। पूर्व वेइल भाजक हैं जबकि पश्चात वाले कार्टियर भाजक हैं।
टोपोलॉजिकल रूप से, वेइल भाजक होमोलॉजी कक्षाओं की भूमिका निभाते हैं, जबकि कार्टियर भाजकसह-समरूपता कक्षाओं का प्रतिनिधित्व करते हैं। सहज विविधता (या अधिक सामान्यतः नियमित योजना) पर, पोंकारे द्वैत के अनुरूप परिणाम कहता है कि वेइल और कार्टियर भाजक समान हैं।
"भाजक" नाम डेडेकाइंड और हेनरिक एम. वेबर के कार्य पर आधारित है, जिन्होंने बीजगणितीय वक्रों के अध्ययन के लिए डेडेकाइंड डोमेन की प्रासंगिकता दिखाई थी।[1] वक्र पर भाजकों का समूह (सभी भाजकों द्वारा उत्पन्न मुक्त एबेलियन समूह) डेडेकाइंड डोमेन के लिए भिन्नात्मक आदर्शों के समूह से निकटता से संबंधित है।
बीजगणितीय चक्र भाजक का उच्च कोडिमेंशन सामान्यीकरण है; परिभाषा के अनुसार, वेइल भाजक संहिता 1 का चक्र है।
रीमैन सतह पर भाजक
रीमैन सतह 1-आयामी समिष्ट मैनिफोल्ड है, और इसलिए इसके कोडिमेंशन-1 सबमैनिफोल्ड्स का आयाम 0 है। सघन रीमैन सतह X पर भाजकों का समूह X के बिंदुओं पर मुक्त एबेलियन समूह है।
समान रूप से, सघन रीमैन सतह X पर भाजक पूर्णांक गुणांक के साथ X के बिंदुओं का सीमित रैखिक संयोजन है। X पर भाजक की 'डिग्री' उसके गुणांकों का योग है।
X पर किसी भी गैर-शून्य मेरोमोर्फिक फलन f के लिए, कोई X ordp(f) में बिंदु p पर f के लुप्त होने के क्रम को परिभाषित कर सकता है। यदि f का ध्रुव p पर है तो यह पूर्णांक, ऋणात्मक है। सघन रीमैन सतह X पर गैर-शून्य मेरोमोर्फिक फलन f के भाजक को इस प्रकार परिभाषित किया गया है:
जो सीमित राशि है। (f) रूप के भाजक को 'मुख्य भाजक' भी कहा जाता है। चूँकि (fg) = (f) + (g), प्रमुख भाजक का समुच्चय भाजक के समूह का उपसमूह है। दो भाजक जो मुख्य भाजक से भिन्न होते हैं उन्हें 'रैखिक समतुल्य' कहा जाता है।
सघन रीमैन सतह पर, मुख्य भाजक की डिग्री शून्य होती है; अर्थात्, मेरोमॉर्फिक फलन के शून्यों की संख्या बहुलता के साथ गणना किये जाने वाले ध्रुवों की संख्या के समान होती है। परिणामस्वरूप, भाजक के रैखिक तुल्यता वर्गों पर डिग्री उचित प्रकार से परिभाषित होती है।
सघन रीमैन सतह D से संबंधित 'लाइन बंडल के अनुभागों का स्थान' है। D की डिग्री इस सदिश समिष्ट के आयाम के विषय में बहुत कुछ कहती है। उदाहरण के लिए, यदि D की डिग्री ऋणात्मक है, तो इसकी सदिश समष्टि शून्य है (क्योंकि मेरोमोर्फिक फलन में ध्रुवों से अधिक शून्य नहीं हो सकते हैं)। यदि D की धनात्मक डिग्री है, तो H0(X, O(mD)) का आयाम m के लिए पर्याप्त रूप से बड़े होने पर रैखिक रूप से बढ़ता है। रीमैन-रोच प्रमेय इन पंक्तियों के साथ अधिक त्रुटिहीन कथन है। दूसरी ओर, निम्न डिग्री के भाजक D के लिए H0(X, O(D)) का त्रुटिहीन आयाम सूक्ष्म है, और D की डिग्री द्वारा पूर्ण रूप से निर्धारित नहीं होता है। सघन रीमैन सतह की विशिष्ट विशेषताएं इन आयामों में परिलक्षित होती हैं।
सघन रीमैन सतह पर प्रमुख भाजक विहित भाजक है। इसे परिभाषित करने के लिए, सबसे पूर्व उपरोक्त पंक्तियों के साथ गैर-शून्य मेरोमोर्फिक 1-रूप के भाजक को परिभाषित किया जाता है। चूँकि मेरोमोर्फिक 1-रूपों की समिष्ट मेरोमोर्फिक कार्यों के क्षेत्र पर 1-आयामी सदिश समिष्ट है, कोई भी दो गैर-शून्य मेरोमोर्फिक 1-रूप रैखिक रूप से समतुल्य भाजक उत्पन्न करते हैं। इस रैखिक तुल्यता वर्ग में किसी भी भाजक को X, KX का 'विहित भाजक' कहा जाता है। X के जीनस g को विहित भाजक से पढ़ा जा सकता है: अर्थात्, KX की डिग्री 2g - 2 है। सघन रीमैन सतहों X के मध्य मुख्य ट्राइकोटॉमी यह है कि क्या विहित भाजक में नकारात्मक डिग्री है (इसलिए X में जीनस शून्य है), शून्य डिग्री (जीनस) एक), या धनात्मक डिग्री (जीनस कम से कम 2)। उदाहरण के लिए, यह निर्धारित करता है कि क्या X के निकट धनात्मक वक्रता, शून्य वक्रता, या नकारात्मक वक्रता वाला काहलर मीट्रिक है। विहित भाजक की डिग्री ऋणात्मक है यदि और केवल X रीमैन क्षेत्र CP1 के लिए समरूपी है।
वेइल भाजक
मान लीजिए कि X अभिन्न स्थानीय नोथेरियन योजना है। X पर 'अभाज्य भाजक' या 'अपरिवर्तनीय भाजक' X में कोडिमेशन 1 का अभिन्न विवृत उपयोजना Z है। X पर वेइल भाजक, X के अभाज्य भाजक Z पर औपचारिक योग है:
जहां संग्रह स्थानीय रूप से सीमित है। यदि X अर्ध-सघन है, तो स्थानीय परिमितता इसके समान है परिमित होता है। सभी वेइल भाजकों के समूह को Div(X) द्वारा दर्शाया गया है। यदि सभी गुणांक गैर-ऋणात्मक हैं तो वेइल भाजक D 'प्रभावी' है। यदि अंतर D − D′ प्रभावी है तो D ≥ D′ लिखा जाता है।
उदाहरण के लिए, किसी क्षेत्र के बीजगणितीय वक्र पर भाजक सीमित रूप से कई विवृत बिंदुओं का औपचारिक योग होता है। Spec Z पर भाजक पूर्णांक गुणांक के साथ अभाज्य संख्याओं का औपचारिक योग है और इसलिए Q में गैर-शून्य भिन्नात्मक आदर्श से युग्मित होता है। समान लक्षण वर्णन भाजक के लिए सत्य है, जहाँ K संख्या क्षेत्र है।
यदि Z ⊂ X अभाज्य भाजक है, तो स्थानीय वलय में क्रुल आयाम है। यदि गैर-शून्य है, तो Z के साथ f के लुप्त होने का क्रम, जिसे ordZ(f) लिखा जाता है, मॉड्यूल की लंबाई है यह लंबाई सीमित है,[2] और यह गुणन के संबंध में योगात्मक है, अर्थात, ordZ(fg) = ordZ(f) + ordZ(g) है।[3] यदि k(X) X पर तर्कसंगत कार्यों का क्षेत्र है, तो किसी भी गैर-शून्य f ∈ k(X) को भागफल g / h के रूप में लिखा जा सकता है, जहां g और h हैं और f के लुप्त होने के क्रम को ordZ(g) − ordZ(h) के रूप में परिभाषित किया गया है।[4] इस परिभाषा के साथ, लुप्त होने का क्रम फलन ordZ : k(X)× → Z है। यदि X सामान्य है, तो स्थानीय वलय भिन्न मूल्यांकन वलय और फलन ordZ संबंधित मूल्यांकन है। X पर गैर-शून्य तर्कसंगत फलन f के लिए, f से जुड़े 'प्रमुख वेइल भाजक' को वेइल भाजक के रूप में परिभाषित किया गया है:
यह दिखाया जा सकता है कि यह योग स्थानीय रूप से सीमित है और इसलिए यह वास्तव में वेइल भाजक को परिभाषित करता है। f से जुड़े प्रमुख वेइल भाजक (f) को भी नोट किया गया है। यदि f नियमित फलन है, तो इसका प्रमुख वेइल भाजक प्रभावी है, किन्तु सामान्यतः यह सत्य नहीं है। लुप्त होने वाले फलन के क्रम की योज्यता का तात्पर्य यह है:
परिणामस्वरूप div समरूपता है, और विशेष रूप से इसकी छवि सभी वेइल भाजकों के समूह का उपसमूह है।
मान लीजिए कि X सामान्य इंटीग्रल नॉथेरियन योजना है। प्रत्येक वेइल भाजक D सुसंगत शीफ X पर निर्धारित करता है। ठोस रूप से इसे तर्कसंगत कार्यों के शीफ के उपशीर्षक के रूप में परिभाषित किया जा सकता है।[5]
अर्थात्, शून्येतर परिमेय फलन f का भाग है U से अधिक यदि और केवल किसी अभाज्य भाजक Z के लिए जो U को प्रतिच्छेद करता है,
जहां nZ D में Z का गुणांक है। यदि D प्रमुख है, इसलिए D परिमेय फलन g का भाजक है, तो समरूपता है:
- तब से प्रभावी भाजक है और इसलिए X की सामान्यता के कारण नियमित है। इसके विपरीत, यदि समरूपी है के रूप में -मॉड्यूल, तो D प्रमुख है। इसका तात्पर्य यह है कि D स्थानीय रूप से प्रमुख है यदि और केवल विपरीत है; अर्थात लाइन बंडल है।
यदि D प्रभावी भाजक है तो से प्रायः उपयोग किया जाने वाला संक्षिप्त त्रुटिहीनअनुक्रम प्राप्त होता है,
इस क्रम की शीफ सहसंरचना यह दर्शाती है में यह सूचना सम्मिलित है कि क्या D पर नियमित कार्य X पर नियमित कार्य के प्रतिबंध हैं।
इसमें समूहों का भी समावेश है:
यह विहित तत्व प्रस्तुत करता है, अर्थात्, वैश्विक भाग 1 की छवि है। इसे विहित अनुभाग कहा जाता है और इसे sD से दर्शाया जा सकता है। जबकि विहित अनुभाग कहीं लुप्त न होने वाले तर्कसंगत फलन की छवि है, इसकी छवि D के साथ लुप्त हो जाता है क्योंकि संक्रमण फलन D के साथ लुप्त हो जाते हैं। जब D सुचारु कार्टियर भाजक होता है, तो उपरोक्त समावेशन के कोकर्नेल की पहचान की जा सकती है; नीचे कार्टियर भाजक देखें।
मान लें कि X क्षेत्र पर परिमित प्रकार की सामान्य अभिन्न पृथक योजना है। मान लीजिए D वेइल भाजक है। तब श्रेणी वन रिफ्लेक्सिव शीफ है, और तब से के उपशीर्षक के रूप में परिभाषित किया गया है। यह भिन्नात्मक आदर्श शीफ है (नीचे देखें)। इसके विपरीत, प्रत्येक श्रेणी रिफ्लेक्सिव शीफ वेइल भाजक से युग्मित होती है: शीफ को नियमित लोकस तक सीमित किया जा सकता है, जहां यह मुक्त हो जाता है और इसलिए कार्टियर भाजक से युग्मित होता है (पुनः, नीचे देखें), और क्योंकि एकवचन लोकस में कम से कम दो कोडिमेंशन होता है, कार्टियर भाजक का विवृत होना वेइल भाजक है।
भाजक वर्ग समूह
वेइल भाजक वर्ग समूह Cl(X) सभी प्रमुख वेइल भाजक के उपसमूह द्वारा Div(X) का भागफल है। दो भाजकों को रैखिक रूप से समतुल्य कहा जाता है यदि उनका अंतर प्रमुख है, इसलिए भाजक वर्ग समूह भाजक मॉड्यूलो रैखिक तुल्यता का समूह है। किसी फ़ील्ड पर आयाम n की विविधता X के लिए, भाजक वर्ग समूह चाउ समूह है; अर्थात्, Cl(X) (n−1)-आयामी चक्रों का चाउ समूह CHn−1(X) है।
मान लीजिए Z, X का विवृत उपसमुच्चय है। यदि Z, कोड आयाम का अपरिवर्तनीय है, तो Cl(X - Z) Z के वर्ग द्वारा Cl(X) के भागफल समूह के लिए समरूपी है। यदि Z का कोड आयाम X में कम से कम 2 है , तो प्रतिबंध Cl(X) → Cl(X − Z) समरूपता है।[6] (ये तथ्य चाउ समूहों के स्थानीयकरण अनुक्रम की विशेष स्थिति है।)
सामान्य इंटीग्रल नोथेरियन योजना X पर, दो वेइल भाजक D, E रैखिक रूप से समतुल्य हैं यदि और केवल और के रूप में समरूपी हैं -मॉड्यूल X पर रिफ्लेक्सिव शीव्स के समरूपी वर्ग मोनोइड बनाते हैं जिसमें उत्पाद को टेंसर उत्पाद के रिफ्लेक्सिव पतवार के रूप में दिया जाता है। तब X के वेइल भाजक वर्ग समूह से X पर श्रेणी-वन रिफ्लेक्सिव शीव्स के समरूपी वर्गों के मोनोइड तक मोनोइड समरूपता को परिभाषित करता है।
उदाहरण
- मान लीजिए k क्षेत्र है, और मान लीजिए n धनात्मक पूर्णांक है। चूँकि बहुपद वलय k[x1, ..., xn] अद्वितीय गुणनखंडन डोमेन है, एफाइन समिष्ट An k का भाजक वर्ग समूह शून्य के समानहै।[7] चूँकि k से हाइपरप्लेन H के ऊपर प्रक्षेप्य समिष्ट Pn, An के समरूपी है, इसलिए यह इस प्रकार है कि Pn का भाजक वर्ग समूह H के वर्ग द्वारा उत्पन्न होता है। वहां से, यह परिक्षण सीधा है कि Cl('P'n) वास्तव में H द्वारा उत्पन्न पूर्णांक 'Z' के समरूपी है। सामान्यतः, इसका तात्पर्य है कि Pn का प्रत्येक कोडिमेशन-1 उप-विविधता को एकल सजातीय बहुपद के लुप्त होने से परिभाषित किया गया है।
- मान लीजिए कि X क्षेत्र k पर बीजगणितीय वक्र है। X में प्रत्येक विवृत बिंदु p में k के कुछ परिमित विस्तार क्षेत्र E के लिए विशिष्ट E का रूप होता है, और p की 'डिग्री' को k के ऊपर E की डिग्री के रूप में परिभाषित किया जाता है। इसे रैखिकता द्वारा विस्तारित करने से X पर भाजक के लिए 'डिग्री' की धारणा मिलती है। यदि X, k पर प्रक्षेप्य वक्र है, तो X पर गैर-शून्य तर्कसंगत फलन f के भाजक की डिग्री शून्य है।[8] परिणामस्वरूप, प्रक्षेप्य वक्र X के लिए, डिग्री समरूपता डिग्री देती है: Cl(X) → 'Z'।
- क्षेत्र k पर प्रक्षेप्य रेखा P1 के लिए, डिग्री समरूपता Cl(P1) ≅ Z देती है। k-तर्कसंगत बिंदु के साथ किसी भी सुचारु प्रक्षेप्य वक्र X के लिए, डिग्री समरूपता विशेषण है, और कर्नेल के समूह के लिए समरूपता है - X की जैकोबियन प्रकार पर k-बिंदु, जो X के जीनस के समान आयाम का एबेलियन प्रकार है। उदाहरण के लिए, यह इस प्रकार है कि समिष्ट अण्डाकार वक्र का भाजक वर्ग समूह अनंत एबेलियन समूह है।
- पिछले उदाहरण को सामान्यीकृत करना: क्षेत्र k पर किसी भी सहज प्रक्षेप्य विविधता X के लिए, जैसे कि X में k-तर्कसंगत बिंदु है, भाजक वर्ग समूह Cl( X) जुड़े हुए समूह योजना के k-बिंदुओं के समूह द्वारा सूक्ष्म रूप से उत्पन्न एबेलियन समूह, नेरॉन-सेवेरी समूह का विस्तार है।[9] विशेषता शून्य के k के लिए, एबेलियन विविधता है, X की पिकार्ड विविधता है।
- R के लिए किसी संख्या क्षेत्र के पूर्णांकों का वलय, भाजक वर्ग समूह Cl(R) := Cl(Spec R) को R का आदर्श वर्ग समूह भी कहा जाता है। यह परिमित एबेलियन समूह है। आदर्श वर्ग समूहों को समझना बीजगणितीय संख्या सिद्धांत का केंद्रीय लक्ष्य है।
- मान लीजिए कि X आयाम 2 का चतुर्भुज शंकु है, जो क्षेत्र के ऊपर एफ़िन 3-समिष्ट में समीकरण xy = z2 द्वारा परिभाषित है। फिर x = z = 0 द्वारा परिभाषित X में रेखा D मूल बिंदु के निकट X पर प्रमुख नहीं है। ध्यान दें कि D को X पर समीकरण द्वारा समुच्चय के रूप में परिभाषित किया जा सकता है, अर्थात् x = 0; किन्तु X पर फलन x, D के अनुदिश क्रम 2 पर लुप्त हो जाता है, और इसलिए हम केवल यह पाते हैं कि 2D, X पर कार्टियर (जैसा कि नीचे परिभाषित है) है। वास्तव में, भाजक वर्ग समूह Cl(X) चक्रीय समूह 'Z'/2 के लिए समरूपी है। जो D के वर्ग द्वारा उत्पन्न होता है।[10]
- मान लीजिए कि X आयाम 3 का चतुर्भुज शंकु है, जो क्षेत्र के ऊपर 4-समिष्ट में समीकरण xy = zw द्वारा परिभाषित है। फिर x = z = 0 द्वारा परिभाषित X में समतल D को मूल बिंदु के निकट समीकरण द्वारा, यहां तक कि समुच्चय के रूप में भी, X में परिभाषित नहीं किया जा सकता है। इससे यह निष्कर्ष निकलता है कि D, X पर 'Q-कार्टियर' नहीं है; अर्थात्, D का कोई भी धनात्मक गुणज कार्टियर नहीं है। वास्तव में, भाजक वर्ग समूह Cl(X) D के वर्ग द्वारा उत्पन्न पूर्णांक 'Z' के समरूपी है।[11]
विहित भाजक
मान लीजिए कि X आदर्श क्षेत्र में सामान्य प्रकार है। X की सहज समिष्ट U विवृत उपसमुच्चय है जिसके पूरक का कोड आयाम कम से कम 2 है। मान लीजिए कि j: U → X समावेशन मानचित्र है, तो प्रतिबंध समरूपता इस प्रकार है:
समरूपता है, क्योंकि X - U का X में कोड आयाम कम से कम 2 कोडिमेंशन है। उदाहरण के लिए, कोई X के विहित भाजक KX को परिभाषित करने के लिए इस समरूपता का उपयोग कर सकता है: यह U पर शीर्ष डिग्री के विभेदक रूपों के लाइन बंडल के अनुरूप वेइल भाजक (रैखिक तुल्यता तक) है। समतुल्य रूप से, शीफ प्रत्यक्ष छवि शीफ है, जहाँ n, X का आयाम है।
'उदाहरण': मान लीजिए X = 'P'n सजातीय निर्देशांक x0, ...,xn के साथ प्रक्षेप्य n-समिष्ट है। माना U = {x0 ≠ 0} तब U निर्देशांक yi = xi/x0 के साथ एफ़िन n-समिष्ट के लिए समरूपी है। मान लीजिए कि:
तब ω U पर तर्कसंगत अंतर रूप है; इस प्रकार, यह तर्कसंगत भाग है। जिसमें Zi= {xi= 0}, i = 1, ..., n के अनुदिश सरल ध्रुव हैं। भिन्न एफ़िन चार्ट पर स्विच करने से केवल ω का चिह्न परिवर्तित होता है और इसलिए हम देखते हैं कि ω में Z0 के साथ सरल ध्रुव भी है। इस प्रकार, ω का भाजक है:
और इसका भाजक वर्ग है:
जहां [H] = [Zi], i = 0, ..., n है। (यूलर अनुक्रम भी देखें।)
कार्टियर भाजक
मान लीजिए कि X अभिन्न नोथेरियन योजना है। तब X के निकट तर्कसंगत फलनों का समूह है सभी नियमित फलन तर्कसंगत फलन हैं, जो संक्षिप्त त्रुटिहीन अनुक्रम की ओर ले जाते हैं:
X पर कार्टियर भाजक का वैश्विक भाग है। जहाँ का संवृत आवरण है का भाग है पर और पर के भाग से गुणा तक है।
कार्टियर भाजक में शीफ-सैद्धांतिक विवरण भी होता है। भिन्नात्मक आदर्श शीफ उप- है -मॉड्यूल का भिन्नात्मक आदर्श शीफ़ J 'विपरीत' है यदि, X में प्रत्येक x के लिए, x का संवृत U उपस्थित है जिस पर J से U का प्रतिबंध समान होता है जहाँ और उत्पाद अंदर ले जाया जाता है प्रत्येक कार्टियर भाजक संग्रह के रूप में कार्टियर भाजक के विवरण का उपयोग करके विपरीत भिन्नात्मक आदर्श शीफ को परिभाषित करता है और इसके विपरीत, व्युत्क्रमणीय भिन्नात्मक आदर्श शीव्स कार्टियर भाजक को परिभाषित करते हैं। यदि कार्टियर भाजक को D निरूपित किया जाता है, तो संबंधित भिन्नात्मक आदर्श शीफ को या L(D) निरूपित किया जाता है।
उपरोक्त त्रुटिहीन अनुक्रम के अनुसार, शीफ़ कोहोलॉजी समूहों का त्रुटिहीन अनुक्रम है:
कार्टियर भाजक को प्रमुख कहा जाता है यदि यह समरूपता की छवि में है, अर्थात्, यदि यह X पर परिमेय फलन का भाजक है। दो कार्टियर भाजक 'रैखिक रूप से समतुल्य' हैं यदि उनका अंतर मूलधन है। इंटीग्रल नोथेरियन योजना X पर प्रत्येक लाइन बंडल L कुछ कार्टियर भाजक का वर्ग है। परिणामस्वरूप, उपरोक्त त्रुटिहीन अनुक्रम कार्टियर डिवाइजर्स मॉड्यूलो रैखिक तुल्यता के समूह के साथ अभिन्न नोथेरियन योजना X पर लाइन बंडलों के पिकार्ड समूह की पहचान करता है। यह सामान्यतः कम नोथेरियन योजनाओं, या नोथेरियन रिंग पर अर्ध-प्रोजेक्टिव योजनाओं के लिए प्रारम्भ होता है,[12] किन्तु यह सामान्य रूप से विफल हो सकता है (यहां तक कि C से अधिक उचित योजनाओं के लिए भी), जो पूर्ण व्यापकता में कार्टियर भाजकों की रुचि को अल्प कर देता है।[13]
मान लें कि D प्रभावी कार्टियर भाजक है। फिर संक्षिप्त त्रुटिहीन क्रम है:
यह क्रम स्थानीय रूप से मुफ़्त है, और इसलिए उस अनुक्रम को टेंसर किया जा रहा है और संक्षिप्त त्रुटिहीन अनुक्रम उत्पन्न करता है। जब D सुचारु हो, X में D का सामान्य बंडल है।
वेइल भाजक और कार्टियर भाजक की तुलना
वेइल भाजक D को 'कार्टियर' कहा जाता है यदि और केवल शीफ विपरीत है। जब ऐसा होता है, (MX में इसके एम्बेडिंग के साथ) कार्टियर भाजक से संबद्ध रेखा बंडल है। अधिक त्रुटिहीन रूप से, यदि विपरीत है, तो ऐसा संवृत आवरण {Ui} उपस्थित है जैसे कि प्रत्येक संवृत समुच्चय पर तुच्छ बंडल तक सीमित है। प्रत्येक Ui के लिए, समरूपता का चयन किया जाता है, की छवि इस मानचित्र के अंतर्गत अनुभाग है। क्योंकि तर्कसंगत फलन के समूह के उपशीर्षक के रूप में परिभाषित किया गया है, 1 की छवि को कुछ तर्कसंगत फलन के साथ पहचाना जा सकता है, संग्रह तब कार्टियर भाजक है। यह उचित प्रकार से परिभाषित है क्योंकि इसमें सम्मिलित एकमात्र विकल्प कवरिंग और समरूपता के थे, जिनमें से कोई भी कार्टियर भाजक को नहीं परिवर्तित करता है। इस कार्टियर भाजक का उपयोग शीफ का उत्पादन करने के लिए किया जा सकता है, जिसे भेद के लिए हम L(D) नोट करेंगे। की समरूपता है संवृत कवर {Ui} पर कार्य करके L(D) के साथ को परिभाषित किया गया है। यह परीक्षण करने के लिए मुख्य तथ्य यह है कि संक्रमण फलन करता है और L(D) संगत हैं, और इसका तात्पर्य यह है कि इन सभी फलनों का रूप है।
विपरीत दिशा में, कार्टियर भाजक इंटीग्रल नोथेरियन योजना पर X प्राकृतिक प्रकार से X पर वेइल भाजक निर्धारित करता है संवृत समुच्चय Ui पर फलन fi के लिए है।
यदि;
नोएथेरियन योजना X को 'फैक्टोरियल' कहा जाता है यदि X के सभी स्थानीय वलय अद्वितीय गुणनखंडन डोमेन हैं।[5] (कुछ लेखक स्थानीय रूप से फैक्टोरियल कहते हैं।) विशेष रूप से, प्रत्येक नियमित योजना तथ्यात्मक होती है।[14] फैक्टोरियल योजना X पर, प्रत्येक वेइल भाजक D स्थानीय रूप से प्रमुख है, और इसी प्रकार सदैव लाइन बंडल होता है।[7] चूँकि, सामान्यतः, सामान्य योजना पर वेइल भाजक को स्थानीय रूप से प्रमुख होने की आवश्यकता नहीं होती है; ऊपर चतुर्भुज शंकु के उदाहरण देखें।
प्रभावी कार्टियर भाजक
प्रभावी कार्टियर भाजक वे होते हैं जो आदर्श शीव्स के अनुरूप होते हैं। वास्तव में, प्रभावी कार्टियर भाजक के सिद्धांत को तर्कसंगत कार्यों के समूह या आंशिक आदर्श समूह के संदर्भ के बिना विकसित किया जा सकता है।
मान लीजिए कि X योजना है। X पर 'प्रभावी कार्टियर भाजक' आदर्श शीफ I है जो विपरीत है और ऐसा है कि X में प्रत्येक बिंदु x के लिए, आधार Ix प्रमुख है। यह आवश्यक है कि प्रत्येक x के निकट, संवृत एफ़िन उपसमुच्चय U = Spec A उपस्थित हो, जैसे कि U ∩ D = Spec A / (f), जहां f, A में गैर-शून्य भाजक है। दो प्रभावी कार्टियर भाजकों का योग आदर्श शीव्स के गुणन से युग्मित होता है।
प्रभावी कार्टियर भाजक के परिवारों का उत्तम सिद्धांत है। मान लीजिए φ : X → S रूपवाद है। X पर S के लिए सापेक्ष प्रभावी कार्टियर भाजक X पर प्रभावी कार्टियर भाजक D है जो S पर समतल है। समतलता धारणा के कारण, प्रत्येक के लिए D से पुलबैक है, और यह पुलबैक प्रभावी कार्टियर भाजक है। विशेष रूप से, यह φ के फाइबर के लिए सत्य है।
कोडैरा की लेम्मा
(बड़े) कार्टियर भाजक के मूल परिणाम के रूप में, कोडैरा का लेम्मा नामक परिणाम होता है:[15][16]
मान लीजिये X एक अघुलनशील है प्रोजेक्टिव किस्म और मान लीजिये D बड़ा कार्टियर विभाजक बनाया जाता है X और मान लीजिये H पर प्रभावी कार्टियर विभाजक बनाया जाता है X तब
- .
सभी के लिए पर्याप्त रूप से बड़ा
कोडैरा की प्रमेयिका बड़े भाजक के विषय में कुछ परिणाम देती है।
कार्यात्मकता
मान लीजिए φ : X → Y अभिन्न स्थानीय नोथेरियन योजनाओं का रूप है। भाजक D को एक योजना से दूसरी योजना में स्थानांतरित करने के लिए φ का उपयोग करना प्रायः—किन्तु सदैव नहीं—संभव होता है। क्या यह संभव है यह इस विषय पर निर्भर करता है कि भाजक वेइल या कार्टियर भाजक है, क्या भाजक को X से Y या इसके विपरीत स्थानांतरित किया जाना है, और φ में कौन से अतिरिक्त गुण हो सकते हैं।
यदि Z, X पर अभाज्य वेइल भाजक है, तो Y का विवृत अपरिवर्तनीय उपयोजना है। φ के आधार पर, यह प्राइम वेइल भाजक हो भी सकता है और नहीं भी। उदाहरण के लिए, यदि φ समतल में किसी बिंदु का ब्लो अप है और Z असाधारण भाजक है, तो इसकी छवि वेइल भाजक नहीं है। इसलिए, φ*Z को परिभाषित किया गया है यदि वह उपयोजना अभाज्य भाजक है और अन्यथा उसे शून्य भाजक के रूप में परिभाषित किया गया है। इसे रैखिकता द्वारा विस्तारित करने पर, यह मानते हुए कि X अर्ध-सघन है, जो समरूपता Div(X) → Div(Y) को परिभाषित करेगा जिसे पुशफॉरवर्ड कहा जाता है। (यदि X अर्ध-सघन नहीं है, तो पुशफॉरवर्ड स्थानीय रूप से सीमित योग होने में विफल हो सकता है।) यह चाउ समूहों पर पुशफॉरवर्ड की विशेष स्थिति है।
यदि Z कार्टियर भाजक है, तो φ पर हल्की परिकल्पना के अंतर्गत, पुलबैक है। शीफ़-सैद्धांतिक रूप से, जब कोई पुलबैक मानचित्र होता है, तो इस पुलबैक का उपयोग कार्टियर भाजकों के पुलबैक को परिभाषित करने के लिए किया जा सकता है। स्थानीय अनुभागों के संदर्भ में, का पुलबैक को द्वारा परिभाषित किया गया है यदि φ प्रभावी है तो पुलबैक को सदैव परिभाषित किया जाता है, किन्तु इसे सामान्य रूप से परिभाषित नहीं किया जा सकता है। उदाहरण के लिए, यदि X = Z और φ, Y में Z का समावेश है, फिर φ*Z अपरिभाषित है क्योंकि संबंधित स्थानीय अनुभाग प्रत्येक समिष्ट पर शून्य होंगे। (चूँकि, संबंधित लाइन बंडल का पुलबैक परिभाषित है।)
यदि φ समतल है, तो वेइल भाजक का पुलबैक परिभाषित किया गया है। इस स्थिति में, Z का पुलबैक φ*Z = φ−1(Z) है। φ की समतलता यह सुनिश्चित करती है कि Z की व्युत्क्रम छवि का कोड आयाम बना रहे। यह उन आकृतियों के लिए विफल हो सकता है जो समतल नहीं हैं, उदाहरण के लिए, छोटे संकुचन के लिए है।
प्रथम चेर्न वर्ग
अभिन्न नोथेरियन योजना;
प्रथम चेर्न वर्ग के रूप में जाना जाता है।[17][18] यदि X सामान्य है तो प्रथम चेर्न वर्ग इंजेक्शन है, और यदि X फैक्टोरियल है (जैसा कि ऊपर परिभाषित है) तो यह समरूपता है। विशेष रूप से, कार्टियर भाजक को किसी भी नियमित योजना पर वेइल भाजक के साथ पहचाना जा सकता है, और इसलिए प्रथम चेर्न वर्ग X नियमित के लिए समरूपता है।
स्पष्ट रूप से, प्रथम चेर्न वर्ग को इस प्रकार परिभाषित किया जा सकता है। इंटीग्रल नोथेरियन योजना तब L के प्रथम चेर्न वर्ग को भाजक के रूप में परिभाषित किया जा सकता है। परिमेय भाग s को परिवर्तित करने से यह भाजक रैखिक तुल्यता द्वारा परिवर्तित किया जाता है, क्योंकि (fs) = (f) + (s) गैर-शून्य परिमेय फलन f और L के गैर-शून्य परिमेय भागs के लिए है। इसलिए Cl(X) में तत्व c1(L) उचित प्रकार से परिभाषित है।
आयाम n का समिष्ट प्रकार;
पश्चात वाले समूह को इसकी शास्त्रीय (यूक्लिडियन) टोपोलॉजी के साथ, X के समिष्ट बिंदुओं के X(C) का उपयोग करके परिभाषित किया गया है। इसी प्रकार, पिकार्ड समूह टोपोलॉजिकल अर्थ में प्रथम चेर्न वर्ग द्वारा इंटीग्रल कोहोमोलॉजी का मानचित्रण करता है:
दो समरूपताएं क्रमविनिमेय आरेख से संबंधित हैं, जहां उचित ऊर्ध्वाधर मानचित्र बोरेल-मूर होमोलॉजी में X के मौलिक वर्ग के साथ कैप उत्पाद है:
'C ' पर X के लिए, दोनों ऊर्ध्वाधर मानचित्र समरूपता हैं।
लाइन बंडलों और रैखिक प्रणालियों के वैश्विक भाग
कार्टियर भाजक प्रभावी होता है यदि इसका स्थानीय परिभाषित फलन fi नियमित हो (केवल तर्कसंगत फलन नहीं)। उस स्थिति में, कार्टियर भाजक को X में कोडिमेंशन 1 की विवृत उप-योजना के साथ पहचाना जा सकता है, उप-योजना को स्थानीय रूप से fi = 0 द्वारा परिभाषित किया गया है। कार्टियर भाजक D प्रभावी भाजक के रैखिक रूप से समतुल्य है यदि और केवल इसकी संबद्ध रेखा बंडल हो गैर-शून्य वैश्विक अनुभाग है; तब D, s के शून्य बिंदुपथ के रैखिक रूप से समतुल्य है।
मान लीजिए कि X क्षेत्र k पर प्रक्षेप्य विविधता है। फिर वैश्विक भाग को गुणा करना k में शून्येतर अदिश द्वारा इसका शून्य स्थान परिवर्तित नहीं किया जाता है। परिणामस्वरूप, वैश्विक वर्गों H0(X, O(D)) के k-सदिश समिष्ट में रेखाओं के प्रक्षेप्य समिष्ट को D के रैखिक रूप से समतुल्य प्रभावी भाजकों के समुच्चय से पहचाना जा सकता है, जिसे D की 'पूर्ण रैखिक प्रणाली' कहा जाता है। इस प्रक्षेप्य समिष्ट के प्रक्षेप्य रैखिक उपसमिष्ट को भाजकों की रैखिक प्रणाली कहा जाता है।
लाइन बंडल के वैश्विक भागों के समिष्ट का अध्ययन करने का कारण किसी दिए गए विविधता से लेकर प्रक्षेप्य समिष्ट तक के संभावित मानचित्रों को समझना है। बीजगणितीय विविधता के वर्गीकरण के लिए यह आवश्यक है। स्पष्ट रूप से, क्षेत्र k पर विविधता X से प्रक्षेप्य समिष्ट Pn तक रूपवाद, X पर लाइन बंडल L निर्धारित करता है, जो मानक लाइन बंडल का पुलबैक बंडल पर Pn है। इसके अतिरिक्त, L n+1 अनुभागों के साथ आता है जिनका आधार समिष्ट रिक्त है। रूपवाद X → Pn निर्धारित करता है।[19] ये अवलोकन कार्टियर भाजक (या लाइन बंडल) के लिए धनात्मकता की कई धारणाओं को उत्पन्न करते हैं, जैसे कि पर्याप्त भाजक और नेफ भाजक है।[20]
क्षेत्र k पर प्रक्षेप्य विविधता X पर भाजक D के लिए, k-सदिश समिष्ट H0(X, O(D)) का सीमित आयाम है। रीमैन-रोच प्रमेय इस सदिश समिष्ट के आयाम की गणना करने के लिए मौलिक उपकरण है जब X प्रक्षेप्य वक्र है। क्रमिक सामान्यीकरण, हिरज़ेब्रुच-रीमैन-रोच प्रमेय और ग्रोथेंडिक-रीमैन-रोच प्रमेय, किसी क्षेत्र पर किसी भी आयाम की प्रक्षेप्य विविधता X के लिए H0(X, O(D)) के आयाम के विषय में कुछ सूचना देते हैं।
क्योंकि विहित भाजक आंतरिक रूप से विविधता से जुड़ा होता है, विविधता के वर्गीकरण में महत्वपूर्ण भूमिका KX और उसके धनात्मक गुणकों द्वारा दिए गए प्रक्षेप्य समिष्ट के मानचित्रों द्वारा निभाई जाती है। X का कोडैरा आयाम प्रमुख द्विवार्षिक अपरिवर्तनीय है, जो m बढ़ने पर सदिश रिक्त समिष्ट H0(X, mKX) (अर्थात् H0(X, O(mKX))) की वृद्धि को मापता है। कोडैरा आयाम सभी n-आयामी विविधता को n+2 वर्गों में विभाजित करता है, जो (सामान्यतः) धनात्मक वक्रता से ऋणात्मक वक्रता की ओर जाते हैं।
Q-भाजक
माना कि X सामान्य प्रकार है। (वेइल) 'Q'-भाजक तर्कसंगत गुणांक के साथ X की इरेड्यूसबल कोडिमेंशन-1 उप-विविधता का सीमित औपचारिक रैखिक संयोजन है। ('R'-भाजक को इसी प्रकार परिभाषित किया गया है।) यदि गुणांक गैर-नकारात्मक हैं तो 'Q'-भाजक 'प्रभावी' होता है। यदि mD किसी धनात्मक पूर्णांक m के लिए कार्टियर भाजक है तो 'Q'-भाजक D 'Q-कार्टियर' है। यदि X सुचारू है, तो प्रत्येक 'Q'-भाजक 'Q'-कार्टियर है।
यदि,
क्यू-भाजक है, तो इसका राउंड-डाउन भाजक है:
जहाँ a से कम या उसके समान सबसे बड़ा पूर्णांक है। शीफ को तब के रूप में परिभाषित किया जाता है।
ग्रोथेंडि-लेफ़्सचेत्ज़ हाइपरप्लेन प्रमेय
लेफ्शेट्ज़ हाइपरप्लेन प्रमेय का तात्पर्य है कि कम से कम 4 आयाम की चिकनी समिष्ट प्रक्षेप्य प्रकार उदाहरण के लिए, यदि Y समिष्ट प्रक्षेप्य में कम से कम 3 आयाम का सहज पूर्ण प्रतिच्छेदन प्रकार है, तो Y का पिकार्ड समूह 'Z' के समरूपी है, जो प्रक्षेप्य समिष्ट पर लाइन बंडल O(1) के प्रतिबंध से उत्पन्न होता है।
ग्रोथेंडिक ने लेफ्शेट्ज़ के प्रमेय को कई दिशाओं में सामान्यीकृत किया, जिसमें इच्छानुसार आधार क्षेत्र, एकवचन प्रकार और प्रक्षेपी प्रकारों के अतिरिक्त स्थानीय वलय पर परिणाम सम्मिलित थे। विशेष रूप से, यदि R पूर्ण प्रतिच्छेदन स्थानीय वलय है, जो अधिकतम 3 कोड आयाम में भाज्य है (उदाहरण के लिए, यदि R के गैर-नियमित स्थान का कोड आयाम कम से कम 4 है), तो R अद्वितीय गुणनभागडोमेन है (और इसलिए प्रत्येक Spec(R) पर वेइल भाजक कार्टियर है)।[21] यहां बंधा हुआ आयाम इष्टतम है, जैसा कि ऊपर दिए गए 3-आयामी क्वाड्रिक शंकु के उदाहरण से दिखाया गया है।
टिप्पणियाँ
- ↑ Dieudonné (1985), section VI.6.
- ↑ Stacks Project, Tag 00PF.
- ↑ Stacks Project, Tag 02MC.
- ↑ Stacks Project, Tag 02MD.
- ↑ 5.0 5.1 Kollár (2013), Notation 1.2.
- ↑ Hartshorne (1977), Proposition II.6.5.
- ↑ 7.0 7.1 Hartshorne (1977), Proposition II.6.2.
- ↑ Stacks Project, Tag 02RS.
- ↑ Kleiman (2005), Theorems 2.5 and 5.4, Remark 6.19.
- ↑ Hartshorne (1977), Example II.6.5.2.
- ↑ Hartshorne(1977), Exercise II.6.5.
- ↑ Grothendieck, EGA IV, Part 4, Proposition 21.3.4, Corollaire 21.3.5.
- ↑ Lazarsfeld (2004), Example 1.1.6.
- ↑ Stacks Project, Tag 0AFW.
- ↑ "Chapter 2. Preliminaries". न्यूनतम मॉडल कार्यक्रम की नींव. Mathematical Society of Japan Memoirs. 2017. pp. 16–47. doi:10.2969/msjmemoirs/03501C020. ISBN 978-4-86497-045-7.
- ↑ (Lazarsfeld 2004, p. 141, Proposition 2.2.6.)
- ↑ For a variety X over a field, the Chern classes of any vector bundle on X act by cap product on the Chow groups of X, and the homomorphism here can be described as L ↦ c1(L) ∩ [X].
- ↑ Eisenbud & Harris 2016, § 1.4.
- ↑ Hartshorne (1977), Theorem II.7.1.
- ↑ (Lazarsfeld 2004, Chapter 1)
- ↑ Grothendieck, SGA 2, Corollaire XI.3.14.
संदर्भ
- Dieudonné, Jean (1985), History of Algebraic Geometry, Wadsworth Mathematics Series, translated by Judith D. Sally, Belmont, CA: Wadsworth International Group, ISBN 0-534-03723-2, MR 0780183
- Eisenbud, David; Harris, Joe (2016), 3264 and All That: A Second Course in Algebraic Geometry, C. U.P., ISBN 978-1107602724
- Grothendieck, Alexandre; Dieudonné, Jean (1967). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatrième partie". Publications Mathématiques de l'IHÉS. 32: 5–361. doi:10.1007/bf02732123. MR 0238860.
- Grothendieck, Alexander; Raynaud, Michèle (2005) [1968], Laszlo, Yves (ed.), Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Documents Mathématiques, vol. 4, Paris: Société Mathématique de France, arXiv:math/0511279, Bibcode:2005math.....11279G, ISBN 978-2-85629-169-6, MR 2171939
- Section II.6 of Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, vol. 52, New York, Heidelberg: Springer-Verlag, doi:10.1007/978-1-4757-3849-0, ISBN 0-387-90244-9, MR 0463157
- Kleiman, Steven (2005), "The Picard scheme", Fundamental Algebraic Geometry, Math. Surveys Monogr., vol. 123, Providence, R.I.: American Mathematical Society, pp. 235–321, arXiv:math/0504020, Bibcode:2005math......4020K, MR 2223410
- Kollár, János (2013), Singularities of the Minimal Model Program, Cambridge University Press, doi:10.1017/CBO9781139547895, ISBN 978-1-107-03534-8, MR 3057950
- Lazarsfeld, Robert (2004), Positivity in Algebraic Geometry, vol. 1, Berlin: Springer-Verlag, doi:10.1007/978-3-642-18808-4, ISBN 3-540-22533-1, MR 2095471
बाहरी संबंध
- The Stacks Project Authors, The Stacks Project