स्थिर-क्रिया सिद्धांत: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
{{about|न्यूनतम कार्रवाई के सिद्धांत का इतिहास|आवेदन|क्रिया (भौतिकी)}} | {{about|न्यूनतम कार्रवाई के सिद्धांत का इतिहास|आवेदन|क्रिया (भौतिकी)}} | ||
'''स्थिर-क्रिया सिद्धांत''' - जिसे कम से कम क्रिया के सिद्धांत के रूप में भी जाना जाता है - एक भिन्नता सिद्धांत है, जिसे जब एक यांत्रिकी प्रणाली के ''कार्य'' पर लागू किया जाता है, उस प्रणाली के लिए गति के समीकरण उत्पन्न करता है। सिद्धांत बताता है कि प्रक्षेपवक्र (अर्थात गति के समीकरणों के समाधान) | '''स्थिर-क्रिया सिद्धांत''' - जिसे कम से कम क्रिया के सिद्धांत के रूप में भी जाना जाता है - एक भिन्नता सिद्धांत है, जिसे जब एक यांत्रिकी प्रणाली के ''कार्य'' पर लागू किया जाता है, उस प्रणाली के लिए गति के समीकरण उत्पन्न करता है। सिद्धांत बताता है कि प्रक्षेपवक्र (अर्थात गति के समीकरणों के समाधान) प्रणाली की क्रिया के स्थिर बिंदु हैं। <ref name=":0">[https://feynmanlectures.caltech.edu/II_19.html The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action]</ref> | ||
सिद्धांत का उपयोग गति के न्यूटोनियन, लैग्रेन्जियन और हैमिल्टनियन समीकरणों और यहां तक कि सामान्य सापेक्षता, साथ ही | सिद्धांत का उपयोग गति के न्यूटोनियन, लैग्रेन्जियन और हैमिल्टनियन समीकरणों और यहां तक कि सामान्य सापेक्षता, साथ ही उत्कृष्ट बिजली का गतिविज्ञान और परिमाण क्षेत्र सिद्धांत को प्राप्त करने के लिए किया जा सकता है।इन सन्दर्भ में, एक अलग क्रिया को न्यूनतम या अधिकतम किया जाना चाहिए। सापेक्षता के लिए, यह आइंस्टीन-हिल्बर्ट क्रिया है। परिमाण क्षेत्र सिद्धांत के लिए, इसमें पथ अभिन्न सूत्रीकरण सम्मिलित है। | ||
उत्कृष्ट यांत्रिकी और विद्युत चुम्बकीय अभिव्यक्तियाँ परिमाण यांत्रिकी का परिणाम हैं। स्थिर क्रिया पद्धति ने परिमाण यांत्रिकी के विकास में मदद की।<ref>[[Richard Feynman]], ''[[The Character of Physical Law]]''.</ref> 1933 में, भौतिक विज्ञानी पॉल डिराक ने आयामों के परिमाण हस्तक्षेप में सिद्धांत के परिमाण यांत्रिक आधार को समझकर प्रदर्शित किया कि इस सिद्धांत का उपयोग परिमाण गणना में कैसे किया जा सकता है।<ref>{{cite journal |last=Dirac |first=Paul A. M. |author-link=Paul Dirac |year=1933 |title=The Lagrangian in Quantum Mechanics |journal=Physikalische Zeitschrift der Sowjetunion |volume=3 |issue=1|pages=64–72 |url=http://www.hep.anl.gov/czachos/soysoy/Dirac33.pdf}}</ref> इसके बाद जूलियन श्विंगर और रिचर्ड फेनमैन ने स्वतंत्र रूप से परिमाण बिजली का गतिविज्ञान में इस सिद्धांत को लागू किया।<ref>R. Feynman, Quantum Mechanics and Path Integrals, McGraw-Hill (1965), {{ISBN|0070206503}}</ref><ref>J. S. Schwinger, Quantum Kinematics and Dynamics, W. A. Benjamin (1970), {{ISBN|0738203033}}</ref> | |||
यह सिद्धांत आधुनिक भौतिक विज्ञान और गणित में केंद्रीय बना हुआ है, जिसे थर्मोडायनामिक्स,<ref>{{cite journal |doi=10.1016/j.aop.2008.04.007 |title=Thermodynamics based on the principle of least abbreviated action: Entropy production in a network of coupled oscillators |journal=Annals of Physics |volume=323 |issue=8 |pages=1844–58 |year=2008 |last1=García-Morales |first1=Vladimir |last2=Pellicer |first2=Julio |last3=Manzanares |first3=José A. |bibcode=2008AnPhy.323.1844G |arxiv=cond-mat/0602186 |s2cid=118464686 }}</ref><ref>{{Cite journal|url=http://www.scholarpedia.org/article/Principle_of_least_action | doi = 10.4249/scholarpedia.8291|title = Principle of least action|year = 2009|last1 = Gray|first1 = Chris|journal = Scholarpedia|volume = 4|issue = 12|page = 8291|bibcode = 2009SchpJ...4.8291G| doi-access = free}}</ref><ref>{{cite journal |bibcode=1942PhDT.........5F |title=The Principle of Least Action in Quantum Mechanics |last1=Feynman |first1=Richard Phillips |year=1942 }}</ref> द्रव यांत्रिकी,<ref>{{Cite web |url=http://www.damtp.cam.ac.uk/user/db275/LeastAction.pdf |title=Principle of Least Action – damtp |access-date=2016-07-18 |archive-url=https://web.archive.org/web/20151010195059/http://www.damtp.cam.ac.uk/user/db275/LeastAction.pdf |archive-date=2015-10-10 |url-status=dead }}</ref> सापेक्षता का सिद्धांत, | यह सिद्धांत आधुनिक भौतिक विज्ञान और गणित में केंद्रीय बना हुआ है, जिसे थर्मोडायनामिक्स,<ref>{{cite journal |doi=10.1016/j.aop.2008.04.007 |title=Thermodynamics based on the principle of least abbreviated action: Entropy production in a network of coupled oscillators |journal=Annals of Physics |volume=323 |issue=8 |pages=1844–58 |year=2008 |last1=García-Morales |first1=Vladimir |last2=Pellicer |first2=Julio |last3=Manzanares |first3=José A. |bibcode=2008AnPhy.323.1844G |arxiv=cond-mat/0602186 |s2cid=118464686 }}</ref><ref>{{Cite journal|url=http://www.scholarpedia.org/article/Principle_of_least_action | doi = 10.4249/scholarpedia.8291|title = Principle of least action|year = 2009|last1 = Gray|first1 = Chris|journal = Scholarpedia|volume = 4|issue = 12|page = 8291|bibcode = 2009SchpJ...4.8291G| doi-access = free}}</ref><ref>{{cite journal |bibcode=1942PhDT.........5F |title=The Principle of Least Action in Quantum Mechanics |last1=Feynman |first1=Richard Phillips |year=1942 }}</ref> द्रव यांत्रिकी,<ref>{{Cite web |url=http://www.damtp.cam.ac.uk/user/db275/LeastAction.pdf |title=Principle of Least Action – damtp |access-date=2016-07-18 |archive-url=https://web.archive.org/web/20151010195059/http://www.damtp.cam.ac.uk/user/db275/LeastAction.pdf |archive-date=2015-10-10 |url-status=dead }}</ref> सापेक्षता का सिद्धांत, परिमाण यांत्रिकी<ref>{{cite journal| author-last=Helzberger |author-first=Max| title=Optics from Euclid to Huygens | journal= Applied Optics | volume=5| issue=9|year=1966|pages=1383–93|doi=10.1364/AO.5.001383| pmid=20057555| bibcode=1966ApOpt...5.1383H| quote = In ''Catoptrics'' the law of reflection is stated, namely that incoming and outgoing rays form the same angle with the surface normal." }}</ref>, कण भौतिक विज्ञान, और स्ट्रिंग सिद्धांत<ref>{{cite book | last=Kline|first=Morris | title=Mathematical Thought from Ancient to Modern Times | url=https://archive.org/details/mathematicalthou0000unse| url-access=registration| publisher=Oxford University Press| location=New York |date=1972| pages= [https://archive.org/details/mathematicalthou0000unse/page/167 167]–68|isbn=0-19-501496-0}}</ref> में लागू किया जा रहा है। और मोर्स सिद्धांत में आधुनिक गणितीय जांच का केंद्र बिंदु है। मौपर्टुइस का सिद्धांत और हैमिल्टन का सिद्धांत स्थिर क्रिया के सिद्धांत का उदाहरण देते हैं। | ||
क्रिया सिद्धांत प्रकाशिकी में पहले के विचारों से पहले आता है। प्राचीन ग्रीस में, यूक्लिड ने अपने कैटोप्ट्रिका में लिखा था कि, दर्पण से परावर्तित होने वाले प्रकाश के पथ के लिए, आपतन कोण प्रतिबिंब के कोण के बराबर होता है।<ref name="mau44">P.L.M. de Maupertuis, ''[[s:fr:Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles|Accord de différentes lois de la nature qui avaient jusqu'ici paru incompatibles.]]'' (1744) Mém. As. Sc. Paris p. 417. ([[s:Accord between different laws of Nature that seemed incompatible|English translation]])</ref> अलेक्जेंड्रिया के | क्रिया सिद्धांत प्रकाशिकी में पहले के विचारों से पहले आता है। प्राचीन ग्रीस में, यूक्लिड ने अपने कैटोप्ट्रिका में लिखा था कि, दर्पण से परावर्तित होने वाले प्रकाश के पथ के लिए, आपतन कोण प्रतिबिंब के कोण के बराबर होता है।<ref name="mau44">P.L.M. de Maupertuis, ''[[s:fr:Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles|Accord de différentes lois de la nature qui avaient jusqu'ici paru incompatibles.]]'' (1744) Mém. As. Sc. Paris p. 417. ([[s:Accord between different laws of Nature that seemed incompatible|English translation]])</ref> अलेक्जेंड्रिया के नायक ने बाद में दिखाया कि यह रास्ता सबसे कम लंबाई और सबसे कम समय का था।<ref name="mau46">P.L.M. de Maupertuis, ''[[s:fr:Les loix du mouvement et du repos déduites d'un principe metaphysique|Le lois de mouvement et du repos, déduites d'un principe de métaphysique.]]'' (1746) Mém. Ac. Berlin, p. 267.([[s:Derivation of the laws of motion and equilibrium from a metaphysical principle|English translation]])</ref> | ||
विद्वान | विद्वान प्रायः कम से कम क्रिया के सिद्धांत को प्रतिपादित करने के लिए पियरे लुईस मौपर्टुइस को श्रेय देते हैं क्योंकि उन्होंने इसके बारे में 1744<ref name="eul44">Leonhard Euler, ''Methodus Inveniendi Lineas Curvas Maximi Minive Proprietate Gaudentes.'' (1744) Bousquet, Lausanne & Geneva. 320 pages. Reprinted in ''Leonhardi Euleri Opera Omnia: Series I vol 24.'' (1952) C. Cartheodory (ed.) Orell Fuessli, Zurich. [http://math.dartmouth.edu/~euler/pages/E065.html Scanned copy of complete text] at ''[http://math.dartmouth.edu/~euler/ The Euler Archive]'', Dartmouth.</ref> और 1746<ref>[[s:fr:Samuel_Koenig,_Appel_au_public,_1752/Lettre_de_Leibniz_contest%C3%A9e_par_Maupertuis |Leibniz's letter to Varignon (not to Hermann)]]. <br>Samuel Koenig, [http://gallica.bnf.fr/ark:/12148/bpt6k5401423n ''Appel au Public du jugement de l'Académie royale de Berlin''], Leide, 1752.</ref> में लिखा था। यद्यपि, लियोनहार्ड यूलर ने भी 1744<ref name="ger98">Gerhardt CI. (1898) "Über die vier Briefe von Leibniz, die Samuel König in dem Appel au public, Leide MDCCLIII, veröffentlicht hat", ''Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften'', '''I''', 419–427.</ref> में इस सिद्धांत पर चर्चा की, और साक्ष्य से पता चलता है कि गॉटफ्रीड लीबनिज़ दोनों से 39 वर्ष पहले थे।<ref name="kab13">Kabitz W. (1913) "Über eine in Gotha aufgefundene Abschrift des von S. König in seinem Streite mit Maupertuis und der Akademie veröffentlichten, seinerzeit für unecht erklärten Leibnizbriefes", ''Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften'', '''II''', 632–638.</ref> | ||
== सामान्य कथन == | == सामान्य कथन == | ||
[[File:Least action principle.svg|250px|thumb|जैसे ही | [[File:Least action principle.svg|250px|thumb|जैसे ही प्रणाली विकसित होता है, q विन्यास स्थान (भौतिक विज्ञान) के माध्यम से एक पथ का पता लगाता है (केवल कुछ दिखाए जाते हैं)। प्रणाली (लाल) द्वारा लिए गए पथ में प्रणाली के विन्यास (''δ''q) में छोटे बदलावों के तहत एक स्थिर क्रिया (''δS'' = 0) है।<ref name=penrose>{{cite book |author=R. Penrose| title=[[The Road to Reality]]| publisher= Vintage books| year=2007 | page = 474|isbn=978-0-679-77631-4}}</ref>]]क्रिया, निरूपित <math> \mathcal{S} </math>, एक भौतिक प्रणाली को समय के उदाहरणों t1 और t2 के बीच लैग्रेंजियन L के अभिन्न अंग के रूप में परिभाषित किया गया है - तकनीकी रूप से N सामान्यीकृत निर्देशांक {{math|1='''q''' = (''q''<sub>1</sub>, ''q''<sub>2</sub>, ... , ''q<sub>N</sub>'')}} का एक कार्यात्मक जो समय के कार्य हैं और प्रणाली के विन्यास को परिभाषित करते हैं: | ||
<math display="block"> \mathbf{q} : \mathbf{R} \to \mathbf{R}^N </math><math display="block"> \mathcal{S}[\mathbf{q}, t_1, t_2] = \int_{t_1}^{t_2} L(\mathbf{q}(t),\mathbf{\dot{q}}(t), t) dt </math> | <math display="block"> \mathbf{q} : \mathbf{R} \to \mathbf{R}^N </math><math display="block"> \mathcal{S}[\mathbf{q}, t_1, t_2] = \int_{t_1}^{t_2} L(\mathbf{q}(t),\mathbf{\dot{q}}(t), t) dt </math> | ||
| Line 21: | Line 21: | ||
गणितीय रूप से सिद्धांत है<ref>Encyclopaedia of Physics (2nd Edition), [[Rita G. Lerner|R.G. Lerner]], G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3</ref><ref name="Analytical Mechanics 2008">Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, {{ISBN|978-0-521-57572-0}}</ref><math display="block"> \delta \mathcal{S} = 0 ,</math> | गणितीय रूप से सिद्धांत है<ref>Encyclopaedia of Physics (2nd Edition), [[Rita G. Lerner|R.G. Lerner]], G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3</ref><ref name="Analytical Mechanics 2008">Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, {{ISBN|978-0-521-57572-0}}</ref><math display="block"> \delta \mathcal{S} = 0 ,</math> | ||
जहां δ (लोअरकेस ग्रीक डेल्टा) का अर्थ एक छोटा सा परिवर्तन है। शब्दों में यह | जहां δ (लोअरकेस ग्रीक डेल्टा) का अर्थ एक छोटा सा परिवर्तन है। शब्दों में यह समझना है<ref name=penrose/> | ||
{{block indent | em = 1.5 | style=font-style:italic; | text = | {{block indent | em = 1.5 | style=font-style:italic; | text = समय के बीच सिस्टम द्वारा अपनाया गया मार्ग {{math|''t''<sub>1</sub>}} and {{math|''t''<sub>2</sub>}} और विन्यास q<sub>1</sub> and q<sub>2</sub> वह है जिसके लिए '''क्रिया''' ''स्थिर (कोई परिवर्तन नहीं)'''' से '''प्रथम क्रम''' है।}} | ||
अनुप्रयोगों में कथन और | न्यूनतम क्रिया के ऐतिहासिक नाम के तथापि, स्थिर क्रिया प्रायः न्यूनतम नहीं होती है।<ref>{{cite encyclopedia |last1=Goodman |first1=Bernard |title=Action |date=1993|encyclopedia=McGraw-Hill Encyclopaedia of Physics |publisher=McGraw-Hill |location=New York |editor=Parker, S. P.|isbn=0-07-051400-3|page=22 |edition=2nd |url=https://archive.org/details/mcgrawhillencycl1993park/page/22/mode/2up}}</ref><ref name=":0" />{{rp|19-6}} यह पथ में पर्याप्त रूप से छोटे, सीमित खंडों के लिए एक न्यूनतम सिद्धांत है।<ref>{{cite encyclopedia |last1=Stehle |first1=Philip M. |title=Least-action principle |date=1993|encyclopedia=McGraw-Hill Encyclopaedia of Physics |publisher=McGraw-Hill |location=New York |editor=Parker, S. P.|isbn=0-07-051400-3|page=670 |edition=2nd |url=https://archive.org/details/mcgrawhillencycl1993park/page/670/mode/2up}}</ref> | ||
<math display="block"> \delta \int_{t_1}^{t_2} L(\mathbf{q}, \mathbf{\dot{q}},t) dt = 0 .</math> | |||
== उत्पत्ति, | अनुप्रयोगों में कथन और क्रिया की परिभाषा को एक साथ लिया जाता है<ref>Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, {{ISBN|0-07-084018-0}}</ref> | ||
<math display="block"> \delta \int_{t_1}^{t_2} L(\mathbf{q}, \mathbf{\dot{q}},t) dt = 0 .</math>क्रिया और लैग्रेंजियन दोनों में हर समय के लिए प्रणाली की गतिशीलता सम्मिलित है। शब्द "पथ" बस विन्यास स्थान में निर्देशांक के संदर्भ में प्रणाली द्वारा अनुरेखण किए गए वक्र को संदर्भित करता है, यानी वक्र {{math|'''q'''(''t'')}}, समय के अनुसार प्राचलयुक्त (इस अवधारणा के लिए प्राचल समीकरण भी देखें)। | |||
== उत्पत्ति, वक्तव्य, और विवाद == | |||
=== फर्मेट === | === फर्मेट === | ||
| Line 34: | Line 35: | ||
===मौपर्टुइस === | ===मौपर्टुइस === | ||
{{Main|Maupertuis principle}} | {{Main|Maupertuis principle}} | ||
कम से कम | कम से कम क्रिया के सिद्धांत के निर्माण का श्रेय आमतौर पर पियरे लुईस मौपर्टुइस को दिया जाता है, जिन्होंने महसूस किया कि "प्रकृति अपने सभी कार्यों में मितव्ययी है", और इस सिद्धांत को व्यापक रूप से लागू किया: | ||
{{Quote|इस सिद्धांत से उत्पन्न गति और विश्राम के नियम बिल्कुल वही हैं जो प्रकृति में देखे गए हैं, हम सभी घटनाओं पर इसके अनुप्रयोग की प्रशंसा कर सकते हैं। पशुओं की गति, पौधों की वानस्पतिक वृद्धि... केवल इसके परिणाम हैं; और ब्रह्माण्ड का दृश्य इतना अधिक भव्य, इतना अधिक सुंदर, इसके रचयिता के योग्य बन जाता है, जब कोई जानता है कि थोड़ी संख्या में, सबसे बुद्धिमानी से स्थापित कानून, सभी गतिविधियों के लिए पर्याप्त हैं।|Pierre Louis Maupertuis<ref>Chris Davis. [http://www.idlex.freeserve.co.uk/idle/evolution/ref/leastact.html ''Idle theory''] {{webarchive|url=https://web.archive.org/web/20060615043538/http://www.idlex.freeserve.co.uk/idle/evolution/ref/leastact.html |date=2006-06-15 }} (1998)</ref>}} | {{Quote|इस सिद्धांत से उत्पन्न गति और विश्राम के नियम बिल्कुल वही हैं जो प्रकृति में देखे गए हैं, हम सभी घटनाओं पर इसके अनुप्रयोग की प्रशंसा कर सकते हैं। पशुओं की गति, पौधों की वानस्पतिक वृद्धि... केवल इसके परिणाम हैं; और ब्रह्माण्ड का दृश्य इतना अधिक भव्य, इतना अधिक सुंदर, इसके रचयिता के योग्य बन जाता है, जब कोई जानता है कि थोड़ी संख्या में, सबसे बुद्धिमानी से स्थापित कानून, सभी गतिविधियों के लिए पर्याप्त हैं।|Pierre Louis Maupertuis<ref>Chris Davis. [http://www.idlex.freeserve.co.uk/idle/evolution/ref/leastact.html ''Idle theory''] {{webarchive|url=https://web.archive.org/web/20060615043538/http://www.idlex.freeserve.co.uk/idle/evolution/ref/leastact.html |date=2006-06-15 }} (1998)</ref>}} | ||
मौपर्टुइस की यह धारणा, | मौपर्टुइस की यह धारणा, यद्यपि आज कुछ सीमा तक नियतात्मक है, यांत्रिकी के अधिकांश सार को ग्रहण करती है। | ||
भौतिक विज्ञान के अनुप्रयोग में, मौपर्टुइस ने सुझाव दिया कि न्यूनतम की जाने वाली मात्रा "विज़ विवा" द्वारा एक प्रणाली के भीतर गति की अवधि (समय) का उत्पाद थी।{{Equation box 1 | भौतिक विज्ञान के अनुप्रयोग में, मौपर्टुइस ने सुझाव दिया कि न्यूनतम की जाने वाली मात्रा "विज़ विवा" द्वारा एक प्रणाली के भीतर गति की अवधि (समय) का उत्पाद थी।{{Equation box 1 | ||
| Line 51: | Line 52: | ||
=== यूलर === | === यूलर === | ||
लियोनहार्ड यूलर ने 1744 में अपने मेथडस इनवेनिएंडी लिनियास कर्वस मैक्सिमी मिनिव प्रोप्राइटेट गौडेंटेस के एडिटामेंटम 2 में बहुत ही पहचाने जाने योग्य शब्दों में | लियोनहार्ड यूलर ने 1744 में अपने मेथडस इनवेनिएंडी लिनियास कर्वस मैक्सिमी मिनिव प्रोप्राइटेट गौडेंटेस के एडिटामेंटम 2 में बहुत ही पहचाने जाने योग्य शब्दों में क्रिया सिद्धांत का सूत्रीकरण दिया। दूसरे अनुच्छेद से प्रारम्भ:: | ||
{{cquote|माना प्रक्षेप्य का द्रव्यमान M है, और अनंत दूरी ds पर चलते समय इसकी गति v है। पिंड में एक संवेग Mv होगा, जिसे दूरी ds से गुणा करने पर, Mv ds देगा, दूरी ds पर एकीकृत पिंड का संवेग। अब मैं दावा करता हूं कि इस प्रकार | {{cquote|माना प्रक्षेप्य का द्रव्यमान M है, और अनंत दूरी ds पर चलते समय इसकी गति v है। पिंड में एक संवेग Mv होगा, जिसे दूरी ds से गुणा करने पर, Mv ds देगा, दूरी ds पर एकीकृत पिंड का संवेग। अब मैं दावा करता हूं कि इस प्रकार निकाय द्वारा वर्णित वक्र (समान समापन बिंदुओं को जोड़ने वाले अन्य सभी वक्रों में से) है जो न्यूनतम करता है | ||
<math display="block">\int Mv\,ds</math> | <math display="block">\int Mv\,ds</math> | ||
या, | या, इसके अलावा 'अनुबंध यह है कि कि एम पथ के साथ स्थिर है, | ||
<math display="block">M\int v\,ds.</math>|20px|20px| | <math display="block">M\int v\,ds.</math>|20px|20px|लेओन्हार्ड यूलर<ref name="eul44" /><ref>Euler, [[s:la:Methodus inveniendi/Additamentum II|Additamentum II]] ([http://math.dartmouth.edu/~euler/docs/originals/E065h external link]), ibid. ([https://en.wikisource.org/w/index.php?title=Translation:Methodus_inveniendi/Additamentum_II&oldid=6399338 English translation])</ref>}} | ||
जैसा कि यूलर कहते हैं, {{math|∫''Mv'' ''ds''}} तय की गई दूरी पर संवेग का अभिन्न अंग है, जो आधुनिक संकेतन में, संक्षिप्त या घटी हुई क्रिया के बराबर है | जैसा कि यूलर कहते हैं, {{math|∫''Mv'' ''ds''}} तय की गई दूरी पर संवेग का अभिन्न अंग है, जो आधुनिक संकेतन में, संक्षिप्त या घटी हुई क्रिया के बराबर है | ||
| Line 66: | Line 67: | ||
|border colour = #0073CF | |border colour = #0073CF | ||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
इस प्रकार, यूलर ने मौपर्टुइस के समान ही वर्ष में परिवर्तनशील सिद्धांत का एक समतुल्य और (स्पष्ट रूप से) स्वतंत्र | इस प्रकार, यूलर ने मौपर्टुइस के समान ही वर्ष में परिवर्तनशील सिद्धांत का एक समतुल्य और (स्पष्ट रूप से) स्वतंत्र वर्णन दिया, भले ही थोड़ा बाद में। कौतूहलपूर्वक यह है कि यूलर ने किसी प्राथमिकता का दावा नहीं किया, जैसा कि निम्नलिखित प्रकरण से पता चलता है। | ||
=== विवादित प्राथमिकता === | === विवादित प्राथमिकता === | ||
मौपर्टुइस की प्राथमिकता पर 1751 में गणितज्ञ सैमुअल कोनिग द्वारा विवाद किया गया था, जिन्होंने दावा किया था कि इसका आविष्कार 1707 में गॉटफ्राइड लाइबनिज द्वारा किया गया था। | मौपर्टुइस की प्राथमिकता पर 1751 में गणितज्ञ सैमुअल कोनिग द्वारा विवाद किया गया था, जिन्होंने दावा किया था कि इसका आविष्कार 1707 में गॉटफ्राइड लाइबनिज द्वारा किया गया था। यद्यपि लाइबनिज के कई तर्कों के समान, सिद्धांत को लाइबनिज के कार्यों में प्रलेखित नहीं किया गया है। कोनिग ने स्वयं सिद्धांत के साथ लाइबनिज से जैकब हरमन को लिखे 1707 के पत्र की एक प्रति दिखाई, लेकिन मूल पत्र खो गया है। विवादास्पद कार्यवाहियों में, कोनिग पर जालसाजी का आरोप लगाया गया था, <ref name="oco03">J J O'Connor and E F Robertson, "[http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Forgery_2.html The Berlin Academy and forgery]", (2003), at ''[http://www-history.mcs.st-andrews.ac.uk/history/ The MacTutor History of Mathematics archive]''.</ref> और यहां तक कि प्रशिया के राजा ने भी मौपर्टुइस (अपनी अकादमी के प्रमुख) का बचाव करते हुए बहस में प्रवेश किया, जबकि वोल्टेयर ने कोनिग का बचाव किया।{{Citation needed|date=July 2017}} | ||
यूलर, प्राथमिकता का दावा करने के बजाय, मौपर्टुइस का एक कट्टर रक्षक था, और यूलर ने स्वयं 13 अप्रैल 1752 को बर्लिन अकादमी के समक्ष जालसाजी के लिए कोनिग पर | यूलर, प्राथमिकता का दावा करने के बजाय, मौपर्टुइस का एक कट्टर रक्षक था, और यूलर ने स्वयं 13 अप्रैल 1752 को बर्लिन अकादमी के समक्ष जालसाजी के लिए कोनिग पर दावा चलाया। जालसाजी के दावों की 150 साल बाद फिर से जांच की गई, और अभिलेखीय कार्य सी.आई. द्वारा किया गया। 1898 में गेरहार्ड्ट<ref name="ger98" /> और 1913 में डब्लू. काबिट्ज़<ref name="kab13" /> ने बर्नौली अभिलेखागार में पत्र की अन्य प्रतियां और कोनिग द्वारा उद्धृत तीन अन्य प्रतियां का खुलासा किया। | ||
== आगे का विकास == | == इससे आगे का विकास == | ||
यूलर ने इस विषय पर लिखना जारी रखा; अपने रिफ्लेक्शंस सुर क्वेल्क्स लोइक्स जेनरालेस डे ला नेचर (1748) में, उन्होंने | यूलर ने इस विषय पर लिखना जारी रखा; अपने रिफ्लेक्शंस सुर क्वेल्क्स लोइक्स जेनरालेस डे ला नेचर (1748) में, उन्होंने क्रिया को "प्रयास" कहा। उनकी अभिव्यक्ति आधुनिक संभावित ऊर्जा से मेल खाती है, और कम से कम क्रिया के उनके वक्तव्य में कहा गया है कि आराम पर निकायों की एक प्रणाली की कुल संभावित ऊर्जा कम हो जाती है, जो आधुनिक स्थैतिकी का सिद्धांत है। | ||
=== लैग्रेंज और हैमिल्टन === | === लैग्रेंज और हैमिल्टन === | ||
{{Main|Hamilton's principle}} | {{Main|Hamilton's principle}} | ||
1760 में जोसफ-लुई लाग्रेंज द्वारा भिन्नताओं की अधिकांश गणनाएं बताई गई थीं<ref>{{cite book|editor=D. J. Struik|title=A Source Book in Mathematics, 1200–1800|publisher=MIT Press|location=Cambridge, Mass|year=1969}} pp. 406–413</ref><ref>{{cite book|last=Kline|first=Morris|title=Mathematical Thought from Ancient to Modern Times|url=https://archive.org/details/mathematicalthou0000unse | url-access=registration|publisher=Oxford University Press|location=New York|year=1972 | isbn=0-19-501496-0}} pp. 582-589</ref> और | 1760 में जोसफ-लुई लाग्रेंज द्वारा भिन्नताओं की अधिकांश गणनाएं बताई गई थीं<ref>{{cite book|editor=D. J. Struik|title=A Source Book in Mathematics, 1200–1800|publisher=MIT Press|location=Cambridge, Mass|year=1969}} pp. 406–413</ref><ref>{{cite book|last=Kline|first=Morris|title=Mathematical Thought from Ancient to Modern Times|url=https://archive.org/details/mathematicalthou0000unse | url-access=registration|publisher=Oxford University Press|location=New York|year=1972 | isbn=0-19-501496-0}} pp. 582-589</ref> और वह इसे गतिशीलता की समस्याओं पर लागू करने के लिए आगे बढ़े। मेकैनिक एनालिटिक (1788) में लैग्रेंज ने एक यांत्रिक पिंड की गति के सामान्य समीकरण निकाले।य की गति के सामान्य लैग्रैंगियन समीकरणों को व्युत्पन्न किया।<ref>{{cite book|last=Lagrange|first=Joseph-Louis|title=Mécanique Analytique|year=1788}} p. 226</ref> विलियम रोवन हैमिल्टन ने 1834 और 1835 में<ref>W. R. Hamilton, "On a General Method in Dynamics", ''Philosophical Transactions of the Royal Society'' [http://www.emis.de/classics/Hamilton/GenMeth.pdf Part I (1834) p.247-308]; [http://www.emis.de/classics/Hamilton/SecEssay.pdf Part II (1835) p. 95-144]. (''From the collection [http://www.emis.de/classics/Hamilton/ Sir William Rowan Hamilton (1805–1865): Mathematical Papers] edited by David R. Wilkins, School of Mathematics, Trinity College, Dublin 2, Ireland. (2000); also reviewed as [http://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Dynamics/ On a General Method in Dynamics]'')</ref> उत्कृष्ट लैग्रेंजियन फ़ंक्शन के लिए परिवर्तनशील सिद्धांत लागू किया <math display="block">L = T - V</math> यूलर-लैग्रेंज समीकरणों को उनके वर्तमान रूप में प्राप्त करने के लिए। | ||
=== जैकोबी, मोर्स और कैराथियोडोरी === | === जैकोबी, मोर्स और कैराथियोडोरी === | ||
1842 में, कार्ल गुस्ताव जैकोबी ने इस समस्या | 1842 में, कार्ल गुस्ताव जैकोबी ने इस समस्या से निपटा कि क्या परिवर्तनशील सिद्धांत हमेशा अन्य स्थिर बिंदुओं (मैक्सिमा या स्थिर काठी बिंदु) के विपरीत न्यूनतम को पाता है; उनका अधिकांश कार्य द्वि-आयामी सतहों पर भू-भौतिकी पर केंद्रित था।<ref>G.C.J. Jacobi, ''Vorlesungen über Dynamik, gehalten an der Universität Königsberg im Wintersemester 1842–1843''. A. Clebsch (ed.) (1866); Reimer; Berlin. 290 pages, available online [http://math-doc.ujf-grenoble.fr/cgi-bin/oeitem?id=OE_JACOBI__8_1_0 Œuvres complètes volume '''8'''] {{Webarchive|url=https://web.archive.org/web/20071122083808/http://math-doc.ujf-grenoble.fr/cgi-bin/oeitem?id=OE_JACOBI__8_1_0 |date=2007-11-22 }} at [http://math-doc.ujf-grenoble.fr/OEUVRES/ Gallica-Math] {{Webarchive|url=https://web.archive.org/web/20081123234823/http://math-doc.ujf-grenoble.fr/OEUVRES/ |date=2008-11-23 }} from the [http://gallica.bnf.fr/ Gallica Bibliothèque nationale de France].</ref> पहला स्पष्ट सामान्य कथन 1920 और 1930 के दशक में मारस्टन मोर्स द्वारा दिया गया था,<ref>Marston Morse (1934). "The Calculus of Variations in the Large", ''American Mathematical Society Colloquium Publication'' '''18'''; New York.</ref> जिसे अब मोर्स सिद्धांत के रूप में जाना जाता है। उदाहरण के लिए, मोर्स ने दिखाया कि एक प्रक्षेपवक्र में संयुग्मित बिंदुओं की संख्या लैग्रेंजियन के दूसरे संस्करण में नकारात्मक आइगेनवैल्यू की संख्या के बराबर है। यूलर-लैग्रेंज समीकरण की एक विशेष रूप से सुंदर व्युत्पत्ति कॉन्स्टेंटिन कैराथियोडोरी द्वारा तैयार की गई थी और उनके द्वारा 1935 में प्रकाशित की गई थी। | ||
=== गॉस और हर्ट्ज === | === गॉस और हर्ट्ज === | ||
उत्कृष्ट यांत्रिकी के अन्य अतिम सिद्धांतों को तैयार किया गया है, जैसे कि गॉस का न्यूनतम अवरोध का सिद्धांत और इसका परिणाम, हर्ट्ज़ का न्यूनतम वक्रता का सिद्धांत। | |||
=== डी'एलेम्बर्ट === | |||
अतिरिक्त-होलोनोमिक बाधाओं वाली प्रणालियों के लिए, हैमिल्टन के सिद्धांत को डी'अलेम्बर्ट सिद्धांत द्वारा प्रतिस्थापित किया जाता है। इस सन्दर्भ में क्रिया केवल विविधताओं के लिए स्थिर होने के लिए लगाया गया है जो बाधाओं के अनुरूप हैं। | |||
== संभावित टेलिऑलॉजिकल पहलुओं के बारे में विवाद == | == संभावित टेलिऑलॉजिकल पहलुओं के बारे में विवाद == | ||
गति के | गति के विभेदक समीकरणों और उनके अभिन्न समकक्ष की गणितीय तुल्यता के महत्वपूर्ण दार्शनिक निहितार्थ हैं। विभेदक समीकरण अंतरिक्ष में एक बिंदु या समय के एक क्षण में स्थानीयकृत मात्राओं के बारे में कथन हैं। उदाहरण के लिए, न्यूटन का दूसरा नियम<math display="block">\mathbf{F} = m\mathbf{a}</math> | ||
<math display="block">\mathbf{F} = m\mathbf{a}</math> | |||
बताता है कि किसी द्रव्यमान m पर लगाया गया तात्क्षणिक बल F उसी क्षण में त्वरण a उत्पन्न करता है। इसके विपरीत, क्रिया सिद्धांत एक बिंदु तक स्थानीयकृत नहीं है; प्रत्युत, इसमें समय के अंतराल पर समाकलित और (क्षेत्र के लिए) स्थान का एक विस्तारित क्षेत्र सम्मिलित होता है। इसके अलावा, उत्कृष्ट क्रिया सिद्धांतों के सामान्य निर्माण में, प्रणाली की प्रारंभिक और अंतिम स्थिति तय होती है, उदाहरण के लिए | |||
{{block indent | em = 1.5 | text = ''यह देखते हुए कि कण समय t1 पर स्थिति x1 से प्रारम्भ होता है और समय t2 पर स्थिति x2 पर समाप्त होता है, इन दो समापन बिंदुओं को जोड़ने वाला भौतिक प्रक्षेपवक्र क्रिया अभिन्न अंग का एक अतिम है''}} | |||
विशेष रूप से, अंतिम स्थिति के निर्धारण की व्याख्या क्रिया सिद्धांत को एक उद्देश्य देने के रूप में की गई है जो ऐतिहासिक रूप से विवादास्पद रहा है। यद्यपि, डब्ल्यू. योरग्राउ और एस. मैंडेलस्टम के अनुसार, दूरसंचार दृष्टिकोण... यह मानता है कि परिवर्तनात्मक सिद्धांतों में स्वयं गणितीय विशेषताएँ होती हैं जो वास्तव में उनके पास नहीं होती हैं। इसके अलावा,कुछ आलोचकों का कहना है कि यह स्पष्ट दूरसंचार प्रश्न पूछे जाने के तरीके के कारण उत्पन्न होती है।.प्रारंभिक और अंतिम दोनों स्थितियों (स्थिति लेकिन वेग नहीं) के कुछ नहीं बल्कि सभी पहलुओं को निर्दिष्ट करके हम अंतिम स्थितियों से प्रारंभिक स्थितियों के बारे में कुछ अनुमान लगा रहे हैं, और यह "पिछड़ा" अनुमान है जिसे एक के रूप में देखा जा सकता है उपर्युक्त सिद्धांत से संबद्ध स्पष्टीकरण. यदि हम उत्कृष्ट विवरण को पथ एकीकरण की परिमाण औपचारिकता के सीमित सन्दर्भ के रूप में मानते हैं, तो प्रयोजनवाद को भी दूर किया जा सकता है, जिसमें सभी संभावित पथों के साथ आयामों के हस्तक्षेप के परिणामस्वरूप स्थिर पथ प्राप्त होते हैं।।<ref name=":0" /> | |||
काल्पनिक कथा लेखक टेड चियांग द्वारा लघु कहानी स्टोरी ऑफ योर लाइफ में फ़र्मेट के सिद्धांत के दृश्य चित्रण के साथ-साथ इसके दूरसंचार आयाम की चर्चा भी सम्मिलित है। कीथ डिवालिन की द मैथ इंस्टिंक्ट में एक अध्याय सम्मिलित है, "एल्विस द वेल्श कॉर्गी हू कैन डू कैलकुलस" जो कुछ जानवरों में निहित कैलकुलस पर चर्चा करता है क्योंकि वे वास्तविक स्थितियों में "कम से कम समय" की समस्या को हल करते हैं। | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 109: | Line 114: | ||
* विविधताओं की गणना | * विविधताओं की गणना | ||
* हैमिल्टनियन यांत्रिकी | * हैमिल्टनियन यांत्रिकी | ||
* | * लग्रांजिएं यांत्रिकी | ||
* ओकाम का उस्तरा | * ओकाम का उस्तरा | ||
{{Div col end}} | {{Div col end}} | ||
| Line 129: | Line 134: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Principle Of Least Action}} | {{DEFAULTSORT:Principle Of Least Action}} | ||
[[de:Prinzip der kleinsten Wirkung]] | [[de:Prinzip der kleinsten Wirkung]] | ||
[[sq:Principi i Hamiltonit]] | [[sq:Principi i Hamiltonit]] | ||
[[Category:All articles with unsourced statements|Principle Of Least Action]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Principle Of Least Action]] | |||
[[Category: | [[Category:Articles with unsourced statements from July 2017|Principle Of Least Action]] | ||
[[Category:Created On 19/01/2023]] | [[Category:CS1 errors]] | ||
[[Category:Created On 19/01/2023|Principle Of Least Action]] | |||
[[Category:Lua-based templates|Principle Of Least Action]] | |||
[[Category:Machine Translated Page|Principle Of Least Action]] | |||
[[Category:Mechanics templates|Principle Of Least Action]] | |||
[[Category:Multi-column templates|Principle Of Least Action]] | |||
[[Category:Pages using div col with small parameter|Principle Of Least Action]] | |||
[[Category:Pages with empty portal template|Principle Of Least Action]] | |||
[[Category:Pages with script errors|Principle Of Least Action]] | |||
[[Category:Physics sidebar templates|Principle Of Least Action]] | |||
[[Category:Portal-inline template with redlinked portals|Principle Of Least Action]] | |||
[[Category:Short description with empty Wikidata description|Principle Of Least Action]] | |||
[[Category:Templates Translated in Hindi|Principle Of Least Action]] | |||
[[Category:Templates Vigyan Ready|Principle Of Least Action]] | |||
[[Category:Templates that add a tracking category|Principle Of Least Action]] | |||
[[Category:Templates that generate short descriptions|Principle Of Least Action]] | |||
[[Category:Templates using TemplateData|Principle Of Least Action]] | |||
[[Category:Templates using under-protected Lua modules|Principle Of Least Action]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:परिवर्तनशील सिद्धांत|Principle Of Least Action]] | |||
[[Category:भौतिकी का इतिहास|Principle Of Least Action]] | |||
[[Category:भौतिकी में अवधारणाएँ|Principle Of Least Action]] | |||
[[Category:वैज्ञानिक कानून|Principle Of Least Action]] | |||
Latest revision as of 18:14, 8 August 2023
| Part of a series on |
| चिरसम्मत यांत्रिकी |
|---|
स्थिर-क्रिया सिद्धांत - जिसे कम से कम क्रिया के सिद्धांत के रूप में भी जाना जाता है - एक भिन्नता सिद्धांत है, जिसे जब एक यांत्रिकी प्रणाली के कार्य पर लागू किया जाता है, उस प्रणाली के लिए गति के समीकरण उत्पन्न करता है। सिद्धांत बताता है कि प्रक्षेपवक्र (अर्थात गति के समीकरणों के समाधान) प्रणाली की क्रिया के स्थिर बिंदु हैं। [1]
सिद्धांत का उपयोग गति के न्यूटोनियन, लैग्रेन्जियन और हैमिल्टनियन समीकरणों और यहां तक कि सामान्य सापेक्षता, साथ ही उत्कृष्ट बिजली का गतिविज्ञान और परिमाण क्षेत्र सिद्धांत को प्राप्त करने के लिए किया जा सकता है।इन सन्दर्भ में, एक अलग क्रिया को न्यूनतम या अधिकतम किया जाना चाहिए। सापेक्षता के लिए, यह आइंस्टीन-हिल्बर्ट क्रिया है। परिमाण क्षेत्र सिद्धांत के लिए, इसमें पथ अभिन्न सूत्रीकरण सम्मिलित है।
उत्कृष्ट यांत्रिकी और विद्युत चुम्बकीय अभिव्यक्तियाँ परिमाण यांत्रिकी का परिणाम हैं। स्थिर क्रिया पद्धति ने परिमाण यांत्रिकी के विकास में मदद की।[2] 1933 में, भौतिक विज्ञानी पॉल डिराक ने आयामों के परिमाण हस्तक्षेप में सिद्धांत के परिमाण यांत्रिक आधार को समझकर प्रदर्शित किया कि इस सिद्धांत का उपयोग परिमाण गणना में कैसे किया जा सकता है।[3] इसके बाद जूलियन श्विंगर और रिचर्ड फेनमैन ने स्वतंत्र रूप से परिमाण बिजली का गतिविज्ञान में इस सिद्धांत को लागू किया।[4][5]
यह सिद्धांत आधुनिक भौतिक विज्ञान और गणित में केंद्रीय बना हुआ है, जिसे थर्मोडायनामिक्स,[6][7][8] द्रव यांत्रिकी,[9] सापेक्षता का सिद्धांत, परिमाण यांत्रिकी[10], कण भौतिक विज्ञान, और स्ट्रिंग सिद्धांत[11] में लागू किया जा रहा है। और मोर्स सिद्धांत में आधुनिक गणितीय जांच का केंद्र बिंदु है। मौपर्टुइस का सिद्धांत और हैमिल्टन का सिद्धांत स्थिर क्रिया के सिद्धांत का उदाहरण देते हैं।
क्रिया सिद्धांत प्रकाशिकी में पहले के विचारों से पहले आता है। प्राचीन ग्रीस में, यूक्लिड ने अपने कैटोप्ट्रिका में लिखा था कि, दर्पण से परावर्तित होने वाले प्रकाश के पथ के लिए, आपतन कोण प्रतिबिंब के कोण के बराबर होता है।[12] अलेक्जेंड्रिया के नायक ने बाद में दिखाया कि यह रास्ता सबसे कम लंबाई और सबसे कम समय का था।[13]
विद्वान प्रायः कम से कम क्रिया के सिद्धांत को प्रतिपादित करने के लिए पियरे लुईस मौपर्टुइस को श्रेय देते हैं क्योंकि उन्होंने इसके बारे में 1744[14] और 1746[15] में लिखा था। यद्यपि, लियोनहार्ड यूलर ने भी 1744[16] में इस सिद्धांत पर चर्चा की, और साक्ष्य से पता चलता है कि गॉटफ्रीड लीबनिज़ दोनों से 39 वर्ष पहले थे।[17]
सामान्य कथन
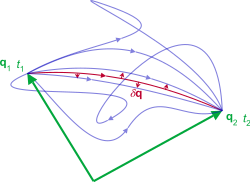
क्रिया, निरूपित , एक भौतिक प्रणाली को समय के उदाहरणों t1 और t2 के बीच लैग्रेंजियन L के अभिन्न अंग के रूप में परिभाषित किया गया है - तकनीकी रूप से N सामान्यीकृत निर्देशांक q = (q1, q2, ... , qN) का एक कार्यात्मक जो समय के कार्य हैं और प्रणाली के विन्यास को परिभाषित करते हैं:
गणितीय रूप से सिद्धांत है[19][20]
न्यूनतम क्रिया के ऐतिहासिक नाम के तथापि, स्थिर क्रिया प्रायः न्यूनतम नहीं होती है।[21][1]: 19–6 यह पथ में पर्याप्त रूप से छोटे, सीमित खंडों के लिए एक न्यूनतम सिद्धांत है।[22]
अनुप्रयोगों में कथन और क्रिया की परिभाषा को एक साथ लिया जाता है[23]
उत्पत्ति, वक्तव्य, और विवाद
फर्मेट
1600 के दशक में, पियरे डी फ़र्मेट ने कहा कि "प्रकाश सबसे कम समय के पथ पर दो दिए गए बिंदुओं के बीच यात्रा करता है," जिसे कम से कम समय के सिद्धांत या फ़र्मेट के सिद्धांत के रूप में जाना जाता है।[20]
मौपर्टुइस
कम से कम क्रिया के सिद्धांत के निर्माण का श्रेय आमतौर पर पियरे लुईस मौपर्टुइस को दिया जाता है, जिन्होंने महसूस किया कि "प्रकृति अपने सभी कार्यों में मितव्ययी है", और इस सिद्धांत को व्यापक रूप से लागू किया:
इस सिद्धांत से उत्पन्न गति और विश्राम के नियम बिल्कुल वही हैं जो प्रकृति में देखे गए हैं, हम सभी घटनाओं पर इसके अनुप्रयोग की प्रशंसा कर सकते हैं। पशुओं की गति, पौधों की वानस्पतिक वृद्धि... केवल इसके परिणाम हैं; और ब्रह्माण्ड का दृश्य इतना अधिक भव्य, इतना अधिक सुंदर, इसके रचयिता के योग्य बन जाता है, जब कोई जानता है कि थोड़ी संख्या में, सबसे बुद्धिमानी से स्थापित कानून, सभी गतिविधियों के लिए पर्याप्त हैं।
— Pierre Louis Maupertuis[24]
मौपर्टुइस की यह धारणा, यद्यपि आज कुछ सीमा तक नियतात्मक है, यांत्रिकी के अधिकांश सार को ग्रहण करती है।
भौतिक विज्ञान के अनुप्रयोग में, मौपर्टुइस ने सुझाव दिया कि न्यूनतम की जाने वाली मात्रा "विज़ विवा" द्वारा एक प्रणाली के भीतर गति की अवधि (समय) का उत्पाद थी।
जो कि प्रणाली की गतिज ऊर्जा T जिसे अब हम कहते हैं, के दोगुने का अभिन्न अंग है।
यूलर
लियोनहार्ड यूलर ने 1744 में अपने मेथडस इनवेनिएंडी लिनियास कर्वस मैक्सिमी मिनिव प्रोप्राइटेट गौडेंटेस के एडिटामेंटम 2 में बहुत ही पहचाने जाने योग्य शब्दों में क्रिया सिद्धांत का सूत्रीकरण दिया। दूसरे अनुच्छेद से प्रारम्भ::
माना प्रक्षेप्य का द्रव्यमान M है, और अनंत दूरी ds पर चलते समय इसकी गति v है। पिंड में एक संवेग Mv होगा, जिसे दूरी ds से गुणा करने पर, Mv ds देगा, दूरी ds पर एकीकृत पिंड का संवेग। अब मैं दावा करता हूं कि इस प्रकार निकाय द्वारा वर्णित वक्र (समान समापन बिंदुओं को जोड़ने वाले अन्य सभी वक्रों में से) है जो न्यूनतम करता है
या, इसके अलावा 'अनुबंध यह है कि कि एम पथ के साथ स्थिर है,
जैसा कि यूलर कहते हैं, ∫Mv ds तय की गई दूरी पर संवेग का अभिन्न अंग है, जो आधुनिक संकेतन में, संक्षिप्त या घटी हुई क्रिया के बराबर है
इस प्रकार, यूलर ने मौपर्टुइस के समान ही वर्ष में परिवर्तनशील सिद्धांत का एक समतुल्य और (स्पष्ट रूप से) स्वतंत्र वर्णन दिया, भले ही थोड़ा बाद में। कौतूहलपूर्वक यह है कि यूलर ने किसी प्राथमिकता का दावा नहीं किया, जैसा कि निम्नलिखित प्रकरण से पता चलता है।
विवादित प्राथमिकता
मौपर्टुइस की प्राथमिकता पर 1751 में गणितज्ञ सैमुअल कोनिग द्वारा विवाद किया गया था, जिन्होंने दावा किया था कि इसका आविष्कार 1707 में गॉटफ्राइड लाइबनिज द्वारा किया गया था। यद्यपि लाइबनिज के कई तर्कों के समान, सिद्धांत को लाइबनिज के कार्यों में प्रलेखित नहीं किया गया है। कोनिग ने स्वयं सिद्धांत के साथ लाइबनिज से जैकब हरमन को लिखे 1707 के पत्र की एक प्रति दिखाई, लेकिन मूल पत्र खो गया है। विवादास्पद कार्यवाहियों में, कोनिग पर जालसाजी का आरोप लगाया गया था, [26] और यहां तक कि प्रशिया के राजा ने भी मौपर्टुइस (अपनी अकादमी के प्रमुख) का बचाव करते हुए बहस में प्रवेश किया, जबकि वोल्टेयर ने कोनिग का बचाव किया।[citation needed]
यूलर, प्राथमिकता का दावा करने के बजाय, मौपर्टुइस का एक कट्टर रक्षक था, और यूलर ने स्वयं 13 अप्रैल 1752 को बर्लिन अकादमी के समक्ष जालसाजी के लिए कोनिग पर दावा चलाया। जालसाजी के दावों की 150 साल बाद फिर से जांच की गई, और अभिलेखीय कार्य सी.आई. द्वारा किया गया। 1898 में गेरहार्ड्ट[16] और 1913 में डब्लू. काबिट्ज़[17] ने बर्नौली अभिलेखागार में पत्र की अन्य प्रतियां और कोनिग द्वारा उद्धृत तीन अन्य प्रतियां का खुलासा किया।
इससे आगे का विकास
यूलर ने इस विषय पर लिखना जारी रखा; अपने रिफ्लेक्शंस सुर क्वेल्क्स लोइक्स जेनरालेस डे ला नेचर (1748) में, उन्होंने क्रिया को "प्रयास" कहा। उनकी अभिव्यक्ति आधुनिक संभावित ऊर्जा से मेल खाती है, और कम से कम क्रिया के उनके वक्तव्य में कहा गया है कि आराम पर निकायों की एक प्रणाली की कुल संभावित ऊर्जा कम हो जाती है, जो आधुनिक स्थैतिकी का सिद्धांत है।
लैग्रेंज और हैमिल्टन
1760 में जोसफ-लुई लाग्रेंज द्वारा भिन्नताओं की अधिकांश गणनाएं बताई गई थीं[27][28] और वह इसे गतिशीलता की समस्याओं पर लागू करने के लिए आगे बढ़े। मेकैनिक एनालिटिक (1788) में लैग्रेंज ने एक यांत्रिक पिंड की गति के सामान्य समीकरण निकाले।य की गति के सामान्य लैग्रैंगियन समीकरणों को व्युत्पन्न किया।[29] विलियम रोवन हैमिल्टन ने 1834 और 1835 में[30] उत्कृष्ट लैग्रेंजियन फ़ंक्शन के लिए परिवर्तनशील सिद्धांत लागू किया
जैकोबी, मोर्स और कैराथियोडोरी
1842 में, कार्ल गुस्ताव जैकोबी ने इस समस्या से निपटा कि क्या परिवर्तनशील सिद्धांत हमेशा अन्य स्थिर बिंदुओं (मैक्सिमा या स्थिर काठी बिंदु) के विपरीत न्यूनतम को पाता है; उनका अधिकांश कार्य द्वि-आयामी सतहों पर भू-भौतिकी पर केंद्रित था।[31] पहला स्पष्ट सामान्य कथन 1920 और 1930 के दशक में मारस्टन मोर्स द्वारा दिया गया था,[32] जिसे अब मोर्स सिद्धांत के रूप में जाना जाता है। उदाहरण के लिए, मोर्स ने दिखाया कि एक प्रक्षेपवक्र में संयुग्मित बिंदुओं की संख्या लैग्रेंजियन के दूसरे संस्करण में नकारात्मक आइगेनवैल्यू की संख्या के बराबर है। यूलर-लैग्रेंज समीकरण की एक विशेष रूप से सुंदर व्युत्पत्ति कॉन्स्टेंटिन कैराथियोडोरी द्वारा तैयार की गई थी और उनके द्वारा 1935 में प्रकाशित की गई थी।
गॉस और हर्ट्ज
उत्कृष्ट यांत्रिकी के अन्य अतिम सिद्धांतों को तैयार किया गया है, जैसे कि गॉस का न्यूनतम अवरोध का सिद्धांत और इसका परिणाम, हर्ट्ज़ का न्यूनतम वक्रता का सिद्धांत।
डी'एलेम्बर्ट
अतिरिक्त-होलोनोमिक बाधाओं वाली प्रणालियों के लिए, हैमिल्टन के सिद्धांत को डी'अलेम्बर्ट सिद्धांत द्वारा प्रतिस्थापित किया जाता है। इस सन्दर्भ में क्रिया केवल विविधताओं के लिए स्थिर होने के लिए लगाया गया है जो बाधाओं के अनुरूप हैं।
संभावित टेलिऑलॉजिकल पहलुओं के बारे में विवाद
गति के विभेदक समीकरणों और उनके अभिन्न समकक्ष की गणितीय तुल्यता के महत्वपूर्ण दार्शनिक निहितार्थ हैं। विभेदक समीकरण अंतरिक्ष में एक बिंदु या समय के एक क्षण में स्थानीयकृत मात्राओं के बारे में कथन हैं। उदाहरण के लिए, न्यूटन का दूसरा नियम
बताता है कि किसी द्रव्यमान m पर लगाया गया तात्क्षणिक बल F उसी क्षण में त्वरण a उत्पन्न करता है। इसके विपरीत, क्रिया सिद्धांत एक बिंदु तक स्थानीयकृत नहीं है; प्रत्युत, इसमें समय के अंतराल पर समाकलित और (क्षेत्र के लिए) स्थान का एक विस्तारित क्षेत्र सम्मिलित होता है। इसके अलावा, उत्कृष्ट क्रिया सिद्धांतों के सामान्य निर्माण में, प्रणाली की प्रारंभिक और अंतिम स्थिति तय होती है, उदाहरण के लिए
विशेष रूप से, अंतिम स्थिति के निर्धारण की व्याख्या क्रिया सिद्धांत को एक उद्देश्य देने के रूप में की गई है जो ऐतिहासिक रूप से विवादास्पद रहा है। यद्यपि, डब्ल्यू. योरग्राउ और एस. मैंडेलस्टम के अनुसार, दूरसंचार दृष्टिकोण... यह मानता है कि परिवर्तनात्मक सिद्धांतों में स्वयं गणितीय विशेषताएँ होती हैं जो वास्तव में उनके पास नहीं होती हैं। इसके अलावा,कुछ आलोचकों का कहना है कि यह स्पष्ट दूरसंचार प्रश्न पूछे जाने के तरीके के कारण उत्पन्न होती है।.प्रारंभिक और अंतिम दोनों स्थितियों (स्थिति लेकिन वेग नहीं) के कुछ नहीं बल्कि सभी पहलुओं को निर्दिष्ट करके हम अंतिम स्थितियों से प्रारंभिक स्थितियों के बारे में कुछ अनुमान लगा रहे हैं, और यह "पिछड़ा" अनुमान है जिसे एक के रूप में देखा जा सकता है उपर्युक्त सिद्धांत से संबद्ध स्पष्टीकरण. यदि हम उत्कृष्ट विवरण को पथ एकीकरण की परिमाण औपचारिकता के सीमित सन्दर्भ के रूप में मानते हैं, तो प्रयोजनवाद को भी दूर किया जा सकता है, जिसमें सभी संभावित पथों के साथ आयामों के हस्तक्षेप के परिणामस्वरूप स्थिर पथ प्राप्त होते हैं।।[1]
काल्पनिक कथा लेखक टेड चियांग द्वारा लघु कहानी स्टोरी ऑफ योर लाइफ में फ़र्मेट के सिद्धांत के दृश्य चित्रण के साथ-साथ इसके दूरसंचार आयाम की चर्चा भी सम्मिलित है। कीथ डिवालिन की द मैथ इंस्टिंक्ट में एक अध्याय सम्मिलित है, "एल्विस द वेल्श कॉर्गी हू कैन डू कैलकुलस" जो कुछ जानवरों में निहित कैलकुलस पर चर्चा करता है क्योंकि वे वास्तविक स्थितियों में "कम से कम समय" की समस्या को हल करते हैं।
यह भी देखें
- क्रिया (भौतिकी)
- पथ अभिन्न सूत्रीकरण
- श्विंगर का क्वांटम एक्शन सिद्धांत
- कम से कम प्रतिरोध का रास्ता
- विश्लेषणात्मक यांत्रिकी
- विविधताओं की गणना
- हैमिल्टनियन यांत्रिकी
- लग्रांजिएं यांत्रिकी
- ओकाम का उस्तरा
नोट्स और संदर्भ
- ↑ 1.0 1.1 1.2 The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action
- ↑ Richard Feynman, The Character of Physical Law.
- ↑ Dirac, Paul A. M. (1933). "The Lagrangian in Quantum Mechanics" (PDF). Physikalische Zeitschrift der Sowjetunion. 3 (1): 64–72.
- ↑ R. Feynman, Quantum Mechanics and Path Integrals, McGraw-Hill (1965), ISBN 0070206503
- ↑ J. S. Schwinger, Quantum Kinematics and Dynamics, W. A. Benjamin (1970), ISBN 0738203033
- ↑ García-Morales, Vladimir; Pellicer, Julio; Manzanares, José A. (2008). "Thermodynamics based on the principle of least abbreviated action: Entropy production in a network of coupled oscillators". Annals of Physics. 323 (8): 1844–58. arXiv:cond-mat/0602186. Bibcode:2008AnPhy.323.1844G. doi:10.1016/j.aop.2008.04.007. S2CID 118464686.
- ↑ Gray, Chris (2009). "Principle of least action". Scholarpedia. 4 (12): 8291. Bibcode:2009SchpJ...4.8291G. doi:10.4249/scholarpedia.8291.
- ↑ Feynman, Richard Phillips (1942). "The Principle of Least Action in Quantum Mechanics". Bibcode:1942PhDT.........5F.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ "Principle of Least Action – damtp" (PDF). Archived from the original (PDF) on 2015-10-10. Retrieved 2016-07-18.
- ↑ Helzberger, Max (1966). "Optics from Euclid to Huygens". Applied Optics. 5 (9): 1383–93. Bibcode:1966ApOpt...5.1383H. doi:10.1364/AO.5.001383. PMID 20057555.
In Catoptrics the law of reflection is stated, namely that incoming and outgoing rays form the same angle with the surface normal."
- ↑ Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 167–68. ISBN 0-19-501496-0.
- ↑ P.L.M. de Maupertuis, Accord de différentes lois de la nature qui avaient jusqu'ici paru incompatibles. (1744) Mém. As. Sc. Paris p. 417. (English translation)
- ↑ P.L.M. de Maupertuis, Le lois de mouvement et du repos, déduites d'un principe de métaphysique. (1746) Mém. Ac. Berlin, p. 267.(English translation)
- ↑ 14.0 14.1 Leonhard Euler, Methodus Inveniendi Lineas Curvas Maximi Minive Proprietate Gaudentes. (1744) Bousquet, Lausanne & Geneva. 320 pages. Reprinted in Leonhardi Euleri Opera Omnia: Series I vol 24. (1952) C. Cartheodory (ed.) Orell Fuessli, Zurich. Scanned copy of complete text at The Euler Archive, Dartmouth.
- ↑ Leibniz's letter to Varignon (not to Hermann).
Samuel Koenig, Appel au Public du jugement de l'Académie royale de Berlin, Leide, 1752. - ↑ 16.0 16.1 Gerhardt CI. (1898) "Über die vier Briefe von Leibniz, die Samuel König in dem Appel au public, Leide MDCCLIII, veröffentlicht hat", Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, I, 419–427.
- ↑ 17.0 17.1 Kabitz W. (1913) "Über eine in Gotha aufgefundene Abschrift des von S. König in seinem Streite mit Maupertuis und der Akademie veröffentlichten, seinerzeit für unecht erklärten Leibnizbriefes", Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, II, 632–638.
- ↑ 18.0 18.1 R. Penrose (2007). The Road to Reality. Vintage books. p. 474. ISBN 978-0-679-77631-4.
- ↑ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
- ↑ 20.0 20.1 Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
- ↑ Goodman, Bernard (1993). "Action". In Parker, S. P. (ed.). McGraw-Hill Encyclopaedia of Physics (2nd ed.). New York: McGraw-Hill. p. 22. ISBN 0-07-051400-3.
- ↑ Stehle, Philip M. (1993). "Least-action principle". In Parker, S. P. (ed.). McGraw-Hill Encyclopaedia of Physics (2nd ed.). New York: McGraw-Hill. p. 670. ISBN 0-07-051400-3.
- ↑ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ↑ Chris Davis. Idle theory Archived 2006-06-15 at the Wayback Machine (1998)
- ↑ Euler, Additamentum II (external link), ibid. (English translation)
- ↑ J J O'Connor and E F Robertson, "The Berlin Academy and forgery", (2003), at The MacTutor History of Mathematics archive.
- ↑ D. J. Struik, ed. (1969). A Source Book in Mathematics, 1200–1800. Cambridge, Mass: MIT Press. pp. 406–413
- ↑ Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. ISBN 0-19-501496-0. pp. 582-589
- ↑ Lagrange, Joseph-Louis (1788). Mécanique Analytique. p. 226
- ↑ W. R. Hamilton, "On a General Method in Dynamics", Philosophical Transactions of the Royal Society Part I (1834) p.247-308; Part II (1835) p. 95-144. (From the collection Sir William Rowan Hamilton (1805–1865): Mathematical Papers edited by David R. Wilkins, School of Mathematics, Trinity College, Dublin 2, Ireland. (2000); also reviewed as On a General Method in Dynamics)
- ↑ G.C.J. Jacobi, Vorlesungen über Dynamik, gehalten an der Universität Königsberg im Wintersemester 1842–1843. A. Clebsch (ed.) (1866); Reimer; Berlin. 290 pages, available online Œuvres complètes volume 8 Archived 2007-11-22 at the Wayback Machine at Gallica-Math Archived 2008-11-23 at the Wayback Machine from the Gallica Bibliothèque nationale de France.
- ↑ Marston Morse (1934). "The Calculus of Variations in the Large", American Mathematical Society Colloquium Publication 18; New York.
बाहरी कड़ियाँ
- Interactive explanation of the principle of least action
- Interactive applet to construct trajectories using principle of least action
- Georgiev, Georgi Yordanov (2012). "A Quantitative Measure, Mechanism and Attractor for Self-Organization in Networked Complex Systems". Self-Organizing Systems. Lecture Notes in Computer Science. Vol. 7166. pp. 90–5. doi:10.1007/978-3-642-28583-7_9. ISBN 978-3-642-28582-0. S2CID 377417.
- Georgiev, Georgi; Georgiev, Iskren (2002). "The Least Action and the Metric of an Organized System". Open Systems and Information Dynamics. 9 (4): 371–380. arXiv:1004.3518. doi:10.1023/a:1021858318296. S2CID 43644348.
- Terekhovich, Vladislav (2018). "Metaphysics of the Principle of Least Action". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 62: 189–201. arXiv:1511.03429. Bibcode:2018SHPMP..62..189T. doi:10.1016/j.shpsb.2017.09.004. S2CID 85528641.
- The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action