प्रभावी क्षेत्र सिद्धांत: Difference between revisions
No edit summary |
m (9 revisions imported from alpha:प्रभावी_क्षेत्र_सिद्धांत) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Type of approximation to an underlying physical theory}} | {{short description|Type of approximation to an underlying physical theory}} | ||
{{Quantum field theory|cTopic=Some models}} | {{Quantum field theory|cTopic=Some models}} | ||
[[भौतिक विज्ञान]] में, एक '''प्रभावी क्षेत्र सिद्धांत''' एक अंतर्निहित भौतिक सिद्धांत, जैसे [[क्वांटम क्षेत्र सिद्धांत]] या एक [[सांख्यिकीय यांत्रिकी]] मॉडल के लिए एक प्रकार का सन्निकटन या [[प्रभावी सिद्धांत]] है। एक प्रभावी क्षेत्र सिद्धांत में चयनित लंबाई | [[भौतिक विज्ञान]] में, एक '''प्रभावी क्षेत्र सिद्धांत''' एक अंतर्निहित भौतिक सिद्धांत, जैसे [[क्वांटम क्षेत्र सिद्धांत]] या एक [[सांख्यिकीय यांत्रिकी]] मॉडल के लिए एक प्रकार का सन्निकटन या [[प्रभावी सिद्धांत]] है। एक प्रभावी क्षेत्र सिद्धांत में चयनित लंबाई माप या ऊर्जा माप पर होने वाली भौतिक घटनाओं का वर्णन करने के लिए स्वतंत्रता की उचित डिग्री (भौतिकी और रसायन विज्ञान) सम्मिलित होती है, जबकि कम दूरी (या, समकक्ष, उच्च ऊर्जा पर) पर उपसंरचना और स्वतंत्रता की डिग्री की अनदेखी की जाती है। सहज रूप से, छोटी लंबाई के माप पर अंतर्निहित सिद्धांत के व्यवहार का औसत निकाला जाता है, जिससे लंबी लंबाई के माप पर एक सरलीकृत मॉडल होने का विश्वाश किया जा सकता है। प्रभावी क्षेत्र सिद्धांत सामान्यतः सबसे अच्छा काम करते हैं जब अभिरुचि की लंबाई के माप और अंतर्निहित गतिशीलता की लंबाई के माप के मध्य एक बड़ा अंतर होता है। प्रभावी क्षेत्र सिद्धांतों का उपयोग [[कण भौतिकी]], सांख्यिकीय यांत्रिकी, [[संघनित पदार्थ भौतिकी]], [[सामान्य सापेक्षता]] और [[ जल-गत्यात्मकता |हाइड्रोडायनामिक्स]] में पाया गया है। वह गणनाओं को सरल करते हैं, और अपव्यय प्रणाली और [[विकिरण]] प्रभावों के उपचार की अनुमति देते हैं।<ref>{{Cite journal|doi=10.1103/PhysRevLett.110.174301|pmid=23679733|title=गैर-रूढ़िवादी प्रणालियों के शास्त्रीय यांत्रिकी|journal=Physical Review Letters|volume=110|issue=17|pages=174301|year=2013|last1=Galley|first1=Chad R.|arxiv=1210.2745|bibcode=2013PhRvL.110q4301G|s2cid=14591873|doi-access=free}}</ref><ref>{{Cite journal |arxiv = 1402.2610|last1 = Birnholtz|first1 = Ofek|title = कार्रवाई के स्तर पर विकिरण प्रतिक्रिया|journal = International Journal of Modern Physics A|volume = 29|issue = 24|pages = 1450132–1450190|last2 = Hadar|first2 = Shahar|last3 = Kol|first3 = Barak|year = 2014|doi = 10.1142/S0217751X14501322|bibcode = 2014IJMPA..2950132B|s2cid = 118541484}}</ref> | ||
== [[पुनर्सामान्यीकरण समूह]] == | == [[पुनर्सामान्यीकरण समूह]] == | ||
वर्तमान में, प्रभावी क्षेत्र सिद्धांतों पर पुनर्सामान्यीकरण समूह (आरजी) के संदर्भ में चर्चा की जाती है जहां कम दूरी की स्वतंत्रता की डिग्री को एकीकृत करने की प्रक्रिया को व्यवस्थित बनाया जाता है। यद्यपि यह विधि प्रभावी क्षेत्र सिद्धांतों के वास्तविक निर्माण की अनुमति देने के लिए पर्याप्त रूप से ठोस नहीं है, | वर्तमान में, प्रभावी क्षेत्र सिद्धांतों पर पुनर्सामान्यीकरण समूह (आरजी) के संदर्भ में चर्चा की जाती है जहां कम दूरी की स्वतंत्रता की डिग्री को एकीकृत करने की प्रक्रिया को व्यवस्थित बनाया जाता है। यद्यपि यह विधि प्रभावी क्षेत्र सिद्धांतों के वास्तविक निर्माण की अनुमति देने के लिए पर्याप्त रूप से ठोस नहीं है, किन्तु आरजी विश्लेषण के माध्यम से उनकी उपयोगिता की सकल समझ स्पष्ट हो जाती है। यह पद्धति [[समरूपता]] के विश्लेषण के माध्यम से प्रभावी क्षेत्र सिद्धांतों के निर्माण की मुख्य विधि को भी विश्वसनीयता प्रदान करती है। यदि सूक्ष्म सिद्धांत में एकल द्रव्यमान मापदंड '<nowiki/>'''M'''<nowiki/>' है, तब प्रभावी क्षेत्र सिद्धांत को '1/'''M'''<nowiki/>' में विस्तार के रूप में देखा जा सकता है। '1/'''M'''<nowiki/>' की कुछ शक्ति के लिए त्रुटिहीन एक प्रभावी क्षेत्र सिद्धांत के निर्माण के लिए '1/'''M'''<nowiki/>' में विस्तार के प्रत्येक क्रम पर मुक्त मापदंडों के एक नए समूह की आवश्यकता होती है। यह विधि [[बिखरने|प्रकीर्णन]] या अन्य प्रक्रियाओं के लिए उपयोगी है जहां अधिकतम संवेग स्केल ''''k'''<nowiki/>' नियम ''''k/M≪1'''<nowiki/>' को संतुष्ट करता है। चूंकि प्रभावी क्षेत्र सिद्धांत छोटे लंबाई के माप पर मान्य नहीं हैं, इसलिए उन्हें पुन: सामान्य करने की आवश्यकता नहीं है। वास्तव में, एक प्रभावी क्षेत्र सिद्धांत के लिए आवश्यक '1/'''M'''<nowiki/>' में प्रत्येक क्रम में मापदंडों की निरंतर बढ़ती संख्या का अर्थ है कि वह सामान्यतः [[क्वांटम इलेक्ट्रोडायनामिक्स]] के समान अर्थ में पुनर्सामान्यीकरण योग्य नहीं हैं, जिसके लिए केवल दो मापदंडों के पुनर्सामान्यीकरण की आवश्यकता होती है। | ||
== प्रभावी क्षेत्र सिद्धांतों के उदाहरण == | == प्रभावी क्षेत्र सिद्धांतों के उदाहरण == | ||
===बीटा क्षय का फर्मी सिद्धांत=== | ===बीटा क्षय का फर्मी सिद्धांत=== | ||
प्रभावी क्षेत्र सिद्धांत का सबसे प्रसिद्ध उदाहरण बीटा क्षय का फर्मी सिद्धांत है। यह सिद्धांत [[परमाणु नाभिक]] के | प्रभावी क्षेत्र सिद्धांत का सबसे प्रसिद्ध उदाहरण बीटा क्षय का फर्मी सिद्धांत है। यह सिद्धांत [[परमाणु नाभिक]] के अशक्त क्षय के प्रारंभिक अध्ययन के समय विकसित किया गया था जब केवल अशक्त क्षय से निकलने वाले [[हैड्रान]] और [[लेपटोन|लेप्टान]] ज्ञात थे। अध्ययन की गई विशिष्ट [[प्राथमिक कण प्रतिक्रिया]]एँ थीं: | ||
::<math> | ::<math> | ||
| Line 18: | Line 18: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
इस सिद्धांत ने इन प्रतिक्रियाओं में सम्मिलित चार [[fermion|फर्मियनों]] के | इस सिद्धांत ने इन प्रतिक्रियाओं में सम्मिलित चार [[fermion|फर्मियनों]] के मध्य एक बिंदु जैसी बातचीत प्रस्तुत की। इस सिद्धांत को बड़ी घटनात्मक सफलता मिली और अंततः [[इलेक्ट्रोवीक इंटरैक्शन]] के [[गेज सिद्धांत]] से उत्पन्न होने के बारे में समझा गया, जो कण भौतिकी के [[मानक मॉडल]] का एक भाग है। इस अधिक मौलिक सिद्धांत में, अंतःक्रियाओं की मध्यस्थता [[स्वाद (कण भौतिकी)|फ्लेवर (कण भौतिकी)]] बदलने वाले [[गेज बोसोन]], W± द्वारा की जाती है। फर्मी सिद्धांत की अपार सफलता इसलिए थी क्योंकि W कण का द्रव्यमान लगभग 80 [[GeV]] है, जबकि प्रारंभिक प्रयोग 10 [[MeV]] से कम के ऊर्जा माप पर किए गए थे। परिमाण के 3 से अधिक आदेशों द्वारा तराजू का ऐसा पृथक्करण, अभी तक किसी भी अन्य स्थिति में पूरा नहीं किया गया है। | ||
=== [[अतिचालकता]] का [[बीसीएस सिद्धांत]] === | === [[अतिचालकता]] का [[बीसीएस सिद्धांत]] === | ||
एक अन्य प्रसिद्ध उदाहरण | एक अन्य प्रसिद्ध उदाहरण अतिचालकता का बीसीएस सिद्धांत है। यहाँ अंतर्निहित सिद्धांत एक [[धातु]] में [[इलेक्ट्रॉन|इलेक्ट्रॉनों]] का सिद्धांत है जो फोनोन नामक जाली कंपन के साथ परस्पर क्रिया करता है। फ़ोनोन कुछ इलेक्ट्रॉनों के मध्य आकर्षक परस्पर क्रिया का कारण बनते हैं, जिससे वह कूपर जोड़े बनाते हैं। इन जोड़ियों की लंबाई का मापदंड [[फोनन]] की तरंग दैर्ध्य की तुलना में बहुत बड़ा है, जिससे फ़ोनों की गतिशीलता की उपेक्षा करना और एक सिद्धांत का निर्माण करना संभव हो जाता है जिसमें दो इलेक्ट्रॉन एक बिंदु पर प्रभावी रूप से परस्पर क्रिया करते हैं। इस सिद्धांत को अतिचालकता पर प्रयोगों के परिणामों का वर्णन और भविष्यवाणी करने में उल्लेखनीय सफलता मिली है। | ||
=== गुरुत्वाकर्षण में प्रभावी क्षेत्र सिद्धांत === | === गुरुत्वाकर्षण में प्रभावी क्षेत्र सिद्धांत === | ||
सामान्य सापेक्षता से अपेक्षा की जाती है कि वह [[ क्वांटम गुरुत्वाकर्षण ]] के पूर्ण सिद्धांत का निम्न ऊर्जा प्रभावी क्षेत्र सिद्धांत हो, जैसे कि [[स्ट्रिंग सिद्धांत]] या [[लूप क्वांटम ग्रेविटी]]। विस्तार | सामान्य सापेक्षता से अपेक्षा की जाती है कि वह [[ क्वांटम गुरुत्वाकर्षण |क्वांटम गुरुत्वाकर्षण]] के पूर्ण सिद्धांत का निम्न ऊर्जा प्रभावी क्षेत्र सिद्धांत हो, जैसे कि [[स्ट्रिंग सिद्धांत]] या [[लूप क्वांटम ग्रेविटी]]। विस्तार मापदंड प्लैंक द्रव्यमान है। | ||
सामान्य सापेक्षता में समस्याओं को सरल बनाने के लिए प्रभावी क्षेत्र सिद्धांतों का भी उपयोग किया गया | |||
विशेष रूप से प्रेरणादायक परिमित आकार की वस्तुओं के [[गुरुत्वाकर्षण तरंग]] हस्ताक्षर की गणना में सामान्य सापेक्षता में समस्याओं को सरल बनाने के लिए प्रभावी क्षेत्र सिद्धांतों का भी उपयोग किया गया है।<ref>{{Cite journal |arxiv = hep-th/0409156|last1 = Goldberger|first1 = Walter|title = विस्तारित वस्तुओं के लिए गुरुत्वाकर्षण का एक प्रभावी क्षेत्र सिद्धांत|journal = Physical Review D|volume = 73|issue = 10|last2 = Rothstein|first2 = Ira|year = 2004|doi = 10.1103/PhysRevD.73.104029|s2cid = 54188791}}</ref> जीआर में सबसे आम ईएफ़टी [[गैर-सापेक्षवादी सामान्य सापेक्षता]] (एनआरजीआर) है,<ref>http://online.kitp.ucsb.edu/online/numrel-m08/buonanno/pdf1/Porto_NumRelData_KITP.pdf {{Bare URL PDF|date=March 2022}}</ref><ref>{{Cite journal |arxiv = 0712.4116|last1 = Kol|first1 = Barak|title = Non-Relativistic Gravitation: From Newton to Einstein and Back|journal = Classical and Quantum Gravity|volume = 25|issue = 14|pages = 145011|last2 = Smolkin|first2 = Lee|year = 2008|doi = 10.1088/0264-9381/25/14/145011|bibcode = 2008CQGra..25n5011K|s2cid = 119216835}}</ref><ref>{{Cite journal |arxiv = gr-qc/0511061|last1 = Porto|first1 = Rafael A|title = NRGR में स्पिनिंग बॉडीज की गति के बाद न्यूटोनियन सुधार|journal = Physical Review D|volume = 73|issue = 104031|pages = 104031|year = 2006|doi = 10.1103/PhysRevD.73.104031|s2cid = 119377563}}</ref> जो न्यूटन के पश्चात् के विस्तार के समान है।<ref>{{Cite journal |doi = 10.1103/PhysRevD.88.104037|title = न्यूटोनियन विकिरण और प्रतिक्रिया के बाद का सिद्धांत|journal = Physical Review D|volume = 88|issue = 10|pages = 104037|year = 2013|last1 = Birnholtz|first1 = Ofek|last2 = Hadar|first2 = Shahar|last3 = Kol|first3 = Barak|arxiv = 1305.6930|bibcode = 2013PhRvD..88j4037B|s2cid = 119170985}}</ref> एक अन्य सामान्य जीआर ईएफटी एक्सट्रीम मास रेशियो (ईएमआर) है, जिसे प्रेरक समस्या के संदर्भ में [[अत्यधिक द्रव्यमान अनुपात प्रेरक]] कहा जाता है। | |||
=== अन्य उदाहरण === | === अन्य उदाहरण === | ||
वर्तमान में, | वर्तमान में, अनेक स्थितियों के लिए प्रभावी क्षेत्र सिद्धांत लिखे गए हैं। | ||
*[[परमाणु भौतिकी]] की एक प्रमुख शाखा क्वांटम हैरोडायनामिक्स है, जहां हैड्रोन की परस्पर क्रियाओं को एक क्षेत्र सिद्धांत के रूप में माना जाता है, जो [[क्वांटम क्रोमोडायनामिक्स]] के अंतर्निहित सिद्धांत से व्युत्पन्न होना चाहिए। [[ क्वांटम हाइड्रोडायनामिक्स ]] [[परमाणु बल]] का सिद्धांत है, इसी | *[[परमाणु भौतिकी]] की एक प्रमुख शाखा क्वांटम हैरोडायनामिक्स है, जहां हैड्रोन की परस्पर क्रियाओं को एक क्षेत्र सिद्धांत के रूप में माना जाता है, जो [[क्वांटम क्रोमोडायनामिक्स]] के अंतर्निहित सिद्धांत से व्युत्पन्न होना चाहिए। [[ क्वांटम हाइड्रोडायनामिक्स |क्वांटम हाइड्रोडायनामिक्स]] [[परमाणु बल]] का सिद्धांत है, इसी प्रकार क्वांटम क्रोमोडायनामिक्स शक्तिशाली अंतःक्रिया का सिद्धांत है और क्वांटम इलेक्ट्रोडायनामिक्स [[विद्युत चुम्बकीय बल]] का सिद्धांत है। यहाँ लंबाई के माप के छोटे पृथक्करण के कारण, इस प्रभावी सिद्धांत में कुछ वर्गीकरण शक्ति है, किन्तु फर्मी सिद्धांत की उत्तम सफलता नहीं है। | ||
*कण भौतिकी में क्वांटम क्रोमोडायनामिक्स के प्रभावी क्षेत्र सिद्धांत जिसे चिरल पर्टर्बेशन सिद्धांत कहा जाता है, को | *कण भौतिकी में क्वांटम क्रोमोडायनामिक्स के प्रभावी क्षेत्र सिद्धांत जिसे चिरल पर्टर्बेशन सिद्धांत कहा जाता है, को उत्तम सफलता मिली है।<ref>{{Cite journal |arxiv = hep-ph/9311274|last1 = Leutwyler|first1 = H|title = चिराल पर्टर्बेशन थ्योरी की नींव पर|journal = Annals of Physics|volume = 235|pages = 165–203|year = 1994|issue = 1|doi = 10.1006/aphy.1994.1094|bibcode = 1994AnPhy.235..165L|s2cid = 16739698}}</ref> यह सिद्धांत पियोन या [[खाना|कोंस]] के साथ हैड्रोन की बातचीत से संबंधित है, जो सहज चिरल समरूपता तोड़ने वाले [[गोल्डस्टोन बोसोन]] हैं। विस्तार पैरामीटर [[pion|पियोन]] ऊर्जा/संवेग है। | ||
*एक भारी [[क्वार्क]] (जैसे [[ निचला क्वार्क ]] या [[ आकर्षण क्वार्क ]]) वाले हैड्रोन के लिए, एक प्रभावी क्षेत्र सिद्धांत जो क्वार्क द्रव्यमान की शक्तियों में विस्तार करता है, जिसे [[भारी क्वार्क प्रभावी सिद्धांत]] (एचक्यूईटी) कहा जाता है, उपयोगी पाया गया है। | *एक भारी [[क्वार्क]] (जैसे [[ निचला क्वार्क |निचला क्वार्क]] या [[ आकर्षण क्वार्क |आकर्षण क्वार्क]] ) वाले हैड्रोन के लिए, एक प्रभावी क्षेत्र सिद्धांत जो क्वार्क द्रव्यमान की शक्तियों में विस्तार करता है, जिसे [[भारी क्वार्क प्रभावी सिद्धांत]] (एचक्यूईटी) कहा जाता है, उपयोगी पाया गया है। | ||
*दो भारी क्वार्क वाले हैड्रोन के लिए, एक प्रभावी क्षेत्र सिद्धांत जो भारी क्वार्क के [[सापेक्ष वेग]] की शक्तियों में विस्तार करता है, जिसे गैर-सापेक्षवादी | *दो भारी क्वार्क वाले हैड्रोन के लिए, एक प्रभावी क्षेत्र सिद्धांत जो भारी क्वार्क के [[सापेक्ष वेग]] की शक्तियों में विस्तार करता है, जिसे गैर-सापेक्षवादी क्यूसीडी (एनआरक्यूसीडी) कहा जाता है, उपयोगी पाया गया है, विशेषकर जब जाली क्यूसीडी के साथ संयोजन में उपयोग किया जाता है। | ||
*हल्के ऊर्जावान ([[समरेख]]) कणों के साथ हैड्रोन प्रतिक्रियाओं के लिए, स्वतंत्रता की कम-ऊर्जावान (नरम) डिग्री के साथ बातचीत को [[नरम संरेख प्रभावी सिद्धांत]] ( | *हल्के ऊर्जावान ([[समरेख]]) कणों के साथ हैड्रोन प्रतिक्रियाओं के लिए, स्वतंत्रता की कम-ऊर्जावान (नरम) डिग्री के साथ बातचीत को [[नरम संरेख प्रभावी सिद्धांत|कोमल संरेख प्रभावी सिद्धांत]] (एससीईटी) द्वारा वर्णित किया गया है। | ||
* अधिकांश संघनित पदार्थ भौतिकी में अध्ययन किए जा रहे पदार्थ की विशेष संपत्ति के लिए प्रभावी क्षेत्र सिद्धांतों को लिखना सम्मिलित है। | * अधिकांश संघनित पदार्थ भौतिकी में अध्ययन किए जा रहे पदार्थ की विशेष संपत्ति के लिए प्रभावी क्षेत्र सिद्धांतों को लिखना सम्मिलित है। | ||
*प्रभावी क्षेत्र सिद्धांतों का उपयोग करके हाइड्रोडायनामिक्स का भी | *प्रभावी क्षेत्र सिद्धांतों का उपयोग करके हाइड्रोडायनामिक्स का भी अभिक्रियित किया जा सकता है<ref>{{Cite journal |arxiv = 1211.6461|last1 = Endlich|first1 = Solomon|title = Dissipation in the effective field theory for hydrodynamics: First order effects|journal = Physical Review D|volume = 88|issue = 10|pages = 105001|last2 = Nicolis|first2 = Alberto|last3 = Porto|first3 = Rafael|last4 = Wang|first4 = Junpu|year = 2013|doi = 10.1103/PhysRevD.88.105001|bibcode = 2013PhRvD..88j5001E|s2cid = 118441607}}</ref> | ||
| Line 50: | Line 51: | ||
== पुस्तकें == | == पुस्तकें == | ||
* ए.ए. पेट्रोव और ए। ब्लेचमैन, '' प्रभावी क्षेत्र सिद्धांत, '' सिंगापुर: विश्व वैज्ञानिक (2016)। {{ISBN|978-981-4434-92-8}} | * ए.ए. पेट्रोव और ए। ब्लेचमैन, ''प्रभावी क्षेत्र सिद्धांत,'' सिंगापुर: विश्व वैज्ञानिक (2016)। {{ISBN|978-981-4434-92-8}} | ||
* सी.पी. बर्गेस, '' इंट्रोडक्शन टू इफेक्टिव फील्ड थ्योरी,'' कैम्ब्रिज यूनिवर्सिटी प्रेस (2020)। {{ISBN|978-052-1195-47-8}} | * सी.पी. बर्गेस, ''इंट्रोडक्शन टू इफेक्टिव फील्ड थ्योरी,'' कैम्ब्रिज यूनिवर्सिटी प्रेस (2020)। {{ISBN|978-052-1195-47-8}} | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
| Line 66: | Line 67: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 03/04/2023]] | [[Category:Created On 03/04/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 11:05, 11 December 2023
| Quantum field theory |
|---|
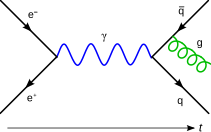 |
| History |
भौतिक विज्ञान में, एक प्रभावी क्षेत्र सिद्धांत एक अंतर्निहित भौतिक सिद्धांत, जैसे क्वांटम क्षेत्र सिद्धांत या एक सांख्यिकीय यांत्रिकी मॉडल के लिए एक प्रकार का सन्निकटन या प्रभावी सिद्धांत है। एक प्रभावी क्षेत्र सिद्धांत में चयनित लंबाई माप या ऊर्जा माप पर होने वाली भौतिक घटनाओं का वर्णन करने के लिए स्वतंत्रता की उचित डिग्री (भौतिकी और रसायन विज्ञान) सम्मिलित होती है, जबकि कम दूरी (या, समकक्ष, उच्च ऊर्जा पर) पर उपसंरचना और स्वतंत्रता की डिग्री की अनदेखी की जाती है। सहज रूप से, छोटी लंबाई के माप पर अंतर्निहित सिद्धांत के व्यवहार का औसत निकाला जाता है, जिससे लंबी लंबाई के माप पर एक सरलीकृत मॉडल होने का विश्वाश किया जा सकता है। प्रभावी क्षेत्र सिद्धांत सामान्यतः सबसे अच्छा काम करते हैं जब अभिरुचि की लंबाई के माप और अंतर्निहित गतिशीलता की लंबाई के माप के मध्य एक बड़ा अंतर होता है। प्रभावी क्षेत्र सिद्धांतों का उपयोग कण भौतिकी, सांख्यिकीय यांत्रिकी, संघनित पदार्थ भौतिकी, सामान्य सापेक्षता और हाइड्रोडायनामिक्स में पाया गया है। वह गणनाओं को सरल करते हैं, और अपव्यय प्रणाली और विकिरण प्रभावों के उपचार की अनुमति देते हैं।[1][2]
पुनर्सामान्यीकरण समूह
वर्तमान में, प्रभावी क्षेत्र सिद्धांतों पर पुनर्सामान्यीकरण समूह (आरजी) के संदर्भ में चर्चा की जाती है जहां कम दूरी की स्वतंत्रता की डिग्री को एकीकृत करने की प्रक्रिया को व्यवस्थित बनाया जाता है। यद्यपि यह विधि प्रभावी क्षेत्र सिद्धांतों के वास्तविक निर्माण की अनुमति देने के लिए पर्याप्त रूप से ठोस नहीं है, किन्तु आरजी विश्लेषण के माध्यम से उनकी उपयोगिता की सकल समझ स्पष्ट हो जाती है। यह पद्धति समरूपता के विश्लेषण के माध्यम से प्रभावी क्षेत्र सिद्धांतों के निर्माण की मुख्य विधि को भी विश्वसनीयता प्रदान करती है। यदि सूक्ष्म सिद्धांत में एकल द्रव्यमान मापदंड 'M' है, तब प्रभावी क्षेत्र सिद्धांत को '1/M' में विस्तार के रूप में देखा जा सकता है। '1/M' की कुछ शक्ति के लिए त्रुटिहीन एक प्रभावी क्षेत्र सिद्धांत के निर्माण के लिए '1/M' में विस्तार के प्रत्येक क्रम पर मुक्त मापदंडों के एक नए समूह की आवश्यकता होती है। यह विधि प्रकीर्णन या अन्य प्रक्रियाओं के लिए उपयोगी है जहां अधिकतम संवेग स्केल 'k' नियम 'k/M≪1' को संतुष्ट करता है। चूंकि प्रभावी क्षेत्र सिद्धांत छोटे लंबाई के माप पर मान्य नहीं हैं, इसलिए उन्हें पुन: सामान्य करने की आवश्यकता नहीं है। वास्तव में, एक प्रभावी क्षेत्र सिद्धांत के लिए आवश्यक '1/M' में प्रत्येक क्रम में मापदंडों की निरंतर बढ़ती संख्या का अर्थ है कि वह सामान्यतः क्वांटम इलेक्ट्रोडायनामिक्स के समान अर्थ में पुनर्सामान्यीकरण योग्य नहीं हैं, जिसके लिए केवल दो मापदंडों के पुनर्सामान्यीकरण की आवश्यकता होती है।
प्रभावी क्षेत्र सिद्धांतों के उदाहरण
बीटा क्षय का फर्मी सिद्धांत
प्रभावी क्षेत्र सिद्धांत का सबसे प्रसिद्ध उदाहरण बीटा क्षय का फर्मी सिद्धांत है। यह सिद्धांत परमाणु नाभिक के अशक्त क्षय के प्रारंभिक अध्ययन के समय विकसित किया गया था जब केवल अशक्त क्षय से निकलने वाले हैड्रान और लेप्टान ज्ञात थे। अध्ययन की गई विशिष्ट प्राथमिक कण प्रतिक्रियाएँ थीं:
इस सिद्धांत ने इन प्रतिक्रियाओं में सम्मिलित चार फर्मियनों के मध्य एक बिंदु जैसी बातचीत प्रस्तुत की। इस सिद्धांत को बड़ी घटनात्मक सफलता मिली और अंततः इलेक्ट्रोवीक इंटरैक्शन के गेज सिद्धांत से उत्पन्न होने के बारे में समझा गया, जो कण भौतिकी के मानक मॉडल का एक भाग है। इस अधिक मौलिक सिद्धांत में, अंतःक्रियाओं की मध्यस्थता फ्लेवर (कण भौतिकी) बदलने वाले गेज बोसोन, W± द्वारा की जाती है। फर्मी सिद्धांत की अपार सफलता इसलिए थी क्योंकि W कण का द्रव्यमान लगभग 80 GeV है, जबकि प्रारंभिक प्रयोग 10 MeV से कम के ऊर्जा माप पर किए गए थे। परिमाण के 3 से अधिक आदेशों द्वारा तराजू का ऐसा पृथक्करण, अभी तक किसी भी अन्य स्थिति में पूरा नहीं किया गया है।
अतिचालकता का बीसीएस सिद्धांत
एक अन्य प्रसिद्ध उदाहरण अतिचालकता का बीसीएस सिद्धांत है। यहाँ अंतर्निहित सिद्धांत एक धातु में इलेक्ट्रॉनों का सिद्धांत है जो फोनोन नामक जाली कंपन के साथ परस्पर क्रिया करता है। फ़ोनोन कुछ इलेक्ट्रॉनों के मध्य आकर्षक परस्पर क्रिया का कारण बनते हैं, जिससे वह कूपर जोड़े बनाते हैं। इन जोड़ियों की लंबाई का मापदंड फोनन की तरंग दैर्ध्य की तुलना में बहुत बड़ा है, जिससे फ़ोनों की गतिशीलता की उपेक्षा करना और एक सिद्धांत का निर्माण करना संभव हो जाता है जिसमें दो इलेक्ट्रॉन एक बिंदु पर प्रभावी रूप से परस्पर क्रिया करते हैं। इस सिद्धांत को अतिचालकता पर प्रयोगों के परिणामों का वर्णन और भविष्यवाणी करने में उल्लेखनीय सफलता मिली है।
गुरुत्वाकर्षण में प्रभावी क्षेत्र सिद्धांत
सामान्य सापेक्षता से अपेक्षा की जाती है कि वह क्वांटम गुरुत्वाकर्षण के पूर्ण सिद्धांत का निम्न ऊर्जा प्रभावी क्षेत्र सिद्धांत हो, जैसे कि स्ट्रिंग सिद्धांत या लूप क्वांटम ग्रेविटी। विस्तार मापदंड प्लैंक द्रव्यमान है।
विशेष रूप से प्रेरणादायक परिमित आकार की वस्तुओं के गुरुत्वाकर्षण तरंग हस्ताक्षर की गणना में सामान्य सापेक्षता में समस्याओं को सरल बनाने के लिए प्रभावी क्षेत्र सिद्धांतों का भी उपयोग किया गया है।[3] जीआर में सबसे आम ईएफ़टी गैर-सापेक्षवादी सामान्य सापेक्षता (एनआरजीआर) है,[4][5][6] जो न्यूटन के पश्चात् के विस्तार के समान है।[7] एक अन्य सामान्य जीआर ईएफटी एक्सट्रीम मास रेशियो (ईएमआर) है, जिसे प्रेरक समस्या के संदर्भ में अत्यधिक द्रव्यमान अनुपात प्रेरक कहा जाता है।
अन्य उदाहरण
वर्तमान में, अनेक स्थितियों के लिए प्रभावी क्षेत्र सिद्धांत लिखे गए हैं।
- परमाणु भौतिकी की एक प्रमुख शाखा क्वांटम हैरोडायनामिक्स है, जहां हैड्रोन की परस्पर क्रियाओं को एक क्षेत्र सिद्धांत के रूप में माना जाता है, जो क्वांटम क्रोमोडायनामिक्स के अंतर्निहित सिद्धांत से व्युत्पन्न होना चाहिए। क्वांटम हाइड्रोडायनामिक्स परमाणु बल का सिद्धांत है, इसी प्रकार क्वांटम क्रोमोडायनामिक्स शक्तिशाली अंतःक्रिया का सिद्धांत है और क्वांटम इलेक्ट्रोडायनामिक्स विद्युत चुम्बकीय बल का सिद्धांत है। यहाँ लंबाई के माप के छोटे पृथक्करण के कारण, इस प्रभावी सिद्धांत में कुछ वर्गीकरण शक्ति है, किन्तु फर्मी सिद्धांत की उत्तम सफलता नहीं है।
- कण भौतिकी में क्वांटम क्रोमोडायनामिक्स के प्रभावी क्षेत्र सिद्धांत जिसे चिरल पर्टर्बेशन सिद्धांत कहा जाता है, को उत्तम सफलता मिली है।[8] यह सिद्धांत पियोन या कोंस के साथ हैड्रोन की बातचीत से संबंधित है, जो सहज चिरल समरूपता तोड़ने वाले गोल्डस्टोन बोसोन हैं। विस्तार पैरामीटर पियोन ऊर्जा/संवेग है।
- एक भारी क्वार्क (जैसे निचला क्वार्क या आकर्षण क्वार्क ) वाले हैड्रोन के लिए, एक प्रभावी क्षेत्र सिद्धांत जो क्वार्क द्रव्यमान की शक्तियों में विस्तार करता है, जिसे भारी क्वार्क प्रभावी सिद्धांत (एचक्यूईटी) कहा जाता है, उपयोगी पाया गया है।
- दो भारी क्वार्क वाले हैड्रोन के लिए, एक प्रभावी क्षेत्र सिद्धांत जो भारी क्वार्क के सापेक्ष वेग की शक्तियों में विस्तार करता है, जिसे गैर-सापेक्षवादी क्यूसीडी (एनआरक्यूसीडी) कहा जाता है, उपयोगी पाया गया है, विशेषकर जब जाली क्यूसीडी के साथ संयोजन में उपयोग किया जाता है।
- हल्के ऊर्जावान (समरेख) कणों के साथ हैड्रोन प्रतिक्रियाओं के लिए, स्वतंत्रता की कम-ऊर्जावान (नरम) डिग्री के साथ बातचीत को कोमल संरेख प्रभावी सिद्धांत (एससीईटी) द्वारा वर्णित किया गया है।
- अधिकांश संघनित पदार्थ भौतिकी में अध्ययन किए जा रहे पदार्थ की विशेष संपत्ति के लिए प्रभावी क्षेत्र सिद्धांतों को लिखना सम्मिलित है।
- प्रभावी क्षेत्र सिद्धांतों का उपयोग करके हाइड्रोडायनामिक्स का भी अभिक्रियित किया जा सकता है[9]
यह भी देखें
- फॉर्म फैक्टर (क्वांटम फील्ड थ्योरी)
- पुनर्सामान्यीकरण समूह
- क्वांटम क्षेत्र सिद्धांत
- क्वांटम तुच्छता
- गिन्ज़बर्ग-लैंडौ सिद्धांत
संदर्भ
- ↑ Galley, Chad R. (2013). "गैर-रूढ़िवादी प्रणालियों के शास्त्रीय यांत्रिकी". Physical Review Letters. 110 (17): 174301. arXiv:1210.2745. Bibcode:2013PhRvL.110q4301G. doi:10.1103/PhysRevLett.110.174301. PMID 23679733. S2CID 14591873.
- ↑ Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2014). "कार्रवाई के स्तर पर विकिरण प्रतिक्रिया". International Journal of Modern Physics A. 29 (24): 1450132–1450190. arXiv:1402.2610. Bibcode:2014IJMPA..2950132B. doi:10.1142/S0217751X14501322. S2CID 118541484.
- ↑ Goldberger, Walter; Rothstein, Ira (2004). "विस्तारित वस्तुओं के लिए गुरुत्वाकर्षण का एक प्रभावी क्षेत्र सिद्धांत". Physical Review D. 73 (10). arXiv:hep-th/0409156. doi:10.1103/PhysRevD.73.104029. S2CID 54188791.
- ↑ http://online.kitp.ucsb.edu/online/numrel-m08/buonanno/pdf1/Porto_NumRelData_KITP.pdf[bare URL PDF]
- ↑ Kol, Barak; Smolkin, Lee (2008). "Non-Relativistic Gravitation: From Newton to Einstein and Back". Classical and Quantum Gravity. 25 (14): 145011. arXiv:0712.4116. Bibcode:2008CQGra..25n5011K. doi:10.1088/0264-9381/25/14/145011. S2CID 119216835.
- ↑ Porto, Rafael A (2006). "NRGR में स्पिनिंग बॉडीज की गति के बाद न्यूटोनियन सुधार". Physical Review D. 73 (104031): 104031. arXiv:gr-qc/0511061. doi:10.1103/PhysRevD.73.104031. S2CID 119377563.
- ↑ Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2013). "न्यूटोनियन विकिरण और प्रतिक्रिया के बाद का सिद्धांत". Physical Review D. 88 (10): 104037. arXiv:1305.6930. Bibcode:2013PhRvD..88j4037B. doi:10.1103/PhysRevD.88.104037. S2CID 119170985.
- ↑ Leutwyler, H (1994). "चिराल पर्टर्बेशन थ्योरी की नींव पर". Annals of Physics. 235 (1): 165–203. arXiv:hep-ph/9311274. Bibcode:1994AnPhy.235..165L. doi:10.1006/aphy.1994.1094. S2CID 16739698.
- ↑ Endlich, Solomon; Nicolis, Alberto; Porto, Rafael; Wang, Junpu (2013). "Dissipation in the effective field theory for hydrodynamics: First order effects". Physical Review D. 88 (10): 105001. arXiv:1211.6461. Bibcode:2013PhRvD..88j5001E. doi:10.1103/PhysRevD.88.105001. S2CID 118441607.
पुस्तकें
- ए.ए. पेट्रोव और ए। ब्लेचमैन, प्रभावी क्षेत्र सिद्धांत, सिंगापुर: विश्व वैज्ञानिक (2016)। ISBN 978-981-4434-92-8
- सी.पी. बर्गेस, इंट्रोडक्शन टू इफेक्टिव फील्ड थ्योरी, कैम्ब्रिज यूनिवर्सिटी प्रेस (2020)। ISBN 978-052-1195-47-8
बाहरी संबंध
- Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (1998). "Effective Field Theory". arXiv:hep-ph/9806303.
- Hartmann, Stephan (2001). "Effective Field Theories, Reductionism and Scientific Explanation" (PDF). Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 32 (2): 267–304. Bibcode:2001SHPMP..32..267H. doi:10.1016/S1355-2198(01)00005-3.
- Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (1997). "Aspects of Heavy Quark Theory". Annual Review of Nuclear and Particle Science. 47: 591–661. arXiv:hep-ph/9703290. Bibcode:1997ARNPS..47..591B. doi:10.1146/annurev.nucl.47.1.591. S2CID 13843227.
- Effective field theory (Interactions, Symmetry Breaking and Effective Fields - from Quarks to Nuclei. an Internet Lecture by Jacek Dobaczewski)