आइसोसर्फेस: Difference between revisions
m (8 revisions imported from alpha:आइसोसर्फेस) |
No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
किसी '''आइसोसर्फेस''' ('''समसतह''') का आइसोसर्फेस त्रि-आयामी एनालॉग होता है। यह एक ऐसी सतह है जो समष्टि आयतन के भीतर एक स्थिर मान(जैसे [[दबाव]], [[तापमान]], [[वेग]], [[घनत्व]]) के बिंदुओं का प्रतिनिधित्व करता है, दूसरे शब्दों में, यह एक सतत फलन(गणित) का एक स्तर समुच्चय है जिसका फलन का क्षेत्र [[3-अंतरिक्ष|3-समष्टि]] है। | |||
किसी समसतह का आइसोसर्फेस त्रि-आयामी एनालॉग होता है। यह एक ऐसी सतह है जो समष्टि आयतन के भीतर एक स्थिर मान(जैसे [[दबाव]], [[तापमान]], [[वेग]], [[घनत्व]]) के बिंदुओं का प्रतिनिधित्व करता है, दूसरे शब्दों में, यह एक सतत फलन(गणित) का एक स्तर समुच्चय है जिसका फलन का क्षेत्र [[3-अंतरिक्ष|3-समष्टि]] है। | |||
'आइसोलाइन' शब्द का प्रयोग कभी-कभी 3 से अधिक आयामों के डोमेन के लिए भी किया जाता है।<ref>{{Citation|title=Hamilton–Jacobi equation|date=2020-12-06|url=https://en.wikipedia.org/w/index.php?title=Hamilton%E2%80%93Jacobi_equation&oldid=992629363|work=Wikipedia|language=en|access-date=2020-12-14}}</ref> | 'आइसोलाइन' शब्द का प्रयोग कभी-कभी 3 से अधिक आयामों के डोमेन के लिए भी किया जाता है।<ref>{{Citation|title=Hamilton–Jacobi equation|date=2020-12-06|url=https://en.wikipedia.org/w/index.php?title=Hamilton%E2%80%93Jacobi_equation&oldid=992629363|work=Wikipedia|language=en|access-date=2020-12-14}}</ref> | ||
| Line 34: | Line 32: | ||
मैनिफोल्ड दोहरी समोच्च रेखण में मैनिफोल्ड सतह की निरंतरता बनाए रखने के लिए ऑक्ट्री निकटतम का विश्लेषण सम्मिलित होता है <ref>{{cite web|author=Scott Schaefer, Tao Ju, Joe Warren|year=2006|title=मैनिफोल्ड डुअल कंटूरिंग|url=http://faculty.cs.tamu.edu/schaefer/research/dualsimp_tvcg.pdf}}</ref><ref>{{cite AV media|date=30 Dec 2015|title=मैनिफोल्ड डुअल कंटूरिंग|author=Lin X|url=https://www.youtube.com/watch?v=l3K-tD3TMqQ|access-date=28 April 2020|archive-date=11 September 2020|archive-url=https://web.archive.org/web/20200911201609/https://www.youtube.com/watch?v=l3K-tD3TMqQ&gl=US&hl=en|url-status=dead}}</ref><ref>{{cite web|title=जीथब रिपॉजिटरी - आइसोसर्फेस|date=23 Oct 2016|author=Lin X|url=https://github.com/Lin20/isosurface}}</ref> | मैनिफोल्ड दोहरी समोच्च रेखण में मैनिफोल्ड सतह की निरंतरता बनाए रखने के लिए ऑक्ट्री निकटतम का विश्लेषण सम्मिलित होता है <ref>{{cite web|author=Scott Schaefer, Tao Ju, Joe Warren|year=2006|title=मैनिफोल्ड डुअल कंटूरिंग|url=http://faculty.cs.tamu.edu/schaefer/research/dualsimp_tvcg.pdf}}</ref><ref>{{cite AV media|date=30 Dec 2015|title=मैनिफोल्ड डुअल कंटूरिंग|author=Lin X|url=https://www.youtube.com/watch?v=l3K-tD3TMqQ|access-date=28 April 2020|archive-date=11 September 2020|archive-url=https://web.archive.org/web/20200911201609/https://www.youtube.com/watch?v=l3K-tD3TMqQ&gl=US&hl=en|url-status=dead}}</ref><ref>{{cite web|title=जीथब रिपॉजिटरी - आइसोसर्फेस|date=23 Oct 2016|author=Lin X|url=https://github.com/Lin20/isosurface}}</ref> | ||
== उदाहरण == | == उदाहरण == | ||
3डी प्रत्योक्षकरण में उपयोग होने वाले '[[मेटाबॉल्स]]' या धब्बायुक्त ऑब्जेक्ट आइसोसर्फ़ेस के उदाहरण हैं। आइसोसर्फ़ेस बनाने का एक अधिक सामान्य तरीका फलन प्रतिनिधित्व का उपयोग करना है। | 3डी प्रत्योक्षकरण में उपयोग होने वाले '[[मेटाबॉल्स]]' या धब्बायुक्त ऑब्जेक्ट आइसोसर्फ़ेस के उदाहरण हैं। आइसोसर्फ़ेस बनाने का एक अधिक सामान्य तरीका फलन प्रतिनिधित्व का उपयोग करना है। | ||
| Line 48: | Line 44: | ||
{{Reflist}} | {{Reflist}} | ||
* {{cite book|author1=Charles D. Hansen|author2=Chris R. Johnson|title=Visualization Handbook|url=https://books.google.com/books?id=ZFrlULckWdAC&pg=PA7|year=2004|publisher=Academic Press|isbn=978-0-12-387582-2|pages=7–11}} | * {{cite book|author1=Charles D. Hansen|author2=Chris R. Johnson|title=Visualization Handbook|url=https://books.google.com/books?id=ZFrlULckWdAC&pg=PA7|year=2004|publisher=Academic Press|isbn=978-0-12-387582-2|pages=7–11}} | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
*[http://www2.imm.dtu.dk/~jab/gallery/polygonization.html Isosurface Polygonization] | *[http://www2.imm.dtu.dk/~jab/gallery/polygonization.html Isosurface Polygonization] | ||
*[https://github.com/AaronWatters/contourist The contourist package for numeric python] generates triangulations of isosurfaces for arbitrary 3 dimensional functions which can be displayed using HTML5 as illustrated in this [https://jsfiddle.net/AaronWatters/9qszgyaj/ jsfiddle] | *[https://github.com/AaronWatters/contourist The contourist package for numeric python] generates triangulations of isosurfaces for arbitrary 3 dimensional functions which can be displayed using HTML5 as illustrated in this [https://jsfiddle.net/AaronWatters/9qszgyaj/ jsfiddle] | ||
[[Category:3डी कंप्यूटर ग्राफिक्स]] | [[Category:3डी कंप्यूटर ग्राफिक्स]] | ||
[[Category: चिकित्सा इमेजिंग]] | [[Category:Articles with short description]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 24/11/2022]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia fully protected templates|Cite web]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:चिकित्सा इमेजिंग]] | |||
[[Category:सतह]] | [[Category:सतह]] | ||
Latest revision as of 12:47, 13 September 2023
किसी आइसोसर्फेस (समसतह) का आइसोसर्फेस त्रि-आयामी एनालॉग होता है। यह एक ऐसी सतह है जो समष्टि आयतन के भीतर एक स्थिर मान(जैसे दबाव, तापमान, वेग, घनत्व) के बिंदुओं का प्रतिनिधित्व करता है, दूसरे शब्दों में, यह एक सतत फलन(गणित) का एक स्तर समुच्चय है जिसका फलन का क्षेत्र 3-समष्टि है।
'आइसोलाइन' शब्द का प्रयोग कभी-कभी 3 से अधिक आयामों के डोमेन के लिए भी किया जाता है।[1]
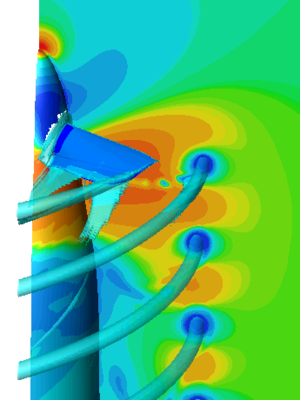
अनुप्रयोग
आइसोसर्फेस को सामान्यतः अभिकलित्र आलेखिकी का उपयोग करके प्रदर्शित किया जाता है, और संगणनात्मक द्रव गतिकी(CFD) में तथ्य प्रत्यक्षण विधियों के रूप में उपयोग किया जाता है, जो अभियन्ता को विमान पंखों जैसे वस्तुओं के चारों ओर तरल प्रवाह(गैस या द्रव) की विशेषताओं का अध्ययन करने की अनुमति देता है जैसे कि समपृष्ठ पराध्वनिक उड़ान में एक व्यक्तिगत प्रघात तरंग को प्रदर्शित कर सकता है, या कई समसतहों को उत्पन्न किया जा सकता है जो किसी पंख के चारों ओर बहने वाली हवा में दाब मानों का अनुक्रम दिखाते हैं। आइसो सतहें आयतन डेटासेट के लिए दृश्यकरण का एक लोकप्रिय रूप हैं क्योंकि इन्हें साधारण बहुकोणीय मॉडल द्वारा प्रस्तुत किया जा सकता है, जिसे बहुत जल्दी स्क्रीन पर निकाला जा सकता है।
चिकित्सा प्रतिबिंबन में, आइसोसर्फेस का उपयोग त्रि-आयामी परिकलित टोमोग्राफी स्कैन में एक विशेष घनत्व के क्षेत्रों का प्रतिनिधित्व करने के लिए किया जा सकता है, जिससे आंतरिक अंग(शरीर रचना), हड्डियों या अन्य संरचनाओं के दृश्य की अनुमति मिलती है।
त्रि-आयामी तथ्य में रुचि रखने वाले कई अन्य विषय सदैव औषध, रसायन विज्ञान, भूभौतिकी और मौसम विज्ञान के बारे में जानकारी प्राप्त करने के लिए आइसोसर्फेस का उपयोग करते हैं।
कार्यान्वयन एल्गोरिदम
मार्चिंग क्यूब्स
मार्चिंग क्यूब्स कलन विधि पहली बार 1987 में लोरेंसन और क्लाइन द्वारा सिग्ग्राफ कार्यवाही में प्रकाशित किया गया था,[2] और यह आयतन ग्रिड के साथ आँकड़े(अभिकलन) आयतन ग्रिड के किनारों को काटकर एक सतह बनाता है। जहां सतह किनारे को काटती है। वहां कलन विधि एक शीर्ष बनाता है। किनारे के प्रतिच्छेदन के विभिन्न नमूना के आधार पर विभिन्न त्रिभुजों की एक तालिका का उपयोग करके कलन विधि एक सतह का निर्माण कर सकती है। इस कलन विधि में सीपीयू और जीपीयू दोनों पर कार्यान्वयन के लिए माध्यम हैं।
स्पर्शोन्मुख निर्णायक
इसमें अस्पष्टता की संभावना को हल करने के लिए स्पर्शोन्मुख निर्णायक कलन विधि को मार्चिंग क्यूब्स के विस्तार के रूप में विकसित किया गया था।
मार्चिंग टेट्राहेड्रा
मार्चिंग टेट्राहेड्रा कलन विधि को उस कलन विधि में अस्पष्टता को हल करने और उच्च गुणवत्ता वाली आउटपुट सतह बनाने के लिए मार्चिंग क्यूब्स के विस्तार के रूप में विकसित किया गया था।
भूतल जाल
सरफेस नेट कलन विधि किनारों के अतिरिक्त आयतन वोक्सल के बीच में एक प्रतिच्छेदी शीर्ष् के रूप में रखता है, जिससे एक चिकनी सतह बनती है।
दोहरी समोच्चता
दोहरी रूपरेखा कलन विधि पहली बार 2002 में जू और लोसासो द्वारा सिगग्राफ की कार्यवाही में प्रकाशित किया गया था।[3] सतह जाल और मार्चिंग क्यूब दोनों के विस्तार के रूप में विकसित किया गया। यह वॉक्सेल के भीतर एक दोहरी बहुफलक शीर्ष् में रखता है। लेकिन अब केंद्र में नहीं है। दोहरी समोच्चता उस स्थिति और सामान्य(ज्यामिति) का लाभ उठाती है जहां सतह वोक्सल के किनारों को पार करती है चूँकि वोक्सल के भीतर दोहरी बहुफलक शीर्ष् की स्थिति को प्रक्षेपित किया जा सके। इसमें तेज या चिकनी सतहों को बनाए रखने का लाभ है जहां सतह के जाल सदैव अवरुद्ध या गलत तरीके से उभरे हुए दिखते हैं।[4] दोहरी समोच्च रेखण सदैव सतह पीढ़ी का उपयोग करती है जो सतह की जटिलता के लिए आउटपुट में त्रिकोणों की संख्या को अनुकूलित करने के लिए एक अनुकूलन के रूप में ऑक्ट्री का लाभ उठाती है।
कई गुना दोहरी समोच्चता
मैनिफोल्ड दोहरी समोच्च रेखण में मैनिफोल्ड सतह की निरंतरता बनाए रखने के लिए ऑक्ट्री निकटतम का विश्लेषण सम्मिलित होता है [5][6][7]
उदाहरण
3डी प्रत्योक्षकरण में उपयोग होने वाले 'मेटाबॉल्स' या धब्बायुक्त ऑब्जेक्ट आइसोसर्फ़ेस के उदाहरण हैं। आइसोसर्फ़ेस बनाने का एक अधिक सामान्य तरीका फलन प्रतिनिधित्व का उपयोग करना है।
यह भी देखें
- त्रिकोणासन(ज्यामिति)
- अंतर्निहित सतह
- मात्रा प्रतिपादन
संदर्भ
- ↑ "Hamilton–Jacobi equation", Wikipedia (in English), 2020-12-06, retrieved 2020-12-14
- ↑ William E. Lorensen, Harvey E. Cline: Marching Cubes: A high resolution 3D surface construction algorithm. In: Computer Graphics, Vol. 21, Nr. 4, July 1987
- ↑ Tao Ju, Frank Losasso, Scott Schaefer, Joe Warren: Dual Contouring of Hermite Data. Archived 2017-09-18 at the Wayback Machine In: ACM Transactions on Graphics, Volume 21 Issue 3, July 2002
- ↑ "चिकना स्वर क्षेत्र (भाग 2)". 12 July 2012.
- ↑ Scott Schaefer, Tao Ju, Joe Warren (2006). "मैनिफोल्ड डुअल कंटूरिंग" (PDF).
{{cite web}}: CS1 maint: multiple names: authors list (link) - ↑ Lin X (30 Dec 2015). मैनिफोल्ड डुअल कंटूरिंग. Archived from the original on 11 September 2020. Retrieved 28 April 2020.
- ↑ Lin X (23 Oct 2016). "जीथब रिपॉजिटरी - आइसोसर्फेस".
- Charles D. Hansen; Chris R. Johnson (2004). Visualization Handbook. Academic Press. pp. 7–11. ISBN 978-0-12-387582-2.
बाहरी संबंध
- Isosurface Polygonization
- The contourist package for numeric python generates triangulations of isosurfaces for arbitrary 3 dimensional functions which can be displayed using HTML5 as illustrated in this jsfiddle