समलम्ब चतुर्भुज: Difference between revisions
(TEXT) |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
{{short description|Convex quadrilateral with at least one pair of parallel sides}} | {{short description|Convex quadrilateral with at least one pair of parallel sides}} | ||
{{Infobox polygon | {{Infobox polygon | ||
| name = | | name = चतुर्भुज (AmE)<br>समलंब (BrE) | ||
| image = Trapezoid.svg | | image = Trapezoid.svg | ||
| caption = | | caption = चतुर्भुज या समलम्ब | ||
| type = [[ | | type = [[चतुष्कोष]] | ||
| edges = 4 | | edges = 4 | ||
| symmetry = | | symmetry = | ||
| area = <math>\tfrac{a + b}{2} h</math> | | area = <math>\tfrac{a + b}{2} h</math> | ||
| properties = [[ | | properties = [[उत्तल बहुभुज|उत्तल]]}} | ||
[[यूक्लिडियन ज्यामिति]] में एक | समानांतर भुजाओं की कम से कम एक जोड़ी के साथ एक चतुर्भुज को अमेरिकी और कनाडाई अंग्रेजी में(समलम्ब)({{IPAc-en|ˈ|t|ɹ|æ|p|ə|z|ɔɪ|d}}) कहा जाता है। ब्रिटिश और अंग्रेजी के अन्य रूपों में, इसे(ट्रैपीज़ियम)({{IPAc-en|t|r|ə|ˈ|p|iː|z|i|ə|m}}) कहा जाता है।<ref>http://www.mathopenref.com/trapezoid.html Mathopenref definition</ref><ref>A. D. Gardiner & C. J. Bradley, ''Plane Euclidean Geometry: Theory and Problems'', UKMT, 2005, p. 34.</ref> [[चार्ल्स हटन]] के गणितीय शब्दकोष में एक त्रुटि के कारण इन दो शब्दों का स्थानान्तरण हुआ। | ||
[[यूक्लिडियन ज्यामिति]] में एक समलम्ब आवश्यक रूप से एक [[उत्तल बहुभुज|उत्तल चतुर्भुज]] है। समानांतर भुजाओं को समलम्ब का आधार कहा जाता है। अन्य दो भुजाओं को लेग(या पार्श्व पक्ष) कहा जाता है यदि वे समानांतर नहीं हैं; अन्यथा, समलम्ब चतुर्भुज एक समांतर चतुर्भुज है, और आधारों के दो जोड़े हैं)। स्केलीन समलम्ब एक ट्रेपोज़ॉइड है जिसमें समान माप की कोई भुजा नहीं होती है,<ref> | |||
[http://www.basic-mathematics.com/types-of-quadrilaterals.html Types of quadrilaterals] | [http://www.basic-mathematics.com/types-of-quadrilaterals.html Types of quadrilaterals] | ||
</ref> नीचे दिए गए विशेष परिस्थितियों के विपरीत। | </ref> नीचे दिए गए विशेष परिस्थितियों के विपरीत। | ||
== | == व्युत्पत्ति विज्ञान और समलम्ब बनाम ट्रैपीज़ियम == | ||
प्राचीन यूनानी गणितज्ञ यूक्लिड ने पाँच प्रकार के चतुर्भुजों को परिभाषित किया, जिनमें से चार में समानांतर भुजाओं के दो समुच्चय थे (अंग्रेजी में वर्ग, आयत, समचतुर्भुज और समचतुर्भुज के रूप में जाना जाता है) और अंतिम में समानांतर भुजाओं के दो समुच्चय नहीं थे - एक τραπέζια (ट्रेपेज़िया)<ref>[http://data.perseus.org/citations/urn:cts:greekLit:tlg1799.tlg001.perseus-grc1:1.def.22 Euclid Elements Book I Definition 22]</ref> शाब्दिक रूप से एक तालिका, स्वयं τετράς (टेट्रास) से, चार + πέζα (पेज़ा), एक आधार; अंत, सीमा, किनारा)।<ref>πέζα is said to be the Doric and Arcadic form of πούς "foot", but recorded only in the sense "instep [of a human foot]", whence the meaning "edge, border". τράπεζα "table" is Homeric. Henry George Liddell, Robert Scott, Henry Stuart Jones, ''A Greek-English Lexicon'', Oxford, Clarendon Press (1940), s.v. [https://www.perseus.tufts.edu/hopper/morph?l=peza&la=greek#lexicon πέζα], | प्राचीन यूनानी गणितज्ञ यूक्लिड ने पाँच प्रकार के चतुर्भुजों को परिभाषित किया, जिनमें से चार में समानांतर भुजाओं के दो समुच्चय थे(अंग्रेजी में वर्ग, आयत, समचतुर्भुज और समचतुर्भुज के रूप में जाना जाता है) और अंतिम में समानांतर भुजाओं के दो समुच्चय नहीं थे - एक τραπέζια(ट्रेपेज़िया)<ref>[http://data.perseus.org/citations/urn:cts:greekLit:tlg1799.tlg001.perseus-grc1:1.def.22 Euclid Elements Book I Definition 22]</ref> शाब्दिक रूप से एक तालिका, स्वयं τετράς(टेट्रास) से, चार + πέζα(पेज़ा), एक आधार; अंत, सीमा, किनारा)।<ref>πέζα is said to be the Doric and Arcadic form of πούς "foot", but recorded only in the sense "instep [of a human foot]", whence the meaning "edge, border". τράπεζα "table" is Homeric. Henry George Liddell, Robert Scott, Henry Stuart Jones, ''A Greek-English Lexicon'', Oxford, Clarendon Press (1940), s.v. [https://www.perseus.tufts.edu/hopper/morph?l=peza&la=greek#lexicon πέζα], | ||
[https://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.04.0057%3Aentry%3Dtra%2Fpeza τράπεζα].</ref> | [https://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.04.0057%3Aentry%3Dtra%2Fpeza τράπεζα].</ref> | ||
[[यूक्लिड के तत्वों]] की पहली पुस्तक पर अपनी टिप्पणी में [[प्रोक्लस]] (412 से 485 ईस्वी) द्वारा दो प्रकार के ट्रैपेज़िया पेश किए गए थे:<ref name="oed">{{cite book|title=ए न्यू इंग्लिश डिक्शनरी ऑन हिस्टोरिकल प्रिंसिपल्स: मुख्य रूप से फिलोलॉजिकल सोसाइटी द्वारा एकत्रित सामग्री पर आधारित|author=James A. H. Murray|volume=X|date=1926|url=https://archive.org/details/oedxaarch/page/n296/mode/1up|page=286 (Trapezium)|publisher=Clarendon Press at Oxford|quote=यूक्लिड के साथ (सी 300 ईसा पूर्व) τραπέζιον में वर्ग, आयत, समचतुर्भुज और समचतुर्भुज को छोड़कर सभी चतुर्भुज आकृतियाँ शामिल थीं; ट्रेपेज़िया की किस्मों में उन्होंने प्रवेश नहीं किया। लेकिन प्रोक्लस, जिसने यूक्लिड के तत्वों की पहली पुस्तक एडी 450 पर टिप्पणी लिखी थी, ने τραπέζιον नाम को केवल समानांतर दो पक्षों वाले चतुर्भुजों के लिए बनाए रखा, इन्हें τραπέζιον ἰσοσκελὲς, समद्विबाहु ट्रेपेज़ियम में विभाजित किया, जिसमें दो गैर-समानांतर भुजाएँ हैं (और उनके आधार) समान हैं, और σκαληνὸν τραπέζιον, स्केलीन ट्रेपेज़ियम, जिसमें ये पक्ष और कोण असमान हैं। ऐसे चतुर्भुजों के लिए जिनका कोई पार्श्व समानांतर नहीं है, प्रोक्लस ने τραπέζοειδὲς ट्रेपेज़ॉइड नाम दिया। इस नामकरण को सभी महाद्वीपीय भाषाओं में रखा गया है, और 18 वीं शताब्दी के अंत तक इंग्लैंड में सार्वभौमिक था, जब शर्तों के आवेदन को स्थानांतरित कर दिया गया था, ताकि अन्य राष्ट्रों के प्रोक्लस और आधुनिक भूगर्भीय आंकड़े विशेष रूप से एक ट्रैपेज़ियम (एफ। ट्रेपेज़, गेर. ट्रेपेज़, ड्यू. ट्रेपेज़ियम, इट. ट्रेपेज़ियो) अधिकांश अंग्रेजी लेखकों के साथ एक ट्रेपेज़ियम बन गया, और प्रोक्लस और अन्य राष्ट्रों का ट्रेपेज़ियम एक ट्रेपेज़ियम बन गया। ट्रैपेज़ॉइड का यह बदला हुआ अर्थ हटन के गणितीय शब्दकोश, 1795 में 'कभी-कभी' के रूप में दिया गया है - वह यह नहीं कहता कि किसके द्वारा; लेकिन उन्होंने खुद दुर्भाग्य से इसे अपनाया और इसका इस्तेमाल किया, और उनका शब्दकोश निस्संदेह इसके प्रसार में मुख्य एजेंट था। हालांकि कुछ जियोमीटर ने अपने मूल अर्थों में शब्दों का उपयोग करना जारी रखा, और 1875 के बाद से यह प्रचलित उपयोग है।}}</ref><ref name="ConwayBurgiel2016">{{cite book|last1=Conway|first1=John H.|last2=Burgiel|first2=Heidi|last3=Goodman-Strauss|first3=Chaim|title=चीजों की समरूपता|url=https://books.google.com/books?id=Drj1CwAAQBAJ&pg=PA286|date=5 April 2016|publisher=CRC Press|isbn=978-1-4398-6489-0|pages=286}}</ref> | [[यूक्लिड के तत्वों]] की पहली पुस्तक पर अपनी टिप्पणी में [[प्रोक्लस]](412 से 485 ईस्वी) द्वारा दो प्रकार के ट्रैपेज़िया पेश किए गए थे:<ref name="oed">{{cite book|title=ए न्यू इंग्लिश डिक्शनरी ऑन हिस्टोरिकल प्रिंसिपल्स: मुख्य रूप से फिलोलॉजिकल सोसाइटी द्वारा एकत्रित सामग्री पर आधारित|author=James A. H. Murray|volume=X|date=1926|url=https://archive.org/details/oedxaarch/page/n296/mode/1up|page=286 (Trapezium)|publisher=Clarendon Press at Oxford|quote=यूक्लिड के साथ (सी 300 ईसा पूर्व) τραπέζιον में वर्ग, आयत, समचतुर्भुज और समचतुर्भुज को छोड़कर सभी चतुर्भुज आकृतियाँ शामिल थीं; ट्रेपेज़िया की किस्मों में उन्होंने प्रवेश नहीं किया। लेकिन प्रोक्लस, जिसने यूक्लिड के तत्वों की पहली पुस्तक एडी 450 पर टिप्पणी लिखी थी, ने τραπέζιον नाम को केवल समानांतर दो पक्षों वाले चतुर्भुजों के लिए बनाए रखा, इन्हें τραπέζιον ἰσοσκελὲς, समद्विबाहु ट्रेपेज़ियम में विभाजित किया, जिसमें दो गैर-समानांतर भुजाएँ हैं (और उनके आधार) समान हैं, और σκαληνὸν τραπέζιον, स्केलीन ट्रेपेज़ियम, जिसमें ये पक्ष और कोण असमान हैं। ऐसे चतुर्भुजों के लिए जिनका कोई पार्श्व समानांतर नहीं है, प्रोक्लस ने τραπέζοειδὲς ट्रेपेज़ॉइड नाम दिया। इस नामकरण को सभी महाद्वीपीय भाषाओं में रखा गया है, और 18 वीं शताब्दी के अंत तक इंग्लैंड में सार्वभौमिक था, जब शर्तों के आवेदन को स्थानांतरित कर दिया गया था, ताकि अन्य राष्ट्रों के प्रोक्लस और आधुनिक भूगर्भीय आंकड़े विशेष रूप से एक ट्रैपेज़ियम (एफ। ट्रेपेज़, गेर. ट्रेपेज़, ड्यू. ट्रेपेज़ियम, इट. ट्रेपेज़ियो) अधिकांश अंग्रेजी लेखकों के साथ एक ट्रेपेज़ियम बन गया, और प्रोक्लस और अन्य राष्ट्रों का ट्रेपेज़ियम एक ट्रेपेज़ियम बन गया। ट्रैपेज़ॉइड का यह बदला हुआ अर्थ हटन के गणितीय शब्दकोश, 1795 में 'कभी-कभी' के रूप में दिया गया है - वह यह नहीं कहता कि किसके द्वारा; लेकिन उन्होंने खुद दुर्भाग्य से इसे अपनाया और इसका इस्तेमाल किया, और उनका शब्दकोश निस्संदेह इसके प्रसार में मुख्य एजेंट था। हालांकि कुछ जियोमीटर ने अपने मूल अर्थों में शब्दों का उपयोग करना जारी रखा, और 1875 के बाद से यह प्रचलित उपयोग है।}}</ref><ref name="ConwayBurgiel2016">{{cite book|last1=Conway|first1=John H.|last2=Burgiel|first2=Heidi|last3=Goodman-Strauss|first3=Chaim|title=चीजों की समरूपता|url=https://books.google.com/books?id=Drj1CwAAQBAJ&pg=PA286|date=5 April 2016|publisher=CRC Press|isbn=978-1-4398-6489-0|pages=286}}</ref> | ||
* समानांतर भुजाओं का एक युग्म – एक समलंबक (τραπέζιον), समद्विबाहु (समान लेग) और स्केलीन (असमान) ट्रैपेज़िया में विभाजित | * समानांतर भुजाओं का एक युग्म – एक समलंबक(τραπέζιον), समद्विबाहु(समान लेग) और स्केलीन(असमान) ट्रैपेज़िया में विभाजित | ||
* कोई समानांतर भुजाएँ नहीं - समलम्ब (τραπεζοειδή, ट्रैपीज़ियम, शाब्दिक रूप से ट्रैपीज़ियम-जैसा (:wikt:εἶδος|εἶδος का अर्थ होता है), ठीक उसी प्रकार जैसे घनाभ का अर्थ घन जैसा होता है और समचतुर्भुज का अर्थ समचतुर्भुज जैसा होता है) | * कोई समानांतर भुजाएँ नहीं - समलम्ब(τραπεζοειδή, ट्रैपीज़ियम, शाब्दिक रूप से ट्रैपीज़ियम-जैसा(:wikt:εἶδος|εἶδος का अर्थ होता है), ठीक उसी प्रकार जैसे घनाभ का अर्थ घन जैसा होता है और समचतुर्भुज का अर्थ समचतुर्भुज जैसा होता है) | ||
सभी यूरोपीय भाषाएं प्रोक्लस की संरचना का पालन करती हैं<ref name="ConwayBurgiel2016"/><ref>For example: French ''trapèze'', Italian ''trapezio'', Portuguese ''trapézio'', Spanish ''trapecio'', German ''Trapez'', Ukrainian "трапеція", e.g. {{cite web|url=http://www.larousse.fr/dictionnaires/francais/trap%C3%A9zo%C3%AFde/79256|title=Larousse definition for trapézoïde}}</ref> जैसा कि 18वीं शताब्दी के अंत तक अंग्रेजी में था, जब तक कि 1795 में चार्ल्स हटन द्वारा प्रकाशित एक प्रभावशाली गणितीय शब्दकोश ने स्पष्टीकरण के बिना शब्दों की एक व्याख्या का समर्थन किया। इस गलती को लगभग 1875 में ब्रिटिश अंग्रेजी में ठीक कर लिया गया था, लेकिन आधुनिक समय में अमेरिकी अंग्रेजी में इसे प्रतिधारित रखा गया था।<ref name="oed"/> | सभी यूरोपीय भाषाएं प्रोक्लस की संरचना का पालन करती हैं<ref name="ConwayBurgiel2016"/><ref>For example: French ''trapèze'', Italian ''trapezio'', Portuguese ''trapézio'', Spanish ''trapecio'', German ''Trapez'', Ukrainian "трапеція", e.g. {{cite web|url=http://www.larousse.fr/dictionnaires/francais/trap%C3%A9zo%C3%AFde/79256|title=Larousse definition for trapézoïde}}</ref> जैसा कि 18वीं शताब्दी के अंत तक अंग्रेजी में था, जब तक कि 1795 में चार्ल्स हटन द्वारा प्रकाशित एक प्रभावशाली गणितीय शब्दकोश ने स्पष्टीकरण के बिना शब्दों की एक व्याख्या का समर्थन किया। इस गलती को लगभग 1875 में ब्रिटिश अंग्रेजी में ठीक कर लिया गया था, लेकिन आधुनिक समय में अमेरिकी अंग्रेजी में इसे प्रतिधारित रखा गया था।<ref name="oed"/> | ||
| Line 38: | Line 39: | ||
| | | | ||
| | | | ||
|यूक्लिड (परिभाषा 22) | |यूक्लिड(परिभाषा 22) | ||
|प्रोक्लस (परिभाषाएं 30-34, पोसिडोनियस को उद्धृत करते हुए) | |प्रोक्लस(परिभाषाएं 30-34, पोसिडोनियस को उद्धृत करते हुए) | ||
|यूक्लिड / प्रोक्लस परिभाषा | |यूक्लिड / प्रोक्लस परिभाषा | ||
|ब्रिटिश अंग्रेजी (और यूरोपीय भाषाएं) | |ब्रिटिश अंग्रेजी(और यूरोपीय भाषाएं) | ||
|अमेरिकी अंग्रेजी | |अमेरिकी अंग्रेजी | ||
|- | |- | ||
| rowspan="2" |समानांतर चतुर्भुज | | rowspan="2" |समानांतर चतुर्भुज | ||
| rowspan="2" |'''2'''|| [[File:Rhombus 2 (PSF).png|100px|frameless]]|| colspan="2" |ῥόμβος (समचतुर्भुज) | | rowspan="2" |'''2'''|| [[File:Rhombus 2 (PSF).png|100px|frameless]]|| colspan="2" |ῥόμβος(समचतुर्भुज) | ||
|समबाहु लेकिन समकोण नहीं | |समबाहु लेकिन समकोण नहीं | ||
| colspan="2" |समचतुर्भुज/समांतर चतुर्भुज | | colspan="2" |समचतुर्भुज/समांतर चतुर्भुज | ||
|- | |- | ||
| [[File:Rhomboid 2 (PSF).png|100px|frameless]]|| colspan="2" |ῥομβοειδὲς (तिर्यग्वर्ग) | | [[File:Rhomboid 2 (PSF).png|100px|frameless]]|| colspan="2" |ῥομβοειδὲς(तिर्यग्वर्ग) | ||
|विपरीत भुजाएँ और कोण एक दूसरे के बराबर लेकिन न तो समबाहु और न ही समकोण | |विपरीत भुजाएँ और कोण एक दूसरे के बराबर लेकिन न तो समबाहु और न ही समकोण | ||
| colspan="2" |समचतुर्भुज/समांतर चतुर्भुज | | colspan="2" |समचतुर्भुज/समांतर चतुर्भुज | ||
|- | |- | ||
| rowspan="3" |नॉन-समानांतर चतुर्भुज | | rowspan="3" |नॉन-समानांतर चतुर्भुज | ||
| rowspan="2" |'''1'''|| [[File:Trapezoid 2 (PSF).png|100px|frameless]]|| rowspan="3" |τραπέζια (ट्रेपेज़िया) | | rowspan="2" |'''1'''|| [[File:Trapezoid 2 (PSF).png|100px|frameless]]|| rowspan="3" |τραπέζια(ट्रेपेज़िया) | ||
|τραπέζιον ἰσοσκελὲς (ट्रेपेज़ियन समद्विबाहु) | |τραπέζιον ἰσοσκελὲς(ट्रेपेज़ियन समद्विबाहु) | ||
|दो समांतर भुजाएँ, और एक सममित रेखा | |दो समांतर भुजाएँ, और एक सममित रेखा | ||
|समद्विबाहु ट्रेपेज़ियम | |समद्विबाहु ट्रेपेज़ियम | ||
|समद्विबाहु चतुर्भुज | |समद्विबाहु चतुर्भुज | ||
|- | |- | ||
| [[File:Trapezoid 3 (PSF).png|100px|frameless]]||τραπέζιον σκαληνὸν (ट्रेपेज़ियन स्केलिनॉन) | | [[File:Trapezoid 3 (PSF).png|100px|frameless]]||τραπέζιον σκαληνὸν(ट्रेपेज़ियन स्केलिनॉन) | ||
|दो समानांतर भुजाएँ, और समरूपता की कोई रेखा नहीं | |दो समानांतर भुजाएँ, और समरूपता की कोई रेखा नहीं | ||
|ट्रैपीज़ियम | |ट्रैपीज़ियम | ||
| | |समलम्ब(अनन्य) | ||
|- | |- | ||
|'''0''' | |'''0''' | ||
| [[File:Trapezium (PSF).png|100px|frameless]] ||τραπέζοειδὲς (ट्रेपेज़ोइड्स) | | [[File:Trapezium (PSF).png|100px|frameless]] ||τραπέζοειδὲς(ट्रेपेज़ोइड्स) | ||
|कोई समानांतर भुजाएँ नहीं | |कोई समानांतर भुजाएँ नहीं | ||
|अनियमित चतुर्भुज/ | |अनियमित चतुर्भुज/ समलम्ब | ||
|ट्रैपीज़ियम | |ट्रैपीज़ियम | ||
|} | |} | ||
== समावेशी बनाम अनन्य परिभाषा == | == समावेशी बनाम अनन्य परिभाषा == | ||
इस बात पर कुछ असहमति है कि क्या समांतर चतुर्भुज, जिसमें समानांतर भुजाओं के दो जोड़े हैं, को समलम्ब ( | इस बात पर कुछ असहमति है कि क्या समांतर चतुर्भुज, जिसमें समानांतर भुजाओं के दो जोड़े हैं, को समलम्ब(समलम्ब) माना जाना चाहिए। कुछ लोग चतुर्भुज को समांतर चतुर्भुज के रूप में परिभाषित करते हैं जिसमें समानांतर भुजाओं(विशेष परिभाषा) की केवल एक जोड़ी होती है, जिससे समांतर चतुर्भुजों को बाहर रखा जाता है।<ref>{{cite web |url=http://www.math.com/school/glossary/defs/trapezoid.html |title="Math.com" से अमेरिकन स्कूल की परिभाषा|access-date=2008-04-14}}</ref> अन्य<ref name=Mathworld>{{MathWorld |title=Trapezoid |urlname=Trapezoid}}</ref> समांतर चतुर्भुज को समांतर भुजाओं की कम से कम एक जोड़ी के साथ चतुर्भुज के रूप में परिभाषित करें(समावेशी परिभाषा<ref>Trapezoids, [http://www.math.washington.edu/~king/coursedir/m444a00/syl/class/trapezoids/Trapezoids.html]. Retrieved 2012-02-24.</ref>), समांतर चतुर्भुज को एक विशेष प्रकार का समलम्ब बनाते हैं। बाद की परिभाषा उच्च गणित जैसे कलन में इसके उपयोग के अनुरूप है। यह लेख समावेशी परिभाषा का उपयोग करता है और समांतर चतुर्भुजों को समलम्ब के विशेष परिस्थितियों के रूप में मानता है। चतुर्भुज वर्गिकी में भी इसकी पक्षपोषित की गई है। | ||
समावेशी परिभाषा के तहत, सभी समांतर चतुर्भुज (समचतुर्भुज, [[वर्ग (ज्यामिति)]] और नॉन -वर्ग [[आयत]] सहित) | समावेशी परिभाषा के तहत, सभी समांतर चतुर्भुज(समचतुर्भुज, [[वर्ग (ज्यामिति)|वर्ग(ज्यामिति)]] और नॉन -वर्ग [[आयत]] सहित) समलम्ब हैं। आयतों के मध्य किनारों पर दर्पण समरूपता होती है; समचतुर्भुजों में शीर्षों पर दर्पण सममिति होती है, यद्यपि वर्गों में मध्य-किनारे और शीर्ष दोनों पर दर्पण सममिति होती है। | ||
== विशेष स्थितियां == | == विशेष स्थितियां == | ||
[[File:Trapezoid special cases.png|280px|thumb| | [[File:Trapezoid special cases.png|280px|thumb|समलम्ब विशेष मामले। नारंगी के आंकड़े समांतर चतुर्भुज के रूप में भी योग्य हैं।]]एक [[समकोण]] चतुर्भुज(जिसे 'समकोण समलम्ब' भी कहा जाता है) में दो आसन्न समकोण होते हैं।<ref name=Mathworld/>एक वक्र के तहत क्षेत्रों का अनुमान लगाने के लिए [[ट्रेपेज़ॉइडल नियम|समलम्ब नियम]] में समकोण चतुर्भुज का उपयोग किया जाता है। | ||
एक तीव्र | एक तीव्र समलम्ब में इसके लंबे ''आधार'' किनारे पर दो समीपवर्ती तीव्र कोण होते हैं, यद्यपि एक अधिक समलंब चतुर्भुज में प्रत्येक ''आधार'' पर एक तीव्र और एक अधिक कोण होता है। | ||
एक समद्विबाहु | एक समद्विबाहु समलम्ब एक समलम्बहै जहाँ आधार कोणों का माप समान होता है। परिणाम स्वरूप दोनों लेग भी समान लंबाई के होते हैं और इसमें [[प्रतिबिंब समरूपता]] होती है। यह तीव्र ट्रेपेज़ोइड्स या समकोण चतुर्भुज(आयत) के लिए संभव है। | ||
समांतर चतुर्भुज समानांतर भुजाओं के दो जोड़े वाला एक समलंब है। एक समांतर चतुर्भुज में केंद्रीय 2-गुना [[घूर्णी समरूपता]] (या [[बिंदु प्रतिबिंब]] समरूपता) होती है। यह [[कुण्ठाग्र चतुर्भुज]] या [[समकोण चतुर्भुज]] (आयतों) के लिए संभव है। | समांतर चतुर्भुज समानांतर भुजाओं के दो जोड़े वाला एक समलंब है। एक समांतर चतुर्भुज में केंद्रीय 2-गुना [[घूर्णी समरूपता]](या [[बिंदु प्रतिबिंब]] समरूपता) होती है। यह [[कुण्ठाग्र चतुर्भुज]] या [[समकोण चतुर्भुज]](आयतों) के लिए संभव है। | ||
एक [[स्पर्शरेखा चतुर्भुज]] एक ट्रेपोज़ॉइड है जिसमें एक अंतःवृत्त होता है। | एक [[स्पर्शरेखा चतुर्भुज]] एक ट्रेपोज़ॉइड है जिसमें एक अंतःवृत्त होता है। | ||
| Line 93: | Line 94: | ||
चार लम्बाई a, c, b, d एक नॉन-समांतर चतुर्भुज, चतुर्भुज की क्रमागत भुजाओं का गठन कर सकते हैं जिसमें केवल a और b समानांतर होते हैं<ref>''Ask Dr. Math'' (2008), [http://mathforum.org/library/drmath/view/72738.html "Area of Trapezoid Given Only the Side Lengths"].</ref> | चार लम्बाई a, c, b, d एक नॉन-समांतर चतुर्भुज, चतुर्भुज की क्रमागत भुजाओं का गठन कर सकते हैं जिसमें केवल a और b समानांतर होते हैं<ref>''Ask Dr. Math'' (2008), [http://mathforum.org/library/drmath/view/72738.html "Area of Trapezoid Given Only the Side Lengths"].</ref> | ||
:<math>\displaystyle |d-c| < |b-a| < d+c.</math> | :<math>\displaystyle |d-c| < |b-a| < d+c.</math> | ||
चतुर्भुज एक समांतर चतुर्भुज है जब <math>d-c = b-a = 0</math>, लेकिन यह एक पूर्व-स्पर्शरेखा चतुर्भुज है (जो कि समलंब नहीं है) जब <math>|d-c| = |b-a| \neq 0</math>.<ref name=Josefsson/>{{rp|p. 35}} | चतुर्भुज एक समांतर चतुर्भुज है जब <math>d-c = b-a = 0</math>, लेकिन यह एक पूर्व-स्पर्शरेखा चतुर्भुज है(जो कि समलंब नहीं है) जब <math>|d-c| = |b-a| \neq 0</math>.<ref name=Josefsson/>{{rp|p. 35}} | ||
== विशेषीकरण == | == विशेषीकरण == | ||
[[File:Trapez mittellinie en labels.svg|thumb|upright=1.0|सामान्य | [[File:Trapez mittellinie en labels.svg|thumb|upright=1.0|सामान्य समलम्ब / ट्रैपीज़ियम:<br/>समानांतर भुजाएँ: <math>a,\, b </math> साथ <math>a<b </math> <br/>लेग: <math> c,\, d</math><br/>विकर्ण: <math>q,\, p </math><br/>मध्य खंड: <math>m </math><br/>लम्बाई/ऊंचाई: <math>h </math>]] | ||
[[File:Trapez mittellinie en labels areas.svg|thumb|upright=1.0| | [[File:Trapez mittellinie en labels areas.svg|thumb|upright=1.0|समलम्ब / ट्रैपीज़ियम चतुर्भुज विपरीत त्रिभुजों के साथ <math>S,\,T </math> विकर्णों द्वारा गठित]]एक उत्तल चतुर्भुज दिया गया है, निम्नलिखित गुण समतुल्य हैं, और प्रत्येक का तात्पर्य है कि चतुर्भुज एक चतुर्भुज है: | ||
*इसके दो आसन्न [[कोण]] हैं जो पूरक कोण हैं, अर्थात, वे 180 [[डिग्री (कोण)|श्रेणी]] तक जोड़ते हैं। | *इसके दो आसन्न [[कोण]] हैं जो पूरक कोण हैं, अर्थात, वे 180 [[डिग्री (कोण)|श्रेणी]] तक जोड़ते हैं। | ||
* एक भुजा और एक [[विकर्ण]] के बीच का कोण विपरीत भुजा और उसी विकर्ण के बीच के कोण के बराबर होता है। | * एक भुजा और एक [[विकर्ण]] के बीच का कोण विपरीत भुजा और उसी विकर्ण के बीच के कोण के बराबर होता है। | ||
* विकर्ण परस्पर समान [[अनुपात]] में एक दूसरे को काटते हैं (यह अनुपात वही है जो समानांतर भुजाओं की लंबाई के बीच है)। | * विकर्ण परस्पर समान [[अनुपात]] में एक दूसरे को काटते हैं(यह अनुपात वही है जो समानांतर भुजाओं की लंबाई के बीच है)। | ||
*विकर्ण चतुर्भुज को चार त्रिभुजों में काटते हैं जिनमें से एक विपरीत युग्म के क्षेत्रफल समान होते हैं।<ref name=Josefsson>Martin Josefsson, [http://forumgeom.fau.edu/FG2013volume13/FG201305.pdf "Characterizations of trapezoids"], Forum Geometricorum, 13 (2013) 23-35.</ref>{{rp|Prop.5}} | *विकर्ण चतुर्भुज को चार त्रिभुजों में काटते हैं जिनमें से एक विपरीत युग्म के क्षेत्रफल समान होते हैं।<ref name=Josefsson>Martin Josefsson, [http://forumgeom.fau.edu/FG2013volume13/FG201305.pdf "Characterizations of trapezoids"], Forum Geometricorum, 13 (2013) 23-35.</ref>{{rp|Prop.5}} | ||
* एक विकर्ण द्वारा निर्मित दो त्रिभुजों के क्षेत्रफलों का गुणनफल दूसरे विकर्ण द्वारा निर्मित दो त्रिभुजों के क्षेत्रफलों के गुणनफल के बराबर होता है।<ref name=Josefsson/>{{rp|Thm.6}} | * एक विकर्ण द्वारा निर्मित दो त्रिभुजों के क्षेत्रफलों का गुणनफल दूसरे विकर्ण द्वारा निर्मित दो त्रिभुजों के क्षेत्रफलों के गुणनफल के बराबर होता है।<ref name=Josefsson/>{{rp|Thm.6}} | ||
| Line 118: | Line 119: | ||
::<math>v=\frac{|a-b|}{2}.</math> | ::<math>v=\frac{|a-b|}{2}.</math> | ||
== [[मध्य]] खंड और ऊंचाई == | == [[मध्य]] खंड और ऊंचाई == | ||
समलम्ब का मध्य खंड(जिसे माध्यिका या मध्य रेखा भी कहा जाता है) वह खंड है जो लेगों के मध्य बिंदुओं से जुड़ता है। यह आधारों के समानांतर है। इसकी लंबाई m ट्रेपोज़ॉइड के आधार a और b की लंबाई के औसत के बराबर है,<ref name=Mathworld/>:<math>m = \frac{a + b}{2}.</math> | |||
समलम्ब चतुर्भुज का मध्य खंड दो चतुर्भुज विशेष रेखा खंडों में से एक है (दूसरा द्विमाध्यक | समलम्ब चतुर्भुज का मध्य खंड दो चतुर्भुज विशेष रेखा खंडों में से एक है(दूसरा द्विमाध्यक समलम्ब को समान क्षेत्रों में विभाजित करता है)। | ||
ऊँचाई (या शीर्षलम्ब) आधारों के बीच की लंबवत दूरी है। इस मामले में कि दो आधारों की लंबाई अलग-अलग है (a ≠ b), एक समलम्बाकार h की ऊंचाई सूत्र का उपयोग करके इसके चारों भुजाओं की लंबाई से निर्धारित की जा सकती है<ref name=Mathworld/>:<math>h= \frac{\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}</math> | ऊँचाई(या शीर्षलम्ब) आधारों के बीच की लंबवत दूरी है। इस मामले में कि दो आधारों की लंबाई अलग-अलग है(a ≠ b), एक समलम्बाकार h की ऊंचाई सूत्र का उपयोग करके इसके चारों भुजाओं की लंबाई से निर्धारित की जा सकती है<ref name=Mathworld/>:<math>h= \frac{\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}</math> | ||
जहाँ c और d लेगों की लंबाई हैं। | जहाँ c और d लेगों की लंबाई हैं। | ||
== क्षेत्र == | == क्षेत्र == | ||
समलम्ब का क्षेत्र K द्वारा दिया गया है<ref name=Mathworld/>: | |||
<math>K = \frac{a + b}{2} \cdot h = mh</math> | <math>K = \frac{a + b}{2} \cdot h = mh</math> | ||
जहाँ a और b समानांतर भुजाओं की लंबाई हैं, h ऊँचाई (इन भुजाओं के बीच की लंबवत दूरी) है, और m दो समानांतर भुजाओं की लंबाई का अंकगणितीय माध्य है। 499 ईस्वी में [[भारतीय गणित]] और [[भारतीय खगोल विज्ञान]] के शास्त्रीय युग के एक महान [[गणितज्ञ]]-खगोलविद [[आर्यभटीय]] (खंड 2.8) में इस पद्धति का उपयोग किया था। यह एक [[त्रिकोण]] के क्षेत्र के लिए एक विशेष मामले के रूप में एक त्रिभुज के क्षेत्र के लिए प्रसिद्ध सूत्र के रूप में उपज देता है, जिसमें एक त्रिभुज को पतित | जहाँ a और b समानांतर भुजाओं की लंबाई हैं, h ऊँचाई(इन भुजाओं के बीच की लंबवत दूरी) है, और m दो समानांतर भुजाओं की लंबाई का अंकगणितीय माध्य है। 499 ईस्वी में [[भारतीय गणित]] और [[भारतीय खगोल विज्ञान]] के शास्त्रीय युग के एक महान [[गणितज्ञ]]-खगोलविद [[आर्यभटीय]](खंड 2.8) में इस पद्धति का उपयोग किया था। यह एक [[त्रिकोण]] के क्षेत्र के लिए एक विशेष मामले के रूप में एक त्रिभुज के क्षेत्र के लिए प्रसिद्ध सूत्र के रूप में उपज देता है, जिसमें एक त्रिभुज को पतित समलम्ब के रूप में माना जाता है जिसमें समानांतर भुजाओं में से एक एक बिंदु तक संकुचन गया है। | ||
7वीं शताब्दी के भारतीय गणितज्ञ भास्कर प्रथम ने लगातार भुजाओं ''a'', ''c'', ''b'', ''d'' के साथ एक | 7वीं शताब्दी के भारतीय गणितज्ञ भास्कर प्रथम ने लगातार भुजाओं ''a'', ''c'', ''b'', ''d'' के साथ एक समलम्ब के क्षेत्र के लिए निम्नलिखित सूत्र निकाला: | ||
:<math>K=\frac{1}{2}(a+b)\sqrt{c^2-\frac{1}{4}\left((b-a)+\frac{c^2-d^2}{b-a}\right)^2}</math> | :<math>K=\frac{1}{2}(a+b)\sqrt{c^2-\frac{1}{4}\left((b-a)+\frac{c^2-d^2}{b-a}\right)^2}</math> | ||
जहां ''a'' और ''b'' समानांतर हैं और ''b'' > ''a''।<ref>T. K. Puttaswamy, ''[https://books.google.com/books?id=8oVRSu692qoC&printsec=frontcover#v=onepage&q=Bhaskara&f=false Mathematical achievements of pre-modern Indian mathematicians]'', Elsevier, 2012, p. 156.</ref> इस सूत्र को अधिक सममित संस्करण में देखा जा सकता है<ref name="Mathworld" />: | जहां ''a'' और ''b'' समानांतर हैं और ''b'' > ''a''।<ref>T. K. Puttaswamy, ''[https://books.google.com/books?id=8oVRSu692qoC&printsec=frontcover#v=onepage&q=Bhaskara&f=false Mathematical achievements of pre-modern Indian mathematicians]'', Elsevier, 2012, p. 156.</ref> इस सूत्र को अधिक सममित संस्करण में देखा जा सकता है<ref name="Mathworld" />: | ||
| Line 137: | Line 138: | ||
<math>K = \frac{a+b}{4|b-a|}\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}.</math> | <math>K = \frac{a+b}{4|b-a|}\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}.</math> | ||
जब समानांतर भुजाओं में से कोई एक बिंदु तक संकुचन जाती है (मान लीजिए a = 0), तो यह सूत्र त्रिभुज के क्षेत्रफल के लिए हीरोन के सूत्र में बदल जाता है। | जब समानांतर भुजाओं में से कोई एक बिंदु तक संकुचन जाती है(मान लीजिए a = 0), तो यह सूत्र त्रिभुज के क्षेत्रफल के लिए हीरोन के सूत्र में बदल जाता है। | ||
क्षेत्र के लिए एक अन्य समतुल्य सूत्र, जो हीरोन के सूत्र के अधिक निकट है, है<ref name="Mathworld" />: | क्षेत्र के लिए एक अन्य समतुल्य सूत्र, जो हीरोन के सूत्र के अधिक निकट है, है<ref name="Mathworld" />: | ||
| Line 143: | Line 144: | ||
<math>K = \frac{a+b}{|b-a|}\sqrt{(s-b)(s-a)(s-b-c)(s-b-d)},</math> | <math>K = \frac{a+b}{|b-a|}\sqrt{(s-b)(s-a)(s-b-c)(s-b-d)},</math> | ||
कहाँ <math>s = \tfrac{1}{2}(a + b + c + d)</math> | कहाँ <math>s = \tfrac{1}{2}(a + b + c + d)</math> समलम्ब का अर्धपरिधि है।(यह सूत्र ब्रह्मगुप्त के सूत्र के समान है, लेकिन यह उससे भिन्न है, जिसमें एक समलम्ब [[चक्रीय चतुर्भुज]](एक वृत्त में खुदा हुआ) नहीं हो सकता है। यह सूत्र एक सामान्य चतुर्भुज के लिए ब्रेट्सच्निदेर के सूत्र का एक विशेष मामला भी है)। | ||
के सूत्र से, यह उसी का अनुसरण करता है | के सूत्र से, यह उसी का अनुसरण करता है | ||
| Line 154: | Line 155: | ||
<math>p= \sqrt{\frac{ab^2-a^2b-ac^2+bd^2}{b-a}},</math> | <math>p= \sqrt{\frac{ab^2-a^2b-ac^2+bd^2}{b-a}},</math> | ||
:<math>q= \sqrt{\frac{ab^2-a^2b-ad^2+bc^2}{b-a}}</math> | :<math>q= \sqrt{\frac{ab^2-a^2b-ad^2+bc^2}{b-a}}</math> | ||
जहाँ a छोटा आधार है, b लंबा आधार है, और c और d | जहाँ a छोटा आधार है, b लंबा आधार है, और c और d समलम्ब लेग हैं। | ||
यदि चतुर्भुज को इसके विकर्ण AC और BD द्वारा चार त्रिभुजों में विभाजित किया जाता है (जैसा कि दाईं ओर दिखाया गया है), O पर प्रतिच्छेद करता है, तो △ ''AOD'' का क्षेत्रफल △ ''BOC'' के बराबर है, और △ ''AOD'' और △ ''BOC'' के क्षेत्रों का उत्पाद △ ''AOB'' और △ ''COD'' के बराबर है। आसन्न त्रिभुजों के प्रत्येक युग्म के क्षेत्रफलों का अनुपात वही है जो समानांतर भुजाओं की लंबाई के बीच है।<ref name="Mathworld" /> | यदि चतुर्भुज को इसके विकर्ण AC और BD द्वारा चार त्रिभुजों में विभाजित किया जाता है(जैसा कि दाईं ओर दिखाया गया है), O पर प्रतिच्छेद करता है, तो △ ''AOD'' का क्षेत्रफल △ ''BOC'' के बराबर है, और △ ''AOD'' और △ ''BOC'' के क्षेत्रों का उत्पाद △ ''AOB'' और △ ''COD'' के बराबर है। आसन्न त्रिभुजों के प्रत्येक युग्म के क्षेत्रफलों का अनुपात वही है जो समानांतर भुजाओं की लंबाई के बीच है।<ref name="Mathworld" /> | ||
बता दें कि | बता दें कि समलम्ब में क्रम में A, B, C और D हैं और समानांतर भुजाएँ AB और DC हैं। मान लीजिए E विकर्णों का प्रतिच्छेदन है, और F भुजा DA पर है और G भुजा BC पर इस प्रकार है कि FEG AB और CD के समांतर है। फिर FG AB और DC का [[अनुकूल माध्य]] है:<ref>''GoGeometry'', [http://www.gogeometry.com/problem/p747-trapezoid-diagonal-parallel-similarity-harmonic-mean-high-school-college.htm]. Retrieved 2012-07-08.</ref> | ||
:<math>\frac{1}{FG}=\frac{1}{2} \left( \frac{1}{AB}+ \frac{1}{DC} \right).</math> | :<math>\frac{1}{FG}=\frac{1}{2} \left( \frac{1}{AB}+ \frac{1}{DC} \right).</math> | ||
विस्तारित असमांतर भुजाओं के प्रतिच्छेदन बिंदु और विकर्णों के प्रतिच्छेदन बिंदु दोनों से होकर जाने वाली रेखा प्रत्येक आधार को समद्विभाजित करती है।<ref name=Byer/> | विस्तारित असमांतर भुजाओं के प्रतिच्छेदन बिंदु और विकर्णों के प्रतिच्छेदन बिंदु दोनों से होकर जाने वाली रेखा प्रत्येक आधार को समद्विभाजित करती है।<ref name=Byer/> | ||
== अन्य गुणधर्म == | == अन्य गुणधर्म == | ||
क्षेत्रफल का केंद्र (एकसमान तलीय पटल के लिए द्रव्यमान का केंद्र) समांतर भुजाओं के मध्यबिंदुओं को मिलाने वाले रेखाखंड के साथ स्थित होता है, जो लंबी भुजा b से लम्बवत दूरी x पर होता है।<ref>''efunda'', General Trapezoid, [http://www.efunda.com/math/areas/Trapezoid.cfm]. Retrieved 2012-07-09.</ref> | क्षेत्रफल का केंद्र(एकसमान तलीय पटल के लिए द्रव्यमान का केंद्र) समांतर भुजाओं के मध्यबिंदुओं को मिलाने वाले रेखाखंड के साथ स्थित होता है, जो लंबी भुजा b से लम्बवत दूरी x पर होता है।<ref>''efunda'', General Trapezoid, [http://www.efunda.com/math/areas/Trapezoid.cfm]. Retrieved 2012-07-09.</ref> | ||
:<math>x = \frac{h}{3} \left( \frac{2a+b}{a+b}\right).</math> | :<math>x = \frac{h}{3} \left( \frac{2a+b}{a+b}\right).</math> | ||
क्षेत्र का केंद्र इस खंड को अनुपात में विभाजित करता है (जब छोटी से लंबी तरफ लिया जाता है)<ref name=AM>{{cite journal|last1=Tom M. Apostol and Mamikon A. Mnatsakanian|title=सर्किलों को घेरते हुए आंकड़े|journal=American Mathematical Monthly|volume=111|issue=10|date=December 2004|pages=853–863|doi=10.2307/4145094|url=http://www.maa.org/sites/default/files/images/upload_library/22/Ford/Apostol853-863.pdf|access-date=2016-04-06|jstor=4145094}}</ref>{{rp|p. 862}} | क्षेत्र का केंद्र इस खंड को अनुपात में विभाजित करता है(जब छोटी से लंबी तरफ लिया जाता है)<ref name=AM>{{cite journal|last1=Tom M. Apostol and Mamikon A. Mnatsakanian|title=सर्किलों को घेरते हुए आंकड़े|journal=American Mathematical Monthly|volume=111|issue=10|date=December 2004|pages=853–863|doi=10.2307/4145094|url=http://www.maa.org/sites/default/files/images/upload_library/22/Ford/Apostol853-863.pdf|access-date=2016-04-06|jstor=4145094}}</ref>{{rp|p. 862}} | ||
:<math>\frac{a+2b}{2a+b}.</math> | :<math>\frac{a+2b}{2a+b}.</math> | ||
यदि कोण A और B के समद्विभाजक P पर प्रतिच्छेद करते हैं, और कोण C और D के समद्विभाजक Q पर प्रतिच्छेद करते हैं, तो<ref name=Byer>Owen Byer, Felix Lazebnik and [[Deirdre Smeltzer]], ''[https://books.google.com/books?id=W4acIu4qZvoC&printsec=frontcover#v=snippet&q=trapezoid&f=false Methods for Euclidean Geometry]'', Mathematical Association of America, 2010, p. 55.</ref> | यदि कोण A और B के समद्विभाजक P पर प्रतिच्छेद करते हैं, और कोण C और D के समद्विभाजक Q पर प्रतिच्छेद करते हैं, तो<ref name=Byer>Owen Byer, Felix Lazebnik and [[Deirdre Smeltzer]], ''[https://books.google.com/books?id=W4acIu4qZvoC&printsec=frontcover#v=snippet&q=trapezoid&f=false Methods for Euclidean Geometry]'', Mathematical Association of America, 2010, p. 55.</ref> | ||
| Line 177: | Line 178: | ||
=== जीव विज्ञान === | === जीव विज्ञान === | ||
[[File:Juanita Vilas Marchant Stenocephalidae Heteroptera HemipteraP.jpg|thumb|एक [[स्टेनोसेफेलिडे]] पर उल्लिखित ट्रेपेज़फ़ॉर्म [[प्रोथोरैक्स]] का उदाहरण]][[आकृति विज्ञान (जीव विज्ञान)]], टैक्सोनॉमी (जीव विज्ञान) और अन्य वर्णनात्मक विषयों में, जिसमें इस तरह के आकार के लिए एक शब्द आवश्यक है, विशेष अंगों या रूपों के विवरण में ट्रैपेज़ॉइडल या ट्रैपेज़फ़ॉर्म जैसे शब्द आमतौर पर उपयोगी होते हैं।<ref name="Capinera2008">{{cite book|author=John L. Capinera|title=एंटोमोलॉजी का विश्वकोश|url=https://books.google.com/books?id=i9ITMiiohVQC&pg=PA1247|date=11 August 2008|publisher=Springer Science & Business Media|isbn=978-1-4020-6242-1|pages=386, 1062, 1247}}</ref> | [[File:Juanita Vilas Marchant Stenocephalidae Heteroptera HemipteraP.jpg|thumb|एक [[स्टेनोसेफेलिडे]] पर उल्लिखित ट्रेपेज़फ़ॉर्म [[प्रोथोरैक्स]] का उदाहरण]][[आकृति विज्ञान (जीव विज्ञान)|आकृति विज्ञान(जीव विज्ञान)]], टैक्सोनॉमी(जीव विज्ञान) और अन्य वर्णनात्मक विषयों में, जिसमें इस तरह के आकार के लिए एक शब्द आवश्यक है, विशेष अंगों या रूपों के विवरण में ट्रैपेज़ॉइडल या ट्रैपेज़फ़ॉर्म जैसे शब्द आमतौर पर उपयोगी होते हैं।<ref name="Capinera2008">{{cite book|author=John L. Capinera|title=एंटोमोलॉजी का विश्वकोश|url=https://books.google.com/books?id=i9ITMiiohVQC&pg=PA1247|date=11 August 2008|publisher=Springer Science & Business Media|isbn=978-1-4020-6242-1|pages=386, 1062, 1247}}</ref> | ||
=== संगणक अभियांत्रिकी === | === संगणक अभियांत्रिकी === | ||
संगणक अभियांत्रिकी में, विशेष रूप से कुंजीपटल तर्कशास्त्र और संगणक वास्तुकला में, ट्रेपेज़ोइड्स का उपयोग विशिष्ट रूप से पर बहुसंकेतक के प्रतीक के लिए किया जाता है। बहुसंकेतक तर्कशास्त्र तत्व हैं जो कई तत्वों के बीच चयन करते हैं और एक विशिष्ट चिन्ह के आधार पर एकल प्रक्षेपण उत्पन्न करते हैं। विशिष्ट अभिकल्पना विशेष रूप से बताए बिना ट्रेपेज़ोइड्स को नियोजित करेंगे कि वे [[बहुसंकेतक]] हैं क्योंकि वे सार्वभौमिक रूप से समकक्ष हैं। | संगणक अभियांत्रिकी में, विशेष रूप से कुंजीपटल तर्कशास्त्र और संगणक वास्तुकला में, ट्रेपेज़ोइड्स का उपयोग विशिष्ट रूप से पर बहुसंकेतक के प्रतीक के लिए किया जाता है। बहुसंकेतक तर्कशास्त्र तत्व हैं जो कई तत्वों के बीच चयन करते हैं और एक विशिष्ट चिन्ह के आधार पर एकल प्रक्षेपण उत्पन्न करते हैं। विशिष्ट अभिकल्पना विशेष रूप से बताए बिना ट्रेपेज़ोइड्स को नियोजित करेंगे कि वे [[बहुसंकेतक]] हैं क्योंकि वे सार्वभौमिक रूप से समकक्ष हैं। | ||
| Line 184: | Line 185: | ||
* छिन्नक, समलम्बाकार फलकों वाला एक ठोस | * छिन्नक, समलम्बाकार फलकों वाला एक ठोस | ||
* [[विनम्र संख्या]], जिसे समलम्बाकार संख्या के रूप में भी जाना जाता है | * [[विनम्र संख्या]], जिसे समलम्बाकार संख्या के रूप में भी जाना जाता है | ||
* [[कील (ज्यामिति)]], दो त्रिभुजों और तीन चतुर्भुज चेहरों द्वारा परिभाषित एक बहुफलक। | * [[कील (ज्यामिति)|कील(ज्यामिति)]], दो त्रिभुजों और तीन चतुर्भुज चेहरों द्वारा परिभाषित एक बहुफलक। | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 195: | Line 196: | ||
* {{MathWorld |title=Right trapezoid |urlname=RightTrapezoid}} | * {{MathWorld |title=Right trapezoid |urlname=RightTrapezoid}} | ||
* [http://www.mathopenref.com/trapezoid.html Trapezoid definition] [http://www.mathopenref.com/trapezoidarea.html Area of a trapezoid] [http://www.mathopenref.com/trapezoidmedian.html Median of a trapezoid] With interactive animations | * [http://www.mathopenref.com/trapezoid.html Trapezoid definition] [http://www.mathopenref.com/trapezoidarea.html Area of a trapezoid] [http://www.mathopenref.com/trapezoidmedian.html Median of a trapezoid] With interactive animations | ||
* [http://www.elsy.at/kurse/index.php?kurs=Trapezoid+%28North+America%29&status=public Trapezoid (North America)] at elsy.at: Animated course (construction, circumference, area) | * [http://www.elsy.at/kurse/index.php?kurs=Trapezoid+%28North+America%29&status=public Trapezoid(North America)] at elsy.at: Animated course(construction, circumference, area) | ||
* [http://numericalmethods.eng.usf.edu/topics/trapezoidal_rule.html Trapezoidal Rule] on ''Numerical Methods for Stem Undergraduate'' | * [http://numericalmethods.eng.usf.edu/topics/trapezoidal_rule.html Trapezoidal Rule] on ''Numerical Methods for Stem Undergraduate'' | ||
* Autar Kaw and E. Eric Kalu, ''[http://www.autarkaw.com/books/numericalmethods/index.html Numerical Methods with Applications]'', (2008) | * Autar Kaw and E. Eric Kalu, ''[http://www.autarkaw.com/books/numericalmethods/index.html Numerical Methods with Applications]'',(2008) | ||
{{Polygons}} | {{Polygons}} | ||
[[Category: | [[Category:All Wikipedia articles written in American English]] | ||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with short description]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 27/11/2022]] | [[Category:Created On 27/11/2022]] | ||
[[Category:Infobox templates|polygon]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Use American English from August 2020]] | |||
[[Category:Wikipedia fully protected templates|Cite web]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:चतुर्भुज के प्रकार]] | |||
[[Category:प्राथमिक आकार]] | |||
Latest revision as of 09:32, 16 December 2022
| चतुर्भुज (AmE) समलंब (BrE) | |
|---|---|
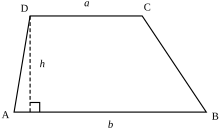 चतुर्भुज या समलम्ब | |
| प्रकार | चतुष्कोष |
| किनारेs और कोने | 4 |
| क्षेत्र | |
| गुण | उत्तल |
समानांतर भुजाओं की कम से कम एक जोड़ी के साथ एक चतुर्भुज को अमेरिकी और कनाडाई अंग्रेजी में(समलम्ब)(/ˈtræpəzɔɪd/) कहा जाता है। ब्रिटिश और अंग्रेजी के अन्य रूपों में, इसे(ट्रैपीज़ियम)(/trəˈpiːziəm/) कहा जाता है।[1][2] चार्ल्स हटन के गणितीय शब्दकोष में एक त्रुटि के कारण इन दो शब्दों का स्थानान्तरण हुआ।
यूक्लिडियन ज्यामिति में एक समलम्ब आवश्यक रूप से एक उत्तल चतुर्भुज है। समानांतर भुजाओं को समलम्ब का आधार कहा जाता है। अन्य दो भुजाओं को लेग(या पार्श्व पक्ष) कहा जाता है यदि वे समानांतर नहीं हैं; अन्यथा, समलम्ब चतुर्भुज एक समांतर चतुर्भुज है, और आधारों के दो जोड़े हैं)। स्केलीन समलम्ब एक ट्रेपोज़ॉइड है जिसमें समान माप की कोई भुजा नहीं होती है,[3] नीचे दिए गए विशेष परिस्थितियों के विपरीत।
व्युत्पत्ति विज्ञान और समलम्ब बनाम ट्रैपीज़ियम
प्राचीन यूनानी गणितज्ञ यूक्लिड ने पाँच प्रकार के चतुर्भुजों को परिभाषित किया, जिनमें से चार में समानांतर भुजाओं के दो समुच्चय थे(अंग्रेजी में वर्ग, आयत, समचतुर्भुज और समचतुर्भुज के रूप में जाना जाता है) और अंतिम में समानांतर भुजाओं के दो समुच्चय नहीं थे - एक τραπέζια(ट्रेपेज़िया)[4] शाब्दिक रूप से एक तालिका, स्वयं τετράς(टेट्रास) से, चार + πέζα(पेज़ा), एक आधार; अंत, सीमा, किनारा)।[5]
यूक्लिड के तत्वों की पहली पुस्तक पर अपनी टिप्पणी में प्रोक्लस(412 से 485 ईस्वी) द्वारा दो प्रकार के ट्रैपेज़िया पेश किए गए थे:[6][7]
- समानांतर भुजाओं का एक युग्म – एक समलंबक(τραπέζιον), समद्विबाहु(समान लेग) और स्केलीन(असमान) ट्रैपेज़िया में विभाजित
- कोई समानांतर भुजाएँ नहीं - समलम्ब(τραπεζοειδή, ट्रैपीज़ियम, शाब्दिक रूप से ट्रैपीज़ियम-जैसा(:wikt:εἶδος|εἶδος का अर्थ होता है), ठीक उसी प्रकार जैसे घनाभ का अर्थ घन जैसा होता है और समचतुर्भुज का अर्थ समचतुर्भुज जैसा होता है)
सभी यूरोपीय भाषाएं प्रोक्लस की संरचना का पालन करती हैं[7][8] जैसा कि 18वीं शताब्दी के अंत तक अंग्रेजी में था, जब तक कि 1795 में चार्ल्स हटन द्वारा प्रकाशित एक प्रभावशाली गणितीय शब्दकोश ने स्पष्टीकरण के बिना शब्दों की एक व्याख्या का समर्थन किया। इस गलती को लगभग 1875 में ब्रिटिश अंग्रेजी में ठीक कर लिया गया था, लेकिन आधुनिक समय में अमेरिकी अंग्रेजी में इसे प्रतिधारित रखा गया था।[6]
निम्नलिखित उपयोगों की तुलना करने वाली एक तालिका है, जिसमें शीर्ष पर सबसे विशिष्ट परिभाषाएं सबसे नीचे सबसे सामान्य हैं।
समावेशी बनाम अनन्य परिभाषा
इस बात पर कुछ असहमति है कि क्या समांतर चतुर्भुज, जिसमें समानांतर भुजाओं के दो जोड़े हैं, को समलम्ब(समलम्ब) माना जाना चाहिए। कुछ लोग चतुर्भुज को समांतर चतुर्भुज के रूप में परिभाषित करते हैं जिसमें समानांतर भुजाओं(विशेष परिभाषा) की केवल एक जोड़ी होती है, जिससे समांतर चतुर्भुजों को बाहर रखा जाता है।[9] अन्य[10] समांतर चतुर्भुज को समांतर भुजाओं की कम से कम एक जोड़ी के साथ चतुर्भुज के रूप में परिभाषित करें(समावेशी परिभाषा[11]), समांतर चतुर्भुज को एक विशेष प्रकार का समलम्ब बनाते हैं। बाद की परिभाषा उच्च गणित जैसे कलन में इसके उपयोग के अनुरूप है। यह लेख समावेशी परिभाषा का उपयोग करता है और समांतर चतुर्भुजों को समलम्ब के विशेष परिस्थितियों के रूप में मानता है। चतुर्भुज वर्गिकी में भी इसकी पक्षपोषित की गई है।
समावेशी परिभाषा के तहत, सभी समांतर चतुर्भुज(समचतुर्भुज, वर्ग(ज्यामिति) और नॉन -वर्ग आयत सहित) समलम्ब हैं। आयतों के मध्य किनारों पर दर्पण समरूपता होती है; समचतुर्भुजों में शीर्षों पर दर्पण सममिति होती है, यद्यपि वर्गों में मध्य-किनारे और शीर्ष दोनों पर दर्पण सममिति होती है।
विशेष स्थितियां
एक समकोण चतुर्भुज(जिसे 'समकोण समलम्ब' भी कहा जाता है) में दो आसन्न समकोण होते हैं।[10]एक वक्र के तहत क्षेत्रों का अनुमान लगाने के लिए समलम्ब नियम में समकोण चतुर्भुज का उपयोग किया जाता है।
एक तीव्र समलम्ब में इसके लंबे आधार किनारे पर दो समीपवर्ती तीव्र कोण होते हैं, यद्यपि एक अधिक समलंब चतुर्भुज में प्रत्येक आधार पर एक तीव्र और एक अधिक कोण होता है।
एक समद्विबाहु समलम्ब एक समलम्बहै जहाँ आधार कोणों का माप समान होता है। परिणाम स्वरूप दोनों लेग भी समान लंबाई के होते हैं और इसमें प्रतिबिंब समरूपता होती है। यह तीव्र ट्रेपेज़ोइड्स या समकोण चतुर्भुज(आयत) के लिए संभव है।
समांतर चतुर्भुज समानांतर भुजाओं के दो जोड़े वाला एक समलंब है। एक समांतर चतुर्भुज में केंद्रीय 2-गुना घूर्णी समरूपता(या बिंदु प्रतिबिंब समरूपता) होती है। यह कुण्ठाग्र चतुर्भुज या समकोण चतुर्भुज(आयतों) के लिए संभव है।
एक स्पर्शरेखा चतुर्भुज एक ट्रेपोज़ॉइड है जिसमें एक अंतःवृत्त होता है।
सैचेरी चतुर्भुज अतिपरवलयिक तल में एक समलंब के समान है, जिसमें दो आसन्न समकोण हैं, यद्यपि यह यूक्लिडियन तल में एक आयत है। अतिशयोक्तिपूर्ण तल में लैम्बर्ट चतुर्भुज में 3 समकोण होते हैं।
अस्तित्व की स्थिति
चार लम्बाई a, c, b, d एक नॉन-समांतर चतुर्भुज, चतुर्भुज की क्रमागत भुजाओं का गठन कर सकते हैं जिसमें केवल a और b समानांतर होते हैं[12]
चतुर्भुज एक समांतर चतुर्भुज है जब , लेकिन यह एक पूर्व-स्पर्शरेखा चतुर्भुज है(जो कि समलंब नहीं है) जब .[13]: p. 35
विशेषीकरण
एक उत्तल चतुर्भुज दिया गया है, निम्नलिखित गुण समतुल्य हैं, और प्रत्येक का तात्पर्य है कि चतुर्भुज एक चतुर्भुज है:
- इसके दो आसन्न कोण हैं जो पूरक कोण हैं, अर्थात, वे 180 श्रेणी तक जोड़ते हैं।
- एक भुजा और एक विकर्ण के बीच का कोण विपरीत भुजा और उसी विकर्ण के बीच के कोण के बराबर होता है।
- विकर्ण परस्पर समान अनुपात में एक दूसरे को काटते हैं(यह अनुपात वही है जो समानांतर भुजाओं की लंबाई के बीच है)।
- विकर्ण चतुर्भुज को चार त्रिभुजों में काटते हैं जिनमें से एक विपरीत युग्म के क्षेत्रफल समान होते हैं।[13]: Prop.5
- एक विकर्ण द्वारा निर्मित दो त्रिभुजों के क्षेत्रफलों का गुणनफल दूसरे विकर्ण द्वारा निर्मित दो त्रिभुजों के क्षेत्रफलों के गुणनफल के बराबर होता है।[13]: Thm.6
- विकर्णों द्वारा बनाए गए चार त्रिभुजों में से कुछ दो विपरीत त्रिभुजों के क्षेत्रफल S और T समीकरण को संतुष्ट करते हैं
- जहाँ K चतुर्भुज का क्षेत्रफल है।[13]: Thm.8
- दो विपरीत भुजाओं के मध्य बिंदु और विकर्णों के प्रतिच्छेदन संरेख होते हैं।[13]: Thm.15
- चतुर्भुज ABCD में कोण संतुष्ट करते हैं [13]: p. 25
- दो आसन्न कोणों के कोसाइन का योग 0 होता है, जैसा कि अन्य दो कोणों के कोसाइन का होता है।[13]: p. 25
- दो आसन्न कोणों का योग 0 होता है, जैसा कि अन्य दो आसन्न कोणों का योग होता है।[13]: p. 26
- एक द्विमाध्यिका चतुर्भुज को समान क्षेत्रफल वाले दो चतुर्भुजों में विभाजित करती है।[13]: p. 26
- दो विपरीत भुजाओं के मध्यबिंदुओं को जोड़ने वाली द्विमाध्यिका की दुगुनी लंबाई अन्य भुजाओं की लंबाई के योग के बराबर होती है।[13]: p. 31
इसके अतिरिक्त, निम्नलिखित गुण समतुल्य हैं, और प्रत्येक का अर्थ है कि विपरीत पक्ष a और b समानांतर हैं:
- क्रमागत भुजाएँ a, c, b, d और विकर्ण p, q समीकरण को संतुष्ट करते हैं[13]: Cor.11
- विकर्णों के मध्यबिंदुओं के बीच की दूरी v समीकरण को संतुष्ट करती है[13]: Thm.12
मध्य खंड और ऊंचाई
समलम्ब का मध्य खंड(जिसे माध्यिका या मध्य रेखा भी कहा जाता है) वह खंड है जो लेगों के मध्य बिंदुओं से जुड़ता है। यह आधारों के समानांतर है। इसकी लंबाई m ट्रेपोज़ॉइड के आधार a और b की लंबाई के औसत के बराबर है,[10]: समलम्ब चतुर्भुज का मध्य खंड दो चतुर्भुज विशेष रेखा खंडों में से एक है(दूसरा द्विमाध्यक समलम्ब को समान क्षेत्रों में विभाजित करता है)।
ऊँचाई(या शीर्षलम्ब) आधारों के बीच की लंबवत दूरी है। इस मामले में कि दो आधारों की लंबाई अलग-अलग है(a ≠ b), एक समलम्बाकार h की ऊंचाई सूत्र का उपयोग करके इसके चारों भुजाओं की लंबाई से निर्धारित की जा सकती है[10]: जहाँ c और d लेगों की लंबाई हैं।
क्षेत्र
समलम्ब का क्षेत्र K द्वारा दिया गया है[10]:
जहाँ a और b समानांतर भुजाओं की लंबाई हैं, h ऊँचाई(इन भुजाओं के बीच की लंबवत दूरी) है, और m दो समानांतर भुजाओं की लंबाई का अंकगणितीय माध्य है। 499 ईस्वी में भारतीय गणित और भारतीय खगोल विज्ञान के शास्त्रीय युग के एक महान गणितज्ञ-खगोलविद आर्यभटीय(खंड 2.8) में इस पद्धति का उपयोग किया था। यह एक त्रिकोण के क्षेत्र के लिए एक विशेष मामले के रूप में एक त्रिभुज के क्षेत्र के लिए प्रसिद्ध सूत्र के रूप में उपज देता है, जिसमें एक त्रिभुज को पतित समलम्ब के रूप में माना जाता है जिसमें समानांतर भुजाओं में से एक एक बिंदु तक संकुचन गया है।
7वीं शताब्दी के भारतीय गणितज्ञ भास्कर प्रथम ने लगातार भुजाओं a, c, b, d के साथ एक समलम्ब के क्षेत्र के लिए निम्नलिखित सूत्र निकाला:
जहां a और b समानांतर हैं और b > a।[14] इस सूत्र को अधिक सममित संस्करण में देखा जा सकता है[10]:
जब समानांतर भुजाओं में से कोई एक बिंदु तक संकुचन जाती है(मान लीजिए a = 0), तो यह सूत्र त्रिभुज के क्षेत्रफल के लिए हीरोन के सूत्र में बदल जाता है।
क्षेत्र के लिए एक अन्य समतुल्य सूत्र, जो हीरोन के सूत्र के अधिक निकट है, है[10]:
कहाँ समलम्ब का अर्धपरिधि है।(यह सूत्र ब्रह्मगुप्त के सूत्र के समान है, लेकिन यह उससे भिन्न है, जिसमें एक समलम्ब चक्रीय चतुर्भुज(एक वृत्त में खुदा हुआ) नहीं हो सकता है। यह सूत्र एक सामान्य चतुर्भुज के लिए ब्रेट्सच्निदेर के सूत्र का एक विशेष मामला भी है)।
के सूत्र से, यह उसी का अनुसरण करता है
समांतर भुजाओं के मध्य बिन्दुओं को मिलाने वाली रेखा क्षेत्रफल को समद्विभाजित करती है।
विकर्ण
विकर्णों की लंबाई हैं[10]:
जहाँ a छोटा आधार है, b लंबा आधार है, और c और d समलम्ब लेग हैं।
यदि चतुर्भुज को इसके विकर्ण AC और BD द्वारा चार त्रिभुजों में विभाजित किया जाता है(जैसा कि दाईं ओर दिखाया गया है), O पर प्रतिच्छेद करता है, तो △ AOD का क्षेत्रफल △ BOC के बराबर है, और △ AOD और △ BOC के क्षेत्रों का उत्पाद △ AOB और △ COD के बराबर है। आसन्न त्रिभुजों के प्रत्येक युग्म के क्षेत्रफलों का अनुपात वही है जो समानांतर भुजाओं की लंबाई के बीच है।[10]
बता दें कि समलम्ब में क्रम में A, B, C और D हैं और समानांतर भुजाएँ AB और DC हैं। मान लीजिए E विकर्णों का प्रतिच्छेदन है, और F भुजा DA पर है और G भुजा BC पर इस प्रकार है कि FEG AB और CD के समांतर है। फिर FG AB और DC का अनुकूल माध्य है:[15]
विस्तारित असमांतर भुजाओं के प्रतिच्छेदन बिंदु और विकर्णों के प्रतिच्छेदन बिंदु दोनों से होकर जाने वाली रेखा प्रत्येक आधार को समद्विभाजित करती है।[16]
अन्य गुणधर्म
क्षेत्रफल का केंद्र(एकसमान तलीय पटल के लिए द्रव्यमान का केंद्र) समांतर भुजाओं के मध्यबिंदुओं को मिलाने वाले रेखाखंड के साथ स्थित होता है, जो लंबी भुजा b से लम्बवत दूरी x पर होता है।[17]
क्षेत्र का केंद्र इस खंड को अनुपात में विभाजित करता है(जब छोटी से लंबी तरफ लिया जाता है)[18]: p. 862
यदि कोण A और B के समद्विभाजक P पर प्रतिच्छेद करते हैं, और कोण C और D के समद्विभाजक Q पर प्रतिच्छेद करते हैं, तो[16]
समुपयोग
वास्तुकला
वास्तुकला में इस शब्द का उपयोग मिस्र की शैली में सममित देहली, खिड़कियां, और आधार पर व्यापक रूप से निर्मित इमारतों, शीर्ष की ओर पतला करने के लिए किया जाता है। यदि इनमें सीधी भुजाएँ और तीखे कोणीय कोने हैं, तो उनकी आकृतियाँ आमतौर पर समद्विबाहु समलम्बाकार होती हैं। इंका वास्तुकला के देहली और खिड़कियों के लिए यह मानक शैली थी।[19]
रेखागणित
सीढ़ी पार करने की समस्या एक राइट ट्रैपेज़ॉइड के समानांतर भुजाओं के बीच की दूरी को खोजने की समस्या है, जिसे विकर्ण लंबाई और लंबवत लेग से विकर्ण चौराहे तक की दूरी दी गई है।
जीव विज्ञान
आकृति विज्ञान(जीव विज्ञान), टैक्सोनॉमी(जीव विज्ञान) और अन्य वर्णनात्मक विषयों में, जिसमें इस तरह के आकार के लिए एक शब्द आवश्यक है, विशेष अंगों या रूपों के विवरण में ट्रैपेज़ॉइडल या ट्रैपेज़फ़ॉर्म जैसे शब्द आमतौर पर उपयोगी होते हैं।[20]
संगणक अभियांत्रिकी
संगणक अभियांत्रिकी में, विशेष रूप से कुंजीपटल तर्कशास्त्र और संगणक वास्तुकला में, ट्रेपेज़ोइड्स का उपयोग विशिष्ट रूप से पर बहुसंकेतक के प्रतीक के लिए किया जाता है। बहुसंकेतक तर्कशास्त्र तत्व हैं जो कई तत्वों के बीच चयन करते हैं और एक विशिष्ट चिन्ह के आधार पर एकल प्रक्षेपण उत्पन्न करते हैं। विशिष्ट अभिकल्पना विशेष रूप से बताए बिना ट्रेपेज़ोइड्स को नियोजित करेंगे कि वे बहुसंकेतक हैं क्योंकि वे सार्वभौमिक रूप से समकक्ष हैं।
यह भी देखें
- छिन्नक, समलम्बाकार फलकों वाला एक ठोस
- विनम्र संख्या, जिसे समलम्बाकार संख्या के रूप में भी जाना जाता है
- कील(ज्यामिति), दो त्रिभुजों और तीन चतुर्भुज चेहरों द्वारा परिभाषित एक बहुफलक।
संदर्भ
- ↑ http://www.mathopenref.com/trapezoid.html Mathopenref definition
- ↑ A. D. Gardiner & C. J. Bradley, Plane Euclidean Geometry: Theory and Problems, UKMT, 2005, p. 34.
- ↑ Types of quadrilaterals
- ↑ Euclid Elements Book I Definition 22
- ↑ πέζα is said to be the Doric and Arcadic form of πούς "foot", but recorded only in the sense "instep [of a human foot]", whence the meaning "edge, border". τράπεζα "table" is Homeric. Henry George Liddell, Robert Scott, Henry Stuart Jones, A Greek-English Lexicon, Oxford, Clarendon Press (1940), s.v. πέζα, τράπεζα.
- ↑ 6.0 6.1 James A. H. Murray (1926). ए न्यू इंग्लिश डिक्शनरी ऑन हिस्टोरिकल प्रिंसिपल्स: मुख्य रूप से फिलोलॉजिकल सोसाइटी द्वारा एकत्रित सामग्री पर आधारित. Vol. X. Clarendon Press at Oxford. p. 286 (Trapezium).
यूक्लिड के साथ (सी 300 ईसा पूर्व) τραπέζιον में वर्ग, आयत, समचतुर्भुज और समचतुर्भुज को छोड़कर सभी चतुर्भुज आकृतियाँ शामिल थीं; ट्रेपेज़िया की किस्मों में उन्होंने प्रवेश नहीं किया। लेकिन प्रोक्लस, जिसने यूक्लिड के तत्वों की पहली पुस्तक एडी 450 पर टिप्पणी लिखी थी, ने τραπέζιον नाम को केवल समानांतर दो पक्षों वाले चतुर्भुजों के लिए बनाए रखा, इन्हें τραπέζιον ἰσοσκελὲς, समद्विबाहु ट्रेपेज़ियम में विभाजित किया, जिसमें दो गैर-समानांतर भुजाएँ हैं (और उनके आधार) समान हैं, और σκαληνὸν τραπέζιον, स्केलीन ट्रेपेज़ियम, जिसमें ये पक्ष और कोण असमान हैं। ऐसे चतुर्भुजों के लिए जिनका कोई पार्श्व समानांतर नहीं है, प्रोक्लस ने τραπέζοειδὲς ट्रेपेज़ॉइड नाम दिया। इस नामकरण को सभी महाद्वीपीय भाषाओं में रखा गया है, और 18 वीं शताब्दी के अंत तक इंग्लैंड में सार्वभौमिक था, जब शर्तों के आवेदन को स्थानांतरित कर दिया गया था, ताकि अन्य राष्ट्रों के प्रोक्लस और आधुनिक भूगर्भीय आंकड़े विशेष रूप से एक ट्रैपेज़ियम (एफ। ट्रेपेज़, गेर. ट्रेपेज़, ड्यू. ट्रेपेज़ियम, इट. ट्रेपेज़ियो) अधिकांश अंग्रेजी लेखकों के साथ एक ट्रेपेज़ियम बन गया, और प्रोक्लस और अन्य राष्ट्रों का ट्रेपेज़ियम एक ट्रेपेज़ियम बन गया। ट्रैपेज़ॉइड का यह बदला हुआ अर्थ हटन के गणितीय शब्दकोश, 1795 में 'कभी-कभी' के रूप में दिया गया है - वह यह नहीं कहता कि किसके द्वारा; लेकिन उन्होंने खुद दुर्भाग्य से इसे अपनाया और इसका इस्तेमाल किया, और उनका शब्दकोश निस्संदेह इसके प्रसार में मुख्य एजेंट था। हालांकि कुछ जियोमीटर ने अपने मूल अर्थों में शब्दों का उपयोग करना जारी रखा, और 1875 के बाद से यह प्रचलित उपयोग है।
- ↑ 7.0 7.1 Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (5 April 2016). चीजों की समरूपता. CRC Press. p. 286. ISBN 978-1-4398-6489-0.
- ↑ For example: French trapèze, Italian trapezio, Portuguese trapézio, Spanish trapecio, German Trapez, Ukrainian "трапеція", e.g. "Larousse definition for trapézoïde".
- ↑ ""Math.com" से अमेरिकन स्कूल की परिभाषा". Retrieved 2008-04-14.
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 Weisstein, Eric W. "Trapezoid". MathWorld.
- ↑ Trapezoids, [1]. Retrieved 2012-02-24.
- ↑ Ask Dr. Math (2008), "Area of Trapezoid Given Only the Side Lengths".
- ↑ 13.00 13.01 13.02 13.03 13.04 13.05 13.06 13.07 13.08 13.09 13.10 13.11 Martin Josefsson, "Characterizations of trapezoids", Forum Geometricorum, 13 (2013) 23-35.
- ↑ T. K. Puttaswamy, Mathematical achievements of pre-modern Indian mathematicians, Elsevier, 2012, p. 156.
- ↑ GoGeometry, [2]. Retrieved 2012-07-08.
- ↑ 16.0 16.1 Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry, Mathematical Association of America, 2010, p. 55.
- ↑ efunda, General Trapezoid, [3]. Retrieved 2012-07-09.
- ↑ Tom M. Apostol and Mamikon A. Mnatsakanian (December 2004). "सर्किलों को घेरते हुए आंकड़े" (PDF). American Mathematical Monthly. 111 (10): 853–863. doi:10.2307/4145094. JSTOR 4145094. Retrieved 2016-04-06.
- ↑ "माचू पिच्चू - इंका ज्यामिति। माचू पिचू - इंका ज्यामिति।". gogeometry.com. Retrieved 2018-02-13.
- ↑ John L. Capinera (11 August 2008). एंटोमोलॉजी का विश्वकोश. Springer Science & Business Media. pp. 386, 1062, 1247. ISBN 978-1-4020-6242-1.
अग्रिम पठन
- D. Fraivert, A. Sigler and M. Stupel : Common properties of trapezoids and convex quadrilaterals
बाहरी संबंध
- "Trapezium" at Encyclopedia of Mathematics
- Weisstein, Eric W. "Right trapezoid". MathWorld.
- Trapezoid definition Area of a trapezoid Median of a trapezoid With interactive animations
- Trapezoid(North America) at elsy.at: Animated course(construction, circumference, area)
- Trapezoidal Rule on Numerical Methods for Stem Undergraduate
- Autar Kaw and E. Eric Kalu, Numerical Methods with Applications,(2008)