पुशफॉरवर्ड (अंतर): Difference between revisions
(Created page with "{{Short description|Linear approximation of smooth maps on tangent spaces}} {{other uses|Pushforward (disambiguation){{!}}Pushforward}} {{Use American English|date = March 201...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Linear approximation of smooth maps on tangent spaces}} | {{Short description|Linear approximation of smooth maps on tangent spaces}} | ||
''अन्य उपयोगों के लिए, पुशफॉरवर्ड देखें।'' | |||
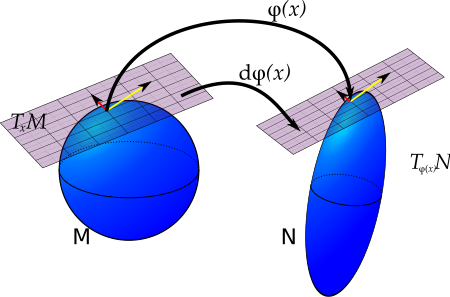
[[File:pushforward.svg|thumb|upright=1.5|alt=यदि एक नक्शा, φ, कई गुना M पर हर बिंदु को कई गुना N तक ले जाता है, तो φ का पुशफॉरवर्ड वेक्टर को स्पर्शरेखा स्थान में M के प्रत्येक बिंदु पर N में प्रत्येक बिंदु पर एक स्पर्शरेखा स्थान पर ले जाता है। | यदि | [[File:pushforward.svg|thumb|upright=1.5|alt=यदि एक नक्शा, φ, कई गुना M पर हर बिंदु को कई गुना N तक ले जाता है, तो φ का पुशफॉरवर्ड वेक्टर को स्पर्शरेखा स्थान में M के प्रत्येक बिंदु पर N में प्रत्येक बिंदु पर एक स्पर्शरेखा स्थान पर ले जाता है। | यदि मानचित्र, φ, प्रत्येक प्रसमष्टि ''M'' से प्रसमष्टि ''N'' पर इंगित करें, फिर φ का पुशफॉरवर्ड वेक्टर को स्पर्शी समष्टि में ''M'' में प्रत्येक बिंदु पर ''N'' में प्रत्येक बिंदु पर स्पर्शी समष्टि पर ले जाता है।]][[ अंतर ज्यामिति | अवकलन ज्यामिति]] में, '''पुशफॉरवर्ड स्पर्शी समष्टि''' पर सरल मानचित्र का एक रैखिक आकलन है। मान लीजिए कि {{nowrap|''φ'' : ''M'' → ''N''}} [[ चिकना कई गुना |सरल प्रसमष्टि]] के बीच एक [[ चिकना नक्शा |सरल मानचित्र]] है; तब φ का अवकलन, <math>d\varphi_x</math>, एक बिंदु x पर, कुछ अर्थों में, x के पास φ का सबसे अच्छा रैखिक आकलन है। इसे साधारण कलन के पूर्ण अवकलज के सामान्यीकरण के रूप में देखा जा सकता है। स्पष्ट रूप से, अवकलन φ (x) पर N के स्पर्शी समष्टि से x पर M के स्पर्शी समष्टि से <math>d\varphi_x: T_xM \to T_{\varphi(x)}N</math> रैखिक मानचित्र है। इसलिए इसका उपयोग N पर स्पर्शरेखा वैक्टर को M पर स्पर्शरेखा वैक्टर को आगे बढ़ाने के लिए किया जा सकता है। विभिन्न लेखकों द्वारा मानचित्र φ के अवकलन को φ का 'अवकलज' या 'पूर्ण अवकलज' भी कहा जाता है। | ||
== | == कारण == | ||
मान लीजिए <math>\varphi: U \to V</math> के विवृत उपसमुच्चय से <math>U</math> का <math>\R^m</math> एक विवृत उपसमुच्चय <math>V</math> का <math>\R^n</math> के लिए एक सुगम मानचित्र बनें, <math>U</math> मे किसी भी बिंदु <math>x</math> के लिए <math>x</math> पर <math>\varphi</math>का जैकबियन आव्यूह और के निर्धारक पर (मानक निर्देशांक के संबंध में) <math>x</math> पर <math>\varphi</math> के पूर्ण अवकलज का [[मैट्रिक्स (गणित)|आव्यूह (गणित)]] प्रतिनिधित्व है जो रैखिक मानचित्र है | |||
:<math>d\varphi_x:T_x\R^m\to T_{\varphi(x)}\R^n</math> | :<math>d\varphi_x:T_x\R^m\to T_{\varphi(x)}\R^n</math> | ||
उनके | उनके स्पर्शी समष्टि के बीच। ध्यान दें स्पर्शरेखा समष्टि क्रमशː <math>T_x\R^m,T_{\varphi(x)}\R^n</math>और <math>\mathbb{R}^m</math> के लिए <math>\mathbb{R}^n</math>, समरूपी हैं। पुशफॉरवर्ड इस निर्माण को इस स्थिति में सामान्यीकृत करता है कि <math>\varphi</math> किसी भी अवकलन प्रसमष्टि <math>M</math> और <math>N</math> के बीच एक सामान्य फलन है। | ||
== | == सरल मानचित्र का अवकलन == | ||
मान लीजिए <math>\varphi \colon M \to N </math> सरल प्रसमष्टि का एक सरल मानचित्र बनें। दिया गया <math> x \in M, </math> का अवकलन <math> \varphi </math> पर <math> x </math> एक रेखीय मानचित्र है | |||
:<math>d\varphi_x \colon\ T_xM\to T_{\varphi(x)}N\,</math> | :<math>d\varphi_x \colon\ T_xM\to T_{\varphi(x)}N\,</math> | ||
<math> x </math> पर <math> M </math> की स्पर्शी समष्टि से <math> N </math> स्पर्शी समष्टि के लिए <math> \varphi(x) </math> पर है। छवि <math> d\varphi_x X </math> एक स्पर्शरेखा सदिश का <math> X \in T_x M </math> अंतर्गत <math> d\varphi_x </math> को कभी-कभी <math> X </math> द्वारा <math> \varphi </math> का पुशफॉरवर्ड कहा जाता है इस पुशफॉरवर्ड की परिशुद्ध परिभाषा स्पर्शरेखा सदिशों के लिए उपयोग की जाने वाली परिभाषा पर निर्भर करती है (विभिन्न परिभाषाओं के लिए स्पर्शी समष्टि देखें)। | |||
यदि स्पर्शरेखा सदिशों को वक्रों के तुल्यता वर्ग | यदि स्पर्शरेखा सदिशों को वक्रों के तुल्यता वर्ग <math>\gamma</math> के रूप में परिभाषित किया जाता है जिसके लिए <math> \gamma(0) = x, </math> तो अवकलन द्वारा दिया जाता है | ||
:<math>d\varphi_x(\gamma'(0)) = (\varphi \circ \gamma)'(0).</math> | :<math>d\varphi_x(\gamma'(0)) = (\varphi \circ \gamma)'(0).</math> | ||
यहाँ, <math> \gamma </math> में वक्र | यहाँ, <math> \gamma </math> में वक्र <math> M </math> साथ <math> \gamma(0) = x </math> है, और <math>\gamma'(0)</math> वक्र के लिए स्पर्शरेखा सदिश <math> \gamma </math> पर <math> 0 </math> है। दूसरे शब्दों में, वक्र के स्पर्शरेखा सदिश का पुशफॉरवर्ड <math> \gamma </math> पर <math> 0 </math> वक्र की स्पर्शरेखा सदिश <math>\varphi \circ \gamma</math> पर <math> 0 </math> है। वैकल्पिक रूप से, यदि स्पर्शरेखा वैक्टर को व्युत्पत्ति (अमूर्त बीजगणित) के रूप में परिभाषित किया जाता है जो सरल वास्तविक-मूल्यवान फलनों पर कार्य करता है, तो अवकलन द्वारा दिया जाता है | ||
वैकल्पिक रूप से, यदि स्पर्शरेखा वैक्टर को व्युत्पत्ति (अमूर्त बीजगणित) के रूप में परिभाषित किया जाता है जो | |||
:<math>d\varphi_x(X)(f) = X(f \circ \varphi),</math> | :<math>d\varphi_x(X)(f) = X(f \circ \varphi),</math> | ||
एकपक्षीय फलन के लिए <math>f \in C^\infty(N)</math> और एकपक्षीय अवकलज <math>X \in T_xM</math> बिंदु पर <math>x \in M</math> (अवकलज (अमूर्त बीजगणित) को एक रेखीय मानचित्र <math>X \colon C^\infty(M) \to \R</math> के रूप में परिभाषित किया गया है, जो उत्पाद नियम को पूरा करता है, देखें: स्पर्शी समष्टि अवकलज के माध्यम से परिभाषा)। परिभाषा के अनुसार, का पुशफॉरवर्ड <math>X</math> में <math>T_{\varphi(x)}N</math> है और इसलिए स्वयं अवकलज <math>d\varphi_x(X) \colon C^\infty(N) \to \R</math> है। | |||
<math> x </math> और <math> \varphi(x), </math> लगभग दो प्रसमष्टि (गणित) चयन करने के बाद <math> \varphi </math> स्थानीय रूप से <math>\widehat{\varphi} \colon U \to V</math> के विवृत समुच्चय के बीच <math>\R^m</math> और <math>\R^n</math> द्वारा सरल मानचित्र द्वारा निर्धारित किया जाता है | |||
:<math>d\varphi_x\left(\frac{\partial}{\partial u^a}\right) = \frac{\partial{\widehat{\varphi}}^b}{\partial u^a} \frac{\partial}{\partial v^b},</math> | :<math>d\varphi_x\left(\frac{\partial}{\partial u^a}\right) = \frac{\partial{\widehat{\varphi}}^b}{\partial u^a} \frac{\partial}{\partial v^b},</math> | ||
आइंस्टीन | आइंस्टीन संकलन संकेतन में, जहां दिए गए मानचित्र में x के अनुरूप U में बिंदु पर आंशिक अवकलज का मूल्यांकन किया जाता है। | ||
रैखिकता द्वारा विस्तार निम्नलिखित | रैखिकता द्वारा विस्तार करने पर निम्नलिखित आव्यूह प्राप्त होता है | ||
:<math>\left(d\varphi_x\right)_a^{\;b} = \frac{\partial{\widehat{\varphi}}^b}{\partial u^a}.</math> | :<math>\left(d\varphi_x\right)_a^{\;b} = \frac{\partial{\widehat{\varphi}}^b}{\partial u^a}.</math> | ||
इस प्रकार | इस प्रकार अवकलन एक रेखीय परिवर्तन है, स्पर्शरेखा समष्टि के बीच, प्रत्येक बिंदु पर सरल मानचित्र <math> \varphi </math> से जुड़ा हुआ है। इसलिए, कुछ चयन किए हुए स्थानीय निर्देशांकों में, यह संबंधित सरल मानचित्र के <math>\R^m</math> को <math>\R^n</math>[[ जैकबियन मैट्रिक्स | जैकबियन आव्यूह]] द्वारा दर्शाया गया है सामान्य रूप से, अवकलन को प्रत्यावर्ती नहीं होना चाहिए। हालांकि, यदि <math> \varphi </math> एक [[स्थानीय भिन्नता|स्थानीय अवकलनीय तद्वता]] है, तब <math> d\varphi_x </math> व्युत्क्रमणीय है, और व्युत्क्रम <math> T_{\varphi(x)} N</math> का [[पुलबैक (अंतर ज्यामिति)|पुलबैक (अवकलन ज्यामिति)]] देता है विभिन्न प्रकार की अन्य सूचनाओं का उपयोग करके अवकलन को प्रायः व्यक्त किया जाता है | ||
विभिन्न प्रकार की अन्य सूचनाओं का उपयोग करके | |||
:<math>D\varphi_x,\left(\varphi_*\right)_x, \varphi'(x),T_x\varphi.</math> | :<math>D\varphi_x,\left(\varphi_*\right)_x, \varphi'(x),T_x\varphi.</math> | ||
यह परिभाषा से अनुसरण करता है कि एक | यह परिभाषा से अनुसरण करता है कि एक सम्मिश्र का अंतर अवकलनों (अर्थात, क्रियात्मक व्यवहार) का सम्मिश्रण है। यह सरल मानचित्रों के लिए शृंखला नियम है। | ||
इसके | इसके अतिरिक्त, स्थानीय अवकलनीय तद्वता का अवकलन स्पर्शी समष्टि का एक [[रैखिक समरूपता]] है। | ||
== [[स्पर्शरेखा बंडल]] पर | == [[स्पर्शरेखा बंडल]] पर अवकलन == | ||
सरल मानचित्र φ का अवकलन, एक स्पष्ट तरीके से, M के स्पर्शरेखा बंडल से N के स्पर्शरेखा बंडल तक [[ बंडल नक्शा |पूल प्रतिचित्र]] (वास्तव में एक [[वेक्टर बंडल समरूपता]]) को प्रेरित करता है, जिसे dφ या φ द्वारा निरूपित किया जाता है<sub>∗</sub>, जो निम्नलिखित क्रमविनिमेय आरेख में निर्धारित होता है: | |||
[[Image:SmoothPushforward-01.svg|center]]जहां | [[Image:SmoothPushforward-01.svg|center]]जहां ''π<sub>M</sub>'' और π<sub>''N''</sub> क्रमशः ''M'' और ''N'' के स्पर्शरेखा बंडलों के बंडल अनुमानों को निरूपित करें। | ||
<math>\operatorname{d}\!\varphi</math> | <math>\operatorname{d}\!\varphi</math> ''TM'' से [[पुलबैक बंडल]] φ<sup>∗</sup> ''TN'' पर ''M'' के माध्यम से पूल प्रतिचित्र प्रेरित करता है | ||
:<math>(m,v_m) \mapsto (m,\operatorname{d}\!\varphi (m,v_m)),</math> | :<math>(m,v_m) \mapsto (m,\operatorname{d}\!\varphi (m,v_m)),</math> | ||
जहाँ <math>m \in M</math> और <math>v_m \in T_mM</math> बाद वाला मानचित्र बदले मे ''M पर'' {{nowrap|Hom(''TM'', ''φ''<sup>∗</sup>''TN'')}} [[वेक्टर बंडल]] के एक भाग (तन्तु बंडल) के रूप में देखा जा सकता है पूल प्रतिचित्र dφ को भी Tφ द्वारा निरूपित किया जाता है और इसे 'स्पर्शरेखा मानचित्र' कहा जाता है। इस प्रकार, T फलननिर्धारक है। | |||
== सदिश क्षेत्रों का पुशफॉरवर्ड == | == वेक्टर (सदिश) क्षेत्रों का पुशफॉरवर्ड == | ||
सरल मानचित्र {{nowrap|''φ'' : ''M'' → ''N''}} और M पर एक सदिश क्षेत्र X दिया, सामान्य रूप से N पर कुछ सदिश क्षेत्र Y के साथ φ द्वारा X के एक पुशफॉरवर्ड की पहचान करना संभव नहीं है। उदाहरण के लिए, यदि मानचित्र φ विशेषण नहीं है, तो वहाँ। φ की छवि के बाहर इस तरह के एक पुशफॉरवर्ड को परिभाषित करने का कोई स्वाभाविक तरीका नहीं है। साथ ही, यदि φ अंतःक्षेपी नहीं है, तो दिए गए बिंदु पर पुशफॉरवर्ड के एक से अधिक विकल्प हो सकते हैं। फिर भी, प्रतिचित्र के साथ एक सदिश क्षेत्र की धारणा का उपयोग करके, कोई भी इस समस्या को परिशुद्ध बना सकता है। | |||
M पर φ∗TN के भाग को φ के साथ एक सदिश क्षेत्र कहा जाता है। उदाहरण के लिए, यदि M, N का उप-प्रसमष्टि है और φ समावेशन है, तो φ के साथ एक सदिश क्षेत्र M के साथ N के स्पर्शरेखा बंडल का एक भाग है; विशेष रूप से, M पर एक वेक्टर क्षेत्र ''TN'' के अंदर ''TM'' को सम्मिलित करने के माध्यम से ऐसे भाग को परिभाषित करता है। यह विचार एकपक्षीय रूप से सरल प्रतिचित्रों का सामान्यीकरण करता है। | |||
मान लीजिए कि X, M पर | मान लीजिए कि X, M पर सदिश क्षेत्र, अर्थात TM का एक भाग है। तब, <math>\operatorname{d}\!\phi \circ X</math> उपरोक्त अर्थ में, पुशफॉरवर्ड ''φ''<sub>∗</sub>X देता है, जो φ के साथ एक सदिश क्षेत्र है, अर्थात, M पर φ∗TN का भाग है | ||
N पर कोई सदिश क्षेत्र Y | N पर कोई सदिश क्षेत्र Y ''φ''<sup>∗</sup>''TN'' के पुलबैक खंड ''φ''<sup>∗</sup>''Y'' को (''φ''<sup>∗</sup>''Y'')<sub>''x''</sub> = ''Y<sub>φ</sub>''<sub>(''x'')</sub> के साथ M पर सदिश क्षेत्र X और N पर सदिश क्षेत्र Y को φ-संबंधित कहा जाता है यदि ''φ''<sub>∗</sub>''X'' = ''φ''<sup>∗</sup>''Y'' के साथ सदिश क्षेत्र के रूप में परिभाषित करता है।। दूसरे शब्दों में, M में सभी x के लिए ''dφ<sub>x</sub>''(''X'') = ''Y<sub>φ</sub>''<sub>(''x'')</sub> परिभाषित किया जाता है। | ||
कुछ स्थितियों में, M पर एक X सदिश क्षेत्र दिया गया है, N पर एक अद्वितीय सदिश क्षेत्र Y है जो φ-X से संबंधित है। यह विशेष रूप से | कुछ स्थितियों में, M पर एक X सदिश क्षेत्र दिया गया है, N पर एक अद्वितीय सदिश क्षेत्र Y है जो φ-X से संबंधित है। यह विशेष रूप से सत्य है जब φ एक अवकलज है। इस स्थिति में, पुशवर्ड N पर वेक्टर क्षेत्र Y को परिभाषित करता है, जिसे दिया गया है | ||
:<math>Y_y = \phi_*\left(X_{\phi^{-1}(y)}\right).</math> | :<math>Y_y = \phi_*\left(X_{\phi^{-1}(y)}\right).</math> | ||
अधिक सामान्य स्थिति तब उत्पन्न होती है जब φ आच्छादक होता है (उदाहरण के लिए [[फाइबर बंडल]] का बंडल प्रक्षेपण)। तब M पर एक वेक्टर क्षेत्र X को 'प्रक्षेप्य' कहा जाता है यदि N में सभी y के लिए, ''dφ<sub>x</sub>''(''X<sub>x</sub>'') ''φ''<sup>−1</sup>({''y''} में x के चयन से स्वतंत्र है। यह ठीक ऐसी स्थिति है जो प्रत्याभूति देती है कि N पर सदिश क्षेत्र के रूप में X का पुशफॉरवर्ड अच्छी तरह से परिभाषित है। | |||
=== उदाहरण === | === उदाहरण === | ||
==== | ==== लाइ समूहों पर गुणन से पुशफॉरवर्ड ==== | ||
लाइ समूह <math>G</math> को देखते हुए, हम गुणन मानचित्र <math>m(-,-):G\times G \to G</math> का उपयोग बायां गुणन प्राप्त करने के लिए <math>L_g = m(g,-)</math> और सही गुणन <math>R_g = m(-,g)</math> कर सकते हैं और <math>G \to G</math> को प्रतिचित्र करता है। इन मानचित्रों का उपयोग बाएँ या दाएँ अपरिवर्तनीय <math>G</math> मूल बिंदु पर इसकी स्पर्शी समष्टि से <math>\mathfrak{g} = T_eG</math> (जो इससे जुड़ा [[झूठ बीजगणित|लाइ बीजगणित]] है) सदिश क्षेत्रों के निर्माण के लिए किया जा सकता है। उदाहरण के लिए दिए गए <math>X \in \mathfrak{g}</math> हमें एक <math>\mathfrak{X}</math> पर <math>G</math> संबंधित वेक्टर क्षेत्र प्रत्येक के लिए <math>g \in G</math> मिलता है। जिसे <math>\mathfrak{X}_g = (L_g)_*(X) \in T_gG</math> द्वारा परिभाषित किया गया है। <blockquote><math>\gamma(0) = e</math> और <math>\gamma'(0) = X</math></blockquote>पुशफॉरवर्ड मानचित्र की वक्र परिभाषा का उपयोग करके इसकी आसानी से गणना की जा सकती है। यदि हमारे पास वक्र | |||
<math>\gamma: (-1,1) \to G</math> | |||
जहाँ <blockquote> मिलता है<math>\begin{align} | |||
(L_g)_*(X) &= (L_g\circ \gamma)'(0) \\ | (L_g)_*(X) &= (L_g\circ \gamma)'(0) \\ | ||
&= (g\cdot \gamma(t))'(0) \\ | &= (g\cdot \gamma(t))'(0) \\ | ||
| Line 72: | Line 73: | ||
&= g \cdot \gamma'(0) | &= g \cdot \gamma'(0) | ||
\end{align}</math></blockquote>चूंकि <math>L_g</math> के संबंध में स्थिर | \end{align}</math></blockquote>चूंकि <math>L_g</math> के संबंध में स्थिर <math>\gamma</math> है। इसका तात्पर्य है कि हम स्पर्शरेखा समष्टि <math>T_gG</math> जैसा <math>T_gG = g\cdot T_eG = g\cdot \mathfrak{g}</math> की व्याख्या कर सकते हैं | ||
==== कुछ लाइ समूहों के लिए पुशफॉरवर्ड ==== | |||
उदाहरण के लिए, यदि <math>G</math> आव्यूह द्वारा दिया गया हाइजेनबर्ग समूह | |||
<math>H = \left\{ | |||
\begin{bmatrix} | \begin{bmatrix} | ||
1 & a & b \\ | 1 & a & b \\ | ||
| Line 81: | Line 84: | ||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{bmatrix} : a,b,c \in \mathbb{R} | \end{bmatrix} : a,b,c \in \mathbb{R} | ||
\right\}</math> | \right\}</math> | ||
इसमें आव्यूह के समुच्चय द्वारा दिया गया लाई बीजगणित है<blockquote><math>\mathfrak{h} = \left\{ | |||
\begin{bmatrix} | \begin{bmatrix} | ||
0 & a & b \\ | 0 & a & b \\ | ||
| Line 87: | Line 92: | ||
0 & 0 & 0 | 0 & 0 & 0 | ||
\end{bmatrix} : a,b,c \in \mathbb{R} | \end{bmatrix} : a,b,c \in \mathbb{R} | ||
\right\}</math></blockquote>क्योंकि हम | \right\}</math></blockquote>क्योंकि हम <math>\gamma:(-1,1) \to H</math> के साथ ऊपरी आव्यूह प्रविष्टियों में से किसी एक में कोई भी वास्तविक संख्या देते हुए एक पथ <math>i < j</math> (i-वें पंक्ति और j-वें स्तंभ) पा सकते हैं। तब, <blockquote> के लिए <math>g = \begin{bmatrix} | ||
1 & 2 & 3 \\ | 1 & 2 & 3 \\ | ||
0 & 1 & 4 \\ | 0 & 1 & 4 \\ | ||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{bmatrix}</math></blockquote>हमारे पास<blockquote> | \end{bmatrix}</math></blockquote>हमारे पास<blockquote> <math>T_gH = g\cdot \mathfrak{h} = | ||
\left\{ | \left\{ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 98: | Line 103: | ||
0 & 0 & 0 | 0 & 0 & 0 | ||
\end{bmatrix} : a,b,c \in \mathbb{R} | \end{bmatrix} : a,b,c \in \mathbb{R} | ||
\right\}</math></blockquote>जो | \right\}</math></blockquote>जो आव्यूह के मूल समुच्चय के बराबर है। यह हमेशा स्थिति नहीं होता है, उदाहरण के लिए, समूह | ||
<math>G = \left\{ | |||
\begin{bmatrix} | \begin{bmatrix} | ||
a & b \\ | a & b \\ | ||
0 & 1/a | 0 & 1/a | ||
\end{bmatrix} : a,b \in \mathbb{R}, a \neq 0 | \end{bmatrix} : a,b \in \mathbb{R}, a \neq 0 | ||
\right\}</math> | \right\}</math> | ||
हमारे पास आव्यूह के समुच्चय के रूप में इसका लाई बीजगणित है<blockquote><math>\mathfrak{g} = \left\{ | |||
\begin{bmatrix} | \begin{bmatrix} | ||
a & b \\ | a & b \\ | ||
0 & -a | 0 & -a | ||
\end{bmatrix} : a,b \in \mathbb{R} | \end{bmatrix} : a,b \in \mathbb{R} | ||
\right\}</math></blockquote>इसलिए कुछ | \right\}</math></blockquote>इसलिए कुछ आव्यूह<blockquote> के लिए <math>g = \begin{bmatrix} | ||
2 & 3 \\ | 2 & 3 \\ | ||
0 & 1/2 | 0 & 1/2 | ||
\end{bmatrix}</math></blockquote>हमारे पास<blockquote> | \end{bmatrix}</math></blockquote>हमारे पास<blockquote> <math>T_gG = \left\{ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
2a & 2b - a/2 \\ | 2a & 2b - a/2 \\ | ||
0 & -a/2 | 0 & -a/2 | ||
\end{bmatrix} : a,b\in \mathbb{R} | \end{bmatrix} : a,b\in \mathbb{R} | ||
\right\}</math></blockquote>जो | \right\}</math></blockquote>जो आव्यूह का समान समुच्चय नहीं है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* पुलबैक ( | * पुलबैक (अवकलन ज्यामिति) | ||
* | * परिणाम आधारित उत्पादक मॉडल | ||
== संदर्भ == | == संदर्भ == | ||
Revision as of 10:11, 14 March 2023
अन्य उपयोगों के लिए, पुशफॉरवर्ड देखें।
अवकलन ज्यामिति में, पुशफॉरवर्ड स्पर्शी समष्टि पर सरल मानचित्र का एक रैखिक आकलन है। मान लीजिए कि φ : M → N सरल प्रसमष्टि के बीच एक सरल मानचित्र है; तब φ का अवकलन, , एक बिंदु x पर, कुछ अर्थों में, x के पास φ का सबसे अच्छा रैखिक आकलन है। इसे साधारण कलन के पूर्ण अवकलज के सामान्यीकरण के रूप में देखा जा सकता है। स्पष्ट रूप से, अवकलन φ (x) पर N के स्पर्शी समष्टि से x पर M के स्पर्शी समष्टि से रैखिक मानचित्र है। इसलिए इसका उपयोग N पर स्पर्शरेखा वैक्टर को M पर स्पर्शरेखा वैक्टर को आगे बढ़ाने के लिए किया जा सकता है। विभिन्न लेखकों द्वारा मानचित्र φ के अवकलन को φ का 'अवकलज' या 'पूर्ण अवकलज' भी कहा जाता है।
कारण
मान लीजिए के विवृत उपसमुच्चय से का एक विवृत उपसमुच्चय का के लिए एक सुगम मानचित्र बनें, मे किसी भी बिंदु के लिए पर का जैकबियन आव्यूह और के निर्धारक पर (मानक निर्देशांक के संबंध में) पर के पूर्ण अवकलज का आव्यूह (गणित) प्रतिनिधित्व है जो रैखिक मानचित्र है
उनके स्पर्शी समष्टि के बीच। ध्यान दें स्पर्शरेखा समष्टि क्रमशː और के लिए , समरूपी हैं। पुशफॉरवर्ड इस निर्माण को इस स्थिति में सामान्यीकृत करता है कि किसी भी अवकलन प्रसमष्टि और के बीच एक सामान्य फलन है।
सरल मानचित्र का अवकलन
मान लीजिए सरल प्रसमष्टि का एक सरल मानचित्र बनें। दिया गया का अवकलन पर एक रेखीय मानचित्र है
पर की स्पर्शी समष्टि से स्पर्शी समष्टि के लिए पर है। छवि एक स्पर्शरेखा सदिश का अंतर्गत को कभी-कभी द्वारा का पुशफॉरवर्ड कहा जाता है इस पुशफॉरवर्ड की परिशुद्ध परिभाषा स्पर्शरेखा सदिशों के लिए उपयोग की जाने वाली परिभाषा पर निर्भर करती है (विभिन्न परिभाषाओं के लिए स्पर्शी समष्टि देखें)।
यदि स्पर्शरेखा सदिशों को वक्रों के तुल्यता वर्ग के रूप में परिभाषित किया जाता है जिसके लिए तो अवकलन द्वारा दिया जाता है
यहाँ, में वक्र साथ है, और वक्र के लिए स्पर्शरेखा सदिश पर है। दूसरे शब्दों में, वक्र के स्पर्शरेखा सदिश का पुशफॉरवर्ड पर वक्र की स्पर्शरेखा सदिश पर है। वैकल्पिक रूप से, यदि स्पर्शरेखा वैक्टर को व्युत्पत्ति (अमूर्त बीजगणित) के रूप में परिभाषित किया जाता है जो सरल वास्तविक-मूल्यवान फलनों पर कार्य करता है, तो अवकलन द्वारा दिया जाता है
एकपक्षीय फलन के लिए और एकपक्षीय अवकलज बिंदु पर (अवकलज (अमूर्त बीजगणित) को एक रेखीय मानचित्र के रूप में परिभाषित किया गया है, जो उत्पाद नियम को पूरा करता है, देखें: स्पर्शी समष्टि अवकलज के माध्यम से परिभाषा)। परिभाषा के अनुसार, का पुशफॉरवर्ड में है और इसलिए स्वयं अवकलज है।
और लगभग दो प्रसमष्टि (गणित) चयन करने के बाद स्थानीय रूप से के विवृत समुच्चय के बीच और द्वारा सरल मानचित्र द्वारा निर्धारित किया जाता है
आइंस्टीन संकलन संकेतन में, जहां दिए गए मानचित्र में x के अनुरूप U में बिंदु पर आंशिक अवकलज का मूल्यांकन किया जाता है।
रैखिकता द्वारा विस्तार करने पर निम्नलिखित आव्यूह प्राप्त होता है
इस प्रकार अवकलन एक रेखीय परिवर्तन है, स्पर्शरेखा समष्टि के बीच, प्रत्येक बिंदु पर सरल मानचित्र से जुड़ा हुआ है। इसलिए, कुछ चयन किए हुए स्थानीय निर्देशांकों में, यह संबंधित सरल मानचित्र के को जैकबियन आव्यूह द्वारा दर्शाया गया है सामान्य रूप से, अवकलन को प्रत्यावर्ती नहीं होना चाहिए। हालांकि, यदि एक स्थानीय अवकलनीय तद्वता है, तब व्युत्क्रमणीय है, और व्युत्क्रम का पुलबैक (अवकलन ज्यामिति) देता है विभिन्न प्रकार की अन्य सूचनाओं का उपयोग करके अवकलन को प्रायः व्यक्त किया जाता है
यह परिभाषा से अनुसरण करता है कि एक सम्मिश्र का अंतर अवकलनों (अर्थात, क्रियात्मक व्यवहार) का सम्मिश्रण है। यह सरल मानचित्रों के लिए शृंखला नियम है।
इसके अतिरिक्त, स्थानीय अवकलनीय तद्वता का अवकलन स्पर्शी समष्टि का एक रैखिक समरूपता है।
स्पर्शरेखा बंडल पर अवकलन
सरल मानचित्र φ का अवकलन, एक स्पष्ट तरीके से, M के स्पर्शरेखा बंडल से N के स्पर्शरेखा बंडल तक पूल प्रतिचित्र (वास्तव में एक वेक्टर बंडल समरूपता) को प्रेरित करता है, जिसे dφ या φ द्वारा निरूपित किया जाता है∗, जो निम्नलिखित क्रमविनिमेय आरेख में निर्धारित होता है:
जहां πM और πN क्रमशः M और N के स्पर्शरेखा बंडलों के बंडल अनुमानों को निरूपित करें।
TM से पुलबैक बंडल φ∗ TN पर M के माध्यम से पूल प्रतिचित्र प्रेरित करता है
जहाँ और बाद वाला मानचित्र बदले मे M पर Hom(TM, φ∗TN) वेक्टर बंडल के एक भाग (तन्तु बंडल) के रूप में देखा जा सकता है पूल प्रतिचित्र dφ को भी Tφ द्वारा निरूपित किया जाता है और इसे 'स्पर्शरेखा मानचित्र' कहा जाता है। इस प्रकार, T फलननिर्धारक है।
वेक्टर (सदिश) क्षेत्रों का पुशफॉरवर्ड
सरल मानचित्र φ : M → N और M पर एक सदिश क्षेत्र X दिया, सामान्य रूप से N पर कुछ सदिश क्षेत्र Y के साथ φ द्वारा X के एक पुशफॉरवर्ड की पहचान करना संभव नहीं है। उदाहरण के लिए, यदि मानचित्र φ विशेषण नहीं है, तो वहाँ। φ की छवि के बाहर इस तरह के एक पुशफॉरवर्ड को परिभाषित करने का कोई स्वाभाविक तरीका नहीं है। साथ ही, यदि φ अंतःक्षेपी नहीं है, तो दिए गए बिंदु पर पुशफॉरवर्ड के एक से अधिक विकल्प हो सकते हैं। फिर भी, प्रतिचित्र के साथ एक सदिश क्षेत्र की धारणा का उपयोग करके, कोई भी इस समस्या को परिशुद्ध बना सकता है।
M पर φ∗TN के भाग को φ के साथ एक सदिश क्षेत्र कहा जाता है। उदाहरण के लिए, यदि M, N का उप-प्रसमष्टि है और φ समावेशन है, तो φ के साथ एक सदिश क्षेत्र M के साथ N के स्पर्शरेखा बंडल का एक भाग है; विशेष रूप से, M पर एक वेक्टर क्षेत्र TN के अंदर TM को सम्मिलित करने के माध्यम से ऐसे भाग को परिभाषित करता है। यह विचार एकपक्षीय रूप से सरल प्रतिचित्रों का सामान्यीकरण करता है।
मान लीजिए कि X, M पर सदिश क्षेत्र, अर्थात TM का एक भाग है। तब, उपरोक्त अर्थ में, पुशफॉरवर्ड φ∗X देता है, जो φ के साथ एक सदिश क्षेत्र है, अर्थात, M पर φ∗TN का भाग है
N पर कोई सदिश क्षेत्र Y φ∗TN के पुलबैक खंड φ∗Y को (φ∗Y)x = Yφ(x) के साथ M पर सदिश क्षेत्र X और N पर सदिश क्षेत्र Y को φ-संबंधित कहा जाता है यदि φ∗X = φ∗Y के साथ सदिश क्षेत्र के रूप में परिभाषित करता है।। दूसरे शब्दों में, M में सभी x के लिए dφx(X) = Yφ(x) परिभाषित किया जाता है।
कुछ स्थितियों में, M पर एक X सदिश क्षेत्र दिया गया है, N पर एक अद्वितीय सदिश क्षेत्र Y है जो φ-X से संबंधित है। यह विशेष रूप से सत्य है जब φ एक अवकलज है। इस स्थिति में, पुशवर्ड N पर वेक्टर क्षेत्र Y को परिभाषित करता है, जिसे दिया गया है
अधिक सामान्य स्थिति तब उत्पन्न होती है जब φ आच्छादक होता है (उदाहरण के लिए फाइबर बंडल का बंडल प्रक्षेपण)। तब M पर एक वेक्टर क्षेत्र X को 'प्रक्षेप्य' कहा जाता है यदि N में सभी y के लिए, dφx(Xx) φ−1({y} में x के चयन से स्वतंत्र है। यह ठीक ऐसी स्थिति है जो प्रत्याभूति देती है कि N पर सदिश क्षेत्र के रूप में X का पुशफॉरवर्ड अच्छी तरह से परिभाषित है।
उदाहरण
लाइ समूहों पर गुणन से पुशफॉरवर्ड
लाइ समूह को देखते हुए, हम गुणन मानचित्र का उपयोग बायां गुणन प्राप्त करने के लिए और सही गुणन कर सकते हैं और को प्रतिचित्र करता है। इन मानचित्रों का उपयोग बाएँ या दाएँ अपरिवर्तनीय मूल बिंदु पर इसकी स्पर्शी समष्टि से (जो इससे जुड़ा लाइ बीजगणित है) सदिश क्षेत्रों के निर्माण के लिए किया जा सकता है। उदाहरण के लिए दिए गए हमें एक पर संबंधित वेक्टर क्षेत्र प्रत्येक के लिए मिलता है। जिसे द्वारा परिभाषित किया गया है।
और
पुशफॉरवर्ड मानचित्र की वक्र परिभाषा का उपयोग करके इसकी आसानी से गणना की जा सकती है। यदि हमारे पास वक्र
जहाँ
मिलता है
चूंकि के संबंध में स्थिर है। इसका तात्पर्य है कि हम स्पर्शरेखा समष्टि जैसा की व्याख्या कर सकते हैं
कुछ लाइ समूहों के लिए पुशफॉरवर्ड
उदाहरण के लिए, यदि आव्यूह द्वारा दिया गया हाइजेनबर्ग समूह
इसमें आव्यूह के समुच्चय द्वारा दिया गया लाई बीजगणित है
क्योंकि हम के साथ ऊपरी आव्यूह प्रविष्टियों में से किसी एक में कोई भी वास्तविक संख्या देते हुए एक पथ (i-वें पंक्ति और j-वें स्तंभ) पा सकते हैं। तब,
के लिए
हमारे पास
जो आव्यूह के मूल समुच्चय के बराबर है। यह हमेशा स्थिति नहीं होता है, उदाहरण के लिए, समूह
हमारे पास आव्यूह के समुच्चय के रूप में इसका लाई बीजगणित है
इसलिए कुछ आव्यूह
के लिए
हमारे पास
जो आव्यूह का समान समुच्चय नहीं है।
यह भी देखें
- पुलबैक (अवकलन ज्यामिति)
- परिणाम आधारित उत्पादक मॉडल
संदर्भ
- Lee, John M. (2003). Introduction to Smooth Manifolds. Springer Graduate Texts in Mathematics. Vol. 218.
- Jost, Jürgen (2002). Riemannian Geometry and Geometric Analysis. Berlin: Springer-Verlag. ISBN 3-540-42627-2. See section 1.6.
- Abraham, Ralph; Marsden, Jerrold E. (1978). Foundations of Mechanics. London: Benjamin-Cummings. ISBN 0-8053-0102-X. See section 1.7 and 2.3.