आधार (ज्यामिति): Difference between revisions
(Created page with "{{Short description|Bottom of a geometric figure}} {{refimprove|date=December 2017}} Image:Pyramid coloured base (geometry).png|thumb|एक कंकाल [[पिरा...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Bottom of a geometric figure}} | {{Short description|Bottom of a geometric figure}} | ||
{{refimprove|date=December 2017}} | {{refimprove|date=December 2017}} | ||
[[Image:Pyramid coloured base (geometry).png|thumb|एक कंकाल [[पिरामिड]] जिसके आधार पर प्रकाश डाला गया है]][[ज्यामिति]] में, एक आधार एक [[बहुभुज]] का एक [[किनारा (ज्यामिति)]] या एक बहुफलक का एक [[चेहरा (ज्यामिति)]] होता है, विशेष रूप से उस दिशा में लंबवत उन्मुख होता है जिसमें ऊंचाई # गणित में मापा जाता है, या जिसे नीचे माना जाता है आंकड़ा।<ref>{{cite book |title=समतल ज्यामिति|first1=C.I.|last1=Palmer|first2=D.P.|last2=Taylor|publisher=Scott, Foresman & Co.|year=1918|pages=38, 315, 353|url=https://books.google.com/books?id=k9oZAAAAYAAJ}}</ref> यह शब्द | [[Image:Pyramid coloured base (geometry).png|thumb|एक कंकाल [[पिरामिड]] जिसके आधार पर प्रकाश डाला गया है]][[ज्यामिति]] में, एक आधार एक [[बहुभुज]] का एक [[किनारा (ज्यामिति)]] या एक बहुफलक का एक [[चेहरा (ज्यामिति)]] होता है, विशेष रूप से उस दिशा में लंबवत उन्मुख होता है जिसमें ऊंचाई # गणित में मापा जाता है, या जिसे नीचे माना जाता है आंकड़ा।<ref>{{cite book |title=समतल ज्यामिति|first1=C.I.|last1=Palmer|first2=D.P.|last2=Taylor|publisher=Scott, Foresman & Co.|year=1918|pages=38, 315, 353|url=https://books.google.com/books?id=k9oZAAAAYAAJ}}</ref> यह शब्द सामान्यतः [[त्रिकोण]], समांतर [[[[चतुर्भुज]]]], ट्रेपेज़ोइड्स, [[सिलेंडर (ज्यामिति)]], [[शंकु (ज्यामिति)]], [[पिरामिड (ज्यामिति)]], समानांतर चतुर्भुज और छिन्नक पर लागू होता है। | ||
== [[क्षेत्र]] और [[आयतन]] गणना में भूमिका == | == [[क्षेत्र]] और [[आयतन]] गणना में भूमिका == | ||
आंकड़ों के क्षेत्रों और मात्राओं की गणना करने के लिए | आंकड़ों के क्षेत्रों और मात्राओं की गणना करने के लिए सामान्यतः आधारों (ऊंचाइयों के साथ) का उपयोग किया जाता है। इन प्रक्रियाओं के बारे में बोलते हुए, किसी आकृति के आधार के माप (लंबाई या क्षेत्र) को अधिकांशतःइसका आधार कहा जाता है। | ||
इस प्रयोग से, समांतर चतुर्भुज का क्षेत्रफल या [[प्रिज्म (ज्यामिति)]] या बेलन के आयतन की गणना इसके आधार को इसकी ऊंचाई से गुणा करके की जा सकती है; इसी तरह, त्रिभुजों का क्षेत्रफल और शंकुओं और पिरामिडों का आयतन उनके आधारों और ऊँचाइयों के गुणनफल के अंश हैं। कुछ आकृतियों के दो समानांतर आधार होते हैं (जैसे कि समलम्बाकार और छिन्नक), जिनमें से दोनों का उपयोग आंकड़ों की सीमा की गणना करने के लिए किया जाता है।<ref>{{Cite book |title=Geometry: Seeing, Doing, Understanding |last=Jacobs |first=Harold R. |authorlink=Harold R. Jacobs |edition=Third |publisher=[[W. H. Freeman and Company]] |location=[[New York City]] |year=2003 |isbn=978-0-7167-4361-3 |page=281}}</ref> | इस प्रयोग से, समांतर चतुर्भुज का क्षेत्रफल या [[प्रिज्म (ज्यामिति)]] या बेलन के आयतन की गणना इसके आधार को इसकी ऊंचाई से गुणा करके की जा सकती है; इसी तरह, त्रिभुजों का क्षेत्रफल और शंकुओं और पिरामिडों का आयतन उनके आधारों और ऊँचाइयों के गुणनफल के अंश हैं। कुछ आकृतियों के दो समानांतर आधार होते हैं (जैसे कि समलम्बाकार और छिन्नक), जिनमें से दोनों का उपयोग आंकड़ों की सीमा की गणना करने के लिए किया जाता है।<ref>{{Cite book |title=Geometry: Seeing, Doing, Understanding |last=Jacobs |first=Harold R. |authorlink=Harold R. Jacobs |edition=Third |publisher=[[W. H. Freeman and Company]] |location=[[New York City]] |year=2003 |isbn=978-0-7167-4361-3 |page=281}}</ref> | ||
| Line 10: | Line 10: | ||
== त्रिकोणमिति में विस्तारित आधार == | == त्रिकोणमिति में विस्तारित आधार == | ||
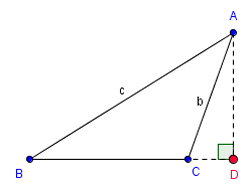
[[Image:Projection formula (3).png|thumb|A से ऊँचाई (त्रिकोण) विस्तारित आधार को D (त्रिकोण के बाहर एक बिंदु) पर काटती है।]]त्रिभुज का विस्तारित आधार (विस्तारित भुजा का एक विशेष मामला) वह [[रेखा (ज्यामिति)]] है जिसमें आधार होता है। विस्तारित आधार अधिक त्रिकोण के संदर्भ में महत्वपूर्ण है: [[तीव्र कोण]] शीर्ष (ज्यामिति) से ऊंचाई (त्रिकोण) त्रिकोण के बाहर हैं और विस्तारित विपरीत आधार ( | [[Image:Projection formula (3).png|thumb|A से ऊँचाई (त्रिकोण) विस्तारित आधार को D (त्रिकोण के बाहर एक बिंदु) पर काटती है।]]त्रिभुज का विस्तारित आधार (विस्तारित भुजा का एक विशेष मामला) वह [[रेखा (ज्यामिति)]] है जिसमें आधार होता है। विस्तारित आधार अधिक त्रिकोण के संदर्भ में महत्वपूर्ण है: [[तीव्र कोण]] शीर्ष (ज्यामिति) से ऊंचाई (त्रिकोण) त्रिकोण के बाहर हैं और विस्तारित विपरीत आधार (किन्तु उचित आधार नहीं) के लंबवत प्रतिच्छेदन हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 19:08, 20 March 2023
This article needs additional citations for verification. (December 2017) (Learn how and when to remove this template message) |
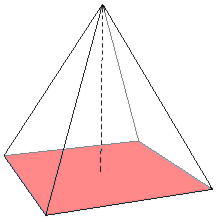
ज्यामिति में, एक आधार एक बहुभुज का एक किनारा (ज्यामिति) या एक बहुफलक का एक चेहरा (ज्यामिति) होता है, विशेष रूप से उस दिशा में लंबवत उन्मुख होता है जिसमें ऊंचाई # गणित में मापा जाता है, या जिसे नीचे माना जाता है आंकड़ा।[1] यह शब्द सामान्यतः त्रिकोण, समांतर [[चतुर्भुज]], ट्रेपेज़ोइड्स, सिलेंडर (ज्यामिति), शंकु (ज्यामिति), पिरामिड (ज्यामिति), समानांतर चतुर्भुज और छिन्नक पर लागू होता है।
क्षेत्र और आयतन गणना में भूमिका
आंकड़ों के क्षेत्रों और मात्राओं की गणना करने के लिए सामान्यतः आधारों (ऊंचाइयों के साथ) का उपयोग किया जाता है। इन प्रक्रियाओं के बारे में बोलते हुए, किसी आकृति के आधार के माप (लंबाई या क्षेत्र) को अधिकांशतःइसका आधार कहा जाता है।
इस प्रयोग से, समांतर चतुर्भुज का क्षेत्रफल या प्रिज्म (ज्यामिति) या बेलन के आयतन की गणना इसके आधार को इसकी ऊंचाई से गुणा करके की जा सकती है; इसी तरह, त्रिभुजों का क्षेत्रफल और शंकुओं और पिरामिडों का आयतन उनके आधारों और ऊँचाइयों के गुणनफल के अंश हैं। कुछ आकृतियों के दो समानांतर आधार होते हैं (जैसे कि समलम्बाकार और छिन्नक), जिनमें से दोनों का उपयोग आंकड़ों की सीमा की गणना करने के लिए किया जाता है।[2]
त्रिकोणमिति में विस्तारित आधार
त्रिभुज का विस्तारित आधार (विस्तारित भुजा का एक विशेष मामला) वह रेखा (ज्यामिति) है जिसमें आधार होता है। विस्तारित आधार अधिक त्रिकोण के संदर्भ में महत्वपूर्ण है: तीव्र कोण शीर्ष (ज्यामिति) से ऊंचाई (त्रिकोण) त्रिकोण के बाहर हैं और विस्तारित विपरीत आधार (किन्तु उचित आधार नहीं) के लंबवत प्रतिच्छेदन हैं।
यह भी देखें
संदर्भ
- ↑ Palmer, C.I.; Taylor, D.P. (1918). समतल ज्यामिति. Scott, Foresman & Co. pp. 38, 315, 353.
- ↑ Jacobs, Harold R. (2003). Geometry: Seeing, Doing, Understanding (Third ed.). New York City: W. H. Freeman and Company. p. 281. ISBN 978-0-7167-4361-3.