प्रतिबाधा अनुरूपता

प्रतिबाधा सादृश्य समान विद्युत प्रणाली द्वारा यांत्रिक प्रणाली का प्रतिनिधित्व करने की विधि है। ऐसा करने का लाभ यह है कि विशेष रूप से इलेक्ट्रॉनिक फिल्टर के क्षेत्र में जटिल विद्युत प्रणालियों से संबंधित सिद्धांत और विश्लेषण तकनीकों का बड़ा समूह है।एक विद्युत प्रतिनिधित्व में परिवर्तित करके, विद्युत डोमेन में इन उपकरणों को बिना किसी संशोधन के सीधे यांत्रिक प्रणाली पर लागू किया जा सकता है। वैद्युतयांत्रिकी में और फायदा होता है: ऐसी प्रणाली के यांत्रिक भाग को विद्युत डोमेन में परिवर्तित करने से पूरे सिस्टम को एकीकृत पूरे के रूप में विश्लेषण करने की अनुमति मिलती है।

सिम्युलेटेड विद्युत प्रणाली का गणितीय व्यवहार प्रस्तुत यांत्रिक प्रणाली के गणितीय व्यवहार के समान है। विद्युत डोमेन में प्रत्येक विद्युत तत्व में यांत्रिक डोमेन में अनुरूप घटक समीकरण के साथ संबंधित तत्व होता है। सर्किट विश्लेषण के सभी नियम, जैसे कि किरचॉफ के सर्किट नियम, जो विद्युत डोमेन में लागू होते हैं, यांत्रिक प्रतिबाधा सादृश्य पर भी लागू होते हैं।

प्रतिबाधा समानता विद्युत डोमेन में यांत्रिक प्रणालियों का प्रतिनिधित्व करने के लिए उपयोग की जाने वाली दो मुख्य यांत्रिक-विद्युत अनुरूपताओं में से है, दूसरी गतिशीलता समानता है। इन दो तरीकों में वोल्टेज और करंट की भूमिका उलट जाती है, और उत्पादित विद्युत प्रतिनिधित्व दूसरे के दोहरे प्रतिबाधा हैं। प्रतिबाधा सादृश्य विद्युत प्रतिबाधा और यांत्रिक प्रतिबाधा के बीच सादृश्य को संरक्षित करता है जबकि गतिशीलता सादृश्य नहीं करता है। दूसरी ओर, गतिशीलता सादृश्य विद्युत डोमेन में स्थानांतरित होने पर यांत्रिक प्रणाली की टोपोलॉजी को संरक्षित करता है जबकि प्रतिबाधा सादृश्य नहीं करता है।

अनुप्रयोग

यांत्रिक फिल्टर के व्यवहार को मॉडल करने के लिए प्रतिबाधा सादृश्य का व्यापक रूप से उपयोग किया जाता है। ये ऐसे फिल्टर हैं जो इलेक्ट्रॉनिक सर्किट में उपयोग के लिए अभिप्रेत हैं, अपितु पूरी तरह से यांत्रिक कंपन तरंगों द्वारा काम करते हैं। ट्रांसड्यूसर विद्युत और यांत्रिक डोमेन के बीच परिवर्तित करने के लिए फ़िल्टर के इनपुट और आउटपुट पर प्रदान किए जाते हैं। एक अन्य बहुत ही सामान्य उपयोग श्रव्य उपकरण के क्षेत्र में है, जैसे लाउडस्पीकर। लाउडस्पीकर में ट्रांसड्यूसर और मैकेनिकल मूविंग पार्ट्स होते हैं। ध्वनिक तरंगें स्वयं यांत्रिक गति की तरंगें हैं: वायु के अणुओं या किसी अन्य द्रव माध्यम की। इस प्रकार का बहुत प्रारंभिक अनुप्रयोग ग्रामोफ़ोन के रसातल ऑडियो प्रदर्शन के लिए यांत्रिक फिल्टर # ध्वनि प्रजनन करना था। 1929 में एडवर्ड लॉरी नॉर्टन ने फोनोग्राफ के यांत्रिक भागों को अधिकतम फ्लैट फिल्टर के रूप में व्यवहार करने के लिए डिजाइन किया, इस प्रकार इलेक्ट्रॉनिक बटरवर्थ फिल्टर की आशंका थी।

तत्व

एक यांत्रिक प्रणाली के लिए विद्युत सादृश्य विकसित करने से पहले, इसे पहले अमूर्त यांत्रिक नेटवर्क के रूप में वर्णित किया जाना चाहिए। यांत्रिक प्रणाली को कई आदर्श तत्वों में विभाजित किया गया है, जिनमें से प्रत्येक को विद्युत एनालॉग के साथ जोड़ा जा सकता है। नेटवर्क आरेखों पर इन यांत्रिक तत्वों के लिए उपयोग किए जाने वाले प्रतीकों को प्रत्येक व्यक्तिगत तत्व पर निम्न अनुभागों में दिखाया गया है।

गांठ वाले विद्युत तत्वों की यांत्रिक उपमाएँ भी गांठ वाले तत्व हैं, अर्थात, यह माना जाता है कि तत्व रखने वाले यांत्रिक घटक इतने छोटे होते हैं कि यांत्रिक तरंगों द्वारा घटक के छोर से दूसरे छोर तक प्रचार करने में लगने वाले समय की उपेक्षा की जा सकती है। पारेषण लाइनों जैसे वितरित तत्वों के लिए समानताएं भी विकसित की जा सकती हैं अपितु लम्प्ड-एलिमेंट सर्किट के साथ सबसे बड़ा लाभ है। तीन निष्क्रिय विद्युत तत्वों, अर्थात् विद्युत प्रतिरोध, अधिष्ठापन और समाई के लिए यांत्रिक उपमाएँ आवश्यक हैं। इन उपमाओं का निर्धारण इस बात से होता है कि प्रयास का प्रतिनिधित्व करने के लिए किस यांत्रिक संपत्ति का चयन किया जाता है, वोल्टेज की सादृश्यता, और प्रवाह का प्रतिनिधित्व करने के लिए चुनी गई संपत्ति, विद्युत प्रवाह की सादृश्यता। प्रतिबाधा सादृश्य में प्रयास चर बल है और प्रवाह चर वेग है।

प्रतिरोध

एक स्पंज (बाएं) और उसके विद्युत सादृश्य (दाएं) के लिए यांत्रिक प्रतीक। प्रतीक का मतलब डैशपोट का विचारोत्तेजक होना है।

विद्युत प्रतिरोध का यांत्रिक सादृश्य घर्षण जैसी प्रक्रियाओं के माध्यम से चलती प्रणाली की ऊर्जा का नुकसान है। प्रतिरोधी के अनुरूप यांत्रिक घटक सदमे अवशोषक है और प्रतिरोध के अनुरूप संपत्ति नमी है। ओम के नियम के संवैधानिक समीकरण द्वारा प्रतिरोधक को नियंत्रित किया जाता है,

$$v=iR\,.$$

यांत्रिक डोमेन में अनुरूप समीकरण है,

$$F=uR_{\mathrm {m} }\,,$$

कहाँ

• $R$ is resistance;
• $v$ is voltage;
• $i$ is current;
• $R_{m}$ is mechanical resistance, or damping;
• $F$ is force; and
• $u$ is velocity induced by the force.

विद्युत प्रतिरोध विद्युत प्रतिबाधा के वास्तविक भाग का प्रतिनिधित्व करता है। इसी तरह, यांत्रिक प्रतिरोध यांत्रिक प्रतिबाधा का वास्तविक हिस्सा है।

अधिष्ठापन

द्रव्यमान के लिए यांत्रिक प्रतीक (बाएं) और इसकी विद्युत सादृश्यता (दाएं)। द्रव्यमान के नीचे का वर्ग कोण यह इंगित करने के लिए है कि द्रव्यमान का संचलन संदर्भ के फ्रेम के सापेक्ष है।

प्रतिबाधा सादृश्य में अधिष्ठापन का यांत्रिक सादृश्य द्रव्यमान है। प्रारंभ करनेवाला के समान यांत्रिक घटक बड़ा, कठोर भार है। प्रारंभ करनेवाला संवैधानिक समीकरण द्वारा शासित होता है,

$$v=L{\frac {di}{dt}}\,.$$

यांत्रिक डोमेन में समरूप समीकरण न्यूटन का गति का दूसरा नियम है,

$$F=M{\frac {du}{dt}}\,,$$

कहाँ

• $L$ is inductance;
• $t$ is time; and
• $M$ is mass.

एक प्रारंभ करनेवाला का प्रतिबाधा विशुद्ध रूप से काल्पनिक संख्या है और इसके द्वारा दिया जाता है,

$$Z=j\omega L\,.$$

अनुरूप यांत्रिक प्रतिबाधा द्वारा दिया जाता है,

$$Z_{\mathrm {m} }=j\omega M\,,$$

कहाँ

• $Z$ is electrical impedance;
• $j$ is the imaginary unit;
• $\omega$ is angular frequency; and
• $Z_{m}$ is mechanical impedance.

समाई

एक कठोरता तत्व (बाएं) और उसके विद्युत सादृश्य (दाएं) के लिए यांत्रिक प्रतीक। प्रतीक का मतलब वसंत का विचारोत्तेजक होना है।

प्रतिबाधा सादृश्य में समाई का यांत्रिक सादृश्य अनुपालन है। यांत्रिकी में कठोरता, अनुपालन के व्युत्क्रम पर चर्चा करना अधिक सामान्य है। विद्युत डोमेन में कठोरता का सादृश्य सामान्यतः कम इस्तेमाल किया जाने वाला लोच है, समाई का व्युत्क्रम। संधारित्र के अनुरूप यांत्रिक घटक वसंत (उपकरण) है। संधारित्र संवैधानिक समीकरण द्वारा शासित होता है,

$$v=D\int idt\,.$$

यांत्रिक डोमेन में समरूप समीकरण हुक के नियम का रूप है,

$$F=S\int udt\,,$$

कहाँ

• $D=1/C$ is elastance;
• $C$ is capacitance; and
• $S$ is stiffness.

एक संधारित्र का प्रतिबाधा विशुद्ध रूप से काल्पनिक है और इसके द्वारा दिया जाता है,

$$Z={\frac {D}{j\omega }}\,.$$

अनुरूप यांत्रिक प्रतिबाधा द्वारा दिया जाता है,

$$Z_{\mathrm {m} }={\frac {S}{j\omega }}\,.$$

वैकल्पिक रूप से, कोई लिख सकता है,

$$Z_{\mathrm {m} }={\frac {1}{j\omega C_{\mathrm {m} }}}\,,$$

कहाँ $C_{m}=1/S$ यांत्रिक अनुपालन है। जब समाई का उपयोग किया जाता है तो यह विद्युत अभिव्यक्ति के अधिक प्रत्यक्ष रूप से अनुरूप होता है।

गुंजयमान यंत्र

एक यांत्रिक गुंजयमान यंत्र में द्रव्यमान तत्व और अनुपालन तत्व दोनों होते हैं। यांत्रिक गुंजयमान यंत्र अधिष्ठापन और समाई से युक्त विद्युत एलसी सर्किट के अनुरूप होते हैं। वास्तविक यांत्रिक घटकों में अनिवार्य रूप से द्रव्यमान और अनुपालन दोनों होते हैं इसलिए अनुनादकों को घटक के रूप में बनाना व्यावहारिक प्रस्ताव है। वास्तव में, शुद्ध द्रव्यमान या शुद्ध अनुपालन को घटक के रूप में बनाना अधिक कठिन है। स्प्रिंग को निश्चित अनुपालन के साथ बनाया जा सकता है और द्रव्यमान को कम से कम किया जा सकता है, या द्रव्यमान को कम से कम अनुपालन के साथ बनाया जा सकता है, अपितु न तो पूरी तरह से समाप्त किया जा सकता है। यांत्रिक गुंजयमान यंत्र यांत्रिक फिल्टर का प्रमुख घटक है।

जेनरेटर

एक निरंतर बल जनरेटर (बाएं) और इसके विद्युत सादृश्य (दाएं) के लिए यांत्रिक प्रतीक

निरंतर वेग जनरेटर (बाएं) और इसके विद्युत सादृश्य (दाएं) के लिए यांत्रिक प्रतीक

वोल्टेज स्रोत और वर्तमान स्रोत (जनरेटर) के सक्रिय विद्युत तत्वों के लिए एनालॉग सम्मिलित हैं। निरंतर वोल्टेज जनरेटर के प्रतिबाधा सादृश्य में यांत्रिक एनालॉग निरंतर बल जनरेटर है। निरंतर चालू जनरेटर का यांत्रिक एनालॉग निरंतर वेग जनरेटर है।

निरंतर बल जनरेटर का उदाहरण निरंतर बल वसंत है। यह वास्तविक वोल्टेज स्रोत के समान है, जैसे कि बैटरी, जो लोड के साथ स्थिर-वोल्टेज के पास रहती है, बशर्ते लोड प्रतिरोध बैटरी के आंतरिक प्रतिरोध से बहुत अधिक हो। व्यावहारिक निरंतर वेग जनरेटर का उदाहरण हल्की लोड वाली शक्तिशाली मशीन है, जैसे विद्युत मोटर , बेल्ट (मैकेनिकल) चला रहा है।

ट्रांसड्यूसर

इलेक्ट्रोमैकेनिक्स को इलेक्ट्रिकल और मैकेनिकल डोमेन के बीच रूपांतरण के लिए ट्रांसड्यूसर की आवश्यकता होती है। वे दो-पोर्ट नेटवर्क के अनुरूप हैं और उन जैसे साथ समीकरणों की जोड़ी और चार मनमाने मापदंडों द्वारा वर्णित किए जा सकते हैं। कई संभावित निरूपण हैं, अपितु प्रतिबाधा सादृश्य के लिए सबसे अधिक लागू रूप में प्रतिबाधा की इकाइयों में स्वैच्छिक पैरामीटर हैं। मैट्रिक्स रूप में (पोर्ट 1 के रूप में लिए गए विद्युत पक्ष के साथ) यह प्रतिनिधित्व है,

$${\begin{bmatrix}v\\F\end{bmatrix}}={\begin{bmatrix}z_{11}&z_{12}\\z_{21}&z_{22}\end{bmatrix}}{\begin{bmatrix}i\\u\end{bmatrix}}\,.$$

तत्व $z_{22}\,$ खुला सर्किट यांत्रिक प्रतिबाधा है, अर्थात, ट्रांसड्यूसर के यांत्रिक पक्ष द्वारा प्रस्तुत प्रतिबाधा जब कोई करंट (ओपन सर्किट) विद्युत पक्ष में प्रवेश नहीं कर रहा होता है। तत्व $z_{11}\,$, इसके विपरीत, क्लैम्प्ड विद्युत प्रतिबाधा है, अर्थात, विद्युत पक्ष को प्रस्तुत प्रतिबाधा जब यांत्रिक पक्ष को क्लैम्प किया जाता है और चलने से रोका जाता है (वेग शून्य है)। शेष दो तत्व, $z_{21}\,$ और $z_{12}\,,$ क्रमशः ट्रांसड्यूसर फॉरवर्ड और रिवर्स ट्रांसफर फ़ंक्शंस का वर्णन करें। वे दोनों प्रतिबाधाओं को स्थानांतरित करने के अनुरूप हैं और विद्युत और यांत्रिक मात्रा के संकर अनुपात हैं।

ट्रांसफॉर्मर

एक ट्रांसफॉर्मर की यांत्रिक समानता साधारण मशीन है जैसे चरखी या लीवर। लोड पर लागू बल इनपुट बल से अधिक या कम हो सकता है, यह इस बात पर निर्भर करता है कि मशीन का यांत्रिक लाभ क्रमशः एकता से अधिक या कम है। यांत्रिक लाभ प्रतिबाधा सादृश्य में ट्रांसफार्मर के घुमावों के अनुपात के अनुरूप है। एकता से अधिक यांत्रिक लाभ स्टेप-अप ट्रांसफार्मर के अनुरूप होता है और एकता से कम स्टेप-डाउन ट्रांसफार्मर के अनुरूप होता है।

शक्ति और ऊर्जा समीकरण

Table of analogous power and energy equations

Electrical quantity	Electrical expression	Mechanical analogy	Mechanical expression
Energy supplied	${\textstyle E=\int vi\ dt}$	Energy supplied	${\textstyle E=\int Fu\ dt}$
Power supplied	$P=vi$	Power supplied	$P=Fu$
Power dissipation in a resistor	$P=i^{2}R={v^{2} \over R}$	Power dissipation in a damper	$P=u^{2}R_{\mathrm {m} }={F^{2} \over R_{\mathrm {m} }}$
Energy stored in an inductor magnetic field	$E={\tfrac {1}{2}}Li^{2}$	Kinetic energy of a moving mass	$E={\tfrac {1}{2}}Mu^{2}$
Energy stored in a capacitor electric field	$E={\tfrac {1}{2}}Cv^{2}$	Potential energy stored in a spring	$E={\tfrac {1}{2}}C_{\mathrm {m} }F^{2}$

उदाहरण

सरल गुंजयमान सर्किट

सरल यांत्रिक गुंजयमान यंत्र (बाएं) और इसकी प्रतिबाधा सादृश्य समकक्ष सर्किट (दाएं)

आंकड़ा द्रव्यमान के मंच की यांत्रिक व्यवस्था को दर्शाता है $M$ जो सब्सट्रेट के ऊपर कठोरता के झरने से निलंबित है $S$ और प्रतिरोध का अवशोषक $R\,.$ प्रतिबाधा सादृश्य समतुल्य परिपथ इस व्यवस्था के दाईं ओर दिखाया गया है और इसमें RLC परिपथ है। इस प्रणाली में गुंजयमान आवृत्ति है, और दोलन की प्राकृतिक आवृत्ति हो सकती है यदि बहुत अधिक अवमंदित न हो।

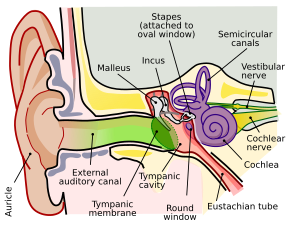
मानव कान का मॉडल

प्रतिबाधा सादृश्य का उपयोग करते हुए मानव कान का समतुल्य परिपथ

कान का एनाटॉमी।

  Brown is outer ear.

  Red is middle ear.

  Purple is inner ear.

सर्किट आरेख मानव कान के प्रतिबाधा सादृश्य मॉडल को दर्शाता है। कान के अंदर की नलिका सेक्शन के बाद कान का परदा का प्रतिनिधित्व करने वाला ट्रांसफॉर्मर होता है। ईयरड्रम कान नहर में हवा में ध्वनिक तरंगों और मध्य कान की हड्डियों में यांत्रिक कंपन के बीच ट्रांसड्यूसर है। कॉक्लिया में यांत्रिक कंपन से कॉक्लिया भरने वाले द्रव में माध्यम का और परिवर्तन होता है। इस प्रकार यह उदाहरण तीन डोमेन (ध्वनिक, यांत्रिक और द्रव प्रवाह) को एकीकृत पूरे में साथ लाने में विद्युत उपमाओं की शक्ति को प्रदर्शित करता है। यदि मस्तिष्क में प्रवाहित होने वाले तंत्रिका आवेगों को भी मॉडल में सम्मिलित किया गया होता तो विद्युत डोमेन ने मॉडल में चार डोमेन सम्मिलित कर लिए होते।

सर्किट का कॉक्लिया भाग कॉक्लियर डक्ट की निरंतर संचरण लाइन के परिमित तत्व विश्लेषण का उपयोग करता है। ऐसी संरचना का आदर्श प्रतिनिधित्व असीम तत्वों का उपयोग करेगा, और इस प्रकार उनमें से अनंत संख्या होगी। इस मॉडल में कोक्लीअ को 350 खंडों में विभाजित किया गया है और प्रत्येक खंड को कम संख्या में गांठ वाले तत्वों का उपयोग करके तैयार किया गया है।

फायदे और नुकसान

इसके विकल्प, गतिशीलता सादृश्य पर प्रतिबाधा सादृश्य का मुख्य लाभ यह है कि यह विद्युत और यांत्रिक प्रतिबाधा के बीच सादृश्य बनाए रखता है। अर्थात्, यांत्रिक प्रतिबाधा को विद्युत प्रतिबाधा के रूप में दर्शाया जाता है और यांत्रिक प्रतिरोध को विद्युत समतुल्य परिपथ में विद्युत प्रतिरोध के रूप में दर्शाया जाता है। बल को वोल्टेज के अनुरूप (जेनरेटर (सर्किट सिद्धांत) वोल्टेज को अधिकांशतः वैद्युतवाहक बल कहा जाता है) और वेग को करंट के अनुरूप माना जाना स्वाभाविक है। यह बुनियादी समानता है जो विद्युत और यांत्रिक प्रतिबाधा के बीच समानता की ओर ले जाती है।

प्रतिबाधा सादृश्य का मुख्य नुकसान यह है कि यह यांत्रिक प्रणाली की टोपोलॉजी को संरक्षित नहीं करता है। यांत्रिक प्रणाली में श्रृंखला में सम्मिलित तत्व विद्युत समतुल्य सर्किट में समानांतर में होते हैं और इसके विपरीत। एक ट्रांसड्यूसर का प्रतिबाधा मैट्रिक्स प्रतिनिधित्व यांत्रिक डोमेन में बल को विद्युत डोमेन में वर्तमान में बदल देता है। इसी तरह, यांत्रिक डोमेन में वेग विद्युत डोमेन में वोल्टेज में परिवर्तित हो जाता है। दो-पोर्ट डिवाइस जो वोल्टेज को समान मात्रा में परिवर्तित करता है, उसे साधारण ट्रांसफॉर्मर के रूप में दर्शाया जा सकता है। उपकरण जो वोल्टेज को वोल्टेज की दोहरी संपत्ति के एनालॉग में बदल देता है (अर्थात, करंट, जिसका एनालॉग वेग है) को जाइरेटर के रूप में दर्शाया गया है। चूँकि बल वोल्टेज के अनुरूप है, करंट नहीं, यह इसके चेहरे पर नुकसान की तरह लग सकता है। हालांकि, कई व्यावहारिक ट्रांसड्यूसर, विशेष रूप से ऑडियो आवृत्ति पर, इलेक्ट्रोमैग्नेटिक इंडक्शन द्वारा काम करते हैं और ऐसे ही रिश्ते द्वारा नियंत्रित होते हैं। उदाहरण के लिए, लोरेंत्ज़ बल # धारावाही तार पर बल | धारावाही चालक पर बल द्वारा दिया जाता है,

$$F=BIl\,,$$

कहाँ

• $B$ is magnetic flux density; and
• $l$ is length of the conductor.

इतिहास

प्रतिबाधा सादृश्य को कभी-कभी मैक्सवेल सादृश्य कहा जाता हैजेम्स क्लर्क मैक्सवेल (1831-1879) के बाद जिन्होंने विद्युत चुम्बकीय क्षेत्रों के बारे में अपने विचारों को समझाने के लिए यांत्रिक सादृश्यता का उपयोग किया। हालांकि, प्रतिबाधा शब्द 1886 तक (ओलिवर हीविसाइड द्वारा) गढ़ा नहीं गया था, जटिल प्रतिबाधा का विचार 1893 में आर्थर ई. केनेली द्वारा पेश किया गया था, और केनेली और आर्थर गॉर्डन वेबस्टर द्वारा 1920 तक प्रतिबाधा की अवधारणा को यांत्रिक डोमेन में विस्तारित नहीं किया गया था। 1907 में हेनरी पॉइनकेयर पहले व्यक्ति थे जिन्होंने ट्रांसड्यूसर को यांत्रिक चर (बल और वेग) से विद्युत चर (वोल्टेज और करंट) से संबंधित रैखिक बीजगणितीय समीकरणों की जोड़ी के रूप में वर्णित किया। वेगेल, 1921 में, यांत्रिक प्रतिबाधा के साथ-साथ विद्युत प्रतिबाधा के रूप में इन समीकरणों को व्यक्त करने वाले पहले व्यक्ति थे।

ग्रन्थसूची

• Beranek, Leo Leroy; Mellow, Tim J., Acoustics: Sound Fields and Transducers, Academic Press, 2012 ISBN 0123914213.
• Busch-Vishniac, Ilene J., Electromechanical Sensors and Actuators, Springer Science & Business Media, 1999 ISBN 038798495X.
• Carr, Joseph J., RF Components and Circuits, Newnes, 2002 ISBN 0-7506-4844-9.
• Darlington, S. "A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors", IEEE Transactions on Circuits and Systems, vol. 31, no. 1, pp. 3–13, 1984.
• Eargle, John, Loudspeaker Handbook, Kluwer Academic Publishers, 2003 ISBN 1402075847.
• Fukazawa, Tatsuya; Tanaka, Yasuo, "Evoked otoacoustic emissions in a cochlear model", pp. 191–196 in Hohmann, D. (ed), ECoG, OAE and Intraoperative Monitoring: Proceedings of the First International Conference, Würzburg, Germany, September 20–24, 1992, Kugler Publications, 1993 ISBN 9062990975.
• Harrison, Henry C. "Acoustic device", U.S. Patent 1,730,425, filed 11 October 1927 (and in Germany 21 October 1923), issued 8 October 1929.
• Hunt, Frederick V., Electroacoustics: the Analysis of Transduction, and its Historical Background, Harvard University Press, 1954 OCLC 2042530.
• Jackson, Roger G., Novel Sensors and Sensing, CRC Press, 2004 ISBN 1420033808.
• Kleiner, Mendel, Electroacoustics, CRC Press, 2013 ISBN 1439836183.
• Martinsen, Orjan G.; Grimnes, Sverre, Bioimpedance and Bioelectricity Basics, Academic Press, 2011 ISBN 0080568807.
• Paik, H. J., "Superconduction accelerometers, gravitational-wave transducers, and gravity gradiometers", pp. 569–598, in Weinstock, Harold, SQUID Sensors: Fundamentals, Fabrication, and Applications, Springer Science & Business Media, 1996 ISBN 0792343506.
• Pierce, Allan D., Acoustics: an Introduction to its Physical Principles and Applications, Acoustical Society of America 1989 ISBN 0883186128.
• Pipes, Louis A.; Harvill, Lawrence R., Applied Mathematics for Engineers and Physicists, Courier Dover Publications, 2014 ISBN 0486779513.
• Poincaré, H., "Study of telephonic reception", Eclairage Electrique, vol. 50, pp. 221–372, 1907.
• Stephens, Raymond William Barrow; Bate, A. E., Acoustics and vibrational physics, Edward Arnold, 1966 OCLC 912579.
• Talbot-Smith, Michael, Audio Engineer's Reference Book, Taylor & Francis, 2013 ISBN 1136119736.
• Taylor, John; Huang, Qiuting, CRC Handbook of Electrical Filters, CRC Press, 1997 ISBN 0849389518.
• Wegel, R. L., "Theory of magneto-mechanical systems as applied to telephone receivers and similar structures", Journal of the American Institute of Electrical Engineers, vol. 40, pp. 791–802, 1921.