ब्राउनियन ब्रिज: Difference between revisions
m (Deepak moved page ब्राउनियन पुल to ब्राउनियन ब्रिज without leaving a redirect) |
No edit summary |
||
| Line 1: | Line 1: | ||
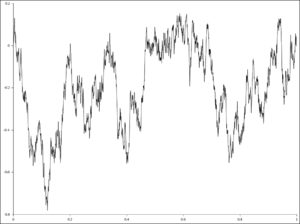
[[Image:Brownian bridge.png|thumb|ब्राउनियन गति, दोनों सिरों पर पिन की गई। यह एक ब्राउनियन ब्रिज का प्रतिनिधित्व करता है।]] | [[Image:Brownian bridge.png|thumb|ब्राउनियन गति, दोनों सिरों पर पिन की गई। यह एक ब्राउनियन ब्रिज का प्रतिनिधित्व करता है।]]'''ब्राउनियन ब्रिज''' एक सतत समय प्रसंभाव्यता प्रक्रिया ''B''(''t'') है जिसका [[प्रायिकता वितरण]] मानक [[वीनर प्रक्रिया]] ''W''(''t'') ([[एक प्रकार कि गति|ब्राउनियन गति]] के गणितीय मॉडल) का सशर्त प्रायिकता वितरण है जो इस शर्त के अधीन है (जब मानकीकृत) कि ''W''(''T'') = 0, ताकि प्रक्रिया को ''t'' = 0 और ''t'' = ''T'' दोनों पर समान मान पर पिन किया जा सके। अधिक सटीक रूप से- | ||
:<math> B_t := (W_t\mid W_T=0),\;t \in [0,T] </math> | :<math> B_t := (W_t\mid W_T=0),\;t \in [0,T] </math> | ||
अंतराल [0,T] में किसी भी t पर | अंतराल [0,''T''] में किसी भी ''t'' पर ब्रिज का अपेक्षित मान विचरण <math>\textstyle\frac{t(T-t)}{T}</math> के साथ शून्य है, जिसका अर्थ है कि सबसे अधिक अनिश्चितता ब्रिज के बीच में है, नोड्स पर शून्य अनिश्चितता है। ''B''(''s'') और ''B''(''t'') का [[सहप्रसरण]] <math>\min(s,t)-\frac{s\,t}{T}</math>, या ''s''(T − ''t'')/T है यदि ''s'' < ''t। ब्राउनियन ब्रिज में वृद्धि स्वतंत्र नहीं है।'' | ||
ब्राउनियन ब्रिज में | |||
== अन्य | == अन्य प्रसंभाव्यता प्रक्रियाओं से संबंध == | ||
यदि W(t) | यदि ''W''(''t'') मानक वीनर प्रक्रिया है (अर्थात्, ''t'' ≥ 0 के लिए, ''W''(''t'') को सामान्यतः अपेक्षित मान 0 और विचरण ''t'' के साथ वितरित किया जाता है, और वृद्धि स्थिर और स्वतंत्र होती है), तो | ||
: <math> B(t) = W(t) - \frac{t}{T} W(T)\,</math> | : <math> B(t) = W(t) - \frac{t}{T} W(T)\,</math> | ||
''t'' ∈ [0, ''T''] के लिए ब्राउनियन ब्रिज है। यह ''W''(''T'') से स्वतंत्र है<ref>Aspects of Brownian motion, Springer, 2008, R. Mansuy, M. Yor page 2</ref> | |||
इसके विपरीत, यदि B(t) | |||
इसके विपरीत, यदि ''B''(''t'') ब्राउनियन ब्रिज है और ''Z'' एक मानक सामान्य यादृच्छिक चर है जो B से स्वतंत्र है, तो प्रक्रिया | |||
: <math>W(t) = B(t) + tZ\,</math> | : <math>W(t) = B(t) + tZ\,</math> | ||
''t'' ∈ [0, 1] के लिए वीनर प्रक्रिया है। अधिक सामान्यतः, ''t'' ∈ [0, ''T''] के लिए वीनर प्रक्रिया ''W''(''t'') को विघटित किया जा सकता है | |||
: <math>W(t) = \sqrt{T}B\left(\frac{t}{T}\right) + \frac{t}{\sqrt{T}} Z.</math> | : <math>W(t) = \sqrt{T}B\left(\frac{t}{T}\right) + \frac{t}{\sqrt{T}} Z.</math> | ||
ब्राउनियन गति पर | ब्राउनियन गति के आधार पर ब्राउनियन ब्रिज का एक और प्रतिनिधित्व, ''t'' ∈ [0, ''T''] के लिए है | ||
: <math> B(t) = \frac{T-t}{\sqrt T} W\left(\frac{t}{T-t}\right).</math> | : <math> B(t) = \frac{T-t}{\sqrt T} W\left(\frac{t}{T-t}\right).</math> | ||
इसके विपरीत, | इसके विपरीत, ''t'' ∈ [0, ∞] के लिए | ||
: <math> W(t) = \frac{T+t}{T} B\left(\frac{Tt}{T+t}\right).</math> | : <math> W(t) = \frac{T+t}{T} B\left(\frac{Tt}{T+t}\right).</math> | ||
ब्राउनियन ब्रिज को | ब्राउनियन ब्रिज को प्रसंभाव्यता गुणांक के साथ फूरियर श्रृंखला के रूप में भी दर्शाया जा सकता है | ||
: <math> B_t = \sum_{k=1}^\infty Z_k \frac{\sqrt{2 T} \sin(k \pi t / T)}{k \pi}</math> | : <math> B_t = \sum_{k=1}^\infty Z_k \frac{\sqrt{2 T} \sin(k \pi t / T)}{k \pi}</math> | ||
जहाँ <math> Z_1, Z_2, \ldots </math>स्वतंत्र रूप से समान रूप से वितरित मानक सामान्य यादृच्छिक चर हैं (करहुनेन-लोव प्रमेय देखें)। | |||
ब्राउनियन ब्रिज [[अनुभवजन्य प्रक्रिया|अनुभवजन्य प्रक्रियाओं]] के क्षेत्र में डोंस्कर के प्रमेय का परिणाम है। इसका उपयोग सांख्यिकीय अनुमान के क्षेत्र में कोल्मोगोरोव-स्मिरनोव परीक्षण में भी किया जाता है। | |||
== सहज | == सहज टिप्पणियाँ == | ||
एक मानक वीनर प्रक्रिया W(0) = 0 को संतुष्ट करती है और इसलिए मूल से बंधी हुई है, लेकिन अन्य बिंदु प्रतिबंधित नहीं हैं। दूसरी ओर ब्राउनियन ब्रिज प्रक्रिया में, न केवल बी (0) = 0 है बल्कि हमें यह भी आवश्यक है कि बी (टी) = 0, यानी प्रक्रिया टी = टी पर भी बंधी हुई है। जैसे शाब्दिक पुल दोनों सिरों पर तोरणों द्वारा समर्थित होता है, वैसे ही अंतराल [0,T] के दोनों सिरों पर शर्तों को पूरा करने के लिए एक ब्राउनियन ब्रिज की आवश्यकता होती है। (थोड़े सामान्यीकरण में, किसी को कभी-कभी बी (टी) की आवश्यकता होती है<sub>1</sub>) = ए और बी (टी<sub>2</sub>) = बी जहां टी<sub>1</sub>, टी<sub>2</sub>, ए और बी ज्ञात स्थिरांक हैं।) | एक मानक वीनर प्रक्रिया W(0) = 0 को संतुष्ट करती है और इसलिए मूल से बंधी हुई है, लेकिन अन्य बिंदु प्रतिबंधित नहीं हैं। दूसरी ओर ब्राउनियन ब्रिज प्रक्रिया में, न केवल बी (0) = 0 है बल्कि हमें यह भी आवश्यक है कि बी (टी) = 0, यानी प्रक्रिया टी = टी पर भी बंधी हुई है। जैसे शाब्दिक पुल दोनों सिरों पर तोरणों द्वारा समर्थित होता है, वैसे ही अंतराल [0,T] के दोनों सिरों पर शर्तों को पूरा करने के लिए एक ब्राउनियन ब्रिज की आवश्यकता होती है। (थोड़े सामान्यीकरण में, किसी को कभी-कभी बी (टी) की आवश्यकता होती है<sub>1</sub>) = ए और बी (टी<sub>2</sub>) = बी जहां टी<sub>1</sub>, टी<sub>2</sub>, ए और बी ज्ञात स्थिरांक हैं।) | ||
मान लीजिए कि हमने कंप्यूटर सिमुलेशन द्वारा वीनर प्रोसेस पाथ के कई बिंदु W(0), W(1), W(2), W(3), आदि उत्पन्न किए हैं। अब यह अंतराल [0,T] में अतिरिक्त बिंदुओं को भरने के लिए वांछित है, जो कि पहले से उत्पन्न बिंदुओं W(0) और W(T) के बीच प्रक्षेपित करना है। इसका समाधान एक ब्राउनियन ब्रिज का उपयोग करना है जो मूल्यों W(0) और W(T) से गुजरने के लिए आवश्यक है। | मान लीजिए कि हमने कंप्यूटर सिमुलेशन द्वारा वीनर प्रोसेस पाथ के कई बिंदु W(0), W(1), W(2), W(3), आदि उत्पन्न किए हैं। अब यह अंतराल [0,T] में अतिरिक्त बिंदुओं को भरने के लिए वांछित है, जो कि पहले से उत्पन्न बिंदुओं W(0) और W(T) के बीच प्रक्षेपित करना है। इसका समाधान एक ब्राउनियन ब्रिज का उपयोग करना है जो मूल्यों W(0) और W(T) से गुजरने के लिए आवश्यक है। | ||
== सामान्य | == सामान्य स्थिति == | ||
सामान्य स्थिति के लिए जब B(t<sub>1</sub>) = | सामान्य स्थिति के लिए जब ''B''(''t''<sub>1</sub>) = ''a'' और ''B''(''t''<sub>2</sub>) = ''b'', समय ''t'' ∈ (''t''<sub>1</sub>, ''t''<sub>2</sub>) पर ''B'' का [[अपेक्षित मूल्य|वितरण माध्य]] के साथ सामान्य होता है | ||
:<math>a + \frac{t-t_1}{t_2-t_1}(b-a)</math> | :<math>a + \frac{t-t_1}{t_2-t_1}(b-a)</math> | ||
| Line 40: | Line 40: | ||
:<math>\frac{(t_2-t)(t-t_1)}{t_2-t_1},</math> | :<math>\frac{(t_2-t)(t-t_1)}{t_2-t_1},</math> | ||
और | और ''B''(''s'') और ''B''(''t'') के बीच सहप्रसरण, ''s'' < ''t'' के साथ है | ||
:<math>\frac{(t_2-t)(s-t_1)}{t_2-t_1}.</math> | :<math>\frac{(t_2-t)(s-t_1)}{t_2-t_1}.</math> | ||
== संदर्भ == | == संदर्भ == | ||
{{Reflist}} | {{Reflist}} | ||
| Line 51: | Line 49: | ||
{{Stochastic processes}} | {{Stochastic processes}} | ||
[[Category: वीनर प्रक्रिया]] [[Category: अनुभवजन्य प्रक्रिया]] | [[Category: वीनर प्रक्रिया]] [[Category: अनुभवजन्य प्रक्रिया]] | ||
Revision as of 00:04, 24 June 2023
ब्राउनियन ब्रिज एक सतत समय प्रसंभाव्यता प्रक्रिया B(t) है जिसका प्रायिकता वितरण मानक वीनर प्रक्रिया W(t) (ब्राउनियन गति के गणितीय मॉडल) का सशर्त प्रायिकता वितरण है जो इस शर्त के अधीन है (जब मानकीकृत) कि W(T) = 0, ताकि प्रक्रिया को t = 0 और t = T दोनों पर समान मान पर पिन किया जा सके। अधिक सटीक रूप से-
अंतराल [0,T] में किसी भी t पर ब्रिज का अपेक्षित मान विचरण के साथ शून्य है, जिसका अर्थ है कि सबसे अधिक अनिश्चितता ब्रिज के बीच में है, नोड्स पर शून्य अनिश्चितता है। B(s) और B(t) का सहप्रसरण , या s(T − t)/T है यदि s < t। ब्राउनियन ब्रिज में वृद्धि स्वतंत्र नहीं है।
अन्य प्रसंभाव्यता प्रक्रियाओं से संबंध
यदि W(t) मानक वीनर प्रक्रिया है (अर्थात्, t ≥ 0 के लिए, W(t) को सामान्यतः अपेक्षित मान 0 और विचरण t के साथ वितरित किया जाता है, और वृद्धि स्थिर और स्वतंत्र होती है), तो
t ∈ [0, T] के लिए ब्राउनियन ब्रिज है। यह W(T) से स्वतंत्र है[1]
इसके विपरीत, यदि B(t) ब्राउनियन ब्रिज है और Z एक मानक सामान्य यादृच्छिक चर है जो B से स्वतंत्र है, तो प्रक्रिया
t ∈ [0, 1] के लिए वीनर प्रक्रिया है। अधिक सामान्यतः, t ∈ [0, T] के लिए वीनर प्रक्रिया W(t) को विघटित किया जा सकता है
ब्राउनियन गति के आधार पर ब्राउनियन ब्रिज का एक और प्रतिनिधित्व, t ∈ [0, T] के लिए है
इसके विपरीत, t ∈ [0, ∞] के लिए
ब्राउनियन ब्रिज को प्रसंभाव्यता गुणांक के साथ फूरियर श्रृंखला के रूप में भी दर्शाया जा सकता है
जहाँ स्वतंत्र रूप से समान रूप से वितरित मानक सामान्य यादृच्छिक चर हैं (करहुनेन-लोव प्रमेय देखें)।
ब्राउनियन ब्रिज अनुभवजन्य प्रक्रियाओं के क्षेत्र में डोंस्कर के प्रमेय का परिणाम है। इसका उपयोग सांख्यिकीय अनुमान के क्षेत्र में कोल्मोगोरोव-स्मिरनोव परीक्षण में भी किया जाता है।
सहज टिप्पणियाँ
एक मानक वीनर प्रक्रिया W(0) = 0 को संतुष्ट करती है और इसलिए मूल से बंधी हुई है, लेकिन अन्य बिंदु प्रतिबंधित नहीं हैं। दूसरी ओर ब्राउनियन ब्रिज प्रक्रिया में, न केवल बी (0) = 0 है बल्कि हमें यह भी आवश्यक है कि बी (टी) = 0, यानी प्रक्रिया टी = टी पर भी बंधी हुई है। जैसे शाब्दिक पुल दोनों सिरों पर तोरणों द्वारा समर्थित होता है, वैसे ही अंतराल [0,T] के दोनों सिरों पर शर्तों को पूरा करने के लिए एक ब्राउनियन ब्रिज की आवश्यकता होती है। (थोड़े सामान्यीकरण में, किसी को कभी-कभी बी (टी) की आवश्यकता होती है1) = ए और बी (टी2) = बी जहां टी1, टी2, ए और बी ज्ञात स्थिरांक हैं।)
मान लीजिए कि हमने कंप्यूटर सिमुलेशन द्वारा वीनर प्रोसेस पाथ के कई बिंदु W(0), W(1), W(2), W(3), आदि उत्पन्न किए हैं। अब यह अंतराल [0,T] में अतिरिक्त बिंदुओं को भरने के लिए वांछित है, जो कि पहले से उत्पन्न बिंदुओं W(0) और W(T) के बीच प्रक्षेपित करना है। इसका समाधान एक ब्राउनियन ब्रिज का उपयोग करना है जो मूल्यों W(0) और W(T) से गुजरने के लिए आवश्यक है।
सामान्य स्थिति
सामान्य स्थिति के लिए जब B(t1) = a और B(t2) = b, समय t ∈ (t1, t2) पर B का वितरण माध्य के साथ सामान्य होता है
और विचरण
और B(s) और B(t) के बीच सहप्रसरण, s < t के साथ है
संदर्भ
- ↑ Aspects of Brownian motion, Springer, 2008, R. Mansuy, M. Yor page 2
- Glasserman, Paul (2004). Monte Carlo Methods in Financial Engineering. New York: Springer-Verlag. ISBN 0-387-00451-3.
- Revuz, Daniel; Yor, Marc (1999). Continuous Martingales and Brownian Motion (2nd ed.). New York: Springer-Verlag. ISBN 3-540-57622-3.