समुच्चय (गणित): Difference between revisions
(Created page with "{{about|what mathematicians call "intuitive" or "naive" set theory|a more detailed account|Naive set theory|a rigorous modern axiomatic treatment of sets|Set theory}} {{Short...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Collection of mathematical objects}} | {{Short description|Collection of mathematical objects}} | ||
| Line 8: | Line 7: | ||
== इतिहास == | == इतिहास == | ||
एक सेट की अवधारणा 19 वीं शताब्दी के अंत में गणित में उभरी। <Ref Name = Ferreirós2007>{{cite book|author=José Ferreirós|title=Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics|url=https://books.google.com/books?id=TXRBwwEACAAJ|date=16 August 2007|publisher=Birkhäuser Basel|isbn=978-3-7643-8349-7}}</ref> सेट के लिए जर्मन शब्द, मेन्ज, को अनंत के अपने काम के विरोधाभासों में बर्नार्ड बोलजानो द्वारा गढ़ा गया था। REF नाम = RUSS2004>{{cite book|author=Steve Russ|title=The Mathematical Works of Bernard Bolzano|url=https://books.google.com/books?id=zp7cLQn0x3gC&pg=PR28|date=9 December 2004|publisher=OUP Oxford|isbn=978-0-19-151370-1}}</ref><ref name="EwaldEwald1996">{{cite book|author1=William Ewald|author2=William Bragg Ewald|title=From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics|url=https://books.google.com/books?id=rykSDAAAQBAJ&pg=PA249|year=1996|publisher=OUP Oxford|isbn=978-0-19-850535-8|page=249}}</ref><रेफ नाम = rusnocksebestík2019>{{cite book|author1=Paul Rusnock|author2=Jan Sebestík|title=Bernard Bolzano: His Life and Work|url=https://books.google.com/books?id=-hqJDwAAQBAJ&pg=PA430|date=25 April 2019|publisher=OUP Oxford|isbn=978-0-19-255683-7|page=430}}</ref>[[File:Passage with the set definition of Georg Cantor.png|thumb|जॉर्ज कैंटर की मूल सेट परिभाषा के अनुवाद के साथ मार्ग।सेट के लिए जर्मन वर्ड मेन्ज का अनुवाद यहां किया गया है।सेट थ्योरी के संस्थापकों में से एक, जॉर्ज कैंटर ने अपने बीटेज ज़ुर बेगुंडुंग डेर ट्रांसफिनिटेन मेंगेनलेहे की शुरुआत में निम्नलिखित परिभाषा दी:<ref name= Cantor >{{cite journal |quote=By an aggregate (Menge) we are to understand any collection into a whole (Zusammenfassung zu einem Gansen) M of definite and 'separate' objects m (p.85)|last1=Cantor |first1=Georg |last2=Jourdain |first2=((Philip E.B. (Translator))) |title=beiträge zur begründung der transfiniten Mengenlehre |journal=Mathematische Annalen |date=1895 |volume=xlvi;xlix |pages=481–512;207–246 |trans-title=contributions to the founding of the theory of transfinite numbers |publisher=New York Dover Publications (1954 English translation) |language=German |url=http://brinkmann-du.de/mathe/fos/fos01_03.htm|archive-url=https://web.archive.org/web/20110610133240/http://brinkmann-du.de/mathe/fos/fos01_03.htm |archive-date=2011-06-10 }}</ref> | एक सेट की अवधारणा 19 वीं शताब्दी के अंत में गणित में उभरी। <Ref Name = Ferreirós2007>{{cite book|author=José Ferreirós|title=Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics|url=https://books.google.com/books?id=TXRBwwEACAAJ|date=16 August 2007|publisher=Birkhäuser Basel|isbn=978-3-7643-8349-7}}</ref> सेट के लिए जर्मन शब्द, मेन्ज, को अनंत के अपने काम के विरोधाभासों में बर्नार्ड बोलजानो द्वारा गढ़ा गया था। REF नाम = RUSS2004>{{cite book|author=Steve Russ|title=The Mathematical Works of Bernard Bolzano|url=https://books.google.com/books?id=zp7cLQn0x3gC&pg=PR28|date=9 December 2004|publisher=OUP Oxford|isbn=978-0-19-151370-1}}</ref><ref name="EwaldEwald1996">{{cite book|author1=William Ewald|author2=William Bragg Ewald|title=From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics|url=https://books.google.com/books?id=rykSDAAAQBAJ&pg=PA249|year=1996|publisher=OUP Oxford|isbn=978-0-19-850535-8|page=249}}</ref><रेफ नाम = rusnocksebestík2019>{{cite book|author1=Paul Rusnock|author2=Jan Sebestík|title=Bernard Bolzano: His Life and Work|url=https://books.google.com/books?id=-hqJDwAAQBAJ&pg=PA430|date=25 April 2019|publisher=OUP Oxford|isbn=978-0-19-255683-7|page=430}}</ref>[[File:Passage with the set definition of Georg Cantor.png|thumb|जॉर्ज कैंटर की मूल सेट परिभाषा के अनुवाद के साथ मार्ग।सेट के लिए जर्मन वर्ड मेन्ज का अनुवाद यहां किया गया है।सेट थ्योरी के संस्थापकों में से एक, जॉर्ज कैंटर ने अपने बीटेज ज़ुर बेगुंडुंग डेर ट्रांसफिनिटेन मेंगेनलेहे की शुरुआत में निम्नलिखित परिभाषा दी:<ref name= Cantor >{{cite journal |quote=By an aggregate (Menge) we are to understand any collection into a whole (Zusammenfassung zu einem Gansen) M of definite and 'separate' objects m (p.85)|last1=Cantor |first1=Georg |last2=Jourdain |first2=((Philip E.B. (Translator))) |title=beiträge zur begründung der transfiniten Mengenlehre |journal=Mathematische Annalen |date=1895 |volume=xlvi;xlix |pages=481–512;207–246 |trans-title=contributions to the founding of the theory of transfinite numbers |publisher=New York Dover Publications (1954 English translation) |language=German |url=http://brinkmann-du.de/mathe/fos/fos01_03.htm|archive-url=https://web.archive.org/web/20110610133240/http://brinkmann-du.de/mathe/fos/fos01_03.htm |archive-date=2011-06-10 }}</ref> | ||
{{quote|A set is a gathering together into a whole of definite, distinct objects of our perception or our thought—which are called elements of the set.}} | {{quote|A set is a gathering together into a whole of definite, distinct objects of our perception or our thought—which are called elements of the set.}} | ||
| Line 17: | Line 15: | ||
=== भोला सेट सिद्धांत === | === भोला सेट सिद्धांत === | ||
एक सेट की सबसे महत्वपूर्ण संपत्ति यह है कि इसमें तत्व हो सकते हैं, जिसे सदस्य भी कहा जाता है।दो सेट समान होते हैं जब उनके समान तत्व होते हैं।अधिक सटीक रूप से, सेट ए और बी समान हैं यदि ए का प्रत्येक तत्व बी का एक तत्व है, और बी का प्रत्येक तत्व ए का एक तत्व है;इस संपत्ति को सेट की एक्सटेंशनलिटी कहा जाता है।{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/2/mode/2up 2]}} एक सेट की सरल अवधारणा गणित में बहुत उपयोगी साबित हुई है, लेकिन: श्रेणी: भोले सेट सिद्धांत के विरोधाभास। विरोधाभास उठते हैं यदि कोई प्रतिबंध नहीं रखा जाता है तो सेट कैसे बनाया जा सकता है: | एक सेट की सबसे महत्वपूर्ण संपत्ति यह है कि इसमें तत्व हो सकते हैं, जिसे सदस्य भी कहा जाता है।दो सेट समान होते हैं जब उनके समान तत्व होते हैं।अधिक सटीक रूप से, सेट ए और बी समान हैं यदि ए का प्रत्येक तत्व बी का एक तत्व है, और बी का प्रत्येक तत्व ए का एक तत्व है;इस संपत्ति को सेट की एक्सटेंशनलिटी कहा जाता है।{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/2/mode/2up 2]}} एक सेट की सरल अवधारणा गणित में बहुत उपयोगी साबित हुई है, लेकिन: श्रेणी: भोले सेट सिद्धांत के विरोधाभास। विरोधाभास उठते हैं यदि कोई प्रतिबंध नहीं रखा जाता है तो सेट कैसे बनाया जा सकता है: | ||
* रसेल के विरोधाभास से पता चलता है कि सभी सेटों का सेट जो स्वयं नहीं है, अर्थात्, यानी, {{mset|''x'' | ''x'' is a set and ''x'' ∉ ''x''}}, मौजूद नहीं हो सकता। | * रसेल के विरोधाभास से पता चलता है कि सभी सेटों का सेट जो स्वयं नहीं है, अर्थात्, यानी, {{mset|''x'' | ''x'' is a set and ''x'' ∉ ''x''}}, मौजूद नहीं हो सकता। | ||
| Line 54: | Line 51: | ||
=== सेट-बिल्डर नोटेशन === | === सेट-बिल्डर नोटेशन === | ||
सेट-बिल्डर नोटेशन तत्वों पर एक स्थिति द्वारा निर्धारित एक बड़े सेट से चयन के रूप में एक सेट को निर्दिष्ट करता है।<ref name="Ruda2011"/><ref name="Lucas1990">{{cite book|author=John F. Lucas|title=Introduction to Abstract Mathematics|url=https://books.google.com/books?id=jklsb5JUgoQC&pg=PA108|year=1990|publisher=Rowman & Littlefield|isbn=978-0-912675-73-2|page=108}}</ref><ref>{{Cite web|last=Weisstein|first=Eric W.|title=Set|url=https://mathworld.wolfram.com/Set.html|access-date=2020-08-19|website=mathworld.wolfram.com|language=en}}</ref> उदाहरण के लिए, एक सेट {{mvar|F}} निम्नानुसार परिभाषित किया जा सकता है: | सेट-बिल्डर नोटेशन तत्वों पर एक स्थिति द्वारा निर्धारित एक बड़े सेट से चयन के रूप में एक सेट को निर्दिष्ट करता है।<ref name="Ruda2011"/><ref name="Lucas1990">{{cite book|author=John F. Lucas|title=Introduction to Abstract Mathematics|url=https://books.google.com/books?id=jklsb5JUgoQC&pg=PA108|year=1990|publisher=Rowman & Littlefield|isbn=978-0-912675-73-2|page=108}}</ref><ref>{{Cite web|last=Weisstein|first=Eric W.|title=Set|url=https://mathworld.wolfram.com/Set.html|access-date=2020-08-19|website=mathworld.wolfram.com|language=en}}</ref> उदाहरण के लिए, एक सेट {{mvar|F}} निम्नानुसार परिभाषित किया जा सकता है: | ||
| Line 68: | Line 64: | ||
== सदस्यता == | == सदस्यता == | ||
यदि {{mvar|B}} एक सेट है और {{mvar|x}} का एक तत्व है {{mvar|B}}, यह शॉर्टहैंड में लिखा गया है {{math|''x'' ∈ ''B''}}, जिसे X के रूप में भी पढ़ा जा सकता है, B से संबंधित है, या X B में है।{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/2/mode/2up 2]}} कथन y b का एक तत्व नहीं है, के रूप में लिखा गया है {{math|''y'' ∉ ''B''}}, जिसे y के रूप में भी पढ़ा जा सकता है, b में नहीं है।<ref name="CapinskiKopp2004">{{cite book|author1=Marek Capinski|author2=Peter E. Kopp|title=Measure, Integral and Probability|url=https://books.google.com/books?id=jdnGYuh58YUC&pg=PA2|year=2004|publisher=Springer Science & Business Media|isbn=978-1-85233-781-0|page=2}}</ref><ref>{{Cite web|title=Set Symbols|url=https://www.mathsisfun.com/sets/symbols.html|access-date=2020-08-19|website=www.mathsisfun.com}}</ref> | यदि {{mvar|B}} एक सेट है और {{mvar|x}} का एक तत्व है {{mvar|B}}, यह शॉर्टहैंड में लिखा गया है {{math|''x'' ∈ ''B''}}, जिसे X के रूप में भी पढ़ा जा सकता है, B से संबंधित है, या X B में है।{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/2/mode/2up 2]}} कथन y b का एक तत्व नहीं है, के रूप में लिखा गया है {{math|''y'' ∉ ''B''}}, जिसे y के रूप में भी पढ़ा जा सकता है, b में नहीं है।<ref name="CapinskiKopp2004">{{cite book|author1=Marek Capinski|author2=Peter E. Kopp|title=Measure, Integral and Probability|url=https://books.google.com/books?id=jdnGYuh58YUC&pg=PA2|year=2004|publisher=Springer Science & Business Media|isbn=978-1-85233-781-0|page=2}}</ref><ref>{{Cite web|title=Set Symbols|url=https://www.mathsisfun.com/sets/symbols.html|access-date=2020-08-19|website=www.mathsisfun.com}}</ref> | ||
उदाहरण के लिए, सेट के संबंध में {{math|1=''A'' = {{mset|1, 2, 3, 4}}}}, {{math|1=''B'' = {{mset|blue, white, red}}}}, तथा {{math|1=''F'' = {{mset|''n'' | ''n'' is an integer, and 0 ≤ ''n'' ≤ 19}}}}, | उदाहरण के लिए, सेट के संबंध में {{math|1=''A'' = {{mset|1, 2, 3, 4}}}}, {{math|1=''B'' = {{mset|blue, white, red}}}}, तथा {{math|1=''F'' = {{mset|''n'' | ''n'' is an integer, and 0 ≤ ''n'' ≤ 19}}}}, | ||
| Line 76: | Line 71: | ||
== खाली सेट == | == खाली सेट == | ||
खाली सेट (या अशक्त सेट) अद्वितीय सेट है जिसमें कोई सदस्य नहीं है।इसे निरूपित किया गया है {{math|∅}} या <math>\emptyset</math> या {{mset| }}{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/8/mode/2up 8]}}<ref name="LeungChen1992">{{cite book|author1=K.T. Leung|author2=Doris Lai-chue Chen|title=Elementary Set Theory, Part I/II|url=https://books.google.com/books?id=cdmy2eOhJdkC&pg=PA27|date=1 July 1992|publisher=Hong Kong University Press|isbn=978-962-209-026-2|page=27}}</ref> या {{math|ϕ}}<ref>{{cite book|title=Understanding ISC Mathematics Class XI|volume=1|first=M.L.|last=Aggarwal|publisher=Arya Publications (Avichal Publishing Company)|year=2021|chapter=1. Sets|page=A=3}}</ref> (या {{mvar|ϕ}})।<ref>{{cite book|title=Chhaya Ganit (Ekadash Shreni)|first=De|last=Sourendra Nath|publisher=Scholar Books Pvt. Ltd.|date=January 2015|chapter=Unit-1 Sets and Functions: 1. Set Theory|page=5}}</ref> | खाली सेट (या अशक्त सेट) अद्वितीय सेट है जिसमें कोई सदस्य नहीं है।इसे निरूपित किया गया है {{math|∅}} या <math>\emptyset</math> या {{mset| }}{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/8/mode/2up 8]}}<ref name="LeungChen1992">{{cite book|author1=K.T. Leung|author2=Doris Lai-chue Chen|title=Elementary Set Theory, Part I/II|url=https://books.google.com/books?id=cdmy2eOhJdkC&pg=PA27|date=1 July 1992|publisher=Hong Kong University Press|isbn=978-962-209-026-2|page=27}}</ref> या {{math|ϕ}}<ref>{{cite book|title=Understanding ISC Mathematics Class XI|volume=1|first=M.L.|last=Aggarwal|publisher=Arya Publications (Avichal Publishing Company)|year=2021|chapter=1. Sets|page=A=3}}</ref> (या {{mvar|ϕ}})।<ref>{{cite book|title=Chhaya Ganit (Ekadash Shreni)|first=De|last=Sourendra Nath|publisher=Scholar Books Pvt. Ltd.|date=January 2015|chapter=Unit-1 Sets and Functions: 1. Set Theory|page=5}}</ref> | ||
== सिंगलटन सेट == | == सिंगलटन सेट == | ||
एक सिंगलटन सेट बिल्कुल एक तत्व के साथ एक सेट है;इस तरह के सेट को यूनिट सेट भी कहा जा सकता है।<ref name="Stoll"/>ऐसे किसी भी सेट को लिखा जा सकता है {{mset|''x''}}, जहां x तत्व है। | एक सिंगलटन सेट बिल्कुल एक तत्व के साथ एक सेट है;इस तरह के सेट को यूनिट सेट भी कहा जा सकता है।<ref name="Stoll"/>ऐसे किसी भी सेट को लिखा जा सकता है {{mset|''x''}}, जहां x तत्व है। | ||
सेट {{mset|''x''}} और तत्व x का मतलब अलग -अलग चीजें हैं;हल्मोस{{sfn|Halmos|1960|loc=[https://archive.org/details/naivesettheory00halm/page/4/mode/2up Sect.2]}} सादृश्य को खींचता है कि टोपी युक्त एक बॉक्स टोपी के समान नहीं है। | सेट {{mset|''x''}} और तत्व x का मतलब अलग -अलग चीजें हैं;हल्मोस{{sfn|Halmos|1960|loc=[https://archive.org/details/naivesettheory00halm/page/4/mode/2up Sect.2]}} सादृश्य को खींचता है कि टोपी युक्त एक बॉक्स टोपी के समान नहीं है। | ||
== सबसेट == | == सबसेट == | ||
यदि सेट A का प्रत्येक तत्व B में भी है, तो A को B के सबसेट के रूप में वर्णित किया गया है, या B में निहित है, A ⊆ B लिखा है,<ref name="Hausdorff2005">{{cite book|author=Felix Hausdorff|title=Set Theory|url=https://books.google.com/books?id=yvVIdH16k0YC&pg=PA30|year=2005|publisher=American Mathematical Soc.|isbn=978-0-8218-3835-8|page=30}}</ref> या बी ⊇ ए।<ref name="Comninos2010">{{cite book|author=Peter Comninos|title=Mathematical and Computer Programming Techniques for Computer Graphics|url=https://books.google.com/books?id=Kdb7-YnnOVwC&pg=PA7|date=6 April 2010|publisher=Springer Science & Business Media|isbn=978-1-84628-292-8|page=7}}</ref> बाद के संकेतन को पढ़ा जा सकता है B में A, B शामिल है, या B शामिल है। A. का एक सुपरसेट है। ⊆ द्वारा स्थापित सेटों के बीच संबंध को समावेश या नियंत्रण कहा जाता है।दो सेट समान हैं यदि वे एक दूसरे को शामिल करते हैं: A ⊆ B और B ⊆ A A = B के बराबर है।<ref name="Lucas1990"/> | यदि सेट A का प्रत्येक तत्व B में भी है, तो A को B के सबसेट के रूप में वर्णित किया गया है, या B में निहित है, A ⊆ B लिखा है,<ref name="Hausdorff2005">{{cite book|author=Felix Hausdorff|title=Set Theory|url=https://books.google.com/books?id=yvVIdH16k0YC&pg=PA30|year=2005|publisher=American Mathematical Soc.|isbn=978-0-8218-3835-8|page=30}}</ref> या बी ⊇ ए।<ref name="Comninos2010">{{cite book|author=Peter Comninos|title=Mathematical and Computer Programming Techniques for Computer Graphics|url=https://books.google.com/books?id=Kdb7-YnnOVwC&pg=PA7|date=6 April 2010|publisher=Springer Science & Business Media|isbn=978-1-84628-292-8|page=7}}</ref> बाद के संकेतन को पढ़ा जा सकता है B में A, B शामिल है, या B शामिल है। A. का एक सुपरसेट है। ⊆ द्वारा स्थापित सेटों के बीच संबंध को समावेश या नियंत्रण कहा जाता है।दो सेट समान हैं यदि वे एक दूसरे को शामिल करते हैं: A ⊆ B और B ⊆ A A = B के बराबर है।<ref name="Lucas1990"/> | ||
| Line 127: | Line 119: | ||
== कार्डिनलिटी == | == कार्डिनलिटी == | ||
एक सेट की कार्डिनलिटी {{math|''S''}}, निरूपित {{math|{{mabs|''S''}}}}, के सदस्यों की संख्या है {{math|''S''}}.<ref name="Moschovakis1994">{{cite book|author=Yiannis N. Moschovakis|title=Notes on Set Theory|url=https://books.google.com/books?id=ndx0_6VCypcC|year=1994|publisher=Springer Science & Business Media|isbn=978-3-540-94180-4}}</ref> उदाहरण के लिए, यदि {{math|''B'' {{=}} {{mset|blue, white, red}}}}, फिर {{math|1={{mabs|B}} = 3}}।रोस्टर संकेतन में बार -बार सदस्यों की गिनती नहीं की जाती है,<ref name="Fleck2001">{{cite book|author=Arthur Charles Fleck|title=Formal Models of Computation: The Ultimate Limits of Computing|url=https://books.google.com/books?id=c42oYf4zBzMC&pg=PA3|year=2001|publisher=World Scientific|isbn=978-981-02-4500-9|page=3}}</ref><ref name="Johnston2015">{{cite book|author=William Johnston|title=The Lebesgue Integral for Undergraduates|url=https://books.google.com/books?id=v4ueCgAAQBAJ&pg=PA7|date=25 September 2015|publisher=The Mathematical Association of America|isbn=978-1-939512-07-9|page=7}}</ref> इसलिए {{math|1={{mabs|{{mset|blue, white, red, blue, white}}}} = 3}}, भी। | एक सेट की कार्डिनलिटी {{math|''S''}}, निरूपित {{math|{{mabs|''S''}}}}, के सदस्यों की संख्या है {{math|''S''}}.<ref name="Moschovakis1994">{{cite book|author=Yiannis N. Moschovakis|title=Notes on Set Theory|url=https://books.google.com/books?id=ndx0_6VCypcC|year=1994|publisher=Springer Science & Business Media|isbn=978-3-540-94180-4}}</ref> उदाहरण के लिए, यदि {{math|''B'' {{=}} {{mset|blue, white, red}}}}, फिर {{math|1={{mabs|B}} = 3}}।रोस्टर संकेतन में बार -बार सदस्यों की गिनती नहीं की जाती है,<ref name="Fleck2001">{{cite book|author=Arthur Charles Fleck|title=Formal Models of Computation: The Ultimate Limits of Computing|url=https://books.google.com/books?id=c42oYf4zBzMC&pg=PA3|year=2001|publisher=World Scientific|isbn=978-981-02-4500-9|page=3}}</ref><ref name="Johnston2015">{{cite book|author=William Johnston|title=The Lebesgue Integral for Undergraduates|url=https://books.google.com/books?id=v4ueCgAAQBAJ&pg=PA7|date=25 September 2015|publisher=The Mathematical Association of America|isbn=978-1-939512-07-9|page=7}}</ref> इसलिए {{math|1={{mabs|{{mset|blue, white, red, blue, white}}}} = 3}}, भी। | ||
| Line 144: | Line 135: | ||
=== कॉन्टिनम परिकल्पना === | === कॉन्टिनम परिकल्पना === | ||
1878 में जॉर्ज कैंटर द्वारा तैयार की गई निरंतरता परिकल्पना, यह कथन है कि कार्डिनलिटी के साथ सख्ती से कोई सेट नहीं है, जो प्राकृतिक संख्याओं की कार्डिनलिटी और एक सीधी रेखा के कार्डिनलिटी के बीच सख्ती से सेट है।<ref name = "Cantor1878">{{Cite journal | 1878 में जॉर्ज कैंटर द्वारा तैयार की गई निरंतरता परिकल्पना, यह कथन है कि कार्डिनलिटी के साथ सख्ती से कोई सेट नहीं है, जो प्राकृतिक संख्याओं की कार्डिनलिटी और एक सीधी रेखा के कार्डिनलिटी के बीच सख्ती से सेट है।<ref name = "Cantor1878">{{Cite journal | ||
| first = Georg | last = Cantor | | first = Georg | last = Cantor | ||
| Line 165: | Line 155: | ||
== पावर सेट == | == पावर सेट == | ||
एक सेट का पावर सेट {{math|''S''}} के सभी सबसेट का सेट है {{math|''S''}}.<ref name="Lucas1990" />खाली सेट और {{math|''S''}} स्वयं के पावर सेट के तत्व हैं {{math|''S''}}, क्योंकि ये दोनों सबसेट हैं {{math|''S''}}।उदाहरण के लिए, का पावर सेट {{math|{{mset|1, 2, 3}}}} है {{math|{{mset|∅, {{mset|1}}, {{mset|2}}, {{mset|3}}, {{mset|1, 2}}, {{mset|1, 3}}, {{mset|2, 3}}, {{mset|1, 2, 3}}}}}}।एक सेट का पावर सेट {{math|''S''}} आमतौर पर लिखा जाता है {{math|''P''(''S'')}} या {{math|2{{sup|''S''}}}}।<ref name="Lucas1990" />{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/18/mode/2up 19]}}<ref name=":1" /> | एक सेट का पावर सेट {{math|''S''}} के सभी सबसेट का सेट है {{math|''S''}}.<ref name="Lucas1990" />खाली सेट और {{math|''S''}} स्वयं के पावर सेट के तत्व हैं {{math|''S''}}, क्योंकि ये दोनों सबसेट हैं {{math|''S''}}।उदाहरण के लिए, का पावर सेट {{math|{{mset|1, 2, 3}}}} है {{math|{{mset|∅, {{mset|1}}, {{mset|2}}, {{mset|3}}, {{mset|1, 2}}, {{mset|1, 3}}, {{mset|2, 3}}, {{mset|1, 2, 3}}}}}}।एक सेट का पावर सेट {{math|''S''}} आमतौर पर लिखा जाता है {{math|''P''(''S'')}} या {{math|2{{sup|''S''}}}}।<ref name="Lucas1990" />{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/18/mode/2up 19]}}<ref name=":1" /> | ||
| Line 174: | Line 163: | ||
== विभाजन == | == विभाजन == | ||
एक सेट एस का एक विभाजन एस के गैर -रिक्त सबसेट का एक सेट है, जैसे कि एस में प्रत्येक तत्व एक्स इन सबसेटों में से एक में है।अर्थात्, सबसेट पेयरवाइज डिसजॉइंट हैं (जिसका अर्थ है कि विभाजन के किसी भी दो सेट में कोई तत्व नहीं होता है), और विभाजन के सभी सबसेटों का संघ एस है।<ref name="Mansour2012">{{cite book|author=Toufik Mansour|title=Combinatorics of Set Partitions|url=https://books.google.com/books?id=5NvrH4w8WGsC|date=27 July 2012|publisher=CRC Press|isbn=978-1-4398-6333-6}}</ref>{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/28/mode/2up 28]}} | एक सेट एस का एक विभाजन एस के गैर -रिक्त सबसेट का एक सेट है, जैसे कि एस में प्रत्येक तत्व एक्स इन सबसेटों में से एक में है।अर्थात्, सबसेट पेयरवाइज डिसजॉइंट हैं (जिसका अर्थ है कि विभाजन के किसी भी दो सेट में कोई तत्व नहीं होता है), और विभाजन के सभी सबसेटों का संघ एस है।<ref name="Mansour2012">{{cite book|author=Toufik Mansour|title=Combinatorics of Set Partitions|url=https://books.google.com/books?id=5NvrH4w8WGsC|date=27 July 2012|publisher=CRC Press|isbn=978-1-4398-6333-6}}</ref>{{sfn|Halmos|1960|p=[https://archive.org/details/naivesettheory00halm/page/28/mode/2up 28]}} | ||
== मूल संचालन == | == मूल संचालन == | ||
दिए गए सेटों से नए सेट बनाने के लिए कई मौलिक संचालन हैं। | दिए गए सेटों से नए सेट बनाने के लिए कई मौलिक संचालन हैं। | ||
=== यूनियनों === | === यूनियनों === | ||
[[File:Venn0111.svg|thumb|<div class = केंद्र> का संघ {{math|''A''}} तथा {{math|''B''}}, निरूपित {{math|''A'' ∪ ''B''}}</div>]] | [[File:Venn0111.svg|thumb|<div class = केंद्र> का संघ {{math|''A''}} तथा {{math|''B''}}, निरूपित {{math|''A'' ∪ ''B''}}</div>]] | ||
दो सेट में शामिल हो सकते हैं: संघ {{math|''A''}} तथा {{math|''B''}}, द्वारा चिह्नित {{math|''A'' ∪ ''B''}}, उन सभी चीजों का सेट है जो ए या बी या दोनों के सदस्य हैं। | दो सेट में शामिल हो सकते हैं: संघ {{math|''A''}} तथा {{math|''B''}}, द्वारा चिह्नित {{math|''A'' ∪ ''B''}}, उन सभी चीजों का सेट है जो ए या बी या दोनों के सदस्य हैं। | ||
| Line 201: | Line 187: | ||
=== चौराहों === | === चौराहों === | ||
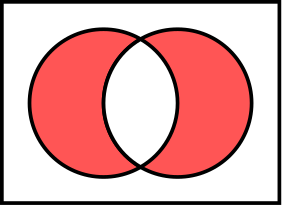
एक नए सेट का निर्माण यह निर्धारित करके भी किया जा सकता है कि कौन से सदस्यों के दो सेट समान हैं।ए और बी के चौराहे, द्वारा निरूपित किया गया {{nowrap|''A'' ∩ ''B'',}} सभी चीजों का सेट है जो ए और बी दोनों के सदस्य हैं {{nowrap|1=''A'' ∩ ''B'' = ∅,}} तब ए और बी को असंतुष्ट कहा जाता है। | एक नए सेट का निर्माण यह निर्धारित करके भी किया जा सकता है कि कौन से सदस्यों के दो सेट समान हैं।ए और बी के चौराहे, द्वारा निरूपित किया गया {{nowrap|''A'' ∩ ''B'',}} सभी चीजों का सेट है जो ए और बी दोनों के सदस्य हैं {{nowrap|1=''A'' ∩ ''B'' = ∅,}} तब ए और बी को असंतुष्ट कहा जाता है। | ||
[[File:Venn0001.svg|thumb|<div class = केंद्र> A और B का चौराहा, निरूपित {{nowrap|''A'' ∩ ''B''.}}</div>]] | [[File:Venn0001.svg|thumb|<div class = केंद्र> A और B का चौराहा, निरूपित {{nowrap|''A'' ∩ ''B''.}}</div>]] | ||
| Line 218: | Line 203: | ||
=== पूरक === | === पूरक === | ||
[[File:Venn0100.svg|thumb|<div class = केंद्र> सापेक्ष पूरक < /div> में B का <br />]] | [[File:Venn0100.svg|thumb|<div class = केंद्र> सापेक्ष पूरक < /div> में B का <br />]] | ||
[[File:Venn1010.svg|thumb|<div class = केंद्र> u का पूरक u </div>]] | [[File:Venn1010.svg|thumb|<div class = केंद्र> u का पूरक u </div>]] | ||
| Line 249: | Line 233: | ||
=== कार्टेशियन उत्पाद === | === कार्टेशियन उत्पाद === | ||
एक नए सेट का निर्माण एक सेट के प्रत्येक तत्व को दूसरे सेट के प्रत्येक तत्व के साथ जोड़कर किया जा सकता है।ए × बी द्वारा निरूपित दो सेट ए और बी के कार्टेशियन उत्पाद, सभी आदेशित जोड़े (ए, बी) का सेट है, जैसे कि ए ए और बी का सदस्य है। बी का एक सदस्य है। | एक नए सेट का निर्माण एक सेट के प्रत्येक तत्व को दूसरे सेट के प्रत्येक तत्व के साथ जोड़कर किया जा सकता है।ए × बी द्वारा निरूपित दो सेट ए और बी के कार्टेशियन उत्पाद, सभी आदेशित जोड़े (ए, बी) का सेट है, जैसे कि ए ए और बी का सदस्य है। बी का एक सदस्य है। | ||
| Line 267: | Line 250: | ||
भोले सेट सिद्धांत के मुख्य अनुप्रयोगों में से एक संबंध के निर्माण में है।एक डोमेन से एक संबंध {{math|''A''}} एक कोडोमैन के लिए {{math|''B''}} कार्टेशियन उत्पाद का एक सबसेट है {{math|''A'' × ''B''}}।उदाहरण के लिए, सेट को देखते हुए {{math|''S'' {{=}} {{mset|rock, paper, scissors}}}} एक ही नाम के खेल में आकृतियाँ, संबंध से धड़कता है {{math|''S''}} प्रति {{math|''S''}} सेट है {{math|''B'' {{=}} {{mset|(scissors,paper), (paper,rock), (rock,scissors)}}}};इस प्रकार {{math|''x''}} धड़कता है {{math|''y''}} खेल में अगर जोड़ी {{math|(''x'',''y'')}} का सदस्य है {{math|''B''}}।एक अन्य उदाहरण सेट है {{math|''F''}} सभी जोड़े की {{math|(''x'', ''x''{{sup|2}})}}, कहाँ पे {{math|''x''}} यह सचमुच का है।यह संबंध एक सबसेट है {{math|'''R''' × '''R'''}}, क्योंकि सभी वर्गों का सेट सभी वास्तविक संख्याओं के सेट का सबसेट है।चूंकि हर के लिए {{math|''x''}} में {{math|'''R'''}}, एक और केवल एक जोड़ी {{math|(''x'',...)}} में पाया जाता है {{math|''F''}}, इसे एक फ़ंक्शन कहा जाता है।कार्यात्मक संकेतन में, इस संबंध को के रूप में लिखा जा सकता है {{math|''F''(''x'') {{=}} ''x''{{sup|2}}}}। | भोले सेट सिद्धांत के मुख्य अनुप्रयोगों में से एक संबंध के निर्माण में है।एक डोमेन से एक संबंध {{math|''A''}} एक कोडोमैन के लिए {{math|''B''}} कार्टेशियन उत्पाद का एक सबसेट है {{math|''A'' × ''B''}}।उदाहरण के लिए, सेट को देखते हुए {{math|''S'' {{=}} {{mset|rock, paper, scissors}}}} एक ही नाम के खेल में आकृतियाँ, संबंध से धड़कता है {{math|''S''}} प्रति {{math|''S''}} सेट है {{math|''B'' {{=}} {{mset|(scissors,paper), (paper,rock), (rock,scissors)}}}};इस प्रकार {{math|''x''}} धड़कता है {{math|''y''}} खेल में अगर जोड़ी {{math|(''x'',''y'')}} का सदस्य है {{math|''B''}}।एक अन्य उदाहरण सेट है {{math|''F''}} सभी जोड़े की {{math|(''x'', ''x''{{sup|2}})}}, कहाँ पे {{math|''x''}} यह सचमुच का है।यह संबंध एक सबसेट है {{math|'''R''' × '''R'''}}, क्योंकि सभी वर्गों का सेट सभी वास्तविक संख्याओं के सेट का सबसेट है।चूंकि हर के लिए {{math|''x''}} में {{math|'''R'''}}, एक और केवल एक जोड़ी {{math|(''x'',...)}} में पाया जाता है {{math|''F''}}, इसे एक फ़ंक्शन कहा जाता है।कार्यात्मक संकेतन में, इस संबंध को के रूप में लिखा जा सकता है {{math|''F''(''x'') {{=}} ''x''{{sup|2}}}}। | ||
== समावेश और बहिष्करण का सिद्धांत == | == समावेश और बहिष्करण का सिद्धांत == | ||
[[Image:A union B.svg|thumb|समावेश-बहिष्करण सिद्धांत का उपयोग सेट के संघ के आकार की गणना करने के लिए किया जाता है: संघ का आकार दो सेटों का आकार है, उनके चौराहे के आकार को माइनस करता है।]] | [[Image:A union B.svg|thumb|समावेश-बहिष्करण सिद्धांत का उपयोग सेट के संघ के आकार की गणना करने के लिए किया जाता है: संघ का आकार दो सेटों का आकार है, उनके चौराहे के आकार को माइनस करता है।]] | ||
समावेश -बहिष्करण सिद्धांत एक गिनती तकनीक है जिसका उपयोग दो सेटों के संघ में तत्वों की संख्या को गिनने के लिए किया जा सकता है - यदि प्रत्येक सेट का आकार और उनके चौराहे के आकार को जाना जाता है।इसे प्रतीकात्मक रूप से व्यक्त किया जा सकता है | समावेश -बहिष्करण सिद्धांत एक गिनती तकनीक है जिसका उपयोग दो सेटों के संघ में तत्वों की संख्या को गिनने के लिए किया जा सकता है - यदि प्रत्येक सेट का आकार और उनके चौराहे के आकार को जाना जाता है।इसे प्रतीकात्मक रूप से व्यक्त किया जा सकता है | ||
Revision as of 10:44, 18 August 2022
एक सेट अलग के संग्रह के लिए गणितीय मॉडल है[1] चीज़ें;[2][3][4] एक सेट में तत्व या सदस्य होते हैं, जो किसी भी प्रकार की गणितीय वस्तुएं हो सकती हैं: संख्या, प्रतीक, अंतरिक्ष, रेखाओं, अन्य ज्यामितीय आकार, चर, या यहां तक कि अन्य सेट भी।[5] बिना किसी तत्व के सेट खाली सेट है;एक एकल तत्व के साथ एक सेट एक सिंगलटन है।एक सेट में तत्वों की एक सीमित संख्या हो सकती है या एक अनंत सेट हो सकता है।दो सेट समान हैं यदि उनके पास ठीक समान तत्व हैं।[6] आधुनिक गणित में सेट सर्वव्यापी हैं।वास्तव में, सेट सिद्धांत, अधिक विशेष रूप से Zermelo -Fraenkel सेट सिद्धांत, 20 वीं शताब्दी की पहली छमाही के बाद से गणित की सभी शाखाओं के लिए कठोर नींव प्रदान करने का मानक तरीका रहा है।[5]
इतिहास
एक सेट की अवधारणा 19 वीं शताब्दी के अंत में गणित में उभरी। [7] सेट के लिए जर्मन शब्द, मेन्ज, को अनंत के अपने काम के विरोधाभासों में बर्नार्ड बोलजानो द्वारा गढ़ा गया था। REF नाम = RUSS2004>Steve Russ (9 December 2004). The Mathematical Works of Bernard Bolzano. OUP Oxford. ISBN 978-0-19-151370-1.</ref>[8]<रेफ नाम = rusnocksebestík2019>Paul Rusnock; Jan Sebestík (25 April 2019). Bernard Bolzano: His Life and Work. OUP Oxford. p. 430. ISBN 978-0-19-255683-7.</ref>[[File:Passage with the set definition of Georg Cantor.png|thumb|जॉर्ज कैंटर की मूल सेट परिभाषा के अनुवाद के साथ मार्ग।सेट के लिए जर्मन वर्ड मेन्ज का अनुवाद यहां किया गया है।सेट थ्योरी के संस्थापकों में से एक, जॉर्ज कैंटर ने अपने बीटेज ज़ुर बेगुंडुंग डेर ट्रांसफिनिटेन मेंगेनलेहे की शुरुआत में निम्नलिखित परिभाषा दी:[1]
A set is a gathering together into a whole of definite, distinct objects of our perception or our thought—which are called elements of the set.
बर्ट्रेंड रसेल ने एक सेट एक वर्ग कहा:[9]
When mathematicians deal with what they call a manifold, aggregate, Menge, ensemble, or some equivalent name, it is common, especially where the number of terms involved is finite, to regard the object in question (which is in fact a class) as defined by the enumeration of its terms, and as consisting possibly of a single term, which in that case is the class.
भोला सेट सिद्धांत
एक सेट की सबसे महत्वपूर्ण संपत्ति यह है कि इसमें तत्व हो सकते हैं, जिसे सदस्य भी कहा जाता है।दो सेट समान होते हैं जब उनके समान तत्व होते हैं।अधिक सटीक रूप से, सेट ए और बी समान हैं यदि ए का प्रत्येक तत्व बी का एक तत्व है, और बी का प्रत्येक तत्व ए का एक तत्व है;इस संपत्ति को सेट की एक्सटेंशनलिटी कहा जाता है।[10] एक सेट की सरल अवधारणा गणित में बहुत उपयोगी साबित हुई है, लेकिन: श्रेणी: भोले सेट सिद्धांत के विरोधाभास। विरोधाभास उठते हैं यदि कोई प्रतिबंध नहीं रखा जाता है तो सेट कैसे बनाया जा सकता है:
- रसेल के विरोधाभास से पता चलता है कि सभी सेटों का सेट जो स्वयं नहीं है, अर्थात्, यानी, {x | x is a set and x ∉ x}, मौजूद नहीं हो सकता।
- कैंटर के विरोधाभास से पता चलता है कि सभी सेटों का सेट मौजूद नहीं हो सकता है।
Nave सेट सिद्धांत अलग-अलग तत्वों के किसी भी अच्छी तरह से परिभाषित संग्रह के रूप में एक सेट को परिभाषित करता है, लेकिन समस्याएं अच्छी तरह से परिभाषित शब्द की अस्पष्टता से उत्पन्न होती हैं।
स्वयंसिद्ध सेट सिद्धांत
भोले सेट सिद्धांत के मूल सूत्रीकरण के समय से इन विरोधाभासों को हल करने के बाद के प्रयासों में, सेट के गुणों को स्वयंसिद्ध द्वारा परिभाषित किया गया है।Axiomatic सेट सिद्धांत एक आदिम धारणा के रूप में एक सेट की अवधारणा को लेता है।[11] स्वयंसिद्धों का उद्देश्य एक बुनियादी ढांचा प्रदान करना है जिसमें से पहले-क्रम के तर्क का उपयोग करके सेट के बारे में विशेष गणितीय प्रस्तावों (कथनों) की सच्चाई या मिथ्या को कम करना है।हालांकि, गोडेल के अपूर्णता प्रमेयों के अनुसार, किसी भी विशेष स्वयंसिद्ध सेट सिद्धांत को यह साबित करने के लिए पहले-क्रम के तर्क का उपयोग करना संभव नहीं है कि वह विरोधाभास से मुक्त हो।[citation needed]
कैसे सेट परिभाषित किए जाते हैं और नोटेशन सेट करते हैं
गणितीय ग्रंथ आमतौर पर बड़े अक्षरों द्वारा सेट को निरूपित करते हैं[12][5] इटैलिक में, जैसे A, B, C.[13] एक सेट को एक संग्रह या परिवार भी कहा जा सकता है, खासकर जब इसके तत्व स्वयं सेट होते हैं।
रोस्टर अंकन
रोस्टर या एन्यूमरेशन नोटेशन एक सेट को घुंघराले कोष्ठक के बीच अपने तत्वों को सूचीबद्ध करके परिभाषित करता है, कॉमा द्वारा अलग किया गया:[14][15][16][17]
एक सेट में, यह सब मायने रखता है कि क्या प्रत्येक तत्व इसमें है या नहीं, इसलिए रोस्टर नोटेशन में तत्वों का आदेश अप्रासंगिक है (इसके विपरीत, एक अनुक्रम में, एक टपल, या एक सेट का क्रमपरिवर्तन, ऑर्डरिंग का आदेशशर्तें मायने रखती हैं)।उदाहरण के लिए, {2, 4, 6} तथा {4, 6, 4, 2} एक ही सेट का प्रतिनिधित्व करते हैं।[18][13][19] कई तत्वों के साथ सेट के लिए, विशेष रूप से एक निहित पैटर्न का पालन करने वाले, सदस्यों की सूची को एक दीर्घवृत्त का उपयोग करके संक्षिप्त किया जा सकता है '...'।[20][21] उदाहरण के लिए, पहले हजार सकारात्मक पूर्णांक के सेट को रोस्टर नोटेशन में निर्दिष्ट किया जा सकता है
रोस्टर अंकन में अनंत सेट
एक अनंत सेट तत्वों की एक अंतहीन सूची के साथ एक सेट है।रोस्टर नोटेशन में एक अनंत सेट का वर्णन करने के लिए, एक एलिप्सिस को सूची के अंत में, या दोनों छोरों पर रखा जाता है, यह इंगित करने के लिए कि सूची हमेशा के लिए जारी रहती है।उदाहरण के लिए, गैर -पूर्णांक का सेट है
और सभी पूर्णांक का सेट है
सिमेंटिक परिभाषा
एक सेट को परिभाषित करने का एक और तरीका यह है कि तत्व क्या हैं यह निर्धारित करने के लिए एक नियम का उपयोग करें:
इस तरह की परिभाषा को एक शब्दार्थ विवरण कहा जाता है।[22][23]
सेट-बिल्डर नोटेशन
सेट-बिल्डर नोटेशन तत्वों पर एक स्थिति द्वारा निर्धारित एक बड़े सेट से चयन के रूप में एक सेट को निर्दिष्ट करता है।[23][24][25] उदाहरण के लिए, एक सेट F निम्नानुसार परिभाषित किया जा सकता है:
परिभाषा के तरीकों को वर्गीकृत करना
दर्शन परिभाषाओं के प्रकारों को वर्गीकृत करने के लिए विशिष्ट शब्दों का उपयोग करता है:
- एक अंतरंग परिभाषा सदस्यता निर्धारित करने के लिए एक नियम का उपयोग करती है।सेट-बिल्डर नोटेशन का उपयोग करके सिमेंटिक परिभाषाएँ और परिभाषाएँ उदाहरण हैं।
- एक व्यापक परिभाषा उसके सभी तत्वों को सूचीबद्ध करके एक सेट का वर्णन करती है।[23]इस तरह की परिभाषाओं को एनुमेरेटिव भी कहा जाता है।
- एक अस्थिर परिभाषा वह है जो तत्वों के उदाहरण देकर एक सेट का वर्णन करती है;एक रोस्टर जिसमें एक एलिप्सिस शामिल है, एक उदाहरण होगा।
सदस्यता
यदि B एक सेट है और x का एक तत्व है B, यह शॉर्टहैंड में लिखा गया है x ∈ B, जिसे X के रूप में भी पढ़ा जा सकता है, B से संबंधित है, या X B में है।[10] कथन y b का एक तत्व नहीं है, के रूप में लिखा गया है y ∉ B, जिसे y के रूप में भी पढ़ा जा सकता है, b में नहीं है।[27][28] उदाहरण के लिए, सेट के संबंध में A = {1, 2, 3, 4}, B = {blue, white, red}, तथा F = {n | n is an integer, and 0 ≤ n ≤ 19},
खाली सेट
खाली सेट (या अशक्त सेट) अद्वितीय सेट है जिसमें कोई सदस्य नहीं है।इसे निरूपित किया गया है ∅ या या { }[29][30] या ϕ[31] (या ϕ)।[32]
सिंगलटन सेट
एक सिंगलटन सेट बिल्कुल एक तत्व के साथ एक सेट है;इस तरह के सेट को यूनिट सेट भी कहा जा सकता है।[6]ऐसे किसी भी सेट को लिखा जा सकता है {x}, जहां x तत्व है। सेट {x} और तत्व x का मतलब अलग -अलग चीजें हैं;हल्मोस[33] सादृश्य को खींचता है कि टोपी युक्त एक बॉक्स टोपी के समान नहीं है।
सबसेट
यदि सेट A का प्रत्येक तत्व B में भी है, तो A को B के सबसेट के रूप में वर्णित किया गया है, या B में निहित है, A ⊆ B लिखा है,[34] या बी ⊇ ए।[35] बाद के संकेतन को पढ़ा जा सकता है B में A, B शामिल है, या B शामिल है। A. का एक सुपरसेट है। ⊆ द्वारा स्थापित सेटों के बीच संबंध को समावेश या नियंत्रण कहा जाता है।दो सेट समान हैं यदि वे एक दूसरे को शामिल करते हैं: A ⊆ B और B ⊆ A A = B के बराबर है।[24]
यदि A B का एक सबसेट है, लेकिन A B के बराबर नहीं है, तो A को B का एक उचित उपसमुच्चय कहा जाता है। इसे एक ⊊ B. इसी तरह लिखा जा सकता है, B ⊋ A MEANS B का एक उचित सुपरसेट है, अर्थात् Bशामिल हैं, और ए के बराबर नहीं है।
ऑपरेटरों की एक तीसरी जोड़ी ⊂ और ⊃ का उपयोग अलग -अलग लेखकों द्वारा अलग -अलग तरीके से किया जाता है: कुछ लेखक एक ⊂ B और B ⊃ A का अर्थ है A का मतलब B का कोई सबसेट है (और जरूरी नहीं कि एक उचित सबसेट) हो,[36][27]जबकि अन्य उन मामलों के लिए ⊂ B और B ⊃ A को आरक्षित करते हैं जहां A B का एक उचित सबसेट है।[34]
उदाहरण:
- सभी मनुष्यों का सेट सभी स्तनधारियों के सेट का एक उचित सबसेट है।
- {1, 3} ⊂ {1, 2, 3, 4}।
- {1, 2, 3, 4} ⊆ {1, 2, 3, 4}।
खाली सेट हर सेट का एक सबसेट है,[29] और हर सेट अपने आप में एक सबसेट है:[36]
- ∅ ⊆ A. A.
- ए ⊆ ए।
यूलर और वेन आरेख
एक यूलर आरेख सेट के संग्रह का एक चित्रमय प्रतिनिधित्व है;प्रत्येक सेट को एक लूप द्वारा संलग्न एक प्लानर क्षेत्र के रूप में दर्शाया गया है, जिसके अंदर उसके तत्व हैं।यदि A का एक सबसेट है B, फिर क्षेत्र का प्रतिनिधित्व करना A पूरी तरह से प्रतिनिधित्व करने वाले क्षेत्र के अंदर है B।यदि दो सेटों में कोई तत्व सामान्य नहीं है, तो क्षेत्र ओवरलैप नहीं करते हैं।
एक वेन आरेख, इसके विपरीत, एक चित्रमय प्रतिनिधित्व है n सेट करता है जिसमें n लूप विमान को विभाजित करें 2n ऐसे जोन ऐसे हैं कि कुछ का चयन करने के प्रत्येक तरीके के लिए n सेट (संभवतः सभी या कोई भी), उन तत्वों के लिए एक क्षेत्र है जो सभी चयनित सेटों से संबंधित हैं और दूसरों में से कोई भी नहीं।उदाहरण के लिए, यदि सेट हैं A, B, तथा C, उन तत्वों के लिए एक क्षेत्र होना चाहिए जो अंदर हैं A तथा C और बाहर B (भले ही ऐसे तत्व मौजूद न हों)।
गणित में संख्याओं के विशेष सेट
इस तरह के गणितीय महत्व के सेट हैं, जिनके लिए गणितज्ञ इतने बार संदर्भित करते हैं, कि उन्होंने उनकी पहचान करने के लिए विशेष नाम और उल्लेखनीय सम्मेलनों का अधिग्रहण किया है।
इनमें से कई महत्वपूर्ण सेटों को गणितीय ग्रंथों में बोल्ड का उपयोग करके दर्शाया गया है (उदा। ) या ब्लैकबोर्ड बोल्ड (उदा। ) टाइपफेस।[37] इसमे शामिल है
- या , सभी प्राकृतिक संख्याओं का सेट: (अक्सर, लेखक बाहर करते हैं 0);[37]* या , सभी पूर्णांक का सेट (चाहे सकारात्मक, नकारात्मक या शून्य): ;[37]* या , सभी तर्कसंगत संख्याओं का सेट (यानी, सभी उचित और अनुचित अंशों का सेट): ।उदाहरण के लिए, −7/4 ∈ Q तथा 5 = 5/1 ∈ Q;[37]* या , सभी वास्तविक संख्याओं का सेट, जिसमें सभी तर्कसंगत संख्या और सभी तर्कहीन संख्याएं शामिल हैं (जिसमें बीजीय संख्या शामिल हैं जैसे इसे अंशों के रूप में फिर से नहीं लिखा जा सकता है, साथ ही ट्रान्सेंडैंटल नंबरों जैसेπतथाe);[37]* या , सभी जटिल संख्याओं का सेट: C = {a + bi | a, b ∈ R}, उदाहरण के लिए, 1 + 2i ∈ C.[37]
संख्याओं के उपरोक्त सेटों में से प्रत्येक में अनंत संख्या में तत्व होते हैं।प्रत्येक इसके नीचे सूचीबद्ध सेटों का एक सबसेट है।
सकारात्मक या नकारात्मक संख्याओं के सेट को कभी -कभी सुपरस्क्रिप्ट प्लस और माइनस संकेतों द्वारा क्रमशः निरूपित किया जाता है।उदाहरण के लिए, सकारात्मक तर्कसंगत संख्याओं के सेट का प्रतिनिधित्व करता है।
कार्य
एक सेट से एक फ़ंक्शन (या मैपिंग) A एक सेट पर B एक नियम है जो प्रत्येक इनपुट तत्व को असाइन करता है A एक आउटपुट जो एक तत्व है B;अधिक औपचारिक रूप से, एक फ़ंक्शन एक विशेष प्रकार का संबंध है, एक जो प्रत्येक तत्व से संबंधित है A के बिल्कुल एक तत्व के लिए B।एक फ़ंक्शन कहा जाता है
- इंजेक्शन (या एक-से-एक) यदि यह किसी भी दो अलग-अलग तत्वों को मैप करता है A के विभिन्न तत्वों के लिए B,
- सर्जिकल (या पर) यदि हर तत्व के लिए B, कम से कम एक तत्व है A कि यह नक्शे, और
- Filejective (या एक-से-एक पत्राचार) यदि फ़ंक्शन इंजेक्टिव और सर्जिकल दोनों है-इस मामले में, प्रत्येक तत्व का A के एक अनूठे तत्व के साथ जोड़ा जाता है B, और प्रत्येक तत्व B के एक अनूठे तत्व के साथ जोड़ा जाता है A, ताकि कोई अप्रकाशित तत्व न हो।
एक इंजेक्शन फ़ंक्शन को एक इंजेक्शन कहा जाता है, एक सर्जिकल फ़ंक्शन को एक अधिसूचना कहा जाता है, और एक द्विध्र हुए फ़ंक्शन को एक बायजमेंट या एक-से-एक पत्राचार कहा जाता है।
कार्डिनलिटी
एक सेट की कार्डिनलिटी S, निरूपित |S|, के सदस्यों की संख्या है S.[38] उदाहरण के लिए, यदि B = {blue, white, red}, फिर |B| = 3।रोस्टर संकेतन में बार -बार सदस्यों की गिनती नहीं की जाती है,[39][40] इसलिए |{blue, white, red, blue, white}| = 3, भी।
अधिक औपचारिक रूप से, दो सेट एक ही कार्डिनलिटी साझा करते हैं यदि उनके बीच एक-से-एक पत्राचार मौजूद है।
खाली सेट की कार्डिनलिटी शून्य है।[41]
अनंत सेट और अनंत कार्डिनलिटी
कुछ सेटों के तत्वों की सूची अंतहीन, या अनंत है।उदाहरण के लिए, सेट प्राकृतिक संख्याओं का अनंत है।[24]वास्तव में, उपरोक्त अनुभाग में उल्लिखित संख्याओं के सभी विशेष सेट अनंत हैं।अनंत सेट में अनंत कार्डिनलिटी होती है।
कुछ अनंत कार्डिनल दूसरों की तुलना में अधिक हैं।संभवतः सेट सिद्धांत से सबसे महत्वपूर्ण परिणामों में से एक यह है कि वास्तविक संख्याओं के सेट में प्राकृतिक संख्याओं के सेट की तुलना में अधिक कार्डिनैलिटी होती है।[42] कार्डिनलिटी के साथ सेट से कम या उसके बराबर गणना योग्य सेट कहा जाता है;ये या तो परिमित सेट या अनगिनत अनंत सेट हैं (उसी कार्डिनलिटी के सेट );कुछ लेखक गिनती के लिए गिनती करने योग्य का उपयोग करते हैं।कार्डिनलिटी के साथ सख्ती से अधिक से अधिक सेट करता है बेशुमार सेट कहा जाता है।
हालांकि, यह दिखाया जा सकता है कि एक सीधी रेखा की कार्डिनलिटी (यानी, एक लाइन पर बिंदुओं की संख्या) उस लाइन के किसी भी खंड की कार्डिनलिटी के समान है, पूरे विमान की, और वास्तव में किसी भी परिमित-आयामी यूक्लिडियन कीअंतरिक्ष।[43]
कॉन्टिनम परिकल्पना
1878 में जॉर्ज कैंटर द्वारा तैयार की गई निरंतरता परिकल्पना, यह कथन है कि कार्डिनलिटी के साथ सख्ती से कोई सेट नहीं है, जो प्राकृतिक संख्याओं की कार्डिनलिटी और एक सीधी रेखा के कार्डिनलिटी के बीच सख्ती से सेट है।[44] 1963 में, पॉल कोहेन ने साबित किया कि कॉन्टिनम परिकल्पना Axiom सिस्टम ZFC से स्वतंत्र है, जिसमें ज़रमेलो -फ्रेनकेल सेट सिद्धांत से मिलकर पसंद है।[45] (ZFC स्वयंसिद्ध सेट सिद्धांत का सबसे व्यापक रूप से अध्ययन किया गया संस्करण है।)
पावर सेट
एक सेट का पावर सेट S के सभी सबसेट का सेट है S.[24]खाली सेट और S स्वयं के पावर सेट के तत्व हैं S, क्योंकि ये दोनों सबसेट हैं S।उदाहरण के लिए, का पावर सेट {1, 2, 3} है {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}।एक सेट का पावर सेट S आमतौर पर लिखा जाता है P(S) या 2S।[24][46][13]
यदि S है n तत्व, फिर P(S) है 2n तत्व।[47] उदाहरण के लिए, {1, 2, 3} में तीन तत्व हैं, और इसका पावर सेट है 23 = 8 तत्व, जैसा कि ऊपर दिखाया गया है।
यदि S अनंत है (चाहे गिनती योग्य हो या बेशुमार), फिर P(S) बेशुमार है।इसके अलावा, पावर सेट हमेशा मूल सेट की तुलना में कड़ाई से बड़ा होता है, इस अर्थ में कि तत्वों को जोड़ने का कोई भी प्रयास S के तत्वों के साथ P(S) के कुछ तत्व छोड़ देंगे P(S) अप्रकाशित।(कभी भी एक बायजेक्शन नहीं है S पर P(S)।)[48]
विभाजन
एक सेट एस का एक विभाजन एस के गैर -रिक्त सबसेट का एक सेट है, जैसे कि एस में प्रत्येक तत्व एक्स इन सबसेटों में से एक में है।अर्थात्, सबसेट पेयरवाइज डिसजॉइंट हैं (जिसका अर्थ है कि विभाजन के किसी भी दो सेट में कोई तत्व नहीं होता है), और विभाजन के सभी सबसेटों का संघ एस है।[49][50]
मूल संचालन
दिए गए सेटों से नए सेट बनाने के लिए कई मौलिक संचालन हैं।
यूनियनों
[[File:Venn0111.svg|thumb|
]]
दो सेट में शामिल हो सकते हैं: संघ A तथा B, द्वारा चिह्नित A ∪ B, उन सभी चीजों का सेट है जो ए या बी या दोनों के सदस्य हैं।
उदाहरण:
- {1, 2} ∪ {1, 2} = {1, 2}.
- {1, 2} ∪ {2, 3} = {1, 2, 3}.
- {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}.
यूनियनों के कुछ बुनियादी गुण:
- A ∪ B = B ∪ A.
- A ∪ (B ∪ C) = (A ∪ B) ∪ C.
- A ⊆ (A ∪ B).
- A ∪ A = A.
- A ∪ ∅ = A.
- A ⊆ B अगर और केवल अगर A ∪ B = B.
चौराहों
एक नए सेट का निर्माण यह निर्धारित करके भी किया जा सकता है कि कौन से सदस्यों के दो सेट समान हैं।ए और बी के चौराहे, द्वारा निरूपित किया गया A ∩ B, सभी चीजों का सेट है जो ए और बी दोनों के सदस्य हैं A ∩ B = ∅, तब ए और बी को असंतुष्ट कहा जाता है।
उदाहरण:
- {1, 2} ∩ {1, 2} = {1, 2}.
- {1, 2} ∩ {2, 3} = {2}.
- {1, 2} ∩ {3, 4} = ∅.
चौराहों के कुछ बुनियादी गुण:
- A ∩ B = B ∩ A.
- A ∩ (B ∩ C) = (A ∩ B) ∩ C.
- A ∩ B ⊆ A.
- A ∩ A = A.
- A ∩ ∅ = ∅.
- A ⊆ B अगर और केवल अगर A ∩ B = A.
पूरक
दो सेटों को भी घटाया जा सकता है।बी के सापेक्ष पूरक (जिसे ए और बी के सेट-थ्योरिटिक अंतर भी कहा जाता है), द्वारा निरूपित किया गया A \ B (या A − B), उन सभी तत्वों का सेट है जो ए के सदस्य हैं, लेकिन बी के सदस्य नहीं हैं। यह एक सेट के सदस्यों को घटाने के लिए मान्य है जो सेट में नहीं हैं, जैसे कि सेट से तत्व हरे को हटाना {1, 2, 3};ऐसा करने से सेट में तत्वों को प्रभावित नहीं किया जाएगा।
कुछ सेटिंग्स में, चर्चा के तहत सभी सेटों को किसी दिए गए सार्वभौमिक सेट यू के सबसेट माना जाता है, ऐसे मामलों में, U \ A निरपेक्ष पूरक या बस के पूरक कहा जाता है, और एक ′ या एक द्वारा निरूपित किया जाता हैC </des>।
- A′ = U \ A
उदाहरण:
- {1, 2} \ {1, 2} = ∅.
- {1, 2, 3, 4} \ {1, 3} = {2, 4}.
- यदि यू पूर्णांक का सेट है, तो ई भी पूर्णांक का सेट है, और ओ विषम पूर्णांक का सेट है, तो u \ e = e ′ = O.
पूरक के कुछ बुनियादी गुणों में निम्नलिखित शामिल हैं:
- A \ B ≠ B \ A के लिये A ≠ B।
- A ∪ A′ = U.
- A ∩ A′ = ∅.
- (A′)′ = A.
- ∅ \ A = ∅.
- A \ ∅ = A.
- A \ A = ∅.
- A \ U = ∅.
- A \ A′ = A तथा A′ \ A = A′.
- U′ = ∅ तथा ∅′ = U.
- A \ B = A ∩ B′।
- यदि A ⊆ B फिर A \ B = ∅.
पूरक का एक विस्तार सममित अंतर है, सेट के लिए परिभाषित किया गया है, बी के रूप में
कार्टेशियन उत्पाद
एक नए सेट का निर्माण एक सेट के प्रत्येक तत्व को दूसरे सेट के प्रत्येक तत्व के साथ जोड़कर किया जा सकता है।ए × बी द्वारा निरूपित दो सेट ए और बी के कार्टेशियन उत्पाद, सभी आदेशित जोड़े (ए, बी) का सेट है, जैसे कि ए ए और बी का सदस्य है। बी का एक सदस्य है।
उदाहरण:
- {1, 2} × {red, white, green} = {(1, red), (1, white), (1, green), (2, red), (2, white), (2, green)}.
- {1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
- {a, b, c} × {d, e, f} = {(a, d), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)}.
कार्टेशियन उत्पादों के कुछ बुनियादी गुण:
- A × ∅ = ∅.
- A × (B ∪ C) = (A × B) ∪ (A × C).
- (A ∪ B) × C = (A × C) ∪ (B × C).
चलो a और b परिमित सेट हो;तब कार्टेशियन उत्पाद की कार्डिनलिटी कार्डिनलिटीज का उत्पाद है:
- | A × B |= | B × A |= | ए |× | B | |
अनुप्रयोग
आधुनिक गणित में सेट सर्वव्यापी हैं।उदाहरण के लिए, अमूर्त बीजगणित में संरचनाएं, जैसे कि समूह, फ़ील्ड और रिंग, एक या अधिक संचालन के तहत बंद सेट हैं।
भोले सेट सिद्धांत के मुख्य अनुप्रयोगों में से एक संबंध के निर्माण में है।एक डोमेन से एक संबंध A एक कोडोमैन के लिए B कार्टेशियन उत्पाद का एक सबसेट है A × B।उदाहरण के लिए, सेट को देखते हुए S = {rock, paper, scissors} एक ही नाम के खेल में आकृतियाँ, संबंध से धड़कता है S प्रति S सेट है B = {(scissors,paper), (paper,rock), (rock,scissors)};इस प्रकार x धड़कता है y खेल में अगर जोड़ी (x,y) का सदस्य है B।एक अन्य उदाहरण सेट है F सभी जोड़े की (x, x2), कहाँ पे x यह सचमुच का है।यह संबंध एक सबसेट है R × R, क्योंकि सभी वर्गों का सेट सभी वास्तविक संख्याओं के सेट का सबसेट है।चूंकि हर के लिए x में R, एक और केवल एक जोड़ी (x,...) में पाया जाता है F, इसे एक फ़ंक्शन कहा जाता है।कार्यात्मक संकेतन में, इस संबंध को के रूप में लिखा जा सकता है F(x) = x2।
समावेश और बहिष्करण का सिद्धांत
समावेश -बहिष्करण सिद्धांत एक गिनती तकनीक है जिसका उपयोग दो सेटों के संघ में तत्वों की संख्या को गिनने के लिए किया जा सकता है - यदि प्रत्येक सेट का आकार और उनके चौराहे के आकार को जाना जाता है।इसे प्रतीकात्मक रूप से व्यक्त किया जा सकता है
डी मॉर्गन के नियम
ऑगस्टस डी मॉर्गन ने कहा कि डी मॉर्गन के कानून | सेट के बारे में दो कानून।
यदि A तथा B फिर भी दो सेट हैं,
- (A ∪ B)′ = A′ ∩ B′के पूरक A संघ B के पूरक के बराबर है A के पूरक के साथ जुड़ा हुआ है B।
- (A ∩ B)′ = A′ ∪ B′के पूरक A के साथ जुड़ा हुआ है B के पूरक के बराबर है A के पूरक के लिए संघ B।
यह भी देखें
- सेट का बीजगणित
- वैकल्पिक सेट सिद्धांत
- सेट की श्रेणी
- वर्ग (सेट सिद्धांत)
- घने सेट
- सेट का परिवार
- फजी सेट
- आंतरिक सेट
- मेरोलॉजी
- मल्टीसेट
- प्रिंसिपिया मैथेमेटिका
- रफ सेट
टिप्पणियाँ
- ↑ 1.0 1.1 Cantor, Georg; Jourdain, Philip E.B. (Translator) (1895). "beiträge zur begründung der transfiniten Mengenlehre" [contributions to the founding of the theory of transfinite numbers]. Mathematische Annalen (in German). New York Dover Publications (1954 English translation). xlvi, xlix: 481–512, 207–246. Archived from the original on 2011-06-10.
By an aggregate (Menge) we are to understand any collection into a whole (Zusammenfassung zu einem Gansen) M of definite and 'separate' objects m (p.85)
{{cite journal}}: CS1 maint: unrecognized language (link) - ↑ P. K. Jain; Khalil Ahmad; Om P. Ahuja (1995). Functional Analysis. New Age International. p. 1. ISBN 978-81-224-0801-0.
- ↑ Samuel Goldberg (1 January 1986). Probability: An Introduction. Courier Corporation. p. 2. ISBN 978-0-486-65252-8.
- ↑ Thomas H. Cormen; Charles E Leiserson; Ronald L Rivest; Clifford Stein (2001). Introduction To Algorithms. MIT Press. p. 1070. ISBN 978-0-262-03293-3.
- ↑ 5.0 5.1 5.2 Halmos 1960, p. 1.
- ↑ 6.0 6.1 Stoll, Robert (1974). Sets, Logic and Axiomatic Theories. W. H. Freeman and Company. pp. 5. ISBN 9780716704577.
- ↑ José Ferreirós (16 August 2007). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Birkhäuser Basel. ISBN 978-3-7643-8349-7.
- ↑ William Ewald; William Bragg Ewald (1996). From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics. OUP Oxford. p. 249. ISBN 978-0-19-850535-8.
- ↑ Bertrand Russell (1903) The Principles of Mathematics, chapter VI: Classes
- ↑ 10.0 10.1 Halmos 1960, p. 2.
- ↑ Jose Ferreiros (1 November 2001). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Springer Science & Business Media. ISBN 978-3-7643-5749-8.
- ↑ Seymor Lipschutz; Marc Lipson (22 June 1997). Schaum's Outline of Discrete Mathematics. McGraw Hill Professional. p. 1. ISBN 978-0-07-136841-4.
- ↑ 13.0 13.1 13.2 "Introduction to Sets". www.mathsisfun.com. Retrieved 2020-08-19.
- ↑ Charles Roberts (24 June 2009). Introduction to Mathematical Proofs: A Transition. CRC Press. p. 45. ISBN 978-1-4200-6956-3.
- ↑ David Johnson; David B. Johnson; Thomas A. Mowry (June 2004). Finite Mathematics: Practical Applications (Docutech Version). W. H. Freeman. p. 220. ISBN 978-0-7167-6297-3.
- ↑ Ignacio Bello; Anton Kaul; Jack R. Britton (29 January 2013). Topics in Contemporary Mathematics. Cengage Learning. p. 47. ISBN 978-1-133-10742-2.
- ↑ Susanna S. Epp (4 August 2010). Discrete Mathematics with Applications. Cengage Learning. p. 13. ISBN 978-0-495-39132-6.
- ↑ Stephen B. Maurer; Anthony Ralston (21 January 2005). Discrete Algorithmic Mathematics. CRC Press. p. 11. ISBN 978-1-4398-6375-6.
- ↑ D. Van Dalen; H. C. Doets; H. De Swart (9 May 2014). Sets: Naïve, Axiomatic and Applied: A Basic Compendium with Exercises for Use in Set Theory for Non Logicians, Working and Teaching Mathematicians and Students. Elsevier Science. p. 1. ISBN 978-1-4831-5039-0.
- ↑ Alfred Basta; Stephan DeLong; Nadine Basta (1 January 2013). Mathematics for Information Technology. Cengage Learning. p. 3. ISBN 978-1-285-60843-3.
- ↑ Laura Bracken; Ed Miller (15 February 2013). Elementary Algebra. Cengage Learning. p. 36. ISBN 978-0-618-95134-5.
- ↑ Halmos 1960, p. 4.
- ↑ 23.0 23.1 23.2 Frank Ruda (6 October 2011). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. p. 151. ISBN 978-1-4411-7413-0.
- ↑ 24.0 24.1 24.2 24.3 24.4 John F. Lucas (1990). Introduction to Abstract Mathematics. Rowman & Littlefield. p. 108. ISBN 978-0-912675-73-2.
- ↑ Weisstein, Eric W. "Set". mathworld.wolfram.com (in English). Retrieved 2020-08-19.
- ↑ Ralph C. Steinlage (1987). College Algebra. West Publishing Company. ISBN 978-0-314-29531-6.
- ↑ 27.0 27.1 Marek Capinski; Peter E. Kopp (2004). Measure, Integral and Probability. Springer Science & Business Media. p. 2. ISBN 978-1-85233-781-0.
- ↑ "Set Symbols". www.mathsisfun.com. Retrieved 2020-08-19.
- ↑ 29.0 29.1 Halmos 1960, p. 8.
- ↑ K.T. Leung; Doris Lai-chue Chen (1 July 1992). Elementary Set Theory, Part I/II. Hong Kong University Press. p. 27. ISBN 978-962-209-026-2.
- ↑ Aggarwal, M.L. (2021). "1. Sets". Understanding ISC Mathematics Class XI. Vol. 1. Arya Publications (Avichal Publishing Company). p. A=3.
- ↑ Sourendra Nath, De (January 2015). "Unit-1 Sets and Functions: 1. Set Theory". Chhaya Ganit (Ekadash Shreni). Scholar Books Pvt. Ltd. p. 5.
- ↑ Halmos 1960, Sect.2.
- ↑ 34.0 34.1 Felix Hausdorff (2005). Set Theory. American Mathematical Soc. p. 30. ISBN 978-0-8218-3835-8.
- ↑ Peter Comninos (6 April 2010). Mathematical and Computer Programming Techniques for Computer Graphics. Springer Science & Business Media. p. 7. ISBN 978-1-84628-292-8.
- ↑ 36.0 36.1 Halmos 1960, p. 3.
- ↑ 37.0 37.1 37.2 37.3 37.4 37.5 George Tourlakis (13 February 2003). Lectures in Logic and Set Theory: Volume 2, Set Theory. Cambridge University Press. p. 137. ISBN 978-1-139-43943-5.
- ↑ Yiannis N. Moschovakis (1994). Notes on Set Theory. Springer Science & Business Media. ISBN 978-3-540-94180-4.
- ↑ Arthur Charles Fleck (2001). Formal Models of Computation: The Ultimate Limits of Computing. World Scientific. p. 3. ISBN 978-981-02-4500-9.
- ↑ William Johnston (25 September 2015). The Lebesgue Integral for Undergraduates. The Mathematical Association of America. p. 7. ISBN 978-1-939512-07-9.
- ↑ Karl J. Smith (7 January 2008). Mathematics: Its Power and Utility. Cengage Learning. p. 401. ISBN 978-0-495-38913-2.
- ↑ John Stillwell (16 October 2013). The Real Numbers: An Introduction to Set Theory and Analysis. Springer Science & Business Media. ISBN 978-3-319-01577-4.
- ↑ David Tall (11 April 2006). Advanced Mathematical Thinking. Springer Science & Business Media. p. 211. ISBN 978-0-306-47203-9.
- ↑ Cantor, Georg (1878). "Ein Beitrag zur Mannigfaltigkeitslehre". Journal für die Reine und Angewandte Mathematik. 1878 (84): 242–258. doi:10.1515/crll.1878.84.242.
- ↑ Cohen, Paul J. (December 15, 1963). "The Independence of the Continuum Hypothesis". Proceedings of the National Academy of Sciences of the United States of America. 50 (6): 1143–1148. Bibcode:1963PNAS...50.1143C. doi:10.1073/pnas.50.6.1143. JSTOR 71858. PMC 221287. PMID 16578557.
- ↑ Halmos 1960, p. 19.
- ↑ Halmos 1960, p. 20.
- ↑ Edward B. Burger; Michael Starbird (18 August 2004). The Heart of Mathematics: An invitation to effective thinking. Springer Science & Business Media. p. 183. ISBN 978-1-931914-41-3.
- ↑ Toufik Mansour (27 July 2012). Combinatorics of Set Partitions. CRC Press. ISBN 978-1-4398-6333-6.
- ↑ Halmos 1960, p. 28.
संदर्भ
- Dauben, Joseph W. (1979). Georg Cantor: His Mathematics and Philosophy of the Infinite. Boston: Harvard University Press. ISBN 0-691-02447-2.
- Halmos, Paul R. (1960). Naive Set Theory. Princeton, N.J.: Van Nostrand. ISBN 0-387-90092-6.
- Stoll, Robert R. (1979). Set Theory and Logic. Mineola, N.Y.: Dover Publications. ISBN 0-486-63829-4.
- Velleman, Daniel (2006). How To Prove It: A Structured Approach. Cambridge University Press. ISBN 0-521-67599-5.
बाहरी संबंध
 The dictionary definition of set at Wiktionary
The dictionary definition of set at Wiktionary- Cantor's "Beiträge zur Begründung der transfiniten Mengenlehre" (in German)