समीकरण: Difference between revisions
(Added Internal link) |
mNo edit summary |
||
| Line 5: | Line 5: | ||
== समीकरण बनाना == | == समीकरण बनाना == | ||
वास्तविक समाधान में जाने से पहले हमें समीकरणों पर कुछ प्रारंभिक संचालन करने की आवश्यकता है। | वास्तविक समाधान में जाने से पहले, हमें समीकरणों पर कुछ प्रारंभिक संचालन करने की आवश्यकता है। | ||
हमें प्रस्तावित समस्या की दी गई शर्तों से समीकरण (''समी-करण, समी-करा या समी-क्रिया''; ''समा, बराबर'' और ''कर्'' से करना; इसलिए शाब्दिक रूप से, समान बनाना) बनाने की आवश्यकता है। इसके लिए बीजगणित या अंकगणित की एक या एक से अधिक मूलभूत संक्रियाओं को लागू करने की आवश्यकता हो सकती है। | हमें प्रस्तावित समस्या की दी गई शर्तों से समीकरण (''समी-करण, समी-करा या समी-क्रिया''; ''समा, बराबर'' और ''कर्'' से करना; इसलिए शाब्दिक रूप से, समान बनाना) बनाने की आवश्यकता है। इसके लिए बीजगणित या अंकगणित की एक या एक से अधिक मूलभूत संक्रियाओं को लागू करने की आवश्यकता हो सकती है। | ||
[[भास्कर द्वितीय]] कहते हैं: "''यावत्-तावत्'' " को अज्ञात मात्रा का मान मान लें। फिर ठीक वैसा ही करें जैसा कि विशेष रूप से बताया गया है- किसी समीकरण के दो बराबर पक्षों को घटाना, जोड़ना, गुणा करना या भाग देना बहुत सावधानी से बनाया जाना चाहिए। | [[भास्कर द्वितीय]] कहते हैं: "''यावत्-तावत्'' " को अज्ञात मात्रा का मान/मूल्य मान लें। फिर ठीक वैसा ही करें, जैसा कि विशेष रूप से बताया गया है- किसी समीकरण के दो बराबर पक्षों को घटाना, जोड़ना, गुणा करना या भाग देना बहुत सावधानी से बनाया जाना चाहिए। | ||
[[File:Equation illustration colour.svg|thumb|बीजीय व्यंजक और बीजीय समीकरण]] | [[File:Equation illustration colour.svg|thumb|बीजीय व्यंजक और बीजीय समीकरण]] | ||
| Line 25: | Line 25: | ||
अत: 'x + 10' एक बीजीय व्यंजक है। | अत: 'x + 10' एक बीजीय व्यंजक है। | ||
बीजगणित प्रतीकों के प्रयोग का उपयोग करता है। ये प्रतीक अज्ञात मात्राओं और उनके साथ किए गए कार्यों का प्रतिनिधित्व करते हैं। निम्नलिखित तालिका में वे प्रतीक दिए गए हैं जिनका उपयोग प्राचीन भारतीय गणितज्ञों द्वारा कुछ बुनियादी कार्यों के लिए किया गया था। | बीजगणित प्रतीकों के प्रयोग का उपयोग करता है। ये प्रतीक अज्ञात मात्राओं और उनके साथ किए गए कार्यों का प्रतिनिधित्व करते हैं। निम्नलिखित तालिका में वे प्रतीक दिए गए हैं, जिनका उपयोग प्राचीन भारतीय गणितज्ञों द्वारा कुछ बुनियादी कार्यों के लिए किया गया था। | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
| Line 109: | Line 109: | ||
|} | |} | ||
अक्षर ''या'' (''यावत्-तावत्'' का संक्षिप्त रूप) अज्ञात मात्रा का सबसे लोकप्रिय प्रतिनिधित्व था। इसके वर्ग को ''याव'' | अक्षर '<nowiki/>''या'' '(''यावत्-तावत्'' का संक्षिप्त रूप),अज्ञात मात्रा का सबसे लोकप्रिय प्रतिनिधित्व था। इसके वर्ग को '<nowiki/>''याव'' ' कहा जाता था, जो ''यावत्-तावत्-वर्ग'' (''वर्ग'' का अर्थ वर्ग) का संक्षिप्त नाम था। स्थिर पद को '''रू'' 'अक्षर से निरूपित किया गया था, जो ''रूपा'' का एक संक्षिप्त नाम है जैसा कि उपरोक्त तालिका में दिखाया गया है। समीकरण में किसी भी ऋणात्मक चिह्न को पद के ऊपर एक बिंदु द्वारा दर्शाया जाता है। | ||
यदि किसी व्यंजक में तीन अज्ञात मात्राएँ हैं, तो प्रयुक्त चिह्न ''या'' , ''का'', और ''नी'' हैं। ये ''यावत्-तावत्,'' ''कालका'' और ''नीलका'' के संक्षिप्त रूप हैं। पहली दो अज्ञात मात्राओं के | यदि किसी व्यंजक में तीन अज्ञात मात्राएँ हैं, तो प्रयुक्त चिह्न ''या'' , ''का'', और ''नी'' हैं। ये ''यावत्-तावत्,'' ''कालका'' और ''नीलका'' के संक्षिप्त रूप हैं। पहली दो अज्ञात मात्राओं के गुणनफल को ''याकाभा'' के रूप में दर्शाया जाता है जहाँ ''या'' और ''का'' दो अज्ञात हैं और ''भा'' उनके गुणनफल के लिए है। | ||
निम्नलिखित तालिका प्राचीन भारतीय गणितज्ञों द्वारा प्रयुक्त कुछ बीजीय व्यंजकों का निरूपण करती है। | निम्नलिखित तालिका प्राचीन भारतीय गणितज्ञों द्वारा प्रयुक्त कुछ बीजीय व्यंजकों का निरूपण करती है। | ||
| Line 155: | Line 155: | ||
x<sup>2</sup>, x<sup>1</sup>, x<sup>0</sup> (स्थिर पद/अवधि) की स्थितियों का निरीक्षण करने पर कुछ स्वरूप मिलता है? समीकरण लिखने का सामान्य तरीका x की उच्चतम घात से प्रारंभ होता है। तब x की घातों को उसके निम्नतम घात तक अवरोही क्रम(descending order) में लिखा गया था। समीकरण लिखने के इस प्रारूप का अनुसरण प्राचीन काल से गणितज्ञों द्वारा किया जाता रहा है। | x<sup>2</sup>, x<sup>1</sup>, x<sup>0</sup> (स्थिर पद/अवधि) की स्थितियों का निरीक्षण करने पर कुछ स्वरूप मिलता है? समीकरण लिखने का सामान्य तरीका x की उच्चतम घात से प्रारंभ होता है। तब x की घातों को उसके निम्नतम घात तक अवरोही क्रम(descending order) में लिखा गया था। समीकरण लिखने के इस प्रारूप का अनुसरण प्राचीन काल से गणितज्ञों द्वारा किया जाता रहा है। | ||
[[ब्रह्मगुप्त]] ने समीकरण को ''समकरण'' या ''संकरण'' | [[ब्रह्मगुप्त]] ने समीकरण को ''समकरण'' या ''संकरण'' कहा है। इसका अर्थ है 'समान बनाना'। एक समीकरण के दो पक्षों (LHS और RHS) को एक के नीचे एक लिखा गया था। प्रतीक '=' का प्रयोग नहीं किया गया था। एक समीकरण के दोनों पक्षों को अज्ञात के लिए उपयुक्त मान (मानों) को खोजने के द्वारा समान बनाया गया था। | ||
चतुर्वेद पृथूदकस्वामिन् (864 ईस्वी) ने ब्रह्म-स्फूट-सिद्धांत पर अपनी टिप्पणी में समीकरण 40x - 48 = x<sup>2</sup> + 51 को नीचे के रूप में लिखा है | चतुर्वेद पृथूदकस्वामिन् (864 ईस्वी) ने ब्रह्म-स्फूट-सिद्धांत पर अपनी टिप्पणी में समीकरण 40x - 48 = x<sup>2</sup> + 51 को नीचे के रूप में लिखा है | ||
| Line 193: | Line 193: | ||
''भागादिकं रूपवदेव शेषं व्यक्ते यदुक्तं गणिते तदत्र ॥''<ref>Bījagaṇita, ch. Avyaktādi-guṇana, vs.6,7, p.8</ref> | ''भागादिकं रूपवदेव शेषं व्यक्ते यदुक्तं गणिते तदत्र ॥''<ref>Bījagaṇita, ch. Avyaktādi-guṇana, vs.6,7, p.8</ref> | ||
"एक संख्यात्मक स्थिरांक और एक अज्ञात मात्रा का गुणनफल एक अज्ञात मात्रा है। दो या तीन समान पदों के गुणनफल उनके वर्ग या घन (क्रमशः) होते हैं। विषम पदों का गुणनफल ''भाविता'' है। भिन्न आदि ज्ञात की स्थति में हैं। अन्य (प्रक्रियाएं) वही हैं जो अंकगणित में बताए गए हैं।" | "एक संख्यात्मक स्थिरांक और एक अज्ञात मात्रा का गुणनफल एक अज्ञात मात्रा है। दो या तीन समान पदों के गुणनफल उनके वर्ग या घन (क्रमशः) होते हैं। विषम पदों का गुणनफल ''भाविता'' है। भिन्न आदि ज्ञात की स्थति में हैं। अन्य (प्रक्रियाएं) वही हैं जो अंकगणित में बताए गए हैं।" | ||
=== बीजीय व्यंजकों का जोड़ और घटाव === | === बीजीय व्यंजकों का जोड़ और घटाव === | ||
| Line 204: | Line 204: | ||
'''व्याख्या:''' | '''व्याख्या:''' | ||
जोड़ और घटाव समान पदों के साथ किया जा सकता है और विपरीत पदों को अलग-अलग रखा जाना है। समान घातों के लिए उठाए गए समान अक्षर चर को समान पदों के रूप में माना जाता है। उदा., ''या ४,या ५, या ६'' समान पद हैं। ''याव ७, याव ८, याव ९'' भी समान पद हैं। ''का ३, का ७, का १५'' भी समान पद हैं। वर्तमान में हम कहते हैं कि 4x, 5x, 6x समान पद हैं। इसी प्रकार 7x<sup>2</sup>, 8x<sup>2</sup>, 9x<sup>2</sup> समान पद हैं। और 3y, 7y, 15y भी समान पद हैं।जब हमारे पास समान पद होते हैं, तो योग और अंतर को सरल बनाया जा सकता है। उदा. 4x + 6x को 10x के रूप में सरल बनाया जा सकता है। 9x<sup>2</sup> - 7x<sup>2</sup> को 2x<sup>2</sup> के रूप में सरल बनाया जा सकता है। | जोड़ और घटाव समान पदों के साथ किया जा सकता है, और विपरीत पदों को अलग-अलग रखा जाना होता है। समान घातों के लिए उठाए गए समान अक्षर चर को समान पदों के रूप में माना जाता है। उदा., ''या ४,या ५, या ६'' समान पद हैं। ''याव ७, याव ८, याव ९'' भी समान पद हैं। ''का ३, का ७, का १५'' भी समान पद हैं। वर्तमान में हम कहते हैं कि 4x, 5x, 6x समान पद हैं। इसी प्रकार 7x<sup>2</sup>, 8x<sup>2</sup>, 9x<sup>2</sup> समान पद हैं। और 3y, 7y, 15y भी समान पद हैं।जब हमारे पास समान पद होते हैं, तो योग और अंतर को सरल बनाया जा सकता है। उदा. 4x + 6x को 10x के रूप में सरल बनाया जा सकता है। 9x<sup>2</sup> - 7x<sup>2</sup> को 2x<sup>2</sup> के रूप में सरल बनाया जा सकता है। | ||
विपरीत पद वे पद हैं जिनमें भिन्न-भिन्न चर या भिन्न-भिन्न घात वाले चर होते हैं। उदा | विपरीत पद वे पद हैं, जिनमें भिन्न-भिन्न चर या भिन्न-भिन्न घात वाले चर होते हैं। उदा: ''या'' ३, ''याव'' ३, ''याघ'' ४, ''का'' ५, ''काव'', ''याकाभा'' । आधुनिक संकेतन में, इन्हें 3x, 3x<sup>2</sup>, 4x<sup>3</sup>, 5y, y<sup>2</sup>, xy के रूप में दर्शाया जाता है। | ||
=== बीजीय व्यंजकों का गुणन === | === बीजीय व्यंजकों का गुणन === | ||
बीजगणित गुणन का नियम देता है - | बीजगणित गुणन का नियम देता इस प्रकार देता है - | ||
''गुण्यः पृथग्गुणकखण्डसमो निवेश्यस्तैः खण्डकैः क्रमहतः सहितो यथोक्त्या।'' | ''गुण्यः पृथग्गुणकखण्डसमो निवेश्यस्तैः खण्डकैः क्रमहतः सहितो यथोक्त्या।'' | ||
| Line 215: | Line 215: | ||
''अव्यक्तवर्गकरणीगणनास चिन्त्यो व्यक्तोक्तखण्डगुणनाविधिरेवमत्र॥''<ref>Bījagaṇita ch. Avyaktādi-guṇana, vs.8, p.8</ref> | ''अव्यक्तवर्गकरणीगणनास चिन्त्यो व्यक्तोक्तखण्डगुणनाविधिरेवमत्र॥''<ref>Bījagaṇita ch. Avyaktādi-guṇana, vs.8, p.8</ref> | ||
"गुण्य को गुणक के पदों के रूप में कई स्थानों पर रखें। गुणक के पदों को अलग-अलग क्रम से गुणा करें और समस्या में निर्देशानुसार परिणाम जोड़ें। यह अज्ञात संख्याओं और करणी (surd/सर्ड) के वर्गों कि स्थिति में भी लागू होता है। अंकगणितीय संख्याओं के स्थिति में बताई गई आंशिक | "गुण्य को गुणक के पदों के रूप में कई स्थानों पर रखें। गुणक के पदों को अलग-अलग क्रम से गुणा करें और समस्या में निर्देशानुसार परिणाम जोड़ें। यह अज्ञात संख्याओं और करणी (surd/सर्ड) के वर्गों कि स्थिति में भी लागू होता है। अंकगणितीय संख्याओं के स्थिति में बताई गई आंशिक गुणनफलों (partial products) की विधि यहां भी लागू होती है।" | ||
'''व्याख्या''' | '''व्याख्या''' | ||
| Line 223: | Line 223: | ||
|- | |- | ||
|यदि या २ रू ४ और या ३ रू ५ क्रमशः गुण्य और गुणक हैं, | |यदि या २ रू ४ और या ३ रू ५ क्रमशः गुण्य और गुणक हैं, | ||
उनका | उनका गुणनफल निम्नानुसार प्राप्त किया जा सकता है: | ||
|यदि 2x + 4 और 3x + 5 क्रमशः गुण्य और गुणक हैं, | |यदि 2x + 4 और 3x + 5 क्रमशः गुण्य और गुणक हैं, | ||
उनका | उनका गुणनफल निम्नानुसार प्राप्त किया जा सकता है: | ||
|- | |- | ||
|गुणक के दो पद होते हैं, अर्थात् या ३ और रू ५ | |गुणक के दो पद होते हैं, अर्थात् या ३ और रू ५ | ||
Revision as of 19:13, 16 August 2022
समीकरण | |
|---|---|
 |
समीकरण बनाना
वास्तविक समाधान में जाने से पहले, हमें समीकरणों पर कुछ प्रारंभिक संचालन करने की आवश्यकता है।
हमें प्रस्तावित समस्या की दी गई शर्तों से समीकरण (समी-करण, समी-करा या समी-क्रिया; समा, बराबर और कर् से करना; इसलिए शाब्दिक रूप से, समान बनाना) बनाने की आवश्यकता है। इसके लिए बीजगणित या अंकगणित की एक या एक से अधिक मूलभूत संक्रियाओं को लागू करने की आवश्यकता हो सकती है।
भास्कर द्वितीय कहते हैं: "यावत्-तावत् " को अज्ञात मात्रा का मान/मूल्य मान लें। फिर ठीक वैसा ही करें, जैसा कि विशेष रूप से बताया गया है- किसी समीकरण के दो बराबर पक्षों को घटाना, जोड़ना, गुणा करना या भाग देना बहुत सावधानी से बनाया जाना चाहिए।
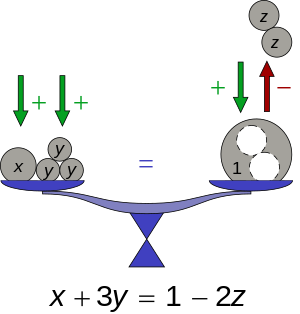
बीजीय व्यंजक और बीजीय समीकरण
बीजीय व्यंजक को निम्न उदाहरण [1]से समझा जा सकता है।
राम कहता है कि उसके पास श्याम से 10 सिक्के ज्यादा हैं। हम ठीक से नहीं जानते कि श्याम के पास कितने सिक्के हैं। उसके पास कितने भी सिक्के हो सकते हैं। लेकिन हम जानते हैं कि राम के सिक्कों की संख्या = श्याम के सिक्कों की संख्या + 10
हम 'श्याम के सिक्कों की संख्या' को अक्षर x से निरूपित करेंगे। यहाँ x अज्ञात है जो 1, 2, 3, 4 आदि हो सकता है।
x का प्रयोग करके हम लिखते हैं,
राम के सिक्कों की संख्या = x+10
अत: 'x + 10' एक बीजीय व्यंजक है।
बीजगणित प्रतीकों के प्रयोग का उपयोग करता है। ये प्रतीक अज्ञात मात्राओं और उनके साथ किए गए कार्यों का प्रतिनिधित्व करते हैं। निम्नलिखित तालिका में वे प्रतीक दिए गए हैं, जिनका उपयोग प्राचीन भारतीय गणितज्ञों द्वारा कुछ बुनियादी कार्यों के लिए किया गया था।
| क्रमांक | बीजीय व्यंजक का संघटक | संस्कृत शब्द | प्रतीक/चिह्न | उदाहरण | |
|---|---|---|---|---|---|
| 1 | अज्ञात | यावत्तावत्
कालकः नीलकः , ...... |
या
का नी , ........ |
या ३५
का १४ नी ८२ |
35x
14y 82z |
| 2 | योगफल | योगः | - | या का
या ३५ का १४ |
x + y
35x + 14y |
| 3 | गुणनफल | भावितम् | भा | याकाभा
याकाभा ३२ |
xy
32xy |
| 4 | वर्ग | वर्गः | व | याव | x2 |
| 5 | घनक्षेत्र | घनः | घ | याघ | x3 |
| 6 | चौथी शक्ति | वर्ग-वर्गः | वव | यावव | x4 |
| 7 | स्थायी अवधि | रूपम् | रू | रू ३२ | 32 |
| 8 | ऋणात्मक | ऋणम् | मात्रा के ऊपर बिंदु (.) | .
रू ४३२ |
-432 |
अक्षर 'या '(यावत्-तावत् का संक्षिप्त रूप),अज्ञात मात्रा का सबसे लोकप्रिय प्रतिनिधित्व था। इसके वर्ग को 'याव ' कहा जाता था, जो यावत्-तावत्-वर्ग (वर्ग का अर्थ वर्ग) का संक्षिप्त नाम था। स्थिर पद को 'रू 'अक्षर से निरूपित किया गया था, जो रूपा का एक संक्षिप्त नाम है जैसा कि उपरोक्त तालिका में दिखाया गया है। समीकरण में किसी भी ऋणात्मक चिह्न को पद के ऊपर एक बिंदु द्वारा दर्शाया जाता है।
यदि किसी व्यंजक में तीन अज्ञात मात्राएँ हैं, तो प्रयुक्त चिह्न या , का, और नी हैं। ये यावत्-तावत्, कालका और नीलका के संक्षिप्त रूप हैं। पहली दो अज्ञात मात्राओं के गुणनफल को याकाभा के रूप में दर्शाया जाता है जहाँ या और का दो अज्ञात हैं और भा उनके गुणनफल के लिए है।
निम्नलिखित तालिका प्राचीन भारतीय गणितज्ञों द्वारा प्रयुक्त कुछ बीजीय व्यंजकों का निरूपण करती है।
| क्रमांक | आधुनिक संकेतन | प्राचीन भारतीय संकेतन |
|---|---|---|
| 1 | x + 17 | या १ रू १७ |
| 2 | 7x - 17 | या ७ रू १७. |
| 3 | 18x – 8 | या १८ रू ८. |
| 4 | 15x2 + 17x - 2 | याव १५ या ७ रू २. |
| 5 | 1x4 + 16x3 + 25x2 + 8x + 6 | यावव १ याघ १६ याव २५ या ८ रू ६ |
| 6 | 8x2 + 12xy - 6xz -16x | याव ८ याकाभा १२ यानीभा ६. या १६. |
हम देखेंगे कि प्राचीन भारतीय गणितज्ञों द्वारा बीजीय व्यंजक कैसे लिखे जाते हैं।
समीकरण 10x - 8 = x2 +1 पर विचार करें
इसे इस प्रकार लिखा जा सकता है,
0x2 + 10x - 8 = 1x2 + 0x + 1
x2, x1, x0 (स्थिर पद/अवधि) की स्थितियों का निरीक्षण करने पर कुछ स्वरूप मिलता है? समीकरण लिखने का सामान्य तरीका x की उच्चतम घात से प्रारंभ होता है। तब x की घातों को उसके निम्नतम घात तक अवरोही क्रम(descending order) में लिखा गया था। समीकरण लिखने के इस प्रारूप का अनुसरण प्राचीन काल से गणितज्ञों द्वारा किया जाता रहा है।
ब्रह्मगुप्त ने समीकरण को समकरण या संकरण कहा है। इसका अर्थ है 'समान बनाना'। एक समीकरण के दो पक्षों (LHS और RHS) को एक के नीचे एक लिखा गया था। प्रतीक '=' का प्रयोग नहीं किया गया था। एक समीकरण के दोनों पक्षों को अज्ञात के लिए उपयुक्त मान (मानों) को खोजने के द्वारा समान बनाया गया था।
चतुर्वेद पृथूदकस्वामिन् (864 ईस्वी) ने ब्रह्म-स्फूट-सिद्धांत पर अपनी टिप्पणी में समीकरण 40x - 48 = x2 + 51 को नीचे के रूप में लिखा है
| देवनागरी | लिप्यंतरण | आधुनिक संकेतन | |
|---|---|---|---|
| याव ० या ४० रू ४८.
याव १ या ० रू ५१ |
याव 0 या 40 rū 48.
याव 1 या 0 rū 51 |
⇒ | 0x2 + 0 x - 8 = 1x2 + 0x + 51 |
भास्कर द्वितीय के बीजगणित से समीकरण का एक और उदाहरण यहां दिया गया है:
x4 - 2x2 - 400x = 9999
इसे इस प्रकार दर्शाया गया है,
यावव १ याव २. या ४.०० रू ०
यावव ० याव ० या ० रू ९९९९
बीजीय व्यंजकों के साथ संक्रिया
भास्कर द्वितीय बीजगणितीय शब्दों का उपयोग करते हुए संक्रियाएँ इस प्रकार देते हैं :
स्याद्रूपवर्णाभिहतौ तु वर्णो द्वित्र्यादिकानां समजातिकानाम् ॥
वधे तु तद्वर्गघनादयः स्युस्तद्भावितं चासमजातिघाते।
भागादिकं रूपवदेव शेषं व्यक्ते यदुक्तं गणिते तदत्र ॥[2]
"एक संख्यात्मक स्थिरांक और एक अज्ञात मात्रा का गुणनफल एक अज्ञात मात्रा है। दो या तीन समान पदों के गुणनफल उनके वर्ग या घन (क्रमशः) होते हैं। विषम पदों का गुणनफल भाविता है। भिन्न आदि ज्ञात की स्थति में हैं। अन्य (प्रक्रियाएं) वही हैं जो अंकगणित में बताए गए हैं।"
बीजीय व्यंजकों का जोड़ और घटाव
भास्कर द्वितीय अज्ञात मात्राओं के जोड़ और घटाव का नियम इस प्रकार देते हैं:
योगोऽन्तरं तेषु समानजात्योर्विभिन्नजात्योश्च पृथक् स्थितिश्च।[3]
"जोड़ और घटाव समान पदों के बीच किया जाता है। विपरीत/विषम शब्दों को अलग रखा जाना चाहिए।"
व्याख्या:
जोड़ और घटाव समान पदों के साथ किया जा सकता है, और विपरीत पदों को अलग-अलग रखा जाना होता है। समान घातों के लिए उठाए गए समान अक्षर चर को समान पदों के रूप में माना जाता है। उदा., या ४,या ५, या ६ समान पद हैं। याव ७, याव ८, याव ९ भी समान पद हैं। का ३, का ७, का १५ भी समान पद हैं। वर्तमान में हम कहते हैं कि 4x, 5x, 6x समान पद हैं। इसी प्रकार 7x2, 8x2, 9x2 समान पद हैं। और 3y, 7y, 15y भी समान पद हैं।जब हमारे पास समान पद होते हैं, तो योग और अंतर को सरल बनाया जा सकता है। उदा. 4x + 6x को 10x के रूप में सरल बनाया जा सकता है। 9x2 - 7x2 को 2x2 के रूप में सरल बनाया जा सकता है।
विपरीत पद वे पद हैं, जिनमें भिन्न-भिन्न चर या भिन्न-भिन्न घात वाले चर होते हैं। उदा: या ३, याव ३, याघ ४, का ५, काव, याकाभा । आधुनिक संकेतन में, इन्हें 3x, 3x2, 4x3, 5y, y2, xy के रूप में दर्शाया जाता है।
बीजीय व्यंजकों का गुणन
बीजगणित गुणन का नियम देता इस प्रकार देता है -
गुण्यः पृथग्गुणकखण्डसमो निवेश्यस्तैः खण्डकैः क्रमहतः सहितो यथोक्त्या।
अव्यक्तवर्गकरणीगणनास चिन्त्यो व्यक्तोक्तखण्डगुणनाविधिरेवमत्र॥[4]
"गुण्य को गुणक के पदों के रूप में कई स्थानों पर रखें। गुणक के पदों को अलग-अलग क्रम से गुणा करें और समस्या में निर्देशानुसार परिणाम जोड़ें। यह अज्ञात संख्याओं और करणी (surd/सर्ड) के वर्गों कि स्थिति में भी लागू होता है। अंकगणितीय संख्याओं के स्थिति में बताई गई आंशिक गुणनफलों (partial products) की विधि यहां भी लागू होती है।"
व्याख्या
| प्राचीन भारतीय संकेतन | आधुनिक संकेतन |
|---|---|
| यदि या २ रू ४ और या ३ रू ५ क्रमशः गुण्य और गुणक हैं,
उनका गुणनफल निम्नानुसार प्राप्त किया जा सकता है: |
यदि 2x + 4 और 3x + 5 क्रमशः गुण्य और गुणक हैं,
उनका गुणनफल निम्नानुसार प्राप्त किया जा सकता है: |
| गुणक के दो पद होते हैं, अर्थात् या ३ और रू ५ | गुणक के दो पद हैं, अर्थात् 3x और 5 |
| गुण्य को दो स्थानों पर रखें। उन्हें गुणक के पदों से अलग से गुणा करें जैसा कि दिखाया गया है।
(या २ रू ४)) X या ३ = याव ६ या १२ (या २ रू ४)) X रू ५ = या १० रू २० |
गुण्य को दो स्थानों पर रखें। उन्हें गुणक के पदों से अलग से गुणा करें जैसा कि दिखाया गया है।
(2x + 4) X 3x = 6x2 + 12x (2x + 4) X 5 = 10x + 20 |
| परिणाम जोड़ें।
गुणन परिणाम है:: याव् ६ या २२ रू २० |
परिणाम जोड़ें।
गुणन परिणाम है: 6x2 + 22x + 20 |
यदि और क्रमशः गुण्य और गुणक हैं, तो उनका गुणनफल निम्नानुसार प्राप्त किया जा सकता है:
गुणक के दो पद हैं, अर्थात् cx और d। गुणक को दो स्थानों पर रखें। उन्हें गुणक के पदों से अलग से गुणा करें जैसा कि दिखाया गया है।
परिणाम जोड़ें।
गुणन परिणाम है:
समीकरणों का वर्गीकरण
लगभग 300 ई.पू. के विहित कार्य में यह पाया गया है कि समीकरणों का हिंदू वर्गीकरण उनकी घातों के अनुसार हुआ है, जैसे कि सरल (तकनीकी रूप से यावत्-तावत् कहा जाता है), द्विघात (वर्ग), घनीय(घन) और द्विघात (वर्ग-वर्ग))।
लेकिन आगे के पुष्ट प्रमाणों के अभाव में, हम इसके बारे में सुनिश्चित नहीं हो सकते। ब्रह्मगुप्त (628) ने समीकरणों को इस प्रकार वर्गीकृत किया है: (I) एक अज्ञात में समीकरण (एक-वर्ण-समीकरण), (2) कई अज्ञात में समीकरण (अनेक-वर्ण-समीकरण), और (3) अज्ञात के उत्पादों से जुड़े समीकरण (भैविता)।
एक अज्ञात में समीकरणों (एक-वर्ण-समीकरण) को फिर से दो उप वर्गों में विभाजित किया जाता है, अर्थात, (i) रैखिक समीकरण, और (ii) द्विघात समीकरण (अव्यक्त-वर्ग-समीकरण)।यहाँ से हमारे पास समीकरणों को उनकी घातों के अनुसार वर्गीकृत करने की हमारी वर्तमान पद्धति की शुरुआत है। चतुर्वेद पृथुदकास्वामी (860) द्वारा अपनाई गई वर्गीकरण की पद्धति थोड़ी भिन्न है। उन्होंने वर्गीकृत किया: (1) एक अज्ञात के साथ रैखिक समीकरण, (2) अधिक अज्ञात के साथ रैखिक समीकरण, (3) उनकी दूसरी और उच्च घातों में एक, दो या अधिक अज्ञात के साथ समीकरण, और (4) अज्ञात के उत्पादों को शामिल करने वाले समीकरण। चूंकि तृतीय वर्ग के समीकरण के समाधान की विधि मध्य पद के उन्मूलन के सिद्धांत पर आधारित है, इसलिए उस वर्ग को मध्यमाहारण (मध्यम से, "मध्य", अहारण "उन्मूलन", इसलिए अर्थ -" मध्य अवधि का उन्मूलन" कहा जाता है।")। अन्य वर्गों के लिए, ब्रह्मगुप्त द्वारा दिए गए पुराने नामों को बरकरार रखा गया है। वर्गीकरण की इस पद्धति का अनुसरण बाद के लेखकों ने किया है।
भास्कर द्वितीय तीसरे वर्ग में दो प्रकारों को अलग करते हैं , अर्थात् "(i) अपनी दूसरी और उच्च घातों में एक अज्ञात में समीकरण और (ii) अपनी दूसरी और उच्च घातों में दो या दो से अधिक अज्ञात में समीकरण।' कृष्ण के अनुसार (1580) समीकरण मुख्य रूप से दो वर्गों के होते हैं: (1) एक अज्ञात में समीकरण और (2) दो या दो से अधिक अज्ञात में समीकरण। पहले वर्गीकरण में दो उपवर्ग शामिल हैं: (i) सरल समीकरण और (ii) द्विघात और उच्च समीकरण। दूसरे वर्गीकरण में तीन उपवर्ग हैं: (i) एक साथ रैखिक समीकरण, (ii) अज्ञात की दूसरी और उच्च घातों वाले समीकरण, और (iii) अज्ञात के उत्पादों को शामिल करने वाले समीकरण। फिर वह देखते हैं कि इन पांच वर्गों को, कक्षा (1) और (2) के दूसरे उपवर्गों को मध्यमाहारण के रूप में एक वर्ग में शामिल करके, घटाकर चार किया जा सकता है।
एक अज्ञात में रैखिक समीकरण
एक रैखिक समीकरण एक समीकरण है जिसमें चर, गुणांक और स्थिरांक की केवल पहली घात होती है। उदाहरण के लिए, समीकरण 4x + 7 = 8 एक चर में एक रैखिक समीकरण है। इसे प्रथम-क्रम समीकरण कहा जाता है क्योंकि चर (x) की घात एक है। यदि समीकरण में x की उच्चतम शक्ति दो के रूप में है, अर्थात x2 , तो यह एक द्विघात (द्वितीय क्रम) समीकरण होगा।
प्रारंभिक समाधान:
जैसा कि पहले ही कहा गया है, एक अज्ञात में एक रैखिक समीकरण का ज्यामितीय समाधान शुल्बसूत्र; śulba में पाया जाता है, जिसमें से सबसे पहला 800 ईसा पूर्व के बाद का नहीं है।
स्थानांग-सूत्र (सी 300 ईसा पूर्व) में इसके नाम (यावत्-तावत्) से एक रैखिक समीकरण का संदर्भ है, जो उस समय के समाधान की विधि का सूचक है।
बख्शाली ग्रंथ में सरल बीजगणितीय समीकरणों और समाधान पद्धति से जुड़ी समस्याएं हैं, जो शायद ईसाई युग की शुरुआत में लिखी गई थीं।
एक समस्या यह है कि "पहले को दी गई राशि ज्ञात नहीं है। दूसरे को पहले की तुलना में दोगुना दिया जाता है, तीसरे को दूसरे से तीन गुना और चौथे को तीसरे से चार गुना अधिक दिया जाता है। वितरित की गई कुल राशि है 132, पहले की राशि क्या है?"
यदि x पहले को दी गई राशि हो, तो समस्या के अनुसार,
असत्य स्थिति का नियम:
इस समीकरण का हल इस प्रकार दिया गया है:
"'किसी भी वांछित मात्रा को रिक्त स्थान पर रखना'; कोई भी वांछित मात्रा 1 है; 'फिर श्रृंखला का निर्माण करें।
| 1 | 2 | 2 3 | 6 4 |
| 1 | 1 | 1 1 | 1 1 |
'गुणा किया हुआ'
| 1 | 2 | 2*3=6 | 6*4 =24 |
| 1 | 2 | 6 | 24 |
जोड़ा गया
1 + 2 + 6 + 24 = 33
जोड़ा गया' 33.
"दृश्यमान मात्रा को विभाजित करें'
| 132
33 |
(जो) कमी करने पर बन जाता है
| 4
1 |
(यह है) दी गई राशि (पहले को)।"
बख्शाली ग्रंथ में समस्याओं के समूह का ,एक और समाधान अंततः ax+ b=p प्रकार के समीकरण की ओर ले जाता है। इसके समाधान के लिए दी गई विधि यह है कि x के लिए कोई मनमाना मान g रखा जाए, ताकि
ag+ b =p' कहा जाए ।
तब सही मान होगा
रैखिक समीकरणों का हल
आर्यभट्ट (499) कहते हैं:
"दो व्यक्तियों से संबंधित ज्ञात "राशि" के अंतर को अज्ञात के गुणांकों के अंतर से विभाजित किया जाना चाहिए। भागफल अज्ञात का मान होगा, यदि उनकी संपत्ति समान हो।"
यह नियम इस प्रकार की समस्या पर विचार करता है: दो व्यक्ति, जो समान रूप से अमीर हैं, के पास क्रमशः c, d के साथ एक निश्चित अज्ञात राशि का a, b गुना है
नकद में पैसे की इकाइयों। वह राशि क्या है?
मान लीजिए x अज्ञात राशि है, दी गई जानकारी के साथ
ax + c = bx+ d
इसलिए
जिस वजह से नियम।
bx + c = dx + e के रूप के रैखिक समीकरण को हल करने का नियम, जहाँ b, c, d और e संख्याएँ दी गई हैं, ब्रह्मगुप्त द्वारा निम्नानुसार दिया गया है।
अव्यक्तान्तरभक्तं व्यस्ततां समानऽव्यक्तं।
कक्षा व्यक्ताः शोध यशद्रूपाणी तदधस्तात II [5]
"पूर्ण संख्याओं का अंतर, उत्क्रम और अज्ञात के अंतर से विभाजित, एक समीकरण में अज्ञात का [मान] है।"
व्याख्या: समीकरण पर विचार करें, bx + c = dx + e
यहाँ x अज्ञात राशि है जिसका मान ज्ञात करना है। अक्षर b और d इसके गुणांक हैं। शेष अक्षर c और e संख्यात्मक स्थिरांक हैं।
निरपेक्ष संख्याओं का अंतर = c-e
उत्क्रमित पूर्ण संख्याओं का अंतर = e-c
अज्ञात के गुणांकों का अंतर = b - d
x के रूप में पाया जाता है
भास्कर द्वितीय बताते हैं कि उपरोक्त सूत्र कैसे प्राप्त किया जाता है।
यावत्तावत् कल्प्यमव्यक्तराशेर्मानं तस्मिन् कुर्वतोद्दिष्टमेव ।
तुल्यौ पक्षौ साधनीयौ प्रयत्नात्त्यक्त्वा क्षिप्त्वा वाऽपि संगुण्य भक्त्वा ॥
एकाव्यक्तं शोधयेदन्यपक्षाद्रूपाण्यन्यस्येतरस्माच्च पक्षात्
शेषाव्यक्तेनोद्धरेद्रूपशेषं व्यक्तं मानं जायतेऽव्यक्तराशेः॥[6]
"अज्ञात मात्रा (x) मान लें। रद्द करने या कम करने या गुणा करने या विभाजित करने के बाद अज्ञात शब्दों से जुड़े कारकों को एक तरफ और स्थिर शब्दों को दूसरी तरफ स्थानांतरित करके वांछित प्रक्रिया करें। अज्ञात के गुणांक से पदों को विभाजित करें और अज्ञात कारक के मान की गणना करें।"
व्याख्या: उदाहरण के लिए, आइए हम निम्नलिखित समीकरण पर विचार करें:
6x - 5 = 2x + 3
(i) अज्ञात पदों वाले कारकों को एक तरफ और अचरों को दूसरी तरफ स्थानांतरित करने पर, हम प्राप्त करते हैं,
6x - 2x = 3 + 5
इसलिए, 4x = 8
ii) अज्ञात के गुणांक द्वारा पदों को विभाजित करने पर, हम प्राप्त करते हैं
x = 2
श्रीपति लिखते हैं:
"पहले ज्ञात पद को छोड़कर किसी भी पक्ष (समीकरण के) से अज्ञात को हटा दें; दूसरी तरफ उत्क्रम (किया जाना चाहिए)। उत्क्रमण (उल्टे क्रम में लिए गए )निरपेक्ष पदों के अंतर को अज्ञात के गुणांकों के अंतर से विभाजित करने पर अज्ञात का मान होगा।
नारायण लिखते हैं:
"एक तरफ से 'अज्ञात' और दूसरी तरफ से ज्ञात मात्रा को निवारक करें(हटा दें), फिर अज्ञात के अवशिष्ट गुणांक द्वारा ज्ञात अवशिष्ट को विभाजित करें। इस प्रकार निश्चित रूप से अज्ञात का मूल्य ज्ञात हो जाएगा।"
उदाहरण के लिए हम ब्रह्मगुप्त द्वारा प्रस्तावित एक समस्या लेते हैं:
"उस समय के लिए बीते हुए दिनों की संख्या बताएं जब शेष डिग्री के बारहवें भाग में एक से चार गुना वृद्धि हुई हो, आठ गुना शेष डिग्री जमा एक के बराबर होगा।"
इसे चतुर्वेद पृथूदकस्वामिन् ने इस प्रकार हल किया है:
"यहाँ अवशिष्ट अंश यावत्-तावत् हैं,
या एक की वृद्धि हुई, या 1 रु 1; इसका बारहवाँ भाग, (या 1 रु 1) / 12
इसका चार गुना, (या 1 रु 1) / 3 ; प्लस निरपेक्ष मात्रा आठ, (या 1 रु 25) / 3 ।
यह अवशिष्ट घात और तत्समक(residual degrees plus unity) के बराबर है। दोनों पक्षों का कथन तीन गुना है
या 1 रु 25
या 3 रु 3
अज्ञात के गुणांकों के बीच का अंतर 2 है। इसके द्वारा निरपेक्ष पदों का अंतर(अर्थात् 22), विभाजित किया जा रहा है, योग 11 की घातों के अवशिष्ट का उत्पादन किया जाता है। इन अवशिष्ट घातों को अलघुकरणीय(irreducible) के रूप में जाना जाता है। बीते हुए दिनों को पहले की तरह (आगे बढ़ते हुए) घटाया जा सकता है।"
दूसरे शब्दों में, हमें समीकरण को हल करना होगा
जो देता है x + 25 = 3x + 3
2x = 22
इसलिए x= 11
निम्नलिखित समस्या और उसका समाधान भास्कर द्वितीय के बीजगणित से हैं:
"एक व्यक्ति के पास तीन सौ सिक्के और छह घोड़े हैं। दूसरे के पास समान मूल्य के दस घोड़े (प्रत्येक) हैं और उस पर सौ सिक्कों का कर्ज भी है। लेकिन वे
समान मूल्य के हैं। घोड़े की कीमत क्या होगी ?
"यहाँ सम-निकासी(equi-clearance) के लिए कथन है कि :
6x + 300 = 10x - 100
अब, नियम के अनुसार, 'एक तरफ से अज्ञात को दूसरी तरफ से घटाएं', पहली तरफ अज्ञात को दूसरी तरफ से घटाया जा रहा है,
शेष 4x है। दूसरी तरफ का निरपेक्ष पद पहली तरफ के निरपेक्ष पद से घटाया जाता है, तो शेष 400 होता है। शेष ज्ञात है।
संख्या 400 को अवशिष्ट अज्ञात 4x के गुणांक से विभाजित किया जा रहा है, भागफल को x, (अर्थात् 100) के मान के रूप में पहचाना जाता है।"
दो अज्ञात के साथ रैखिक समीकरण
संगमन/सहमति का नियम
लगभग सभी हिंदू लेखकों द्वारा आमतौर पर चर्चा किए जाने वाले एक विषय को सन्निपतन/संक्रमण (संगमन/सहमति) के विशेष नाम से जाना जाता है। नारायण (1350) के अनुसार इसे संक्रम और संक्रमा भी कहते हैं। ब्रह्मगुप्त (628) ने इसे बीजगणित में शामिल किया है जबकि अन्य इसे अंकगणित के दायरे में आने के रूप में मानते हैं। जैसा कि समीक्षक गंगाधर (1420) द्वारा समझाया गया है, यहां चर्चा का विषय "दो राशियों की जांच समवर्ती या उनके योग और अंतर के रूप में एक साथ उगाई बढ़ी।"
दूसरे शब्दों में संक्रमण समकालिक समीकरणों का समाधान है
x+ y= a, x-y= b
समाधान के लिए ब्रह्मगुप्त का नियम है: "योग को अंतर से बढ़ाया और घटाया जाता है और दो से विभाजित किया जाता है; (परिणाम दो अज्ञात मात्रा होगी): यह है संगमन/सहमति। एक ही नियम को उन्होंने अलग-अलग मौकों पर समस्या और उसके समाधान के रूप में दोहराया है।
"दो (स्वर्गीय पिंडों) के अवशेषों का योग और अंतर, घात और काल (degrees and minutes) में जाना जाता है। अवशेष क्या हैं? अंतर को योग से जोड़ा और घटाया जाता है और आधा किया जाता है, परिणाम अवशेष हैं।
रेखीय समीकरण
महावीर निम्नलिखित उदाहरण देते हैं जो प्रत्येक के समाधान के नियमों के साथ-साथ एक समकालिक रैखिक समीकरण की ओर ले जाते हैं।
उदाहरण। "9 नींबू और 7 सुगंधित बेल की एक साथ कीमत 107 है, फिर से 7 नींबू और 9 सुगंधित बेलों की कीमत एक साथ ली गई है 101 है। हे गणितज्ञ, मुझे जल्दी से एक नींबू और एक सुगंधित बेल की कीमत अलग-अलग बताओ।"
यदि x, y क्रमशः एक नींबू और एक सुगंधित बेल की कीमतें हों, तो
9x+7y= 107,
7x+9y = 101.
या, सामान्य तौर पर,
ax+ by = m
bx + ay = n
समाधान: "बड़ी मात्रा में (संबंधित) चीजों की बड़ी संख्या से गुणा की गई चीजों की छोटी संख्या (संबंधित) से छोटी मात्रा को गुणा करके घटाया जाता है।(शेष) वस्तुओं की संख्या के वर्गों के अंतर से विभाजित प्रत्येक वस्तु की बड़ी संख्या का मूल्य होगा। दूसरे का मूल्य गुणकों की उत्क्रमी (reversing the multipliers) पर प्राप्त होगा।
इस प्रकार ,
इसके समाधान के साथ निम्नलिखित उदाहरण भास्कर द्वितीय के बीजगणित से लिया गया है:
उदाहरण। "एक कहता है, 'मुझे सौ दो, मित्र, तब मैं तुमसे दुगना धनवान बन जाऊँगा।' दूसरा जवाब देता है, 'यदि आप मुझे दस देते हैं, तो मैं छह गुना अमीर हो जाऊंगा जैसे आप।' मुझे बताओ कि उनकी (संबंधित) पूंजी की राशि क्या है?"
समीकरण हैं
x + 100 = 2(y - 100) (1)
y + 10 = 6(x - 10) (2)
भास्कर द्वितीय ने इन समीकरणों को हल करने के दो तरीकों को इंगित किया है। वे काफी हद तक इस प्रकार हैं:
पहली विधि:
मान लीजिए x = 2z - 100, y = z + 100,
ताकि समीकरण (1) समान रूप से संतुष्ट हो। स्थानापन्न
दूसरे समीकरण में ये मान, हम प्राप्त करते हैं
z + 110 = 12z- 660;
इसलिये z =70 , जिसकी वजह से, x = 40 , y = 170
दूसरी विधि:
समीकरण (1) से, हम प्राप्त करते हैं
x =2y - 300,
और समीकरण (2) से
x के इन दो मानों को समकारी करने पर हमें प्राप्त होता है
अत: y= 170. y के इस मान को x के दो व्यंजकों में से किसी में प्रतिस्थापित करने पर, हमें x = 40 प्राप्त होता है।
विविध/कई अज्ञात के साथ रैखिक समीकरण
रैखिक समीकरणों का एक प्रकार
बख्शाली ग्रंथ कई अज्ञात से जुड़े रैखिक समीकरणों के यथाशीध्र हिंदू समाधान के बारे में बात करता है।
इसमें एक समस्या इस प्रकार है:
"[तीन व्यक्तियों में से प्रत्येक के पास निश्चित मात्रा में धन है।] पहले और दूसरे की दौलत एक साथ मिलाकर 13 हो गई है; दूसरी और तीसरी की दौलत एक साथ मिलाकर14 हो गई; और पहिले और तीसरे की मिलाकर 15 का धन हुआ।
हर एक की दौलत बताओ
यदि x1, x2, x3 क्रमशः तीन व्यापारियों की संपत्ति हो, तो x1 + x2 = 13, x2 + x3 = 14, x3 + x1 = 15.
एक और समस्या यह है कि "पांच व्यक्तियों के पास एक निश्चित मात्रा में धन होता है। पहले और दूसरे के धन को मिलाकर 16 की राशि मिलती है; दूसरे और तीसरे के धन को मिलाकर 17 माना जाता है; तीसरे का धन और चौथे को मिलाकर 18 माना जाता है; चौथे और पांचवें को मिलाकर धन 19 है; और पहले और पांचवें का धन मिलाकर 20 है। मुझे बताओ कि प्रत्येक की राशि क्या है
x₁ + x₂ = 16, x₂ + x₃ = 17, x₃+ x₄ = 18, x₄ + x₅ = 19, x₅ + x₁ = 20
काम में इसी तरह की कुछ और समस्याएं हैं। उनमें से हर एक प्रकार के रैखिक समीकरणों की एक प्रणाली से संबंधित है
x₁ + x₂ = a1, x₂ + x₃ = a2 ..., xn + x₁ = an n विषम होना।
असत्य स्थिति से समाधान
इस प्रकार के रैखिक समीकरणों की एक प्रणाली बख्शाली ग्रंथ में हल की गई है जैसा कि नीचे दिखाया गया है।
x₁ के लिए एक स्वेच्छ मान(arbitrary value) p मान लें और फिर उसके अनुरूप x₂, x₃, ... के मानों की गणना करें। अंत में xn + x₁ का परिकलित मान b के बराबर होने दें
(कल्पना करें )। तब x₁ का सही मान सूत्र द्वारा प्राप्त किया जाता है
एक विशिष्ट स्थिति में (1) लेखक x के लिए स्वेच्छ मान 5 मानता है; फिर क्रमशः x₂ = 8, x₃ = 6 और x₃ + x₁ = 11 के मानों की गणना की जाती है
इसलिए सही मान हैं,
x₁= 5 + (15 - 11)/2 = 7, x₂ = 6, x₃= 8
तर्काधार/ कारण विवरण ,जो हम उन्मूलन की प्रक्रिया से हम प्राप्त करते हैं
समीकरण (I)
(a2-a1)+(a4-a3)+· ... +(an-1 - an-2) + 2x1 = an
कल्पना करें x1 = p; ताकि
(a2-a1)+(a4-a3)+· ... +(an-1 - an-2) + 2p = b कहें।
घटाना 2(x1 - p) = a - b
अतः
दूसरा प्रकार
समीकरणों के प्रकार (I) का एक विशिष्ट स्थिति जिसके लिए n = 3, को भी रैखिक समीकरणों के एक अलग प्रकार के प्रणाली से संबंधित माना जा सकता है।
Σx - x1 = a1 , Σx - x2 = a2, Σx - xn = an
जहाँ Σx का अर्थ है x1 + x2 +....+xn
लेकिन यह कहना उचित नहीं होगा कि बख्शिली ग्रंथ में इस प्रकार के समीकरणों का उपचार किया गया है। हालाँकि, आर्यभट्ट (499) और महावीर (850) द्वारा उन्हें हल किया गया है।
आर्यभट कहते हैं: "कुछ (अज्ञात) संख्याओं के योग (दिए गए) अलग-अलग जोड़ दिए जाते हैं,अनुक्रम में एक संख्या को छोड़कर, और एक से कम पदों की संख्या से विभाजित किए जाते हैं; वह (भागफल) संपूर्ण का मान होगा।
महावीर समाधान इस प्रकार बताते हैं: "एक साथ जोड़ी गई वस्तुओं की बताई गई मात्रा को पुरुषों की संख्या से कम से विभाजित किया जाना चाहिए। भागफल कुल मूल्य (सभी वस्तुओं का) होगा। प्रत्येक बताई गई राशि को उसमें से घटाया जा रहा है, (मूल्य) हाथों में (प्रत्येक का मिल जाएगा)।
अपना शासन बनाने में महावीर ने निम्नलिखित उदाहरण को ध्यान में रखा था:
"चार व्यापारियों से प्रत्येक से सीमा शुल्क अधिकारी द्वारा उनकी वस्तुओं के कुल मूल्य के बारे में अलग-अलग पूछा गया।
पहले व्यापारी ने अपने स्वयं के निवेश को छोड़कर, कुल मूल्य 22 बताया; दूसरे ने इसे 23, तीसरे ने 24 और चौथे ने 27 को बताया; उनमें से प्रत्येक ने निवेश में अपनी राशि काट ली।
हे मित्र, प्रत्येक के स्वामित्व वाली वस्तु का (हिस्सा) मूल्य अलग से बताओ।"
यहाँ
इसलिए x1 = 10, x2 = 9, x3 = 8, x4 = 5.
नारायण कहते हैं: "कुल राशि है "एक से कम व्यक्तियों की संख्या से विभाजित कम राशि का योग। इसमें से बताई गई राशि को अलग-अलग घटाने पर अलग-अलग राशियां मिल जाएंगी।"
तीसरा प्रकार
रैखिक समीकरणों की एक अधिक सामान्यीकृत प्रणाली होगी
, ......,
..........................................(III)
इसलिए
अतः ....................(I)
r = I, 2, 3..... n
इस प्रकार की एक विशिष्ट स्थिति महावीर के निम्नलिखित उदाहरण द्वारा प्रस्तुत कि गयी है:
"तीन व्यापारी आपस में एक-दूसरे से भीख माँगते थे। पहला दूसरे से 4 और तीसरे से 5 भीख माँगने पर दूसरे की तुलना में दुगना धनी हो गया। दूसरा पहले से 4 और तीसरे से 6 होने पर तीन गुना धनी हो गया। तीसरा आदमी पहले से 5 और दूसरे से 6 भीख माँगने पर दूसरों की तुलना में पाँच गुना अमीर बन गया। हे गणितज्ञ, यदि आप चित्रा-कुट्टाक-मिश्रा जानते हैं तो मुझे जल्दी से बताओ कि प्रत्येक के हाथ में कितनी राशि थी। "
यानी हमें समीकरण मिलते हैं
x + 4 + 5 = 2(y + z - 4 - 5),
y + 4 + 6 = 3(z + x - 4 - 6),
z + 5 + 6 = 5 (x + y - 5 - 6);
or 2(x + y + z) - 3x = 27,
3(x + y + z) - 4y = 40 ;
5 (x + y +z) - 6z = 66;
प्रणाली की एक विशिष्ट स्थिति (III) में प्रतिस्थापन करने पर
(I), हम पाते हैं
x = 7, Y = 8, Z = 9
ब्रह्मगुप्त का नियम: ब्रह्मगुप्त (628) कई अज्ञात से जुड़े रैखिक समीकरणों को हल करने के लिए निम्नलिखित नियम बताते हैं :
"पहले अज्ञात के पक्ष से अन्य अज्ञात को हटाकर और पहले अज्ञात के गुणांक से विभाजित करके, पहले अज्ञात का मान प्राप्त किया जाता है।पहले अज्ञात के अधिक मूल्यों के मामले में, दो और दो (उनमें से) चाहिए उन्हें आम भाजक में कम करने के बाद विचार किया जाना चाहिए। और इसी तरह बार-बार किया जाना चाहिए। यदि अंतिम समीकरण में अधिक अज्ञात रहते हैं, तो चूर्णित्र(pulveriser) की विधि को नियोजित किया जाना चाहिए। फिर विपरीत तरीके से आगे बढ़ने पर अन्य अज्ञात के मान मिल सकते हैं।"
चतुर्वेद पृथुदका स्वामी (860) ने इसे इस प्रकार समझाया है: "एक ऐसे उदाहरण में जिसमें दो या दो से अधिक अज्ञात मात्राएँ, रंगों जैसे हों यावत्-तावत् , आदि को उनके मूल्यों के लिए ग्रहण किया जाना चाहिए। उन पर उदाहरण के कथन के अनुरूप सभी संचालन किए जाने चाहिए और इस प्रकार दो या दो से अधिक पक्षों और समीकरणों को भी ध्यान से तैयार किया जाना चाहिए।पहले दो और दो के बीच सम-निकासी( Equi-clearance) की जानी चाहिए और इसी तरह अंतिम तक: एक तरफ से एक अज्ञात को हटा देना चाहिए, अन्य अज्ञात को एक सामान्य भाजक में घटाया जाना चाहिए और साथ ही विपरीत पक्ष से निरपेक्ष संख्या को हटा देना चाहिए।अन्य अज्ञात के अवशेषों को पहले अज्ञात के अवशिष्ट गुणांक से विभाजित किया जा रहा है, जो पहले अज्ञात का मान देगा।यदि ऐसे कई मान प्राप्त हों, तो उनमें से दो और दो के साथ, सामान्य हर में कमी के बाद समीकरण बनाए जाने चाहिए।इस तरह से अंत तक आगे बढ़ते हुए एक अज्ञात के मूल्य का पता लगाएं। यदि वह मान किसी अन्य अज्ञात के पदों में हो तो उन दोनों के गुणांक पारस्परिक रूप से दो अज्ञात के मान होंगे।यदि, हालांकि, उस मूल्य में और अधिक अज्ञात मौजूद हैं, तो चूर्णित्र(pulveriser) की विधि को नियोजित किया जाना चाहिए। कुछ अज्ञातों के लिए मनमाना मूल्य तब माना जा सकता है। "उपरोक्त नियम अनिश्चित और साथ ही निर्धारित समीकरणों को स्वीकार करता है। नियम के चित्रण में ब्रह्मगुप्त द्वारा दिए गए सभी उदाहरण अनिश्चित चरित्र के हैं।
भास्कर का नियम: भास्कर द्वितीय ने ब्रह्मगुप्त के समान नियम दिया है, जिसमें कई अज्ञात को शामिल करते हुए समकालिक रैखिक समीकरणों को हल किया जाता है।
हम उनके कार्यों से निम्नलिखित दृष्टांत लेते हैं।
उदाहरण 1. "आठ माणिक, दस पन्ने, और एक सौ मोती जो आपके कान में हैं, वह मेरे द्वारा आपके लिए समान राशि पर खरीदे गए थे; तीन प्रकार के रत्नों की कीमत दरों का योग सौ के आधे से तीन कम है। ओ प्रिय! शुभ महिला, यदि आप गणित में निपुण हैं तो, प्रत्येक की कीमत मुझे बताओ।"
यदि x, y, z क्रमशः एक माणिक, पन्ना और मोती के मूल्य हों, तो 8x = 10y = 100z
x+y+z = 47
भास्कर द्वितीय कहते हैं, समान राशि को w मान लें, तो हम प्राप्त करेंगे
x = w/8, y = w/10, z = w/100
शेष समीकरण में प्रतिस्थापित करने पर, हमें w = 200 प्राप्त होता है। इसलिए
x = 25, y = 20, z = 2
द्विघातीय समीकरण
जैनियों (500-300 ईसा पूर्व) के प्रारंभिक विहित कार्यों में हम सरल द्विघात समीकरण का ज्यामितीय समाधान देखते हैं
और इसके अलावा उमास्वती (सी 150 ई.पू.) के तत्त्वाधिगमा-सूत्र के रूप में भी पाया जाता है।
श्रीधर का शासन: श्रीधर (सी। 750) द्विघात समीकरण को हल करने की उनकी विधि को स्पष्ट रूप से इंगित करते हैं ।
बीजगणित पर उनका ग्रंथ अब खो गया है। लेकिन इसका प्रासंगिक अंश भास्कर द्वितीय और अन्य के उद्धरणों में संरक्षित है।
श्रीधर की विधि है:
"दोनों पक्षों (एक समीकरण के) को अज्ञात के वर्ग के गुणांक के चार गुणा के बराबर ज्ञात मात्रा से गुणा करें; दोनों पक्षों में अज्ञात के (मूल) गुणांक के वर्ग के बराबर एक ज्ञात मात्रा जोड़ें: फिर मूल निकालें ।"
अर्थात् समीकरण को हल करने के लिए
दोनों पक्षों में 4a से गुणा करें
श्रीपति के नियम: श्रीपति (1039) द्विघात को हल करने की दो विधियों को इंगित करते हैं । पहली विधि का वर्णन करने वाले नियम में हमारी पांडुलिपि में एक कमी/अंतर है, लेकिन इसे आसानी से श्रीधर के विधि के समान माना जा सकता है।
"अज्ञात के वर्ग के गुणांक से चार गुना गुणा करें और अज्ञात के गुणांक के वर्ग को जोड़ें; फिर अज्ञात के वर्ग के गुणांक के दोगुने से विभाजित वर्गमूल निकालें, इसे अज्ञात का मूल्य कहा जाता है।"
"या अज्ञात के वर्ग के गुणांक से गुणा करके और अज्ञात के गुणांक के आधे के वर्ग को जोड़कर, वर्गमूल निकालें। फिर पहले की तरह आगे बढ़ते हुए, यह अज्ञात के गुणांक के आधे से कम हो जाता है और गुणांक से विभाजित हो जाता है अज्ञात के वर्ग का। इस भागफल को अज्ञात का मान कहा जाता है।"
या
इसलिए
भास्कर द्वितीय के नियम : भास्कर द्वितीय (1150) कहते हैं : "जब अज्ञात का वर्ग रहता है, तो दोनों पक्षों (समीकरण के) को कुछ उपयुक्त मात्राओं से गुणा करते हुए, उनमें अन्य उपयुक्त मात्राएँ जोड़ी जानी चाहिए ताकि अज्ञात वाली भुजा एक मूल (पद-प्रद) उत्पन्न करने में सक्षम हो जाए।फिर इस पक्ष के मूल और ज्ञात पक्ष के मूल के साथ फिर से समीकरण बनाना चाहिए। इस प्रकार अज्ञात का मान उस समीकरण से प्राप्त होता है।
इस नियम को लेखक ने आगे इस प्रकार स्पष्ट किया है : .
"जब दोनों पक्षों की पूर्ण निकासी के बाद, एक तरफ अज्ञात का वर्ग, आदि रहता है और दूसरी तरफ केवल पूर्ण शब्द होता है, तो, दोनों पक्षों को कुछ उपयुक्त वैकल्पिक मात्रा से गुणा या विभाजित किया जाना चाहिए; कुछ समान मात्राओं को आगे दोनों पक्षों से जोड़ा या घटाया जाना चाहिए ताकि अज्ञात पक्ष एक मूल देने में सक्षम हो जाए। उस पक्ष की मूल दूसरी तरफ के निरपेक्ष पदों के मूल के बराबर होनी चाहिए। एक साथ समान जोड़, आदि द्वारा के लिए,दो समान पक्षों में समानता बनी रहती है। इसलिए इन मूलों के साथ फिर से एक समीकरण बनाने से अज्ञात का मान मिल जाता है।"
भास्कर प्रथम ने अंकगणित पर अपने ग्रंथ में हमेशा अज्ञात के वर्ग के गुणांक से विभाजित करने की आधुनिक पद्धति का पालन किया है।
ज्ञानराज (1503) और गणेश (1545) द्विघात को हल करने के लिए भास्कर द्वितीय के समान सामान्य तरीकों का वर्णन करते हैं।
मध्य अवधि का उन्मूलन : मध्यमहारना या "मध्य का उन्मूलन"(मध्यम = मध्य और अहारना = हटाने, या नष्ट करने, यानी उन्मूलन), तकनीकी पदनाम जिसके माध्यम से हिंदू बीजगणितविदों ने द्विघात समीकरण को हल करने की विधि दी।
इस नाम की उत्पत्ति विधि के अंतर्निहित सिद्धांत से हुई है।
सामान्य तौर पर द्विघात समीकरण में तीन पद होते हैं जिनमें एक मध्य पद होता है। इस विधि द्वारा इसे केवल दो पदों के साथ सरल समीकरणों में परिवर्तित किया जाएगा, जहां मध्य पद को हटा दिया जाता है। इसलिए नाम मध्यमहारना
भास्कर द्वितीय ने देखा है, "यह भी विशेष रूप से विद्वान शिक्षकों द्वारा मध्यमहारना के रूप में नामित किया गया है। क्योंकि, द्विघात के दो शब्दों में से एक(बीच वाला) को हटा दिया जाता है,इसके द्वारा होता है।:हालाँकि, नाम को एक विस्तारित अर्थ में भी नियोजित किया जाता है ताकि घन और द्विघात को हल करने के तरीकों को अपनाया जा सके, जहाँ कुछ शर्तों को भी समाप्त कर दिया जाता है। यह ब्रह्मगुप्त (628) के कार्यों के रूप में यथाशीध्र होता है।
द्विघात के दो मूल : हिंदुओं ने जल्दी ही पहचान लिया कि द्विघात की आम तौर पर दो मूल होते हैं।इस संबंध में भास्कर द्वितीय ने पद्मनाभ नाम के एक प्राचीन लेखक से निम्नलिखित नियम उद्धृत किया है जिसका बीजगणित पर ग्रंथ अब उपलब्ध नहीं है।"यदि मूलों को निकालने के बाद द्विघात की निरपेक्ष भुजा का वर्गमूल दूसरी ओर के ऋणात्मक निरपेक्ष पद से कम हो, तो इसे ऋणात्मक और धनात्मक लेने पर अज्ञात के दो मान मिलते हैं।"
भास्कर कुछ विशिष्ट दृष्टांतों की मदद से बताते हैं कि हालांकि द्विघात की ये दोहरी मूले सैद्धांतिक रूप से सही हैं, वे कभी-कभी असंगति की ओर ले जाती हैं और इसलिए हमेशा स्वीकार नहीं किया जाना चाहिए।इसलिए वह नियम को इस प्रकार संशोधित करते है:"यदि द्विघात के ज्ञात पक्ष का वर्गमूल अज्ञात पक्ष के वर्गमूल में आने वाले ऋणात्मक निरपेक्ष पद से कम हो तो उसे ऋणात्मक और धनात्मक बनाते हुए अज्ञात के दो मान ज्ञात करने चाहिए।यह कभी-कभी किया जाना है।"
उदाहरण 1."बंदरों की एक टोली का आठवां हिस्सा(वर्ग), जंगल के अंदर कूद रहा था, खुशी से उससे जुड़ा हुआ था। बारह को पहाड़ी पर चिल्लाते और चिल्लाते हुए देखा गया था। वे कितने थे?"
समाधान। "यहाँ बन्दरों की टोली x है। इसके आठवें भाग का वर्ग 12 को मिलाकर सेना के बराबर है। तो दोनों पक्ष इस प्रकार हैं
इन्हें एक सामान्य भाजक में कम करना और फिर हर को हटाना, और निकासी भी करना दोनों पक्ष बन जाते हैं
x² - 64x + 0 = 0x2 + 0x - 768
दोनों पक्षों में 32 का वर्ग जोड़ने पर और वर्गमूल निकालने पर, हम यह प्राप्त करते हैं
x- 32 = ± (0x + 16)
इस उदाहरण में ज्ञात पक्ष पर निरपेक्ष पद अज्ञात के पक्ष में ऋणात्मक निरपेक्ष पद से छोटा है; इसलिए इसे सकारात्मक के साथ-साथ नकारात्मक भी लिया जाता है; x के दो मान 48, 16 पाए जाते हैं।
उच्च घात के समीकरण
घन और द्विघात: घन और द्विघात समीकरणों को हल करने में हिंदुओं की कोई खास उपलब्धि नहीं है। भास्कर द्वितीय(1150) ने मध्यमाहारन (मध्य का उन्मूलन) पद्धति को उन समीकरणों पर भी लागू करने की कोशिश की ताकि लाभप्रद परिवर्तनों के माध्यम से उन्हें कम किया जा सके और सहायक मात्राओं को क्रमशः सरल और द्विघात समीकरणों में शामिल किया जा सके।इस प्रकार उन्होंने द्विघात को हल करने के आधुनिक तरीकों में से एक का अनुमान लगाया। "यदि, हालांकि," भास्कर द्वितीय का कहना है, "घन, द्विघात, आदि की उपस्थिति के कारण, अज्ञात पक्ष के मूल के अभाव में, इस तरह के संचालन के प्रदर्शन के बाद, कमी का कार्य आगे नहीं बढ़ सकता है ( एक समीकरण का), तो अज्ञात का मान सरलता (गणितज्ञ के) द्वारा प्राप्त किया जाना चाहिए।उन्होंने दो उदाहरण दिए हैं, एक घन का और दूसरा द्विघात का, जिसमें ऐसी कमी संभव है।
उदाहरण 1. "वह कौन सी संख्या है, जिसे बारह से गुणा किया जाता है और संख्या के घन से बढ़ा दिया जाता है, जो पैंतीस के साथ जोड़ी गई संख्या के वर्ग के छह गुणा के बराबर होती है।
समाधान : "यहाँ संख्या x है। इसे बारह से गुणा करने पर संख्या का घन x³ + 12x हो जाता है। यह 6x² + 35 के बराबर होता है। निकासी करने पर, एक तरफ x³ - 6x² + 12x; दूसरी तरफ 35 दोनों पक्षों में ऋणात्मक आठ जोड़ने पर और घनमूल निकालने पर हमें x - 2. = 0x + 3 प्राप्त होता है और इस समीकरण से संख्या 5 होती है।
उदाहरण 2. "वह कौन सी संख्या है जिसे 200 से गुणा करके संख्या के वर्ग में जोड़ा जाता है, और फिर 2 से गुणा किया जाता है और संख्या की चौथी घात से घटाया जाता है, तो वह असंख्य कम एकांक बन जाएगी? वह संख्या बताएं।
समाधान: "यहाँ संख्या x है; 200 से गुणा करने पर यह 200x हो जाता है; संख्या के वर्ग में जोड़ने पर x² + 200x हो जाता है; इसे दो से गुणा करने पर, 2x² + 400x; इससे संख्या की चौथी घात कम हो जाती है, अर्थात्, यह x4- 2x² - 400x हो जाता है। यह असंख्य कम एकांक के बराबर है। सम-निकासी होने के बाद, दोनों पक्ष इस तरह होंगे,
x4- 2x² - 400x = 0x4 + 0x² + 0x + 9999
यहाँ पर पहली भुजा में चार सौ x जमा एकता जोड़ने पर मूल निकाला जा सकता है, लेकिन दूसरी भुजा में समान जोड़ने पर उसकी मूल नहीं बनेगा । इस प्रकार कार्य (कमी का) आगे नहीं बढ़ता है। यहाँ दोनों पक्षों को x के वर्ग के चार गुणा, चार सौ x और एकांक में जोड़ने पर और फिर मूल निकालने पर, हम प्राप्त करते हैं
x² + 0x+ 1 = 0x² + 2x + 100।
फिर से इनके साथ समीकरण बनाकर और पहले की तरह आगे बढ़ते हुए, x का मान 11 के रूप में प्राप्त होता है।"
समकालिक द्विघात समीकरण
सामान्य रूप हिंदू लेखकों ने समकालिक द्विघात समीकरणों के निम्नलिखित रूपों पर विचार किया है।:
x - y = d ; xy = b ......(1)
x + y = a ; xy = b ......(2
x² + y² = c ; xy = b ......(3)
x² + y² = c ; x + y = a ......(4)
(1) के समाधान के लिए,आर्यभट्ट प्रथम (499) निम्नलिखित नियम बताते हैं :
" गुणन(दो मात्राओं का) के चार गुना का वर्गमूल उनके अंतर के वर्ग के साथ जोड़ा जाता है,उनके अंतर और आधा से जोड़ा और घटाया जा रहा है, जो दो गुणक देता है।"
,
ब्रह्मगुप्त (628) कहते हैं: "अवशेषों के अंतर के वर्ग के योग का वर्गमूल और अवशेषों के गुणनफल का दो वर्ग गुना, अवशेषों के अंतर से जोड़ा और घटाया जाता है, और आधा (देता है) वांछित अवशेष क्रम से किया जाता है ।"
नारायण (1357) लिखते हैं: "दो मात्राओं के अंतर के वर्ग का वर्गमूल और उनके गुणनफल का चार गुना उनका योग होता है।"
"मात्राओं के अंतर का वर्ग उनके गुणनफल के दुगुने के साथ उनके वर्गों के योग के बराबर होता है। इस परिणाम का वर्गमूल गुणनफल का दोगुना योग होता है।"
(2) के समाधान के लिए महावीर (850) द्वारा निम्नलिखित नियम दिया गया है: "अर्ध-परिधि के वर्ग से क्षेत्रफल (एक आयत का) का चार गुना घटाएँ, फिर उस (शेष) के वर्गमूल और अर्ध-परिधि के बीच संक्रमण द्वारा आधार/समतल और उर्ध्वाधर प्राप्त होते हैं।"
नारायण कहते हैं: "योग के वर्ग का वर्गमूल घटा गुणनफल के चार गुना का अंतर है।"
(3) के लिए महावीर नियम देते हैं: "विकर्ण के वर्ग से (एक आयत के) क्षेत्र को दो बार जोड़ें और घटाएं और वर्गमूल निकालें। इनमें से बड़े और छोटे (मूलों) के बीच संक्रमण द्वारा, आधार/समतल और उर्ध्वाधर पाए जाते हैं।
(4) समीकरणों के लिए आर्यभट प्रथम लिखते हैं : "योग(दो राशियों का) के वर्ग से, उनके वर्गों का योग घटाएं। शेष का आधा उनका गुणनफल है।"
शेष संक्रियाएं समीकरणों (2) के समान होंगी; ताकि
ब्रह्मगुप्त कहते हैं: "योग के वर्ग को वर्गों के योग के दोगुने से घटाएं; शेष का वर्गमूल योग में जोड़ा और घटाया और आधा किया जाता है, जो वांछित अवशेष देता है।"
नारायण ने समकालिक द्विघात समीकरणों के दो अन्य रूप दिए हैं, अर्थात्,
x - y = d.....(5)
xy = b ......(6)
(5) के समाधान के लिए ,वह यह नियम देते हैं : "वर्गों के योग के दोगुने का वर्गमूल अंतर के वर्ग द्वारा घटाए गए योग के बराबर है।"
इसलिए
(6) के लिए नारायण लिखते हैं: "-
"मान लीजिए कि गुणनफल का वर्ग दो मात्राओं का गुणनफल है और वर्गों का अंतर उनके अंतर के रूप में है। उनसे संक्रमण द्वारा (वर्ग) मात्राएँ प्राप्त की जाएंगी। उनके वर्गमूल अलग-अलग आवश्यक मात्राएँ देंगे।"
हमारे पास है
x² - y² =m
x² y² = b2
ये रूप (1) के हैं। इसलिए
अब हम x और y के मान प्राप्त करते हैं।
बाहरी संपर्क
यह भी देखें
संदर्भ
- ↑ A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1. Samskrit Promotion Foundation. 2021. ISBN 978-81-951757-2-7.
- ↑ Bījagaṇita, ch. Avyaktādi-guṇana, vs.6,7, p.8
- ↑ Bījagaṇita ch. Avyakta-saṅkalana-vyavakalana, vs.6, p.7
- ↑ Bījagaṇita ch. Avyaktādi-guṇana, vs.8, p.8
- ↑ Brāhma-sphuṭa-siddhānta, Ch 18, vs.43,p.314
- ↑ (Bijagaṇita, ch. Ekavarṇa-samīkaraṇa, vs.1, 2, pp.43,44)