एफ वितरण: Difference between revisions
(Created page with "{{Short description|Continuous probability distribution}} {{About|the central F-distribution|the generalized distribution|noncentral F-distribution|other uses|F-ratio (disambi...") |
(TEXT) |
||
| Line 1: | Line 1: | ||
{{Short description|Continuous probability distribution}} | {{Short description|Continuous probability distribution}} | ||
{{About| | {{About|केंद्रीय एफ-वितरण|सामान्यीकृत वितरण|अकेंद्रीय एफ-वितरण|अन्य उपयोग|एफ-अनुपात (disambiguation){{!}}F-ratio}} | ||
{{distinguish|text=[[ | {{distinguish|text=[[एफ-सांख्यिकी|''एफ''-सांख्यिकी]] as used in [[जनसंख्या आनुवंशिकी]]}} | ||
{{DISPLAYTITLE:''F''-distribution}} | {{DISPLAYTITLE:''F''-distribution}} | ||
{{Probability distribution | {{Probability distribution | ||
| Line 23: | Line 23: | ||
}} | }} | ||
संभाव्यता सिद्धांत और सांख्यिकी में, ''एफ''-वितरण या एफ-अनुपात, जिसे स्नेडेकोर के ''एफ'' वितरण या फिशर-स्नेडेकोर वितरण ([[रोनाल्ड फिशर]] और जॉर्ज डब्ल्यू. स्नेडेकोर के बाद) के रूप में भी जाना जाता है, एक सतत | संभाव्यता सिद्धांत और सांख्यिकी में, ''एफ''-वितरण या एफ-अनुपात, जिसे स्नेडेकोर के ''एफ'' वितरण या फिशर-स्नेडेकोर वितरण ([[रोनाल्ड फिशर]] और जॉर्ज डब्ल्यू. स्नेडेकोर के बाद) के रूप में भी जाना जाता है, एक सतत प्रायिकता वितरण है, जो लगातार शून्य वितरण के रूप में उत्पन्न होता है। एक परीक्षण सांख्यिकी, विशेष रूप से प्रसरण (एनोवा) और अन्य एफ-परीक्षणों के विश्लेषण में है।<ref name=johnson>{{cite book | last = Johnson | ||
| first = Norman Lloyd | | first = Norman Lloyd | ||
|author2=Samuel Kotz |author3=N. Balakrishnan | |author2=Samuel Kotz |author3=N. Balakrishnan | ||
| Line 36: | Line 36: | ||
| year = 1974 | | year = 1974 | ||
| isbn = 0-07-042864-6}}</ref> | | isbn = 0-07-042864-6}}</ref> | ||
== परिभाषा == | == परिभाषा == | ||
''d''<sub>1</sub> और ''d''<sub>2</sub> के साथ एफ-वितरण स्वतंत्रता की डिग्री का वितरण है | |||
: <math> X = \frac{S_1/d_1}{S_2/d_2} </math> | : <math> X = \frac{S_1/d_1}{S_2/d_2} </math> | ||
कहाँ <math display=inline>S_1</math> और <math display=inline>S_2</math> स्वतंत्रता | कहाँ <math display=inline>S_1</math> और <math display=inline>S_2</math> स्वतंत्रता <math display="inline">d_1</math>और <math display="inline">d_2</math> की संबंधित डिग्री के साथ [[ची-स्क्वायर वितरण|ची-वर्ग वितरण]] के साथ स्वतंत्र यादृच्छिक चर हैं। | ||
यह अनुसरण करने के लिए दिखाया जा सकता है कि | यह अनुसरण करने के लिए दिखाया जा सकता है कि ''X'' के लिए प्रायिकता घनत्व फलन (पीडीएफ) द्वारा दिया गया है | ||
: <math> | : <math> | ||
| Line 53: | Line 51: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
[[वास्तविक संख्या]] x > 0 के लिए यहाँ <math>\mathrm{B}</math> बीटा | [[वास्तविक संख्या]] x > 0 के लिए यहाँ <math>\mathrm{B}</math> बीटा फलन है। कई अनुप्रयोगों में, प्राचल (पैरामीटर) ''d''<sub>1</sub> और ''d''<sub>2</sub> [[सकारात्मक पूर्णांक]] हैं, लेकिन वितरण इन प्राचल के सकारात्मक वास्तविक मूल्यों के लिए अच्छी तरह से परिभाषित है। | ||
संचयी वितरण | संचयी वितरण फलन है | ||
:<math>F(x; d_1,d_2)=I_{d_1 x/(d_1 x + d_2)}\left (\tfrac{d_1}{2}, \tfrac{d_2}{2} \right) ,</math> | :<math>F(x; d_1,d_2)=I_{d_1 x/(d_1 x + d_2)}\left (\tfrac{d_1}{2}, \tfrac{d_2}{2} \right) ,</math> | ||
जहां I [[नियमित अधूरा बीटा फ़ंक्शन]] है। | जहां ''I'' [[नियमित अधूरा बीटा फ़ंक्शन|नियमित अपूर्ण बीटा फलन]] है। | ||
F(d | F(''d''<sub>1</sub>, ''d''<sub>2</sub>)) के बारे में अपेक्षा, प्रसरण और अन्य विवरण साइडबॉक्स में दिए गए हैं; ''d''<sub>2</sub> > 8 के लिए, अतिरिक्त ककुदता है | ||
:<math>\gamma_2 = 12\frac{d_1(5d_2-22)(d_1+d_2-2)+(d_2-4)(d_2-2)^2}{d_1(d_2-6)(d_2-8)(d_1+d_2-2)}.</math> | :<math>\gamma_2 = 12\frac{d_1(5d_2-22)(d_1+d_2-2)+(d_2-4)(d_2-2)^2}{d_1(d_2-6)(d_2-8)(d_1+d_2-2)}.</math> | ||
F(''d''<sub>1</sub>, ''d''<sub>2</sub>) वितरण का k-वाँ क्षण उपस्थित है और केवल तभी परिमित है जब 2k <d<sub>2</sub> और यह इसके समान है | |||
:<math>\mu _X(k) =\left( \frac{d_2}{d_1}\right)^k \frac{\Gamma \left(\tfrac{d_1}{2}+k\right) }{\Gamma \left(\tfrac{d_1}{2}\right)} \frac{\Gamma \left(\tfrac{d_2}{2}-k\right) }{\Gamma \left( \tfrac{d_2}{2}\right) }.</math> <ref name=taboga>{{cite web | last1 = Taboga | first1 = Marco | url = http://www.statlect.com/F_distribution.htm | title = The F distribution}}</ref> | :<math>\mu _X(k) =\left( \frac{d_2}{d_1}\right)^k \frac{\Gamma \left(\tfrac{d_1}{2}+k\right) }{\Gamma \left(\tfrac{d_1}{2}\right)} \frac{\Gamma \left(\tfrac{d_2}{2}-k\right) }{\Gamma \left( \tfrac{d_2}{2}\right) }.</math> <ref name=taboga>{{cite web | last1 = Taboga | first1 = Marco | url = http://www.statlect.com/F_distribution.htm | title = The F distribution}}</ref> | ||
एफ- | एफ-वितरण [[बीटा प्राइम वितरण|बीटा प्रमुख वितरण]] का एक विशेष प्राचलीकरण है, जिसे दूसरी तरह का बीटा वितरण भी कहा जाता है। | ||
विशेषता | विशेषता फलन कई मानक संदर्भों (जैसे) में अशुद्ध रूप से सूचीबद्ध है।<ref name=abramowitz /> सही अभिव्यक्ति <ref>Phillips, P. C. B. (1982) "The true characteristic function of the F distribution," ''[[Biometrika]]'', 69: 261–264 {{JSTOR|2335882}}</ref> है | ||
:<math>\varphi^F_{d_1, d_2}(s) = \frac{\Gamma\left(\frac{d_1+d_2}{2}\right)}{\Gamma\left(\tfrac{d_2}{2}\right)} U \! \left(\frac{d_1}{2},1-\frac{d_2}{2},-\frac{d_2}{d_1} \imath s \right)</math> | :<math>\varphi^F_{d_1, d_2}(s) = \frac{\Gamma\left(\frac{d_1+d_2}{2}\right)}{\Gamma\left(\tfrac{d_2}{2}\right)} U \! \left(\frac{d_1}{2},1-\frac{d_2}{2},-\frac{d_2}{d_1} \imath s \right)</math> | ||
जहां U(a, b, z) दूसरी तरह का [[संगम हाइपरज्यामितीय समारोह]] है। | जहां U(a, b, z) दूसरी तरह का [[संगम हाइपरज्यामितीय समारोह|संगमी हाइपरज्यामितीय फलन]] है। | ||
== | == अभिलक्षण == | ||
प्राचल <math>d_1</math> और <math>d_2</math> के साथ एफ-वितरण का एक [[यादृच्छिक चर]] दो उचित रूप से स्केल किए गए ची-वर्ग वितरण के अनुपात के रूप में उत्पन्न होता है:<ref>M.H. DeGroot (1986), ''Probability and Statistics'' (2nd Ed), Addison-Wesley. {{ISBN|0-201-11366-X}}, p. 500</ref> | |||
:<math>X = \frac{U_1/d_1}{U_2/d_2}</math> | :<math>X = \frac{U_1/d_1}{U_2/d_2}</math> | ||
जहाँ | |||
*<math>U_1</math> और <math>U_2</math> के | *<math>U_1</math> और <math>U_2</math> के क्रमशः स्वतंत्रता की <math>d_1</math> और <math>d_2</math> डिग्री के साथ ची-वर्ग वितरण हैं, और | ||
*<math>U_1</math> और <math>U_2</math> [[सांख्यिकीय स्वतंत्रता]] हैं। | *<math>U_1</math> और <math>U_2</math> [[सांख्यिकीय स्वतंत्रता|स्वतंत्र]] हैं। | ||
ऐसे उदाहरणों में जहां एफ-वितरण का उपयोग किया जाता है, उदाहरण के लिए | ऐसे उदाहरणों में जहां एफ-वितरण का उपयोग किया जाता है, उदाहरण के लिए प्रसरण विश्लेषण, कोचरन के प्रमेय को आवेदन करके <math>U_1</math> और <math>U_2</math> की स्वतंत्रता का प्रदर्शन किया जा सकता है। | ||
समतुल्य रूप से, | समतुल्य रूप से, एफ-वितरण का यादृच्छिक चर भी लिखा जा सकता है | ||
:<math>X = \frac{s_1^2}{\sigma_1^2} \div \frac{s_2^2}{\sigma_2^2},</math> | :<math>X = \frac{s_1^2}{\sigma_1^2} \div \frac{s_2^2}{\sigma_2^2},</math> | ||
जहाँ <math>s_1^2 = \frac{S_1^2}{d_1}</math> और <math>s_2^2 = \frac{S_2^2}{d_2}</math>, <math>S_1^2</math> सामान्य वितरण <math>N(0,\sigma_1^2)</math> से <math>d_1</math> यादृच्छिक चर के वर्गों का योग है और <math>S_2^2</math> सामान्य वितरण <math>N(0,\sigma_2^2)</math> से <math>d_2</math> यादृच्छिक चर के वर्गों का योग है। | |||
[[फ़्रीक्वेंटिस्ट]] संदर्भ में, एक स्केल किया हुआ | [[फ़्रीक्वेंटिस्ट]] संदर्भ में, एक स्केल किया हुआ एफ-वितरण इसलिए प्रायिकता <math>p(s_1^2/s_2^2 \mid \sigma_1^2, \sigma_2^2)</math> देता है, स्वयं एफ-वितरण के साथ, बिना किसी स्केलिंग के, जहां <math>\sigma_1^2</math> को <math>\sigma_2^2</math> के समान लिया जा रहा है। यह वह संदर्भ है जिसमें एफ-वितरण सबसे सामान्यतः पर एफ-परीक्षणों में प्रकट होता है: जहां शून्य परिकल्पना यह है कि दो स्वतंत्र सामान्य प्रसरण समान हैं, और कुछ उचित रूप से चयनित वर्गों के देखे गए योगों की जांच की जाती है कि क्या उनका अनुपात शून्य परिकल्पना के साथ महत्वपूर्ण रूप से असंगत है। | ||
यदि <math>\sigma_1^2</math> और <math>\sigma_2^2</math> की पूर्वप्रायिकताएं के लिए एक असूचनात्मक पुनर्विक्रय-अपरिवर्तक जेफरीस पूर्व लिया जाता है, तो मात्रा <math>X</math> बायेसियन सांख्यिकी में समान वितरण होता है।<ref>G. E. P. Box and G. C. Tiao (1973), ''Bayesian Inference in Statistical Analysis'', Addison-Wesley. p. 110</ref> इस संदर्भ में, एक स्केल किया गया एफ-वितरण इस प्रकार पश्च प्रायिकता <math>p(\sigma^2_2 /\sigma_1^2 \mid s^2_1, s^2_2)</math> देता है, जहां देखे गए योग <math>s^2_1</math> और <math>s^2_2</math> अब ज्ञात के रूप में लिया जाता है। | |||
== | == गुण और संबंधित वितरण == | ||
*अगर <math>X \sim \chi^2_{d_1}</math> और <math>Y \sim \chi^2_{d_2}</math> (ची | *अगर <math>X \sim \chi^2_{d_1}</math> और <math>Y \sim \chi^2_{d_2}</math> (ची वर्ग वितरण) [[स्वतंत्रता (संभाव्यता सिद्धांत)|स्वतंत्र]] हैं, तो <math> \frac{X / d_1}{Y / d_2} \sim \mathrm{F}(d_1, d_2)</math> | ||
*अगर <math>X_k \sim \Gamma(\alpha_k,\beta_k)\,</math> ([[गामा वितरण]]) | *अगर <math>X_k \sim \Gamma(\alpha_k,\beta_k)\,</math> ([[गामा वितरण]]) स्वतंत्र हैं, तो <math> \frac{\alpha_2\beta_1 X_1}{\alpha_1\beta_2 X_2} \sim \mathrm{F}(2\alpha_1, 2\alpha_2)</math> | ||
*अगर <math>X \sim \operatorname{Beta}(d_1/2,d_2/2)</math> ([[बीटा वितरण]]) | *अगर <math>X \sim \operatorname{Beta}(d_1/2,d_2/2)</math> ([[बीटा वितरण]]) तो <math>\frac{d_2 X}{d_1(1-X)} \sim \operatorname{F}(d_1,d_2)</math> | ||
*समान रूप से, यदि <math>X \sim F(d_1, d_2)</math>, | *समान रूप से, यदि <math>X \sim F(d_1, d_2)</math>, तो <math>\frac{d_1 X/d_2}{1+d_1 X/d_2} \sim \operatorname{Beta}(d_1/2,d_2/2)</math> | ||
*अगर <math>X \sim F(d_1, d_2)</math>, | *अगर <math>X \sim F(d_1, d_2)</math>, तो <math>\frac{d_1}{d_2}X</math> एक बीटा मुख्य वितरण है: <math>\frac{d_1}{d_2}X \sim \operatorname{\beta^\prime}\left(\tfrac{d_1}{2},\tfrac{d_2}{2}\right)</math> | ||
*अगर <math>X \sim F(d_1, d_2)</math> | *अगर <math>X \sim F(d_1, d_2)</math> तो <math>Y = \lim_{d_2 \to \infty} d_1 X</math> ची-वर्ग वितरण <math>\chi^2_{d_1}</math> है। | ||
*<math>F(d_1, d_2)</math> | *<math>F(d_1, d_2)</math> स्केल किए गए हॉटेलिंग के टी-वर्ग वितरण <math>\frac{d_2}{d_1(d_1+d_2-1)} \operatorname{T}^2 (d_1, d_1 +d_2-1) </math> के समतुल्य है। | ||
*अगर <math>X \sim F(d_1, d_2)</math> | *अगर <math>X \sim F(d_1, d_2)</math> तो <math>X^{-1} \sim F(d_2, d_1)</math> | ||
*अगर <math>X\sim t_{(n)}</math> — छात्र का टी-वितरण — | *अगर <math>X\sim t_{(n)}</math> — छात्र का टी-वितरण — तब: <math display="block">\begin{align} | ||
X^{2} &\sim \operatorname{F}(1, n) \\ | X^{2} &\sim \operatorname{F}(1, n) \\ | ||
X^{-2} &\sim \operatorname{F}(n, 1) | X^{-2} &\sim \operatorname{F}(n, 1) | ||
\end{align}</math> | \end{align}</math> | ||
*एफ-वितरण | *एफ-वितरण प्ररूप 6 [[पियर्सन वितरण]] का एक विशेष प्रकरण है | ||
*अगर <math>X</math> और <math>Y</math> | *अगर <math>X</math> और <math>Y</math> स्वतंत्र हैं, तो <math>X,Y\sim</math> [[Laplace(μ, b)]] के साथ <math display="block"> \frac{|X-\mu|}{|Y-\mu|} \sim \operatorname{F}(2,2) </math> | ||
*अगर <math>X\sim F(n,m)</math> | *अगर <math>X\sim F(n,m)</math> तो <math>\tfrac{\log{X}}{2} \sim \operatorname{FisherZ}(n,m)</math> (फिशर का जेड-वितरण) | ||
* | *अकेंद्रीय एफ-वितरण, एफ-वितरण को सरल बनाता है यदि <math>\lambda=0</math> | ||
* | *दोगुना अकेंद्रीय एफ-वितरण, एफ-वितरण को सरल बनाता है यदि <math> \lambda_1 = \lambda_2 = 0 </math> | ||
*अगर <math>\operatorname{Q}_X(p)</math> | *अगर <math>\operatorname{Q}_X(p)</math> <math>X\sim F(d_1,d_2)</math> के लिए विभाजक ''p'' है और <math>\operatorname{Q}_Y(1-p)</math> <math>Y\sim F(d_2,d_1)</math> के लिए विभाजक <math>1-p</math> है, तो <math display="block">\operatorname{Q}_X(p)=\frac{1}{\operatorname{Q}_Y(1-p)}</math> | ||
* एफ-वितरण [[अनुपात वितरण]] का एक उदाहरण है | * एफ-वितरण [[अनुपात वितरण]] का एक उदाहरण है | ||
== यह भी देखें == | == यह भी देखें == | ||
{{Colbegin}} | {{Colbegin}} | ||
* बीटा प्राइम | * बीटा प्राइम वितरण | ||
* ची | * ची वर्ग वितरण | ||
* [[चाउ परीक्षण]] | * [[चाउ परीक्षण]] | ||
* गामा वितरण | * गामा वितरण | ||
| Line 123: | Line 120: | ||
* विल्क्स का लैम्ब्डा वितरण | * विल्क्स का लैम्ब्डा वितरण | ||
* [[विशार्ट वितरण]] | * [[विशार्ट वितरण]] | ||
* [[संशोधित | * [[संशोधित अर्ध-सामान्य वितरण]]<ref name="Sun, Kong and Pal">{{cite journal |last1=Sun |first1=Jingchao |last2=Kong |first2=Maiying |last3=Pal |first3=Subhadip |title=The Modified-Half-Normal distribution: Properties and an efficient sampling scheme |journal=Communications in Statistics - Theory and Methods |date=22 June 2021 |pages=1–23 |doi=10.1080/03610926.2021.1934700 |s2cid=237919587 |url=https://www.tandfonline.com/doi/abs/10.1080/03610926.2021.1934700?journalCode=lsta20 |issn=0361-0926}}</ref> पीडीएफ के साथ <math>(0, \infty)</math> के रूप में दिया गया है <math> f(x)= \frac{2\beta^{\frac{\alpha}{2}} x^{\alpha-1} \exp(-\beta x^2+ \gamma x )}{\Psi{\left(\frac{\alpha}{2}, \frac{ \gamma}{\sqrt{\beta}}\right)}}</math>, जहाँ <math>\Psi(\alpha,z)={}_1\Psi_1\left(\begin{matrix}\left(\alpha,\frac{1}{2}\right)\\(1,0)\end{matrix};z \right)</math> [[फॉक्स-राइट साई फलन]] को दर्शाता है। | ||
{{Colend}} | {{Colend}} | ||
Revision as of 00:52, 27 March 2023
|
Probability density function 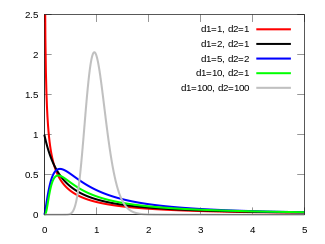 | |||
|
Cumulative distribution function  | |||
| Parameters | d1, d2 > 0 deg. of freedom | ||
|---|---|---|---|
| Support | if , otherwise | ||
| CDF | |||
| Mean |
for d2 > 2 | ||
| Mode |
for d1 > 2 | ||
| Variance |
for d2 > 4 | ||
| Skewness |
for d2 > 6 | ||
| Ex. kurtosis | see text | ||
| Entropy |
[1] | ||
| MGF | does not exist, raw moments defined in text and in [2][3] | ||
| CF | see text | ||
संभाव्यता सिद्धांत और सांख्यिकी में, एफ-वितरण या एफ-अनुपात, जिसे स्नेडेकोर के एफ वितरण या फिशर-स्नेडेकोर वितरण (रोनाल्ड फिशर और जॉर्ज डब्ल्यू. स्नेडेकोर के बाद) के रूप में भी जाना जाता है, एक सतत प्रायिकता वितरण है, जो लगातार शून्य वितरण के रूप में उत्पन्न होता है। एक परीक्षण सांख्यिकी, विशेष रूप से प्रसरण (एनोवा) और अन्य एफ-परीक्षणों के विश्लेषण में है।[2][3][4][5]
परिभाषा
d1 और d2 के साथ एफ-वितरण स्वतंत्रता की डिग्री का वितरण है
कहाँ और स्वतंत्रता और की संबंधित डिग्री के साथ ची-वर्ग वितरण के साथ स्वतंत्र यादृच्छिक चर हैं।
यह अनुसरण करने के लिए दिखाया जा सकता है कि X के लिए प्रायिकता घनत्व फलन (पीडीएफ) द्वारा दिया गया है
वास्तविक संख्या x > 0 के लिए यहाँ बीटा फलन है। कई अनुप्रयोगों में, प्राचल (पैरामीटर) d1 और d2 सकारात्मक पूर्णांक हैं, लेकिन वितरण इन प्राचल के सकारात्मक वास्तविक मूल्यों के लिए अच्छी तरह से परिभाषित है।
संचयी वितरण फलन है
जहां I नियमित अपूर्ण बीटा फलन है।
F(d1, d2)) के बारे में अपेक्षा, प्रसरण और अन्य विवरण साइडबॉक्स में दिए गए हैं; d2 > 8 के लिए, अतिरिक्त ककुदता है
F(d1, d2) वितरण का k-वाँ क्षण उपस्थित है और केवल तभी परिमित है जब 2k <d2 और यह इसके समान है
एफ-वितरण बीटा प्रमुख वितरण का एक विशेष प्राचलीकरण है, जिसे दूसरी तरह का बीटा वितरण भी कहा जाता है।
विशेषता फलन कई मानक संदर्भों (जैसे) में अशुद्ध रूप से सूचीबद्ध है।[3] सही अभिव्यक्ति [7] है
जहां U(a, b, z) दूसरी तरह का संगमी हाइपरज्यामितीय फलन है।
अभिलक्षण
प्राचल और के साथ एफ-वितरण का एक यादृच्छिक चर दो उचित रूप से स्केल किए गए ची-वर्ग वितरण के अनुपात के रूप में उत्पन्न होता है:[8]
जहाँ
- और के क्रमशः स्वतंत्रता की और डिग्री के साथ ची-वर्ग वितरण हैं, और
- और स्वतंत्र हैं।
ऐसे उदाहरणों में जहां एफ-वितरण का उपयोग किया जाता है, उदाहरण के लिए प्रसरण विश्लेषण, कोचरन के प्रमेय को आवेदन करके और की स्वतंत्रता का प्रदर्शन किया जा सकता है।
समतुल्य रूप से, एफ-वितरण का यादृच्छिक चर भी लिखा जा सकता है
जहाँ और , सामान्य वितरण से यादृच्छिक चर के वर्गों का योग है और सामान्य वितरण से यादृच्छिक चर के वर्गों का योग है।
फ़्रीक्वेंटिस्ट संदर्भ में, एक स्केल किया हुआ एफ-वितरण इसलिए प्रायिकता देता है, स्वयं एफ-वितरण के साथ, बिना किसी स्केलिंग के, जहां को के समान लिया जा रहा है। यह वह संदर्भ है जिसमें एफ-वितरण सबसे सामान्यतः पर एफ-परीक्षणों में प्रकट होता है: जहां शून्य परिकल्पना यह है कि दो स्वतंत्र सामान्य प्रसरण समान हैं, और कुछ उचित रूप से चयनित वर्गों के देखे गए योगों की जांच की जाती है कि क्या उनका अनुपात शून्य परिकल्पना के साथ महत्वपूर्ण रूप से असंगत है।
यदि और की पूर्वप्रायिकताएं के लिए एक असूचनात्मक पुनर्विक्रय-अपरिवर्तक जेफरीस पूर्व लिया जाता है, तो मात्रा बायेसियन सांख्यिकी में समान वितरण होता है।[9] इस संदर्भ में, एक स्केल किया गया एफ-वितरण इस प्रकार पश्च प्रायिकता देता है, जहां देखे गए योग और अब ज्ञात के रूप में लिया जाता है।
गुण और संबंधित वितरण
- अगर और (ची वर्ग वितरण) स्वतंत्र हैं, तो
- अगर (गामा वितरण) स्वतंत्र हैं, तो
- अगर (बीटा वितरण) तो
- समान रूप से, यदि , तो
- अगर , तो एक बीटा मुख्य वितरण है:
- अगर तो ची-वर्ग वितरण है।
- स्केल किए गए हॉटेलिंग के टी-वर्ग वितरण के समतुल्य है।
- अगर तो
- अगर — छात्र का टी-वितरण — तब:
- एफ-वितरण प्ररूप 6 पियर्सन वितरण का एक विशेष प्रकरण है
- अगर और स्वतंत्र हैं, तो Laplace(μ, b) के साथ
- अगर तो (फिशर का जेड-वितरण)
- अकेंद्रीय एफ-वितरण, एफ-वितरण को सरल बनाता है यदि
- दोगुना अकेंद्रीय एफ-वितरण, एफ-वितरण को सरल बनाता है यदि
- अगर के लिए विभाजक p है और के लिए विभाजक है, तो
- एफ-वितरण अनुपात वितरण का एक उदाहरण है
यह भी देखें
- बीटा प्राइम वितरण
- ची वर्ग वितरण
- चाउ परीक्षण
- गामा वितरण
- होटलिंग का टी-वर्ग वितरण
- विल्क्स का लैम्ब्डा वितरण
- विशार्ट वितरण
- संशोधित अर्ध-सामान्य वितरण[10] पीडीएफ के साथ के रूप में दिया गया है , जहाँ फॉक्स-राइट साई फलन को दर्शाता है।
संदर्भ
- ↑ Lazo, A.V.; Rathie, P. (1978). "On the entropy of continuous probability distributions". IEEE Transactions on Information Theory. IEEE. 24 (1): 120–122. doi:10.1109/tit.1978.1055832.
- ↑ 2.0 2.1 Johnson, Norman Lloyd; Samuel Kotz; N. Balakrishnan (1995). Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27). Wiley. ISBN 0-471-58494-0.
- ↑ 3.0 3.1 3.2 Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 26". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 946. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- ↑ NIST (2006). Engineering Statistics Handbook – F Distribution
- ↑ Mood, Alexander; Franklin A. Graybill; Duane C. Boes (1974). सांख्यिकी के सिद्धांत का परिचय (Third ed.). McGraw-Hill. pp. 246–249. ISBN 0-07-042864-6.
- ↑ Taboga, Marco. "The F distribution".
- ↑ Phillips, P. C. B. (1982) "The true characteristic function of the F distribution," Biometrika, 69: 261–264 JSTOR 2335882
- ↑ M.H. DeGroot (1986), Probability and Statistics (2nd Ed), Addison-Wesley. ISBN 0-201-11366-X, p. 500
- ↑ G. E. P. Box and G. C. Tiao (1973), Bayesian Inference in Statistical Analysis, Addison-Wesley. p. 110
- ↑ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). "The Modified-Half-Normal distribution: Properties and an efficient sampling scheme". Communications in Statistics - Theory and Methods: 1–23. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.