बलयुग्म (यांत्रिकी): Difference between revisions
m (Abhishek moved page युगल (यांत्रिकी) to बलयुग्म (यांत्रिकी) without leaving a redirect) |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Pair of equal and opposite forces acting along different lines of action of force on a rigid body}}{{Classical mechanics|cTopic=Fundamental concepts}} | {{Short description|Pair of equal and opposite forces acting along different lines of action of force on a rigid body}}{{Classical mechanics|cTopic=Fundamental concepts}} | ||
[[यांत्रिकी]] में | [[यांत्रिकी]] में बलयुग्म परिणामी बल (या [[शुद्ध बल]] या योग) बलाघूर्ण के साथ बलों की प्रणाली है। लेकिन कोई परिणामी बल नहीं है।<ref name=Kane>''Dynamics, Theory and Applications'' by T.R. Kane and D.A. Levinson, 1985, pp. 90-99: [http://ecommons.library.cornell.edu/handle/1813/638 Free download]</ref> | ||
एक बेहतर शब्द बल युगल या शुद्ध क्षण है। इसका प्रभाव कोणीय [[गति]] प्रदान करना है लेकिन कोई रैखिक गति नहीं है। [[कठोर शरीर की गतिशीलता]] में, बल जोड़े 'मुक्त [[सदिश स्थल]]' हैं, जिसका अर्थ है कि शरीर पर उनके प्रभाव आवेदन के बिंदु से स्वतंत्र हैं। | एक बेहतर शब्द बल युगल या शुद्ध क्षण है। इसका प्रभाव कोणीय [[गति]] प्रदान करना है लेकिन कोई रैखिक गति नहीं है। [[कठोर शरीर की गतिशीलता]] में, बल जोड़े 'मुक्त [[सदिश स्थल]]' हैं, जिसका अर्थ है कि शरीर पर उनके प्रभाव आवेदन के बिंदु से स्वतंत्र हैं। | ||
Revision as of 23:16, 24 March 2023
| Part of a series on |
| चिरसम्मत यांत्रिकी |
|---|
यांत्रिकी में बलयुग्म परिणामी बल (या शुद्ध बल या योग) बलाघूर्ण के साथ बलों की प्रणाली है। लेकिन कोई परिणामी बल नहीं है।[1] एक बेहतर शब्द बल युगल या शुद्ध क्षण है। इसका प्रभाव कोणीय गति प्रदान करना है लेकिन कोई रैखिक गति नहीं है। कठोर शरीर की गतिशीलता में, बल जोड़े 'मुक्त सदिश स्थल' हैं, जिसका अर्थ है कि शरीर पर उनके प्रभाव आवेदन के बिंदु से स्वतंत्र हैं।
एक जोड़े का परिणामी क्षण पल का एक विशेष मामला होता है। एक जोड़े के पास संपत्ति है कि वह संदर्भ बिंदु से स्वतंत्र है।
साधारण युगल
- परिभाषा
एक जोड़ी बलों की एक जोड़ी है, परिमाण में बराबर, विपरीत दिशा में निर्देशित, और लंबवत दूरी या पल से विस्थापित।
सबसे सरल प्रकार के युगल में दो समान और विपरीत बल होते हैं जिनकी क्रिया रेखा मेल नहीं खाती। इसे कहते हैं सिंपल कपल।[1] बलों का एक मोड़ प्रभाव या क्षण होता है जिसे अक्ष के बारे में एक टोक़ कहा जाता है जो बलों के विमान के लिए सामान्य (ज्यामिति) (लंबवत) होता है। युगल के बलाघूर्ण के लिए SI इकाई न्यूटन मीटर है।
यदि दो बल हैं F और −F, तो टॉर्क का यूक्लिडियन वेक्टर निम्न सूत्र द्वारा दिया जाता है:
- युगल का क्षण है
- F बल का परिमाण है
- d दो समानांतर बलों के बीच लंबवत दूरी (आघूर्ण) है
टॉर्क का परिमाण बराबर है F • d, इकाई वेक्टर द्वारा दिए गए टॉर्क की दिशा के साथ , जो दो बलों वाले विमान के लंबवत है और धनात्मक एक वामावर्त युगल है। कब d बलों की कार्रवाई के बिंदुओं के बीच एक सदिश के रूप में लिया जाता है, तो टोक़ का क्रॉस उत्पाद है d और F, अर्थात।
संदर्भ बिंदु की स्वतंत्रता
किसी बल के क्षण को केवल एक निश्चित बिंदु के संबंध में परिभाषित किया जाता है P (यह पल के बारे में कहा जाता है P ) और, सामान्य तौर पर, जब P बदल जाता है, पल बदल जाता है। हालाँकि, युगल का क्षण (टोक़) संदर्भ बिंदु से स्वतंत्र है P: कोई भी बिंदु वही क्षण देगा।[1]दूसरे शब्दों में, एक युगल, किसी भी अधिक सामान्य क्षणों के विपरीत, एक मुक्त सदिश है। (इस तथ्य को पियरे वैरिग्नन का सेकंड मोमेंट प्रमेय कहा जाता है।)[2] इस दावे का प्रमाण इस प्रकार है: मान लीजिए बल सदिशों का एक समुच्चय है F1, F2, आदि जो एक जोड़ी बनाते हैं, स्थिति वैक्टर के साथ (कुछ मूल के बारे में P), r1, r2, आदि, क्रमशः। के बारे में क्षण P है
अब हम एक नया संदर्भ बिंदु चुनते हैं P' से भिन्न है P वेक्टर द्वारा r. नया क्षण है
अब क्रॉस उत्पाद की वितरण संपत्ति का तात्पर्य है
हालाँकि, एक बल युगल की परिभाषा का अर्थ है
इसलिए,
यह साबित करता है कि क्षण संदर्भ बिंदु से स्वतंत्र है, जो इस बात का प्रमाण है कि युगल एक मुक्त सदिश है।
बल और युगल
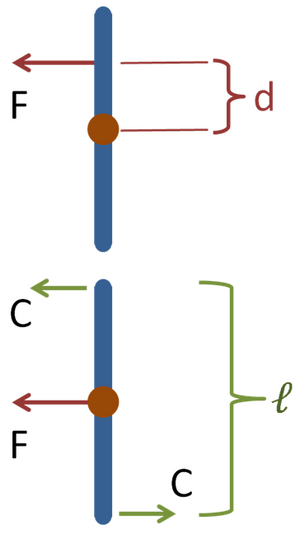
द्रव्यमान के केंद्र से दूरी d पर एक कठोर शरीर पर लगाए गए बल F का वही प्रभाव होता है जो समान बल सीधे द्रव्यमान के केंद्र पर लागू होता है और एक जोड़े Cℓ = Fd। युगल जोड़े के तल पर समकोण पर कठोर शरीर का कोणीय त्वरण उत्पन्न करता है।[3] द्रव्यमान के केंद्र में बल बल की दिशा में बल की दिशा में अभिविन्यास में बदलाव के बिना शरीर को गति देता है। सामान्य प्रमेय हैं:[3]: एक कठोर पिंड के किसी भी बिंदु O' पर कार्य करने वाला एक बल किसी भी बिंदु O पर समान और समानांतर बल F द्वारा प्रतिस्थापित किया जा सकता है और F के समानांतर बलों वाला एक युगल जिसका क्षण M = Fd है, d का पृथक्करण है ओ और ओ'। इसके विपरीत, युगल के तल में एक युगल और एक बल को उचित रूप से स्थित एक बल द्वारा प्रतिस्थापित किया जा सकता है।
- किसी भी जोड़े को एक ही दिशा और क्षण के समान विमान में किसी भी वांछित बल या किसी वांछित भुजा के द्वारा प्रतिस्थापित किया जा सकता है।[3]
अनुप्रयोग
मैकेनिकल इंजीनियरिंग और भौतिक विज्ञान में जोड़े बहुत महत्वपूर्ण हैं। कुछ उदाहरण हैं:
- किसी के हाथ से पेचकस पर लगने वाला बल
- पेचकश की नोक द्वारा पेंच के सिर पर लगाया गया बल
- कताई प्रोपेलर पर कार्य करने वाले बलों को खींचें
- एक समान विद्युत क्षेत्र में विद्युत द्विध्रुव पर बल।
- एक अंतरिक्ष यान पर प्रतिक्रिया नियंत्रण प्रणाली।
- स्टीयरिंग व्हील पर हाथों द्वारा लगाया गया बल।
यह भी देखें
- ट्रैक्शन (इंजीनियरिंग)
- टॉर्क
- पल (भौतिकी)
- ताकत
संदर्भ
- H.F. Girvin (1938) Applied Mechanics, §28 Couples, pp 33,4, Scranton Pennsylvania: International Textbook Company.