एह्रेसमैन कनेक्शन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
== परिचय == | == परिचय == | ||
डिफरेंशियल ज्योमेट्री में सहसंयोजक व्युत्पन्न रेखीय अंतर ऑपरेटर है जो सहसंयोजक प्रकार से [[वेक्टर बंडल|सदिश बंडल]] के खंड के [[दिशात्मक व्युत्पन्न]] को लेता है। यह सदिश की दिशा में बंडल के [[समानांतर परिवहन|समानांतर]] खंड की धारणा तत्पर करने की भी अनुमति देता है: सदिश ''X'' के साथ खंड समानांतर है यदि <math>\nabla_X s = 0</math> है। तो सहसंयोजक व्युत्पन्न अल्प से अल्प दो चीजें प्रदान करता है: अंतर ऑपरेटर, और प्रत्येक दिशा में समानांतर होने का अर्थ क्या है। 'एह्रेसमैन कनेक्शन' डिफरेंशियल ऑपरेटर को प्रत्येक प्रकार से विस्थापित कर देता है और प्रत्येक दिशा में समानांतर अनुभागों के संदर्भ में स्वयंसिद्ध रूप से कनेक्शन को परिभाषित करता है {{harv|एह्रेसमैन|1950}} विशेष रूप से, एह्रेस्मान कनेक्शन फाइबर बंडल के कुल स्थान के लिए प्रत्येक [[स्पर्शरेखा स्थान]] के [[वेक्टर उप-स्थान|सदिश उप-स्थान]] को एकल करता है, जिसे क्षैतिज स्थान कहा जाता है। खंड s तब क्षैतिज (अर्थात, समानांतर) दिशा X में है यदि <math>{\rm d}s(X)</math> क्षैतिज स्थान में स्थित है। यहाँ हम फलन के रूप में s के सम्बन्ध में बता रहे हैं <math>s\colon M\to E</math> आधार M से फाइबर बंडल E तक, जिससे कि <math>{\rm d}s\colon TM\to s^*TE</math> तब स्पर्शरेखा सदिशों का पुशफॉरवर्ड है। क्षैतिज रिक्त स्थान मिलकर सदिश | डिफरेंशियल ज्योमेट्री में सहसंयोजक व्युत्पन्न रेखीय अंतर ऑपरेटर है जो सहसंयोजक प्रकार से [[वेक्टर बंडल|सदिश बंडल]] के खंड के [[दिशात्मक व्युत्पन्न]] को लेता है। यह सदिश की दिशा में बंडल के [[समानांतर परिवहन|समानांतर]] खंड की धारणा तत्पर करने की भी अनुमति देता है: सदिश ''X'' के साथ खंड समानांतर है यदि <math>\nabla_X s = 0</math> है। तो सहसंयोजक व्युत्पन्न अल्प से अल्प दो चीजें प्रदान करता है: अंतर ऑपरेटर, और प्रत्येक दिशा में समानांतर होने का अर्थ क्या है। 'एह्रेसमैन कनेक्शन' डिफरेंशियल ऑपरेटर को प्रत्येक प्रकार से विस्थापित कर देता है और प्रत्येक दिशा में समानांतर अनुभागों के संदर्भ में स्वयंसिद्ध रूप से कनेक्शन को परिभाषित करता है {{harv|एह्रेसमैन|1950}} विशेष रूप से, एह्रेस्मान कनेक्शन फाइबर बंडल के कुल स्थान के लिए प्रत्येक [[स्पर्शरेखा स्थान]] के [[वेक्टर उप-स्थान|सदिश उप-स्थान]] को एकल करता है, जिसे क्षैतिज स्थान कहा जाता है। खंड s तब क्षैतिज (अर्थात, समानांतर) दिशा X में है यदि <math>{\rm d}s(X)</math> क्षैतिज स्थान में स्थित है। यहाँ हम फलन के रूप में s के सम्बन्ध में बता रहे हैं <math>s\colon M\to E</math> आधार M से फाइबर बंडल E तक, जिससे कि <math>{\rm d}s\colon TM\to s^*TE</math> तब स्पर्शरेखा सदिशों का पुशफॉरवर्ड है। क्षैतिज रिक्त स्थान मिलकर सदिश उपबंडल बनाते <math>TE</math> हैं। | ||
यह मात्र सदिश बंडलों की तुलना में संरचनाओं के व्यापक वर्ग पर निश्चित होने का तत्काल लाभ है। विशेष रूप से, यह सामान्य फाइबर बंडल पर उचित प्रकार से परिभाषित है। इसके अतिरिक्त, सहसंयोजक व्युत्पन्न की अनेक विशेषताएं अभी भी बनी हुई हैं: समानांतर परिवहन, [[वक्रता]] और समरूपता। | यह मात्र सदिश बंडलों की तुलना में संरचनाओं के व्यापक वर्ग पर निश्चित होने का तत्काल लाभ है। विशेष रूप से, यह सामान्य फाइबर बंडल पर उचित प्रकार से परिभाषित है। इसके अतिरिक्त, सहसंयोजक व्युत्पन्न की अनेक विशेषताएं अभी भी बनी हुई हैं: समानांतर परिवहन, [[वक्रता]] और समरूपता। | ||
| Line 17: | Line 17: | ||
===क्षैतिज उपस्थानों के माध्यम से परिभाषा === | ===क्षैतिज उपस्थानों के माध्यम से परिभाषा === | ||
''E'' पर एह्रेसमैन कनेक्शन स्मूथ | ''E'' पर एह्रेसमैन कनेक्शन स्मूथ उपबंडल ''H'' है <math>TE</math>, कनेक्शन का [[क्षैतिज बंडल]] कहा जाता है, जो ''V'' का पूरक है, इस अर्थ में कि यह सदिश बंडलों के अपघटन के प्रत्यक्ष योग <math>TE=H\oplus V</math> को परिभाषित करता है,{{sfnp|Kolář|Michor|Slovák|1993|p={{pn|date=November 2021}}}} अधिक विस्तार से, क्षैतिज बंडल में निम्नलिखित गुण होते हैं। | ||
* प्रत्येक बिंदु के लिए <math>e\in E</math>, <math>H_e</math> स्पर्शरेखा स्थान का सदिश स्थान है <math>T_e E</math> से ''E'' पर ''e'', ''e'' पर कनेक्शन के क्षैतिज उप-स्थान कहा जाता है। | * प्रत्येक बिंदु के लिए <math>e\in E</math>, <math>H_e</math> स्पर्शरेखा स्थान का सदिश स्थान है <math>T_e E</math> से ''E'' पर ''e'', ''e'' पर कनेक्शन के क्षैतिज उप-स्थान कहा जाता है। | ||
* <math>H_e</math> सरलता से ''e'' पर निर्भर करता है। | * <math>H_e</math> सरलता से ''e'' पर निर्भर करता है। | ||
* प्रत्येक के लिए <math>e\in E</math>, <math>H_e \cap V_e = \{0\}</math> | * प्रत्येक के लिए <math>e\in E</math>, <math>H_e \cap V_e = \{0\}</math> होता है। | ||
* T<sub>''e''</sub>E में कोई स्पर्शरेखा सदिश (किसी भी e∈E के लिए) क्षैतिज और ऊर्ध्वाधर घटक का योग है, जिससे कि T<sub>''e''</sub>E = H<sub>''e''</sub> + V<sub>''e''</sub> प्राप्त होता है। | * T<sub>''e''</sub>E में कोई स्पर्शरेखा सदिश (किसी भी e∈E के लिए) क्षैतिज और ऊर्ध्वाधर घटक का योग है, जिससे कि T<sub>''e''</sub>E = H<sub>''e''</sub> + V<sub>''e''</sub> प्राप्त होता है। | ||
| Line 31: | Line 31: | ||
* {{mvar|Φ}} V =Im {{mvar|Φ}} पर तत्समक है। | * {{mvar|Φ}} V =Im {{mvar|Φ}} पर तत्समक है। | ||
इसके विपरीत यदि {{mvar|Φ}} TE का सदिश बंडल [[एंडोमोर्फिज्म]] है जो इन दो गुणों को संतुष्ट करता है, तो H = ker {{mvar|Φ}} एह्रेस्मान कनेक्शन का क्षैतिज | इसके विपरीत यदि {{mvar|Φ}} TE का सदिश बंडल [[एंडोमोर्फिज्म]] है जो इन दो गुणों को संतुष्ट करता है, तो H = ker {{mvar|Φ}} एह्रेस्मान कनेक्शन का क्षैतिज उपबंडल है। | ||
अंत में, ध्यान दें कि {{mvar|Φ}}, अपने आप में प्रत्येक स्पर्शरेखा स्थान का रेखीय मानचित्रण होने के सम्बन्ध में, E पर TE-मूल्यवान 1-रूप के रूप में भी माना जा सकता है। यह आने वाले अनुभागों में उपयोगी परिप्रेक्ष्य होगा। | अंत में, ध्यान दें कि {{mvar|Φ}}, अपने आप में प्रत्येक स्पर्शरेखा स्थान का रेखीय मानचित्रण होने के सम्बन्ध में, E पर TE-मूल्यवान 1-रूप के रूप में भी माना जा सकता है। यह आने वाले अनुभागों में उपयोगी परिप्रेक्ष्य होगा। | ||
| Line 56: | Line 56: | ||
या, दूसरे शब्दों में, | या, दूसरे शब्दों में, | ||
:<math>R\left(X,Y\right) = \left[X_H,Y_H\right]_V</math>, | :<math>R\left(X,Y\right) = \left[X_H,Y_H\right]_V</math>, | ||
जहां एक्स = एक्स<sub>H</sub> + एक्स<sub>V</sub> क्रमशः एच और वी घटकों में प्रत्यक्ष योग अपघटन को दर्शाता है। वक्रता के लिए इस अंतिम अभिव्यक्ति से, यह समान रूप से गायब होने के लिए देखा जाता है, और केवल अगर, क्षैतिज उपबंडल फ्रोबेनियस एकीकरण प्रमेय है। इस प्रकार वक्रता क्षैतिज | जहां एक्स = एक्स<sub>H</sub> + एक्स<sub>V</sub> क्रमशः एच और वी घटकों में प्रत्यक्ष योग अपघटन को दर्शाता है। वक्रता के लिए इस अंतिम अभिव्यक्ति से, यह समान रूप से गायब होने के लिए देखा जाता है, और केवल अगर, क्षैतिज उपबंडल फ्रोबेनियस एकीकरण प्रमेय है। इस प्रकार वक्रता क्षैतिज उपबंडल के लिए फाइबर बंडल ई → एम के अनुप्रस्थ वर्गों को प्राप्त करने के लिए [[अभिन्नता की स्थिति]] है। | ||
एह्रेस्मान कनेक्शन की वक्रता भी [[बियांची पहचान]] के संस्करण को संतुष्ट करती है: | एह्रेस्मान कनेक्शन की वक्रता भी [[बियांची पहचान]] के संस्करण को संतुष्ट करती है: | ||
| Line 98: | Line 98: | ||
=== [[संबद्ध बंडल]] === | === [[संबद्ध बंडल]] === | ||
फाइबर बंडल (संरचना समूह के साथ संपन्न) पर एह्रेस्मान कनेक्शन कभी-कभी संबंधित बंडल पर एह्रेस्मान कनेक्शन को उत्पन्न करता है। उदाहरण के लिए, सदिश बंडल ''E में'' | फाइबर बंडल (संरचना समूह के साथ संपन्न) पर एह्रेस्मान कनेक्शन कभी-कभी संबंधित बंडल पर एह्रेस्मान कनेक्शन को उत्पन्न करता है। उदाहरण के लिए, सदिश बंडल ''E में'' (रैखिक) कनेक्शन, ऊपर के रूप में ''E'' की समानता देने के सम्बन्ध में सोचा, ''E'' के फ्रेम P''E'' के जुड़े बंडल पर कनेक्शन प्रेरित करता है। इसके विपरीत, P''E'' में कनेक्शन ''E'' में (रैखिक) कनेक्शन को उत्पन्न करता है, P''E'' में कनेक्शन फ्रेम पर सामान्य रैखिक समूह के संबंध में समतुल्य है (और इस प्रकार कनेक्शन (प्रमुख बंडल))। एह्रेसमैन कनेक्शन के लिए स्वाभाविक रूप से संबद्ध बंडल पर कनेक्शन को प्रेरित करना सदैव संभव नहीं होता है। उदाहरण के लिए, सदिश बंडल के फ्रेम के बंडल पर गैर-समतुल्य एह्रेसमैन कनेक्शन सदिश बंडल पर कनेक्शन को प्रेरित नहीं कर सकता है। | ||
मान लीजिए कि E, P का संबद्ध बंडल है, जिससे कि E = P × <sub>G</sub>''F'' है। E पर ''''''G'''''-कनेक्शन' एह्रेस्मान कनेक्शन है जैसे समानांतर परिवहन मानचित्र τ: ''F''<sub>x</sub> → ''F''<sub>x′</sub> तंतुओं के ''G''-परिवर्तन द्वारा दिया जाता है (पर्याप्त रूप से निकट के बिंदु x और x 'M में वक्र से जुड़ा हुआ है)।<ref>See also {{harvp|Lumiste|2001b|loc="Connections on a manifold"}}.</ref> | मान लीजिए कि E, P का संबद्ध बंडल है, जिससे कि E = P × <sub>G</sub>''F'' है। E पर ''''''G'''''-कनेक्शन' एह्रेस्मान कनेक्शन है जैसे समानांतर परिवहन मानचित्र τ: ''F''<sub>x</sub> → ''F''<sub>x′</sub> तंतुओं के ''G''-परिवर्तन द्वारा दिया जाता है (पर्याप्त रूप से निकट के बिंदु x और x 'M में वक्र से जुड़ा हुआ है)।<ref>See also {{harvp|Lumiste|2001b|loc="Connections on a manifold"}}.</ref> | ||
P पर प्रमुख कनेक्शन दिया गया है, | P पर प्रमुख कनेक्शन दिया गया है, पुलबैक के माध्यम से संबंधित फाइबर बंडल ''E'' = ''P'' ×<sub>G</sub> ''F'' पर ''G''-कनेक्शन प्राप्त करता है। | ||
इसके विपरीत, E पर ''G''-कनेक्शन दिया गया है, संबंधित प्रमुख बंडल ''P'' पर प्रमुख कनेक्शन को पुनर्प्राप्त करना संभव है। इस प्रमुख कनेक्शन को पुनर्प्राप्त करने के लिए, सामान्य फाइबर ''F'' पर फ्रेम की धारणा प्रस्तुत करता है। चूंकि G परिमित-आयामी है<ref>For convenience, we assume that ''G'' is finite-dimensional, although this assumption can safely be dropped with minor modifications.</ref> जो F पर प्रभावी रूप से कार्य करता है, | इसके विपरीत, E पर ''G''-कनेक्शन दिया गया है, संबंधित प्रमुख बंडल ''P'' पर प्रमुख कनेक्शन को पुनर्प्राप्त करना संभव है। इस प्रमुख कनेक्शन को पुनर्प्राप्त करने के लिए, सामान्य फाइबर ''F'' पर फ्रेम की धारणा प्रस्तुत करता है। चूंकि G परिमित-आयामी है<ref>For convenience, we assume that ''G'' is finite-dimensional, although this assumption can safely be dropped with minor modifications.</ref> जो F पर प्रभावी रूप से कार्य करता है, F के अंदर बिंदुओं (y<sub>1</sub>,...,y<sub>m</sub>) का परिमित विन्यास उपस्थित होना चाहिए जैसे कि G-कक्षा R = {(gy<sub>1</sub>,...,''gy''<sub>m</sub>) | ''g'' ∈ ''G''} ''G'' का प्रमुख सजातीय स्थान है। ''F'' पर ''G''-एक्शन के लिए फ्रेम की धारणा का सामान्यीकरण देने के रूप में ''R'' के विषय में विचार कर सकते हैं। ध्यान दें कि, चूंकि ''R, G'' के लिए प्रमुख सजातीय स्थान है, विशिष्ट फाइबर ''R'' के साथ E से जुड़ा बंडल E(R) E से जुड़ा प्रमुख बंडल है। किन्तु यह स्वयं के साथ ''E'' के ''m''-फोल्ड उत्पाद बंडल का उपबंडल भी है। E पर क्षैतिज रिक्त स्थान का वितरण इस उत्पाद बंडल पर रिक्त स्थान के वितरण को प्रेरित करता है। चूंकि कनेक्शन से जुड़े समानांतर परिवहन मानचित्र ''G''-मानचित्र हैं, वे उप-स्थान E(R) को संरक्षित करते हैं, और इसलिए ''G''-कनेक्शन E(R) पर प्रमुख ''G''-कनेक्शन के लिए उतरता है। | ||
सारांश में, संबंधित फाइबर बंडलों के प्रमुख कनेक्शनों के अवरोही और संबंधित फाइबर बंडलों पर जी-कनेक्शन के मध्य पत्राचार (समतुल्यता तक) है। इस कारण से, संरचना समूह जी के साथ फाइबर बंडलों की श्रेणी में, प्रमुख कनेक्शन में संबंधित बंडलों पर जी-कनेक्शन के लिए सभी प्रासंगिक जानकारी होती है। इसलिए, जब तक संबंधित बंडलों पर कनेक्शन पर विचार करने के लिए कोई प्रमुख कारण नहीं है (जैसा कि, उदाहरण के लिए, [[कार्टन कनेक्शन]] के स्थिति में है) सामान्यतः मुख्य कनेक्शन के साथ सीधे काम करता है। | सारांश में, संबंधित फाइबर बंडलों के प्रमुख कनेक्शनों के अवरोही और संबंधित फाइबर बंडलों पर जी-कनेक्शन के मध्य पत्राचार (समतुल्यता तक) है। इस कारण से, संरचना समूह जी के साथ फाइबर बंडलों की श्रेणी में, प्रमुख कनेक्शन में संबंधित बंडलों पर जी-कनेक्शन के लिए सभी प्रासंगिक जानकारी होती है। इसलिए, जब तक संबंधित बंडलों पर कनेक्शन पर विचार करने के लिए कोई प्रमुख कारण नहीं है (जैसा कि, उदाहरण के लिए, [[कार्टन कनेक्शन]] के स्थिति में है) सामान्यतः मुख्य कनेक्शन के साथ सीधे काम करता है। | ||
Revision as of 10:27, 26 April 2023
विभेदक ज्यामिति में, एह्रेसमैन कनेक्शन (फ्रांसीसी गणितज्ञ चार्ल्स एह्रेसमैन के पश्चात, जिन्होंने प्रथम बार इस अवधारणा को औपचारिक रूप दिया था) कनेक्शन की धारणा का संस्करण है, जो किसी भी चिकनी फाइबर बंडल पर समझ में आता है। विशेष रूप से, यह अंतर्निहित फाइबर बंडल की संभावित सदिश बंडल संरचना पर निर्भर नहीं करता है, किन्तु फिर भी, रैखिक कनेक्शन को विशेष स्थिति के रूप में देखा जा सकता है। एह्रेसमैन कनेक्शन की अन्य महत्वपूर्ण विशेष स्थिति प्रमुख बंडलपर प्रमुख कनेक्शन हैं, जो कि प्रमुख लाइ समूह एक्शन में समकक्ष होना आवश्यक है।
परिचय
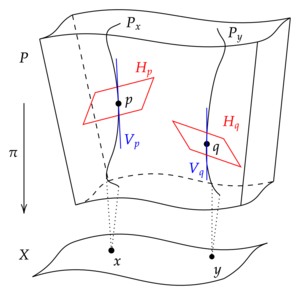
डिफरेंशियल ज्योमेट्री में सहसंयोजक व्युत्पन्न रेखीय अंतर ऑपरेटर है जो सहसंयोजक प्रकार से सदिश बंडल के खंड के दिशात्मक व्युत्पन्न को लेता है। यह सदिश की दिशा में बंडल के समानांतर खंड की धारणा तत्पर करने की भी अनुमति देता है: सदिश X के साथ खंड समानांतर है यदि है। तो सहसंयोजक व्युत्पन्न अल्प से अल्प दो चीजें प्रदान करता है: अंतर ऑपरेटर, और प्रत्येक दिशा में समानांतर होने का अर्थ क्या है। 'एह्रेसमैन कनेक्शन' डिफरेंशियल ऑपरेटर को प्रत्येक प्रकार से विस्थापित कर देता है और प्रत्येक दिशा में समानांतर अनुभागों के संदर्भ में स्वयंसिद्ध रूप से कनेक्शन को परिभाषित करता है (एह्रेसमैन 1950) विशेष रूप से, एह्रेस्मान कनेक्शन फाइबर बंडल के कुल स्थान के लिए प्रत्येक स्पर्शरेखा स्थान के सदिश उप-स्थान को एकल करता है, जिसे क्षैतिज स्थान कहा जाता है। खंड s तब क्षैतिज (अर्थात, समानांतर) दिशा X में है यदि क्षैतिज स्थान में स्थित है। यहाँ हम फलन के रूप में s के सम्बन्ध में बता रहे हैं आधार M से फाइबर बंडल E तक, जिससे कि तब स्पर्शरेखा सदिशों का पुशफॉरवर्ड है। क्षैतिज रिक्त स्थान मिलकर सदिश उपबंडल बनाते हैं।
यह मात्र सदिश बंडलों की तुलना में संरचनाओं के व्यापक वर्ग पर निश्चित होने का तत्काल लाभ है। विशेष रूप से, यह सामान्य फाइबर बंडल पर उचित प्रकार से परिभाषित है। इसके अतिरिक्त, सहसंयोजक व्युत्पन्न की अनेक विशेषताएं अभी भी बनी हुई हैं: समानांतर परिवहन, वक्रता और समरूपता।
रैखिकता के अतिरिक्त, कनेक्शन का गुप्त घटक सहप्रसरण है। शास्त्रीय सहसंयोजक डेरिवेटिव के साथ, सहप्रसरण डेरिवेटिव की पश्चवर्ती विशेषता है। उनके निर्माण में क्रिस्टोफेल प्रतीकों के परिवर्तन नियम को निर्दिष्ट करता है- जो कि सहसंयोजक नहीं है - और फिर परिणामस्वरूप व्युत्पन्न का सामान्य सहप्रसरण होता है। एह्रेसमैन कनेक्शन के लिए, फाइबर बंडल के तंतुओं पर अभिनय करने वाले लाई समूह को प्रारंभ करके सामान्यीकृत सहप्रसरण सिद्धांत प्रारंभ करना संभव है। उचित नियम यह है कि क्षैतिज रिक्त स्थान निश्चित अर्थ में, समूह क्रिया के संबंध में समकक्ष हो।
एह्रेस्मान कनेक्शन के लिए परिष्कृत स्पर्श यह है कि इसे अंतर रूप में प्रदर्शित किया जा सकता है, उसी प्रकार जैसे कनेक्शन प्रपत्र के स्थिति में। यदि समूह तंतुओं पर कार्य करता है और कनेक्शन समतुल्य है, तो रूप भी समतुल्य होगा। इसके अतिरिक्त, कनेक्शन फॉर्म वक्रता की परिभाषा को वक्रता रूप के रूप में भी अनुमति देता है।
औपचारिक परिभाषा
माना चिकना फाइबर बंडल बनें।[1] मान लीजिये,
- 'E' के तंतुओं, अर्थात 'V ' के तंतु पर स्पर्शरेखा सदिशों से युक्त ऊर्ध्वाधर बंडल बनें है का यह उपसमूह आधार स्थान M के लिए कोई विहित उप-स्पर्श स्पर्शरेखा नहीं होने पर भी विहित रूप से परिभाषित किया गया है। (बेशक, यह विषमता फाइबर बंडल की परिभाषा से आती है, जिसमें केवल प्रक्षेपण है जबकि उत्पाद दो होंगे।)
क्षैतिज उपस्थानों के माध्यम से परिभाषा
E पर एह्रेसमैन कनेक्शन स्मूथ उपबंडल H है , कनेक्शन का क्षैतिज बंडल कहा जाता है, जो V का पूरक है, इस अर्थ में कि यह सदिश बंडलों के अपघटन के प्रत्यक्ष योग को परिभाषित करता है,[2] अधिक विस्तार से, क्षैतिज बंडल में निम्नलिखित गुण होते हैं।
- प्रत्येक बिंदु के लिए , स्पर्शरेखा स्थान का सदिश स्थान है से E पर e, e पर कनेक्शन के क्षैतिज उप-स्थान कहा जाता है।
- सरलता से e पर निर्भर करता है।
- प्रत्येक के लिए , होता है।
- TeE में कोई स्पर्शरेखा सदिश (किसी भी e∈E के लिए) क्षैतिज और ऊर्ध्वाधर घटक का योग है, जिससे कि TeE = He + Ve प्राप्त होता है।
अधिक परिष्कृत शब्दों में, इन गुणों को संतुष्ट करने वाले क्षैतिज रिक्त स्थान का ऐसा असाइनमेंट जेट बंडल J1E → E के चिकने खंड से त्रुटिहीन रूप से युग्मित होता है।
कनेक्शन फार्म के माध्यम से परिभाषा
समतुल्य रूप से, Φ को ऊर्ध्वाधर बंडल V पर H के साथ प्रक्षेपण होने दें (जिससे कि H = ker Φ)। यह TE के क्षैतिज और ऊर्ध्वाधर भागों में उपरोक्त प्रत्यक्ष योग अपघटन द्वारा निर्धारित किया जाता है और इसे कभी-कभी एह्रेसमैन कनेक्शन का कनेक्शन रूप कहा जाता है। इस प्रकार Φ निम्नलिखित गुणों (सामान्य रूप से अनुमानों) के साथ TE से स्वयं के लिए सदिश बंडल समरूपता है:
- Φ2 = Φ;
- Φ V =Im Φ पर तत्समक है।
इसके विपरीत यदि Φ TE का सदिश बंडल एंडोमोर्फिज्म है जो इन दो गुणों को संतुष्ट करता है, तो H = ker Φ एह्रेस्मान कनेक्शन का क्षैतिज उपबंडल है।
अंत में, ध्यान दें कि Φ, अपने आप में प्रत्येक स्पर्शरेखा स्थान का रेखीय मानचित्रण होने के सम्बन्ध में, E पर TE-मूल्यवान 1-रूप के रूप में भी माना जा सकता है। यह आने वाले अनुभागों में उपयोगी परिप्रेक्ष्य होगा।
क्षैतिज लिफ्टों के माध्यम से समानांतर परिवहन
एह्रेस्मान कनेक्शन भी फाइबर बंडल E के कुल स्थान में बेस मैनिफोल्ड M से वक्र उठाने के लिए विधि निर्धारित करता है जिससे कि वक्र के स्पर्शक क्षैतिज हों।[2][3] ये क्षैतिज लिफ्ट कनेक्शन औपचारिकता के अन्य संस्करणों के लिए समानांतर परिवहन का प्रत्यक्ष एनालॉग हैं।
विशेष रूप से, मान लें कि γ(t), M में बिंदु x = γ(0) से होते हुए चिकना वक्र है। मान लीजिए e ∈ Ex x के ऊपर फाइबर में बिंदु है। E के माध्यम से γ का 'लिफ्ट' वक्र है कुल स्थान E में ऐसा है:
- , और
लिफ्ट क्षैतिज है यदि, इसके अतिरिक्त, वक्र का प्रत्येक स्पर्शरेखा TE के क्षैतिज उपबंडल में स्थित है:
इसे π और Φ पर प्रारम्भ श्रेणी-शून्यता प्रमेय का उपयोग करके दिखाया जा सकता है कि प्रत्येक सदिश X∈TxM में सदिश के लिए अद्वितीय क्षैतिज लिफ्ट है। विशेष रूप से, γ के लिए स्पर्शरेखा क्षेत्र पुलबैक बंडल γ*E के कुल स्थान में क्षैतिज सदिश क्षेत्र उत्पन्न करता है। पिकार्ड-लिंडेलोफ प्रमेय के अनुसार, यह सदिश क्षेत्र पूर्णांकीय है। इस प्रकार, किसी वक्र γ और बिंदु e पर x = γ(0) के लिए, छोटे समय t के लिए γ से e तक का अद्वितीय क्षैतिज लिफ़्ट उपस्थित है।
ध्यान दें कि, सामान्य एह्रेस्मान कनेक्शन के लिए, क्षैतिज लिफ्ट पथ-निर्भर है। जब M में दो चिकने वक्र, γ1(0) = γ2(0) = x0 पर युग्मित होते हैं और अन्य बिंदु x1∈ M पर प्रतिच्छेद करते हैं, समान e ∈ π के माध्यम से क्षैतिज रूप से E तक उठाये जाते हैं-1(x0), वे सामान्यतः π के विभिन्न बिंदुओं से गुजरेंगे-1(x1). फाइबर बंडलों के विभेदक ज्यामिति के लिए इसका महत्वपूर्ण परिणाम है: एच के वर्गों का स्थान ई पर सदिश फ़ील्ड्स के स्थान का झूठ बोलना नहीं है, क्योंकि यह झूठ व्युत्पन्न के तहत (सामान्य रूप से) बंद नहीं है। लाई ब्रैकेट के नीचे बंद होने की इस विफलता को वक्रता द्वारा मापा जाता है।
गुण
वक्रता
होने देना Φ एह्रेस्मान कनेक्शन हो। फिर की वक्रता Φ द्वारा दिया गया है[2]
जहां [-,-] फ्रॉलीशर-निजेनहुइस ब्रैकेट को दर्शाता है {{mvar|Φ}∈ Ω1(ई, टीई) स्वयं के साथ। इस प्रकार आर ∈ Ω2(E,TE) E पर दो रूप है जिसमें TE द्वारा परिभाषित मान हैं
- ,
या, दूसरे शब्दों में,
- ,
जहां एक्स = एक्सH + एक्सV क्रमशः एच और वी घटकों में प्रत्यक्ष योग अपघटन को दर्शाता है। वक्रता के लिए इस अंतिम अभिव्यक्ति से, यह समान रूप से गायब होने के लिए देखा जाता है, और केवल अगर, क्षैतिज उपबंडल फ्रोबेनियस एकीकरण प्रमेय है। इस प्रकार वक्रता क्षैतिज उपबंडल के लिए फाइबर बंडल ई → एम के अनुप्रस्थ वर्गों को प्राप्त करने के लिए अभिन्नता की स्थिति है।
एह्रेस्मान कनेक्शन की वक्रता भी बियांची पहचान के संस्करण को संतुष्ट करती है:
जहां फिर से [-,-] फ्रॉलीशर-निजेनहुइस का ब्रैकेट है {{mvar|Φ}∈ Ω1(ई, टीई) और आर ∈ Ω2(ई, टीई)।
पूर्णता
एह्रेस्मान कनेक्शन घटता को अद्वितीय क्षैतिज लिफ्ट स्थानीय संपत्ति रखने की अनुमति देता है। पूर्ण एह्रेस्मान कनेक्शन के लिए, वक्र क्षैतिज रूप से अपने संपूर्ण डोमेन पर उठाया जा सकता है।
होलोनॉमी
कनेक्शन की सपाटता स्थानीय रूप से क्षैतिज रिक्त स्थान के फ्रोबेनियस प्रमेय (अंतर टोपोलॉजी) से मेल खाती है। दूसरे चरम पर, गैर-लुप्त होने वाली वक्रता का तात्पर्य कनेक्शन की समग्रता की उपस्थिति से है।[4]
विशेष स्थिति
प्रमुख बंडल और प्रमुख कनेक्शन
मान लीजिए कि E स्मूथ प्रमुख बंडल है| M के ऊपर प्रमुख G-बंडल है। फिर E पर एह्रेसमैन कनेक्शन H को 'प्रमुख (एह्रेसमैन ) कनेक्शन' कहा जाता है।[3] यदि यह E पर G क्रिया के संबंध में इस अर्थ में अपरिवर्तनीय है
- किसी भी e∈E और g∈G के लिए; यहाँ ई पर ई पर जी के समूह क्रिया (गणित) के अंतर को दर्शाता है।
जी के एक-पैरामीटर उपसमूह ई पर लंबवत रूप से कार्य करते हैं। इस क्रिया का अंतर किसी को उप-स्थान की पहचान करने की अनुमति देता है समूह 'जी' के झूठ बीजगणित जी के साथ, मानचित्र द्वारा कहें . एह्रेसमैन कनेक्शन के कनेक्शन फॉर्म v को तब ω(X)=ι(v(X)) द्वारा परिभाषित 'g' में मानों के साथ E पर 1-फॉर्म ω के रूप में देखा जा सकता है।
इस प्रकार पुनर्व्याख्या की गई, कनेक्शन फॉर्म ω निम्नलिखित दो गुणों को संतुष्ट करता है:
- यह G क्रिया के तहत समान रूप से रूपांतरित होता है: सभी h∈G के लिए, जहाँ Rh* सही क्रिया के तहत पुलबैक (अंतर ज्यामिति) है और विज्ञापन इसके लाई बीजगणित पर G का आसन्न प्रतिनिधित्व है।
- यह लाई बीजगणित के उनके संबंधित तत्वों के लिए लंबवत सदिश फ़ील्ड को मैप करता है: ω(X)=ι(X) सभी X∈V के लिए।
इसके विपरीत, यह दिखाया जा सकता है कि प्रमुख बंडल पर ऐसा 'जी'-मूल्यवान 1-रूप उपरोक्त गुणों को संतुष्ट करने वाला क्षैतिज वितरण उत्पन्न करता है।
स्थानीय तुच्छीकरण को देखते हुए क्षैतिज सदिश क्षेत्रों में ω को अल्प किया जा सकता है (इस तुच्छीकरण में)। यह पुलबैक (डिफरेंशियल ज्योमेट्री) के माध्यम से बी पर 1-फॉर्म ω' को परिभाषित करता है। फॉर्म ω' ω को प्रत्येक प्रकार से निर्धारित करता है, किन्तु यह तुच्छीकरण के विकल्प पर निर्भर करता है। (इस फॉर्म को अक्सर 'कनेक्शन फॉर्म' भी कहा जाता है और इसे केवल ω द्वारा दर्शाया जाता है।)
सदिश बंडल और सहपरिवर्ती डेरिवेटिव
मान लीजिए कि E, M के ऊपर स्मूथ सदिश बंडल है। फिर E पर एह्रेसमैन कनेक्शन H को 'रैखिक (एह्रेसमैन ) कनेक्शन' कहा जाता है यदि He ई ∈ ई पर रैखिक रूप से निर्भर करता हैx प्रत्येक x ∈ M के लिए। इसे सटीक बनाने के लिए, मान लीजिए Sλ ई पर λ द्वारा स्केलर गुणा को निरूपित करें। फिर एच रैखिक है अगर और केवल अगर किसी भी ई ∈ ई और अदिश λ के लिए।
चूँकि E सदिश बंडल है, इसका वर्टिकल बंडल V π*E के लिए आइसोमॉर्फिक है। इसलिए यदि s, E का भाग है, तब v(ds):TM→s*V=s*π*E=E. यह सदिश बंडल आकारिकी है, और इसलिए सदिश बंडल होम (टीएम, ई) के खंड ∇s द्वारा दिया जाता है। तथ्य यह है कि एह्रेसमैन कनेक्शन रैखिक है, इसका अर्थ यह है कि इसके अतिरिक्त यह प्रत्येक कार्य के लिए सत्यापित करता है पर लीबनिज नियम, यानी , और इसलिए s का कनेक्शन (सदिश बंडल) है।
इसके विपरीत कनेक्शन (सदिश बंडल) ∇ सदिश बंडल पर H को परिभाषित करके रैखिक एह्रेसमैन कनेक्शन को परिभाषित करता हैe, x=π(e) के साथ e ∈ E के लिए, प्रतिबिंब ds होना चाहिएx(टीxM) जहां s, s(x) = e और ∇ के साथ E का खंड हैXएस = 0 सभी एक्स ∈ टी के लिएxएम।
ध्यान दें कि (ऐतिहासिक कारणों से) शब्द रेखीय जब कनेक्शन पर लागू होता है, तो कभी-कभी स्पर्शरेखा बंडल या फ्रेम बंडल पर परिभाषित कनेक्शन को संदर्भित करने के लिए उपयोग किया जाता है (जैसे शब्द affine - Affine कनेक्शन देखें)।
संबद्ध बंडल
फाइबर बंडल (संरचना समूह के साथ संपन्न) पर एह्रेस्मान कनेक्शन कभी-कभी संबंधित बंडल पर एह्रेस्मान कनेक्शन को उत्पन्न करता है। उदाहरण के लिए, सदिश बंडल E में (रैखिक) कनेक्शन, ऊपर के रूप में E की समानता देने के सम्बन्ध में सोचा, E के फ्रेम PE के जुड़े बंडल पर कनेक्शन प्रेरित करता है। इसके विपरीत, PE में कनेक्शन E में (रैखिक) कनेक्शन को उत्पन्न करता है, PE में कनेक्शन फ्रेम पर सामान्य रैखिक समूह के संबंध में समतुल्य है (और इस प्रकार कनेक्शन (प्रमुख बंडल))। एह्रेसमैन कनेक्शन के लिए स्वाभाविक रूप से संबद्ध बंडल पर कनेक्शन को प्रेरित करना सदैव संभव नहीं होता है। उदाहरण के लिए, सदिश बंडल के फ्रेम के बंडल पर गैर-समतुल्य एह्रेसमैन कनेक्शन सदिश बंडल पर कनेक्शन को प्रेरित नहीं कर सकता है।
मान लीजिए कि E, P का संबद्ध बंडल है, जिससे कि E = P × GF है। E पर 'G-कनेक्शन' एह्रेस्मान कनेक्शन है जैसे समानांतर परिवहन मानचित्र τ: Fx → Fx′ तंतुओं के G-परिवर्तन द्वारा दिया जाता है (पर्याप्त रूप से निकट के बिंदु x और x 'M में वक्र से जुड़ा हुआ है)।[5]
P पर प्रमुख कनेक्शन दिया गया है, पुलबैक के माध्यम से संबंधित फाइबर बंडल E = P ×G F पर G-कनेक्शन प्राप्त करता है।
इसके विपरीत, E पर G-कनेक्शन दिया गया है, संबंधित प्रमुख बंडल P पर प्रमुख कनेक्शन को पुनर्प्राप्त करना संभव है। इस प्रमुख कनेक्शन को पुनर्प्राप्त करने के लिए, सामान्य फाइबर F पर फ्रेम की धारणा प्रस्तुत करता है। चूंकि G परिमित-आयामी है[6] जो F पर प्रभावी रूप से कार्य करता है, F के अंदर बिंदुओं (y1,...,ym) का परिमित विन्यास उपस्थित होना चाहिए जैसे कि G-कक्षा R = {(gy1,...,gym) | g ∈ G} G का प्रमुख सजातीय स्थान है। F पर G-एक्शन के लिए फ्रेम की धारणा का सामान्यीकरण देने के रूप में R के विषय में विचार कर सकते हैं। ध्यान दें कि, चूंकि R, G के लिए प्रमुख सजातीय स्थान है, विशिष्ट फाइबर R के साथ E से जुड़ा बंडल E(R) E से जुड़ा प्रमुख बंडल है। किन्तु यह स्वयं के साथ E के m-फोल्ड उत्पाद बंडल का उपबंडल भी है। E पर क्षैतिज रिक्त स्थान का वितरण इस उत्पाद बंडल पर रिक्त स्थान के वितरण को प्रेरित करता है। चूंकि कनेक्शन से जुड़े समानांतर परिवहन मानचित्र G-मानचित्र हैं, वे उप-स्थान E(R) को संरक्षित करते हैं, और इसलिए G-कनेक्शन E(R) पर प्रमुख G-कनेक्शन के लिए उतरता है।
सारांश में, संबंधित फाइबर बंडलों के प्रमुख कनेक्शनों के अवरोही और संबंधित फाइबर बंडलों पर जी-कनेक्शन के मध्य पत्राचार (समतुल्यता तक) है। इस कारण से, संरचना समूह जी के साथ फाइबर बंडलों की श्रेणी में, प्रमुख कनेक्शन में संबंधित बंडलों पर जी-कनेक्शन के लिए सभी प्रासंगिक जानकारी होती है। इसलिए, जब तक संबंधित बंडलों पर कनेक्शन पर विचार करने के लिए कोई प्रमुख कारण नहीं है (जैसा कि, उदाहरण के लिए, कार्टन कनेक्शन के स्थिति में है) सामान्यतः मुख्य कनेक्शन के साथ सीधे काम करता है।
टिप्पणियाँ
- ↑ These considerations apply equally well to the more general situation in which is a surjective submersion: i.e., E is a fibered manifold over M. In an alternative generalization, due to Lang (1999) and Eliason (1967), E and M are permitted to be Banach manifolds, with E a fiber bundle over M as above.
- ↑ 2.0 2.1 2.2 Kolář, Michor & Slovák (1993), p. [page needed].
- ↑ 3.0 3.1 Kobayashi & Nomizu (1996a), p. [page needed], Vol. 1.
- ↑ Holonomy for Ehresmann connections in fiber bundles is sometimes called the Ehresmann-Reeb holonomy or leaf holonomy in reference to the first detailed study using Ehresmann connections to study foliations in (Reeb 1952)
- ↑ See also Lumiste (2001b), "Connections on a manifold".
- ↑ For convenience, we assume that G is finite-dimensional, although this assumption can safely be dropped with minor modifications.
संदर्भ
- Ehresmann, Charles (1950), Les connexions infinitésimales dans un espace fibré différentiable (PDF), Colloque de Topologie, Bruxelles, Georges Thone, Liège; Masson & cie, Paris, pp. 29–55
- Ehresmann, Charles (1952), Les connexions infinitésimales dans un espace fibré différentiable (PDF), Séminaire N. Bourbaki, vol. 24, pp. 153–168
- Eliason, H (1967), "Geometry of manifolds of maps", Journal of Differential Geometry, 1: 169–194
- Kobayashi, Shoshichi (1957), "Theory of connections", Ann. Mat. Pura Appl., 43: 119–194, doi:10.1007/BF02411907, MR 0096276, S2CID 120972987
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996a), Foundations of Differential Geometry, vol. 1 (New ed.), Wiley-Interscience, ISBN 0-471-15733-3
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996b), Foundations of Differential Geometry, vol. 2 (New ed.), Wiley-Interscience, ISBN 978-0-471-15732-8
- Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag, archived from the original (PDF) on 2017-03-30, retrieved 2007-04-25
- Lang, Serge (1999), Fundamentals of differential geometry, Springer-Verlag, ISBN 0-387-98593-X
- Lumiste, Ülo (2001a) [1994], "Connection on a fibre bundle", Encyclopedia of Mathematics, EMS Press
- Lumiste, Ülo (2001b) [1994], "Connections on a manifold", Encyclopedia of Mathematics, EMS Press
- Reeb, Georges (1952), Sur certaines propriétés topologiques des variétés feuilletées, Paris: Herman
अग्रिम पठन
- Raoul Bott (1970) "Topological obstruction to integrability", Proc. Symp. Pure Math., 16 Amer. Math. Soc., Providence, RI.
- Kubarski, Jan; Pradines, Jean; Rybicki, Tomasz; Wolak, Robert, eds. (2007). Geometry and topology of manifolds: The mathematical legacy of Charles Ehresmann on the occasion of the hundredth anniversary of his birthday. Banach Center Publications. Vol. 76. Warsaw: Polish Academy of Sciences. MR 2284825.