ब्राउनियन ब्रिज: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
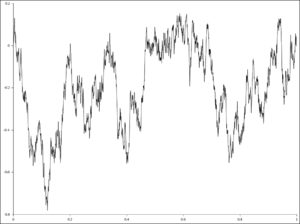
[[Image:Brownian bridge.png|thumb|ब्राउनियन गति, दोनों सिरों पर पिन की गई। यह | [[Image:Brownian bridge.png|thumb|ब्राउनियन गति, दोनों सिरों पर पिन की गई। यह ब्राउनियन ब्रिज का प्रतिनिधित्व करती है।]]'''ब्राउनियन ब्रिज''' एक सतत समय प्रसंभाव्यता प्रक्रिया ''B''(''t'') है जिसका [[प्रायिकता वितरण]] मानक [[वीनर प्रक्रिया]] ''W''(''t'') ([[एक प्रकार कि गति|ब्राउनियन गति]] के गणितीय मॉडल) का सशर्त प्रायिकता वितरण है जो इस शर्त के अधीन है (जब मानकीकृत) कि ''W''(''T'') = 0, ताकि प्रक्रिया को ''t'' = 0 और ''t'' = ''T'' दोनों पर समान मान पर पिन किया जा सके। अधिक सटीक रूप से- | ||
:<math> B_t := (W_t\mid W_T=0),\;t \in [0,T] </math> | :<math> B_t := (W_t\mid W_T=0),\;t \in [0,T] </math> | ||
अंतराल [0,''T''] में किसी भी ''t'' पर ब्रिज का अपेक्षित मान विचरण <math>\textstyle\frac{t(T-t)}{T}</math> के साथ शून्य है, जिसका अर्थ है कि सबसे अधिक अनिश्चितता ब्रिज के बीच में है, नोड्स पर शून्य अनिश्चितता है। ''B''(''s'') और ''B''(''t'') का [[सहप्रसरण]] <math>\min(s,t)-\frac{s\,t}{T}</math>, या ''s''(T − ''t'')/T है यदि ''s'' < ''t। ब्राउनियन ब्रिज में वृद्धि स्वतंत्र नहीं है।'' | अंतराल [0,''T''] में किसी भी ''t'' पर ब्रिज का अपेक्षित मान विचरण <math>\textstyle\frac{t(T-t)}{T}</math> के साथ शून्य है, जिसका अर्थ है कि सबसे अधिक अनिश्चितता ब्रिज के बीच में है, नोड्स पर शून्य अनिश्चितता है। ''B''(''s'') और ''B''(''t'') का [[सहप्रसरण]] <math>\min(s,t)-\frac{s\,t}{T}</math>, या ''s''(T − ''t'')/T है यदि ''s'' < ''t। ब्राउनियन ब्रिज में वृद्धि स्वतंत्र नहीं है।'' | ||
Revision as of 00:19, 24 June 2023
ब्राउनियन ब्रिज एक सतत समय प्रसंभाव्यता प्रक्रिया B(t) है जिसका प्रायिकता वितरण मानक वीनर प्रक्रिया W(t) (ब्राउनियन गति के गणितीय मॉडल) का सशर्त प्रायिकता वितरण है जो इस शर्त के अधीन है (जब मानकीकृत) कि W(T) = 0, ताकि प्रक्रिया को t = 0 और t = T दोनों पर समान मान पर पिन किया जा सके। अधिक सटीक रूप से-
अंतराल [0,T] में किसी भी t पर ब्रिज का अपेक्षित मान विचरण के साथ शून्य है, जिसका अर्थ है कि सबसे अधिक अनिश्चितता ब्रिज के बीच में है, नोड्स पर शून्य अनिश्चितता है। B(s) और B(t) का सहप्रसरण , या s(T − t)/T है यदि s < t। ब्राउनियन ब्रिज में वृद्धि स्वतंत्र नहीं है।
अन्य प्रसंभाव्यता प्रक्रियाओं से संबंध
यदि W(t) मानक वीनर प्रक्रिया है (अर्थात्, t ≥ 0 के लिए, W(t) को सामान्यतः अपेक्षित मान 0 और विचरण t के साथ वितरित किया जाता है, और वृद्धि स्थिर और स्वतंत्र होती है), तो
t ∈ [0, T] के लिए ब्राउनियन ब्रिज है। यह W(T) से स्वतंत्र है[1]
इसके विपरीत, यदि B(t) ब्राउनियन ब्रिज है और Z एक मानक सामान्य यादृच्छिक चर है जो B से स्वतंत्र है, तो प्रक्रिया
t ∈ [0, 1] के लिए वीनर प्रक्रिया है। अधिक सामान्यतः, t ∈ [0, T] के लिए वीनर प्रक्रिया W(t) को विघटित किया जा सकता है
ब्राउनियन गति के आधार पर ब्राउनियन ब्रिज का एक और प्रतिनिधित्व, t ∈ [0, T] के लिए है
इसके विपरीत, t ∈ [0, ∞] के लिए
ब्राउनियन ब्रिज को प्रसंभाव्यता गुणांक के साथ फूरियर श्रृंखला के रूप में भी दर्शाया जा सकता है
जहाँ स्वतंत्र रूप से समान रूप से वितरित मानक सामान्य यादृच्छिक चर हैं (करहुनेन-लोव प्रमेय देखें)।
ब्राउनियन ब्रिज अनुभवजन्य प्रक्रियाओं के क्षेत्र में डोंस्कर के प्रमेय का परिणाम है। इसका उपयोग सांख्यिकीय अनुमान के क्षेत्र में कोल्मोगोरोव-स्मिरनोव परीक्षण में भी किया जाता है।
सहज टिप्पणियाँ
मानक वीनर प्रक्रिया W(0) = 0 को संतुष्ट करती है और इसलिए मूल से "बंधी" होती है, लेकिन अन्य बिंदु प्रतिबंधित नहीं होते हैं। दूसरी ओर, ब्राउनियन ब्रिज प्रक्रिया में, न केवल B(0) = 0 है, बल्कि हमें यह भी आवश्यक है कि B(T) = 0 है, अर्थात यह प्रक्रिया t = T पर भी "बंधी हुई" है। जिस तरह एक शाब्दिक ब्रिज को दोनों सिरों पर स्तंभों द्वारा समर्थित किया जाता है, उसी तरह ब्राउनियन ब्रिज को अंतराल [0,T] के दोनों सिरों पर शर्तों को पूरा करने की आवश्यकता होती है। (थोड़े सामान्यीकरण में, कभी-कभी किसी को B(t1) = a और B(t1) = a की आवश्यकता होती है जहां t1, t2, a और b ज्ञात स्थिरांक होते हैं।)
मान लीजिए कि हमने कंप्यूटर अनुकरण द्वारा वीनर प्रक्रिया पथ के कई बिंदु W(0), W(1), W(2), W(3), आदि उत्पन्न किए हैं। अब अंतराल [0,T] में अतिरिक्त अंक पूर्ण करना वांछित है, अर्थात पहले से उत्पन्न बिंदुओं W(0) और W(T) के बीच अंतर्वेशन करना है। इसका हल ब्राउनियन ब्रिज का उपयोग करना है जो W(0) और W(T) मानों से गुजरने के लिए आवश्यक है।
सामान्य स्थिति
सामान्य स्थिति के लिए जब B(t1) = a और B(t2) = b, समय t ∈ (t1, t2) पर B का वितरण माध्य के साथ सामान्य होता है
और विचरण
और B(s) और B(t) के बीच सहप्रसरण, s < t के साथ है
संदर्भ
- ↑ Aspects of Brownian motion, Springer, 2008, R. Mansuy, M. Yor page 2
- Glasserman, Paul (2004). Monte Carlo Methods in Financial Engineering. New York: Springer-Verlag. ISBN 0-387-00451-3.
- Revuz, Daniel; Yor, Marc (1999). Continuous Martingales and Brownian Motion (2nd ed.). New York: Springer-Verlag. ISBN 3-540-57622-3.