ची वितरण

chi

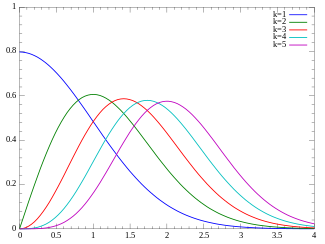
Probability density function
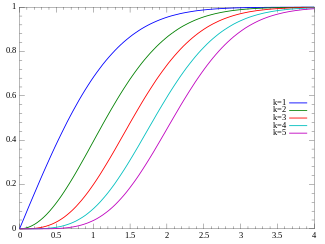
Cumulative distribution function
Parameters	$k>0\,$ (degrees of freedom)
Support	$x\in [0,\infty )$
PDF	${\frac {1}{2^{(k/2)-1}\Gamma (k/2)}}\;x^{k-1}e^{-x^{2}/2}$
CDF	$P(k/2,x^{2}/2)\,$
Mean	$\mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}$
Median	$\approx {\sqrt {k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}}}$
Mode	${\sqrt {k-1}}\,$ for $k\geq 1$
Variance	$\sigma ^{2}=k-\mu ^{2}\,$
Skewness	$\gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})$
Ex. kurtosis	${\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})$
Entropy	$\ln(\Gamma (k/2))+\,$ ${\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))$
MGF	Complicated (see text)
CF	Complicated (see text)

संभाव्यता सिद्धांत और सांख्यिकी में, ची वितरण एक सतत संभाव्यता वितरण है। यह एक मानक सामान्य वितरण के बाद स्वतंत्र यादृच्छिक चर के एक सेट के वर्गों के योग के सकारात्मक वर्गमूल का वितरण है, या समकक्ष, मूल से यादृच्छिक चर की यूक्लिडियन दूरी का वितरण है। इस प्रकार यह ची-वर्ग वितरण का पालन करने वाले एक चर के सकारात्मक वर्गमूलों के वितरण का वर्णन करके ची-वर्ग वितरण से संबंधित है।

अगर $Z_{1},\ldots ,Z_{k}$ हैं $k$ माध्य 0 और मानक विचलन 1 के साथ स्वतंत्र, सामान्य वितरण यादृच्छिक चर, फिर आँकड़ा

$Y={\sqrt {\sum _{i=1}^{k}Z_{i}^{2}}}$

ची वितरण के अनुसार वितरित किया जाता है। ची वितरण का एक पैरामीटर है, $k$, जो स्वतंत्रता की डिग्री (सांख्यिकी) की संख्या निर्दिष्ट करता है (यानी यादृच्छिक चर की संख्या $Z_{i}$).

सबसे परिचित उदाहरण हैं रेले वितरण (स्वतंत्रता की दो डिग्री के साथ ची वितरण) और एक आदर्श गैस में आणविक गति का मैक्सवेल-बोल्ट्ज़मैन वितरण (स्वतंत्रता की तीन डिग्री के साथ ची वितरण)।

परिभाषाएँ

संभाव्यता घनत्व फ़ंक्शन

ची-वितरण की संभाव्यता घनत्व फ़ंक्शन (पीडीएफ) है

$f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geq 0;\\0,&{\text{otherwise}}.\end{cases}}$

कहाँ $\Gamma (z)$ गामा फ़ंक्शन है.

संचयी वितरण फलन

संचयी वितरण फ़ंक्शन द्वारा दिया गया है:

$F(x;k)=P(k/2,x^{2}/2)\,$

कहाँ $P(k,x)$ Incomplete_gamma_function#Regularized_gamma_functions_and_Poisson_random_variables है।

कार्य उत्पन्न करना

क्षण-उत्पन्न करने वाला कार्य इस प्रकार दिया गया है:

$M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+t{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right),$

कहाँ $M(a,b,z)$ कुमेर का संगम हाइपरज्यामितीय फलन है। विशेषता फ़ंक्शन (संभावना सिद्धांत) द्वारा दिया गया है:

$\varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+it{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right).$

गुण

क्षण

कच्चा क्षण (गणित) तब दिया जाता है:

$\mu _{j}=\int _{0}^{\infty }f(x;k)x^{j}\mathrm {d} x=2^{j/2}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+j)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}$

कहाँ $\ \Gamma (z)\$ गामा फ़ंक्शन है. इस प्रकार पहले कुछ कच्चे क्षण हैं:

$\mu _{1}={\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+1)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}$

$\mu _{2}=k\ ,$

$\mu _{3}=2{\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+3)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}=(k+1)\ \mu _{1}\ ,$ :$\mu _{4}=(k)(k+2)\ ,$

$\mu _{5}=4{\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k\!+\!5)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}=(k+1)(k+3)\ \mu _{1}\ ,$

$\mu _{6}=(k)(k+2)(k+4)\ ,$

जहां गामा फ़ंक्शन के लिए पुनरावृत्ति संबंध का उपयोग करके सबसे सही अभिव्यक्ति प्राप्त की जाती है:

$\Gamma (x+1)=x\ \Gamma (x)~.$

इन अभिव्यक्तियों से हम निम्नलिखित संबंध प्राप्त कर सकते हैं:

अर्थ: $\mu ={\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+1)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}\ ,$ जो करीब है ${\sqrt {k-{\tfrac {1}{2}}\ }}\$ बड़े के लिए k.

विचरण: $V=k-\mu ^{2}\ ,$ जो पास आता है $\ {\tfrac {1}{2}}\$ जैसा k बढ़ती है।

तिरछापन: $\gamma _{1}={\frac {\mu }{\ \sigma ^{3}\ }}\left(1-2\sigma ^{2}\right)~.$ कर्टोसिस की अधिकता: $\gamma _{2}={\frac {2}{\ \sigma ^{2}\ }}\left(1-\mu \ \sigma \ \gamma _{1}-\sigma ^{2}\right)~.$

एंट्रॉपी

एन्ट्रापी निम्न द्वारा दी गई है:

$S=\ln(\Gamma (k/2))+{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi ^{0}(k/2))$

कहाँ $\psi ^{0}(z)$ बहुविवाह फ़ंक्शन है.

बड़ा एन सन्निकटन

हम ची वितरण के माध्य और विचरण का बड़ा n=k+1 सन्निकटन पाते हैं। इसमें एप्लिकेशन है उदा. सामान्य रूप से वितरित जनसंख्या के नमूने के मानक विचलन का वितरण ज्ञात करने में, जहाँ n नमूना आकार है।

तब माध्य है:

$\mu ={\sqrt {2}}\,\,{\frac {\Gamma (n/2)}{\Gamma ((n-1)/2)}}$

हम लिखने के लिए Multiplication_theorem#Gamma_function–Legendre_formula का उपयोग करते हैं:

$2^{n-2}\,\Gamma ((n-1)/2)\cdot \Gamma (n/2)={\sqrt {\pi }}\Gamma (n-1)$,

ताकि:

$\mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {(\Gamma (n/2))^{2}}{\Gamma (n-1)}}$

गामा फ़ंक्शन के लिए स्टर्लिंग के सन्निकटन का उपयोग करते हुए, हमें माध्य के लिए निम्नलिखित अभिव्यक्ति मिलती है:

$\mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}$

$=(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]$

$={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{2n}}+O({\frac {1}{n^{2}}})\right]\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]$

$={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]$

और इस प्रकार भिन्नता है:

$V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}}\,\cdot \left[1+O({\frac {1}{n}})\right]$

संबंधित वितरण

• अगर $X\sim \chi _{k}$ तब $X^{2}\sim \chi _{k}^{2}$ (ची-वर्ग वितरण)
• $\lim _{k\to \infty }{\tfrac {\chi _{k}-\mu _{k}}{\sigma _{k}}}\xrightarrow {d} \ N(0,1)\,$ (सामान्य वितरण)
• अगर $X\sim N(0,1)\,$ तब $|X|\sim \chi _{1}\,$
• अगर $X\sim \chi _{1}\,$ तब $\sigma X\sim HN(\sigma )\,$ (अर्ध-सामान्य वितरण) किसी के लिए $\sigma >0\,$
• $\chi _{2}\sim \mathrm {Rayleigh} (1)\,$ (रेले वितरण)
• $\chi _{3}\sim \mathrm {Maxwell} (1)\,$ (मैक्सवेल वितरण)
• $\|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|_{2}\sim \chi _{k}$, बहुभिन्नरूपी_सामान्य_वितरण का मानक (गणित)#यूक्लिडियन मानदंड#मानक_सामान्य_यादृच्छिक_वेक्टर साथ में $k$ आयाम, के साथ ची वितरण के अनुसार वितरित किया जाता है $k$ स्वतंत्रता की डिग्री (सांख्यिकी)
• ची वितरण सामान्यीकृत गामा वितरण या नाकागामी वितरण या गैर-केंद्रीय ची वितरण का एक विशेष मामला है
• ची वितरण का माध्य (वर्गमूल के आधार पर मापा गया)। $n-1$) सामान्य वितरण के लिए मानक विचलन#परिणामों के निष्पक्ष अनुमान में सुधार कारक उत्पन्न करता है।

Various chi and chi-squared distributions

Name	Statistic
chi-squared distribution	$\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}$
noncentral chi-squared distribution	$\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}$
chi distribution	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}$
noncentral chi distribution	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}$

यह भी देखें

• नाकागामी वितरण

संदर्भ

• Martha L. Abell, James P. Braselton, John Arthur Rafter, John A. Rafter, Statistics with Mathematica (1999), 237f.
• Jan W. Gooch, Encyclopedic Dictionary of Polymers vol. 1 (2010), Appendix E, p. 972.

बाहरी संबंध

• http://mathworld.wolfram.com/ChiDistribution.html