अधिकतम और न्यूनतम: Difference between revisions
No edit summary |
No edit summary |
||
| Line 80: | Line 80: | ||
{{main|दूसरा आंशिक व्युत्पन्न परीक्षण}} | {{main|दूसरा आंशिक व्युत्पन्न परीक्षण}} | ||
[[File:Modell einer Peanoschen Fläche -Schilling XLIX, 1-.jpg|thumb|left|पीआनो सतह, 19वीं शताब्दी के स्थानीय अधिकतम के कुछ मानदंडों का प्रति उदाहरण]][[File:MaximumParaboloid.png|thumb|right|वैश्विक अधिकतम शीर्ष पर स्थित बिंदु है]] | [[File:Modell einer Peanoschen Fläche -Schilling XLIX, 1-.jpg|thumb|left|पीआनो सतह, 19वीं शताब्दी के स्थानीय अधिकतम के कुछ मानदंडों का प्रति उदाहरण]][[File:MaximumParaboloid.png|thumb|right|वैश्विक अधिकतम शीर्ष पर स्थित बिंदु है]] | ||
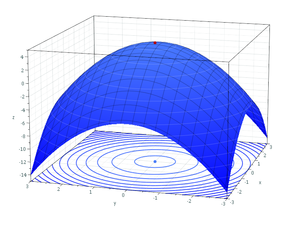
[[File:MaximumCounterexample.png|thumb|right|प्रति उदाहरण: लाल बिंदु एक स्थानीय न्यूनतम दिखाता है जो वैश्विक न्यूनतम नहीं है]]एक से अधिक चर वाले फलनों के लिए समान शर्तें प्रयुक्त होती हैं। उदाहरण के लिए, दाईं ओर (विस्तारित) आकृति में, स्थानीय अधिकतम के लिए आवश्यक शर्तें केवल एक चर वाले फलन के समान होती हैं। Z के रूप में पहला आंशिक | [[File:MaximumCounterexample.png|thumb|right|प्रति उदाहरण: लाल बिंदु एक स्थानीय न्यूनतम दिखाता है जो वैश्विक न्यूनतम नहीं है]]एक से अधिक चर वाले फलनों के लिए समान शर्तें प्रयुक्त होती हैं। उदाहरण के लिए, दाईं ओर (विस्तारित) आकृति में, स्थानीय अधिकतम के लिए आवश्यक शर्तें केवल एक चर वाले फलन के समान होती हैं। Z के रूप में पहला आंशिक व्युत्पन्न (अधिकतम किया जाने वाला चर) अधिकतम पर शून्य है (चित्र में शीर्ष पर चमकता हुआ बिंदु)। दूसरा आंशिक व्युत्पन्न नकारात्मक है। एक काठी बिंदु की संभावना के कारण ये केवल आवश्यक हैं, पर्याप्त नहीं हैं, एक स्थानीय अधिकतम के लिए शर्तें। अधिकतम के लिए समाधान करने के लिए इन स्थितियों के उपयोग के लिए, फलन z को भी अलग-अलग फलन होना चाहिए। [[दूसरा आंशिक व्युत्पन्न परीक्षण]] बिंदु को सापेक्ष अधिकतम या सापेक्ष न्यूनतम के रूप में वर्गीकृत करने में सहायता कर सकता है। | ||
इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के फलनों और एक से अधिक चर के फलनों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय न्यूनतम है, तो यह एक वैश्विक न्यूनतम भी है ([[मध्यवर्ती मूल्य प्रमेय]] और रोले के प्रमेय का उपयोग करके इसे सिद्ध करें [[विरोधाभास द्वारा प्रमाण]])। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है | इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के फलनों और एक से अधिक चर के फलनों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय न्यूनतम है, तो यह एक वैश्विक न्यूनतम भी है ([[मध्यवर्ती मूल्य प्रमेय]] और रोले के प्रमेय का उपयोग करके इसे सिद्ध करें [[विरोधाभास द्वारा प्रमाण]])। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है | ||
:<math>f(x,y)= x^2+y^2(1-x)^3,\qquad x,y \in \R,</math> | :<math>f(x,y)= x^2+y^2(1-x)^3,\qquad x,y \in \R,</math> | ||
जिसका एकमात्र महत्वपूर्ण बिंदु (0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय न्यूनतम है। चूंकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5। | जिसका एकमात्र महत्वपूर्ण बिंदु (0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय न्यूनतम है। चूंकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5। | ||
'''एक फलनात्मक की अधिकतम या न्यूनतम''' | |||
यदि किसी फलन का डोमेन जिसके लिए एक एक्सट्रीम पाया जाना है, में स्वयं | |||
यदि किसी फलन का डोमेन जिसके लिए एक एक्सट्रीम पाया जाना है, में स्वयं फलन सम्मिलित हैं (अर्थात यदि एक एक्सट्रीमम को एक [[कार्यात्मक (गणित)|फलनात्मक (गणित)]] पाया जाना है), तो एक्सट्रीम को विविधताओं के कैलकुलस का उपयोग करके पाया जाता है। | |||
== समुच्चय के संबंध में == | == समुच्चय के संबंध में == | ||
अधिकतम और न्यूनतम को समुच्चय के लिए भी परिभाषित किया जा सकता है। विस्तृत रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे | अधिकतम और न्यूनतम को समुच्चय के लिए भी परिभाषित किया जा सकता है। विस्तृत रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे <math>\max(S)</math> रूप में भी निरूपित किया जाता है. इसके अतिरिक्त, यदि एस एक आदेशित समुच्चय T का एक उपसमुच्चय है और एम एस का सबसे बड़ा तत्व है (T द्वारा प्रेरित ऑर्डर के संबंध में), तो M टी में एस का सर्वोच्च है। इसी प्रकार के परिणाम [[कम से कम तत्व]], [[न्यूनतम तत्व]] और अल्प. समुच्चय के लिए अधिकतम और न्यूनतम फलन का उपयोग [[डेटाबेस]] में किया जाता है, और इसकी गणना तेजी से की जा सकती है, क्योंकि एक समुच्चय के अधिकतम (या न्यूनतम) की गणना एक विभाजन की अधिकतम सीमा से की जा सकती है; औपचारिक रूप से, वे स्व-विघटन योग्य एकत्रीकरण फलन हैं। | ||
एक सामान्य [[आंशिक आदेश]] के स्थिति में, '[[सबसे कम]] तत्व' (अर्थात, जो अन्य सभी की तुलना में छोटा है) को 'न्यूनतम तत्व' (कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी प्रकार, आंशिक रूप से ऑर्डर किए गए समुच्चय (पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के अंदर निहित होता है, चूँकि पॉसमुच्चय | एक सामान्य [[आंशिक आदेश]] के स्थिति में, '[[सबसे कम]] तत्व' (अर्थात, जो अन्य सभी की तुलना में छोटा है) को 'न्यूनतम तत्व' (कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी प्रकार, आंशिक रूप से ऑर्डर किए गए समुच्चय (पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के अंदर निहित होता है, चूँकि पॉसमुच्चय A का 'अधिकतम तत्व' m A का एक तत्व होता है जैसे कि यदि m ≤ b (a में किसी भी b के लिए), फिर m = b। पोसमुच्चय का कोई भी न्यूनतम तत्व या सबसे बड़ा तत्व अद्वितीय है, किन्तुएक पॉसमुच्चय में कई न्यूनतम या अधिकतम तत्व हो सकते हैं। यदि किसी पॉसमुच्चय में एक से अधिक अधिकतम तत्व हैं, तो ये तत्व परस्पर तुलनीय नहीं होंगे। | ||
कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में अधिकतम एक न्यूनतम तत्व और अधिकतम एक अधिकतम तत्व हो सकता है। फिर, आपसी तुलना के कारण, न्यूनतम तत्व भी सबसे छोटा तत्व होगा, और अधिकतम तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी प्रकार से व्यवस्थित समुच्चय में, हम केवल 'न्यूनतम' और 'अधिकतम' शब्दों का उपयोग कर सकते हैं। | कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में अधिकतम एक न्यूनतम तत्व और अधिकतम एक अधिकतम तत्व हो सकता है। फिर, आपसी तुलना के कारण, न्यूनतम तत्व भी सबसे छोटा तत्व होगा, और अधिकतम तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी प्रकार से व्यवस्थित समुच्चय में, हम केवल 'न्यूनतम' और 'अधिकतम' शब्दों का उपयोग कर सकते हैं। | ||
यदि एक श्रृंखला परिमित है, तो इसमें सदैव अधिकतम और न्यूनतम होगा। यदि एक शृंखला अनंत है, तो उसके लिए अधिकतम या न्यूनतम की आवश्यकता नहीं है। उदाहरण के लिए, [[प्राकृतिक संख्या]]ओं के समुच्चय का कोई अधिकतम नहीं है, चूंकि इसमें न्यूनतम है। यदि एक अनंत श्रृंखला एस परिबद्ध है, तो समुच्चय के [[टोपोलॉजिकल क्लोजर]] सीएल (एस) में कभी-कभी न्यूनतम और अधिकतम होता है, इस स्थिति में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय | यदि एक श्रृंखला परिमित है, तो इसमें सदैव अधिकतम और न्यूनतम होगा। यदि एक शृंखला अनंत है, तो उसके लिए अधिकतम या न्यूनतम की आवश्यकता नहीं है। उदाहरण के लिए, [[प्राकृतिक संख्या]]ओं के समुच्चय का कोई अधिकतम नहीं है, चूंकि इसमें न्यूनतम है। यदि एक अनंत श्रृंखला एस परिबद्ध है, तो समुच्चय के [[टोपोलॉजिकल क्लोजर]] सीएल (एस) में कभी-कभी न्यूनतम और अधिकतम होता है, इस स्थिति में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय S की 'कम से कम [[ऊपरी सीमा]]' कहा जाता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 15:30, 17 February 2023
गणितीय विश्लेषण में अधिकतम (पीएल: अधिकतम या अधिकतम) और न्यूनतम (पीएल: न्यूनतम या न्यूनतम) , जिसे सामान्य रूप से उच्च (पीएल: उच्चततम) के रूप में जाना जाता है, फलन का सबसे बड़ा और सबसे छोटा मान, या तो दिए गए अंतराल (गणित) ("स्थानीय" या "रिश्तेदार") के अंदर, या किसी फलन के पूरे डोमेन ( वैश्विक या पूर्ण उच्चतम) पर होता हैं।[1][2][3] पियरे डी फर्मेट उन पहले गणितज्ञों में से एक थे जिन्होंने फलन की अधिकतम और न्यूनतम खोजने के लिए एक सामान्य विधि , पर्याप्तता का प्रस्ताव दिया था।
जैसा कि समुच्चय सिद्धांत में परिभाषित किया गया है, एक समुच्चय (गणित) का अधिकतम और न्यूनतम क्रमशः समुच्चय में सबसे बड़ा और सबसे कम तत्व हैं। असीम अनंत समुच्चय, जैसे कि वास्तविक संख्याओं का समुच्चय, का कोई न्यूनतम या अधिकतम नहीं होता है।
परिभाषा
एक डोमेन X पर परिभाषित एक वास्तविक-मूल्यवान फलन (गणित) f में X में सभी x के लिए, यदि f(x∗) ≥ f(x) पर 'वैश्विक' (या 'पूर्ण') 'अधिकतम बिंदु' x∗ हैं। इसी प्रकार, फलन का X में सभी x के लिए, यदि f(x∗) ≤ f(x) 'वैश्विक' (या 'पूर्ण') 'न्यूनतम बिंदु' x∗ है। किसी अधिकतम बिंदु पर फलन के मान को फलन का अधिकतम मान कहा जाता है, जिसे निरूपित किया जाता है, और न्यूनतम बिंदु पर फलन के मान कों न्यूनतम मान कहा जाता है। प्रतीकात्मक रूप से, इसे इस प्रकार लिखा जा सकता है:
- फलन का वैश्विक अधिकतम बिंदु है यदि
वैश्विक न्यूनतम बिंदु की परिभाषा भी इसी प्रकार आगे बढ़ती है।
यदि डोमेन X एक मीट्रिक स्थान है, तो f को बिंदु x∗ पर एक 'स्थानीय' (या 'सापेक्ष') 'अधिकतम बिंदु' कहा जाता है, यदि कुछ ε > 0 ऐसा उपस्थित है जैसे कि f(x∗) ≥ f(x) X में सभी x∗ के लिए एक्स की दूरी ε के अंदर है। इसी प्रकार, फ़ंक्शन का x∗ पर एक स्थानीय न्यूनतम बिंदु है, यदि f(x∗) ≤ f(x) x के सभी x के लिए x∗ की दूरी ε के अन्दर है। इसी प्रकार की परिभाषा का उपयोग तब किया जा सकता है जब एक्स एक स्थलीय स्थान है, क्योंकि अभी दी गई परिभाषा को पड़ोस के संदर्भ में फिर से परिभाषित किया जा सकता है। गणितीय रूप से, दी गई परिभाषा इस प्रकार लिखी गई है:
- मान ले एक मीट्रिक स्थान और फलन हो. तब फलन का एक स्थानीय अधिकतम बिंदु है यदि जैसे कि
स्थानीय न्यूनतम बिंदु की परिभाषा भी इसी प्रकार आगे बढ़ सकती है।
वैश्विक और स्थानीय दोनों स्थितियों में, सख्त चरम सीमा की अवधारणा कों परिभाषित किया जा सकता। उदाहरण के लिए, x∗ एक निश्चित वैश्विक अधिकतम बिंदु है यदि x ≠ x∗ के साथ x में X सभी के लिए , अपने पास f(x∗) > f(x), और x∗ सख्त स्थानीय अधिकतम बिंदु हैं यदि कुछ ε > 0 उपस्थित है जैसे कि, X में सभी x के लिए x∗ की दूरी ε के अंदर x ≠ x∗ के साथ, अपने पास f(x∗) > f(x) है। ध्यान दें कि एक बिंदु एक सख्त वैश्विक अधिकतम बिंदु है यदि और केवल यदि यह अद्वितीय वैश्विक अधिकतम बिंदु है और इसी तरह न्यूनतम बिंदुओं के लिए है।
सघन जगह डोमेन के साथ एक सतत फलन वास्तविक-मूल्यवान फलन में सदैव अधिकतम बिंदु और न्यूनतम बिंदु होता है। एक महत्वपूर्ण उदाहरण एक फलन है जिसका डोमेन वास्तविक संख्याओं का एक बंद और परिबद्ध अंतराल (गणित) है (ऊपर ग्राफ देखें)।
खोज
वैश्विक अधिकतम और न्यूनतम ढूँढना गणितीय अनुकूलन का लक्ष्य है। यदि कोई फलन एक बंद अंतराल पर निरंतर है, तो उच्च मूल्य प्रमेय द्वारा वैश्विक अधिकतम और निम्निष्ठ उपस्थित हैं। इसके अतिरिक्त, एक वैश्विक अधिकतम (या न्यूनतम) या तो डोमेन के आंतरिक भाग में एक स्थानीय अधिकतम (या न्यूनतम) होना चाहिए, या डोमेन की सीमा पर स्थित होना चाहिए। तो एक वैश्विक अधिकतम (या न्यूनतम) खोजने की एक विधि इंटीरियर में सभी स्थानीय अधिकतम (या न्यूनतम) को देखना है, और सीमा पर बिंदुओं के अधिकतम (या न्यूनतम) को भी देखना है, और सबसे बड़ा मान ( या सबसे छोटा) लेना है।
अलग-अलग फलनों के लिए, फर्मेट के प्रमेय (स्थिर बिंदु) में कहा गया है कि एक डोमेन के इंटीरियर में स्थानीय एक्स्ट्रेमा महत्वपूर्ण बिंदु (गणित) (या अंक जहां व्युत्पन्न शून्य के बराबर होता है) पर होना चाहिए।[4] चूंकि, सभी महत्वपूर्ण बिंदु एक्स्ट्रीमा नहीं हैं। पहला व्युत्पन्न परीक्षण, व्युत्पन्न परीक्षण द्वितीय-व्युत्पन्न परीक्षण (एकल चर), या उच्च-क्रम व्युत्पन्न परीक्षण का उपयोग करके एक महत्वपूर्ण बिंदु एक स्थानीय अधिकतम या स्थानीय न्यूनतम है, पर्याप्त भिन्नता दी गई है।[5]
किसी भी फलन के लिए जिसे टुकड़े के रूप में परिभाषित किया गया है, प्रत्येक टुकड़े के अधिकतम (या न्यूनतम) को अलग-अलग ढूंढकर अधिकतम (या न्यूनतम) पाता है, और फिर यह देखते हुए कि कौन सा सबसे बड़ा (या सबसे छोटा) है।
उदाहरण
| Function | Maxima and minima |
|---|---|
| x2 | Unique global minimum at x = 0. |
| x3 | No global minima or maxima. Although the first derivative (3x2) is 0 at x = 0, this is an inflection point. (2nd derivative is 0 at that point.) |
| Unique global maximum at x = e. (See figure at right) | |
| x−x | Unique global maximum over the positive real numbers at x = 1/e. |
| x3/3 − x | First derivative x2 − 1 and second derivative 2x. Setting the first derivative to 0 and solving for x gives stationary points at −1 and +1. From the sign of the second derivative, we can see that −1 is a local maximum and +1 is a local minimum. This function has no global maximum or minimum. |
| |x| | Global minimum at x = 0 that cannot be found by taking derivatives, because the derivative does not exist at x = 0. |
| cos(x) | Infinitely many global maxima at 0, ±2π, ±4π, ..., and infinitely many global minima at ±π, ±3π, ±5π, .... |
| 2 cos(x) − x | Infinitely many local maxima and minima, but no global maximum or minimum. |
| cos(3πx)/x with 0.1 ≤ x ≤ 1.1 | Global maximum at x = 0.1 (a boundary), a global minimum near x = 0.3, a local maximum near x = 0.6, and a local minimum near x = 1.0. (See figure at top of page.) |
| x3 + 3x2 − 2x + 1 defined over the closed interval (segment) [−4,2] | Local maximum at x = −1−√15/3, local minimum at x = −1+√15/3, global maximum at x = 2 and global minimum at x = −4. |
एक व्यावहारिक उदाहरण के लिए,[6] मान लें कि ऐसी स्थिति है जहाँ किसी के पास है फेंसिंग के फीट और एक आयताकार बाड़े के वर्ग छवि को अधिकतम करने की कोशिश कर रहा है, जहां लंबाई, चौड़ाई है, और क्षेत्र है:
के संबंध में व्युत्पन्न है:
इस समुच्चय कों के बराबर करना है
पता चलता हैं कि हमारा एकमात्र महत्वपूर्ण बिंदु (गणित) है।
अब उस अंतराल को निर्धारित करके समापन बिंदु को पुनः प्राप्त करें जिससे प्रतिबंधित है। चूँकि चौड़ाई धनात्मक है, तब , और तबसे , इसका तात्पर्य है कि .
महत्वपूर्ण बिंदु , में प्लग करें, साथ ही समापन बिंदु और , में , और और क्रमश परिणाम हैं।
इसलिए, आयत के साथ प्राप्य सबसे बड़ा क्षेत्र फीट की बाड़ . है
एक से अधिक चर के फलन
एक से अधिक चर वाले फलनों के लिए समान शर्तें प्रयुक्त होती हैं। उदाहरण के लिए, दाईं ओर (विस्तारित) आकृति में, स्थानीय अधिकतम के लिए आवश्यक शर्तें केवल एक चर वाले फलन के समान होती हैं। Z के रूप में पहला आंशिक व्युत्पन्न (अधिकतम किया जाने वाला चर) अधिकतम पर शून्य है (चित्र में शीर्ष पर चमकता हुआ बिंदु)। दूसरा आंशिक व्युत्पन्न नकारात्मक है। एक काठी बिंदु की संभावना के कारण ये केवल आवश्यक हैं, पर्याप्त नहीं हैं, एक स्थानीय अधिकतम के लिए शर्तें। अधिकतम के लिए समाधान करने के लिए इन स्थितियों के उपयोग के लिए, फलन z को भी अलग-अलग फलन होना चाहिए। दूसरा आंशिक व्युत्पन्न परीक्षण बिंदु को सापेक्ष अधिकतम या सापेक्ष न्यूनतम के रूप में वर्गीकृत करने में सहायता कर सकता है।
इसके विपरीत, वैश्विक एक्स्ट्रेमा की पहचान में एक चर के फलनों और एक से अधिक चर के फलनों के बीच पर्याप्त अंतर हैं। उदाहरण के लिए, यदि वास्तविक रेखा में एक बंद अंतराल पर परिभाषित परिबद्ध अवकलनीय फलन f का एक एकल महत्वपूर्ण बिंदु है, जो एक स्थानीय न्यूनतम है, तो यह एक वैश्विक न्यूनतम भी है (मध्यवर्ती मूल्य प्रमेय और रोले के प्रमेय का उपयोग करके इसे सिद्ध करें विरोधाभास द्वारा प्रमाण)। दो और अधिक आयामों में, यह तर्क विफल हो जाता है। यह समारोह द्वारा सचित्र है
जिसका एकमात्र महत्वपूर्ण बिंदु (0,0) पर है, जो f(0,0) = 0 के साथ एक स्थानीय न्यूनतम है। चूंकि, यह वैश्विक नहीं हो सकता, क्योंकि f(2,3) = −5।
एक फलनात्मक की अधिकतम या न्यूनतम
यदि किसी फलन का डोमेन जिसके लिए एक एक्सट्रीम पाया जाना है, में स्वयं फलन सम्मिलित हैं (अर्थात यदि एक एक्सट्रीमम को एक फलनात्मक (गणित) पाया जाना है), तो एक्सट्रीम को विविधताओं के कैलकुलस का उपयोग करके पाया जाता है।
समुच्चय के संबंध में
अधिकतम और न्यूनतम को समुच्चय के लिए भी परिभाषित किया जा सकता है। विस्तृत रूप से, यदि एक क्रमित समुच्चय S में सबसे बड़ा अवयव m है, तो m समुच्चय का एक उच्चिष्ठ अवयव है, जिसे रूप में भी निरूपित किया जाता है. इसके अतिरिक्त, यदि एस एक आदेशित समुच्चय T का एक उपसमुच्चय है और एम एस का सबसे बड़ा तत्व है (T द्वारा प्रेरित ऑर्डर के संबंध में), तो M टी में एस का सर्वोच्च है। इसी प्रकार के परिणाम कम से कम तत्व, न्यूनतम तत्व और अल्प. समुच्चय के लिए अधिकतम और न्यूनतम फलन का उपयोग डेटाबेस में किया जाता है, और इसकी गणना तेजी से की जा सकती है, क्योंकि एक समुच्चय के अधिकतम (या न्यूनतम) की गणना एक विभाजन की अधिकतम सीमा से की जा सकती है; औपचारिक रूप से, वे स्व-विघटन योग्य एकत्रीकरण फलन हैं।
एक सामान्य आंशिक आदेश के स्थिति में, 'सबसे कम तत्व' (अर्थात, जो अन्य सभी की तुलना में छोटा है) को 'न्यूनतम तत्व' (कुछ भी छोटा नहीं है) के साथ भ्रमित नहीं होना चाहिए। इसी प्रकार, आंशिक रूप से ऑर्डर किए गए समुच्चय (पॉसमुच्चय) का एक 'महानतम तत्व' समुच्चय का ऊपरी भाग होता है जो समुच्चय के अंदर निहित होता है, चूँकि पॉसमुच्चय A का 'अधिकतम तत्व' m A का एक तत्व होता है जैसे कि यदि m ≤ b (a में किसी भी b के लिए), फिर m = b। पोसमुच्चय का कोई भी न्यूनतम तत्व या सबसे बड़ा तत्व अद्वितीय है, किन्तुएक पॉसमुच्चय में कई न्यूनतम या अधिकतम तत्व हो सकते हैं। यदि किसी पॉसमुच्चय में एक से अधिक अधिकतम तत्व हैं, तो ये तत्व परस्पर तुलनीय नहीं होंगे।
कुल क्रम समुच्चय, या श्रृंखला में, सभी तत्व परस्पर तुलनीय हैं, इसलिए ऐसे समुच्चय में अधिकतम एक न्यूनतम तत्व और अधिकतम एक अधिकतम तत्व हो सकता है। फिर, आपसी तुलना के कारण, न्यूनतम तत्व भी सबसे छोटा तत्व होगा, और अधिकतम तत्व भी सबसे बड़ा तत्व होगा। इस प्रकार पूरी प्रकार से व्यवस्थित समुच्चय में, हम केवल 'न्यूनतम' और 'अधिकतम' शब्दों का उपयोग कर सकते हैं।
यदि एक श्रृंखला परिमित है, तो इसमें सदैव अधिकतम और न्यूनतम होगा। यदि एक शृंखला अनंत है, तो उसके लिए अधिकतम या न्यूनतम की आवश्यकता नहीं है। उदाहरण के लिए, प्राकृतिक संख्याओं के समुच्चय का कोई अधिकतम नहीं है, चूंकि इसमें न्यूनतम है। यदि एक अनंत श्रृंखला एस परिबद्ध है, तो समुच्चय के टोपोलॉजिकल क्लोजर सीएल (एस) में कभी-कभी न्यूनतम और अधिकतम होता है, इस स्थिति में उन्हें 'सबसे बड़ी निचली सीमा' और समुच्चय S की 'कम से कम ऊपरी सीमा' कहा जाता है।
यह भी देखें
- आर्ग मैक्स
- व्युत्पन्न परीक्षण
- निम्नतम और उच्चतम
- श्रेष्ठ को सीमित करें और हीन को सीमित करें
- अधिकतम-न्यूनतम पहचान
- यांत्रिक संतुलन
- मेक्स (गणित)
- नमूना अधिकतम और न्यूनतम
- लादने की सीमा
संदर्भ
- ↑ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.
- ↑ Larson, Ron; Edwards, Bruce H. (2009). Calculus (9th ed.). Brooks/Cole. ISBN 978-0-547-16702-2.
- ↑ Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.
- ↑ Weisstein, Eric W. "न्यूनतम". mathworld.wolfram.com (in English). Retrieved 2020-08-30.
- ↑ Weisstein, Eric W. "अधिकतम". mathworld.wolfram.com (in English). Retrieved 2020-08-30.
- ↑ Garrett, Paul. "न्यूनतमकरण और अधिकतमकरण पुनश्चर्या".
बाहरी संबंध
- Thomas Simpson's work on Maxima and Minima at Convergence
- Application of Maxima and Minima with sub pages of solved problems
- Jolliffe, Arthur Ernest (1911). . Encyclopædia Britannica (in English). Vol. 17 (11th ed.). pp. 918–920.