स्पेक्ट्रल घनत्व अनुमान
सांख्यिकीय संकेत प्रसंस्करण में, वर्णक्रमीय घनत्व अनुमान (एसडीई) या केवल वर्णक्रमीय अनुमान का लक्ष्य संकेत के समय नमूनों के अनुक्रम से संकेत के वर्णक्रमीय घनत्व (जिसे शक्ति की वर्णक्रमीय घनत्व के रूप में भी जाना जाता है) का अनुमान लगाना है।[1] सहज रूप से कहें तो, वर्णक्रमीय घनत्व संकेत की आवृत्ति सामग्री को दर्शाता है। वर्णक्रमीय घनत्व का अनुमान लगाने का एक उद्देश्य इन आवधिकों के अनुरूप आवृत्तियों पर चोटियों को देखकर, आँकड़े में किसी भी आवधिकता का पता लगाना है।
कुछ एसडीई तकनीकों का मानना है, कि एक संकेत उत्पन्न आवृत्तियों की एक सीमित (सामान्यतः छोटी) संख्या और ध्वनि से निर्मित होता है, और उत्पन्न आवृत्तियों के स्थान और तीव्रता को खोजने का प्रयास करता है। अन्य घटकों की संख्या पर कोई धारणा नहीं बनाते हैं, और संपूर्ण उत्पादक उत्पन्न करने का अनुमान लगाना चाहते हैं।
अवलोकन
वर्णक्रम विश्लेषण, जिसे वर्णक्रमीय अनुमान विश्लेषण या वर्णक्रमीय घनत्व अनुमान के रूप में भी जाना जाता है, एक जटिल संकेत को सरल भागों में विघटित करने की तकनीकी प्रक्रिया है। जैसा कि ऊपर बताया गया है, कई भौतिक प्रक्रियाओं को कई अलग-अलग आवृत्ति घटकों के योग के रूप में वर्णित किया गया है। कोई भी प्रक्रिया जो विभिन्न राशियों (जैसे आयाम, शक्तियाँ, तीव्रता) बनाम आवृत्ति (या चरण (तरंगें)) की मात्रा निर्धारित करती है, उसे वर्णक्रम विश्लेषण कहा जा सकता है।
वर्णक्रम विश्लेषण पूरे संकेत पर किया जा सकता है। वैकल्पिक रूप से, एक संकेत को छोटे खंडों में तोड़ा जा सकता है (कभी-कभी फ्रेम कहा जाता है), और इन अलग-अलग खंडों पर वर्णक्रम विश्लेषण लागू किया जा सकता है। आवधिक कार्य (जैसे ) इस उप-विभाजन के लिए विशेष रूप से उपयुक्त हैं। गैर-आवधिक कार्यों के विश्लेषण के लिए सामान्य गणितीय विधियाँ सांध्वनिक विश्लेषण की श्रेणी में आती हैं।
फलन का सांध्वनिक रूपांतरण एक आवृत्ति वर्णक्रम उत्पन्न करता है, जिसमें मूल संकेत के विषय में सभी जानकारी होती है, परन्तु एक अलग रूप में। इसका तात्पर्य यह है, कि प्रतिलोम संध्वनिक रूपांतरण द्वारा मूल कार्य को पूरी तरह से पुनर्निर्मित (संश्लेषित) किया जा सकता है। सही पुनर्निर्माण के लिए, वर्णक्रम विश्लेषक को प्रत्येक आवृत्ति घटक के आयाम और चरण (तरंगों) दोनों को संरक्षित करना चाहिए। जानकारी के इन दो टुकड़ों को 2-आयामी वेक्टर के रूप में, एक जटिल संख्या के रूप में, या परिमाण (आयाम) और चरण के रूप में ध्रुवीय निर्देशांक (अर्थात, एक चरण के रूप में) के रूप में दर्शाया जा सकता है। संकेत प्रसंस्करण में एक सामान्य विधि वर्ग आयाम, या शक्ति (भौतिकी) पर विचार करना है; इस विषय में परिणामी भूखंड को शक्ति वर्णक्रम कहा जाता है।
प्रतिवर्तीता के कारण, सान्ध्वनिक रूपांतरण को समय के अतिरिक्त आवृत्ति के संदर्भ में फलन का प्रतिनिधित्व कहा जाता है; इस प्रकार, यह एक आवृत्ति कार्यक्षेत्र प्रतिनिधित्व है। रैखिक संचालन जो समय कार्यक्षेत्र में किए जा सकते हैं, उनके समकक्ष हैं, जो प्रायः आवृत्ति कार्यक्षेत्र में अधिक सरलता से किए जा सकते हैं। बारंबारता विश्लेषण भी रैखिक और गैर-रैखिक दोनों तरह के विभिन्न समय -कार्यक्षेत्र संचालनों के प्रभावों की समझ और व्याख्या को सरल करता है। उदाहरण के लिए, केवल गैर-रैखिक या समय-भिन्न प्रणाली आवृत्ति वर्णक्रम में नई आवृत्तियां निर्मित कर सकते हैं।
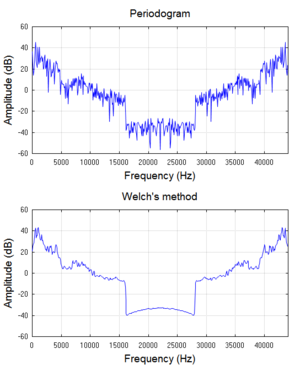
व्यवहार में, लगभग सभी सॉफ्टवेयर और वैद्युत्कीय उपकरण जो आवृत्ति स्पेक्ट्रा उत्पन्न करते हैं, एक विशेष फूरियर परिवर्तन (डीएफटी) का उपयोग करते हैं, जो संकेत के नमूनों पर कार्य करता है, और पूर्ण समाकलित समाधान के लिए एक गणितीय अनुमान प्रदान करता है। जो संकेत के नमूनाकरण पर संचालित होता है, और जो पूर्ण अभिन्न समाधान के लिए गणितीय समीपता प्रदान करता है। डीएफटी लगभग अनिवार्य रूप से [[असतत फूरियर रूपांतरण]] (एफएफटी) नामक एक कुशल कलन विधि द्वारा कार्यान्वित किया जाता है। एक डीएफटी के वर्ग-परिमाण घटकों की सारणी एक प्रकार का शक्ति वर्णक्रम है, जिसे पीरियोग्राम कहा जाता है, जिसका व्यापक रूप से आवेग प्रतिक्रिया और विंडो फलन जैसे ध्वनि-मुक्त कार्यों की आवृत्ति विशेषताओं की जांच के लिए उपयोग किया जाता है। परन्तु कम संकेत-से-ध्वनि अनुपात पर ध्वनि जैसा संकेत या यहां तक कि ज्यावक्र पर लागू होने पर पीरियडोग्राम प्रसंस्करण-लाभ प्रदान नहीं करता है। दूसरे शब्दों में, किसी दी गई आवृत्ति पर इसके वर्णक्रमीय अनुमान का प्रसरण कम नहीं होता है, क्योंकि संगणना में उपयोग किए जाने वाले नमूनों की संख्या बढ़ जाती है। इसे समय के साथ औसत करके कम किया जा सकता है, (वेल्च की विधि[1]) या अधिक आवृत्ति (चौरसाई)। वेल्च की विधि व्यापक रूप से वर्णक्रमीय घनत्व अनुमान (एसडीई) के लिए उपयोग की जाती है। यद्यपि, पीरियोग्राम-आधारित तकनीकें छोटे पूर्वाग्रहों का परिचय देती हैं जो कुछ अनुप्रयोगों में अस्वीकार्य हैं। इसलिए अन्य विकल्प अगले भाग में प्रस्तुत किए गए हैं।
तकनीक
आधारभूत आवर्त सारणी की कमियों को कम करने के लिए वर्णक्रमीय आकलन की कई अन्य तकनीकें विकसित की गई हैं। इन तकनीकों को सामान्यतः गैर- प्राचलिक, प्राचलिक और हाल ही में अर्ध- प्राचलिक (जिन्हें विरल भी कहा जाता है) विधियों में विभाजित किया जा सकता है।[3] गैर- प्राचलिक दृष्टिकोण स्पष्ट रूप से सहप्रसरण या प्रक्रिया के वर्णक्रम का अनुमान लगाते हैं, अतिरिक्त यह माने कि प्रक्रिया में कोई विशेष संरचना है। आधारभूत अनुप्रयोगों (उदाहरण के लिए वेल्च की विधि) के लिए उपयोग में आने वाले कुछ सबसे आम अनुमानक गैर- प्राचलिक अनुमानक हैं, जो आवर्त सारणी से निकटता से संबंधित हैं। इसके विपरीत, प्राचलिक दृष्टिकोण यह मानते हैं, कि अंतर्निहित स्थिर प्रसंभाव्य प्रक्रिया में एक निश्चित संरचना होती है, जिसे कम संख्या में मापदंडों का उपयोग करके वर्णित किया जा सकता है, (उदाहरण के लिए, एक स्वतः-प्रतिगामी या चलती औसत प्रारूप का उपयोग करके)। इन दृष्टिकोणों में, कार्य उस प्रारूप के मापदंडों का अनुमान लगाना है, जो प्रसंभाव्य प्रक्रिया का वर्णन करता है। अर्ध-प्राचलिक विधियों का उपयोग करते समय, अंतर्निहित प्रक्रिया को गैर-प्राचलिक ढांचे का उपयोग करके प्रारूपित किया जाता है, अतिरिक्त धारणा के साथ कि प्रारूप के गैर-शून्य घटकों की संख्या छोटी है, (अर्थात, प्रारूप विरल है)। इसी तरह के विधियों का उपयोग विलुप्त आँकड़े की रिकवरी [4] के साथ-साथ संकेत पुनर्निर्माण के लिए भी किया जा सकता है, एवं साथ ही संपीड़ित संवेदन भी।
निम्नलिखित गैर- प्राचलिक वर्णक्रमीय घनत्व अनुमान तकनीकों की आंशिक सूची है:
- आवर्त सारणी, असतत फूरियर रूपांतरण का मापांक वर्ग है-
- लोम्ब-स्कार्ल पीरियोग्राम, जिसके लिए आँकड़े को समान रूप से स्थान देने की आवश्यकता नहीं है,
- बार्टलेट की विधि वर्णक्रमीय घनत्व अनुमान के विचरण को कम करने के लिए संकेत के कई खंडों से लिए गए पीरियडोग्राम का औसत है
- वेल्च की विधि बार्टलेट की विधि का एक खिड़की वाला संस्करण है जो ओवरलैपिंग सेगमेंट का उपयोग करता है
- मल्टीटेपर एक पीरियडोग्राम-आधारित विधि है, जो वर्णक्रमीय घनत्व अनुमान के विचरण को कम करने के लिए वर्णक्रमीय घनत्व के स्वतंत्र अनुमान बनाने के लिए कई टेपर्स या विंडो का उपयोग करती है।
- कम से कम वर्ग वर्णक्रमीय विश्लेषण, ज्ञात आवृत्तियों के लिए कम से कम वर्गों के आधार पर,
- गैर-समान असतत फूरियर रूपांतरण का उपयोग तब किया जाता है जब संकेत नमूने असमान रूप से समय श्रृंखला में होते हैं,
- एकवचन वर्णक्रम विश्लेषण एक गैर प्राचलिक विधि है जो वर्णक्रमीय घनत्व का अनुमान लगाने के लिए सहप्रसरण मैट्रिक्स के एकवचन मूल्य अपघटन का उपयोग करती है,
- शॉर्ट-टाइम फूरियर रूपांतरण
- सूचना क्षेत्र सिद्धांत महत्वपूर्ण फ़िल्टर सूचना क्षेत्र सिद्धांत पर आधारित एक गैर- प्राचलिक विधि है जो ध्वनि, अपूर्ण आँकड़े और वाद्य प्रतिक्रिया कार्यों से निपट सकता है,
नीचे प्राचलिक तकनीकों की आंशिक सूची दी गई है:
- ऑटोरेग्रेसिव प्रारूप (एआर) आकलन, जो मानता है कि एनटीएच् नमूना पिछले पी नमूनों के साथ सहसंबद्ध है।
- मूविंग-एवरेज प्रारूप (एमए) का अनुमान, जो मानता है कि एनटीएच् नमूना पिछले पी नमूनों में रव की शर्तों के साथ सहसंबद्ध है।
- ऑटोरेग्रेसिव मूविंग एवरेज (एआरएमए) अनुमान, जो एआर और एमए प्रारूप का सामान्यीकरण करता है।
- संगीत (एल्गोरिदम) (संगीत) एक लोकप्रिय सुपर-प्रस्ताव इमेजिंग विधि है।
- अधिकतम एन्ट्रॉपी वर्णक्रमीय अनुमान एसडीई के लिए उपयोगी एक सर्व-ध्रुवीय विधि है, जब एकवचन वर्णक्रमीय विशेषताओं, जैसे तीव्र चोटियों की अपेक्षा की जाती है।
और अंत में अर्ध- प्राचलिक तकनीकों के कुछ उदाहरण:
- स्पार्स इटरेटिव कोवैरियंस-आधारित अनुमान (स्पाइस) अनुमान,[2]और अधिक सामान्यीकृत -मसाला।[3] * पुनरावृत्त अनुकूली दृष्टिकोण (आईएए) अनुमान।[4] *लास्सो (सांख्यिकी), कम से कम वर्ग वर्णक्रमीय विश्लेषण के समान परन्तु एक विरलता लागू करने वाले दंड के साथ।[5]
प्राचलिक अनुमान
प्राचलिक वर्णक्रमीय अनुमान में, कोई मानता है, कि संकेत एक स्थिर प्रक्रिया द्वारा निर्माण किया गया है, जिसमें वर्णक्रमीय घनत्व फलन (एसडीएफ) है। यह आवृत्ति का एक कार्य है और मापदण्ड .[6] अनुमान समस्या तब इन मापदण्ड का आकलन करने में से एक निर्माणित हो जाती है।
प्राचलिक एसडीएफ अनुमान का सबसे सामान्य रूप एक प्रारूप के रूप में एक स्वत:प्रतिगामी प्रारूप का उपयोग करता है, आदेश की .[6]: 392 एक संकेत अनुक्रम शून्य माध्य का पालन करना एवं प्रक्रिया समीकरण को संतुष्ट करती है,
जहां निश्चित गुणांक हैं और शून्य माध्य और नवीनता विचरण के साथ एक श्वेत रव प्रक्रिया है . इस प्रक्रिया के लिए एसडीएफ है,
साथ नमूना समय अंतराल और Nyquist आवृत्ति।
मापदंडों का अनुमान लगाने के लिए कई दृष्टिकोण हैं की प्रक्रिया और इस प्रकार वर्णक्रमीय घनत्व:[6]: 452-453
- स्वत:प्रतिगामी यूल-वॉकर अनुमानक एक प्रक्रिया के लिए यूल-वॉकर समीकरणों को पुनरावर्ती रूप से हल करके पाए जाते हैं,
- बर्ग अनुमानक यूल-वॉकर समीकरणों को सामान्य न्यूनतम वर्ग समस्या के रूप में मानते हुए पाए जाते हैं। बर्ग अनुमानकों को सामान्यतः यूल-वाकर अनुमानकों से उत्तम माना जाता है।[6]: 452 बर्ग ने इन्हें अधिकतम परिक्षय वर्णक्रमीय अनुमान के साथ संबद्ध किया।[7]
- आगे-पीछे न्यूनतम-वर्ग अनुमानक इसका इलाज करते हैं, प्रतिगमन समस्या के रूप में प्रक्रिया करें और आगे-पीछे विधि का उपयोग करके उस समस्या को हल करें। वे बर्ग अनुमानकों के साथ प्रतिस्पर्धी हैं।
- अधिकतम संभावना अनुमानक अधिकतम संभावना दृष्टिकोण का उपयोग करके मापदंडों का अनुमान लगाते हैं। इसमें एक गैर-रैखिक अनुकूलन सम्मिलित है, और प्रथम तीन की तुलना में अधिक जटिल है।
अधिकतम संभावना अनुमानक अधिकतम संभावना दृष्टिकोण का उपयोग करके मापदंडों का अनुमान लगाते हैं। इसमें एक अरेखीय अनुकूलन सम्मिलित है, और यह प्रथम तीन की तुलना में अधिक जटिल है।
आवृत्ति अनुमान
आवृत्ति अनुमान, अवयव की संख्या के विषय में दी गई धारणाओं के ध्वनि की उपस्थिति में अंकीय संकेत प्रक्रिया की आवृत्ति, विपुलता और चरण-परिवर्तन के आकलन सिद्धांत की प्रक्रिया है।[8] यह उपरोक्त सामान्य विधियों के विपरीत है, जो घटकों के बारे में पूर्व धारणा नहीं बनाते हैं।
एकल स्वर
यदि कोई केवल एक ही सबसे तीव्र आवृत्ति का अनुमान लगाना चाहता है, तो वह ध्वनि पहचान कलन विधि का उपयोग कर सकता है। यदि प्रमुख आवृत्ति समय के साथ परिवर्तित है, तो समस्या तात्कालिक आवृत्ति का अनुमान बन जाती है, जैसा कि समय-आवृत्ति प्रतिनिधित्व में परिभाषित किया गया है। तात्क्षणिक आवृत्ति अनुमान के विधियों में विग्नर-विल वितरण और उच्च क्रम अस्पष्टता कार्यों पर आधारित सम्मिलित हैं।[9]
यदि कोई प्राप्त संकेत (संचारित संकेत और ध्वनि सहित) के सभी (संभवतः जटिल) आवृत्ति घटकों को जानना चाहता है, तो एक बहु-टोन दृष्टिकोण का उपयोग करता है।
एकाधिक स्वर
एक संकेत के लिए एक विशिष्ट प्रारूप का योग होता है सफेद ध्वनि की उपस्थिति में जटिल घातांक,
- .
की शक्ति वर्णक्रमीय घनत्व से बना है रव के कारण वर्णक्रमीय घनत्व समारोह के अलावा आवेग कार्य करता है।
आवृत्ति अनुमान के लिए सबसे सरलतम विधियों में इन घटकों को निकालने के लिए ध्वनि रैखिक उप-स्थान की पहचान करना सम्मिलित है। ये विधियाँ एक संकेत उप-स्थान और एक ध्वनि उप-क्षेत्र में स्वतःसंबंध मैट्रिक्स के एजकम्पोजीशन पर आधारित हैं। इन उप-स्थानों की पहचान के पश्चात, ध्वनि उप-स्थान से घटक आवृत्तियों को खोजने के लिए एक आवृत्ति अनुमान फलन का उपयोग किया जाता है। ध्वनि उप-स्थान आधारित आवृत्ति आकलन के सबसे लोकप्रिय विधि हैं, पिसारेंको हार्मोनिक, पिसारेंको की विधि, एकाधिक संकेत वर्गीकरण (संगीत) विधि, आइजन्वेक्टर विधि और न्यूनतम मानदंड विधि।
- पिसारेंको हार्मोनिक अपघटन | पिसारेंको की विधि
- एकाधिक संकेत वर्गीकरण
- ,
- ईजेनवेक्टर विधि
- न्यूनतम मानदंड विधि
उदाहरण गणना
कल्पना करना , से को शून्य माध्य के साथ एक समय श्रृंखला (असतत समय) है। मान लीजिए कि यह आवधिक घटकों की एक परिमित संख्या का योग है, (सभी आवृत्तियाँ धनात्मक हैं):
का विचरण ऊपर दिए गए शून्य-माध्य फ़ंक्शन के लिए है
यदि ये आँकड़े एक विद्युत संकेत से लिए गए नमूने थे, तो यह इसकी औसत शक्ति होगी (शक्ति प्रति इकाई समय में ऊर्जा है, इसलिए यह विचरण के अनुरूप है यदि ऊर्जा आयाम वर्ग के अनुरूप है)।
अब, सरलता के लिए, मान लें कि संकेत समय में अनंतता तक फैलता है, इसलिए हम इसे सीमा के रूप में ले जाते हैं यदि औसत शक्ति परिबद्ध है, जो वास्तविकता में लगभग सदैव ही होती है, तो निम्नलिखित सीमा उपस्थित होती है, और यह आँकड़े का विचरण है।
तत्पश्चात, सरलता के लिए, हम निरंतर समय को पास करेंगे, और यह मानेंगे कि संकेत दोनों दिशाओं में समय में असीमित रूप से विस्तारित होता है। तब ये दो सूत्र बन जाते हैं
और
का मूल माध्य वर्ग है , इसलिए का विचरण है , की औसत शक्ति में योगदान आवृत्ति के साथ घटक से आ रहा है है ये सभी योगदान की औसत शक्ति को जोड़ते हैं
इसके पश्चात आवृत्ति के कार्य के रूप में शक्ति है और इसका सांख्यिकीय संचयी वितरण कार्य होगा
एक समारोह की ओर कदम बढ़ाएं है, नीरस रूप से गैर-घटता है। इसकी छलांग अवधि (रिंग) के घटकों की आवृत्तियों पर होती है , और प्रत्येक छलांग का मान उस घटक की शक्ति या भिन्नता है।
प्रसरण स्वयं के साथ आँकड़े का सहप्रसरण है। यदि हम अब समान आँकड़े पर विचार करें, परन्तु एक अंतराल के साथ ,को हम सहप्रसरण ले सकते हैं, साथ , और इसे स्वतः सहसंबंध फलन के रूप में परिभाषित करें संकेत (या डेटा) के :
यदि यह अस्तित्व में है, तो यह का एक कार्य भी है, यदि औसत शक्ति परिबद्ध है, तब हर जगह उपस्थित है एवं परिमित है, और इससे घिरा हुआ है जो आँकड़े की औसत शक्ति या भिन्नता है।
यह दिखाया जा सकता है,कि के रूप में : एक ही अवधि के साथ आवधिक घटकों में विघटित किया जा सकता है:
यह वास्तव में वर्णक्रमीय अपघटन है, और विभिन्न आवृत्तियों पर शक्ति के वितरण से संबंधित है, आवृत्तियों पर: के एक आवृत्ति घटक का आयाम संकेत की औसत शक्ति में इसका योगदान होता है।
इस उदाहरण की शक्ति वर्णक्रम निरंतर नहीं है, इसलिए इसका अवकलन नहीं होता है, और इसलिए इस संकेत का शक्ति स्पेक्ट्रल घनत्व फलन नहीं होता है। सामान्य रूप से, शक्ति वर्णक्रम दो हिस्सों का योग होता है: एक ऐसी रेखा वर्णक्रम जैसा इस उदाहरण में है, जो निरंतर नहीं है, और जिसका घनत्व फलन नहीं होता है, और एक शेष, जो पूरी तरह से निरंतर होता है,एवं जिसका घनत्व फलन होता है।
यह भी देखें
- बहुआयामी वर्णक्रमीय अनुमान
- पीरियोडोग्राम
- सिगस्पेक
- spectrogram
- समय-आवृत्ति विश्लेषण
- समय-आवृत्ति प्रतिनिधित्व
- कम संभावना
- वर्णक्रमीय बिजली वितरण
संदर्भ
- ↑ Welch, P. D. (1967), "The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms", IEEE Transactions on Audio and Electroacoustics, AU-15 (2): 70–73, Bibcode:1967ITAE...15...70W, doi:10.1109/TAU.1967.1161901
- ↑ Stoica, Petre; Babu, Prabhu; Li, Jian (January 2011). "अलग-अलग मॉडल में विरल पैरामीटर अनुमान की नई विधि और अनियमित रूप से सैंपल किए गए डेटा के स्पेक्ट्रल विश्लेषण के लिए इसका उपयोग". IEEE Transactions on Signal Processing. 59 (1): 35–47. Bibcode:2011ITSP...59...35S. doi:10.1109/TSP.2010.2086452. ISSN 1053-587X. S2CID 15936187.
- ↑ Sward, Johan; Adalbjornsson, Stefan Ingi; Jakobsson, Andreas (March 2017). "विरल पुनरावृत्त सहप्रसरण-आधारित अनुमानक का एक सामान्यीकरण". 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE: 3954–3958. doi:10.1109/icassp.2017.7952898. ISBN 978-1-5090-4117-6. S2CID 5640068.
- ↑ Yardibi, Tarik; Li, Jian; Stoica, Petre; Xue, Ming; Baggeroer, Arthur B. (January 2010). "Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares". IEEE Transactions on Aerospace and Electronic Systems. 46 (1): 425–443. Bibcode:2010ITAES..46..425Y. doi:10.1109/TAES.2010.5417172. hdl:1721.1/59588. ISSN 0018-9251. S2CID 18834345.
- ↑ Panahi, Ashkan; Viberg, Mats (February 2011). "LASSO-आधारित DOA आकलन पद्धति के संकल्प पर". 2011 International ITG Workshop on Smart Antennas. IEEE: 1–5. doi:10.1109/wsa.2011.5741938. ISBN 978-1-61284-075-8. S2CID 7013162.
- ↑ 6.0 6.1 6.2 6.3 Percival, Donald B.; Walden, Andrew T. (1992). भौतिक अनुप्रयोगों के लिए वर्णक्रमीय विश्लेषण. Cambridge University Press. ISBN 9780521435413.
- ↑ Burg, J.P. (1967) "Maximum Entropy Spectral Analysis", Proceedings of the 37th Meeting of the Society of Exploration Geophysicists, Oklahoma City, Oklahoma.
- ↑ Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.
- ↑ Lerga, Jonatan. "सिग्नल तात्कालिक आवृत्ति अनुमान विधियों का अवलोकन" (PDF). University of Rijeka. Retrieved 22 March 2014.
अग्रिम पठन
- Porat, B. (1994). Digital Processing of Random Signals: Theory & Methods. Prentice Hall. ISBN 978-0-13-063751-2.
- Priestley, M.B. (1991). Spectral Analysis and Time Series. Academic Press. ISBN 978-0-12-564922-3.
- Stoica, P.; Moses, R. (2005). Spectral Analysis of Signals. Prentice Hall. ISBN 978-0-13-113956-5.
- Thomson, D. J. (1982). "Spectrum estimation and harmonic analysis". Proceedings of the IEEE. 70 (9): 1055–1096. Bibcode:1982IEEEP..70.1055T. CiteSeerX 10.1.1.471.1278. doi:10.1109/PROC.1982.12433. S2CID 290772.