तीव्रतम अवतरण की विधि
गणित में, तीव्रतम अवतरण की विधि या सैडल-बिंदु की विधि इंटीग्रल का अनुमान लगाने के लिए लाप्लास की विधि का विस्तार है, जहां स्थिर बिंदु (सैडल बिंदु) के समीप से निकलने के लिए कठोर समतल में समोच्च इंटीग्रल को तीव्रतम अवतरण या स्थिर चरण की दिशा में विकृत किया जाता है। सैडल-पॉइंट सन्निकटन का उपयोग कठोर समतल में इंटीग्रल्स के साथ किया जाता है, जबकि लाप्लास की विधि का उपयोग वास्तविक इंटीग्रल्स के साथ किया जाता है।
अनुमान लगाया जाने वाला इंटीग्रल प्रायः निम्नलिखित रूप का होता है
जहां C समोच्च है, और λ बड़ा है। तीव्रतम अवतरण की विधि का संस्करण एकीकरण C के समोच्च को नवीन पथ एकीकरण C' में विकृत कर देता है जिससे निम्नलिखित स्थितियाँ बनी रहें:
- C′ व्युत्पन्न g′(z) के एक या अधिक शून्य से होकर निकलता है,
- g(z) का काल्पनिक भाग C′ पर स्थिर है।
तीव्रतम अवतरण की विधि सर्वप्रथम किसके द्वारा प्रकाशित की गई थी? डेबी (1909), जिन्होंने बेसेल फलन का अनुमान लगाने के लिए इसका उपयोग किया और बताया कि यह हाइपरज्यामितीय फलन के विषय में रीमैन (1863) अप्रकाशित नोट में हुआ था। तीव्रतम अवतरण के समोच्च में न्यूनतम गुण होता है, देखें फेडोर्युक (2001) देखें। सीगल (1932) रीमैन के कुछ अन्य अप्रकाशित नोट्स का वर्णन किया, जहां उन्होंने रीमैन-सीगल सूत्र प्राप्त करने के लिए इस विधि का उपयोग किया था।
मूल विचार
तीव्रतम अवतरण की विधि प्रपत्र के कठोर इंटीग्रल का अनुमान लगाने की विधि है
व्युत्पत्ति
विश्लेषणात्मक होने के कारण इस विधि को तीव्रतम अवतरण की विधि कहा जाता है, स्थिर चरण समोच्च तीव्रतम अवरोही समोच्चों के समतुल्य हैं।
यदि का विश्लेषणात्मक फलन है, यह कॉची-रीमैन समीकरण को संतुष्ट करता है,
साधारण अनुमान
मान लीजिए f, S : Cn → C और C ⊂ Cn, यदि
जहाँ वास्तविक भाग को दर्शाता है, और धनात्मक वास्तविक संख्या λ0 सम्मिलित है जो इस प्रकार है,
तो निम्नलिखित अनुमान मान्य है:[2]
सरल अनुमान का प्रमाण:
एकल गैर-क्षतिग्रस्त सैडल बिंदु का विषय
मूल धारणाएँ और संकेतन
मान लीजिए x सशक्त n-आयामी सदिश है, और
किसी फलन S(x) के लिए हेस्सियन आव्यूह को निरूपित किया जाता है, यदि
सदिश फलन है, तो इसके जैकोबियन आव्यूह और निर्धारक को इस प्रकार परिभाषित किया गया है,
अपतित सैडल बिंदु, z0 ∈ Cn, होलोमोर्फिक फलन S(z) का महत्वपूर्ण बिंदु है (अर्थात, ∇S(z0) = 0) जहां फलन के हेसियन आव्यूह में गैर-लुप्त होने वाला निर्धारक (अर्थात, ) है।
गैर-अपक्षयी सैडल बिंदु के विषय में इंटीग्रल के एसिम्प्टोटिक्स के निर्माण के लिए निम्नलिखित मुख्य उपकरण है:
कॉम्प्लेक्स मोर्स लेम्मा
वास्तविक-मूल्यवान फलन के लिए मोर्स लेम्मा होलोमोर्फिक फलन के लिए निम्नानुसार सामान्यीकृत करता है।[3] होलोमोर्फिक फलन S(z) के अपतित सैडल बिंदु z0 के पास, ऐसे निर्देशांक होते हैं जिनके संदर्भ में S(z) − S(z0) सम्पूर्ण द्विघात है। इसे त्रुटिहीन बनाने के लिए S डोमेन W ⊂ Cn के साथ होलोमोर्फिक फलन मान लीजिए, और W में z0 को S का अपतित सैडल बिंदु मान लीजिए, अर्थात, ∇S(z0) = 0 और , फिर z0 के नेबर U ⊂ W और w = 0 के V ⊂ Cn और φ(0) के साथ विशेषण होलोमोर्फिक फलन सम्मिलित है, φ: V → U φ : V → U साथ φ(0) = z0 इस प्रकार है कि
यहां μj आव्यूह के आइगेनवैल्यूज़ एवं आइगेनसदिश्स हैं।
The following proof is a straightforward generalization of the proof of the real Morse Lemma, which can be found in.[4] We begin by demonstrating
- Auxiliary statement. Let f : Cn → C be holomorphic in a neighborhood of the origin and f (0) = 0. Then in some neighborhood, there exist functions gi : Cn → C such that where each gi is holomorphic and
From the identity
we conclude that
and
Without loss of generality, we translate the origin to z0, such that z0 = 0 and S(0) = 0. Using the Auxiliary Statement, we have
Since the origin is a saddle point,
we can also apply the Auxiliary Statement to the functions gi(z) and obtain
-
(1)
Recall that an arbitrary matrix A can be represented as a sum of symmetric A(s) and anti-symmetric A(a) matrices,
The contraction of any symmetric matrix B with an arbitrary matrix A is
-
(2)
i.e., the anti-symmetric component of A does not contribute because
Thus, hij(z) in equation (1) can be assumed to be symmetric with respect to the interchange of the indices i and j. Note that
hence, det(hij(0)) ≠ 0 because the origin is a non-degenerate saddle point.
Let us show by induction that there are local coordinates u = (u1, ... un), z = ψ(u), 0 = ψ(0), such that
-
(3)
First, assume that there exist local coordinates y = (y1, ... yn), z = φ(y), 0 = φ(0), such that
-
(4)
where Hij is symmetric due to equation (2). By a linear change of the variables (yr, ... yn), we can assure that Hrr(0) ≠ 0. From the chain rule, we have
Therefore:
whence,
The matrix (Hij(0)) can be recast in the Jordan normal form: (Hij(0)) = LJL−1, were L gives the desired non-singular linear transformation and the diagonal of J contains non-zero eigenvalues of (Hij(0)). If Hij(0) ≠ 0 then, due to continuity of Hij(y), it must be also non-vanishing in some neighborhood of the origin. Having introduced , we write
Motivated by the last expression, we introduce new coordinates z = η(x), 0 = η(0),
The change of the variables y ↔ x is locally invertible since the corresponding Jacobian is non-zero,
Therefore,
-
(5)
Comparing equations (4) and (5), we conclude that equation (3) is verified. Denoting the eigenvalues of by μj, equation (3) can be rewritten as
-
(6)
Therefore,
-
(7)
From equation (6), it follows that . The Jordan normal form of reads , where Jz is an upper diagonal matrix containing the eigenvalues and det P ≠ 0; hence, . We obtain from equation (7)
If , then interchanging two variables assures that .
एकल अपतित सैडल बिंदु के विषय में स्पर्शोन्मुख विस्तार
मान लीजिए
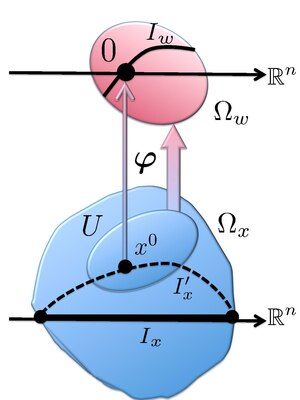
- f (z) और S(z) संवृत, परिबद्ध,और साधारण रूप से जुड़े हुए समुच्चय Ωx ⊂ Cn में होलोमोर्फिक फलन हैं जैसे कि Ix = Ωx ∩ Rn जुड़ा हुआ है;
- के x0 ∈ Ix सम्पूर्ण बिंदु के लिए एकल अधिकतम है;
- x0 अपतित सैडल बिंदु (अर्थात, ∇S(x0) = 0 और ) है,
फिर, निम्नलिखित स्पर्शोन्मुख धारण करता है,
-
(8)
जहाँ μj हेस्सियन आव्यूह और के आइगेनवैल्यू हैं जो नियमों से परिभाषित किये गये हैं,
-
(9)
यह कथन फेडोर्युक (1987) में प्रस्तुत अधिक सामान्य परिणामों का विशेष विषय है।[5]
First, we deform the contour Ixinto a new contour passing through the saddle point x0 and sharing the boundary with Ix. This deformation does not change the value of the integral I(λ). We employ the Complex Morse Lemma to change the variables of integration. According to the lemma, the function φ(w) maps a neighborhood x0 ∈ U ⊂ Ωx onto a neighborhood Ωw containing the origin. The integral I(λ) can be split into two: I(λ) = I0(λ) + I1(λ), where I0(λ) is the integral over , while I1(λ) is over (i.e., the remaining part of the contour I′x). Since the latter region does not contain the saddle point x0, the value of I1(λ) is exponentially smaller than I0(λ) as λ → ∞;[6] thus, I1(λ) is ignored. Introducing the contour Iw such that , we have
-
(10)
Recalling that x0 = φ(0) as well as , we expand the pre-exponential function into a Taylor series and keep just the leading zero-order term
-
(11)
Here, we have substituted the integration region Iw by Rn because both contain the origin, which is a saddle point, hence they are equal up to an exponentially small term.[7] The integrals in the r.h.s. of equation (11) can be expressed as
-
(12)
From this representation, we conclude that condition (9) must be satisfied in order for the r.h.s. and l.h.s. of equation (12) to coincide. According to assumption 2, is a negatively defined quadratic form (viz., ) implying the existence of the integral , which is readily calculated
समीकरण (8) को इस प्रकार भी लिखा जा सकता है
-
(13)
निम्नानुसार चयन किया गया है,
महत्वपूर्ण विषयों पर विचार करें:
- यदि S(x), Rn (अर्थात, बहुआयामी लाप्लास विधि) में वास्तविक x और x0 के लिए वास्तविक मूल्य है, फिर[8]
- यदि S(x) x के लिए वास्तव में पूर्णतया काल्पनिक है (अर्थात, सभी के लिए x में Rn) और x0 में Rn (अर्थात, बहुआयामी स्थिर चरण विधि),[9] तब[10] जहाँ आव्यूह के जड़त्व के नियम को दर्शाता है। प्रमेय का कथन , जो ऋणात्मक आइगेनवैल्यू की संख्या घटाकर धनात्मक आइगेनवैल्यू की संख्या के समान है। यह उल्लेखनीय है कि क्वांटम यांत्रिकी (साथ ही प्रकाशिकी में) में बहुआयामी WKB सन्पासन के लिए स्थिर चरण विधि के अनुप्रयोगों में, Ind मास्लोव सूचकांक से संबंधित है, उदाहरण के लिए, चाइचियन & डेमीचेव (2001) और शुलमैन (2005) है।
एकाधिक अक्षतिग्रस्त सैडल बिंदुओं का विषय
यदि फलन S(x) में कई भिन्न-भिन्न अपतित सैडल बिंदु हैं, अर्थात,
जहाँ
Ωx का संवृत आवरण है, तो एकता के विभाजन को नियोजित करके इंटीग्रल एसिम्प्टोटिक की गणना को एकल सैडल बिंदु के विषय में कम कर दिया जाता है। एकता का विभाजन हमें निरंतर फलन ρk(x) : Ωx → [0, 1], 1 ≤ k ≤ K, का समुच्चय बनाने की अनुमति देता है जो इस प्रकार है,
जहाँ से,
इसलिए जैसे λ → ∞ हमारे पास है:
जहां अंतिम चरण में समीकरण (13) और पूर्व-घातीय फलन का उपयोग किया गया था f (x) कम से कम निरंतर होना चाहिए।
अन्य विषय
जब ∇S(z0) = 0 और , बिंदु z0 ∈ Cn को किसी फलन S(z) का अपतित सैडल पॉइंट कहा जाता है।
स्पर्शोन्मुख की गणना
जब λ → ∞, f (x) सतत है, और S(z) में पतित सैडल बिंदु है, यह बहुत ही समृद्ध समस्या है, जिसका समाधान अधिकतम सीमा तक कैटास्ट्रोफे सिद्धांत पर निर्भर करता है। यहां, कैटास्ट्रोफे सिद्धांत मोर्स लेम्मा की विधि को, S(z) विहित अभ्यावेदन से एक में परिवर्तित करने के लिए प्रतिस्थापित करता है जो केवल अपतित विषय में मान्य है। अधिक जानकारी के लिए, उदाहरण, पोस्टन & स्टीवर्ट (1978) और फेडोर्युक (1987) है।
विकृत सैडल बिंदुओं वाले इंटीग्रल स्वाभाविक रूप से कास्टिक (प्रकाशिकी) और क्वांटम यांत्रिकी में बहुआयामी डब्ल्यूकेबी सन्पासन सहित कई अनुप्रयोगों में दिखाई देते हैं।
अन्य विषय जैसे f (x) और S(x) असंतत हैं या जब S(x) का शीर्ष एकीकरण क्षेत्र की सीमा पर स्थित है,तो विशेष सुरक्षा की आवश्यकता है, उदाहरण के लिए, फेडोर्युक (1987) और वोंग (1989) है।
विस्तार और सामान्यीकरण
सबसे तीव्र अवतरण विधि का विस्तार तथाकथित अरेखीय स्थिर चरण/सबसे तीव्र अवतरण विधि है। यहां, इंटीग्रल के अतिरिक्त, किसी को रीमैन-हिल्बर्ट फ़ैक्टराइज़ेशन समस्याओं के स्पर्शोन्मुख समाधानों का मूल्यांकन करने की आवश्यकता है।
कठोर क्षेत्र में समोच्च C को देखते हुए, उस समोच्च पर परिभाषित फलन f और विशेष बिंदु, मान लीजिए अनंत, समोच्च C से दूर फलन f C में निर्धारित जंप के साथ, और अनंत पर दिए गए सामान्यीकरण के साथ होलोमोर्फिक की शोध करता है। यदि f और इसलिए M अदिश के अतिरिक्त आव्यूह हैं तो यह ऐसी समस्या है जो सामान्य रूप से स्पष्ट समाधान स्वीकार नहीं करती है।
तब रैखिक स्थिर चरण/तीव्रतम अवतरण विधि की के विषय पर स्पर्शोन्मुख मूल्यांकन संभव है। विचार यह है कि दी गई रीमैन-हिल्बर्ट समस्या के समाधान को असम्बद्ध रूप से कम करके सरल, स्पष्ट रूप से समाधान करने योग्य, रीमैन-हिल्बर्ट समस्या बना दिया जाए। कॉची के प्रमेय का उपयोग जम्प समोच्च की विकृतियों को उचित बताने के लिए किया जाता है।
रूसी गणितज्ञ अलेक्जेंडर इट्स के पूर्व फलन के आधार पर, 1993 में डेफ्ट और झोउ द्वारा नॉनलाइनियर स्थिर चरण का प्रारम्भ किया गया था। लैक्स, लीवरमोर, डेफ्ट, वेनाकिड्स और झोउ के पूर्व फलन के आधार पर, 2003 में फलनविसिस, के. मैकलॉघलिन और पी. मिलर द्वारा नॉनलाइनियर स्टीपेस्ट डीसेंट विधि प्रस्तुत की गई थी। जैसा कि रैखिक विषय में होता है, सबसे तीव्र अवरोही आकृतियाँ न्यूनतम-अधिकतम समस्या का समाधान करती हैं। अरैखिक विषय में वे S-वक्र बन जाते हैं (80 के दशक में स्टाल, गोन्चर और राखमनोव द्वारा भिन्न संदर्भ में परिभाषित)।
नॉनलाइनियर स्थिर चरण/तीव्रतम अवतरण विधि में सॉलिटन समीकरणों और एकीकृत प्रारूप, यादृच्छिक आव्यूह और साहचर्य के सिद्धांत के अनुप्रयोग हैं।
अन्य विस्तार सैडल बिंदुओं और एकसमान स्पर्शोन्मुख विस्तारों को संयोजित करने के लिए चेस्टर-फ़्रीडमैन-उर्सेल की विधि है।
यह भी देखें
- पियर्सी इंटीग्रल
- स्थिर चरण सन्पासन
- लाप्लास की विधि
टिप्पणियाँ
- ↑ Bender, Carl M.; Orszag, Steven A. (1999). वैज्ञानिकों और इंजीनियरों के लिए उन्नत गणितीय तरीके I (in English). New York, NY: Springer New York. doi:10.1007/978-1-4757-3069-2. ISBN 978-1-4419-3187-0.
- ↑ A modified version of Lemma 2.1.1 on page 56 in Fedoryuk (1987).
- ↑ Lemma 3.3.2 on page 113 in Fedoryuk (1987)
- ↑ Poston & Stewart (1978), page 54; see also the comment on page 479 in Wong (1989).
- ↑ Fedoryuk (1987), pages 417-420.
- ↑ This conclusion follows from a comparison between the final asymptotic for I0(λ), given by equation (8), and a simple estimate for the discarded integral I1(λ).
- ↑ This is justified by comparing the integral asymptotic over Rn [see equation (8)] with a simple estimate for the altered part.
- ↑ See equation (4.4.9) on page 125 in Fedoryuk (1987)
- ↑ Rigorously speaking, this case cannot be inferred from equation (8) because the second assumption, utilized in the derivation, is violated. To include the discussed case of a purely imaginary phase function, condition (9) should be replaced by
- ↑ See equation (2.2.6') on page 186 in Fedoryuk (1987)
संदर्भ
- Chaichian, M.; Demichev, A. (2001), Path Integrals in Physics Volume 1: Stochastic Process and Quantum Mechanics, Taylor & Francis, p. 174, ISBN 075030801X
- Debye, P. (1909), "Näherungsformeln für die Zylinderfunktionen für große Werte des Arguments und unbeschränkt veränderliche Werte des Index", Mathematische Annalen, 67 (4): 535–558, doi:10.1007/BF01450097, S2CID 122219667 English translation in Debye, Peter J. W. (1954), The collected papers of Peter J. W. Debye, Interscience Publishers, Inc., New York, ISBN 978-0-918024-58-9, MR 0063975
- Deift, P.; Zhou, X. (1993), "A steepest descent method for oscillatory Riemann-Hilbert problems. Asymptotics for the MKdV equation", Ann. of Math., The Annals of Mathematics, Vol. 137, No. 2, vol. 137, no. 2, pp. 295–368, arXiv:math/9201261, doi:10.2307/2946540, JSTOR 2946540, S2CID 12699956.
- Erdelyi, A. (1956), Asymptotic Expansions, Dover.
- Fedoryuk, M. V. (2001) [1994], "Saddle point method", Encyclopedia of Mathematics, EMS Press.
- Fedoryuk, M. V. (1987), Asymptotic: Integrals and Series, Nauka, Moscow [in Russian].
- Kamvissis, S.; McLaughlin, K. T.-R.; Miller, P. (2003), "Semiclassical Soliton Ensembles for the Focusing Nonlinear Schrödinger Equation", Annals of Mathematics Studies, Princeton University Press, vol. 154.
- Riemann, B. (1863), Sullo svolgimento del quoziente di due serie ipergeometriche in frazione continua infinita (Unpublished note, reproduced in Riemann's collected papers.)
- Siegel, C. L. (1932), "Über Riemanns Nachlaß zur analytischen Zahlentheorie", Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, 2: 45–80 Reprinted in Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966.
- Translated in Deift, Percy; Zhou, Xin (2018), "On Riemanns Nachlass for Analytic Number Theory: A translation of Siegel's Uber", arXiv:1810.05198 [math.HO].
- Poston, T.; Stewart, I. (1978), Catastrophe Theory and Its Applications, Pitman.
- Schulman, L. S. (2005), "Ch. 17: The Phase of the Semiclassical Amplitude", Techniques and Applications of Path Integration, Dover, ISBN 0486445283
- Wong, R. (1989), Asymptotic approximations of integrals, Academic Press.