पुशफॉरवर्ड (अंतर)

For other uses, see Pushforward.

यदि एक नक्शा, φ, हर मैनिफोल्ड एम से कई गुना एन पर इंगित करें, फिर φ का पुशफॉरवर्ड वेक्टर को स्पर्शरेखा स्थान में एम में प्रत्येक बिंदु पर एन में प्रत्येक बिंदु पर स्पर्शरेखा स्थान पर ले जाता है।

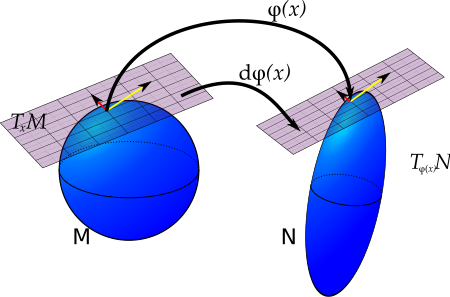
अंतर ज्यामिति में, पुशफॉरवर्ड टेंगेंट स्पेस पर चिकने मैप्स का एक रैखिक सन्निकटन है। लगता है कि φ : M → N चिकना कई गुना ्स के बीच एक चिकना नक्शा है; फिर φ का अंतर, $d\varphi _{x}$, एक बिंदु x पर, कुछ अर्थों में, x के पास φ का सबसे अच्छा रैखिक सन्निकटन है। इसे साधारण कलन के कुल व्युत्पन्न के सामान्यीकरण के रूप में देखा जा सकता है। स्पष्ट रूप से, अंतर φ (x) पर N के स्पर्शरेखा स्थान से x पर M के स्पर्शरेखा स्थान से एक रैखिक मानचित्र है। $d\varphi _{x}:T_{x}M\to T_{\varphi (x)}N$. इसलिए इसका उपयोग N पर स्पर्शरेखा वैक्टर को M पर स्पर्शरेखा वैक्टर को आगे बढ़ाने के लिए किया जा सकता है। विभिन्न लेखकों द्वारा मानचित्र φ के अंतर को φ का 'व्युत्पन्न' या 'कुल व्युत्पन्न' भी कहा जाता है।

प्रेरणा

होने देना $\varphi :U\to V$ एक स्मूथ फंक्शन बनें # ओपन सबसेट # यूक्लिडियन स्पेस से मैनिफोल्ड्स के बीच स्मूद फंक्शन $U$ का $\mathbb {R} ^{m}$ एक खुले उपसमुच्चय के लिए $V$ का $\mathbb {R} ^{n}$. किसी भी बिंदु के लिए $x$ में $U$, जैकोबियन मैट्रिक्स और के निर्धारक $\varphi$ पर $x$ (मानक निर्देशांक के संबंध में) के कुल व्युत्पन्न का मैट्रिक्स (गणित) प्रतिनिधित्व है $\varphi$ पर $x$, जो एक रेखीय नक्शा है

$d\varphi _{x}:T_{x}\mathbb {R} ^{m}\to T_{\varphi (x)}\mathbb {R} ^{n}$

उनके स्पर्शरेखा रिक्त स्थान के बीच। स्पर्शरेखा रिक्त स्थान पर ध्यान दें $T_{x}\mathbb {R} ^{m},T_{\varphi (x)}\mathbb {R} ^{n}$ के लिए आइसोमॉर्फिक हैं $\mathbb {R} ^{m}$ और $\mathbb {R} ^{n}$, क्रमश। पुशफॉरवर्ड इस निर्माण को इस मामले में सामान्यीकृत करता है कि $\varphi$ किसी भी मैनिफोल्ड # डिफरेंशिएबल मैनिफोल्ड के बीच एक सहज कार्य है $M$ और $N$.

चिकने मानचित्र का अंतर

होने देना $\varphi \colon M\to N$ चिकने मैनिफोल्ड का एक चिकना नक्शा बनें। दिया गया $x\in M,$ का अंतर $\varphi$ पर $x$ एक रेखीय नक्शा है

$d\varphi _{x}\colon \ T_{x}M\to T_{\varphi (x)}N\,$

के स्पर्शरेखा स्थान से $M$ पर $x$ स्पर्शरेखा स्थान के लिए $N$ पर $\varphi (x).$ छवि $d\varphi _{x}X$ एक स्पर्शरेखा सदिश का $X\in T_{x}M$ अंतर्गत $d\varphi _{x}$ को कभी-कभी का पुशफॉरवर्ड कहा जाता है $X$ द्वारा $\varphi .$ इस पुशफॉरवर्ड की सटीक परिभाषा स्पर्शरेखा सदिशों के लिए उपयोग की जाने वाली परिभाषा पर निर्भर करती है (विभिन्न परिभाषाओं के लिए स्पर्शरेखा स्थान देखें)।

यदि स्पर्शरेखा सदिशों को वक्रों के तुल्यता वर्ग के रूप में परिभाषित किया जाता है $\gamma$ जिसके लिए $\gamma (0)=x,$ तो अंतर द्वारा दिया जाता है

$d\varphi _{x}(\gamma '(0))=(\varphi \circ \gamma )'(0).$

यहाँ, $\gamma$ में वक्र है $M$ साथ $\gamma (0)=x,$ और $\gamma '(0)$ वक्र के लिए स्पर्शरेखा सदिश है $\gamma$ पर $0.$ दूसरे शब्दों में, वक्र के स्पर्शरेखा सदिश का पुशफॉरवर्ड $\gamma$ पर $0$ वक्र की स्पर्शरेखा सदिश है $\varphi \circ \gamma$ पर $0.$ वैकल्पिक रूप से, यदि स्पर्शरेखा वैक्टर को व्युत्पत्ति (अमूर्त बीजगणित) के रूप में परिभाषित किया जाता है जो सुचारू वास्तविक-मूल्यवान कार्यों पर कार्य करता है, तो अंतर द्वारा दिया जाता है

$d\varphi _{x}(X)(f)=X(f\circ \varphi ),$

एक मनमाना समारोह के लिए $f\in C^{\infty }(N)$ और एक मनमाना व्युत्पत्ति $X\in T_{x}M$ बिंदु पर $x\in M$ (एक व्युत्पत्ति (सार बीजगणित) को एक रेखीय मानचित्र के रूप में परिभाषित किया गया है $X\colon C^{\infty }(M)\to \mathbb {R}$ जो उत्पाद नियम को संतुष्ट करता है, देखें: स्पर्शरेखा स्थान # व्युत्पन्न के माध्यम से परिभाषा)। परिभाषा के अनुसार, का पुशफॉरवर्ड $X$ में है $T_{\varphi (x)}N$ और इसलिए स्वयं एक व्युत्पत्ति है, $d\varphi _{x}(X)\colon C^{\infty }(N)\to \mathbb {R}$.

चारों ओर दो मैनिफोल्ड (गणित) चुनने के बाद $x$ और चारों ओर $\varphi (x),$ $\varphi$ स्थानीय रूप से एक चिकने मानचित्र द्वारा निर्धारित किया जाता है ${\widehat {\varphi }}\colon U\to V$ के खुले सेट के बीच $\mathbb {R} ^{m}$ और $\mathbb {R} ^{n}$, और

$d\varphi _{x}\left({\frac {\partial }{\partial u^{a}}}\right)={\frac {\partial {\widehat {\varphi }}^{b}}{\partial u^{a}}}{\frac {\partial }{\partial v^{b}}},$

आइंस्टीन सारांश संकेतन में, जहां आंशिक डेरिवेटिव का मूल्यांकन बिंदु पर किया जाता है $U$ तदनुसार $x$ दिए गए चार्ट में।

रैखिकता द्वारा विस्तार निम्नलिखित मैट्रिक्स देता है

$\left(d\varphi _{x}\right)_{a}^{\;b}={\frac {\partial {\widehat {\varphi }}^{b}}{\partial u^{a}}}.$

इस प्रकार अंतर एक रेखीय परिवर्तन है, स्पर्शरेखा रिक्त स्थान के बीच, चिकनी मानचित्र से जुड़ा हुआ है $\varphi$ प्रत्येक बिंदु पर। इसलिए, कुछ चुने हुए स्थानीय निर्देशांकों में, यह संबंधित चिकने मानचित्र के जैकबियन मैट्रिक्स द्वारा दर्शाया गया है $\mathbb {R} ^{m}$ को $\mathbb {R} ^{n}$. सामान्य तौर पर, अंतर को उलटा नहीं होना चाहिए। हालांकि, यदि $\varphi$ एक स्थानीय भिन्नता है, फिर $d\varphi _{x}$ व्युत्क्रमणीय है, और व्युत्क्रम का पुलबैक (अंतर ज्यामिति) देता है $T_{\varphi (x)}N.$ विभिन्न प्रकार की अन्य सूचनाओं का उपयोग करके अंतर को अक्सर व्यक्त किया जाता है

$D\varphi _{x},\left(\varphi _{*}\right)_{x},\varphi '(x),T_{x}\varphi .$

यह परिभाषा से अनुसरण करता है कि एक फ़ंक्शन रचना का अंतर अंतरों (यानी, क्रियात्मक व्यवहार) का सम्मिश्रण है। यह चिकने नक्शों के लिए चेन नियम है।

इसके अलावा, एक स्थानीय भिन्नता का अंतर स्पर्शरेखा रिक्त स्थान का एक रैखिक समरूपता है।

स्पर्शरेखा बंडल पर अंतर

एक चिकने मानचित्र φ का अंतर, एक स्पष्ट तरीके से, M के स्पर्शरेखा बंडल से N के स्पर्शरेखा बंडल तक एक बंडल नक्शा (वास्तव में एक वेक्टर बंडल समरूपता) को प्रेरित करता है, जिसे dφ या φ द्वारा निरूपित किया जाता है।_∗, जो निम्नलिखित क्रमविनिमेय आरेख में फिट बैठता है:

जहां प_M और π_N क्रमशः एम और एन के स्पर्शरेखा बंडलों के बंडल अनुमानों को निरूपित करें।

$\operatorname {d} \!\varphi$ टीएम से पुलबैक बंडल φ के लिए एक बंडल मैप प्रेरित करता है^∗टीएन ओवर एम वाया

$(m,v_{m})\mapsto (m,\operatorname {d} \!\varphi (m,v_{m})),$

कहाँ $m\in M$ और $v_{m}\in T_{m}M.$ बाद वाला नक्शा वेक्टर बंडल के एक खंड (फाइबर बंडल) के रूप में देखा जा सकता है Hom(TM, φ^∗TN) ओवर एम। बंडल मैप dφ को भी Tφ द्वारा निरूपित किया जाता है और इसे 'स्पर्शरेखा मानचित्र' कहा जाता है। इस प्रकार, T एक फ़नकार है।

सदिश क्षेत्रों का पुशफॉरवर्ड

एक चिकना नक्शा दिया φ : M → N और M पर एक सदिश क्षेत्र X, आमतौर पर N पर कुछ सदिश क्षेत्र Y के साथ φ द्वारा X के एक पुशफॉरवर्ड की पहचान करना संभव नहीं है। φ की छवि के बाहर धक्का दें। साथ ही, यदि φ अंतःक्षेपी नहीं है, तो दिए गए बिंदु पर पुशफॉरवर्ड के एक से अधिक विकल्प हो सकते हैं। फिर भी, एक मानचित्र के साथ एक सदिश क्षेत्र की धारणा का उपयोग करके, कोई भी इस कठिनाई को सटीक बना सकता है।

φ का एक वेक्टर बंडल^∗M पर TN को 'φ के साथ सदिश क्षेत्र' कहा जाता है। उदाहरण के लिए, यदि M, N का सबमेनिफोल्ड है और φ समावेशन है, तो φ के साथ एक सदिश क्षेत्र M के साथ N के स्पर्शरेखा बंडल का एक खंड है; विशेष रूप से, एम पर एक वेक्टर फ़ील्ड टीएन के अंदर टीएम को शामिल करने के माध्यम से ऐसे खंड को परिभाषित करता है। यह विचार मनमाने ढंग से चिकने नक्शों का सामान्यीकरण करता है।

मान लीजिए कि X, M पर एक सदिश क्षेत्र है, यानी TM का एक खंड। तब, $\operatorname {d} \!\phi \circ X$ पैदावार, उपरोक्त अर्थ में, पुशफॉरवर्ड φ_∗X, जो φ के साथ एक सदिश क्षेत्र है, यानी, φ का एक खंड^∗टीएन ओवर एम.

N पर कोई सदिश क्षेत्र Y एक पुलबैक बंडल φ को परिभाषित करता है^∗ φ का वाई^∗टीएन के साथ (φ^∗Y)_x = Y_φ(x). M पर सदिश क्षेत्र X और N पर सदिश क्षेत्र Y को 'φ-संबंधित' कहा जाता है यदि φ_∗X = φ^∗Y φ के साथ सदिश क्षेत्रों के रूप में। दूसरे शब्दों में, M में सभी x के लिए, dφ_x(X) = Y_φ(x).

कुछ स्थितियों में, M पर एक X सदिश क्षेत्र दिया गया है, N पर एक अद्वितीय सदिश क्षेत्र Y है जो φ-X से संबंधित है। यह विशेष रूप से सच है जब φ एक भिन्नता है। इस मामले में, पुशवर्ड एन पर वेक्टर फ़ील्ड वाई को परिभाषित करता है, जिसे दिया गया है

$Y_{y}=\phi _{*}\left(X_{\phi ^{-1}(y)}\right).$

एक अधिक सामान्य स्थिति तब उत्पन्न होती है जब φ आच्छादक होता है (उदाहरण के लिए फाइबर बंडल का फाइबर बंडल)। तब M पर एक वेक्टर फ़ील्ड X को 'प्रोजेक्टेबल' कहा जाता है यदि N में सभी y के लिए, dφ_x(एक्स_x) φ में x की पसंद से स्वतंत्र है⁻¹({y})। यह ठीक ऐसी स्थिति है जो गारंटी देती है कि N पर सदिश क्षेत्र के रूप में X का एक पुशफॉरवर्ड अच्छी तरह से परिभाषित है।

उदाहरण

झूठ समूहों पर गुणन से आगे बढ़ना

एक झूठ समूह दिया $G$, हम गुणन मानचित्र का उपयोग कर सकते हैं $m(-,-):G\times G\to G$ बायां गुणन प्राप्त करने के लिए $L_{g}=m(g,-)$ और सही गुणन $R_{g}=m(-,g)$ एमएपीएस $G\to G$. इन मानचित्रों का उपयोग बाएँ या दाएँ अपरिवर्तनीय सदिश क्षेत्रों के निर्माण के लिए किया जा सकता है $G$ मूल बिंदु पर इसकी स्पर्शरेखा स्थान से ${\mathfrak {g}}=T_{e}G$ (जो इससे जुड़ा झूठ बीजगणित है)। उदाहरण के लिए दिया $X\in {\mathfrak {g}}$ हमें एक संबंधित वेक्टर फ़ील्ड मिलता है ${\mathfrak {X}}$ पर $G$ <ब्लॉककोट> द्वारा परिभाषित${\mathfrak {X}}_{g}=(L_{g})_{*}(X)\in T_{g}G$प्रत्येक के लिए $g\in G$. पुशफॉरवर्ड मैप्स की वक्र परिभाषा का उपयोग करके इसकी आसानी से गणना की जा सकती है। यदि हमारे पास वक्र <ब्लॉककोट> है$\gamma :(-1,1)\to G$कहाँ

$\gamma (0)=e$ और $\gamma '(0)=X$

हमें

मिलता है${\begin{aligned}(L_{g})_{*}(X)&=(L_{g}\circ \gamma )'(0)\\&=(g\cdot \gamma (t))'(0)\\&={\frac {dg}{d\gamma }}\gamma (0)+g\cdot {\frac {d\gamma }{dt}}(0)\\&=g\cdot \gamma '(0)\end{aligned}}$

चूंकि $L_{g}$ के संबंध में स्थिर है $\gamma$. इसका तात्पर्य है कि हम स्पर्शरेखा रिक्त स्थान की व्याख्या कर सकते हैं $T_{g}G$ जैसा $T_{g}G=g\cdot T_{e}G=g\cdot {\mathfrak {g}}$.

झूठ बोलने वाले कुछ समूहों के लिए आगे बढ़ें

उदाहरण के लिए, यदि $G$ मैट्रिसेस <ब्लॉककोट> द्वारा दिया गया हाइजेनबर्ग समूह है$H=\left\{{\begin{bmatrix}1&a&b\\0&1&c\\0&0&1\end{bmatrix}}:a,b,c\in \mathbb {R} \right\}$इसमें मेट्रिसेस के सेट द्वारा दिया गया लाई बीजगणित है

${\mathfrak {h}}=\left\{{\begin{bmatrix}0&a&b\\0&0&c\\0&0&0\end{bmatrix}}:a,b,c\in \mathbb {R} \right\}$

क्योंकि हम एक रास्ता खोज सकते हैं $\gamma :(-1,1)\to H$ ऊपरी मैट्रिक्स प्रविष्टियों में से किसी एक में कोई वास्तविक संख्या देना $i<j$ (i-वें पंक्ति और j-वें स्तंभ)। फिर,

के लिए$g={\begin{bmatrix}1&2&3\\0&1&4\\0&0&1\end{bmatrix}}$

हमारे पास

है$T_{g}H=g\cdot {\mathfrak {h}}=\left\{{\begin{bmatrix}0&a&2b+3c\\0&0&c\\0&0&0\end{bmatrix}}:a,b,c\in \mathbb {R} \right\}$

जो मैट्रिक्स के मूल सेट के बराबर है। यह हमेशा मामला नहीं होता है, उदाहरण के लिए, समूह <ब्लॉककोट> में$G=\left\{{\begin{bmatrix}a&b\\0&1/a\end{bmatrix}}:a,b\in \mathbb {R} ,a\neq 0\right\}$हमारे पास मैट्रिक्स के सेट के रूप में इसका लाई बीजगणित है

${\mathfrak {g}}=\left\{{\begin{bmatrix}a&b\\0&-a\end{bmatrix}}:a,b\in \mathbb {R} \right\}$

इसलिए कुछ मैट्रिक्स

के लिए$g={\begin{bmatrix}2&3\\0&1/2\end{bmatrix}}$

हमारे पास

है$T_{g}G=\left\{{\begin{bmatrix}2a&2b-a/2\\0&-a/2\end{bmatrix}}:a,b\in \mathbb {R} \right\}$

जो मैट्रिक्स का समान सेट नहीं है।

यह भी देखें

• पुलबैक (अंतर ज्यामिति)
• सामान्य प्रवाह

संदर्भ

• Lee, John M. (2003). Introduction to Smooth Manifolds. Springer Graduate Texts in Mathematics. Vol. 218.
• Jost, Jürgen (2002). Riemannian Geometry and Geometric Analysis. Berlin: Springer-Verlag. ISBN 3-540-42627-2. See section 1.6.
• Abraham, Ralph; Marsden, Jerrold E. (1978). Foundations of Mechanics. London: Benjamin-Cummings. ISBN 0-8053-0102-X. See section 1.7 and 2.3.