प्रभाव रेखा

चित्र 1: (ए) यह सरल समर्थित बीम एक इकाई भार के साथ बाएं छोर से x दूरी पर दिखाया गया है। चार अलग-अलग कार्यों के लिए इसकी प्रभाव रेखाएं: (बी) बाएं समर्थन पर प्रतिक्रिया (निरूपित ए), (सी) सही समर्थन पर प्रतिक्रिया (निरूपित सी), (डी) बीम के साथ एक बिंदु बी पर कतरनी के लिए, और (ई) एक पल के लिए भी बिंदु बी पर।

इंजीनियरिंग में, एक प्रभाव रेखा एक बीम (संरचना) पर एक विशिष्ट बिंदु पर एक फ़ंक्शन (जैसे कतरनी, क्षण आदि। एक संरचनात्मक सदस्य में महसूस किया जाता है) की भिन्नता को रेखांकन करती है या किसी भी बिंदु पर रखे गए यूनिट लोड के कारण ट्रस होती है। संरचना। प्रभाव रेखाओं के साथ अध्ययन किए जाने वाले सामान्य कार्यों में प्रतिक्रियाएँ शामिल हैं (ताकतें जो संरचना के समर्थन को स्थिर रहने के लिए संरचना के लिए लागू होनी चाहिए), कतरनी बल, झुकने का क्षण, और विक्षेपण (इंजीनियरिंग) (विरूपण)। पुल, क्रेन रेल, कन्वेयर बेल्ट, फर्श गर्डर्स और अन्य संरचनाओं में उपयोग किए जाने वाले बीम और ट्रस को डिजाइन करने में प्रभाव रेखाएं महत्वपूर्ण हैं जहां भार उनके विस्तार के साथ आगे बढ़ेगा।प्रभाव रेखाएँ दिखाती हैं कि अध्ययन किए गए किसी भी कार्य के लिए भार कहाँ अधिकतम प्रभाव पैदा करेगा।

प्रभाव रेखाएँ अदिश (गणित) और योज्य मानचित्र दोनों हैं।इसका मतलब यह है कि उनका उपयोग तब भी किया जा सकता है जब लागू किया जाने वाला भार एक इकाई भार नहीं है या यदि कई भार लागू होते हैं। किसी संरचना पर किसी गैर-इकाई भार के प्रभाव का पता लगाने के लिए, प्रभाव रेखा द्वारा प्राप्त समन्वय परिणाम को लागू किए जाने वाले वास्तविक भार के परिमाण से गुणा किया जाता है। संपूर्ण प्रभाव रेखा को बढ़ाया जा सकता है, या केवल रेखा के साथ अधिकतम और न्यूनतम प्रभावों का अनुभव किया जा सकता है। स्केल किए गए अधिकतम और न्यूनतम महत्वपूर्ण परिमाण हैं जिन्हें बीम या ट्रस में डिज़ाइन किया जाना चाहिए।

ऐसे मामलों में जहां कई भार प्रभाव में हो सकते हैं, कुल प्रभाव प्राप्त करने के लिए अलग-अलग भारों के लिए प्रभाव रेखाओं को एक साथ जोड़ा जा सकता है, जो किसी दिए गए बिंदु पर संरचना को महसूस करता है। प्रभाव रेखाओं को एक साथ जोड़ते समय, संरचना में भार के अंतर के कारण उपयुक्त ऑफ़सेट शामिल करना आवश्यक है। उदाहरण के लिए, संरचना पर एक ट्रक लोड लागू होता है। रियर एक्सल, बी, फ्रंट एक्सल, ए से तीन फीट पीछे है, तो संरचना के साथ x फीट पर A का प्रभाव संरचना के साथ (x - 3) फीट पर B के प्रभाव में जोड़ा जाना चाहिए - पर B का प्रभाव नहीं x फीट संरचना के साथ।

कई भार केंद्रित होने के बजाय वितरित किए जाते हैं। प्रभाव रेखाओं का उपयोग या तो केंद्रित या वितरित लोडिंग के साथ किया जा सकता है। एक केंद्रित (या बिंदु) भार के लिए, एक इकाई बिंदु भार को संरचना के साथ ले जाया जाता है। किसी दिए गए चौड़ाई के वितरित भार के लिए, समान चौड़ाई के एक इकाई-वितरित भार को संरचना के साथ ले जाया जाता है, यह देखते हुए कि जैसे-जैसे भार सिरों के पास आता है और संरचना से हटता है, कुल भार का केवल एक हिस्सा संरचना द्वारा वहन किया जाता है। वितरित इकाई भार का प्रभाव संरचनाओं की इसी लंबाई पर बिंदु भार की प्रभाव रेखा को एकीकृत करके भी प्राप्त किया जा सकता है।

निर्धारित संरचनाओं की प्रभाव रेखाएँ एक तंत्र बन जाती हैं जबकि अनिश्चित संरचनाओं की प्रभाव रेखाएँ केवल निर्धारित हो जाती हैं।

बेट्टी के प्रमेय से प्रदर्शन

प्रभाव रेखाएँ बेट्टी के प्रमेय पर आधारित हैं। वहां से, दो बाहरी बल प्रणालियों पर विचार करें, $F_{i}^{P}$ और $F_{i}^{Q}$, प्रत्येक एक विस्थापन क्षेत्र से जुड़ा है जिसका विस्थापन बल के अनुप्रयोग बिंदु में मापा जाता है $d_{i}^{P}$ और $d_{i}^{Q}$.

विचार करें कि $F_{i}^{P}$ प्रणाली संरचना पर लागू वास्तविक बलों का प्रतिनिधित्व करती है, जो संतुलन में हैं। विचार करें कि $F_{i}^{Q}$ प्रणाली एक बल द्वारा बनाई गई है, $F^{Q}$. विस्थापन क्षेत्र $d_{i}^{Q}$ इस बल से जुड़े को उस बिंदु पर कार्य करने वाले संरचनात्मक प्रतिबंधों को जारी करके परिभाषित किया गया है $F^{Q}$ लागू किया जाता है और एक सापेक्ष इकाई विस्थापन लगाया जाता है जो नकारात्मक दिशा में किनेमेटिक रूप से स्वीकार्य है, जिसे दर्शाया गया है $d_{1}^{Q}=-1$. बेट्टी के प्रमेय से, हम निम्नलिखित परिणाम प्राप्त करते हैं:

$-F_{1}^{P}+\sum _{i=2}^{n}F_{i}^{P}d_{i}^{Q}=F^{Q}\times 0\iff F_{1}^{P}=\sum _{i=2}^{n}F_{i}^{P}d_{i}^{Q}$

अवधारणा

बीम या ट्रस को डिजाइन करते समय, संरचना सदस्यों के भीतर अधिकतम अपेक्षित प्रतिक्रियाओं, कैंची और क्षणों के कारण परिदृश्यों के लिए डिजाइन करना आवश्यक है ताकि यह सुनिश्चित किया जा सके कि संरचना के जीवन के दौरान कोई सदस्य विफल न हो। डेड और लाइव लोड (भार जो कभी नहीं चलते हैं, जैसे कि संरचना का वजन) के साथ काम करते समय, यह अपेक्षाकृत आसान होता है क्योंकि लोड की भविष्यवाणी करना और योजना बनाना आसान होता है। मृत और जीवित भार के लिए (कोई भी भार जो संरचना के जीवन के दौरान चलता है, जैसे कि फर्नीचर और लोग), यह अनुमान लगाना बहुत कठिन हो जाता है कि भार कहाँ होगा या वे संरचना के पूरे जीवन में कितने केंद्रित या वितरित होंगे।

प्रभाव रेखाएँ एक बीम या ट्रस की प्रतिक्रिया को रेखांकन करती हैं क्योंकि एक इकाई भार इसके पार जाता है। प्रभाव रेखा डिजाइनरों को यह पता लगाने में मदद करती है कि निम्नलिखित कार्यों में से प्रत्येक के लिए अधिकतम परिणामी प्रतिक्रिया की गणना करने के लिए लाइव लोड कहां रखा जाए: प्रतिक्रिया, कतरनी या पल। इसके बाद डिजाइनर प्रत्येक कार्य की अधिकतम प्रतिक्रिया की गणना करने के लिए अधिकतम अपेक्षित भार द्वारा प्रभाव रेखा को स्केल कर सकता है जिसके लिए बीम या ट्रस को डिजाइन किया जाना चाहिए। लागू इकाई भार के लिए अन्य कार्यों (जैसे विक्षेपण या अक्षीय बल) की प्रतिक्रियाओं को खोजने के लिए प्रभाव रेखाओं का भी उपयोग किया जा सकता है, लेकिन प्रभाव रेखाओं के ये उपयोग कम आम हैं।

प्रभाव रेखाओं के निर्माण की विधियाँ

प्रभाव रेखा के निर्माण के लिए तीन विधियों का उपयोग किया जाता है। सबसे पहले संरचना के साथ कई बिंदुओं के लिए प्रभाव मानों को सारणीबद्ध करना है, फिर प्रभाव रेखा बनाने के लिए उन बिंदुओं का उपयोग करना है।दूसरा प्रभाव-रेखा समीकरणों को निर्धारित करना है जो संरचना पर लागू होते हैं, जिससे x के संदर्भ में प्रभाव रेखा के साथ सभी बिंदुओं को हल किया जाता है, जहां x संरचना की शुरुआत से उस बिंदु तक पैरों की संख्या है जहां इकाई भार लागू की गई है। तीसरी विधि को मुलर-ब्रेस्लाउ का सिद्धांत कहा जाता है। यह एक गुणात्मक डेटा प्रभाव रेखा बनाता है।यह प्रभाव रेखा अभी भी डिज़ाइनर को एक सटीक विचार प्रदान करेगी कि इकाई भार अध्ययन किए जा रहे बिंदु पर किसी फ़ंक्शन की सबसे बड़ी प्रतिक्रिया कहां उत्पन्न करेगा, लेकिन इसका उपयोग सीधे यह गणना करने के लिए नहीं किया जा सकता है कि प्रतिक्रिया कितनी परिमाण होगी, जबकि प्रभाव पहले दो तरीकों से उत्पादित लाइनें कर सकते हैं।

मूल्यों को सारणीबद्ध करें

संरचना पर कुछ बिंदु A के संबंध में प्रभाव मूल्यों को सारणीबद्ध करने के लिए, संरचना के साथ विभिन्न बिंदुओं पर एक इकाई भार रखा जाना चाहिए। स्थिति-विज्ञान का उपयोग यह गणना करने के लिए किया जाता है कि बिंदु ए पर फ़ंक्शन (प्रतिक्रिया, कतरनी या क्षण) का मूल्य क्या है। आमतौर पर ऊपर की ओर प्रतिक्रिया को सकारात्मक रूप में देखा जाता है। कतरनी और पल आरेखों के लिए उपयोग किए जाने वाले समान सम्मेलनों के अनुसार कतरनी और क्षणों को सकारात्मक या नकारात्मक मान दिए जाते हैं।

आरसी हिबेलर ने अपनी पुस्तक स्ट्रक्चरल एनालिसिस में कहा है, "सभी स्थिर रूप से निर्धारित बीमों में प्रभाव रेखाएं होंगी जिनमें सीधी रेखा खंड शामिल होंगे।"इसलिए, उन बिंदुओं को पहचान कर संगणनाओं की संख्या को कम करना संभव है जो प्रभाव रेखा के ढलान में परिवर्तन का कारण बनेंगे और केवल उन बिंदुओं पर मूल्यों की गणना करेंगे। विभक्ति रेखा का ढलान समर्थन, मध्य-विस्तार और जोड़ों पर बदल सकता है।

किसी दिए गए फ़ंक्शन के लिए एक प्रभाव रेखा, जैसे प्रतिक्रिया, अक्षीय बल, कतरनी बल, या झुकने का क्षण, एक ग्राफ है जो किसी भी इकाई भार के आवेदन के कारण संरचना पर किसी दिए गए बिंदु पर उस फ़ंक्शन की भिन्नता को दर्शाता है। संरचना पर बिंदु।

किसी फ़ंक्शन के लिए प्रभाव रेखा कतरनी, अक्षीय या झुकने वाले क्षण आरेख से भिन्न होती है। एक संरचना पर कई बिंदुओं पर एक इकाई भार को स्वतंत्र रूप से लागू करके और इस भार के कारण फ़ंक्शन के मूल्य का निर्धारण करके, यानी कतरनी, अक्षीय और वांछित स्थान पर पल के द्वारा प्रभाव रेखाएं उत्पन्न की जा सकती हैं। प्रत्येक फ़ंक्शन के लिए परिकलित मान तब प्लॉट किए जाते हैं जहां लोड लागू किया गया था और फिर फ़ंक्शन के लिए प्रभाव रेखा उत्पन्न करने के लिए एक साथ जुड़ा हुआ था।

एक बार प्रभाव मानों को सारणीबद्ध कर लेने के बाद, बिंदु A पर फ़ंक्शन के लिए प्रभाव रेखा x के संदर्भ में खींची जा सकती है। सबसे पहले, सारणीबद्ध मूल्यों को स्थित होना चाहिए। सारणीबद्ध बिंदुओं के बीच के वर्गों के लिए, प्रक्षेप आवश्यक है। इसलिए, बिंदुओं को जोड़ने के लिए सीधी रेखाएँ खींची जा सकती हैं। एक बार यह हो जाने के बाद, प्रभाव रेखा पूरी हो जाती है।

प्रभाव-रेखा समीकरण

किसी संरचना की संपूर्ण अवधि में प्रभाव रेखा को परिभाषित करने वाले समीकरण बनाना संभव है। यह एक विशिष्ट दूरी के बजाय संरचना के साथ x फीट पर रखे गए एक इकाई भार के कारण बिंदु A पर प्रतिक्रिया, कतरनी या क्षण के लिए हल करके किया जाता है। यह विधि सारणीबद्ध मान पद्धति के समान है, लेकिन एक संख्यात्मक समाधान प्राप्त करने के बजाय, परिणाम x के संदर्भ में एक समीकरण है।

यह समझना महत्वपूर्ण है कि इस पद्धति के लिए प्रभाव रेखा का ढलान कहां बदलता है क्योंकि प्रभाव रेखा के प्रत्येक रैखिक खंड के लिए प्रभाव-रेखा समीकरण बदल जाएगा। इसलिए, प्रभाव रेखा के प्रत्येक रैखिक खंड के लिए एक अलग प्रभाव-रेखा समीकरण के साथ पूर्ण समीकरण एक टुकड़ा-वार रैखिक कार्य है।

मुलर-ब्रेसलाऊ का सिद्धांत

Www.public.iastate.edu के अनुसार, "मुलर-ब्रेसलाऊ का सिद्धांत। मुलर-ब्रेसलाऊ सिद्धांत का उपयोग गुणात्मक डेटा प्रभाव रेखाएँ खींचने के लिए किया जा सकता है, जो वास्तविक प्रभाव रेखा के सीधे आनुपातिक हैं।" एक बीम के साथ एक इकाई भार को स्थानांतरित करने के बजाय, मुलर-ब्रेस्लाउ सिद्धांत पहले अध्ययन किए जा रहे बिंदु पर बीम को छोड़ने और फिर अध्ययन किए जा रहे कार्य (प्रतिक्रिया, कतरनी, या क्षण) को लागू करने के कारण बीम के विक्षेपित आकार का पता लगाता है। वह बिंदु। सिद्धांत कहता है कि किसी फ़ंक्शन की प्रभाव रेखा में एक स्केल आकार होगा जो बीम के विक्षेपित आकार के समान होता है जब बीम पर फ़ंक्शन द्वारा कार्य किया जाता है।

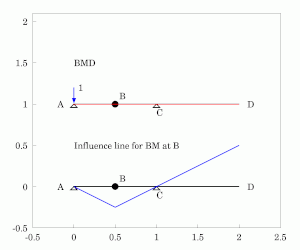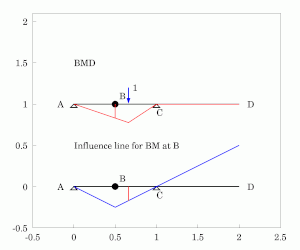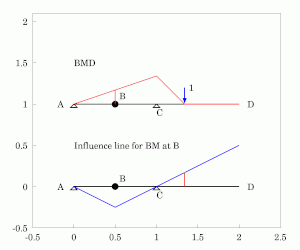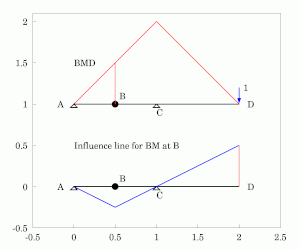
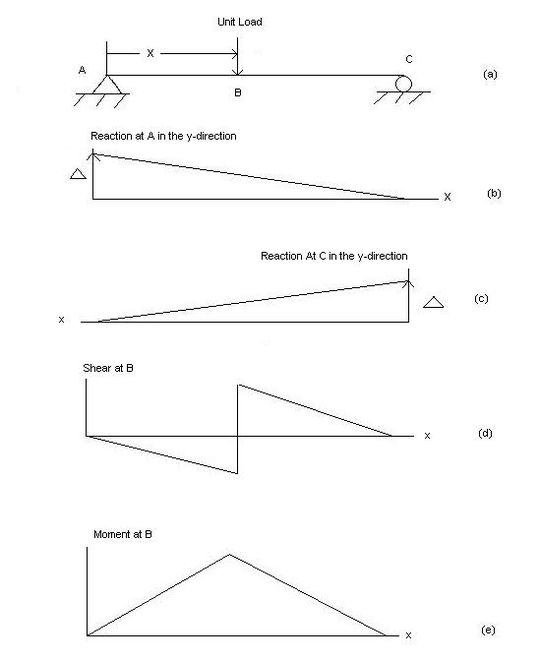
यह समझने के लिए कि फ़ंक्शन के तहत बीम कैसे विक्षेपित होता है, फ़ंक्शन का विरोध करने के लिए बीम की क्षमता को हटाना आवश्यक है। नीचे इस बात की व्याख्या दी गई है कि सरल रूप से समर्थित, कठोर बीम (जैसे चित्र 1 में प्रदर्शित एक) की प्रभाव रेखाओं को कैसे खोजा जाए।

* समर्थन पर होने वाली प्रतिक्रिया का निर्धारण करते समय, समर्थन को एक रोलर से बदल दिया जाता है, जो एक ऊर्ध्वाधर प्रतिक्रिया का विरोध नहीं कर सकता।फिर ऊपर की ओर (सकारात्मक) प्रतिक्रिया उस बिंदु पर लागू होती है जहां समर्थन था। चूंकि समर्थन हटा दिया गया है, बीम ऊपर की ओर घूमेगा, और चूंकि बीम कठोर है, यह दूसरे समर्थन पर बिंदु के साथ एक त्रिभुज बनाएगा। यदि बीम दूसरे समर्थन से परे एक कैंटिलीवर के रूप में फैली हुई है, तो कैंटिलीवर स्थिति के नीचे एक समान त्रिकोण का गठन किया जाएगा। इसका मतलब है कि प्रतिक्रिया की प्रभाव रेखा दूसरे समर्थन के स्थान पर शून्य के मान के साथ एक सीधी, झुकी हुई रेखा होगी।

* बीम के साथ किसी बिंदु बी पर होने वाली कतरनी का निर्धारण करते समय, बीम को काटा जाना चाहिए और एक रोलर-गाइड (जो क्षणों का विरोध करने में सक्षम है लेकिन कतरनी नहीं) बिंदु बी पर डाला जाना चाहिए।फिर, उस बिंदु पर एक सकारात्मक कतरनी लगाने से, यह देखा जा सकता है कि बाईं ओर नीचे की ओर घूमेगा, लेकिन दाईं ओर ऊपर की ओर घूमेगा। यह एक असंतुलित प्रभाव रेखा बनाता है जो समर्थन पर शून्य तक पहुंचती है और जिसका ढलान विच्छिन्नता के दोनों ओर समान होता है। यदि बिंदु बी एक समर्थन पर है, तो बिंदु बी और किसी भी अन्य समर्थन के बीच का विक्षेपण अभी भी एक त्रिकोण बना देगा, लेकिन यदि बीम कैंटिलीवर है, तो संपूर्ण कैंटिलीवर पक्ष एक आयत बनाते हुए ऊपर या नीचे जाएगा।

* बीम के साथ किसी बिंदु बी पर होने वाले पल का निर्धारण करते समय, बिंदु बी पर एक हिंज रखा जाएगा, इसे क्षणों तक जारी किया जाएगा लेकिन कतरनी का विरोध किया जाएगा।फिर जब बिंदु B पर एक सकारात्मक क्षण रखा जाता है, तो बीम के दोनों किनारे ऊपर की ओर घूमेंगे। यह एक सतत प्रभाव रेखा बनाएगा, लेकिन ढलान बिंदु B पर हिंज के दोनों ओर समान और विपरीत होगा। चूंकि बीम केवल समर्थित है, इसका अंत समर्थन (पिन) पल का विरोध नहीं कर सकता है; इसलिए, यह देखा जा सकता है कि समर्थन कभी भी स्थिर स्थिति में क्षणों का अनुभव नहीं करेगा, भले ही भार कहीं भी रखा गया हो।

मुलर-ब्रेस्लाउ सिद्धांत केवल गुणात्मक प्रभाव रेखाएँ उत्पन्न कर सकता है।इसका मतलब यह है कि इंजीनियर इसका उपयोग यह निर्धारित करने के लिए कर सकते हैं कि अधिकतम कार्य करने के लिए भार कहां रखा जाए, लेकिन उस अधिकतम के परिमाण की गणना प्रभाव रेखा से नहीं की जा सकती। इसके बजाय, उस लोडिंग मामले में फ़ंक्शन मान को हल करने के लिए इंजीनियर को स्टैटिक्स का उपयोग करना चाहिए।

वैकल्पिक लोडिंग मामले

एकाधिक भार

सबसे सरल लोडिंग मामला एकल बिंदु भार है, लेकिन कई भारों और वितरित भारों के कारण प्रतिक्रियाओं को निर्धारित करने के लिए प्रभाव रेखाओं का भी उपयोग किया जा सकता है। कभी-कभी यह ज्ञात होता है कि अलग-अलग निश्चित दूरी पर कई भार होंगे। उदाहरण के लिए, एक पुल पर कारों या ट्रकों के पहिए पॉइंट लोड बनाते हैं जो अपेक्षाकृत मानक दूरी पर कार्य करते हैं।

एक प्रभाव रेखा का उपयोग करके इन सभी बिंदु भारों के लिए एक फ़ंक्शन की प्रतिक्रिया की गणना करने के लिए, प्रभाव रेखा के साथ पाए जाने वाले परिणामों को प्रत्येक भार के लिए बढ़ाया जा सकता है, और फिर स्केल किए गए परिमाणों को उस कुल प्रतिक्रिया को खोजने के लिए अभिव्यक्त किया जा सकता है जिसे संरचना को झेलना होगा।बिंदु भार में अलग-अलग परिमाण हो सकते हैं, लेकिन भले ही वे संरचना पर समान बल लागू करते हों, उन्हें अलग-अलग मापना आवश्यक होगा क्योंकि वे संरचना के साथ अलग-अलग दूरी पर कार्य करते हैं। उदाहरण के लिए, यदि कार के पहिए 10 फीट अलग हैं, तो जब पहला सेट पुल पर 13 फीट होगा, तो दूसरा सेट पुल पर केवल 3 फीट होगा। यदि पहियों का पहला सेट पुल पर 7 फीट है, तो दूसरा सेट अभी तक पुल तक नहीं पहुंचा है, और इसलिए केवल पहला सेट पुल पर भार डाल रहा है।

इसके अलावा, यदि दो भारों के बीच, भारों में से एक भारी है, तो भार को दोनों लोडिंग ऑर्डर (दाईं ओर बड़ा भार और बाईं ओर बड़ा भार) में जांचना चाहिए ताकि यह सुनिश्चित हो सके कि अधिकतम भार पाया जाता है। यदि तीन या अधिक भार हैं, तो जांच किए जाने वाले मामलों की संख्या बढ़ जाती है।

वितरित भार

कई भार बिंदु भार के रूप में कार्य नहीं करते हैं, बल्कि वितरित भार के रूप में विस्तारित लंबाई या क्षेत्र पर कार्य करते हैं। उदाहरण के लिए, निरंतर पटरियों वाला एक ट्रैक्टर प्रत्येक ट्रैक की लंबाई पर वितरित भार लागू करेगा।

वितरित भार के प्रभाव का पता लगाने के लिए, डिज़ाइनर संरचना की प्रभावित दूरी पर एक बिंदु भार का उपयोग करके पाई जाने वाली प्रभाव रेखा को एकीकृत कर सकता है।उदाहरण के लिए, यदि तीन फुट लंबा ट्रैक बीम के साथ 5 फीट और 8 फीट के बीच काम करता है, तो उस बीम की प्रभाव रेखा 5 और 8 फीट के बीच एकीकृत होनी चाहिए। प्रभाव रेखा का एकीकरण वह प्रभाव देता है जो वितरित भार में इकाई परिमाण होने पर महसूस किया जाएगा। इसलिए, एकीकृत करने के बाद, वितरित भार के वास्तविक प्रभाव को प्राप्त करने के लिए डिजाइनर को अभी भी परिणामों को मापना चाहिए।

अनिश्चित संरचनाएं

जबकि स्थैतिक रूप से निर्धारित संरचनाओं की प्रभाव रेखाएँ (जैसा कि ऊपर उल्लेख किया गया है) सीधी रेखा खंडों से बनी हैं, वही अनिश्चित संरचनाओं के लिए सही नहीं है। अनिश्चित संरचनाओं को कठोर नहीं माना जाता है; इसलिए, उनके लिए खींची जाने वाली प्रभाव रेखाएँ सीधी रेखाएँ नहीं होंगी, बल्कि वक्र होंगी। संरचना के लिए प्रभाव रेखाओं को निर्धारित करने के लिए उपरोक्त विधियों का अभी भी उपयोग किया जा सकता है, लेकिन कार्य अधिक जटिल हो जाता है क्योंकि बीम के गुणों को ही ध्यान में रखा जाना चाहिए।

यह भी देखें

• बीम (संरचना)
• कतरनी और पल आरेख
• डेड और लाइव लोड
• मुलर-ब्रेस्लाउ का सिद्धांत