योजक सफेद गाउसियन रव
This article relies largely or entirely on a single source. (February 2020) |
योजक सफेद गाउसियन रव (एडब्ल्यूजीएन) एक मूल रव प्रारूप है जिसका उपयोग प्रकृति में होने वाली कई यादृच्छिक प्रक्रियाओं के प्रभाव की नकल करने के लिए सूचना सिद्धांत में किया जाता है। संशोधक विशिष्ट विशेषताओं को दर्शाते हैं:
- योजक क्योंकि यह किसी भी रव में जोड़ा जाता है जो सूचना पद्धति में अंतर्निहित हो सकता है।
- सफेद इस विचार को संदर्भित करता है कि इसमें सूचना पद्धति के लिए आवृत्ति बैंड में एक समान शक्ति स्पेक्ट्रमी घनत्व है। यह सफेद रंग का एक सादृश्य है जिसे दृश्य स्पेक्ट्रम में सभी आवृत्तियों पर समान उत्सर्जनों द्वारा महसूस किया जा सकता है।
- गाउसियन क्योंकि इसका काल प्रक्षेत्र में औसत काल प्रक्षेत्र मान शून्य (गाउसियन प्रक्रिया) के साथ एक सामान्य वितरण है।
विस्तृत बैंड रव कई प्राकृतिक रव स्रोतों से आता है, जैसे संवाहकों में परमाणुओं के ऊष्मीय कंपन (ऊष्मीय रव या जॉनसन-नाइक्विस्ट रव के रूप में जाना जाता है), शॉट रव, पृथ्वी और अन्य गर्म वस्तुओं से कृष्णिका विकिरण, और सूर्य जैसे खगोलीय स्रोतों से। प्रायिकता सिद्धांत की केंद्रीय सीमा प्रमेय निर्दिष्ट करती है कि कई यादृच्छिक प्रक्रियाओं के योग में गाऊसी या सामान्य नामक वितरण होगा।
एडब्ल्यूजीएन को अधिकतर एक प्रणाल प्रारूप के रूप में उपयोग किया जाता है जिसमें संचार में एकमात्र बाधा नियत वर्णक्रमीय घनत्व (बैंड विड्थ के प्रति हर्ट्ज़ वाट के रूप में व्यक्त) और आयाम के गाऊसी वितरण के साथ वाइडबैंड या सफेद रव का एक रैखिक जोड़ है। प्रतिरूप म्लानन (फडिंग), आवृत्ति चयनात्मकता, हस्तक्षेप, अरैखिकता या परिक्षेपण को ध्यान में नहीं रखता है। हालाँकि, यह सरल और सुव्यवस्थित गणितीय प्रतिरूप तैयार करता है जो इन अन्य परिघटनाओं पर विचार करने से पहले किसी पद्धति के अंतर्निहित व्यवहार में अंतर्दृष्टि प्राप्त करने के लिए उपयोगी होते हैं।
एडब्ल्यूजीएन प्रणाल कई उपग्रहों और गहन अंतरिक्ष संचार कड़ियों के लिए एक अच्छा प्रतिरूप है। बहुपथ, भूभाग अवरोधन, हस्तक्षेप आदि के कारण अधिकांश स्थलीय कड़ियों के लिए यह एक अच्छा प्रतिरूप नहीं है। हालाँकि, स्थलीय पथ प्रतिरूपण के लिए, एडब्ल्यूजीएन का उपयोग आमतौर पर अध्ययन के अंतर्गत प्रणाल के पृष्ठभूमि रव का अनुकरण करने के लिए किया जाता है, इसके अतिरिक्त बहुपथ, भू भाग अवरोधन, हस्तक्षेप, भू अपचित्र और स्वयं हस्तक्षेप का उपयोग आधुनिक रेडियो प्रणाली स्थलीय संचालन में करते हैं।
प्रणाल क्षमता
एडब्ल्यूजीएन प्रणाल को असतत समय घटना सूचकांक पर आउटपुट की एक श्रृंखला द्वारा दर्शाया गया है। इनपुट और रव, का योग है, जहां स्वतंत्र है और प्रसरण N (रव) के साथ शून्य-माध्य सामान्य वितरण से समान रूप से वितरित और खींचा गया है। यह भी माना जाता है कि का के साथ कोई संबंध नहीं है।
प्रणाल की क्षमता अनंत है जब तक कि रव शून्येतर है, और पर्याप्त रूप से प्रतिबंधित हैं| इनपुट पर सबसे साधारण व्यवरोध तथाकथित "शक्ति" व्यवरोध है, प्रणाल के माध्यम से प्रसारित संकेत शब्दों के लिए इसकी आवश्यकता होती है, हमारे पास,
- है
जहां अधिकतम प्रणाल शक्ति का निरुपण करता है। इसलिए, शक्ति-प्रतिबंधित प्रणाल के लिए प्रणाल क्षमता इस प्रकार दी गई है:
जहां , का वितरण है | का विस्तार करें, इसे विभेदक एन्ट्रापी के पदों में लिखें:
लेकिन और स्वतंत्र हैं, इसलिए:
गाऊसी की विभेदक एन्ट्रापी का मूल्यांकन करने पर यह मिलता है:
क्योंकि और स्वतंत्र हैं और उनका योग देता है:
इस सीमा से, हम विभेदक एन्ट्रापी के एक गुण से अनुमान लगाते हैं
इसलिए, प्रणाल क्षमता पारस्परिक जानकारी पर उच्चतम प्राप्य सीमा द्वारा दी गई है:
जहां अधिकतम तब होता है जब:
इस प्रकार एडब्ल्यूजीएन प्रणाल के लिए प्रणाल क्षमता C इस प्रकार दी गई है:
प्रणाल क्षमता और गोला संकुलन
मान लीजिए कि हम से तक के सूचकांक वाले प्रणाल के माध्यम से संदेश भेज रहे हैं, जो कि सुस्पष्ट संभावित संदेशों की संख्या है। यदि हम संदेशों को बिट्स में कोडन करते हैं, तो हम दर को इस प्रकार परिभाषित करते हैं:
एक दर को प्राप्त करने योग्य कहा जाता है यदि कोड का एक अनुक्रम होता है ताकि त्रुटि की अधिकतम संभावना शून्य हो जाए क्योंकि n अनंत तक पहुंचता है। क्षमता उच्चतम प्राप्य दर है।
रव स्तर के साथ एडब्ल्यूजीएन प्रणाल के माध्यम से भेजे गए लंबाई के कोड शब्द पर विचार करें। प्राप्त होने पर, कोड शब्द सदिश प्रसरण अब है, और इसका माध्य भेजा गया कोड शब्द है। भेजे गए कोड शब्द के चारों ओर त्रिज्या के एक गोले में सदिश के समाहित होने की बहुत संभावना है। यदि हम इस गोले के केंद्र में कोड शब्द पर प्राप्त प्रत्येक संदेश को प्रतिचित्रिण करके विकोडन करते हैं, तो त्रुटि तभी होती है जब प्राप्त सदिश इस गोले के बाहर होता है, जो बहुत ही असंभव है।
प्रत्येक कोड शब्द सदिश में प्राप्त कोड शब्द सदिश का एक संबद्ध गोला होता है जिसे इसमें विकोडन किया जाता है और ऐसे प्रत्येक गोले को एक कोड शब्द पर विशिष्ट रूप से प्रतिचित्रित किया जाना चाहिए। चूँकि ये गोले एक दूसरे को नहीं काटने चाहिए, इसलिए हमें गोला संकुलन की समस्या का सामना करना पड़ता है। हम अपने -बिट कोड शब्द सदिश में कितने सुस्पष्ट कोड शब्द पैक कर सकते हैं? प्राप्त सदिश में की अधिकतम ऊर्जा होती है और इसलिए उसे त्रिज्या का एक गोला घेरना चाहिए। प्रत्येक कोड शब्द गोले की त्रिज्या है। एक n-विमीय गोले का आयतन सीधे के समानुपाती होता है, इसलिए संचरण क्षमता P के साथ हमारे गोले में संकुलित किए जा सकने वाले विशिष्ट डिकोडेबल गोलों की अधिकतम संख्या है:
इस तर्क के अनुसार, दर R, से अधिक नहीं हो सकती है।
साध्यता
इस भाग में, हम अंतिम भाग से दर पर ऊपरी सीमा की प्राप्ति दर्शाते हैं।
कोडक और विकोडक दोनों के लिए ज्ञात एक कोड पुस्तक, लंबाई n, i.i.d. के कोड शब्दों को चयन करके तैयार की जाती है। प्रसरण और माध्य शून्य के साथ गाऊसी। बड़े n के लिए, कोड पुस्तक का अनुभवजन्य प्रसरण इसके वितरण के विचरण के बहुत सटीक होगा, जिससे संभावित रूप से शक्ति व्यवरोध के उल्लंघन से बचा जा सकेगा।
प्राप्त संदेशों को कोड पुस्तक में एक संदेश में डिकोड किया जाता है जो विशिष्ट रूप से संयुक्त रूप से विशिष्ट है। यदि ऐसा कोई संदेश नहीं है या यदि शक्ति की कमी का उल्लंघन किया गया है, तो विकोडन त्रुटि घोषित की जाती है।
मान लें कि संदेश के लिए कोड शब्द को दर्शाता है, जबकि , प्राप्त सदिश से पहले की तरह है। निम्नलिखित तीन घटनाओं को परिभाषित करें:
- घटना : प्राप्त संदेश की शक्ति से बड़ी है।
- घटना : प्रेषित और प्राप्त कोड शब्द संयुक्त रूप से विशिष्ट नहीं हैं।
- घटना : , में है, विशिष्ट समुच्चय जहां , जिसका अर्थ है कि गलत कोड शब्द प्राप्त सदिश के साथ संयुक्त रूप से विशिष्ट है।
इसलिए त्रुटि तब होती है जब , या कोई घटित होता है। बड़ी संख्या के नियम के अनुसार, जैसे-जैसे n अनंतधा के सटीक पहुंचता है, शून्य पर चला जाता है, और संयुक्त अनंतस्पर्शी समविभाजन गुण द्वारा पर भी यही लागू होता है। इसलिए, पर्याप्त रूप से बड़े के लिए के लिए, और दोनों से कम हैं। चूँकि के लिए और स्वतंत्र हैं, हमारे पास यह है कि और भी स्वतंत्र हैं। इसलिए, संयुक्त एईपी द्वारा, | यह हमें , त्रुटि की संभावना की गणना करने की अनुमति देता है:
इसलिए, जैसे-जैसे n अनंतधा की ओर बढ़ता है, शून्य और पर जाता है। इसलिए, पहले प्राप्त क्षमता के सटीक स्वेच्छतः दर R का एक कोड है।
कोडिंग प्रमेय का व्युत्क्रम
यहां हम दिखाते हैं कि क्षमता से ऊपर की दरें प्राप्त नहीं की जा सकतीं हैं।
मान लीजिए कि एक कोड पुस्तक के लिए शक्ति का व्यवरोध पूर्ण हो गया है, और आगे यह भी मान लीजिए कि संदेश एक समान वितरण का पालन करते हैं। मान लीजिए कि इनपुट संदेश हैं और आउटपुट संदेश हैं। इस प्रकार से सूचना का प्रवाह होता है:
फ़ानो की असमानता का उपयोग करने से मिलता है:
जहां जैसा
मान लीजिए कि कोड शब्द सूचकांक i का विकोडित संदेश है। तब:
मान लीजिए सूचकांक i के कोड शब्द की औसत शक्ति है:
जहां योग सभी इनपुट संदेशों से अधिक है। और स्वतंत्र हैं, इस प्रकार रव स्तर के लिए की शक्ति की अपेक्षा है:
और, यदि सामान्य रूप से वितरित है, हमारे पास वह है
इसलिए,
हम जेन्सेन की समता को लागू कर सकते हैं, जो x का एक उन्मुख (नीचे की ओर) फलन है, प्राप्त करने के लिए:
चूँकि प्रत्येक कोड शब्द व्यक्तिगत रूप से शक्ति व्यवरोध को संतुष्ट करता है, औसत भी शक्ति व्यवरोध को संतुष्ट करता है। इसलिए,
जिसे हम उपरोक्त असमानता को सरल बनाने के लिए लागू कर सकते हैं और प्राप्त कर सकते हैं:
इसलिए, यह वह चाहिए। इसलिए, R को स्वेच्छतः से पहले व्युत्पन्न क्षमता के सटीक एक मान से कम होना चाहिए, जैसे कि |
काल प्रक्षेत्र में प्रभाव
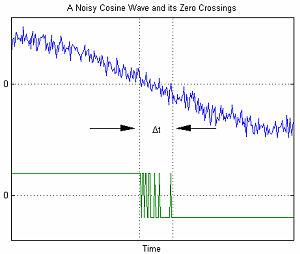
क्रमिक डेटा संचार में, एडब्ल्यूजीएन गणितीय प्रतिरूप का उपयोग यादृच्छिक कँपन (आरजे) के कारण होने वाली कालन त्रुटि को प्रतिरूपित करने के लिए किया जाता है।
दाईं ओर का ग्राफ़ एडब्ल्यूजीएन से जुड़ी कालन संबंधी त्रुटियों का एक उदाहरण दिखाता है। चर Δt शून्य पारण में अनिश्चितता का निरुपण करता है। जैसे-जैसे एडब्ल्यूजीएन का आयाम बढ़ता है, संकेत रव अनुपात कम हो जाता है। इसके परिणामस्वरूप अनिश्चितता Δt बढ़ जाती है।[1]
एडब्ल्यूजीएन के प्रभाव से, साइन (ज्या) तरंग को इनपुट के रूप में लेते हुए एक संकीर्ण बैंड पारक फिल्टर के आउटपुट पर प्रति सेकंड या तो धनात्मक या ऋणात्मक जाने वाले शून्य पारणों की औसत संख्या
- होती है,
जहां
- ƒ0 = फ़िल्टर की केंद्र आवृत्ति,
- B = फिल्टर बैंडविड्थ,
- SNR = रैखिक पदों में संकेत रव शक्ति अनुपात।
फ़ेसर प्रक्षेत्र में प्रभाव
आधुनिक संचार प्रणालियों में, बैंड सीमित एडब्ल्यूजीएन को नजरअंदाज नहीं किया जा सकता है। जब फेज़र प्रक्षेत्र में बैंड सीमित एडब्ल्यूजीएन का प्रतिरूपण किया जाता है, तो सांख्यिकीय विश्लेषण से पता चलता है कि वास्तविक और काल्पनिक योगदान के आयाम स्वतंत्र चर हैं जो गाउसीय वितरण प्रतिरूप का पालन करते हैं। संयुक्त होने पर, परिणामी चरण का परिमाण एक रेले वितरण होता है| संयुक्त होने पर, परिणामी फ़ेजर का परिमाण एक रैले-वितरित यादृच्छिक चर होता है, जबकि फेज समान रूप से 0 से 2π तक वितरित होता है।
दाईं ओर का ग्राफ़ एक उदाहरण दिखाता है कि बैंड सीमित एडब्ल्यूजीएन एक संसक्त वाहक संकेत को कैसे प्रभावित कर सकता है। रव सदिश की तात्क्षणिक अनुक्रिया का सटीक अनुमान नहीं लगाया जा सकता है, हालांकि, इसकी समय-औसत अनुक्रिया का सांख्यिकीय रूप से अनुमान लगाया जा सकता है। जैसा कि ग्राफ में दिखाया गया है, हम विश्वासपूर्वक अनुमान लगाते हैं कि रव फ़ेजर 1σ वृत्त के भीतर लगभग 38% समय, 2σ वृत्त के भीतर लगभग 86% समय और 3σ वृत्त के भीतर लगभग 98% समय रहेगा।[1]