आधार (ज्यामिति)
This article needs additional citations for verification. (December 2017) (Learn how and when to remove this template message) |
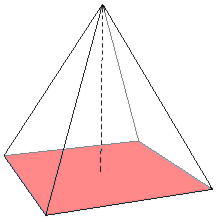
ज्यामिति में, एक आधार एक बहुभुज का एक किनारा (ज्यामिति) या एक बहुफलक का एक चेहरा (ज्यामिति) होता है, विशेष रूप से उस दिशा में लंबवत उन्मुख होता है जिसमें ऊंचाई गणित में मापा जाता है, या जिसे "नीचे" माना जाता है आंकड़ा।[1] यह शब्द सामान्यतः त्रिकोण, समांतर [[चतुर्भुज]], ट्रेपेज़ोइड्स, सिलेंडर (ज्यामिति), शंकु (ज्यामिति), पिरामिड (ज्यामिति), समानांतर चतुर्भुज और छिन्नक पर लागू होता है।
क्षेत्र और आयतन गणना में भूमिका
आंकड़ों के क्षेत्रों और मात्राओं की गणना करने के लिए सामान्यतः आधारों (ऊंचाइयों के साथ) का उपयोग किया जाता है। इन प्रक्रियाओं के बारे में बोलते हुए, किसी आकृति के आधार के माप (लंबाई या क्षेत्र) को अधिकांशतः इसका "आधार" कहा जाता है।
इस प्रयोग से, एक समांतर चतुर्भुज का क्षेत्रफल या एक प्रिज्म (ज्यामिति) या बेलन के आयतन की गणना इसके "आधार" को इसकी ऊंचाई से गुणा करके की जा सकती है; इसी तरह, त्रिभुजों का क्षेत्रफल और शंकुओं और पिरामिडों का आयतन उनके आधारों और ऊँचाइयों के गुणनफल के अंश हैं। कुछ आकृतियों के दो समानांतर आधार होते हैं (जैसे कि समलम्बाकार और छिन्नक), जिनमें से दोनों का उपयोग आंकड़ों की सीमा की गणना करने के लिए किया जाता है।[2]
त्रिकोणमिति में विस्तारित आधार
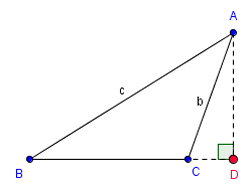
त्रिभुज का विस्तारित आधार (विस्तारित भुजा का एक विशेष मामला) वह रेखा (ज्यामिति) है जिसमें आधार होता है। विस्तारित आधार को अधिक त्रिकोण के संदर्भ में महत्वपूर्ण होते है: तीव्र कोण शीर्ष (ज्यामिति) से ऊंचाई (त्रिकोण) त्रिकोण के बाहर हैं और विस्तारित रूप से विपरीत आधार (किन्तु उचित आधार नहीं) के लंबवत को प्रतिच्छेदन करते हैं।
यह भी देखें
संदर्भ
- ↑ Palmer, C.I.; Taylor, D.P. (1918). समतल ज्यामिति. Scott, Foresman & Co. pp. 38, 315, 353.
- ↑ Jacobs, Harold R. (2003). Geometry: Seeing, Doing, Understanding (Third ed.). New York City: W. H. Freeman and Company. p. 281. ISBN 978-0-7167-4361-3.