समुचित अनुक्रम

समुचित अनुक्रम वस्तुओं के बीच आकारिकी का एक क्रम है, उदाहरण के लिए, समूह (गणित), वृत्त (गणित), मापदंड (गणित), और अधिक सामान्यतः एक एबेलियन श्रेणी की वस्तुएं इत्यादि। समुचित अनुक्रम में एक आकारिकी की छवि कर्नेल की अगली छवि के बराबर होती है।
परिभाषा
समूह सिद्धांत के संदर्भ में, एक अनुक्रम
अगर है तो समूहों और समूह समरूपताओं को पर समुचित कहा जाता है। अनुक्रम को तब भी समुचित कहा जाता है यदि सभी के लिए प्रत्येक ,पर समुचित हो यानी, यदि प्रत्येक समरूपता की छवि अगले छवि के कर्नेल के बराबर हो।
समूहों और समरूपताओं का क्रम या तो सीमित या अनंत हो सकता है।
इसी तरह की परिभाषा अन्य बीजगणितीय संरचनाओं के लिए भी बनाई जा सकती है। उदाहरण के लिए, किसी के पास रेखीय स्थान और रैखिक मानचित्र, या मापदंड और मापदंड समरूपता का समुचित अनुक्रम हो सकता है। विशेष रूप से एबेलियन श्रेणियों में इसका उपयोग व्यापक रूप से किया जाता है और सामान्यतौर पर, एक समुचित अनुक्रम की धारणा किसी भी श्रेणी में कर्नेल श्रेणी सिद्धांत और कोकर्नेल के साथ अधिक अर्थपूर्ण होती है।
सामान्य स्तिथियाँ
परिभाषा को समझने के लिए, अपेक्षाकृत सरल स्तिथियों पर विचार करना सहायक होता है जहां समूह समरूपता का अनुक्रम सीमित है, और शून्य समूह के साथ शुरू या समाप्त होता है। परंपरागत रूप से,सामान्यतौर पर जब समूह एबेलियन होते हैं तब एकल पहचान तत्व के साथ योगात्मक संकेतन '0' को दर्शाया जाता है, या गुणात्मक संकेतन '1' को दर्शाया जाता है।
- अनुक्रम 0 → A→ B पर विचार करें। सबसे बाएं मानचित्र की छवि 0 है, अगर और केवल अगर सबसे दाहिने मानचित्र (A से B तक) में कर्नेल {0} है तो यह अनुक्रम समुचित है ; यानी, अगर और केवल अगर वह नक्शा एकरूपता अंतःक्षेपक, या एक-से-एक है।
- दोहरे अनुक्रम B → C → 0 पर विचार करें। सबसे दाहिने मानचित्र का कर्नेल C है, अगर और केवल अगर बाईं ओर के मानचित्र की छवि (B से C तक) सभी C की है तो यह अनुक्रम समुचित है; यानी, अगर और केवल अगर वह नक्शा एक अधिरूपता प्रक्षेपण या एक पर एक है।
- इसलिए, अनुक्रम 0 → X → Y → 0 समुचित है अगर और केवल अगर X से Y तक का मानचित्र एक एकरूपता और अधिरूपता यानी, एक द्विरूपता है, और इसलिए सामान्यतौर पर X से Y तक एक समरूपता 'समुच्चय' जैसी समुचित श्रेणियों में आता है।
लघु समुचित अनुक्रम
लघु समुचित अनुक्रम प्रपत्र के समुचित अनुक्रम हैं
ऊपर स्थापित किये गए सूत्र के अनुसार, किसी भी छोटे समुचित अनुक्रम के लिए, f एक एकरूपता है और g एक अधिरूपता है। इसके अतिरिक्त , f की छवि g के कर्नेल के बराबर है। A को f के साथ B के उपवस्तु के रूप में और A को B और C को संबंधित कारक वस्तु (या भागफल वस्तु) में अन्तः स्थापित करने के साथ, B/A के रूप में सोचना मददगार होता है, जिसमें g एक समरूपता को प्रेरित करता है।
लघु समुचित अनुक्रम
यदि h : C → B समरूपता मौजूद है जैसे कि रचना g ∘ h C पर पहचान मानचित्र है तो इसे विभाजित समुचित अनुक्रम कहा जाता है। यह इस प्रकार है कि यदि ये एबेलियन समूह का अनुसरण करता हैं, तो Aऔर C के प्रत्यक्ष योग के लिए B समरूपता है:
दीर्घ समुचित अनुक्रम
एक छोटे समुचित अनुक्रम के विशेष स्तिथियों से अलग करने के लिए, एक सामान्य समुचित अनुक्रम को कभी-कभी एक दीर्घ समुचित अनुक्रम कहा जाता है।[1]
एक दीर्घ समुचित अनुक्रम निम्नलिखित अर्थों में लघु समुचित अनुक्रमों के श्रेणी के बराबर है: एक दीर्घ अनुक्रम दिया गया
(1)
n ≥ 2 के साथ, हम इसे लघु अनुक्रमों में विभाजित कर सकते हैं
(2)
जहाँ प्रत्येक के लिए ,सूत्र संरचना के द्वारा, पर अनुक्रम (2) समुचित हैं। इसके अतिरिक्त, (1) एक दीर्घ समुचित अनुक्रम है अगर और केवल अगर सभी (2) लघु समुचित अनुक्रम हैं।
उदाहरण
दो पूर्णांक गुणनखंड
एबेलियन समूहों के निम्नलिखित अनुक्रम पर विचार करें:
पहला समरूपता पूर्णांक 'Z' के समुच्चय में प्रत्येक तत्व i को 'Z' के तत्व 2i में मानचित्र करता है। दूसरा समरूपता 'Z' के प्रत्येक तत्व i को भागफल समूह के एक तत्व j में मानचित्र करता है; वह है, j = i mod 2. यहाँ अंकुश निशान इंगित करता है कि Z से Z तक का नक्शा 2× एक एकरूपता है, और दो-सिरे वाला निशान है इंगित करता है कि मानचित्र मॉड 2 एक अधिरूपता है। यह एक समुचित क्रम है क्योंकि एकरूपता की छवि 2Z अधिरूपता का कर्नेल है। अनिवार्य रूप से उसी क्रम को इस रूप में भी लिखा जा सकता है
इस स्तिथियों में एकरूपता 2n ↦ 2n है और यद्यपि यह एक पहचान कार्य की तरह दिखता है, यह आच्छादित नहीं है (अर्थात, एपिमोर्फिज़्म नहीं है) क्योंकि विषम संख्याएँ 2'Z' से संबंधित नहीं हैं। इस एकरूपता के माध्यम से 2'Z' की छवि हालांकि 'Z' का बिल्कुल वही उपसमुच्चय है, जो पिछले अनुक्रम में प्रयुक्त n ↦ 2n के माध्यम से 'Z' की छवि है। यह बाद वाला क्रम पिछले एक से अपनी पहली वस्तु की ठोस प्रकृति में भिन्न होता है क्योंकि 2'Z' 'Z' के समान सेट नहीं है, भले ही दोनों समूह के रूप में आइसोमोर्फिक हों।
एकरूपता और अधिरूपता के लिए विशेष प्रतीकों का उपयोग किए बिना पहला अनुक्रम भी लिखा जा सकता है:
यहाँ 0 तुच्छ समूह को दर्शाता है, Z से Z का नक्शा 2 से गुणा है, और Z से कारक समूह Z/2Z का नक्शा पूर्णांक मापदंडर अंकगणित 2 को कम करके दिया गया है। यह वास्तव में एक समुचित क्रम है:
- मानचित्र 0 → Z की छवि {0} है, और 2 से गुणन की गिरी भी {0} है, इसलिए अनुक्रम पहले Z पर समुचित है।
- 2 से गुणन की छवि 2Z है, और मॉडुलो 2 को कम करने की गिरी भी 2Z है, इसलिए अनुक्रम दूसरे Z पर समुचित है।
- मोडुलो 2 को कम करने की छवि Z/2Z है, और शून्य मानचित्र का कर्नेल भी Z/2Z है, इसलिए अनुक्रम Z/2Z की स्थिति पर समुचित है।
Z की अनंत प्रकृति के कारण पहला और तीसरा क्रम कुछ विशेष मामला है। एक परिमित समूह के लिए खुद के एक उचित उपसमूह के रूप में समावेशन (अर्थात, एक एकरूपता द्वारा) द्वारा मानचित्र किया जाना संभव नहीं है। इसके बजाय पहले समरूपता प्रमेय से निकलने वाला क्रम है
परिमित समूहों पर एक समुचित अनुक्रम के अधिक ठोस उदाहरण के रूप में:
कहाँ क्रम n और का चक्रीय समूह है 2n कोटि का डायहेड्रल समूह है, जो एक गैर-अबेलियन समूह है।
प्रतिच्छेदन और मापदंड का योग
होने देना I और J एक रिंग के दो आइडियल (रिंग थ्योरी) हों R. तब
का समुचित क्रम है R-मापदंड, जहां मापदंड समरूपता प्रत्येक तत्व को मानचित्र करता है x का तत्व को {{tmath|(x,x)}प्रत्यक्ष राशि का } , और समरूपता प्रत्येक तत्व को मानचित्र करता है का को .
ये समरूपता समान रूप से परिभाषित समरूपता के प्रतिबंध हैं जो लघु समुचित अनुक्रम बनाते हैं
- भागफल मापदंड के पास जाने से एक और समुचित अनुक्रम प्राप्त होता है
अंतरात्मक रेखागणित में ग्रेड, कर्ल और डिव
एक और उदाहरण अंतरात्मक रेखागणित से प्राप्त किया जा सकता है, विशेष रूप से मैक्सवेल समीकरणों पर काम के लिए प्रासंगिक।
हिल्बर्ट अंतरिक्ष पर विचार करें तीन आकारों पर अदिश-मूल्यवान वर्ग-अभिन्न कार्य . किसी फंक्शन का ग्रेडियेंट लेना हमें के उपसमुच्चय में ले जाता है , सदिश मूल्य का स्थान, एक ही डोमेन पर अभी भी वर्ग-अभिन्न कार्य - विशेष रूप से, ऐसे कार्यों का सेट जो रूढ़िवादी सदिश क्षेत्रों का प्रतिनिधित्व करते हैं। (सामान्यीकृत स्टोक्स प्रमेय ने पूर्णता को संरक्षित रखा है।)
सबसे पहले, ध्यान दें कि ऐसे सभी क्षेत्रों का कर्ल (गणित) शून्य है - चूंकि
ऐसे सभी के लिए f. हालाँकि, यह केवल यह साबित करता है कि ढाल की छवि कर्ल के कर्नेल का एक उपसमुच्चय है। यह साबित करने के लिए कि वे वास्तव में एक ही सेट हैं, इसका विलोम सिद्ध करें: कि यदि एक सदिश क्षेत्र का कर्ल है 0 है, तो कुछ अदिश फलन का ग्रेडिएंट है। यह स्टोक्स के प्रमेय से लगभग तुरंत अनुसरण करता है (रूढ़िवादी बल#गणितीय विवरण पर प्रमाण देखें।) ग्रेडिएंट की छवि तब ठीक कर्ल की गिरी है, और इसलिए हम कर्ल को अपना अगला रूप ले सकते हैं, हमें ले जा रहे हैं फिर से एक (अलग) उपसमुच्चय के लिए .
इसी तरह, हम ध्यान दें
तो कर्ल की छवि विचलन के कर्नेल का एक उपसमुच्चय है। बातचीत कुछ हद तक शामिल है:
| Proof that = 0 implies for some |
|---|
| We shall proceed by construction: given a vector field such that , we produce a field such that
First, note that since as proved above , we can add the gradient of any scalar function to without changing the curl. We can use this gauge freedom to set any one component of to zero without changing its curl; choosing arbitrarily the z-component, we thus require simply that Then by simply integrating the first two components, and noting that the 'constant' of integration may still depend on any variable not integrated over, we find that Note that since the two integration terms both depend only on x and y and not on z, then we can add another gradient of some function that also does not depend on z. This permits us to eliminate either of the terms in favor of the other, without spoiling our earlier work that set to zero. Choosing to eliminate and applying the last component as a constraint, we have By assumption, , and so Since the fundamental theorem of calculus requires that the first term above be precisely plus a constant in z, a solution to the above system of equations is guaranteed to exist. |
इस प्रकार यह साबित करने के बाद कि कर्ल की छवि वास्तव में विचलन की गिरी है, यह आकारिकी हमें उस स्थान पर वापस ले जाती है जहां से हमने शुरू किया था . चूंकि निश्चित रूप से हम अभिन्न कार्यों के एक स्थान पर उतरे हैं, ऐसा कोई भी कार्य (कम से कम औपचारिक रूप से) एक सदिश क्षेत्र का निर्माण करने के लिए एकीकृत किया जा सकता है जो विचलन वह कार्य है - इसलिए विचलन की छवि पूरी तरह से है , और हम अपना क्रम पूरा कर सकते हैं:
समतुल्य रूप से, हम इसके विपरीत तर्क दे सकते थे: सरल रूप से जुड़े हुए स्थान में, एक कर्ल-मुक्त सदिश क्षेत्र (कर्ल के कर्नेल में एक फ़ील्ड) को हमेशा एक रूढ़िवादी सदिश क्षेत्र के रूप में लिखा जा सकता है (और इस प्रकार ढाल की छवि में है) ). इसी प्रकार, अपसरण रहित क्षेत्र को दूसरे क्षेत्र के कर्ल के रूप में लिखा जा सकता है।[2] (इस दिशा में तर्क इस तथ्य का उपयोग करता है कि 3-आयामी स्थान सांस्थितिक रूप से तुच्छ है।)
यह छोटा समुचित अनुक्रम भी हेल्महोल्ट्ज़ अपघटन की वैधता के एक बहुत छोटे प्रमाण की अनुमति देता है जो ब्रूट-बल सदिश कलन पर निर्भर नहीं करता है। अनुवर्ती पर विचार करें
चूँकि ढाल का विचलन लाप्लासियन है, और चूंकि वर्ग-अभिन्न कार्यों के हिल्बर्ट स्थान को लाप्लासियन के ईजेनफंक्शन द्वारा फैलाया जा सकता है, हम पहले से ही देखते हैं कि कुछ व्युत्क्रम मानचित्रण मौजूद होना चाहिए। स्पष्ट रूप से इस तरह के व्युत्क्रम का निर्माण करने के लिए, हम सदिश लाप्लासियन की परिभाषा से शुरू कर सकते हैं
चूंकि हम ढाल के साथ कुछ फ़ंक्शन बनाकर एक पहचान मानचित्रण बनाने की कोशिश कर रहे हैं, हम जानते हैं कि हमारे स्तिथियों में . फिर अगर हम दोनों पक्षों का विचलन लेते हैं
हम देखते हैं कि यदि कोई फलन सदिश लाप्लासियन का एक ईजेनफंक्शन है, तो इसका डाइवर्जेंस उसी आइगेनवैल्यू के साथ स्केलर लाप्लासियन का एक ईजेनफंक्शन होना चाहिए। तब हम अपने व्युत्क्रम कार्य का निर्माण कर सकते हैं बस किसी भी समारोह को तोड़कर सदिश-लाप्लासियन ईगेनबेसिस में, प्रत्येक को उनके आइगेनवेल्यू के व्युत्क्रम द्वारा मापना, और विचलन लेना; की कार्रवाई इस प्रकार स्पष्ट रूप से पहचान है। इस प्रकार विभाजन लेम्मा द्वारा,
- ,
या समतुल्य, कोई भी वर्ग-पूर्णांक सदिश क्षेत्र पर एक ढाल और एक कर्ल के योग में तोड़ा जा सकता है - जिसे हम साबित करने के लिए निर्धारित करते हैं।
गुण
बंटवारे लेम्मा में कहा गया है कि यदि लघु समुचित अनुक्रम
रूपवाद को स्वीकार करता है t : B → A ऐसा है कि t ∘ f पर पहचान है A तार्किक संयोजन एक रूपवाद u: C → B ऐसा है कि g ∘ u पर पहचान है C, तब B का प्रत्यक्ष योग है A और C (गैर-कम्यूटेटिव समूहों के लिए, यह एक अर्ध-प्रत्यक्ष उत्पाद है)। एक का कहना है कि इतना छोटा समुचित क्रम टूट जाता है।
साँप लेम्मा दिखाता है कि कैसे दो समुचित पंक्तियों वाला एक क्रमविनिमेय आरेख एक लंबे समुचित अनुक्रम को जन्म देता है। नौ लेम्मा एक विशेष मामला है।
पांच लेम्मा ऐसी स्थितियाँ देती है जिसके तहत 5 लंबाई की समुचित पंक्तियों के साथ एक क्रमविनिमेय आरेख में मध्य मानचित्र एक समरूपता है; लघु पांच लेम्मा इसका एक विशेष मामला है जो लघु समुचित अनुक्रमों पर लागू होता है।
लघु समुचित अनुक्रमों के महत्व को इस तथ्य से रेखांकित किया जाता है कि प्रत्येक समुचित अनुक्रम कई अतिव्यापी लघु समुचित अनुक्रमों को एक साथ बुनने से उत्पन्न होता है। उदाहरण के लिए समुचित क्रम पर विचार करें
जिसका तात्पर्य है कि उद्देश्य सी मौजूद हैkऐसी श्रेणी में
- .
इसके अतिरिक्त मान लीजिए कि प्रत्येक रूपवाद का कोकर्नेल मौजूद है, और अनुक्रम में अगले आकारिकी की छवि के लिए समरूप है:
(यह कई दिलचस्प श्रेणियों के लिए सही है, जिसमें एबेलियन समूह जैसे कोई भी एबेलियन श्रेणी शामिल है; लेकिन यह उन सभी श्रेणियों के लिए सही नहीं है जो समुचित अनुक्रमों की अनुमति देते हैं, और विशेष रूप से समूहों की श्रेणी के लिए सही नहीं है, जिसमें कोकर ( f) : G → H, H/im(f) नहीं है लेकिन , im(f) के संयुग्मन समापन द्वारा H का भागफल।) तब हमें एक क्रमविनिमेय आरेख प्राप्त होता है जिसमें सभी विकर्ण छोटे समुचित क्रम होते हैं:
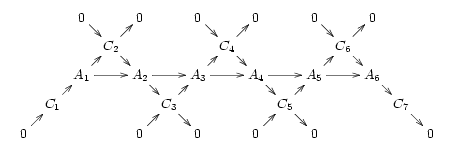 इस आरेख का एकमात्र भाग जो कोकरनेल की स्थिति पर निर्भर करता है वह वस्तु है और morphisms की अंतिम जोड़ी . अगर कोई वस्तु मौजूद है और आकृतिवाद ऐसा है कि समुचित है, तो की समुचितता सुनिश्चित किया जाता है। फिर से समूहों की श्रेणी का उदाहरण लेते हुए, तथ्य यह है कि आईएम (एफ) एच पर कुछ समरूपता का कर्नेल है, यह दर्शाता है कि यह एक सामान्य उपसमूह है, जो इसके संयुग्मित समापन के साथ मेल खाता है; इस प्रकार कोकर (एफ) अगले रूपवाद की छवि एच/आईएम (एफ) के लिए आइसोमोर्फिक है।
इस आरेख का एकमात्र भाग जो कोकरनेल की स्थिति पर निर्भर करता है वह वस्तु है और morphisms की अंतिम जोड़ी . अगर कोई वस्तु मौजूद है और आकृतिवाद ऐसा है कि समुचित है, तो की समुचितता सुनिश्चित किया जाता है। फिर से समूहों की श्रेणी का उदाहरण लेते हुए, तथ्य यह है कि आईएम (एफ) एच पर कुछ समरूपता का कर्नेल है, यह दर्शाता है कि यह एक सामान्य उपसमूह है, जो इसके संयुग्मित समापन के साथ मेल खाता है; इस प्रकार कोकर (एफ) अगले रूपवाद की छवि एच/आईएम (एफ) के लिए आइसोमोर्फिक है।
इसके विपरीत, अतिव्यापी छोटे समुचित अनुक्रमों की किसी भी सूची को देखते हुए, उनके मध्य शब्द उसी तरह एक समुचित अनुक्रम बनाते हैं।
समुचित अनुक्रमों के अनुप्रयोग
एबेलियन श्रेणियों के सिद्धांत में, लघु समुचित अनुक्रमों को अक्सर उप-वस्तु और कारक वस्तुओं के बारे में बात करने के लिए एक सुविधाजनक भाषा के रूप में उपयोग किया जाता है।
विस्तार की समस्या अनिवार्य रूप से प्रश्न है एक छोटे समुचित अनुक्रम के अंत शर्तों ए और सी को देखते हुए, मध्य अवधि बी के लिए क्या संभावनाएं मौजूद हैं? समूहों की श्रेणी में, यह प्रश्न के समतुल्य है, कौन से समूह B में सामान्य उपसमूह के रूप में A और संबंधित कारक समूह के रूप में C है? परिमित सरल समूहों के वर्गीकरण में यह समस्या महत्वपूर्ण है। बाहरी ऑटोमोर्फिज्म समूह भी देखें।
ध्यान दें कि एक समुचित क्रम में रचना fi+1 ∘ चi मानचित्र एi ए में 0 तकi+2, इसलिए प्रत्येक समुचित क्रम एक श्रृंखला परिसर है। इसके अतिरिक्त , केवल एफiए के तत्वों की छवियांi f द्वारा 0 पर मानचित्र किए गए हैंi+1, इसलिए इस श्रृंखला परिसर की समरूपता (गणित) तुच्छ है। अधिक संक्षेप में:
- समुचित अनुक्रम समुचित रूप से वे श्रृंखला परिसर हैं जो चक्रीय परिसर हैं।
किसी भी चेन कॉम्प्लेक्स को देखते हुए, इसकी समरूपता को उस डिग्री के माप के रूप में माना जा सकता है जिस पर यह समुचित नहीं हो पाता है।
यदि हम श्रृंखला परिसरों से जुड़े छोटे समुचित अनुक्रमों की एक श्रृंखला लेते हैं (अर्थात, श्रृंखला परिसरों का एक छोटा समुचित अनुक्रम, या दूसरे दृष्टिकोण से, लघु समुचित अनुक्रमों का एक श्रृंखला परिसर), तो हम इससे एक लंबा समुचित प्राप्त कर सकते हैं ज़िगज़ैग लेम्मा के अनुप्रयोग द्वारा समरूपता पर अनुक्रम (अर्थात, प्राकृतिक संख्याओं द्वारा अनुक्रमित एक समुचित अनुक्रम)। यह रिश्तेदार समरूपता के अध्ययन में बीजगणितीय टोपोलॉजी में आता है; मेयर-विटोरिस अनुक्रम एक अन्य उदाहरण है। छोटे समुचित अनुक्रमों से प्रेरित लंबे समुचित अनुक्रम भी व्युत्पन्न फ़ैक्टरों की विशेषता हैं।
समुचित ऑपरेटर ऐसे फ़ंक्टर हैं जो समुचित अनुक्रमों को समुचित अनुक्रमों में बदलते हैं।
संदर्भ
- Citations
- ↑ "exact sequence in nLab, Remark 2.3". ncatlab.org. Retrieved 2021-09-05.
{{cite web}}: CS1 maint: url-status (link) - ↑ "विचलन रहित क्षेत्र". December 6, 2009.
- Sources
- Spanier, Edwin Henry (1995). Algebraic Topology. Berlin: Springer. p. 179. ISBN 0-387-94426-5.
- Eisenbud, David (1995). Commutative Algebra: with a View Toward Algebraic Geometry. Springer-Verlag New York. p. 785. ISBN 0-387-94269-6.