जाइरोमैग्नेटिक अनुपात

भौतिकी में, जाइरोमैग्नेटिक अनुपात (जिसे कभी-कभी मैग्नेटोग्यरिक अनुपात के रूप में भी जाना जाता है अन्य विषयों में) एक कण या प्रणाली के चुंबकीय क्षण का उसके कोणीय गति का अनुपात है, और इसे अक्सर प्रतीक गामा द्वारा निरूपित किया जाता है|γ, गामा। इसकी SI इकाई कांति प्रति सेकंड प्रति टेस्ला (इकाई) (rad⋅s⁻¹⋅T⁻¹) या, समकक्ष, कूलम्ब प्रति किलोग्राम (C⋅kg^-1).

जाइरोमैग्नेटिक अनुपात शब्द का प्रयोग अक्सर किया जाता है एक अलग लेकिन बारीकी से संबंधित मात्रा के पर्याय के रूप में, जी-कारक (भौतिकी) |g-कारक। वह g-कारक केवल जाइरोमैग्नेटिक अनुपात से आयाम रहित होने में भिन्न होता है।

क्लासिकल रोटेटिंग बॉडी के लिए

एक विद्युत प्रतिरोधकता और चालकता पर विचार करें समरूपता के अक्ष के बारे में घूमते हुए बिजली का आवेश बॉडी। शास्त्रीय भौतिकी के नियमों के अनुसार, इसमें आवेश की गति के कारण चुंबकीय द्विध्रुवीय क्षण और इसके घूर्णन से उत्पन्न द्रव्यमान की गति के कारण कोणीय गति दोनों होती है। यह दिखाया जा सकता है कि जब तक इसका आवेश और द्रव्यमान घनत्व और प्रवाह समान रूप से और घूर्णी रूप से सममित रूप से वितरित किया जाता है, तब तक इसका जाइरोमैग्नेटिक अनुपात होता है

$\gamma ={\frac {q}{2m}}$

कहाँ ${q}$ इसका चार्ज है और ${m}$ इसका द्रव्यमान है।

इस संबंध की व्युत्पत्ति इस प्रकार है। यह शरीर के भीतर एक असीम रूप से संकीर्ण गोलाकार वलय के लिए इसे प्रदर्शित करने के लिए पर्याप्त है, क्योंकि सामान्य परिणाम तब एक अभिन्न से होता है। मान लीजिए कि रिंग की त्रिज्या है r, क्षेत्र A = πr², द्रव्यमान m, शुल्क q, और कोणीय गति L = mvr. फिर चुंबकीय द्विध्रुवीय क्षण का परिमाण है

$\mu =IA={\frac {qv}{2\pi r}}\,\pi r^{2}={\frac {q}{2m}}\,mvr={\frac {q}{2m}}L~.$

एक पृथक इलेक्ट्रॉन के लिए

एक पृथक इलेक्ट्रॉन का एक कोणीय संवेग होता है और एक चुंबकीय क्षण होता है जो इसके स्पिन (भौतिकी) से उत्पन्न होता है। जबकि एक इलेक्ट्रॉन के स्पिन को कभी-कभी अक्ष के बारे में शाब्दिक रोटेशन के रूप में देखा जाता है, इसे चार्ज के समान वितरित द्रव्यमान के लिए जिम्मेदार नहीं ठहराया जा सकता है। उपरोक्त शास्त्रीय संबंध धारण नहीं करता है, इलेक्ट्रॉन के जी-कारक (भौतिकी) के निरपेक्ष मान द्वारा गलत परिणाम देता है|g-कारक, जिसे निरूपित किया जाता है g_e:

$$\gamma _{\mathrm {e} }={\frac {-e}{2m_{\mathrm {e} }}}\,|g_{\mathrm {e} }|={\frac {g_{\mathrm {e} }\mu _{\mathrm {B} }}{\hbar }}\,,$$

कहाँ μ_B बोहर चुंबक है।

इलेक्ट्रॉन स्पिन के कारण जाइरोमैग्नेटिक अनुपात एक इलेक्ट्रॉन की परिक्रमा के कारण दोगुना होता है।

सापेक्षतावादी क्वांटम यांत्रिकी के ढांचे में,

$$g_{\mathrm {e} }=-2\left(1+{\frac {\alpha }{\,2\pi \,}}+\cdots \right)~,$$

कहाँ $\alpha$ ठीक-संरचना स्थिरांक है। यहाँ सापेक्षतावादी परिणाम के लिए छोटे सुधार g = 2 विषम चुंबकीय द्विध्रुव आघूर्ण की क्वांटम क्षेत्र सिद्धांत गणना से आते हैं। इलेक्ट्रॉन g-कारक को एक-इलेक्ट्रॉन साइक्लोट्रॉन में इलेक्ट्रॉन चुंबकीय क्षण को मापकर बारह दशमलव स्थानों तक जाना जाता है:

$$g_{\mathrm {e} }=-2.002\,319\,304\,362\,56(35).$$

इलेक्ट्रॉन जाइरोमैग्नेटिक अनुपात है

$$\gamma _{\mathrm {e} }=\mathrm {-1.760\,859\,630\,23(53)\times 10^{11}\,rad{\cdot }s^{-1}{\cdot }T^{-1}}$$

$${\frac {\gamma _{\mathrm {e} }}{2\pi }}=\mathrm {-28\,024.951\,4242(85)\,MHz{\cdot }T^{-1}} .$$

इलेक्ट्रॉन g-कारक और γ सिद्धांत के साथ उत्कृष्ट समझौते में हैं; विवरण के लिए क्यूईडी के सटीक परीक्षण देखें।

जाइरोमैग्नेटिक कारक सापेक्षता के परिणाम के रूप में नहीं

चूंकि डायराक के समीकरण से 2 के बराबर एक जाइरोमैग्नेटिक कारक होता है, इसलिए यह सोचना एक गलत धारणा है कि जी-फैक्टर (भौतिकी) |g-फैक्टर 2 सापेक्षता का परिणाम है; यह नहीं है। कारक 2 श्रोडिंगर समीकरण और सापेक्षवादी क्लेन-गॉर्डन समीकरण (जो डिराक की ओर जाता है) दोनों के रैखिककरण से प्राप्त किया जा सकता है। दोनों ही मामलों में एक 4-स्पिनर प्राप्त होता है और दोनों रैखिककरणों के लिए जी-फैक्टर (भौतिकी)|g-कारक 2 के बराबर पाया जाता है; इसलिए, कारक 2 न्यूनतम युग्मन और स्थान और समय के लिए डेरिवेटिव के समान क्रम होने के तथ्य का परिणाम है। फिजिकल स्पिन 1/2 कण जिन्हें रैखिक गेज डायराक समीकरण द्वारा वर्णित नहीं किया जा सकता है, द्वारा विस्तारित गेज क्लेन-गॉर्डन समीकरण को संतुष्ट करते हैं g e/4 σ^μν F_μν अवधि के अनुसार,:$\left[\,\left(\partial ^{\mu }\,u+i\,e\,A^{\mu }\right)\,\left(\partial _{\mu }+i\,e\,A_{\mu }\right)+g\,{\frac {e}{\,4\,}}\,\sigma ^{\mu \nu }\,F_{\mu \nu }+m^{2}\,\right]\;\psi \;=\;0~,\quad g\neq 2~.$ यहाँ, 1/2σ^μν और F^μν Dirac अंतरिक्ष में लोरेंत्ज़ समूह जनरेटर और क्रमशः विद्युत चुम्बकीय टेंसर के लिए खड़ा है, जबकि A^μ विद्युत चुम्बकीय चार-विभव है। ऐसे कण के लिए एक उदाहरण, स्पिन है 1/2 स्पिन का साथी 3/2 में D^(½,1) ⊕ D^(1,½) लोरेंत्ज़ समूह का प्रतिनिधित्व सिद्धांत। इस कण की विशेषता दिखाई गई है g = −+2/3 और फलस्वरूप वास्तव में द्विघात फ़र्मियन के रूप में व्यवहार करने के लिए।

एक नाभिक के लिए

जाइरोमैग्नेटिक अनुपात का संकेत, γ, अग्रगमन की भावना निर्धारित करता है। जबकि चुंबकीय क्षण (काले तीर) के दोनों मामलों के लिए समान उन्मुख होते हैं γ, पुरस्सरण विपरीत दिशाओं में है। स्पिन और चुंबकीय क्षण एक ही दिशा में होते हैं γ > 0 (प्रोटॉन के लिए)।

प्रोटॉन, न्यूट्रॉन, और कई नाभिक परमाणु स्पिन ले जाते हैं, जो ऊपर के रूप में जाइरोमैग्नेटिक अनुपात को जन्म देता है। सादगी और स्थिरता के लिए अनुपात पारंपरिक रूप से प्रोटॉन द्रव्यमान और आवेश के संदर्भ में लिखा जाता है, यहां तक ​​कि न्यूट्रॉन और अन्य नाभिकों के लिए भी। सूत्र है:

$\gamma _{\rm {n}}={\frac {e}{\,2m_{p}\,}}\,g_{\rm {n}}=g_{\rm {n}}\,{\frac {\,\mu _{\mathrm {N} }\,}{\hbar }}~,$

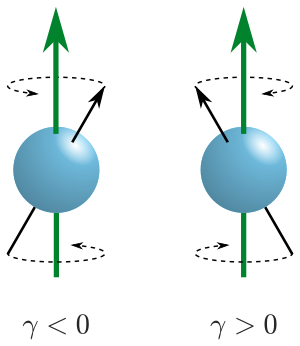
कहाँ $\mu _{\mathrm {N} }$ परमाणु मैग्नेटन है, और $g_{\rm {n}}$ जी-कारक (भौतिकी) है |g-प्रश्न में नाभिक या नाभिक का कारक। के अनुपात $\,{\frac {\gamma _{n}}{\,2\pi \,g_{\rm {n}}\,}}\,,$ के बराबर $\mu _{\mathrm {N} }/h$, 7.622593285(47) मेगाहर्ट्ज/टी है। नाभिक का जाइरोमैग्नेटिक अनुपात परमाणु चुंबकीय अनुनाद (NMR) और चुंबकीय अनुनाद इमेजिंग (MRI) में भूमिका निभाता है। ये प्रक्रियाएं इस तथ्य पर भरोसा करती हैं कि परमाणु स्पिन के कारण थोक चुंबकीयकरण एक चुंबकीय क्षेत्र में लार्मर आवृत्ति नामक दर से आगे बढ़ता है, जो कि चुंबकीय क्षेत्र की ताकत के साथ जाइरोमैग्नेटिक अनुपात का उत्पाद है। इस घटना के साथ, का संकेत γ पुरस्सरण का अर्थ (दक्षिणावर्त बनाम वामावर्त) निर्धारित करता है।

सबसे आम नाभिक जैसे ¹एच और ¹³C का धनात्मक जाइरोमैग्नेटिक अनुपात है। कुछ सामान्य नाभिकों के अनुमानित मान नीचे तालिका में दिए गए हैं।

Nucleus	$\gamma _{n}$ (106 rad⋅s−1⋅T−1)	$\gamma _{n}/(2\pi )$ (MHz⋅T−1)
1H	267.52218744(11)	42.577478518(18)
1H (in H2O)	267.5153151(29)	42.57638474(46)
2H	41.065	6.536
3H	285.3508	45.415
3He	−203.7894569(24)	−32.43409942(38)
7Li	103.962	16.546
13C	67.2828	10.7084
14N	19.331	3.077
15N	−27.116	−4.316
17O	−36.264	−5.772
19F	251.815	40.078
23Na	70.761	11.262
27Al	69.763	11.103
29Si	−53.190	−8.465
31P	108.291	17.235
57Fe	8.681	1.382
63Cu	71.118	11.319
67Zn	16.767	2.669
129Xe	−73.997	−11.777

लार्मर पुरस्सरण

Main article: Larmor precession

किसी बाहरी चुंबकीय क्षेत्र में रखे जाने पर एक स्थिर जाइरोमैग्नेटिक अनुपात के साथ कोई भी मुक्त प्रणाली, जैसे कि आवेशों की एक कठोर प्रणाली, एक परमाणु नाभिक, या एक इलेक्ट्रॉनB (टेस्ला में मापा गया) जो अपने चुंबकीय क्षण के साथ संरेखित नहीं है, एक आवृत्ति पर अग्रगमन होगा f (हेटर्स में मापा जाता है), जो बाहरी क्षेत्र के समानुपाती होता है:

$f={\frac {\gamma }{2\pi }}B.$

इस कारण से, के मान γ/ 2 π , हर्ट्ज़ प्रति टेस्ला (यूनिट) (Hz/T) की इकाइयों में, इसके बजाय अक्सर उद्धृत किया जाता है γ.

अनुमानी व्युत्पत्ति

इस संबंध की व्युत्पत्ति इस प्रकार है: पहले हमें यह सिद्ध करना होगा कि एक चुंबकीय आघूर्ण के अधीन होने से उत्पन्न बलाघूर्ण $\mathbf {m}$ एक चुंबकीय क्षेत्र के लिए $\mathbf {B}$ है

 $\,{\boldsymbol {\mathrm {T} }}=\mathbf {m} \times \mathbf {B} \,.$ स्थिर विद्युत और चुंबकीय क्षेत्रों के कार्यात्मक रूप की पहचान ने चुंबकीय द्विध्रुवीय क्षण के परिमाण को समान रूप से परिभाषित करने के लिए प्रेरित किया है $m=I\pi r^{2}$, या निम्नलिखित तरीके से, क्षण का अनुकरण करना{{math|p}एक विद्युत द्विध्रुव का }: चुंबकीय द्विध्रुव को काल्पनिक चुंबकीय आवेशों के साथ कम्पास की सुई द्वारा दर्शाया जा सकता है $\pm q_{\rm {m}}$ दो ध्रुवों पर और ध्रुवों के बीच सदिश दूरी $\mathbf {d}$ पृथ्वी के चुंबकीय क्षेत्र के प्रभाव में $\,\mathbf {B} \,.$ शास्त्रीय यांत्रिकी द्वारा इस सुई पर बलाघूर्ण होता है $\,{\boldsymbol {\mathrm {T} }}=q_{\rm {m}}(\mathbf {d} \times \mathbf {B} )\,.$ लेकिन जैसा कि पहले कहा गया है $\,q_{\rm {m}}\mathbf {d} =I\pi r^{2}{\hat {\mathbf {d} }}=\mathbf {m} \,,$ इसलिए वांछित सूत्र सामने आता है। ${\hat {\mathbf {d} }}$ इकाई दूरी वेक्टर है।

व्युत्पत्ति में हमारे द्वारा उपयोग किए जाने वाले कताई इलेक्ट्रॉन के मॉडल में जाइरोस्कोप के साथ एक स्पष्ट सादृश्य है। किसी भी घूर्णन पिंड के लिए कोणीय गति के परिवर्तन की दर $\,\mathbf {J} \,$ लागू बल आघूर्ण के बराबर होता है $\mathbf {T}$:

${\frac {d\mathbf {J} }{dt}}=\mathbf {T} ~.$

एक उदाहरण के रूप में जाइरोस्कोप के पुरस्सरण पर ध्यान दें। पृथ्वी का गुरुत्वाकर्षण आकर्षण जाइरोस्कोप पर ऊर्ध्वाधर दिशा में एक बल या टॉर्क लागू करता है, और जाइरोस्कोप की धुरी के साथ कोणीय गति सदिश धुरी के माध्यम से एक ऊर्ध्वाधर रेखा के बारे में धीरे-धीरे घूमता है। जाइरोस्कोप के स्थान पर अक्ष के चारों ओर घूमने वाले एक गोले की कल्पना करें और जाइरोस्कोप की धुरी पर इसके केंद्र के साथ, और जाइरोस्कोप की धुरी के साथ दो विपरीत दिशा वाले वैक्टर दोनों गोले के केंद्र में उत्पन्न हुए, ऊपर की ओर $\mathbf {J}$ और नीचे $\mathbf {m} .$ गुरुत्वाकर्षण को चुंबकीय प्रवाह घनत्व से बदलें

$\,\mathbf {B} ~.$

${\frac {\,\operatorname {d} \mathbf {J} \,}{\,\operatorname {d} t\,}}$ तीर के पाइक के रैखिक वेग का प्रतिनिधित्व करता है $\,\mathbf {J} \,$ एक वृत्त के साथ जिसकी त्रिज्या है $\,J\sin {\phi }\,,$ कहाँ $\,\phi \,$ के बीच का कोण है $\,\mathbf {J} \,$ और लंबवत। इसलिए स्पिन के घूर्णन का कोणीय वेग है

$\omega =2\pi \,f={\frac {1}{\,J\,\sin {\phi }\,}}\,\left|{\frac {\,{\rm {{d}\,\mathbf {J} \,}}}{\,{\rm {{d}\,t\,}}}}\right|={\frac {\,\left|\mathbf {T} \right|\,}{\,J\,\sin {\phi }\,}}={\frac {\,\left|\mathbf {m} \times \mathbf {B} \right|\,}{\,J\,\sin {\phi }\,}}={\frac {\,m\,B\sin {\phi }\,}{\,J\,\sin {\phi }\,}}={\frac {\,m\,B\,}{J}}=\gamma \,B~.$

फलस्वरूप, $f={\frac {\gamma }{\,2\pi \,}}\,B~.\quad {\text{q.e.d.}}$ यह संबंध दो समतुल्य शब्दों के बीच एक स्पष्ट विरोधाभास की भी व्याख्या करता है, जाइरोमैग्नेटिक अनुपात बनाम मैग्नेटोग्यरिक अनुपात: जबकि यह एक चुंबकीय गुण (अर्थात चुंबकीय क्षण) का एक 'गाइरिक' (घूर्णी, से) का अनुपात है। Greek: γύρος, टर्न ) संपत्ति (यानी कोणीय गति), यह एक ही समय में, कोणीय आवृत्ति (एक अन्य gyric संपत्ति) के बीच का अनुपात भी है। ω = 2 π f और चुंबकीय क्षेत्र।

कोणीय पुरस्सरण आवृत्ति का एक महत्वपूर्ण भौतिक अर्थ है: यह साइक्लोट्रॉन अनुनाद है, जब हम एक उच्च आवृत्ति विद्युत चुम्बकीय क्षेत्र को अध्यारोपित करते हैं, तो एक आयनित प्लाज़्मा की अनुनाद आवृत्ति एक स्थिर परिमित चुंबकीय क्षेत्र के प्रभाव में होती है।

यह भी देखें

• चार्ज-टू-मास अनुपात
• रासायनिक पारी
• लांडे जी-फैक्टर|लांडे g--कारक
• लार्मर समीकरण
• प्रोटॉन जाइरोमैग्नेटिक अनुपात