गैर-यादृच्छिक दो-तरल मॉडल

क्लोरोफॉर्म और मेथनॉल प्लस एनआरटीएल के मिश्रण का वाष्प-तरल संतुलन फिट और विभिन्न दबावों के लिए एक्सट्रपलेशन

गैर-यादृच्छिक दो-तरल मॉडल (संक्षिप्त एनआरटीएल मॉडल) एक सक्रियता गुणांक मॉडल है जो सक्रियता गुणांकों $\gamma _{i}$ को ग्रामअणु अंश $x_{i}$के साथ एक यौगिक को तरल कला में परस्पर संबंधित करता है। कला संतुलन की गणना करने के लिए प्रायः इसे रसायन इंजीनियरिंग के क्षेत्र में लागू किया जाता है। एनआरटीएल की अवधारणा विल्सन की परिकल्पना पर आधारित है कि एक अणु के आसपास की स्थानीय सांद्रता थोक सांद्रता से भिन्न होती है। यह अंतर केंद्रीय अणु अपनी तरह के अणुओं $U_{ii}$ और वह दूसरी तरह के अणुओं के साथ $U_{ij}$ के साथ परस्पर क्रिया ऊर्जा के बीच अंतर के कारण है। ऊर्जा अंतर भी स्थानीय आणविक स्तर पर एक गैर-यादृच्छिकता का परिचय देता है। एनआरटीएल मॉडल तथाकथित स्थानीय-रचना मॉडल से संबंधित है। इस प्रकार के अन्य मॉडल विल्सन मॉडल, यूएन आईक्यूयूएसी मॉडल और समूह योगदान मॉडल यूएनआईएफएसी हैं। ये स्थानीय-रचना मॉडल वास्तविक मिश्रण के लिए एक-द्रव मॉडल के सन्दर्भ में ऊष्मागतिक रूप से सुसंगत नहीं हैं, इस धारणा के कारण कि अणु i के आसपास की स्थानीय संरचना अणु j के आसपास की स्थानीय संरचना से स्वतंत्र है। यह धारणा सत्य नहीं है, जैसा कि 1976 में फ्लेमर द्वारा दिखाया गया था। हालांकि, यदि एक काल्पनिक दो-तरल मॉडल का उपयोग किया जाता है तो वे संगत होते हैं।

व्युत्पत्ति

विल्सन (1964) की तरह, रेनॉन और प्रुस्निट्ज़ (1968) ने स्थानीय रचना सिद्धांत के साथ प्रारम्भिक शुरुआत की, लेकिन विल्सन के रूप में फ्लोरी-हगिंस आयतनमितीय अभिव्यक्ति का उपयोग करने के अतिरिक्त, उन्होंने स्थानीय रचनाओं का अनुसरण किया,

${\frac {x_{21}}{x_{11}}}={\frac {x_{2}}{x_{1}}}{\frac {\exp(-\alpha _{21}g_{21}/RT)}{\exp(-\alpha _{11}g_{11}/RT)}}$

तब एक नए गैर-यादृच्छिकता प्राचल निरूपक α के साथ अतिरिक्त गिब्स मुक्त ऊर्जा होना निर्धारित किया गया था,

${\frac {G^{ex}}{RT}}=\sum _{i}^{N}x_{i}{\frac {\sum _{j}^{N}\tau _{ji}G_{ji}x_{j}}{\sum _{k}^{N}G_{ki}x_{k}}}$.

विल्सन के समीकरण के विपरीत, यह आंशिक रूप से गलत मिश्रण की पूर्वानुमान धारणा कर सकता है। ऊर्जा अंतर भी स्थानीय आणविक स्तर पर एक गैर-यादृच्छिकता का परिचय देता है। हालांकि, वोहल के विस्तार की तरह क्रॉस टर्म $H^{\text{ex}}$, $G^{\text{ex}}$ के अतिरिक्त अधिक उपयुक्त है, और प्रयोगात्मक डेटा सदैव तीन सार्थक मूल्यों को प्राप्त करने के लिए पर्याप्त रूप से प्रचुर मात्रा में नहीं होता है, इसलिए बाद में विल्सन के समीकरण को आंशिक मिश्रणीयता तक विस्तारित करने का प्रयास किया गया (या विल्सन के विभिन्न आकार के अणुओं के लिए गैर-यादृच्छिक मिश्रण के लिए गुगेनहाइम के अर्ध-रासायनिक सिद्धांत का विस्तार करने के लिए) अंततः यूएनआईक्यूयूएसी जैसे भिन्नरूपों का उत्पादन किया जाता है।

बाइनरी मिश्रण के लिए समीकरण

बाइनरी मिश्रण के लिए निम्नलिखित फलन का उपयोग किया जाता है:

$\left\{{\begin{matrix}\ln \ \gamma _{1}=x_{2}^{2}\left[\tau _{21}\left({\frac {G_{21}}{x_{1}+x_{2}G_{21}}}\right)^{2}+{\frac {\tau _{12}G_{12}}{(x_{2}+x_{1}G_{12})^{2}}}\right]\\\\\ln \ \gamma _{2}=x_{1}^{2}\left[\tau _{12}\left({\frac {G_{12}}{x_{2}+x_{1}G_{12}}}\right)^{2}+{\frac {\tau _{21}G_{21}}{(x_{1}+x_{2}G_{21})^{2}}}\right]\end{matrix}}\right.$

साथ

$\left\{{\begin{matrix}\ln \ G_{12}=-\alpha _{12}\ \tau _{12}\\\ln \ G_{21}=-\alpha _{21}\ \tau _{21}\end{matrix}}\right.$

यहाँ, $\tau _{12}$ और $\tau _{21}$ विराम रहित अन्योन्यक्रिया प्राचल निरूपक हैं, जो अन्योन्यक्रिया ऊर्जा प्राचल निरूपक $\Delta g_{12}$ और $\Delta g_{21}$ से संबंधित हैं:

$\left\{{\begin{matrix}\tau _{12}={\frac {\Delta g_{12}}{RT}}={\frac {U_{12}-U_{22}}{RT}}\\\tau _{21}={\frac {\Delta g_{21}}{RT}}={\frac {U_{21}-U_{11}}{RT}}\end{matrix}}\right.$

यहाँ R गैस स्थिरांक है और T पूर्ण तापमान है, और U_ijआणविक सतह i और j के बीच की ऊर्जा है। U_ii वाष्पीकरण की ऊर्जा है। यहां U_ij U_jiके बराबर होना चाहिए, लेकिन $\Delta g_{ij}$ के बराबर $\Delta g_{ji}$ आवश्यक नहीं है।

प्राचल निरूपक $\alpha _{12}$ और $\alpha _{21}$ तथाकथित गैर-यादृच्छिकता प्राचल निरूपक हैं, जिसके लिए सामान्यतः $\alpha _{12}$ के बराबर $\alpha _{21}$ सेट किया गया है। एक तरल के लिए, जिसमें केंद्र अणु के आसपास स्थानीय वितरण यादृच्छिक है, प्राचल निरूपक $\alpha _{12}=0$. उस स्थिति में समीकरण एक-प्राचल निरूपक मार्ग्यूल्स सक्रियता मॉडल में कम हो जाते हैं:

$\left\{{\begin{matrix}\ln \ \gamma _{1}=x_{2}^{2}\left[\tau _{21}+\tau _{12}\right]=Ax_{2}^{2}\\\ln \ \gamma _{2}=x_{1}^{2}\left[\tau _{12}+\tau _{21}\right]=Ax_{1}^{2}\end{matrix}}\right.$

व्यवहार में, $\alpha _{12}$ 0.2, 0.3 या 0.48 पर सेट है। बाद वाला मूल्य प्रायः जलीय प्रणालियों के लिए उपयोग किया जाता है। उच्च मूल्य हाइड्रोजन बंधों के कारण होने वाली क्रमबद्ध संरचना को दर्शाता है। ऊर्जा अंतर भी स्थानीय आणविक स्तर पर एक गैर-यादृच्छिकता का परिचय देता है। हालांकि, तरल-तरल संतुलन के विवरण में गलत तरल-तरल विवरण से बचने के लिए गैर-यादृच्छिकता प्राचल निरूपक 0.2 पर सेट किया गया है। कुछ मामलों में सेटिंग द्वारा एक बेहतर कला संतुलन विवरण $\alpha _{12}=-1$ प्राप्त किया जाता है, हालाँकि यह गणितीय समाधान भौतिक दृष्टिकोण से असंभव है, क्योंकि कोई भी प्रणाली यादृच्छिक से अधिक ($\alpha _{12}$ =0) यादृच्छिक नहीं हो सकती है, अतिरिक्त गैर-यादृच्छिकता मापदंडों के कारण सामान्य रूप से एनआरटीएल अन्य सक्रियता मॉडल की तुलना में कला संतुलन के विवरण में अधिक लचीलापन प्रदान करता है। हालाँकि, व्यवहार में यह लचीलापन कम हो जाता है ताकि प्रतिगामी डेटा की सीमा के बाहर गलत संतुलन विवरण से बचा जा सके।

सीमित सक्रियता गुणांक, जिसे अनंत कमजोर पड़ने पर सक्रियता गुणांक के रूप में भी जाना जाता है, की गणना निम्न द्वारा की जाती है:

$\left\{{\begin{matrix}\ln \ \gamma _{1}^{\infty }=\left[\tau _{21}+\tau _{12}\exp {(-\alpha _{12}\ \tau _{12})}\right]\\\ln \ \gamma _{2}^{\infty }=\left[\tau _{12}+\tau _{21}\exp {(-\alpha _{12}\ \tau _{21})}\right]\end{matrix}}\right.$

निर्दिष्ट मान बताते हैं कि $\alpha _{12}=0$ पर सीमित सक्रियता गुणांक बराबर हैं। यह स्थिति समान आकार के, लेकिन विभिन्न ध्रुवों के अणुओं के लिए होती है।
यह इस तथ्य को भी दर्शाता है, क्योंकि तीन प्राचल निरूपक उपलब्ध हैं, और समाधान के कई सेट संभव हैं।

सामान्य समीकरण

इसके लिए सामान्य समीकरण $\ln(\gamma _{i})$ प्रजातियों के लिए $i$ के मिश्रण में $n$ घटक है:

$\ln(\gamma _{i})={\frac {\displaystyle \sum _{j=1}^{n}{x_{j}\tau _{ji}G_{ji}}}{\displaystyle \sum _{k=1}^{n}{x_{k}G_{ki}}}}+\sum _{j=1}^{n}{\frac {x_{j}G_{ij}}{\displaystyle \sum _{k=1}^{n}{x_{k}G_{kj}}}}{\left({\tau _{ij}-{\frac {\displaystyle \sum _{m=1}^{n}{x_{m}\tau _{mj}G_{mj}}}{\displaystyle \sum _{k=1}^{n}{x_{k}G_{kj}}}}}\right)}$

इसके साथ

$G_{ij}=\exp \left({-\alpha _{ij}\tau _{ij}}\right)$

$\alpha _{ij}=\alpha _{ij_{0}}+\alpha _{ij_{1}}T$

$\tau _{i,j}=A_{ij}+{\frac {B_{ij}}{T}}+{\frac {C_{ij}}{T^{2}}}+D_{ij}\ln {\left({T}\right)}+E_{ij}T^{F_{ij}}$

के लिए कई अलग-अलग समीकरण रूप $\alpha _{ij}$ और $\tau _{ij}$ हैं, जिनमें से सबसे सामान्य समीकरण ऊपर दिखाए गए हैं।

तापमान पर निर्भर पैरामीटर

एक बड़े तापमान सिद्धांत पर कला संतुलन का वर्णन करने के लिए (अर्थात 50 K से बड़ा) अंतःक्रियात्मक प्राचल निरूपक को तापमान पर निर्भर करना पड़ता है।

इसमें दो स्वरूपों का प्रायः उपयोग किया जाता है। इस प्रकार विस्तारित एंटोनी समीकरण प्रारूप:

$\tau _{ij}=f(T)=a_{ij}+{\frac {b_{ij}}{T}}+c_{ij}\ \ln \ T+d_{ij}T$

यहाँ लघुगणकीय और रैखिक शब्दों का उपयोग मुख्य रूप से तरल-तरल संतुलन (गलतपन अंतर) के विवरण में किया जाता है।

दूसरा प्रारूप एक दूसरे क्रम बहुपद प्रारूप के समान है:

$\Delta g_{ij}=f(T)=a_{ij}+b_{ij}\cdot T+c_{ij}T^{2}$

प्राचल निरूपक निर्धारण

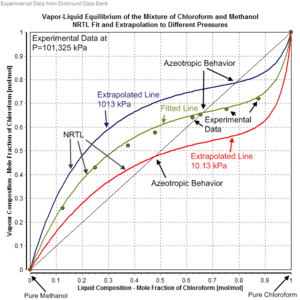
एनआरटीएल मापदंडों को सक्रियता गुणांकों के लिए फिट किया जाता है जो प्रायोगिक रूप से निर्धारित कला संतुलन डेटा (वाष्प-तरल, तरल-तरल, ठोस-तरल) के साथ-साथ मिश्रण के ताप से प्राप्त किए गए हैं। प्रायोगिक डेटा का स्रोत प्रायः डॉर्टमुंड डाटा बैंक जैसे तथ्यात्मक डेटा बैंक होते हैं। अन्य विकल्प प्रत्यक्ष प्रयोगात्मक फलन और यूएनआईएफएसी और इसी तरह के मॉडल के साथ अनुमानित सक्रियता गुणांक हैं।

उल्लेखनीय है कि एक ही तरल मिश्रण के लिए कई एनआरटीएल प्राचल निरूपक सेट उपस्थित हो सकते हैं। उपयोग करने के लिए निर्धारित एनआरटीएल प्राचल निरूपक कला संतुलन (अर्थात ठोस-तरल (एसएल), तरल-तरल (एलएल), वाष्प-तरल (वीएल)) के प्रकार पर निर्भर करता है। वाष्प-तरल संतुलन के विवरण के स्थिति में यह जानना आवश्यक है कि शुद्ध घटकों के संतृप्त वाष्प दबाव का उपयोग किया गया था और कई प्रयोगों द्वारा यह भी जानने का प्रयास किया गया कि क्या गैस कला को आदर्श या वास्तविक गैस के रूप में माना गया था। ऊर्जा अंतर भी स्थानीय आणविक स्तर पर एक गैर-यादृच्छिकता का परिचय देता है। सटीक संतृप्त वाष्प दबाव मान निर्धारण या स्थिरक्वाथी के विवरण में महत्वपूर्ण हैं। गैस फुगसिटी गुणांक ज्यादातर एकता (आदर्श गैस धारणा) पर सेट होते हैं, लेकिन उच्च दबाव (अर्थात > 10 बार) पर वाष्प-तरल संतुलन के लिए वास्तविक गैस विवरण के लिए गैस फ्यूगेस गुणांक की गणना करने के लिए अवस्था के एक समीकरण की आवश्यकता होती है।

एलएलई डेटा से एनआरटीएल मापदंडों का निर्धारण वीएलई डेटा से प्राचल निरूपक प्रतिगमन की तुलना में अधिक जटिल है क्योंकि इसमें निष्क्रिय समीकरणों को हल करना सम्मिलित है जो अत्यधिक गैर-रैखिक हैं। ऊर्जा अंतर भी स्थानीय आणविक स्तर पर एक गैर-यादृच्छिकता का परिचय देता है। इसके अतिरिक्त, डेटा प्रतिगमन में घटकों के सक्रियता मूल्यों पर ज्ञान की कमी के कारण एलएलई से प्राप्त प्राचल निरूपक सदैव घटकों की वास्तविक सक्रियता का प्रतिनिधित्व नहीं कर सकते हैं। इस कारण से रचनाओं की पूरी श्रृंखला (बाइनरी सबसिस्टम, प्रायोगिक और परिकलित असत्य-रेखाएं, हेस्सियन मैट्रिक्स, सहित आदि) में प्राप्त मापदंडों की स्थिरता की पुष्टि करना आवश्यक है।