समाकलित बहुभुज

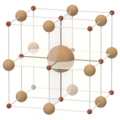
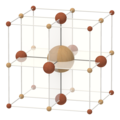
घन	क्यूबोक्टहेड्रॉन	अष्टफलक	छिन्न अष्टफलक
(±1, ±1, ±1)	(0, ±1, ±1)	(0, 0, ±1)	(0, ±1, ±2)
त्रि-आयामों चार पूर्णांक पॉलिटोप

ज्यामिति और बहुभुज संख्यात्मक विज्ञान में, पूर्णांकीय बहुभुज एक ऐसा अभिन्न बहुभुज होता है जिसके सभी शीर्षों के, कार्तेसीय समन्वयी निर्देशांक होते हैं। अर्थात, यह एक ऐसा बहुभुज है जो अपनी पूर्णांकीय बिंदुओं के अवमुख समावरक के समान होता है।पूर्णांकीय बहुभुजों को लैटिस बहुभुज या जेड-बहुभुज भी कहा जाता है। दो- और त्रि-आयामी पूर्णांकीय बहुभुजो के विशेष परिप्रेक्ष्य को क्रमशः पॉलीटोप्स के अतिरिक्त बहुभुज या बहुकोणीय आकृति कहा जा सकता है।

उदाहरण

किसी एन-आयामी नियमित संकेतन को, $\mathbb {R} ^{n+1}$ में एक पूर्णांकीय बहुभुज के रूप में प्रस्तुत किया जा सकता है, जहां पूर्णांकीय बिंदुओं का एक आधार एक है और बाकी सभी बिन्दुओ का आधार शून्य हैं। एक और महत्वपूर्ण प्रकार का पूर्णांकीय सिम्प्लेक्स, विषमकोण आयत, को उन पूर्णांकीय बिंदुओं के अवमुख समावरक द्वारा निर्मित किया जा सकता है, जिनके निर्देशांकों का प्रारंभ कुछ संयुक्त पूर्णांकों के साथ होती है जिसके उपरांत शेष सभी निर्देशांक शून्य होते हैं। $\mathbb {R} ^{n}$ में n-आयामीक इकाई घन के कोण उन सभी पूर्णांक बिंदुओं से मिलते हैं जिनके निर्देशांक शून्य या एक होतें हैं।एक पर्म्युटाहेड्रन के कोण उस सदिश $(1,2,...,n)$. पर सभी संभव क्रमचयों को लागू करके प्राप्त किए जाने वाले निर्देशांक होते हैं। लोडे के उच्चतम वास्तविकीकरण में एक असोसिएहेड्रन भी एक पूर्णांक पॉलिटोप और पर्म्युटाहेड्रन का विकर्ण होता है।

अनुकूलन में

रैखिक प्रोग्रामिंग और गणितीय अनुकूलन में संबंधित समस्याओं के संदर्भ में, उत्तल पॉलीटोप्स को अक्सर रैखिक असमानता की एक प्रणाली द्वारा वर्णित किया जाता है, जो कि उनके बिंदुओं का पालन करना चाहिए। जब एक पॉलीटॉप अभिन्न होता है, तो दी गई असमानताओं की प्रणाली के लिए पूर्णांक प्रोग्रामिंग समस्याओं को हल करने के लिए रैखिक प्रोग्रामिंग का उपयोग किया जा सकता है, एक समस्या जो अन्यथा अधिक कठिन हो सकती है।

संयोजी इष्टतमीकरण समस्याओं से उत्पन्न होने वाले कुछ बहुफलक स्वचालित रूप से अभिन्न हैं। उदाहरण के लिए, यह किसी भी आंशिक रूप से ऑर्डर किए गए सेट के पॉलीटॉप ऑर्डर करें के बारे में सच है, सेट में तुलनीय तत्वों के अनुरूप निर्देशांक के बीच जोड़ीदार असमानताओं द्वारा परिभाषित एक पॉलीटोप। संयोजी अनुकूलन में एक अन्य प्रसिद्ध पोलीटोप मेल खाने वाला पोलीटोप है। स्पष्ट रूप से, कोई मैचिंग को एल्गोरिथम से ढूंढना चाहता है और एक तकनीक रैखिक प्रोग्रामिंग है। रेखीय कार्यक्रम द्वारा वर्णित पॉलीटोप प्रति शीर्ष पर लिए गए किनारों के योग को द्विदलीय रेखांकन के मामले में अभिन्न है, अर्थात यह मिलान वाले पॉलीटोप का सटीक वर्णन करता है, जबकि सामान्य रेखांकन के लिए यह गैर-अभिन्न है। इसलिए, द्विदलीय रेखांकन के लिए, यह एक वैध मिलान (ग्राफ सिद्धांत) प्राप्त करने के लिए संबंधित रैखिक कार्यक्रम को हल करने के लिए पर्याप्त है। सामान्य रेखांकन के लिए, हालांकि, मेल खाने वाले पॉलीटॉप के दो अन्य लक्षण हैं, जिनमें से एक कोने के विषम उपसमुच्चय के लिए ब्लॉसम असमानता का उपयोग करता है और इसलिए वैध मिलान प्राप्त करते हुए पूर्णांक कार्यक्रम को एक रेखीय कार्यक्रम में शिथिल करने की अनुमति देता है। ये विशेषताएँ ब्लॉसम एल्गोरिथम में और अधिक रुचि रखती हैं। एडमंड्स का प्रसिद्ध ब्लॉसम एल्गोरिथम सामान्य ग्राफ़ में ऐसे मिलानों को खोजने के लिए उपयोग किया जाता है।

कम्प्यूटेशनल जटिलता

रेखीय असमानताओं द्वारा वर्णित एक पॉलीटॉप के लिए, जब पॉलीटॉप गैर-अभिन्न होता है, तो कोई ऐसा शीर्ष ढूंढकर अपनी गैर-अभिन्नता साबित कर सकता है जिसका निर्देशांक पूर्णांक नहीं हैं। इस तरह के शीर्ष को असमानताओं के एक सबसेट को निर्दिष्ट करके संयुक्त रूप से वर्णित किया जा सकता है, जब रैखिक समीकरणों की एक प्रणाली में बदल दिया जाता है, तो एक अद्वितीय समाधान होता है, और यह सत्यापित करता है कि यह समाधान बिंदु अन्य सभी असमानताओं का पालन करता है। इसलिए, परीक्षण अभिन्नता समस्याओं की जटिलता वर्ग coNP से संबंधित है, जिसके लिए एक नकारात्मक उत्तर आसानी से सिद्ध किया जा सकता है। अधिक विशेष रूप से, यह coNP-पूर्ण है।

संबंधित वस्तुएं

एक अभिन्न पॉलीटॉप के कई महत्वपूर्ण गुण, इसकी मात्रा और वर्टिकल की संख्या सहित, इसके एहरहार्ट बहुपद द्वारा एन्कोड किए गए हैं।

इंटीग्रल पॉलीटॉप्स को प्रमुख रूप से टॉरिक किस्म के सिद्धांत में चित्रित किया गया है, जहां वे ध्रुवीकृत प्रोजेक्टिव टॉरिक किस्मों के अनुरूप हैं। उदाहरण के लिए, एक सिंप्लेक्स से संबंधित टोरिक किस्म एक प्रक्षेपण स्थान है। एक इकाई घन के अनुरूप टोरिक किस्म की सेग्रे एम्बेडिंग है $n$ प्रक्षेप्य रेखा का -गुना उत्पाद।

बीजगणितीय ज्यामिति में, जाली पॉलीटोप्स का एक महत्वपूर्ण उदाहरण जिसे न्यूटन पॉलीटोप्स कहा जाता है, एक बहुपद के संदर्भ में प्रत्येक चर के घातांक का प्रतिनिधित्व करने वाले वैक्टर के उत्तल पतवार हैं। उदाहरण के लिए, बहुपद $xy+2x^{2}+y^{5}+4$ चार पद हैं, $xy$ एक्सपोनेंट वेक्टर (1,1) के साथ, $2x^{2}$ एक्सपोनेंट वेक्टर (2,0) के साथ, $y^{5}$ एक्सपोनेंट वेक्टर (0,5) के साथ, और $4$ एक्सपोनेंट वेक्टर (0,0) के साथ। इसका न्यूटन पॉलीटॉप चार बिंदुओं (1,1), (2,0), (0,5), और (0,0) का उत्तल पतवार है। यह पतवार एक अभिन्न त्रिभुज है जिसमें बिंदु (1,1) त्रिकोण के आंतरिक और अन्य तीन बिंदु इसके शीर्ष के रूप में हैं।

यह भी देखें

• रीव टेट्राहेड्रॉन