परिक्षेपण (प्रकाशिकी)

This article is about प्रकाशिकी में तरंगों का फैलाव. For other uses, see फैलाव (बहुविकल्पी).

एक प्रसार प्रिज्म में, सामग्री प्रसार (एक तरंग दैर्ध्य -निर्भर अपवर्तक सूचकांक ) विभिन्न रंगों को अलग-अलग कोणों पर अपवर्तन का कारण बनता है, सफेद प्रकाश को स्पेक्ट्रम में विभाजित करता है।

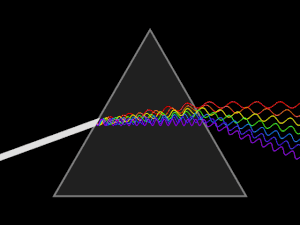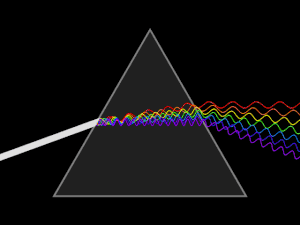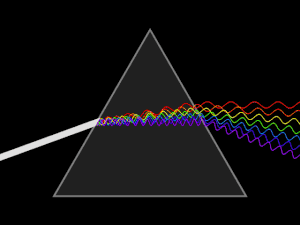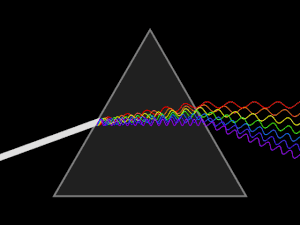
प्रकाशिकी में एमीसी डायरेक्ट-विज़न प्रिज्म PNr° के माध्यम से देखे गए कॉम्पैक्ट फ्लोरोसेंट लैंप का प्रकाश प्रसार प्रिज्म के माध्यम से देखा जाने वाला कॉम्पैक्ट फ्लोरोसेंट लैंप हैं।

प्रकाशिकी में सादृश्य द्वारा तरंग प्रसार से संबंधित भौतिकी की अन्य शाखाएं, प्रसार की वह घटना है जिसमें तरंग का चरण वेग उसकी आवृत्ति पर निर्भर करता है, कभी-कभी वर्णिक परिक्षेपण शब्द का प्रयोग विशेष रूप से प्रकाशिकी की विशिष्टता के लिए किया जाता है।

इस सामान्य गुण वाले माध्यम को प्रसार माध्यम (बहुवचन प्रसारित वाला मीडिया) कहा जा सकता है।

यद्यपि प्रकाश और अन्य विद्युत चुम्बकीय तरंगों का वर्णन करने के लिए प्रकाशिकी के क्षेत्र में शब्दों का उपयोग किया जाता है, उसी अर्थ में प्रसार किसी भी प्रकार की तरंग गति पर लागू हो सकता है जैसे ध्वनि और भूकंपीय तरंगों की स्थिति में ध्वनिक प्रसार, और गुरुत्वाकर्षण तरंगों (महासागर) में तरंग की हैं। प्रकाशिकी के भीतर प्रसार संचरण रेखाओं (जैसे समाक्षीय केबल में माइक्रोवेव ) या प्रकाशित तंतु में प्रकाश की तरंग के साथ दूरसंचार संकेतों की संपत्ति है। भौतिक रूप से, प्रसार अवशोषण के माध्यम से गतिज ऊर्जा के हानि में परिवर्तित हो जाता है।

प्रकाशिकी में प्रसार का महत्वपूर्ण और परिचित परिणाम प्रकाश के विभिन्न रंगों के अपवर्तन कोण में परिवर्तन है, जैसा कि प्रसार चश्मे द्वारा उत्पादित स्पेक्ट्रम और लेंस के रंगीन विपथन में देखा जाता है। इस प्रकार मिश्रित अक्रोमेटिक लेंस का प्रारूप जिसमें रंगीन विपथन को अधिक सीमा तक निरस्त कर दिया जाता है, इसके एब्बे नंबर द्वारा दिए गए ग्लास के प्रसार की मात्रा का उपयोग करता है, जहां कम एबे संख्या दृश्यमान स्पेक्ट्रम पर अधिक प्रसार के अनुरूप होती है। इस प्रकार दूरसंचार जैसे कुछ अनुप्रयोगों में, तरंग का निरपेक्ष चरण अधिकांशतः महत्वपूर्ण नहीं होता है, अपितु केवल तरंग पैकेट या तरंग का प्रसार होता है, उस स्थिति में कोई केवल आवृत्ति के साथ समूह वेग की विविधताओं में रुचि रखता है, तथाकथित समूह वेग प्रसार या समूह-वेग प्रसार सम्मिलित हैं।

आवृत्ति के कार्य के रूप में सभी सामान्य प्रेषक मीडिया क्षीणन (ट्रांसमिशन लंबाई के लिए सामान्यीकृत) में भी भिन्न होते हैं, जिससे क्षीणन विरूपण होता है, यह प्रसार नहीं है, चूंकि कभी-कभी सघनता से दूरी प्रतिबाधा संयोजन (उदाहरण के लिए केबल में क्रिम्प्ड सेगमेंट) पर प्रतिबिंब संकेत विरूपण उत्पन्न कर सकते हैं और संकेत बैंडविड्थ में देखे गए असंगत पारगमन समय को और बढ़ा सकते हैं।

उदाहरण

प्रसार का सबसे परिचित उदाहरण संभवतः इंद्रधनुष है, जिसमें प्रसार सफेद प्रकाश के विभिन्न तरंग दैर्ध्य (विभिन्न रंगों) के घटकों में स्थानिक पृथक्करण का कारण बनता है। चूंकि कई अन्य परिस्थितियों में भी प्रसार का प्रभाव पड़ता है: उदाहरण के लिए समूह वेग प्रसार तरंग (संकेत प्रोसेसिंग) को ऑप्टिकल फाइबर में प्रसारित करने का कारण बनता है, इस प्रकार लंबी दूरी पर इस प्रकार के संकेतों को इसके अतिरिक्त समूह-वेग प्रसार और गैर-रेखीय प्रभावों के बीच निरस्त करने से सॉलिटन तरंगें उत्पन्न होती हैं।

सामग्री और वेवगाइड प्रसार

सबसे अधिक बार रंगीन प्रसार वेवगाइड सामग्री प्रसार को संदर्भित करता है, अर्थात ऑप्टिकल आवृत्ति के साथ अपवर्तक सूचकांक में परिवर्तित करे देता हैं। चूंकि वेवगाइड में वेवगाइड प्रसार की घटना भी होती है, जिस स्थिति में संरचना में तरंग का चरण वेग संरचना की ज्यामिति के कारण इसकी आवृत्ति पर निर्भर करता है। इसके कारण सामान्यतः किसी भी अमानवीय संरचना (जैसे, फोटोनिक क्रिस्टल ) के माध्यम से प्रसार करने वाली तरंगों के लिए वेवगाइड प्रसार हो सकता है, संभवतः तरंगे किसी क्षेत्र तक ही सीमित हों या न हों। वेवगाइड में दोनों प्रकार के प्रसार सामान्यतः सम्मिलित होते हैं, चूंकि वे कठोरता से योगात्मक नहीं होते हैं। उदाहरण के लिए, फाइबर ऑप्टिक्स में सामग्री और वेवगाइड प्रसार तेजी से फाइबर-ऑप्टिक संचार के लिए महत्वपूर्ण शून्य-प्रसार तरंगदैर्ध्य का उत्पादन करने के लिए एक-दूसरे को प्रभावी ढंग से निरस्त कर सकते हैं।

प्रकाशिकी में सामग्री प्रसार

विभिन्न चश्मे के लिए अपवर्तक सूचकांक बनाम वैक्यूम तरंग दैर्ध्य की भिन्नता। दृश्य प्रकाश की तरंग दैर्ध्य ग्रे रंग में छायांकित होती है।

File:Spidergraph Dispersion.GIF

एक विशिष्ट बेस ग्लास (एन .) के औसत प्रसार पर चयनित ग्लास घटक परिवर्धन का प्रभाव_F λ = 486 एनएम (नीला), n . के लिए मान्य_C λ = 656 एनएम (लाल) के लिए मान्य)

ऑप्टिकल अनुप्रयोगों में सामग्री प्रसार वांछनीय या अवांछनीय प्रभाव हो सकता है। इस प्रकार कांच के प्रिज्म द्वारा प्रकाश के प्रसार का उपयोग स्पेक्ट्रोमीटर और स्पेक्ट्रोमाडोमीटर के निर्माण के लिए किया जाता है। चूंकि, लेंस में, प्रसार रंगीन विपथन का कारण बनता है, अवांछित प्रभाव जो सूक्ष्मदर्शी, दूरबीन और फोटोग्राफिक उद्देश्यों में प्रतिबिंबों को नीचा दिखा सकता है।

किसी दिए गए एकसमान माध्यम में तरंग का चरण वेग, v, द्वारा दिया जाता है

$v={\frac {c}{n}}$

जहाँ c निर्वात में प्रकाश की गति है और n माध्यम का अपवर्तनांक है।

सामान्यतः अपवर्तनांक प्रकाश की आवृत्ति f का कुछ कार्य होता है, इस प्रकार n = n(f), या वैकल्पिक रूप से, तरंग की तरंग दैर्ध्य n = n(λ) के संबंध में उपयोग किया जाता हैं। इस प्रकार किसी सामग्री के अपवर्तनांक की तरंगदैर्घ्य निर्भरता को सामान्यतः इसकी एब्बे संख्या या इसके गुणांकों द्वारा अनुभवजन्य सूत्र जैसे कि कॉची के समीकरण या सेलमीयर समीकरण द्वारा निर्धारित किया जाता है।

क्रेमर्स-क्रोनिग संबंधों के कारण, अपवर्तक सूचकांक के वास्तविक भाग की तरंग दैर्ध्य निर्भरता सामग्री अवशोषण (विद्युत चुम्बकीय विकिरण) से संबंधित है, जो अपवर्तक सूचकांक के काल्पनिक भाग द्वारा वर्णित है (जिसे अपवर्तक सूचकांक प्रसार और अवशोषण भी कहा जाता है।) इस प्रकार विशेष रूप से गैर-चुंबकीय सामग्रियों के लिए (पारगम्यता (विद्युत चुंबकत्व) या μ = चुंबकीय स्थिरांक या μ_{0e= n² − 1}) रैखिक प्रतिक्रिया फंक्शन जो क्रेमर्स-क्रोनिग संबंधों में प्रकट होता है, जो इसकी विद्युत संवेदनशीलता है।

प्रकाशिकी में प्रसार का सबसे अधिक देखा जाने वाला परिणाम विद्युतचुंबकीय स्पेक्ट्रम का पृथक्करण है, इस कारण दृश्य विकिरण (प्रकाश) त्रिकोणीय प्रिज्म (प्रकाशिकी) द्वारा ऑप्टिकल स्पेक्ट्रम में उपयोग किया जाता हैं। इस प्रकार स्नेल के नियम से यह देखा जा सकता है कि प्रिज्म में प्रकाश के अपवर्तन का कोण प्रिज्म सामग्री के अपवर्तनांक पर निर्भर करता है। चूंकि वह अपवर्तनांक तरंग दैर्ध्य के साथ परिवर्तित रहता है, इसलिए यह इस प्रकार है कि जिस कोण से प्रकाश अपवर्तित होता है वह तरंग दैर्ध्य के साथ भी भिन्न होता है, जिससे कोणीय प्रसार के रूप में ज्ञात रंगों का कोणीय पृथक्करण होता है।

इस दृश्य प्रकाश के लिए, अधिकांश पारदर्शी सामग्री (जैसे, वायु, चश्मा) के अपवर्तन सूचकांक n बढ़ते तरंग दैर्ध्य के साथ घटते हैं :

$1<n(\lambda _{\rm {red}})<n(\lambda _{\rm {yellow}})<n(\lambda _{\rm {blue}})\ ,$

या वैकल्पिक रूप से:

${\frac {dn}{d\lambda }}<0.$

इस स्थिति में, माध्यम को सामान्य प्रसार कहा जाता है। जबकि, यदि सूचकांक बढ़ती तरंग दैर्ध्य के साथ बढ़ता है (जो सामान्यतः पराबैंगनी में होता है), माध्यम को विषम प्रसार कहा जाता है।

वायु या वैक्यूम (~ 1 का सूचकांक) के साथ ऐसी सामग्री के इंटरफेस पर, स्नेल का नियम भविष्यवाणी करता है कि सतह के कोण पर कोण पर प्रकाश की घटना सामान्य कोण (sin θ/n) पर अपवर्तित होगी। इस प्रकार उच्च अपवर्तनांक वाला नीला प्रकाश, लाल प्रकाश की तुलना में अधिक मजबूती से विचलित होगी, जिसके परिणामस्वरूप प्रसिद्ध इंद्रधनुष पैटर्न बन जाता हैं।

समूह वेग प्रसार

काल्पनिक प्रसार माध्यम (k=w^2) में छोटी तरंग का समय विकास यह दर्शाता है कि लंबी तरंग दैर्ध्य घटक छोटी तरंग दैर्ध्य (धनात्मक जीवीडी) की तुलना में तेजी से यात्रा करते हैं, जिसके परिणामस्वरूप प्रसारित होती है और यह तरंग चौड़ी होती है।

तरंग दैर्ध्य पर चरण वेग में परिवर्तन का वर्णन करने के अलावा, कई अनुप्रयोगों में प्रसार का और अधिक गंभीर परिणाम समूह वेग प्रसार (जीवीडी) कहा जाता है। जबकि चरण वेग v को v = . के रूप में परिभाषित किया गया है c/n, यह केवल आवृत्ति घटक का वर्णन करता है। जब विभिन्न आवृत्ति घटकों को संयोजित किया जाता है, जैसे कि संकेत या तरंग पर विचार करते समय, अधिकांशतः समूह वेग में अधिक रुचि होती है जो उस गति का वर्णन करती है जिस पर तरंग (मॉड्यूलेशन) पर आरोपित सूचना पर प्रसारित होता है। इसके साथ में एनीमेशन में यह देखा जा सकता है कि तरंग स्वयं (नारंगी-भूरा) चरण वेग से यात्रा करती है जो कि काले इनवलप गति से बहुत तेज है जो समूह वेग से मेल खाती है। उदाहरण के लिए, यह तरंग संचार संकेत हो सकता है, और इसकी जानकारी केवल समूह वेग दर पर यात्रा करती है, भले ही इसमें तेज दर (चरण वेग) पर आगे बढ़ने वाले वेवफ्रंट सम्मिलित होती हैं।

समूह वेग की गणना अपवर्तनांक वक्र n(ω) या अधिक से सीधे वेवनंबर k = n/c से करना संभव है जहां रेडियन आवृत्ति ω=2πf है। जबकि चरण वेग के लिए व्यंजक v_p=ω/k है, समूह वेग को व्युत्पन्न का उपयोग करके व्यक्त किया जा सकता है: v_g= dω / dk या चरण वेग v_p के संदर्भ में,

${v_{g}}={\frac {v_{p}}{1-{\frac {\omega }{v_{p}}}{\frac {dv_{p}}{d\omega }}}}.$

जब प्रसार सम्मिलित होता है, तो न केवल समूह वेग चरण वेग के बराबर नहीं होगा, बल्कि सामान्यतः तरंगदैर्ध्य के साथ परिवर्तित रहता है। इसे समूह वेग प्रसार के रूप में जाना जाता है और प्रकाश की छोटी तरंग को चौड़ा करने का कारण बनता है, क्योंकि तरंग के भीतर विभिन्न आवृत्ति घटक विभिन्न वेगों पर यात्रा करते हैं। समूह वेग प्रसार को रेडियन आवृत्ति के संबंध में समूह वेग के व्युत्क्रम के व्युत्पन्न के रूप में निर्धारित किया जाता है जिसके परिणामस्वरूप समूह वेग प्रसार =d²k/dω² होता है।

यदि प्रकाश तरंग को धनात्मक समूह-वेग प्रसार वाली सामग्री के माध्यम से प्रचारित किया जाता है, तो छोटे तरंग दैर्ध्य घटक लंबे तरंग दैर्ध्य घटकों की तुलना में धीमी गति से यात्रा करते हैं। इसलिए तरंग को धनात्मक रूप से विचलित होती है, या समय के साथ आवृत्ति में वृद्धि होती है। दूसरी ओर, यदि तरंग ऋणात्मक समूह-वेग प्रसार वाली सामग्री के माध्यम से यात्रा करती है, तो छोटे तरंग दैर्ध्य घटक लंबे समय से अधिक तेजी से यात्रा करते हैं, और तरंग ऋणात्मक रूप से विचलित होती है, या समय के साथ आवृत्ति में कमी आती है।

ध्वनिक डोमेन में ऋणात्मक रूप से विचलित होने वाले संकेत का दैनिक उदाहरण वेल्डेड ट्रैक पर विकृतियों से संघट्ट होकर उत्पन्न होने वाली ट्रेन का है। इस ट्रेन के कारण होने वाली ध्वनि स्वयं आवेगी होती है, और हवा की तुलना में धातु की पटरियों में बहुत तेजी से यात्रा करती है, जिससे कि ट्रेन आने से पहले अच्छी तरह से सुनी जा सके। चूंकि दूर से इसे आवेगों के कारण के रूप में नहीं सुना जाता है, अपितु ट्रैक के कंपन मोड की जटिलता के कारण होने वाली गूंज के बीच विशिष्ट अवरोही विचलन की ओर जाता है। इस प्रकार समूह वेग प्रसार को सुना जा सकता है कि ध्वनियों की मात्रा आश्चर्यजनक रूप से लंबे समय तक, कई सेकंड तक श्रव्य रहती है।

समूह वेग प्रसार पैरामीटर:

$D={\frac {1}{c}}\,{\frac {dn}{d\lambda }}.$

अधिकांशतः जीवीडी को मापने के लिए प्रयोग किया जाता है, जो कि ऋणात्मक कारक के माध्यम से डी के समानुपाती होता है:

$D=-{\frac {2\pi c}{\lambda ^{2}}}\,{\frac {d^{2}k}{d\omega ^{2}}}.$

कुछ लेखकों के अनुसार माध्यम को निश्चित निर्वात तरंग दैर्ध्य के लिए सामान्य प्रसार/विसंगत प्रसार कहा जाता है। यदि अपवर्तन सूचकांक के दूसरे व्युत्पन्न की गणना λ₀ में की जाती है। इस प्रकार इसका मान धनात्मक/ऋणात्मक होता है, समान्य रूप से, यदि D(λ .)₀) ऋणात्मक/धनात्मक है। यह परिभाषा समूह वेग प्रसार से संबंधित है और इसे पिछले खंड में दिए गए के साथ भ्रमित नहीं होती हैं। इस कारण दो परिभाषाएँ सामान्य रूप से मेल नहीं खाती हैं, इसलिए पाठक को संदर्भ को समझना आवश्यक होता हैं।

प्रसार नियंत्रण

जीवीडी का परिणाम चाहे ऋणात्मक हो या धनात्मक, अंततः इ, तरंग का अस्थायी प्रसार करता है। यह ऑप्टिकल फाइबर पर आधारित ऑप्टिकल संचार प्रणालियों में प्रसार प्रबंधन को अत्यंत महत्वपूर्ण बनाता है, क्योंकि यदि प्रसार बहुत अधिक है, तो बिट-स्ट्रीम का प्रतिनिधित्व करने वाले तरंग का समूह समय में फैल जाएगा और विलय हो जाएगा, जिससे बिट-स्ट्रीम को समझ में नहीं आता हैं। यह फाइबर की लंबाई को सीमित करता है कि पुनर्जनन के बिना संकेत नीचे भेजा जा सकता है। इस समस्या का संभावित उत्तर ऑप्टिकल फाइबर को तरंग दैर्ध्य पर संकेत भेजना है जहां जीवीडी शून्य है (उदाहरण के लिए, सिलिका फाइबर में लगभग 1.3-1.5 माइक्रोन), इसलिए इस तरंग दैर्ध्य पर तरंग को प्रसार से कम से कम फैलता है। व्यवहार में, चूंकि, यह दृष्टिकोण हल करने की तुलना में अधिक समस्याओं का कारण बनता है क्योंकि शून्य जीवीडी अस्वीकार्य रूप से अन्य गैर-रेखीय प्रभावों (जैसे चार तरंग मिश्रण) को बढ़ाता है। अन्य संभावित विकल्प ऋणात्मक प्रसार के प्रभाव में सॉलिटॉन (प्रकाशिकी) तरंग का उपयोग करना है, ऑप्टिकल तरंग का रूप जो अपने आकार को स्वयं बनाए रखने के लिए गैर-रेखीय प्रकाशिकी प्रभाव का उपयोग करता है। चूंकि, सॉलिटॉन के पास व्यावहारिक समस्या है कि उन्हें तरंग में निश्चित शक्ति स्तर बनाए रखने की आवश्यकता होती है जिससे कि गैर-रेखीय प्रभाव सही शक्ति का होता हैं। इसके अतिरिक्त, वर्तमान समय में व्यवहार में उपयोग किया जाने वाले हल के लिए यह प्रसार क्षतिपूर्ति करता है, सामान्यतः फाइबर को विपरीत-चिह्न प्रसार के दूसरे फाइबर के साथ संयोजन करके जिससे कि प्रसार प्रभाव निरस्त हो जाए, इस प्रकार की क्षतिपूर्ति अंततः स्व-चरण मॉडुलन जैसे गैर-रेखीय प्रभावों द्वारा सीमित होती है, जो प्रसार के साथ परस्पर क्रिया करती है जिससे इसे पूर्ववत करना बहुत कठिन हो जाता है।

अल्ट्राशॉर्ट तरंग उत्पन्न करने वाले लेज़रों में प्रसार नियंत्रण भी महत्वपूर्ण है। लेजर द्वारा उत्सर्जित स्पंदों की अवधि निर्धारित करने में लेजर निर्माण का समग्र प्रसार प्रमुख कारक है। प्रिज्म (प्रकाशिकी) की जोड़ी को शुद्ध ऋणात्मक प्रसार उत्पन्न करने के लिए व्यवस्थित किया जा सकता है, जिसका उपयोग लेजर माध्यम के सामान्यतः धनात्मक प्रसार को संतुलित करने के लिए किया जा सकता है। विवर्तन झंझरी का उपयोग प्रसार प्रभाव उत्पन्न करने के लिए भी किया जा सकता है, इनका उपयोग अधिकांशतः उच्च-शक्ति वाले लेजर प्रवर्धक यूक्ति में किया जाता है। वर्तमान समय में प्रिज्म का विकल्प विकसित किया गया है: विचलित होने वाले दर्पण के रूप में जिसे उपयोग किया जाता हैं। यह दर्पण मुख्यतः लेपित होते हैं जिससे कि विभिन्न तरंग दैर्ध्य में अलग-अलग प्रवेश लंबाई हो, और इसलिए अलग-अलग समूह देरी होती हैं। इस प्रकार शुद्ध ऋणात्मक प्रसार प्राप्त करने के लिए लेप चढ़ी हुई इन परतों को संयोजित किया जाता है।

वेवगाइड में

वेवगाइड्स उनकी ज्यामिति (केवल उनकी भौतिक संरचना के अतिरिक्त) के कारण अत्यधिक प्रसार वाले होते हैं। ऑप्टिकल फाइबर आधुनिक दूरसंचार प्रणालियों में व्यापक रूप से उपयोग की जाने वाली ऑप्टिकल आवृत्तियों (प्रकाश) के लिए प्रकार का वेवगाइड है। जिस दर पर डेटा को फाइबर पर ले जाया जा सकता है वह अन्य घटनाओं के बीच रंगीन प्रसार के कारण तरंग ब्रॉडिंग द्वारा सीमित है।

सामान्य तौर पर, वेवगाइड मोड के लिए कोणीय आवृत्ति ω (β) के साथ प्रसार स्थिरांक β (जिससे कि प्रसार दिशा में विद्युत चुम्बकीय क्षेत्र z^i(βz−ωt) ई के आनुपातिक रूप से दोलन करते हैं), समूह-वेग प्रसार पैरामीटर D को इस प्रकार परिभाषित किया गया है:

$D=-{\frac {2\pi c}{\lambda ^{2}}}{\frac {d^{2}\beta }{d\omega ^{2}}}={\frac {2\pi c}{v_{g}^{2}\lambda ^{2}}}{\frac {dv_{g}}{d\omega }}$

जहां =2πc/ω निर्वात तरंगदैर्घ्य है और v_g = dω/dβ समूह वेग है। यह सूत्र सजातीय मीडिया के लिए पिछले अनुभाग में को सामान्य करता है, और इसमें वेवगाइड प्रसार और सामग्री प्रसार दोनों सम्मिलित हैं। परिक्षेपण को इस प्रकार परिभाषित करने का कारण यह है कि |D| (एसिम्प्टोटिक) टेम्पोरल तरंग फैल रहा है। जो t प्रति यूनिट बैंडविड्थ प्रति इकाई दूरी की यात्रा, सामान्यतः ऑप्टिकल फाइबर के लिए पीकोसैकन्ड / नैनोमीटर / किलोमीटर में रिपोर्ट की जाती है।

बहु-मोड ऑप्टिकल फाइबर की स्थिति में, तथाकथित मोडल प्रसार भी तरंग को चौड़ा कर देता हैं। सिंगल-मोड फाइबर में भी, ध्रुवीकरण मोड प्रसार के परिणामस्वरूप तरंग चौड़ीकरण हो सकता है (क्योंकि अभी भी दो ध्रुवीकरण मोड हैं)। ये रंगीन प्रसार के उदाहरण नहीं हैं क्योंकि ये तरंगदैर्घ्य पर निर्भर नहीं हैं या स्पंदनों के वर्णक्रमीय लिनिविथ प्रचारित नहीं हैं।

व्यापक बैंडविड्थ पर उच्च-क्रम प्रसार

जब एकल तरंग पैकेट में आवृत्तियों की विस्तृत श्रृंखला (एक व्यापक बैंडविड्थ) सम्मिलित होती है, जैसे कि अल्ट्राशॉर्ट तरंग या चिरप्ड तरंग ट्रांसमिशन के अन्य रूपों में, यह स्थिरांक द्वारा प्रसार का अनुमान लगाने के लिए सटीक नहीं हो सकता है। संपूर्ण बैंडविड्थ और तरंग स्प्रेडिंग जैसे प्रभावों की गणना करने के लिए अधिक जटिल गणनाओं की आवश्यकता होती है।

विशेष रूप से, ऊपर परिभाषित प्रसार पैरामीटर डी समूह वेग के केवल व्युत्पन्न से प्राप्त होता है। इस प्रकार उच्च व्युत्पन्न को उच्च-क्रम प्रसार के रूप में जाना जाता है। ये शब्द किसी विशेष आवृत्ति के आसपास माध्यम या वेवगाइड के प्रसार संबंध β(ω) के टेलर श्रृंखला विस्तार हैं। उनके प्रभावों की गणना तरंग के फूरियर रूपांतरणों के संख्यात्मक मूल्यांकन के माध्यम से की जा सकती है, उच्च-क्रम के धीरे-धीरे अलग-अलग लिफाफा सन्निकटन के एकीकरण के माध्यम से, विभाजन-चरण विधि द्वारा (जो टेलर श्रृंखला के अतिरिक्त सटीक प्रसार संबंध का उपयोग कर सकते हैं), या प्रत्यक्ष द्वारा अनुमानित इनवलप समीकरण के अतिरिक्त पूर्ण मैक्सवेल के समीकरणों का अनुकरण किया जाता हैं।

स्थानिक प्रसार

Main article: स्थानिक प्रसार

इलेक्ट्रोमैग्नेटिक्स और ऑप्टिक्स में इस शब्द का प्रसार सामान्यतः उपरोक्त अस्थायी या आवृत्ति प्रसार को संदर्भित करता है। इस प्रकार स्थानिक प्रसार अंतरिक्ष में माध्यम की गैर-स्थानीय प्रतिक्रिया को संदर्भित करता है, इसे परमितीकरण की तरंग सदिश निर्भरता के रूप में पुनः लिखा जा सकता है। इस कारण अनुकरणीय एनिसोट्रॉपिक माध्यम के लिए, विद्युत क्षेत्र और विद्युत विस्थापन क्षेत्र के बीच स्थानिक संबंध को संकल्प के रूप में व्यक्त किया जा सकता है:

$D_{i}(t,r)=E_{i}(t,r)+\int _{0}^{\infty }\int f_{ik}(\tau ;r,r')E_{k}(t-\tau ,r')dV'd\tau ,$

जहां इंटीग्रल ट्रांसफॉर्म $f_{ik}$ लेपित करके प्रतिक्रिया (संवेदनशीलता) है, इसके सूचकांक माध्यम के अनिसोट्रॉपी के लिए इसे सामान्य रूप से टेन्सर बनाते हैं। अधिकांश मैक्रोस्कोपिक स्थितियों में स्थानिक प्रसार नगण्य है, जहां भिन्नता का पैमाना $E_{k}(t-\tau ,r')$ परमाणु आयामों की तुलना में बहुत बड़ा है, क्योंकि लेपित होने वाला कर्नेल मैक्रोस्कोपिक दूरी पर समाप्त हो जाता है। इसके अतिरिक्त इसके परिणामस्वरूप गैर-नगण्य मैक्रोस्कोपिक प्रभाव हो सकते हैं, विशेष रूप से धातु ओं, इलेक्ट्रोलाइट्स और प्लाज्मा (भौतिकी) जैसे मीडिया के संचालन में इसका उपयोग किया जाता हैं। इस प्रकार स्थानिक प्रसार ऑप्टिकल रोटेशन और डॉपलर चौड़ीकरण में भी भूमिका निभाता है, साथ ही मेटामटेरियल्स के सिद्धांत में भी उपयोग किया जाता हैं।

रत्न विज्ञान में

खनिजों का प्रसार मान

Name	B–G	C–F
Cinnabar (HgS)	0.40	—
Synth. rutile	0.330	0.190
Rutile (TiO2)	0.280	0.120–0.180
Anatase (TiO2)	0.213–0.259	—
Wulfenite	0.203	0.133
Vanadinite	0.202	—
Fabulite	0.190	0.109
Sphalerite (ZnS)	0.156	0.088
Sulfur (S)	0.155	—
Stibiotantalite	0.146	—
Goethite (FeO(OH))	0.14	—
Brookite (TiO2)	0.131	0.12–1.80
Zincite (ZnO)	0.127	—
Linobate	0.13	0.075
Synthetic moissanite (SiC)	0.104	—
Cassiterite (SnO2)	0.071	0.035
Zirconia (ZrO2)	0.060	0.035
Powellite (CaMoO4)	0.058	—
Andradite	0.057	—
Demantoid	0.057	0.034
Cerussite	0.055	0.033–0.050
Titanite	0.051	0.019–0.038
Benitoite	0.046	0.026
Anglesite	0.044	0.025
Diamond (C)	0.044	0.025
Flint glass	0.041	—
Hyacinth	0.039	—
Jargoon	0.039	—
Starlite	0.039	—
Zircon (ZrSiO4)	0.039	0.022
GGG	0.038	0.022
Scheelite	0.038	0.026
Dioptase	0.036	0.021
Whe Vinay wellite	0.034	—
Alabaster	0.033	—
Gypsum	0.033	0.008
Epidote	0.03	0.012–0.027
Achroite	0.017	—
Cordierite	0.017	0.009
Danburite	0.017	0.009
Dravite	0.017	—
Elbaite	0.017	—
Herderite	0.017	0.008–0.009
Hiddenite	0.017	0.010
Indicolite	0.017	—
Liddicoatite	0.017	—
Kunzite	0.017	0.010
Rubellite	0.017	0.008–0.009
Schorl	0.017	—
Scapolite	0.017	—
Spodumene	0.017	0.010
Tourmaline	0.017	0.009–0.011
Verdelite	0.017	—
Andalusite	0.016	0.009
Baryte (BaSO4)	0.016	0.009
Euclase	0.016	0.009
Alexandrite	0.015	0.011
Chrysoberyl	0.015	0.011
Hambergite	0.015	0.009–0.010
Phenakite	0.01	0.009
Rhodochrosite	0.015	0.010–0.020
Sillimanite	0.015	0.009–0.012
Smithsonite	0.014–0.031	0.008–0.017
Amblygonite	0.014–0.015	0.008
Aquamarine	0.014	0.009–0.013
Beryl	0.014	0.009–0.013
Brazilianite	0.014	0.008
Celestine	0.014	0.008
Goshenite	0.014	—
Heliodor	0.014	0.009–0.013
Morganite	0.014	0.009–0.013
Pyroxmangite	0.015	—
Synth. scheelite	0.015	—
Dolomite	0.013	—
Magnesite (MgCO3)	0.012	—
Synth. emerald	0.012	—
Synth. alexandrite	0.011	—
Synth. sapphire (Al2O3)	0.011	—
Phosphophyllite	0.010–0.011	—
Enstatite	0.010	—
Anorthite	0.009–0.010	—
Actinolite	0.009	—
Jeremejevite	0.009	—
Nepheline	0.008–0.009	—
Apophyllite	0.008	—
Hauyne	0.008	—
Natrolite	0.008	—
Synth. quartz (SiO2)	0.008	—
Aragonite	0.007–0.012	—
Augelite	0.007	—
Tanzanite	0.030	0.011
Thulite	0.03	0.011
Zoisite	0.03	—
YAG	0.028	0.015
Almandine	0.027	0.013–0.016
Hessonite	0.027	0.013–0.015
Spessartine	0.027	0.015
Uvarovite	0.027	0.014–0.021
Willemite	0.027	—
Pleonaste	0.026	—
Rhodolite	0.026	—
Boracite	0.024	0.012
Cryolite	0.024	—
Staurolite	0.023	0.012–0.013
Pyrope	0.022	0.013–0.016
Diaspore	0.02	—
Grossular	0.020	0.012
Hemimorphite	0.020	0.013
Kyanite	0.020	0.011
Peridot	0.020	0.012–0.013
Spinel	0.020	0.011
Vesuvianite	0.019–0.025	0.014
Clinozoisite	0.019	0.011–0.014
Labradorite	0.019	0.010
Axinite	0.018–0.020	0.011
Ekanite	0.018	0.012
Kornerupine	0.018	0.010
Corundum (Al2O3)	0.018	0.011
Rhodizite	0.018	—
Ruby (Al2O3)	0.018	0.011
Sapphire (Al2O3)	0.018	0.011
Sinhalite	0.018	0.010
Sodalite	0.018	0.009
Synth. corundum	0.018	0.011
Diopside	0.018–0.020	0.01
Emerald	0.014	0.009–0.013
Topaz	0.014	0.008
Amethyst (SiO2)	0.013	0.008
Anhydrite	0.013	—
Apatite	0.013	0.010
Apatite	0.013	0.008
Aventurine	0.013	0.008
Citrine	0.013	0.008
Morion	0.013	—
Prasiolite	0.013	0.008
Quartz (SiO2)	0.013	0.008
Smoky quartz (SiO2)	0.013	0.008
Rose quartz (SiO2)	0.013	0.008
Albite	0.012	—
Bytownite	0.012	—
Feldspar	0.012	0.008
Moonstone	0.012	0.008
Orthoclase	0.012	0.008
Pollucite	0.012	0.007
Sanidine	0.012	—
Sunstone	0.012	—
Beryllonite	0.010	0.007
Cancrinite	0.010	0.008–0.009
Leucite	0.010	0.008
Obsidian	0.010	—
Strontianite	0.008–0.028	—
Calcite (CaCO3)	0.008–0.017	0.013–0.014
Fluorite (CaF2)	0.007	0.004
Hematite	0.500	—
Synthetic cassiterite (SnO2)	0.041	—
Gahnite	0.019–0.021	—
Datolite	0.016	—
Tremolite	0.006–0.007	—

जेमोलॉजी की विधि में प्रसार बी और जी (686.7 नैनोमीटर और 430.8 एनएम) या सी और एफ (656.3 एनएम और 486.1 एनएम) फ्रौनहोफर लाइन्स पर सामग्री के अपवर्तक सूचकांक में अंतर है, और यह व्यक्त करने के लिए है जिस सीमा तक रत्न से काटे गए प्रिज्म में आग दिखाई देती है। अग्नि बोलचाल का शब्द है जिसका उपयोग जेमोलॉजिस्ट द्वारा रत्न की प्रसार प्रकृति या उसके अभाव का वर्णन करने के लिए किया जाता है। प्रसार भौतिक संपत्ति है। इस प्रकार किसी दिए गए रत्न द्वारा प्रदर्शित आग की मात्रा रत्न के पहलू कोणों, पॉलिश की गुणवत्ता, प्रकाश वातावरण, सामग्री के अपवर्तक सूचकांक, रंग की संतृप्ति और रत्न के सापेक्ष दर्शक के उन्मुखीकरण का कार्य है।

इमेजिंग में

फोटोग्राफिक और सूक्ष्म लेंस में, प्रसार रंगीन विपथन का कारण बनता है, जिससे छवि में विभिन्न रंग ठीक से ओवरलैप नहीं होते हैं। इसका प्रतिकार करने के लिए विभिन्न तकनीकों का विकास किया गया है, जैसे कि अक्रोमैट का उपयोग, विभिन्न प्रसार के चश्मे के साथ बहु-तत्व लेंस। उनका निर्माण इस तरह से किया जाता है कि विभिन्न भागों के रंगीन विपथन निरस्त हो जाते हैं।

पलसर उत्सर्जन

पलसर न्यूट्रॉन मुख्यतः तारों को प्रकाशित करते हैं जो मिलीसेकंड से लेकर सेकंड तक बहुत नियमित अंतराल पर तरंग का उत्सर्जन करते हैं। इस प्रकार खगोलविदों का मानना ​​​​है कि तरंग को साथ व्यापक आवृत्तियों पर उत्सर्जित किया जाता है। चूंकि जैसा कि पृथ्वी पर देखा गया है, उच्च रेडियो आवृत्तियों पर उत्सर्जित प्रत्येक तरंग के घटक कम आवृत्तियों पर उत्सर्जित होने से पहले आते हैं। इस प्रकार यह प्रसार तारे के बीच के माध्यम के आयनित घटक के कारण होता है, मुख्यतः मुक्त इलेक्ट्रॉन, जो समूह वेग आवृत्ति को निर्भर करते हैं। इस आवृत्ति पर अतिरिक्त विलंब जोड़ा गया ν है।

$t=k_{\mathrm {DM} }\cdot \left({\frac {\mathrm {DM} }{\nu ^{2}}}\right)$

जहां प्रसार निरंतर k_DM द्वारा दिया गया है

$k_{\mathrm {DM} }={\frac {e^{2}}{2\pi m_{\mathrm {e} }c}}\simeq 4.149\,\mathrm {GHz} ^{2}\,\mathrm {pc} ^{-1}\,\mathrm {cm} ^{3}\,\mathrm {ms} ,$

और प्रसार माप (DM) मुक्त इलेक्ट्रॉनों का स्तंभ घनत्व (कुल इलेक्ट्रॉन सामग्री ) है - अर्ताथ इलेक्ट्रॉनों की संख्या घनत्व n_e (इलेक्ट्रॉन/सेमी³) तरंगर से पृथ्वी तक फोटॉन द्वारा यात्रा किए गए पथ के साथ एकीकृत - और द्वारा दिया गया है

$\mathrm {DM} =\int _{0}^{d}{n_{e}\,dl}$

प्रति घन सेंटीमीटर पारसेक की इकाइयों के साथ (1 pc/cm³ = 30.857 × 10²¹ m^-2) मान प्रदर्शित करता हैं।

सामान्यतः खगोलीय टिप्पणियों के लिए, इस देरी को सीधे नहीं मापा जा सकता है, क्योंकि उत्सर्जन का समय अज्ञात है। जो मापा जा सकता है वह दो अलग-अलग आवृत्तियों पर आगमन के समय में अंतर है। उच्च आवृत्ति के बीच देरी t ν_hi और कम आवृत्ति ν_lo तरंग का घटक होता हैं।

$\Delta t=k_{\mathrm {DM} }\cdot \mathrm {DM} \cdot \left({\frac {1}{\nu _{\mathrm {lo} }^{2}}}-{\frac {1}{\nu _{\mathrm {hi} }^{2}}}\right)$

t के संदर्भ में उपरोक्त समीकरण को फिर से लिखना किसी आवृत्तियों पर तरंग आगमन समय को मापकर डीएम निर्धारित करने की अनुमति देता है। यह इसके अतिरिक्त इंटरस्टेलर माध्यम का अध्ययन करने के लिए उपयोग किया जा सकता है, साथ ही साथ विभिन्न आवृत्तियों पर तरंगर के अवलोकनों को संयोजित करने की अनुमति देता है।

यह भी देखें

• एब्बे नंबर
• कांच के गुणों की गणना सहित प्रसार
• कॉची का समीकरण
• विक्षेपण संबंध
• तेज रेडियो फट (खगोल विज्ञान)
• उतार-चढ़ाव प्रमेय
• हरा-कुबो संबंध
• समूह देरी
• इंट्रामॉडल प्रसार
• क्रेमर्स-क्रोनिग संबंध
• रैखिक प्रतिक्रिया फलन
• बहु-प्रिज्म फैलाव सिद्धांत
• सेलमेयर समीकरण
• अल्ट्राशॉर्ट तरंग
• वस्तुतः छविबद्ध चरणबद्ध सरणी

बाहरी संबंध

• Dispersive Wiki – discussing the mathematical aspects of dispersion.
• Dispersion – Encyclopedia of Laser Physics and Technology
• Animations demonstrating optical dispersion by QED
• Interactive webdemo for chromatic dispersion Institute of Telecommunications, University of Stuttgart