यूलर की पहचान
| Part of a series of articles on the |
| mathematical constant e |
|---|
 |
| Properties |
| Applications |
| Defining e |
|
| People |
| Related topics |
गणित में, यूलर की पहचान[note 1] (यूलर के समीकरण के रूप में भी जाना जाता है) समानता (गणित) है
- e यूलर की संख्या प्राकृतिक लघुगणक का आधार है
- i एक काल्पनिक इकाई है, जो परिभाषा के अनुसार i2 = −1 और को संतुष्ट करती है
- π एक वृत्त की परिधि और उसके व्यास का अनुपात पाई है।
यूलर की पहचान स्विस गणितज्ञ लियोनहार्ड यूलर के नाम पर है। यह यूलर के सूत्र का एक विशेष स्थिति है जब x = π के लिए मूल्यांकन किया जाता है। यूलर की पहचान को गणितीय सुंदरता का एक उदाहरण माना जाता है क्योंकि यह गणित में सबसे मौलिक संख्याओं के बीच गहरा संबंध दर्शाता है। इसके अतिरिक्त यह सीधे तौर पर एक प्रमाण में उपयोग किया जाता है कि π पारलौकिक है[3][4] जिसका अर्थ है कि वृत्त को चौकोर करना असंभव है।
गणितीय सौंदर्य
यूलर की पहचान को अधिकांशतः गहरे गणितीय सौंदर्य के उदाहरण के रूप में उद्धृत किया जाता है। तीन मूल अंकगणितीय ऑपरेशन ठीक एक बार होते हैं: जोड़ गुणा और घातांक पहचान पांच मूलभूत गणितीय स्थिरांकों को भी जोड़ती है:[5]
- 0, योगात्मक पहचान।
- 1, गुणक तत्समक।
- संख्या π (π = 3.1415...) मूल वृत्त स्थिरांक।
- संख्या e (e = 2.718...) जिसे यूलर संख्या के रूप में भी जाना जाता है, जो गणितीय विश्लेषण में व्यापक रूप से पाई जाती है।
- संख्या i सम्मिश्र संख्याओं की काल्पनिक इकाई है।
इसके अतिरिक्त समीकरण शून्य के समान अभिव्यक्ति सेट के रूप में दिया जाता है, जो गणित के कई क्षेत्रों में सामान्य अभ्यास है।
स्टैनफोर्ड विश्वविद्यालय के गणित के प्रोफेसर कीथ डिवालिन ने कहा है शेक्सपियर के गाथा की तरह जो प्यार के सार को पकड़ता है या एक पेंटिंग जो मानव रूप की सुंदरता को सामने लाती है जो सिर्फ त्वचा की गहराई से कहीं अधिक है यूलर का समीकरण बहुत गहराई तक पहुंचता है अस्तित्व का[6] और पॉल नाहिन न्यू हैम्पशायर विश्वविद्यालय में एक प्रोफेसर एमेरिटस जिन्होंने यूलर के सूत्र और फूरियर विश्लेषण में इसके अनुप्रयोगों को समर्पित एक पुस्तक लिखी है यूलर की पहचान को उत्कृष्ट सौंदर्य के रूप में वर्णित करता है।[7]
गणित लेखक कॉन्स्टेंस रीड ने कहा है कि यूलर की पहचान सभी गणित में सबसे प्रसिद्ध सूत्र है।[8] 19वीं सदी के एक अमेरिकी दार्शनिक, गणितज्ञ और हार्वर्ड विश्वविद्यालय के प्रोफेसर बेंजामिन पीयर्स ने एक व्याख्यान के समय यूलर की पहचान को सिद्ध करने के बाद कहा कि पहचान पूर्ण रूप से विरोधाभासी है; हम इसे समझ नहीं सकते हैं और हम नहीं जानते कि इसका क्या अर्थ है किन्तु हमने इसे सिद्ध कर दिया है और इसलिए हम जानते हैं कि यह सच होना चाहिए।[9]
1990 में गणितीय बुद्धिजीवी द्वारा आयोजित पाठकों के एक सर्वेक्षण में यूलर की पहचान को गणित में सबसे सुंदर प्रमेय के रूप में नामित किया गया था।[10] 2004 में भौतिकी की दुनिया द्वारा आयोजित पाठकों के एक अन्य सर्वेक्षण में यूलर की पहचान मैक्सवेल के समीकरणों (विद्युत चुंबकत्व के) के साथ अब तक के सबसे बड़े समीकरण के रूप में जुड़ी हुई है।[11]
यूलर की पहचान के बारे में लोकप्रिय गणित में कम से कम तीन पुस्तकें प्रकाशित हुई हैं:
- डॉ यूलर का शानदार सूत्र: पॉल नाहिन (2011) द्वारा कई गणितीय बीमारियों का इलाज[12]
- ए मोस्ट एलिगेंट इक्वेशन: डेविड स्टिप (2017) द्वारा यूलर का सूत्र और गणित की सुंदरता[13]
- यूलर का अग्रणी समीकरण: रॉबिन विल्सन (गणितज्ञ) (2018) द्वारा गणित में सबसे सुंदर प्रमेय।[14]
स्पष्टीकरण
काल्पनिक घातांक

मौलिक रूप से, यूलर की पहचान का प्रमाणित है कि -1 के समान है। व्यंजक , व्यंजक का एक विशेष मामला है, जहाँ z कोई सम्मिश्र संख्या है। सामान्यतः को जटिल z के लिए वास्तविक एक्सपोनेंट से जटिल एक्सपोनेंट तक एक्सपोनेंशियल फलन की परिभाषाओं में से एक को विस्तारित करके परिभाषित किया जाता है। उदाहरण के लिए, एक सामान्य परिभाषा है:
यूलर की पहचान इसलिए बताती है कि की सीमा, जैसे n अनंत तक पहुँचती है, -1 के समान है। यह सीमा एनीमेशन में दाईं ओर सचित्र है।
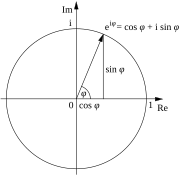
यूलर की पहचान यूलर के सूत्र का एक विशेष स्थिति है जो बताता है कि किसी भी वास्तविक संख्या x के लिए
जहां त्रिकोणमिति साइन और कोसाइन के इनपुट कांति में दिए गए हैं।
विशेष रूप से, जब x = π,
तब से
और
यह इस प्रकार है कि
जो यूलर की पहचान देता है:
ज्यामितीय व्याख्या
किसी भी सम्मिश्र संख्या को सम्मिश्र तल पर बिंदु द्वारा दर्शाया जा सकता है। इस बिंदु को ध्रुवीय निर्देशांक में के रूप में भी दर्शाया जा सकता है, जहां r z (मूल से दूरी) का निरपेक्ष मान है, और z का तर्क है (धनात्मक x-अक्ष से वामावर्त कोण) . साइन और कोसाइन की परिभाषाओं के अनुसार, इस बिंदु में के कार्टेशियन निर्देशांक हैं, जिसका अर्थ है कि यूलर के सूत्र के अनुसार, यह कहने के समान है।
यूलर की पहचान कहती है कि चूंकि , r = 1 और के लिए है, इसे जटिल तल पर संख्या −1 के तथ्य के रूप में समझा जा सकता है: मूल बिंदु से इसकी दूरी 1 है, और धनात्मक x-अक्ष से इसका कोण रेडियन है।
इसके अतिरिक्त, जब किसी सम्मिश्र संख्या z को से गुणा किया जाता है, तो इसका जटिल तल पर के कोण से z वामावर्त घुमाने का प्रभाव होता है। चूँकि −1 से गुणन मूल बिंदु पर एक बिंदु को दर्शाता है यूलर की पहचान को यह कहते हुए व्याख्या किया जा सकता है कि मूल के चारों ओर किसी भी बिंदु रेडियन को घुमाने का वही प्रभाव होता है जो मूल बिंदु पर बिंदु को दर्शाता है। इसी तरह, को के समान सेट करने से संबंधित समीकरण प्राप्त होता है, जिसे यह कहते हुए समझा जा सकता है कि किसी भी बिंदु को मूल के चारों ओर एक चक्कर लगाने से वह अपने मूल स्थिति पर वापस आ जाता है।
सामान्यीकरण
यूलर की पहचान भी अधिक सामान्य पहचान का एक विशेष स्थिति है कि एकता की n वीं जड़ें, n > 1 के लिए, 0 तक जोड़ती हैं:
यूलर की पहचान वह स्थिति है जहां n = 2.है |
गणित के एक अन्य क्षेत्र में, चतुष्कोणीय घातांक का उपयोग करके कोई यह दिखा सकता है कि समान पहचान चतुष्कोणों पर भी प्रयुक्त होती है। होने देना {i, j, k} आधार तत्व हो; तब,
सामान्यतः वास्तविक a1, a2, और a3 ऐसे दिए गए हैं कि a12 + a22 + a32 = 1, फिर,
ऑक्टोनियंस के लिए वास्तविक an के साथ a12 + a22 + ... + a72 = 1 और ऑक्टोनियन आधार तत्वों {i1, i2, ..., i7}के साथ,
इतिहास
जबकि यूलर की पहचान यूलर के सूत्र का प्रत्यक्ष परिणाम है, जो 1748 में उनके गणितीय विश्लेषण के स्मारकीय कार्य में प्रकाशित हुआ था, एनालिसिस इनफिनिटोरम में परिचय,[15] यह संदेहास्पद है कि क्या पांच मूलभूत स्थिरांकों को एक कॉम्पैक्ट रूप में जोड़ने की विशेष अवधारणा का श्रेय स्वयं यूलर को दिया जा सकता है क्योंकि हो सकता है कि उन्होंने इसे व्यक्त नहीं किया होगा।[16]
रॉबिन विल्सन (गणितज्ञ) निम्नलिखित कहते हैं।[17]
हमने देखा है कि कैसे यह [यूलर की पहचान] आसानी से जोहान बर्नौली और रोजर कोट्स के परिणामों से निकाली जा सकती है, किन्तु ऐसा लगता है कि उनमें से किसी ने भी ऐसा नहीं किया है। ऐसा प्रतीत होता है कि यूलर ने भी इसे स्पष्ट रूप से नहीं लिखा है - और निश्चित रूप से यह उनके किसी भी प्रकाशन में प्रकट नहीं होता है - चूँकि उन्होंने निश्चित रूप से यह अनुभव किया होगा कि यह उनकी पहचान [अर्थात। यूलर का सूत्र], eix = cos x + i sin x . इसके अलावा, यह अज्ञात प्रतीत होता है जिसने सबसे पहले परिणाम को स्पष्ट रूप से बताया….
यह भी देखें
- डी मोइवर का सूत्र
- घातांक प्रकार्य
- गेलफॉन्ड स्थिरांक
टिप्पणियाँ
- ↑ The term "Euler's identity" (or "Euler identity") is also used elsewhere to refer to other concepts, including the related general formula eix = cos x + i sin x,[1] and the Euler product formula.[2] See also List of things named after Leonhard Euler.
संदर्भ
- ↑ Dunham, 1999, p. xxiv.
- ↑ Stepanov, S.A. (2001) [1994], "Euler identity", Encyclopedia of Mathematics, EMS Press
- ↑ Milla, Lorenz (2020), The Transcendence of π and the Squaring of the Circle, arXiv:2003.14035
- ↑ Hines, Robert. "ई पारलौकिक है" (PDF). University of Colorado. Archived (PDF) from the original on 2021-06-23.
- ↑ Paulos, 1992, p. 117.
- ↑ Nahin, 2006, p. 1.
- ↑ Nahin, 2006, p. xxxii.
- ↑ Reid, chapter e.
- ↑ Maor, p. 160, and Kasner & Newman, p. 103–104.
- ↑ Wells, 1990.
- ↑ Crease, 2004.
- ↑ Nahin, Paul (2011). Dr. Euler's fabulous formula : cures many mathematical ills (in English). Princeton University Press. ISBN 978-0691118222.
- ↑ Stipp, David (2017). A most elegant equation : Euler's formula and the beauty of mathematics (in English) (First ed.). Basic Books. ISBN 978-0465093779.
- ↑ Wilson, Robin (2018). Euler's pioneering equation : the most beautiful theorem in mathematics (in English). Oxford: Oxford University Press. ISBN 978-0198794936.
- ↑ Conway & Guy, p. 254–255.
- ↑ Sandifer, p. 4.
- ↑ Wilson, p. 151-152.
स्रोत
- जॉन हॉर्टन कॉनवे|कॉनवे, जॉन एच., और रिचर्ड के. गाय|गाइ, रिचर्ड के. (1996), द बुक ऑफ़ नंबर, स्प्रिंगर ISBN 978-0-387-97993-9
- रॉबर्ट पी. क्रीज़ | क्रीज़, रॉबर्ट पी. (10 मई 2004), अब तक का सबसे महान समीकरण , भौतिकी विश्व [पंजीकरण आवश्यक]
- विलियम डनहम (गणितज्ञ) | डनहम, विलियम (1999), यूलर: द मास्टर ऑफ अस ऑल, अमेरिका का गणितीय संघ ISBN 978-0-88385-328-3
- यूलर, लियोनहार्ड (1922), लियोनहार्ड यूलर के कार्य। 1, गणितीय कार्य। वॉल्यूम VIII, लिओनार्ड यूलर का इन्फिनिटिमल्स के विश्लेषण का परिचय। टॉमस प्राइमस, लीपज़िग: बी. जी. टेबनेरी
- एडवर्ड कास्नर | कास्नर, ई., और जेम्स आर. न्यूमैन | न्यूमैन, जे. (1940), गणित और कल्पना, साइमन एंड शूस्टर
- एली मौर|माओर, एली (1998),e: द स्टोरी ऑफ़ ए नंबर, प्रिंसटन यूनिवर्सिटी प्रेस ISBN 0-691-05854-7
- नाहिन, पॉल जे. (2006), डॉ. यूलर का शानदार सूत्र: कई गणितीय बीमारियों का इलाज, प्रिंसटन यूनिवर्सिटी प्रेस ISBN 978-0-691-11822-2
- जॉन एलेन पॉलोस | पॉलोस, जॉन एलन (1992), बियॉन्ड न्यूमरेसी: एन अनकॉमन डिक्शनरी ऑफ मैथेमेटिक्स, पेंगुइन पुस्तकें ISBN 0-14-014574-5
- रीड, कॉन्स्टेंस (विभिन्न संस्करण)शून्य से अनंत तक, मैथमेटिकल एसोसिएशन ऑफ अमेरिका
- सैंडिफ़र, सी. एडवर्ड (2007), यूलर ग्रेटेस्ट हिट्स, मैथमैटिकल एसोसिएशन ऑफ़ अमेरिका ISBN 978-0-88385-563-8
- Stipp, David (2017), A Most Elegant Equation: Euler's formula and the beauty of mathematics, Basic Books
- Wells, David (1990). "क्या ये सबसे खूबसूरत हैं?". The Mathematical Intelligencer. 12 (3): 37–41. doi:10.1007/BF03024015. S2CID 121503263.
- Wilson, Robin (2018), Euler's Pioneering Equation: The most beautiful theorem in mathematics, Oxford University Press, ISBN 978-0-192-51406-6
- Zeki, S.; Romaya, J. P.; Benincasa, D. M. T.; Atiyah, M. F. (2014), "The experience of mathematical beauty and its neural correlates", Frontiers in Human Neuroscience, 8: 68, doi:10.3389/fnhum.2014.00068, PMC 3923150, PMID 24592230
