बराबर का चिन्ह

From Vigyanwiki
Revision as of 16:41, 29 May 2023 by alpha>Abhishek (→‎इतिहास)
Several terms redirect here. For other uses, see बराबर (बहुविकल्पी) (disambiguation), डबल हाइफ़न (disambiguation), असाइनमेंट (कंप्यूटर विज्ञान) (disambiguation) and गणितीय प्रतीकों की शब्दावली # समानता, समानता और समानता (disambiguation).
=
बराबर का चिन्ह
In UnicodeU+003D = EQUALS SIGN (=)
Related
See alsoU+2260 ≠ NOT EQUAL TO
U+2248 ≈ ALMOST EQUAL TO
U+2261 ≡ IDENTICAL TO
एक प्रसिद्ध समानता (गणित) जिसमें समान चिह्न है

बराबर चिह्न ब्रिटिश अंग्रेजी या बराबर चिह्न अमेरिकी अंग्रेजी से लिया गया हैं, जिसे समानता सूचक चिह्न के रूप में भी जाना जाता है, इसका गणितीय प्रतीक = है, जिसका उपयोग अच्छी तरह से परिभाषित किए गए अर्थों में समानता को इंगित करने के लिए किया जाता है।[1] इस प्रकार किसी समीकरण में इसे दो व्यंजकों के बीच रखा जाता है जिनका मान समान होता है, या जिनके लिए कोई उन स्थितियों का अध्ययन करना होता है, जिनके अंतर्गत इनका मान समान होता है।

यूनिकोड और आस्की कोड में, इसका कोड बिंदु U+003D है।[2] इसका आविष्कार 1557 में रॉबर्ट रिकॉर्डे ने किया था।

इतिहास

समान शब्द की व्युत्पत्ति लैटिन शब्द इक्वालिस से हुई है,[3] इसके मौलिक अर्थ के रूप में समान या बराबर, एक्वुअस स्तर के लिए उपयोग होता हैं ।

आधुनिक संकेतन में 14x+15=71 के तुल्य समान चिह्न का पहला प्रयोग। रॉबर्ट रिकॉर्डे द्वारा द वेटस्टोन ऑफ़ विट (1557) से।
रिकॉर्डे का परिचय =

=}== प्रतीक, जिसे अब समानता के लिए गणित में सार्वभौमिक रूप से स्वीकार किया जाता है, पहली बार वेल्श गणितज्ञ रॉबर्ट रिकॉर्डे द्वारा द वेटस्टोन ऑफ विट (1557) में इसे उपयोग किया गया था।[4] इस प्रतीक का मूल रूप वर्तमान स्वरूप से कहीं अधिक व्यापक था। अपनी पुस्तक में रिकॉर्डे जेमोवे लाइनों के अपने डिजाइन की व्याख्या करता है जिसका अर्थ है दो समान रेखाएँ तथा लैटिन में विक्षनरी से: जेमेलस कहा जाता हैं।[5]

'इन शब्दों की पुनरावृत्ति को रोकने के लिए: बराबर है: मैं टेट करूंगा जैसा कि मैं अधिकांशतः काम में करता हूं, समानांतरों की एक जोड़ी, या Gemowe एक लम्बाई की रेखाएं हैं, इस प्रकार: =, बाइका नोए .2. थिंजेस, मोरे इक्वल हो सकते हैं.[6]

— इन शब्दों की थकाऊ पुनरावृत्ति से बचने के लिए: "के बराबर है" मैं सेट करूँगा जैसा कि मैं अधिकांशतः काम के उपयोग में करता हूं, समानांतर की एक जोड़ी, या duplicate एक [समान] लंबाई की रेखाएँ, इस प्रकार: =, क्योंकि कोई भी 2 चीजें अधिक समान नहीं हो सकतीं हैं।

प्रतीक = तुरंत लोकप्रिय नहीं हुआ। प्रतीक || का उपयोग कुछ और द्वारा किया गया था æ (या œ), लैटिन शब्द से aequalis अर्थ बराबर, 1700 के दशक में व्यापक रूप से उपयोग किया गया था (गणित का इतिहास, सेंट एंड्रयूज विश्वविद्यालय)।[7]

गणित और कंप्यूटर प्रोग्रामिंग में उपयोग

गणित में, समान चिह्न का उपयोग किसी विशिष्ट स्थितियों में तथ्य के सरल कथन के रूप में किया जा सकता है (x = 2), या परिभाषाएँ बनाने के लिए (let x = 2), सशर्त प्रमाण के लिए (if x = 2, then ...), या सार्वभौमिक तुल्यता व्यक्त करने के लिए ((x + 1)² = x² + 2x + 1) द्वारा इन्हें प्रदर्शित करते हैं।

समान चिह्न का उपयोग करने वाली पहली महत्वपूर्ण कंप्यूटर प्रोग्रामिंग भाषा फोरट्रान, फोरट्रान I का मूल संस्करण था, जिसे 1954 में डिज़ाइन किया गया था और 1957 में लागू किया गया था। फोरट्रान में, = असाइनमेंट (कंप्यूटर विज्ञान) ऑपरेटर के रूप में कार्य करता है: X = 2 का मान सेट करता है X से 2. यह कुछ सीमा तक इसका उपयोग जैसा दिखता है, = गणितीय परिभाषा में, किन्तु विभिन्न शब्दार्थों के साथ: निम्नलिखित अभिव्यक्ति = का मूल्यांकन पहले किया जाता है, और इसके पिछले मान को संदर्भित कर सकता है X. उदाहरण के लिए, असाइनमेंट X = X + 2 का मान X द्वारा 2 के रूप में बढ़ाता है।

एलगोल भाषा के मूल संस्करण द्वारा प्रतिद्वंद्वी प्रोग्रामिंग-भाषा का उपयोग किया गया था, जिसे 1958 में डिज़ाइन किया गया था और 1960 में लागू किया गया था। एलगोल भाषा में रिलेशनल ऑपरेटर सम्मिलित था जो समानता के लिए परीक्षण करता था, जैसे निर्माण की अनुमति देता है if x = 2 अनिवार्य रूप से ही अर्थ के साथ = गणित में सशर्त उपयोग किया जाता हैं। इस उपयोग के लिए समान चिह्न आरक्षित किया गया था।

21 वीं सदी के प्रारंभ में दोनों का उपयोग विभिन्न प्रोग्रामिंग भाषाओं में सरल है। इसके साथ ही फोरट्रान, = का उपयोग C (प्रोग्रामिंग लैंग्वेज), पर्ल, पायथन (प्रोग्रामिंग लैंग्वेज), एडब्ल्यूके, और उनके पैरेन्ट्स जैसी भाषाओं में असाइनमेंट के लिए किया जाता है। किन्तु = का उपयोग पास्कल (प्रोग्रामिंग भाषा) परिवार, एडा (प्रोग्रामिंग भाषा), एफिल (प्रोग्रामिंग भाषा), एपीएल (प्रोग्रामिंग भाषा), और अन्य भाषाओं में समानता और असाइनमेंट के लिए नहीं किया जाता है।

कुछ भाषाओं, जैसे कि बेसिक और पीएल/आई, ने समान चिह्न का उपयोग किया है, जिसका अर्थ असाइनमेंट और समानता दोनों है, जो संदर्भ से अलग है। चूंकि, अधिकांश भाषाओं में जहाँ = का इनमें से अर्थ है, अलग वर्ण या, अधिक बार, वर्णों के अनुक्रम का उपयोग दूसरे अर्थ के लिए किया जाता है। एलगोल भाषा के बाद, अधिकांश भाषाएँ जो उपयोग करती हैं = समानता के उपयोग के लिए := असाइनमेंट के लिए, चूंकि एपीएल, अपने विशेष वर्ण सेट के साथ, बाएं ओर इंगित करते हुए तीर का उपयोग करता है।

फोरट्रान के पास समानता ऑपरेटर नहीं था, फोरट्रान तक अंकगणित IF कथन का उपयोग करके अभिव्यक्ति की तुलना शून्य से करना संभव था, इस प्रकार IV को 1962 में प्रस्तुत किया गया था, तब से इसने चार वर्णों का उपयोग किया है, इस प्रकार .EQ. का उपयोग समानता के लिए परीक्षण करने के लिए किया जाता है। इस प्रकार B प्रोग्रामिंग भाषा के प्रयोग के प्रारंभ की == इस अर्थ के साथ, जिसे इसके वंशज सी और बाद की अधिकांश भाषाओं द्वारा कॉपी किया गया है, यहाँ पर = का अर्थ असाइनमेंट है ।

एट्रिब्यूट-वैल्यू पेयर को परिभाषित करने के लिए समान चिह्न का भी उपयोग किया जाता है, जिसमें ऐट्रिब्यूट (कंप्यूटिंग) को वैल्यू (कंप्यूटर विज्ञान) असाइन किया जाता है।[citation needed]

विभिन्न समान संकेत

PHP में,

अन्य उपयोग

भाषा

स्वर पत्र

समान चिह्न का उपयोग कांगो-किंशासा में बुडू भाषा की वर्तनी में, क्रुमेन भाषा में, मवान भाषा में और हाथीदांत का किनारा में दान भाषा में व्याकरणिक स्वर पत्र के रूप में भी किया जाता है।[8][9] टोन अक्षर के लिए प्रयुक्त यूनिकोड वर्ण (U+A78A)[10] गणितीय प्रतीक (यू+003डी) से अलग है।

व्यक्तिगत नाम

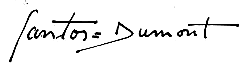
सैंटोस-ड्यूमॉन्ट का हस्ताक्षर, डबल हाइफ़न दिखा रहा है जो समान चिह्न जैसा दिखता है।

किसी व्यक्ति के नाम में यूरोपीय उपयोग के समान चिह्न का संभवतः अलग स्थिति विशेषतः दोनाली नाम में, अग्रणी एविएटर अल्बर्टो सैंटोस-ड्यूमॉन्ट द्वारा किया गया था, क्योंकि उन्हें न केवल अधिकांशतः डबल हाइफ़न का उपयोग करने के लिए जाना जाता है। इस प्रकार ⹀ समान चिह्न जैसा दिखता है = हाइफ़न के स्थान पर अपने दोनाली नाम के बीच, किन्तु यह भी लगता है कि व्यक्तिगत रूप से उस प्रथा को पसंद किया है, अपने पिता की फ्रांसीसी जातीयता और अपनी मां की ब्राजीलियाई जातीयता के लिए समान सम्मान प्रदर्शित करने के लिए उपयोग की जाती हैं।[11]

डबल हाइफ़न के अतिरिक्त, कभी-कभी जापानी में नामों के बीच विभाजक के रूप में समान चिह्न का उपयोग किया जाता है। ओजिब्वे में, कीबोर्ड पर सरलता से उपलब्ध समान चिह्न का उपयोग डबल हाइफ़न के विकल्प के रूप में किया जाता है।

भाषाविज्ञान

भाषाई इंटरलीनियर ग्लॉस में, समान चिह्न पारंपरिक रूप से क्लिटिक सीमाओं को चिह्नित करने के लिए उपयोग किया जाता है: क्लिटिक और क्लिटिक से जुड़े शब्द के बीच समान चिह्न रखा जाता है।[12]

रसायन विज्ञान

रासायनिक सूत्र में, दोहरे बंधन को दर्शाने वाली दो समानांतर रेखाएँ सामान्यतः समान चिह्न का उपयोग करके प्रस्तुत की जाती हैं।

एलजीबीटी प्रतीक

हाल के वर्षों में एलजीबीटी प्रतीकों एलजीबीटी अधिकारों के लिए समान चिह्न का उपयोग किया गया है। इस प्रकार प्रतीक का उपयोग 1995 से मानवाधिकार अभियान द्वारा किया गया है, जो विवाह समानता की पैरवी करता है, और बाद में संयुक्त राष्ट्र स्वतंत्र और समान द्वारा, जो संयुक्त राष्ट्र में एलजीबीटी अधिकारों को बढ़ावा देता है।[13]

हेट स्पीच

≠ प्रतीक कुछ श्वेत श्रेष्ठता और अन्य समूहों द्वारा अपनाया गया है।[14]

टेलीग्राम और टेलेक्स

मोर्स कोड में, बराबर चिह्न को अक्षरों B (-...) और T (-) द्वारा साथ (-...-) चलाया जाता है। अक्षर BT विराम पाठ के लिए खड़ा है, और इस प्रकार टेलिक्स के माध्यम से भेजे गए संदेशों में अनुच्छेदों, या अनुच्छेदों के समूहों के बीच रखा जाता है, मानकीकृत टेली-टाइपराइटर या किसी संदेश के पाठ को हस्ताक्षर से अलग करने के लिए तार के अंत में ब्रेक टेक्स्ट के लिए उपयोग किया जाने वाला चिह्न दिया जाता है।

संबंधित प्रतीक

See also: यूनिकोड गणितीय ऑपरेटर

सन्निकटन बराबर चिह्न

Main article: सन्निकटन §  टाइपोग्राफी

सन्निकटन बराबर चिह्न वस्तुओं को निरूपित करने के लिए उपयोग किए जाने वाले प्रतीकों में निम्नलिखित सम्मिलित हैं:[15]

  • अवधि की शैली = फ़ॉन्ट-आकार: 200%; रेखा-ऊंचाई: 50%; >≈ (U+2248 ≈ ALMOST EQUAL TO, कंडोम \approx)
  • ≃ (U+2243 ≃ ASYMPTOTICALLY EQUAL TO, LaTeX \ simeq), का संयोजन ≈ और =, स्पर्शोन्मुख विश्लेषण को इंगित करने के लिए भी उपयोग किया जाता है
  • ≅ (U+2245 ≅ APPROXIMATELY EQUAL TO, LaTeX \cong), ≈ और = का अन्य संयोजन, जो कभी-कभी तुल्याकारिता या सर्वांगसमता संबंध को इंगित करने के लिए भी प्रयोग किया जाता है
  • ∼ (U+223C ∼ TILDE OPERATOR, LaTeX \sim), जिसका उपयोग कभी-कभी आनुपातिकता (गणित) या समानता (ज्यामिति) को इंगित करने के लिए भी किया जाता है, जो तुल्यता संबंध से संबंधित होता है, या यह इंगित करने के लिए कि विशिष्ट संभाव्यता वितरण के अनुसार यादृच्छिक चर वितरित किया जाता है (टिल्ड भी देखें) ), या वैकल्पिक रूप से दो मात्राओं के बीच इंगित करने के लिए कि वे परिमाण के समान क्रम के हैं।
  • ∽ (U+223D ∽ REVERSED TILDE, LaTex \backsim), जिसका उपयोग आनुपातिकता (गणित) को इंगित करने के लिए भी किया जाता है
  • ≐ (U+2250 ≐ APPROACHES THE LIMIT, LaTeX \doteq), जिसका उपयोग चर के सीमा (गणित) के दृष्टिकोण का प्रतिनिधित्व करने के लिए भी किया जा सकता है।
  • ≒ (U+2252 ≒ APPROXIMATELY EQUAL TO OR THE IMAGE OF, LaTeX \fallingdotseq), सामान्यतः जापान, ताइवान और कोरिया में उपयोग किया जाता है।
  • ≓ (U+2253 ≓ IMAGE OF OR APPROXIMATELY EQUAL TO, लैटेक्स \risingdotseq)

जापान जैसे पूर्वी एशिया के कुछ क्षेत्रों में, ≒ का अर्थ है कि दो शब्द लगभग बराबर हैं, किन्तु अन्य क्षेत्रों और गणित जैसे विशेष साहित्य में, ≃ का प्रयोग अधिकांशतः किया जाता है। इसके गणितीय अर्थ के अतिरिक्त यह कभी-कभी जापानी वाक्यों में लगभग उसी की आशा से प्रयोग किया जाता है।

असमानता

असमानता को निरूपित करने के लिए प्रयुक्त प्रतीक, जब आइटम समान नहीं होते हैं तब उपयोग होता हैं, जिसका समान चिह्न ≠ स्लैश (विराम चिह्न) है। लाटेक्स में, यह \neq कमांड के साथ किया जाता है।

अधिकांश प्रोग्रामिंग लैंग्वेज, खुद को आस्की कोड या 7-बिट आस्की कोड अक्षरों का समूह और QWERTY तक सीमित रखते हुए, उपयोग करती हैं ~=, !=, /=, या <> उनके बूलियन तर्क असमानता ऑपरेटर का प्रतिनिधित्व करने के लिए उपयोग किया जाता हैं।

प्रतीक

ट्रिपल बार प्रतीक ≡ (U+2261, LaTeX \equiv) का प्रयोग अधिकांशतः पहचान (गणित) को इंगित करने के लिए किया जाता है, इसकी परिभाषा U+225D ≝ EQUAL TO BY DEFINITION या U+2254 ≔ COLON EQUALS), या मॉड्यूलर अंकगणित में सर्वांगसम संबंध के द्वारा भी दर्शाया जा सकता है।

समरूपता

प्रतीक ≅ का उपयोग अधिकांशतः समरूप बीजगणितीय संरचनाओं या सर्वांगसमता (ज्यामिति) ज्यामितीय आकृतियों को इंगित करने के लिए किया जाता है।

तर्क में

सत्य मान की समानता (द्वि-निहितार्थ या तार्किक तुल्यता के माध्यम से), सहित विभिन्न प्रतीकों =, ~, और ⇔ द्वारा निरूपित किया जा सकता है।

अन्य संबंधित प्रतीक

यूनिकोड में समान चिह्न से संबंधित अंकन के लिए कोड बिंदुओं के साथ अतिरिक्त पूर्वनिर्मित वर्ण में सम्मिलित हैं:[15]

  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≌ (U+224C ≌ ALL EQUAL TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≔ (U+2254 ≔ COLON EQUALS) (इसके लिए असाइनमेंट (कंप्यूटर साइंस) भी देखें :=)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≕ (U+2255 ≕ EQUALS COLON)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≖ (U+2256 ≖ RING IN EQUAL TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≗ (U+2257 ≗ RING EQUAL TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≘ (U+2258 ≘ CORRESPONDS TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≙ (U+2259 ≙ ESTIMATES)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≚ (U+225A ≚ EQUIANGULAR TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≛ (U+225B ≛ STAR EQUALS)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≜ (U+225C ≜ DELTA EQUAL TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≞ (U+225E ≞ MEASURED BY)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >≟ (U+225F ≟ QUESTIONED EQUAL TO)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >⩴ (U+2A74 ⩴ DOUBLE COLON EQUAL) (बैकस-नौर फॉर्म भी देखें ::=)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >⩵ (U+2A75 ⩵ TWO CONSECUTIVE EQUALS SIGNS)
  • <अवधि शैली = फ़ॉन्ट-आकार: 150%; रेखा-ऊंचाई: 50%; >⩶ (U+2A76 ⩶ THREE CONSECUTIVE EQUALS SIGNS)

गलत उपयोग

समानता दिखाने के अतिरिक्त (विशेष रूप से शुरुआती गणित के छात्रों द्वारा) गणित के चरणों को गैर-मानक तरीके से जोड़ने के लिए गणितीय तर्क के भीतर कभी-कभी बराबर चिह्न का गलत तरीके से उपयोग किया जाता है।

उदाहरण के लिए, यदि कोई संख्या 1, 2, 3, 4, और 5 का योग खोज रहा है, तो कोई गलत लिख सकता है

1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15।

संरचनात्मक रूप से, यह के लिए आशुलिपि है

([(1 + 2 = 3) + 3 = 6] + 4 = 10) + 5 = 15,

किन्तु अंकन गलत है, क्योंकि समानता के प्रत्येक भाग का अलग मूल्य है। यदि इसे कठोरता से व्याख्या की जाती है जैसा कि यह कहता है, तो इसका अर्थ यह होगा

3 = 6 = 10 = 15 = 15।

तर्क का सही संस्करण होगा

1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15।

यह कठिनाई शिक्षा में संकेत के सूक्ष्म रूप से विभिन्न उपयोगों से उत्पन्न होती है। शुरुआती, अंकगणित-केंद्रित ग्रेड में, समान चिह्न चालू हो सकता है; इलेक्ट्रॉनिक कैलकुलेटर पर बराबर बटन के समान यह गणना के परिणाम की मांग करता है। बीजगणित पाठ्यक्रमों में प्रारंभ होने पर, संकेत दो गणनाओं के बीच समानता का संबंधपरक अर्थ लेता है। संकेत के दो उपयोगों के बीच भ्रम कभी-कभी विश्वविद्यालय स्तर पर बना रहता है।[16]

एनकोडिंग

  • U+003D = EQUALS SIGN (&equals;)

संबंधित:

  • U+2260 ≠ NOT EQUAL TO (&ne;, &NotEqual;)
  • U+FE66 ﹦ SMALL EQUALS SIGN
  • U+FF1D ＝ FULLWIDTH EQUALS SIGN
  • U+1F7F0 🟰 HEAVY EQUALS SIGN

यह भी देखें

Look up = in Wiktionary, the free dictionary.
Look up Appendix:Variations of "=" in Wiktionary, the free dictionary.

टिप्पणियाँ

  1. ↑ Weisstein, Eric W. "बराबर". mathworld.wolfram.com (in English). Retrieved 2020-08-09.
  2. ↑ "C0 Controls and Basic Latin Range: 0000–007F" (PDF). Unicode Consortium. p. 0025 – 0041.
  3. ↑ "EQUAL की परिभाषा". www.merriam-webster.com (in English). Retrieved 2020-08-09.
  4. ↑ "गणित में समानता प्रतीकों का इतिहास". Sciencing (in English). Retrieved 2020-08-09.
  5. ↑ See also geminus and Gemini.
  6. ↑ Recorde, Robert (1557). The Whetstone of Witte'. London, England: John Kyngstone. the third page of the chapter "The rule of equation, commonly called Algebers Rule."
  7. ↑ "रॉबर्ट रिकॉर्डे". MacTutor History of Mathematics archive. Retrieved 19 October 2013.
  8. ↑ Peter G. Constable; Lorna A. Priest (31 July 2006). अतिरिक्त ऑर्थोग्राफिक और संशोधक वर्णों को एनकोड करने का प्रस्ताव (PDF). Retrieved 19 October 2013.
  9. ↑ Hartell, Rhonda L., ed. (1993). अफ्रीका के अक्षर. Dakar: UNESCO and SIL. Retrieved 19 October 2013.
  10. ↑ "यूनिकोड लैटिन विस्तारित-डी कोड चार्ट" (PDF). Unicode.org. Retrieved 19 October 2013.
  11. ↑ Gray, Carroll F. (November 2006). "The 1906 Santos=Dumont No. 14bis". World War I Aeroplanes. No. 194: 4.
  12. ↑ "इंटरलीनियर मॉर्फेम-बाय-मॉर्फिम ग्लोस के लिए कन्वेंशन". Retrieved 2017-11-20.
  13. ↑ "HRC Story: Our Logo." The Human Rights Campaign. HRC.org, Retrieved 4 December 2018.
  14. ↑ "सम नही". Anti-Defamation League (in English). Retrieved 2021-02-25.
  15. ↑ 15.0 15.1 "गणितीय ऑपरेटर्स" (PDF). Unicode.org. Retrieved 19 October 2013.
  16. ↑ Capraro, Robert M.; Capraro, Mary Margaret; Yetkiner, Ebrar Z.; Corlu, Sencer M.; Ozel, Serkan; Ye, Sun; Kim, Hae Gyu (2011). "पाठ्यपुस्तकों में समस्या के प्रकारों और संबंधपरक समानता की छात्रों की समझ के बीच एक अंतर्राष्ट्रीय परिप्रेक्ष्य". Mediterranean Journal for Research in Mathematics Education. 10 (1–2): 187–213. Retrieved 19 October 2013.


संदर्भ


बाहरी संबंध

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=बराबर_का_चिन्ह&oldid=172516’