अरैखिक आयामीता अवकरण

शीर्ष-बाएँ: मध्य में एक आयताकार छेद के साथ एक सर्पिलिंग बैंड (उर्फ स्विस रोल) में 1000 बिंदुओं का एक 3D आंकड़ा समुच्चय। टॉप-राइट: मूल 2D बहुविध जिसका उपयोग 3D आंकड़ा समुच्चय उत्पन्न करने के लिए किया जाता है। नीचे बाएँ और दाएँ: मॉड्यूलर आकड़ों प्रोसेसिंग टूलकिट द्वारा कार्यान्वित नॉनलाइनियर विमीयता न्यूनीकरण#स्थानीय-रैखिक अंतःस्थापन और नॉनलाइनियर विमीयता न्यूनीकरण#हेसियन लोकल-लीनियर अंतःस्थापन (हेसियन एलएलई) कलन विधि का उपयोग करके क्रमशः बहुविध की 2डी रिकवरी।

अरैखिक आयामीता अवकरण, जिसे बहुविध अधिगम के रूप में भी जाना जाता है, विभिन्न संबंधित प्रविधियों को संदर्भित करता है, जिसका उद्देश्य निम्न आयामी समष्टि में आकड़ों को दृष्टिगत करने या मानचित्रण अधिगम के लक्ष्य के साथ उच्च-आयामी आकड़ों को निम्न-आयामी अव्यक्त बहुविध पर प्रक्षेप करना है (या तो उच्च-आयामी समष्टि से निम्न-आयामी अंतःस्थापन या इसके विपरीत)।^[1]^[2] नीचे वर्णित प्रविधियों को रेखीय अपघटन विधियों के सामान्यीकरण के रूप में समझा जा सकता है, जो आयामीता अवकरण के लिए उपयोग की जाती हैं, जैसे कि अद्वितीय मान अपघटन और प्रमुख घटक विश्लेषण है।

एनएलडीआर के अनुप्रयोग

एक आव्यूह (या एक आंकड़ाकोष तालिका) के रूप में दर्शाए गए आंकड़ा समुच्चय पर विचार करें, जैसे कि प्रत्येक पंक्ति विशेषताओं (या सुविधाओं या आयामों) के एक समुच्चय का प्रतिनिधित्व करती है जो किसी विशेष उदाहरण का वर्णन करती है। यदि विशेषताओं की संख्या बड़ी है, तो अद्वितीय संभावित पंक्तियों का समष्टि घातीय रूप से बड़ा है। इस प्रकार, आयाम जितना बड़ा होता है, समष्टि का प्रतिरूप लेना उतना ही कठिन हो जाता है। इससे अनेक समस्याएं होती हैं। कलन विधि जो उच्च-आयामी आकड़ों पर कार्य करते हैं, उनमें बहुत अधिक समय जटिलता होती है। अनेक यंत्र अधिगम कलन विधि, उदाहरण के लिए, उच्च-आयामी आकड़ों के साथ संघर्ष करते हैं। आकड़ों को कम आयामों में कम करना प्रायः विश्लेषण कलन विधि को अधिक कुशल बनाता है, और यंत्र अधिगम कलन विधि को अधिक सटीक भविष्यवाणी करने में सहायता कर सकता है।

मनुष्यों को प्रायः उच्च आयामों में आकड़ों को समझने में कठिनाई होती है। इस प्रकार, आकड़ों को कम संख्या में आयामों तक कम करना प्रत्योक्षकरण उद्देश्यों के लिए उपयोगी है।

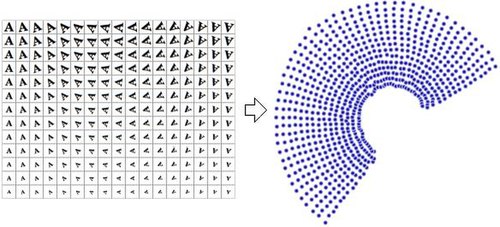
एनएलडीआर कलन विधि का उपयोग करने के परिणामस्वरूप द्वि-आयामी बिंदुओं का क्षेत्रक। इस स्थिति में, बहुविध स्कल्प्टिंग का उपयोग आकड़ों को केवल दो आयामों (वर्तन और पैमाने) में कम करने के लिए किया जाता है।

आकड़ों के निम्न-आयामी प्रतिनिधित्व को प्रायः "आंतरिक चर" के रूप में संदर्भित किया जाता है। इस विवरण का तात्पर्य है कि ये वे मान हैं जिनसे आकड़ों का उत्पादन किया गया था। उदाहरण के लिए, एक ऐसे आँकड़े समुच्चय पर विचार करें जिसमें 'A' अक्षर की छवियां हों, जिसे अलग-अलग मात्रा में अनुमाप और घूर्णन किया गया हो। प्रत्येक छवि में 32×32 चित्रांश हैं। प्रत्येक छवि को 1024 चित्रांश मानों के सदिश के रूप में दर्शाया जा सकता है। प्रत्येक पंक्ति 1024-आयामी समष्टि (एक हैमिंग समष्टि) में द्वि-आयामी बहुविध पर एक प्रतिरूप है। आंतरिक आयाम दो है, क्योंकि आकड़ों उत्पन्न करने के लिए दो चर (वर्तन और पैमाने) भिन्न थे। अक्षर 'A' के आकार या रूप के विषय में सूचना अंतस्थ चर का भाग नहीं है क्योंकि यह प्रत्येक उदाहरण में समान है। अरैखिक आयामीता अवकरण संबंधित सूचना (अक्षर 'A') को छोड़ देगा और केवल अलग-अलग सूचना (वर्तन और पैमाने) को पुनर्प्राप्त करेगा। दाईं ओर की छवि इस आंकड़ा समुच्चय से प्रतिरूप छवियां दर्शाती है (समष्टि को बचाने के लिए, सभी निविष्टि छवियां नहीं दिखाई जाती हैं), और द्वि-आयामी बिंदुओं का एक क्षेत्रक जो एनएलडीआर कलन विधि का उपयोग करने के परिणामस्वरूप होता है (इस स्थिति में, बहुविध मूर्तिकला का उपयोग किया गया था) आकड़ों को केवल दो आयामों में कम करने के लिए है।

पीसीए (एक रैखिक आयामी कमी कलन विधि) का उपयोग इसी आंकड़ा समुच्चय को दो आयामों में कम करने के लिए किया जाता है, परिणामी मान इतनी अच्छी तरह व्यवस्थित नहीं होते हैं।

तुलनात्मक रूप से, यदि प्रमुख घटक विश्लेषण, जो कि एक रैखिक आयामी अवकरण कलन विधि है, जिसका उपयोग इसी आंकड़ा समुच्चय को दो आयामों में कम करने के लिए किया जाता है, तो परिणामी मान इतनी अच्छी तरह व्यवस्थित नहीं होते हैं। यह दर्शाता है कि उच्च-आयामी सदिश (प्रत्येक अक्षर 'A' का प्रतिनिधित्व करते हैं) जो इस बहुविध का प्रतिरूप गैर-रैखिक तरीके से भिन्न होते हैं।

इसलिए, यह स्पष्ट होना चाहिए कि एनएलडीआर के अभिकलक दृष्टि के क्षेत्र में अनेक अनुप्रयोग हैं। उदाहरण के लिए, एक ऐसे यंत्रमानव पर विचार करें जो संवृत्त स्थैतिक वातावरण में संचालन करने के लिए छायाचित्रक का उपयोग करता है। उस छायाचित्रक द्वारा प्राप्त छवियों को उच्च-आयामी समष्टि में बहुविध प्रतिरूप माना जा सकता है, और उस बहुविध के आंतरिक चर यंत्रमानव की स्थिति और अभिविन्यास का प्रतिनिधित्व करेंगे।

गतिशील प्रणाली में प्रतिरूप अनुक्रम अवकरण के लिए अपरिवर्तनीय बहुविध सामान्य रुचि है। विशेष रूप से, यदि चरण समष्टि में एक आकर्षक अपरिवर्तनीय बहुविध है, तो आस-पास के प्रक्षेपवक्र उस पर अभिसरण करेंगे और उस पर अनिश्चित काल तक बने रहेंगे, जिससे यह गतिशील प्रणाली की आयामीता अवकरण के लिए एक प्रत्याशी बन जाएगा। जबकि इस तरह के बहुविध सामान्य रूप से उपस्थित होने की प्रत्याभूति नहीं देते है, वर्णक्रमीय उप-बहुविध (SSM) का सिद्धांत गतिशील प्रणालियों के एक व्यापक वर्ग में अद्वितीय आकर्षक अपरिवर्तनीय वस्तुओं के अस्तित्व के लिए प्रतिबन्ध देता है।^[3] एनएलडीआर में सक्रिय शोध, मॉडलिंग प्रविधियों को विकसित करने के लिए गतिशील प्रणालियों से जुड़े बहुविध अवलोकन प्रकट करना चाहता है।^[4]

कुछ अधिक प्रमुख अरैखिक आयामी अवकरण प्रविधियों नीचे सूचीबद्ध हैं।

महत्वपूर्ण अवधारणाएँ

सैमन की मानचित्रण

सैमन का मानचित्रण पहली और सबसे लोकप्रिय एनएलडीआर प्रविधियों में से एक है।

एक आयामी स्व-संगठित मानचित्र (लाल वर्गों के साथ एक टूटी हुई रेखा, 20 नोड्स) द्वारा एक प्रमुख वक्र का अनुमान। पहला प्रधान घटक विश्लेषण एक नीली सीधी रेखा द्वारा प्रस्तुत किया गया है। आकड़ों बिंदु छोटे धूसर वृत्त होते हैं। पीसीए के लिए, इस उदाहरण में अस्पष्ट विचरण का अंश 23.23% है, एसओएम के लिए यह 6.86% है।^[5]

स्व-आयोजन मानचित्र

स्व-संगठित मानचित्र (SOM, जिसे कोहोनेन मानचित्र भी कहा जाता है) और इसके संभाव्य भिन्नरूप उत्पादक स्थलाकृतिक मानचित्रण (GTM) अंत:स्थापित समष्टि में एक बिंदु प्रतिनिधित्व का उपयोग करते हैं ताकि अंत:स्थापित समष्टि से उच्च आयामी समष्टि तक गैर-रैखिक मानचित्रण के आधार पर एक अव्यक्त चर प्रतिरूप बनाया जा सके।^[6] ये प्रविधियां घनत्व संजाल पर कार्य करने से संबंधित हैं, जो समान संभाव्य प्रतिरूप के निकटवर्ती भी आधारित हैं।

कर्नेल प्रमुख घटक विश्लेषण

संभवतः आयामी अवकरण के लिए सबसे व्यापक रूप से उपयोग किया जाने वाला कलन विधि कर्नेल पीसीए है।^[7] पीसीए सहप्रसरण आव्यूह $m\times n$ आव्यूह $\mathbf {X}$ की गणना से प्रारंभ होता है

C={\frac {1}{m}}\sum _{i=1}^{m}{\mathbf {x} _{i}\mathbf {x} _{i}^{\mathsf {T}}}.

यह तब आकड़ों को उस आव्यूह के पहले k आइजन सदिश पर प्रक्षेप करता है। तुलनात्मक रूप से, केपीसीए एक उच्च-आयामी समष्टि में परिवर्तित होने के पश्चात आकड़ों के सहप्रसरण आव्यूह की गणना करके प्रारंभ होता है,

C={\frac {1}{m}}\sum _{i=1}^{m}{\Phi (\mathbf {x} _{i})\Phi (\mathbf {x} _{i})^{\mathsf {T}}}.

यह तब पीसीए की तरह, उस आव्यूह के पहले k आइजन सदिश पर रूपांतरित आकड़ों को प्रक्षेप करता है। यह अधिकांश संगणनाओं को दूर करने के लिए कर्नेल क्रमभंग का उपयोग करता है, जैसे कि पूर्ण प्रक्रिया वास्तव में संगणना $\Phi (\mathbf {x} )$ के बिना की जा सकती है। बिल्कुल, $\Phi$ इस तरह चयन किया जाना चाहिए कि इसमें ज्ञात संबंधित कर्नेल हो। दुर्भाग्य से, दी गई समस्या के लिए एक अच्छा कर्नेल खोजना तुच्छ नहीं है, इसलिए केपीसीए मानक कर्नेल का उपयोग करते समय कुछ समस्याओं के साथ अच्छे परिणाम नहीं देता है। उदाहरण के लिए, यह स्विस रोल बहुविध पर इन कर्नेल के साथ खराब प्रदर्शन करने के लिए जाना जाता है। हालांकि, हालांकि, आंकड़े-निर्भर कर्नेल आव्यूह का निर्माण करके कर्नेल पीसीए के विशेष स्थितियों के रूप में कुछ अन्य तरीकों को देखा जा सकता है जो इस तरह की समायोजन में अच्छा प्रदर्शन करते हैं (उदाहरण के लिए, लाप्लासियन ईजेनमैप्स, एलएलई)।^[8]

केपीसीए के पास एक आंतरिक प्रतिरूप है, इसलिए इसका उपयोग इसके अंतःस्थापन पर उन बिंदुओं को प्रतिचित्र करने के लिए किया जा सकता है जो प्रशिक्षण के समय उपलब्ध नहीं थे।

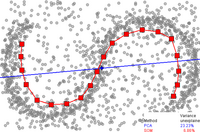
प्रधान वक्र और बहुविध

प्रधान कर्व्स का अनुप्रयोग: जीवन सूचकांक की अरैखिक गुणवत्ता।^[9] अंक 4 संकेतकों के मूल्यों द्वारा गठित 4-आयामी समष्टि में संयुक्त राष्ट्र के 171 देशों के आकड़ों का प्रतिनिधित्व करते हैं: सकल घरेलू उत्पाद, जीवन प्रत्याशा, शिशु मृत्यु दर, तपेदिक घटना। विभिन्न रूप और रंग विभिन्न भौगोलिक स्थानों के अनुरूप हैं। रेड बोल्ड लाइन आंकड़ा समुच्चय का अनुमान लगाते हुए प्रमुख वक्र का प्रतिनिधित्व करती है। यह प्रमुख वक्र लोचदार मानचित्र की विधि द्वारा निर्मित किया गया था। सॉफ्टवेयर मुफ्त गैर-व्यावसायिक उपयोग के लिए उपलब्ध है।^[10]^[11]

प्रधान वक्र और बहुविध अरैखिक आयामीता न्यूनीकरण के लिए प्राकृतिक ज्यामितीय संरचना देते हैं और स्पष्ट रूप से एक अंत:स्थापित बहुविध का निर्माण करके, और बहुविध पर मानक ज्यामितीय प्रक्षेपण का उपयोग करके कूटलेखन द्वारा पीसीए की ज्यामितीय व्याख्या का विस्तार करते हैं। यह दृष्टिकोण मूल रूप से ट्रेवर हेस्टी द्वारा उनके 1984 थीसिस में प्रस्तावित किया गया था,^[12] जिसे उन्होंने औपचारिक रूप से 1989 में प्रस्तुत किया था।^[13] इस विचार को अनेक लेखकों ने आगे खोजा है।^[14]

बहुविध की "सरलता" को कैसे परिभाषित किया जाए, यह समस्या पर निर्भर है, हालांकि, इसे सामान्यतः आंतरिक विमीयता और/या बहुविध की सहजता से मापा जाता है। सामान्यतः, प्रधान बहुविध को अनुकूलन समस्या के समाधान के रूप में परिभाषित किया जाता है। उदेश्य फलन में आंकड़े सन्निकटन की गुणवत्ता और बहुविध बंकन के लिए कुछ दंड शब्द सम्मिलित हैं। लोकप्रिय प्रारंभिक अनुमान रैखिक पीसीए और कोहोनेन के एसओएम द्वारा उत्पन्न होते हैं।

लाप्लासियन ईजेनमैप्स

लाप्लासियन ईजेन मानचित्र आयामीता में कमी करने के लिए वर्णक्रमीय प्रविधियों का उपयोग करता है।^[15] यह प्रविधि मूलभूत धारणा पर निर्भर करती है कि आंकड़े उच्च-आयामी समष्टि में निम्न-आयामी बहुविध में स्थित है।^[16] यह कलन विधि प्रतिरूप से बाह्य बिंदुओं को अंतःस्थापित नहीं कर सकता है, परन्तु इस क्षमता को जोड़ने के लिए कर्नेल हिल्बर्ट समष्टि का पुनरुत्पादन नियमितीकरण पर आधारित प्रविधि उपस्थित हैं।^[17] ऐसी प्रविधियों को अन्य गैर-रैखिक आयामी अवकरण कलन विधि पर भी अनुप्रयुक्त किया जा सकता है।

प्रमुख घटक विश्लेषण जैसी पारंपरिक प्रविधियों आकड़ों की आंतरिक ज्यामिति पर विचार नहीं करती हैं। लाप्लासियन ईजेन मानचित्र आकड़ों समुच्चय निकटवर्ती की सूचना से एक आलेख बनाता है। प्रत्येक आकड़ों बिंदु आलेख पर एक बिंदु के रूप में कार्य करता है और बिंदु के मध्य संयोजकता निकटवर्ती बिंदुओं की निकटता द्वारा नियंत्रित होती है (उदाहरण के लिए k-निकटतम निकटवर्ती कलन विधि का उपयोग करके)। इस प्रकार उत्पन्न आलेख को उच्च-आयामी समष्टि में निम्न-आयामी बहुविध के असतत सन्निकटन के रूप में माना जा सकता है। आलेख के आधार पर लागत फलन का न्यूनीकरण यह सुनिश्चित करता है कि बहुविध पर एक-दूसरे के निकट के बिंदुओं को निम्न-आयामी समष्टि में एक-दूसरे के निकट प्रतिचित्र किया जाता है, स्थानीय दूरी को संरक्षित करता है। बहुविध पर लाप्लास-बेल्ट्रामी प्रचालक के ईजेनफलन अंतःस्थापन आयामों के रूप में कार्य करते हैं, क्योंकि सौम्य परिस्थितियों में इस प्रचालक के पास एक गणनीय वर्णक्रम होता है जो कि बहुविध पर वर्ग पूर्णांक फलनों के लिए एक आधार होता है। लाप्लासियन ईजेन मानचित्र को ठोस सैद्धांतिक आधार पर रखने का प्रयास कुछ सफलता के साथ मिला है, जैसा कि कुछ गैर-प्रतिबंधात्मक मान्यताओं के अंतर्गत, आलेख लाप्लासियन आव्यूह को लाप्लास-बेल्ट्रामी प्रचालक में अभिसरण करने के लिए दर्शाया गया है क्योंकि अंकों की संख्या अनंत तक जाती है।^[16]

आइसोमैप

आइसोमैप^[18] उत्कृष्ट बहुआयामी सोपानन के साथ फ्लोयड-वॉर्शल कलन विधि का एक संयोजन है। उत्कृष्ट बहुआयामी सोपानन (MDS) सभी बिंदुओं के मध्य युग्म-वार दूरी का एक आव्यूह लेता है और प्रत्येक बिंदु के लिए एक स्थिति की गणना करता है। आइसोमैप मानता है कि युग्म-वार दूरी केवल निकटवर्ती बिंदुओं के मध्य ही जानी जाती है, और अन्य सभी बिंदुओं के मध्य युग्म-वार दूरी की गणना करने के लिए फ़्लॉइड-वॉर्शल कलन विधि का उपयोग करती है। यह प्रभावी रूप से सभी बिंदुओं के मध्य युग्म-वार अल्पांतरी दूरियों के पूर्ण आव्यूह का अनुमान लगाता है। आइसोमैप तब सभी बिंदुओं की निम्न-आयामी स्थिति की गणना करने के लिए उत्कृष्ट एमडीएस का उपयोग करता है। लैंडमार्क-आइसोमैप इस कलन विधि का एक प्रकार है जो कुछ सटीकता की कीमत पर गति बढ़ाने के लिए सीमाचिह्न का उपयोग करता है।

बहुविध अधिगम में, निविष्टि आकड़ों को निम्न आयामी बहुविध से प्रतिरूप माना जाता है जो उच्च-आयामी सदिश समष्टि के भीतर अंत:स्थापित होता है। एमवीयू के पीछे मुख्य अंतर्ज्ञान बहुविध की स्थानीय रैखिकता का लाभ उठाना है और एक मानचित्रण बनाना है जो अंतर्निहित बहुविध के प्रत्येक बिंदु पर स्थानीय निकटवर्ती को संरक्षित करता है।

स्थानीय-रैखिक अंतःस्थापन

स्थानीय-रैखिक अंतःस्थापन (LLE) को लगभग उसी समय प्रस्तुत किया गया था जब आइसोमैप को प्रस्तुत किया गया था।^[19]आइसोमैप पर इसके अनेक लाभ हैं, जिसमें विरल आव्यूह कलन विधि का लाभ उठाने के लिए अनुप्रयुक्त किए जाने पर तीव्र अनुकूलन और अनेक समस्याओं के साथ उन्नत परिणाम सम्मिलित हैं। एलएलई भी प्रत्येक बिंदु के निकटतम सहवासियों का एक समुच्चय ढूंढकर प्रारंभ होता है। इसके बाद यह प्रत्येक बिंदु के लिए भार के एक समुच्चय की गणना करता है जो बिंदु को अपने सहवासियों के रैखिक संयोजन के रूप में सर्वोत्तम रूप से वर्णित करता है। अंत में, यह बिंदुओं के निम्न-आयामी अंतःस्थापन को खोजने के लिए एक ईजेनसदिश-आधारित अनुकूलन प्रविधि का उपयोग करता है, जैसे कि प्रत्येक बिंदु अभी भी अपने सहवासियों के समान रैखिक संयोजन के साथ वर्णित है। एलएलई गैर-समान प्रतिरूप घनत्व को अनुचित तरीके से नियंत्रित करता है क्योंकि भार को अपवाही से रोकने के लिए कोई निश्चित इकाई नहीं है क्योंकि विभिन्न क्षेत्र प्रतिरूप घनत्व में भिन्न होते हैं। एलएलई का कोई आंतरिक प्रतिरूप नहीं है।

एलएलई अपने सहवासियों X_j के आधार पर एक बिंदु X_i के बैरीसेंट्रिक निर्देशांक की गणना करता है। मूल बिंदु को उसके सहवासियों के भार आव्यूह W_ij द्वारा दिए गए रैखिक संयोजन द्वारा पुनर्निर्मित किया जाता है। पुनर्निर्माण त्रुटि लागत फलन E(W) द्वारा दी गई है

E(W)=\sum _{i}\left|\mathbf {X} _{i}-\sum _{j}{\mathbf {W} _{ij}\mathbf {X} _{j}}\right|^{2}

भार W_ij बिंदु X के पुनर्निर्माण के पर्यन्त बिंदु X_j के योगदान की मात्रा को संदर्भित करता है। लागत फलन दो बाधाओं के अंतर्गत कम किया गया है: (a) प्रत्येक आंकड़े बिंदु X_j को केवल अपने सहवासियों से पुनर्निर्मित किया जाता है, इस प्रकार W_ij को शून्य होने के लिए विवश किया जाता है यदि बिंदु X_j बिंदु X_i का निकटवर्ती नहीं है और (b) की प्रत्येक पंक्ति का योग भार आव्यूह 1 के समान है

\sum _{j}{\mathbf {W} _{ij}}=1

मूल आंकड़े बिंदुओं को एक D आयामी समष्टि में एकत्र किया जाता है और कलन विधि का लक्ष्य आयामी को कम करना है जैसे कि D >> d है। D आयामी समष्टि में iवें आंकड़े बिंदुओं को पुनः बनाने वाले वही भार W_ij का उपयोग निम्न d आयामी समष्टि में उसी बिंदु को पुनः बनाने के लिए किया जाएगा। इस विचार के आधार पर निकटवर्ती को संरक्षित करने वाला प्रतिचित्र बनाया जाता है। D आयामी समष्टि में, प्रत्येक बिंदु X_i को लागत फलन को कम करके d आयामी समष्टि में एक बिंदु Y_i पर प्रतिचित्र किया जाता है

C(Y)=\sum _{i}\left|\mathbf {Y} _{i}-\sum _{j}{\mathbf {W} _{ij}\mathbf {Y} _{j}}\right|^{2}

इस लागत फलन में, पिछले वाले के विपरीत, भार W_ij निश्चित रखा जाता है और बिंदुओं Y पर न्यूनीकरण किया जाता है_i निर्देशांक का अनुकूलन करने के लिए। इस न्यूनीकरण की समस्या को एक आव्यूह (N आकड़ों बिंदुओं की संख्या होने के नाते) के विरल N X N Eigendecomposition को हल करके हल किया जा सकता है, जिसका निचला d नॉनज़रो ईजेन सदिश निर्देशांक का एक ऑर्थोगोनल समुच्चय प्रदान करता है। सामान्यतः यूक्लिडियन दूरी द्वारा मापे गए K निकटतम सहवासियों से आकड़ों बिंदुओं का पुनर्निर्माण किया जाता है। इस तरह के कार्यान्वयन के लिए कलन विधि में केवल एक मुक्त मापदण्ड K है, जिसे क्रॉस सत्यापन द्वारा चुना जा सकता है।

हेसियन स्थानीय-रैखिक अंतःस्थापन (हेस्सियन एलएलई)

LLE की तरह, Hessian LLE भी विरल आव्यूह प्रविधि पर आधारित है।^[20] यह एलएलई की तुलना में बहुत अधिक गुणवत्ता वाले परिणाम देता है। दुर्भाग्य से, इसकी एक बहुत ही महंगी कम्प्यूटेशनल जटिलता है, इसलिए यह भारी प्रतिरूप बहुविध के लिए उपयुक्त नहीं है। इसका कोई आंतरिक प्रतिरूप नहीं है।

संशोधित स्थानीय-रैखिक अंतःस्थापन (MLLE)

संशोधित एलएलई (एमएलएलई)^[21] एक अन्य एलएलई संस्करण है जो स्थानीय भार आव्यूह कंडीशनिंग समस्या को दूर करने के लिए प्रत्येक निकटवर्ती में अनेक भारों का उपयोग करता है जो एलएलई मानचित्रों में विकृतियों की ओर जाता है। शिथिल रूप से अनेक भार बोलना एलएलई द्वारा उत्पादित मूल भार का स्थानीय ऑर्थोगोनल प्रक्षेपण है। इस नियमित संस्करण के निर्माता स्थानीय स्पर्शरेखा समष्टि संरेखण (एलटीएसए) के लेखक भी हैं, जो एमएलएलई फॉर्मूलेशन में निहित है, जब यह महसूस किया जाता है कि प्रत्येक भार सदिश के ऑर्थोगोनल अनुमानों का वैश्विक अनुकूलन, संक्षेप में, स्थानीय स्पर्शरेखा रिक्त समष्टि को संरेखित करता है। प्रत्येक आकड़ों बिंदु का। इस कलन विधि के सही अनुप्रयोग से सैद्धांतिक और अनुभवजन्य निहितार्थ दूरगामी हैं।^[22]

स्थानीय स्पर्शरेखा समष्टि संरेखण

स्थानीय स्पर्शरेखा समष्टि संरेखण^[23] अंतर्ज्ञान पर आधारित है कि जब एक बहुविध को सही ढंग से प्रकट किया जाता है, तो बहुविध के सभी स्पर्शरेखा हाइपरप्लेन संरेखित हो जाएंगे। यह हर बिंदु के k-निकटतम सहवासियों की गणना करके प्रारंभ होता है। यह प्रत्येक स्थानीय निकटवर्ती में डी-प्रथम प्रमुख घटकों की गणना करके प्रत्येक बिंदु पर स्पर्शरेखा समष्टि की गणना करता है। यह तब एक अंतःस्थापन खोजने के लिए अनुकूलित करता है जो स्पर्शरेखा रिक्त समष्टि को संरेखित करता है।

प्रकट होने वाला अधिकतम विचरण

अधिकतम भिन्नता प्रकट करना , आइसोमैप और स्थानीय रूप से लीनियर अंतःस्थापन इस धारणा पर निर्भर एक सामान्य अंतर्ज्ञान साझा करते हैं कि यदि बहुविध ठीक से अनफोल्ड किया जाता है, तो बिंदुओं पर विचरण अधिकतम हो जाता है। इसका प्रारंभिक चरण, जैसे आइसोमैप और स्थानीय रूप से रैखिक अंतःस्थापन, प्रत्येक बिंदु के के-निकटतम सहवासियों को ढूंढ रहा है। इसके बाद यह सभी गैर-निकटवर्ती बिंदुओं के मध्य की दूरी को अधिकतम करने की समस्या को हल करना चाहता है, इस तरह व्यवरूद्ध किया जाता है कि निकटवर्ती बिंदुओं के मध्य की दूरी संरक्षित रहे। इस कलन विधि का प्राथमिक योगदान इस समस्या को एक अर्ध-निश्चित प्रोग्रामिंग समस्या के रूप में ढालने की एक प्रविधि है। दुर्भाग्य से, अर्ध-निश्चित प्रोग्रामिंग सॉल्वरों की उच्च कम्प्यूटेशनल लागत होती है। स्थानीय रूप से रैखिक अंतःस्थापन की तरह, इसका कोई आंतरिक प्रतिरूप नहीं है।

autoencoder

एक ऑटोएन्कोडर एक फीड-फॉरवर्ड तंत्रिका संजाल है जिसे पहचान फलन का अनुमान लगाने के लिए प्रशिक्षित किया जाता है। यही है, इसे मूल्यों के सदिश से उसी सदिश में प्रतिचित्र करने के लिए प्रशिक्षित किया जाता है। जब आयाम अवकरण के उद्देश्यों के लिए उपयोग किया जाता है, तो संजाल में छिपी हुई परतों में से एक में केवल कुछ ही संजाल इकाइयां होती हैं। इस प्रकार, संजाल को सदिश को कम संख्या में आयामों में एन्कोड करना सीखना चाहिए और फिर इसे मूल समष्टि पर वापस डिकोड करना चाहिए। इस प्रकार, संजाल का पहला भाग एक ऐसा प्रतिरूप है जो उच्च से निम्न-आयामी समष्टि तक प्रतिचित्र करता है, और दूसरी छमाही निम्न से उच्च-आयामी समष्टि तक प्रतिचित्र करता है। हालांकि ऑटोएन्कोडर का विचार काफी पुराना है,^[24] डीप ऑटोएन्कोडर का प्रशिक्षण हाल ही में प्रतिबंधित बोल्ट्जमैन मशीनों और स्टैक्ड डीनोइजिंग ऑटोएनकोडर्स के उपयोग के माध्यम से संभव हुआ है। Autoencoders से संबंधित न्यूरोस्केल कलन विधि है, जो उच्च-आयामी से अंत:स्थापित समष्टि तक गैर-रैखिक मानचित्रण अधिगम के लिए बहुआयामी सोपानन और सैमॉन मानचित्रण (ऊपर देखें) से प्रेरित तनाव फलनों का उपयोग करता है। NeuroScale संपो की मानचित्रण रेडियल आधार फलन संजाल पर आधारित हैं।

गाऊसी प्रक्रिया अव्यक्त चर प्रतिरूप

गाऊसी प्रक्रिया अव्यक्त चर प्रतिरूप (GPLVM)^[25] संभाव्य आयामी कमी के तरीके हैं जो उच्च आयामी आकड़ों के निम्न आयामी गैर-रैखिक अंतःस्थापन को खोजने के लिए गॉसियन प्रक्रियाओं (जीपी) का उपयोग करते हैं। वे पीसीए के संभाव्य सूत्रीकरण का विस्तार हैं। प्रतिरूप को संभावित रूप से परिभाषित किया गया है और अव्यक्त चर तब हाशिए पर हैं और संभावना को अधिकतम करके मापदण्ड प्राप्त किए जाते हैं। कर्नेल पीसीए की तरह वे एक गैर रेखीय मानचित्रण (गाऊसी प्रक्रिया के रूप में) बनाने के लिए एक कर्नेल फलन का उपयोग करते हैं। हालाँकि, GPLVM में मानचित्रण अंत:स्थापित (अव्यक्त) समष्टि से आकड़ों समष्टि (जैसे घनत्व संजाल और GTM) तक है जबकि कर्नेल PCA में यह विपरीत दिशा में है। यह मूल रूप से उच्च आयामी आकड़ों के प्रत्योक्षकरण के लिए प्रस्तावित किया गया था, परन्तु दो अवलोकन स्थानों के मध्य एक साझा बहुविध प्रतिरूप बनाने के लिए इसका विस्तार किया गया है। जीपीएलवीएम और इसके अनेक रूपों को विशेष रूप से मानव गति मॉडलिंग के लिए प्रस्तावित किया गया है, उदाहरण के लिए, बैक कंस्ट्रेन्ड जीपीएलवीएम, जीपी डायनामिक प्रतिरूप (जीपीडीएम), संतुलित जीपीडीएम (बी-जीपीडीएम) और टोपोलॉजिकल रूप से बाधित जीपीडीएम। गैट विश्लेषण में पोज़ और गैट बहुविध के युग्मन प्रभाव को पकड़ने के लिए, एक मल्टी-लेयर ज्वाइंट गैट-पोज़ बहुविध प्रस्तावित किया गया था।^[26]

टी-वितरित स्टोकेस्टिक निकटवर्ती अंतःस्थापन

टी-वितरित स्टोकेस्टिक निकटवर्ती अंतःस्थापन (टी-एसएनई)^[27] व्यापक रूप से उपयोग किया जाता है। यह स्टोचैस्टिक निकटवर्ती अंतःस्थापन विधियों के परिवार में से एक है। कलन विधि संभावना की गणना करता है कि उच्च-आयामी समष्टि में डेटापॉइंट्स के जोड़े संबंधित हैं, और फिर निम्न-आयामी अंतःस्थापन चुनते हैं जो एक समान वितरण उत्पन्न करते हैं।

अन्य कलन विधि

संबंधपरक परिप्रेक्ष्य मानचित्र

रिलेशनल पर्सपेक्टिव प्रतिचित्र एक बहुआयामी सोपानन कलन विधि है। कलन विधि एक संवृत्त बहुविध पर एक बहु-कण गतिशील प्रणाली का अनुकरण करके बहुविध आकड़ों बिंदुओं का एक विन्यास पाता है, जहां आकड़ों बिंदुओं को कणों और दूरी (या असमानता) के लिए प्रतिचित्र किया जाता है, आकड़ों बिंदुओं के मध्य एक प्रतिकारक बल का प्रतिनिधित्व करता है। चूंकि बहुविध धीरे-धीरे आकार में बढ़ता है, बहु-कण प्रणाली धीरे-धीरे शांत हो जाती है और कॉन्फ़िगरेशन में परिवर्तित हो जाती है जो आकड़ों बिंदुओं की दूरी की सूचना को दर्शाती है।

संबंधपरक परिप्रेक्ष्य नक्शा एक भौतिक प्रतिरूप से प्रेरित था जिसमें सकारात्मक रूप से आवेशित कण एक गेंद की सतह पर स्वतंत्र रूप से चलते हैं। कणों के मध्य चार्ल्स ऑगस्टिन डी कूलम्ब कूलम्ब के नियम द्वारा निर्देशित, कणों का न्यूनतम ऊर्जा विन्यास कणों के मध्य प्रतिकारक बलों की ताकत को प्रतिबिंबित करेगा।

संबंधपरक परिप्रेक्ष्य मानचित्र में प्रस्तुत किया गया था।^[28] कलन विधि ने सर्वप्रथम फ्लैट टोरस्र्स को इमेज बहुविध के रूप में उपयोग किया, फिर इसे विस्तारित किया गया है (सॉफ़्टवेयर VisuMap में अन्य प्रकार के संवृत्त बहुविध, जैसे वृत्त, प्रक्षेपण समष्टि , और क्लेन का उपयोग करने के लिए बोतल, छवि बहुविध के रूप में।

संक्रमण के नक्शे

कॉन्टैगियन मैप्स एक बिंदु क्लाउड के रूप में नोड्स को प्रतिचित्र करने के लिए एक संजाल पर अनेक छूत का उपयोग करते हैं।^[29] वैश्विक कैस्केड प्रतिरूप के स्थिति में प्रसार की गति को थ्रेसहोल्ड मापदण्ड के साथ समायोजित किया जा सकता है $t\in [0,1]$ . के लिए $t=0$ छूत का नक्शा आइसोमैप कलन विधि के बराबर है।

वक्रीय घटक विश्लेषण

Curvilinear घटक विश्लेषण (CCA) आउटपुट समष्टि में बिंदुओं के विन्यास की तलाश करता है जो आउटपुट समष्टि में छोटी दूरी पर ध्यान केंद्रित करते हुए यथासंभव मूल दूरी को संरक्षित करता है (इसके विपरीत सैमन की मानचित्रण जो मूल समष्टि में छोटी दूरी पर ध्यान केंद्रित करती है)।^[30] यह ध्यान दिया जाना चाहिए कि CCA, एक पुनरावृत्त अधिगम के कलन विधि के रूप में, वास्तव में बड़ी दूरी (जैसे सैमन कलन विधि) पर ध्यान केंद्रित करना प्रारंभ करता है, फिर धीरे-धीरे छोटी दूरी पर ध्यान केंद्रित करता है। यदि दोनों के मध्य समझौता करना पड़े तो छोटी दूरी की सूचना बड़ी दूरी की सूचना को अधिलेखित कर देगी।

CCA का स्ट्रेस फंक्शन राइट ब्रेगमैन डायवर्जेंस के योग से संबंधित है।^[31]

वक्रीय दूरी विश्लेषण

सीडीए^[30]एक स्व-संगठित तंत्रिका संजाल को बहुविध फिट करने के लिए प्रशिक्षित करता है और इसके अंतःस्थापन में भूगर्भीय दूरी को संरक्षित करने की कोशिश करता है। यह Curvilinear घटक विश्लेषण पर आधारित है (जो सैमन के मानचित्रण को विस्तारित करता है), परन्तु इसके बजाय अल्पांतरी दूरी का उपयोग करता है।

डिफियोमॉर्फिक विमीयता न्यूनीकरण

डिफियोमॉर्फिक विमीयता न्यूनीकरण या डिफियोमैप^[32] एक चिकनी डिफियोमोर्फिक मानचित्रण सीखता है जो आकड़ों को निम्न-आयामी रैखिक उप-समष्टि पर स्थानांतरित करता है। विधियाँ एक सुचारू समय अनुक्रमित सदिश क्षेत्र के लिए हल करती हैं जैसे कि क्षेत्र के साथ प्रवाह जो आकड़ों बिंदुओं पर प्रारंभ होता है, एक निम्न-आयामी रैखिक उप-समष्टि पर समाप्त होगा, जिससे आगे और उलटा मानचित्रण दोनों के अंतर्गत जोड़ीदार अंतर को संरक्षित करने का प्रयास किया जाएगा।

बहुविध संरेखण

बहुविध संरेखण इस धारणा का लाभ उठाता है कि समान जनरेटिंग प्रक्रियाओं द्वारा उत्पादित अलग-अलग आकड़ों समुच्चय एक समान अंतर्निहित बहुविध प्रतिनिधित्व साझा करेंगे। प्रत्येक मूल समष्टि से साझा बहुविध तक प्रक्षेपण सीखकर, पत्राचार पुनर्प्राप्त किया जाता है और एक डोमेन से ज्ञान दूसरे में स्थानांतरित किया जा सकता है। अधिकांश बहुविध संरेखण प्रविधि केवल दो आकड़ों सेटों पर विचार करती है, परन्तु यह अवधारणा मनमाने ढंग से अनेक प्रारंभिक आकड़ों सेटों तक फैली हुई है।^[33]

प्रसार मानचित्र

डिफ्यूजन मैप्स हीट डिफ्यूजन और यादृच्छिक चाल (मार्कोव चेन) के मध्य संबंध का लाभ उठाते हैं; बहुविध पर प्रसार प्रचालक और आलेख पर परिभाषित फलनों पर कार्य कर रहे एक मार्कोव संक्रमण आव्यूह के मध्य एक सादृश्य तैयार किया गया है, जिनके नोड्स को बहुविध से प्रतिरूप लिया गया था।^[34] विशेष रूप से, आकड़ों समुच्चय को किसके द्वारा दर्शाया जाना चाहिए $\mathbf {X} =[x_{1},x_{2},\ldots ,x_{n}]\in \Omega \subset \mathbf {R^{D}}$ . प्रसार मानचित्र की अंतर्निहित धारणा यह है कि उच्च-आयामी आकड़ों आयाम के निम्न-आयामी बहुविध पर स्थित है $\mathbf {d}$ . X आकड़ों समुच्चय का प्रतिनिधित्व करते हैं और $\mu$ एक्स पर आकड़ों बिंदुओं के वितरण का प्रतिनिधित्व करते हैं। इसके अलावा, एक कर्नेल को परिभाषित करें जो एक्स में बिंदुओं की समानता की कुछ धारणा का प्रतिनिधित्व करता है। कर्नेल ${\mathit {k}}$ निम्नलिखित गुण हैं^[35]

k(x,y)=k(y,x),

k सममित है

k(x,y)\geq 0\qquad \forall x,y,k

k सकारात्मकता को बनाए रखने वाला है

इस प्रकार कोई व्यक्ति व्यक्तिगत आकड़ों बिंदुओं को एक आलेख के नोड्स के रूप में और कर्नेल k को उस आलेख पर किसी प्रकार की आत्मीयता को परिभाषित करने के रूप में सोच सकता है। आलेख निर्माण द्वारा सममित है क्योंकि कर्नेल सममित है। यहां यह देखना आसान है कि टपल ('एक्स', 'के') से एक उत्क्रमणीय मार्कोव श्रृंखला का निर्माण किया जा सकता है। यह प्रविधि विभिन्न प्रकार के क्षेत्रों के लिए सामान्य है और इसे आलेख लाप्लासियन के रूप में जाना जाता है।

उदाहरण के लिए, गॉसियन कर्नेल का उपयोग करके आलेख 'के' = (एक्स, ई) का निर्माण किया जा सकता है।

K_{ij}={\begin{cases}e^{-\|x_{i}-x_{j}\|_{2}^{2}/\sigma ^{2}}&{\text{if }}x_{i}\sim x_{j}\\0&{\text{otherwise}}\end{cases}}

उपरोक्त समीकरण में, $x_{i}\sim x_{j}$ दर्शाता है $x_{i}$ का निकटतम निकटवर्ती है $x_{j}$ . उचित रूप से, अल्पांतरी दूरी का उपयोग वास्तव में बहुविध दूरियों को मापने के लिए किया जाना चाहिए। चूंकि बहुविध की सटीक संरचना उपलब्ध नहीं है, निकटतम सहवासियों के लिए अल्पांतरी दूरी यूक्लिडियन दूरी द्वारा अनुमानित है। विकल्प $\sigma$ निकटता की हमारी धारणा को इस अर्थ में संशोधित करता है कि यदि $\|x_{i}-x_{j}\|_{2}\gg \sigma$ तब $K_{ij}=0$ और अगर $\|x_{i}-x_{j}\|_{2}\ll \sigma$ तब $K_{ij}=1$ . पूर्व का अर्थ है कि बहुत कम प्रसार हुआ है जबकि बाद का अर्थ है कि प्रसार प्रक्रिया लगभग पूरी हो चुकी है। चुनने के लिए विभिन्न रणनीतियाँ $\sigma$ में पाए जा सकते हैं।^[36] मार्कोव आव्यूह का ईमानदारी से प्रतिनिधित्व करने के लिए, $K$ इसी डिग्री आव्यूह द्वारा सामान्यीकृत किया जाना चाहिए $D$ :

P=D^{-1}K.

$P$ अब एक मार्कोव श्रृंखला का प्रतिनिधित्व करता है। $P(x_{i},x_{j})$ से स्थानांतरित होने की संभावना है $x_{i}$ को $x_{j}$ एक बार के चरण में। इसी प्रकार से संक्रमण की संभावना $x_{i}$ को $x_{j}$ t समय चरणों द्वारा दिया गया है $P^{t}(x_{i},x_{j})$ . यहाँ $P^{t}$ आव्यूह है $P$ अपने आप से गुणा टी बार।

मार्कोव आव्यूह $P$ आकड़ों समुच्चय X की स्थानीय ज्यामिति की कुछ धारणा का गठन करता है। प्रसार मानचित्रों और प्रमुख घटक विश्लेषण के मध्य प्रमुख अंतर यह है कि आकड़ों के केवल स्थानीय विशेषताओं को प्रसार मानचित्रों में माना जाता है, क्योंकि पूरे आकड़ों समुच्चय के सहसंबंधों को लेने का विरोध किया जाता है।

$K$ आकड़ों समुच्चय पर एक यादृच्छिक चलना परिभाषित करता है जिसका अर्थ है कि कर्नेल आकड़ों समुच्चय के कुछ स्थानीय ज्यामिति को कैप्चर करता है। मार्कोव श्रृंखला कर्नेल मूल्यों के माध्यम से प्रसार की तेज और धीमी दिशाओं को परिभाषित करती है। जैसे-जैसे चलना समय के साथ आगे बढ़ता है, स्थानीय ज्यामिति की सूचना गतिशील प्रणाली के स्थानीय संक्रमण (अंतर समीकरणों द्वारा परिभाषित) के समान होती है।^[35]प्रसार का रूपक पारिवारिक प्रसार दूरी की परिभाषा से उत्पन्न होता है $\{D_{t}\}_{t\in N}$

D_{t}^{2}(x,y)=\|p_{t}(x,\cdot )-p_{t}(y,\cdot )\|^{2}

निश्चित टी के लिए, $D_{t}$ पथ कनेक्टिविटी के आधार पर आकड़ों समुच्चय के किसी भी दो बिंदुओं के मध्य की दूरी को परिभाषित करता है: का मान $D_{t}(x,y)$ x से y और इसके विपरीत कनेक्ट करने वाले अधिक पथ छोटे होंगे। क्योंकि मात्रा $D_{t}(x,y)$ लंबाई टी के सभी पथों का योग सम्मिलित है, $D_{t}$ अल्पांतरी दूरी की तुलना में आकड़ों में शोर के प्रति अधिक प्रबल है। $D_{t}$ दूरी की गणना करते समय बिंदु x और y के मध्य सभी संबंधों को ध्यान में रखता है और केवल यूक्लिडियन दूरी या यहां तक कि भूगर्भीय दूरी की तुलना में निकटता की बेहतर धारणा के रूप में कार्य करता है।

स्थानीय बहुआयामी सोपानन

स्थानीय बहुआयामी सोपानन स्थानीय क्षेत्रों में बहुआयामी सोपानन करता है, और फिर सभी टुकड़ों को एक साथ फिट करने के लिए उत्तल अनुकूलन का उपयोग करता है।^[37]

नॉनलाइनियर पीसीए

Nonlinear PCA (NLPCA) एक बहु-परत परसेप्ट्रॉन (MLP) को बहुविध फिट करने के लिए प्रशिक्षित करने के लिए backpropagation का उपयोग करता है।^[38] ठेठ एमएलपी प्रशिक्षण के विपरीत, जो केवल वज़न को अद्यतन करता है, एनएलपीसीए वज़न और निविष्टि दोनों को अद्यतन करता है। अर्थात्, वज़न और निविष्टि दोनों को अव्यक्त मान के रूप में माना जाता है। प्रशिक्षण के बाद, अव्यक्त निविष्टि देखे गए वैक्टरों का एक निम्न-आयामी प्रतिनिधित्व है, और एमएलपी उस निम्न-आयामी प्रतिनिधित्व से उच्च-आयामी अवलोकन समष्टि पर प्रतिचित्र करता है।

आकड़ों-चालित उच्च-आयामी सोपानन

आकड़ों-संचालित उच्च-आयामी सोपानन (DD-HDS)^[39] सैमन के मानचित्रण और घुमावदार घटक विश्लेषण से निकटता से संबंधित है, सिवाय इसके कि (1) यह मूल और आउटपुट दोनों जगहों में छोटी दूरी पर ध्यान केंद्रित करके झूठे निकटवर्ती और आँसू को एक साथ दंडित करता है, और यह (2) यह भार घटाने के द्वारा माप घटना की एकाग्रता के लिए खाता है दूरी वितरण के लिए कार्य।

बहुविध मूर्तिकला

बहुविध मूर्तिकला^[40] अंतःस्थापन खोजने के लिए स्नातक किए गए अनुकूलन का उपयोग करता है। अन्य कलन विधि की तरह, यह के-निकटतम सहवासियों की गणना करता है और एक अंतःस्थापन की तलाश करने की कोशिश करता है जो स्थानीय निकटवर्ती में संबंधों को संरक्षित करता है। यह धीरे-धीरे उच्च आयामों से विचरण करता है, साथ ही साथ उन संबंधों को बनाए रखने के लिए निचले आयामों में बिंदुओं को समायोजित करता है। यदि सोपानन की दर छोटी है, तो यह बहुत ही सटीक अंतःस्थापन पा सकता है। यह अनेक समस्याओं वाले अन्य कलन विधि की तुलना में उच्च अनुभवजन्य सटीकता का दावा करता है। इसका उपयोग अन्य बहुविध अधिगम वाले कलन विधि से परिणामों को परिष्कृत करने के लिए भी किया जा सकता है। हालांकि, जब तक बहुत धीमी सोपानन दर का उपयोग नहीं किया जाता है, तब तक यह बहुविध प्रकट करने के लिए संघर्ष करता है। इसका कोई प्रतिरूप नहीं है।

हैंडऑल

HandsAll^[41] दूरी के बजाय निकटवर्ती के क्रम को संरक्षित करने के लिए रूपांकित किया गया है। रैंकविसु विशेष रूप से कठिन फलनों में उपयोगी है (जब दूरी का संरक्षण संतोषजनक रूप से प्राप्त नहीं किया जा सकता है)। दरअसल, निकटवर्ती की क्रम दूरी की तुलना में कम जानकारीपूर्ण है (क्रम को दूरी से घटाया जा सकता है परन्तु दूरी को क्रम से नहीं घटाया जा सकता है) और इसका संरक्षण इस प्रकार आसान है।

स्थैतिक रूप से व्यवरूद्ध सममितीय अंतःस्थापन

स्थैतिक रूप से व्यवरूद्ध सममितीय अंतःस्थापन (टीसीआईई)^[42] यूक्लिडियन मापीय के साथ असंगत जियोडेसिक्स को छानने के बाद लगभग अल्पांतरी दूरियों पर आधारित एक कलन विधि है। जब आइसोमैप का उपयोग आंतरिक रूप से गैर-उत्तल आकड़ों को प्रतिचित्र करने के लिए किया जाता है, तो होने वाली विकृतियों को ठीक करने के उद्देश्य से, टीसीआईई अधिक सटीक मानचित्रण प्राप्त करने के लिए वेट लेस-स्क्वायर एमडीएस का उपयोग करता है। टीसीआईई कलन विधि पहले आकड़ों में संभावित सीमा बिंदुओं का पता लगाता है, और अल्पांतरी लंबाई की गणना के दौरान असंगत जियोडेसिक्स को चिन्हित करता है, जिसे भारित तनाव प्रमुखता में एक छोटा भार दिया जाता है।

समान बहुविध सन्निकटन और प्रक्षेपण

समरूप बहुविध सन्निकटन और प्रक्षेपण (UMAP) एक नॉनलाइनियर विमीयता न्यूनीकरण प्रविधि है।^[43] दृष्टिगत रूप से, यह टी-एसएनई के समान है, परन्तु यह मानता है कि आंकड़े समान रूप से स्थानीय रूप से जुड़े रीमैनियन बहुविध पर वितरित किया जाता है और यह कि रीमैनियन मापीय स्थानीय रूप से स्थिर या लगभग स्थानीय रूप से स्थिर है।^[44]

निकटता मैट्रिक्स पर आधारित तरीके

निकटता मैट्रिक्स पर आधारित एक विधि वह है जहां आकड़ों को समानता आव्यूह या दूरी आव्यूह के रूप में कलन विधि में प्रस्तुत किया जाता है। ये विधियाँ मापीय बहुआयामी सोपानन के व्यापक वर्ग के अंतर्गत आती हैं। निकटता आकड़ों की गणना कैसे की जाती है, इसमें विविधताएं अंतर होती हैं; उदाहरण के लिए, आइसोमैप, स्थानीय रूप से रैखिक अंतःस्थापन, अधिकतम विचरण का विकास, और सैममोन का प्रक्षेपण (जो वास्तव में मानचित्रण नहीं है) मापीय बहुआयामी सोपानन विधियों के उदाहरण हैं।

यह भी देखें

बहुविध परिकल्पना
स्पेक्ट्रल उप-बहुविध
टेकेंस की प्रमेय|टेकेंस की प्रमेय
व्हिटनी अंतःस्थापन प्रमेय
विभेदक विश्लेषण
लोचदार नक्शा
फ़ीचर अधिगम
बढ़ता हुआ स्व-संगठित मानचित्र (जीएसओएम)
स्व-आयोजन मानचित्र (SOM)

संदर्भ

↑ Lawrence, Neil D (2012). "A unifying probabilistic perspective for spectral dimensionality reduction: insights and new models". Journal of Machine Learning Research. 13 (May): 1609–38. arXiv:1010.4830. Bibcode:2010arXiv1010.4830L.
↑ Lee, John A.; Verleysen, Michel (2007). नॉनलाइनियर डायमेंशनलिटी रिडक्शन. Springer. ISBN 978-0-387-39350-6.
↑ Haller, George; Ponsioen, Sten (2016). "Nonlinear normal modes and spectral submanifolds: Existence, uniqueness and use in model reduction". Nonlinear Dynamics. 86 (3): 1493–1534. arXiv:1602.00560. doi:10.1007/s11071-016-2974-z. S2CID 44074026.
↑ Gashler, M.; Martinez, T. (2011). टेम्पोरल नॉनलाइनियर डायमेंशनलिटी रिडक्शन (PDF). Proceedings of the International Joint Conference on Neural Networks IJCNN'11. pp. 1959–66.
↑ The illustration is prepared using free software: Mirkes, E.M. (2011). "Principal Component Analysis and Self-Organizing Maps: applet". University of Leicester.
↑ Yin, Hujun (2007). "3. Learning Nonlinear Principal Manifolds by Self-Organising Maps". In Gorban, A.N.; Kégl, B.; Wunsch, D.C.; Zinovyev, A. (eds.). डेटा विज़ुअलाइज़ेशन और डायमेंशन रिडक्शन के लिए प्रिंसिपल मैनिफोल्ड्स. Lecture Notes in Computer Science and Engineering. Vol. 58. Springer. pp. 68–95. ISBN 978-3-540-73749-0.
↑ Schölkopf, B.; Smola, A.; Müller, K.-R. (1998). "कर्नेल आइगेनवैल्यू प्रॉब्लम के रूप में नॉनलाइनियर कंपोनेंट एनालिसिस". Neural Computation. MIT Press. 10 (5): 1299–1319. doi:10.1162/089976698300017467. S2CID 6674407.
↑ Ham, Jihun; Lee, Daniel D.; Mika, Sebastian; Schölkopf, Bernhard. "मैनिफोल्ड्स की डायमेंशनलिटी रिडक्शन का एक कर्नेल व्यू". Proceedings of the 21st International Conference on Machine Learning, Banff, Canada, 2004. doi:10.1145/1015330.1015417.
↑ Gorban, A. N.; Zinovyev, A. (2010). "Principal manifolds and graphs in practice: from molecular biology to dynamical systems". International Journal of Neural Systems. 20 (3): 219–232. arXiv:1001.1122. doi:10.1142/S0129065710002383. PMID 20556849. S2CID 2170982.
↑ A. Zinovyev, ViDaExpert - Multidimensional Data Visualization Tool (free for non-commercial use). Institut Curie, Paris.
↑ Zinovyev, A. "ViDaExpert सिंहावलोकन" (PDF). Bures-Sur-Yvette, Île-de-France: IHES (Institut des Hautes Études Scientifiques).
↑ Hastie, T. (November 1984). प्रधान वक्र और सतहें (PDF) (PhD). Stanford Linear Accelerator Center, Stanford University. Archived (PDF) from the original on August 2, 2019.
↑ Hastie, T.; Stuetzle, W. (June 1989). "प्रधान वक्र" (PDF). Journal of the American Statistical Association. 84 (406): 502–6. doi:10.1080/01621459.1989.10478797.
↑ Gorban, A. N.; Kégl, B.; Wunsch, D. C.; Zinovyev, A., eds. (2007). डेटा विज़ुअलाइज़ेशन और डायमेंशन रिडक्शन के लिए प्रिंसिपल मैनिफोल्ड्स. Lecture Notes in Computer Science and Engineering (LNCSE). Vol. 58. Springer. ISBN 978-3-540-73749-0.
↑ Belkin, Mikhail; Niyogi, Partha (2001). "एम्बेडिंग और क्लस्टरिंग के लिए लाप्लासियन ईजेनमैप्स और स्पेक्ट्रल तकनीक" (PDF). Advances in Neural Information Processing Systems. MIT Press. 14: 586–691. ISBN 0-262-27173-7. OCLC 52710683.
↑ ^16.0 ^16.1 Belkin, Mikhail (August 2003). कई गुना सीखने की समस्याएं (PhD). Department of Mathematics, The University of Chicago. Matlab code for Laplacian Eigenmaps can be found in algorithms at Ohio-state.edu
↑ Bengio, Yoshua; Paiement, Jean-Francois; Vincent, Pascal; Delalleau, Olivier; Le Roux, Nicolas; Ouimet, Marie (2004). "Out-of-Sample Extensions for LLE, Isomap, MDS, Eigenmaps, and Spectral Clustering" (PDF). न्यूरल इन्फर्मेशन प्रोसेसिंग सिस्टम्स में प्रगति. Vol. 16. ISBN 0-262-20152-6.
↑ Tenenbaum, J B.; de Silva, V.; Langford, J.C. (2000). "नॉनलाइनियर डायमेंशनलिटी रिडक्शन के लिए एक ग्लोबल जियोमेट्रिक फ्रेमवर्क" (PDF). Science. 290: 2319–23.
↑ Roweis, S. T.; Saul, L. K. (2000). "स्थानीय रूप से रैखिक एम्बेडिंग द्वारा गैर-रैखिक आयाम में कमी". Science. 290 (5500): 2323–6. Bibcode:2000Sci...290.2323R. doi:10.1126/science.290.5500.2323. PMID 11125150. S2CID 5987139.
↑ Donoho, D.; Grimes, C. (2003). "Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data". Proc Natl Acad Sci U S A. 100 (10): 5591–6. Bibcode:2003PNAS..100.5591D. doi:10.1073/pnas.1031596100. PMC 156245. PMID 16576753.
↑ Zhang, Z.; Wang, J. (2006). "MLLE: Modified Locally Linear Embedding Using Multiple Weights". NIPS'06: Proceedings of the 19th International Conference on Neural Information Processing Systems: 1593–1600.
↑ Sidhu, Gagan (2019). "मनोरोग वर्गीकरण में स्थानीय रूप से रैखिक एंबेडिंग और fMRI विशेषता चयन". IEEE Journal of Translational Engineering in Health and Medicine. 7: 1–11. arXiv:1908.06319. doi:10.1109/JTEHM.2019.2936348. PMC 6726465. PMID 31497410. S2CID 201832756.
↑ Zhang, Zhenyue; Hongyuan Zha (2005). "प्रिंसिपल मैनिफोल्ड्स और नॉनलाइनियर डायमेंशन रिडक्शन वाया लोकल टैंजेंट स्पेस एलाइनमेंट". SIAM Journal on Scientific Computing. 26 (1): 313–338. CiteSeerX 10.1.1.211.9957. doi:10.1137/s1064827502419154.
↑ DeMers, D.; Cottrell, G.W. (1993). "Non-linear dimensionality reduction". न्यूरल इन्फर्मेशन प्रोसेसिंग सिस्टम्स में प्रगति. Vol. 5. pp. 580–7. ISBN 1558600159. OCLC 928936290.
↑ Lawrence, N. (2005). "गाऊसी प्रक्रिया अव्यक्त चर मॉडल के साथ संभाव्य गैर-रैखिक प्रमुख घटक विश्लेषण". Journal of Machine Learning Research. 6: 1783–1816.
↑ Ding, M.; Fan, G. (2015). "ह्यूमन गैट मोशन मॉडलिंग के लिए मल्टीलेयर जॉइंट गैट-पोज मैनिफोल्ड्स". IEEE Transactions on Cybernetics. 45 (11): 2413–24. doi:10.1109/TCYB.2014.2373393. PMID 25532201. S2CID 15591304.
↑ van der Maaten, L.J.P.; Hinton, G.E. (2008). "t-SNE का उपयोग करके उच्च-आयामी डेटा की कल्पना करना" (PDF). Journal of Machine Learning Research. 9: 2579–2605.
↑ Li, James X. (2004). "संबंधपरक परिप्रेक्ष्य मानचित्र के साथ उच्च-आयामी डेटा की कल्पना करना" (PDF). Information Visualization. 3: 49–59. doi:10.1057/palgrave.ivs.9500051. S2CID 7566939.
↑ Taylor, D.; Klimm, F.; Harrington, H. A.; Kramár, M.; Mischaikow, K.; Porter, M. A.; Mucha, P. J. (2015). "नेटवर्क पर प्रसार प्रक्रियाओं की जांच के लिए संक्रामक मानचित्रों का सामयिक डेटा विश्लेषण". Nature Communications. 6: 7723. arXiv:1408.1168. Bibcode:2015NatCo...6.7723T. doi:10.1038/ncomms8723. PMC 4566922. PMID 26194875.
↑ ^30.0 ^30.1 Demartines, P.; Hérault, J. (1997). "Curvilinear Component Analysis: A Self-Organizing Neural Network for Nonlinear Mapping of Data Sets" (PDF). IEEE Transactions on Neural Networks. 8 (1): 148–154. doi:10.1109/72.554199. PMID 18255618.
↑ Sun, Jigang; Crowe, Malcolm; Fyfe, Colin (2010). "Curvilinear component analysis and Bregman divergences" (PDF). कृत्रिम तंत्रिका नेटवर्क पर यूरोपीय संगोष्ठी (Esan). d-side publications. pp. 81–86.
↑ Walder, Christian; Schölkopf, Bernhard (2009). "Diffeomorphic Dimensionality Reduction" (PDF). न्यूरल इन्फर्मेशन प्रोसेसिंग सिस्टम्स में प्रगति. Vol. 22. MIT Press. pp. 1713–20.
↑ Wang, Chang; Mahadevan, Sridhar (July 2008). Procrustes विश्लेषण का उपयोग करते हुए मैनिफोल्ड एलाइनमेंट (PDF). The 25th International Conference on Machine Learning. pp. 1120–7.
↑ Lafon, Stephane (May 2004). डिफ्यूजन मैप्स और जियोमेट्रिक हार्मोनिक्स (PhD). Yale University.
↑ ^35.0 ^35.1 Coifman, Ronald R.; Lafon, Stephane (July 2006). "प्रसार मानचित्र" (PDF). Applied and Computational Harmonic Analysis. 21 (1): 5–30. doi:10.1016/j.acha.2006.04.006. S2CID 17160669.
↑ Bah, B. (2008). Diffusion Maps: Applications and Analysis (Masters). University of Oxford.
↑ Venna, J.; Kaski, S. (2006). "स्थानीय बहुआयामी स्केलिंग". Neural Networks. 19 (6–7): 889–899. doi:10.1016/j.neunet.2006.05.014. PMID 16787737.
↑ Scholz, M.; Kaplan, F.; Guy, C. L.; Kopka, J.; Selbig, J. (2005). "Non-linear PCA: a missing data approach". Bioinformatics. Oxford University Press. 21 (20): 3887–95. doi:10.1093/bioinformatics/bti634. PMID 16109748.
↑ S. Lespinats, M. Verleysen, A. Giron, B. Fertil, DD-HDS: a tool for visualization and exploration of high-dimensional data, IEEE Transactions on Neural Networks 18 (5) (2007) 1265–1279.
↑ Gashler, M. and Ventura, D. and Martinez, T., Iterative Non-linear Dimensionality Reduction with Manifold Sculpting, In Platt, J.C. and Koller, D. and Singer, Y. and Roweis, S., editor, Advances in Neural Information Processing Systems 20, pp. 513–520, MIT Press, Cambridge, MA, 2008
↑ Lespinats S., Fertil B., Villemain P. and Herault J., Rankvisu: Mapping from the neighbourhood network, Neurocomputing, vol. 72 (13–15), pp. 2964–2978, 2009.
↑ Rosman, G.; Bronstein, M.M.; Bronstein, A.M.; Kimmel, R. (2010). "स्थलाकृतिक रूप से बाधित आइसोमेट्रिक एंबेडिंग द्वारा नॉनलाइनियर डायमेंशनलिटी रिडक्शन" (PDF). International Journal of Computer Vision. 89 (1): 56–68. doi:10.1007/s11263-010-0322-1. S2CID 1365750.
↑ McInnes, Leland; Healy, John; Melville, James (2018-12-07). "डायमेंशन रिडक्शन के लिए यूनिफ़ॉर्म मैनिफोल्ड सन्निकटन और प्रोजेक्शन". arXiv:1802.03426.
↑ "UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction — umap 0.3 documentation". umap-learn.readthedocs.io. Retrieved 2019-05-04.

अग्रिम पठन

Murphy, Kevin P. (2022). "Manifold Learning". Probabilistic Machine Learning. MIT Press. pp. 682–699. ISBN 978-0-262-04682-4.

बाहरी संबंध

Isomap
Generative Topographic Mapping
Mike Tipping's Thesis
Gaussian Process Latent Variable Model
Locally Linear Embedding
Relational Perspective Map
Waffles is an open source C++ library containing implementations of LLE, Manifold Sculpting, and some other manifold learning algorithms.
DD-HDS homepage
RankVisu homepage
Short review of Diffusion Maps
Nonlinear PCA by autoencoder neural networks

[1] Lawrence, Neil D (2012). "A unifying probabilistic perspective for spectral dimensionality reduction: insights and new models". Journal of Machine Learning Research. 13 (May): 1609–38. arXiv:1010.4830. Bibcode:2010arXiv1010.4830L.

[2] Lee, John A.; Verleysen, Michel (2007). नॉनलाइनियर डायमेंशनलिटी रिडक्शन. Springer. ISBN 978-0-387-39350-6.

[3] Haller, George; Ponsioen, Sten (2016). "Nonlinear normal modes and spectral submanifolds: Existence, uniqueness and use in model reduction". Nonlinear Dynamics. 86 (3): 1493–1534. arXiv:1602.00560. doi:10.1007/s11071-016-2974-z. S2CID 44074026.

[4] Gashler, M.; Martinez, T. (2011). टेम्पोरल नॉनलाइनियर डायमेंशनलिटी रिडक्शन (PDF). Proceedings of the International Joint Conference on Neural Networks IJCNN'11. pp. 1959–66.

[5] The illustration is prepared using free software: Mirkes, E.M. (2011). "Principal Component Analysis and Self-Organizing Maps: applet". University of Leicester.

[6] Yin, Hujun (2007). "3. Learning Nonlinear Principal Manifolds by Self-Organising Maps". In Gorban, A.N.; Kégl, B.; Wunsch, D.C.; Zinovyev, A. (eds.). डेटा विज़ुअलाइज़ेशन और डायमेंशन रिडक्शन के लिए प्रिंसिपल मैनिफोल्ड्स. Lecture Notes in Computer Science and Engineering. Vol. 58. Springer. pp. 68–95. ISBN 978-3-540-73749-0.

[7] Schölkopf, B.; Smola, A.; Müller, K.-R. (1998). "कर्नेल आइगेनवैल्यू प्रॉब्लम के रूप में नॉनलाइनियर कंपोनेंट एनालिसिस". Neural Computation. MIT Press. 10 (5): 1299–1319. doi:10.1162/089976698300017467. S2CID 6674407.

[8] Ham, Jihun; Lee, Daniel D.; Mika, Sebastian; Schölkopf, Bernhard. "मैनिफोल्ड्स की डायमेंशनलिटी रिडक्शन का एक कर्नेल व्यू". Proceedings of the 21st International Conference on Machine Learning, Banff, Canada, 2004. doi:10.1145/1015330.1015417.

[9] Gorban, A. N.; Zinovyev, A. (2010). "Principal manifolds and graphs in practice: from molecular biology to dynamical systems". International Journal of Neural Systems. 20 (3): 219–232. arXiv:1001.1122. doi:10.1142/S0129065710002383. PMID 20556849. S2CID 2170982.

[10] A. Zinovyev, ViDaExpert - Multidimensional Data Visualization Tool (free for non-commercial use). Institut Curie, Paris.

[11] Zinovyev, A. "ViDaExpert सिंहावलोकन" (PDF). Bures-Sur-Yvette, Île-de-France: IHES (Institut des Hautes Études Scientifiques).

[12] Hastie, T. (November 1984). प्रधान वक्र और सतहें (PDF) (PhD). Stanford Linear Accelerator Center, Stanford University. Archived (PDF) from the original on August 2, 2019.

[13] Hastie, T.; Stuetzle, W. (June 1989). "प्रधान वक्र" (PDF). Journal of the American Statistical Association. 84 (406): 502–6. doi:10.1080/01621459.1989.10478797.

[14] Gorban, A. N.; Kégl, B.; Wunsch, D. C.; Zinovyev, A., eds. (2007). डेटा विज़ुअलाइज़ेशन और डायमेंशन रिडक्शन के लिए प्रिंसिपल मैनिफोल्ड्स. Lecture Notes in Computer Science and Engineering (LNCSE). Vol. 58. Springer. ISBN 978-3-540-73749-0.

[15] Belkin, Mikhail; Niyogi, Partha (2001). "एम्बेडिंग और क्लस्टरिंग के लिए लाप्लासियन ईजेनमैप्स और स्पेक्ट्रल तकनीक" (PDF). Advances in Neural Information Processing Systems. MIT Press. 14: 586–691. ISBN 0-262-27173-7. OCLC 52710683.

[Belkin-16] 16.0 ^16.1 Belkin, Mikhail (August 2003). कई गुना सीखने की समस्याएं (PhD). Department of Mathematics, The University of Chicago. Matlab code for Laplacian Eigenmaps can be found in algorithms at Ohio-state.edu

[17] Bengio, Yoshua; Paiement, Jean-Francois; Vincent, Pascal; Delalleau, Olivier; Le Roux, Nicolas; Ouimet, Marie (2004). "Out-of-Sample Extensions for LLE, Isomap, MDS, Eigenmaps, and Spectral Clustering" (PDF). न्यूरल इन्फर्मेशन प्रोसेसिंग सिस्टम्स में प्रगति. Vol. 16. ISBN 0-262-20152-6.

[18] Tenenbaum, J B.; de Silva, V.; Langford, J.C. (2000). "नॉनलाइनियर डायमेंशनलिटी रिडक्शन के लिए एक ग्लोबल जियोमेट्रिक फ्रेमवर्क" (PDF). Science. 290: 2319–23.

[19] Roweis, S. T.; Saul, L. K. (2000). "स्थानीय रूप से रैखिक एम्बेडिंग द्वारा गैर-रैखिक आयाम में कमी". Science. 290 (5500): 2323–6. Bibcode:2000Sci...290.2323R. doi:10.1126/science.290.5500.2323. PMID 11125150. S2CID 5987139.

[20] Donoho, D.; Grimes, C. (2003). "Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data". Proc Natl Acad Sci U S A. 100 (10): 5591–6. Bibcode:2003PNAS..100.5591D. doi:10.1073/pnas.1031596100. PMC 156245. PMID 16576753.

[21] Zhang, Z.; Wang, J. (2006). "MLLE: Modified Locally Linear Embedding Using Multiple Weights". NIPS'06: Proceedings of the 19th International Conference on Neural Information Processing Systems: 1593–1600.

[borntolose-22] Sidhu, Gagan (2019). "मनोरोग वर्गीकरण में स्थानीय रूप से रैखिक एंबेडिंग और fMRI विशेषता चयन". IEEE Journal of Translational Engineering in Health and Medicine. 7: 1–11. arXiv:1908.06319. doi:10.1109/JTEHM.2019.2936348. PMC 6726465. PMID 31497410. S2CID 201832756.

[23] Zhang, Zhenyue; Hongyuan Zha (2005). "प्रिंसिपल मैनिफोल्ड्स और नॉनलाइनियर डायमेंशन रिडक्शन वाया लोकल टैंजेंट स्पेस एलाइनमेंट". SIAM Journal on Scientific Computing. 26 (1): 313–338. CiteSeerX 10.1.1.211.9957. doi:10.1137/s1064827502419154.

[24] DeMers, D.; Cottrell, G.W. (1993). "Non-linear dimensionality reduction". न्यूरल इन्फर्मेशन प्रोसेसिंग सिस्टम्स में प्रगति. Vol. 5. pp. 580–7. ISBN 1558600159. OCLC 928936290.

[25] Lawrence, N. (2005). "गाऊसी प्रक्रिया अव्यक्त चर मॉडल के साथ संभाव्य गैर-रैखिक प्रमुख घटक विश्लेषण". Journal of Machine Learning Research. 6: 1783–1816.

[26] Ding, M.; Fan, G. (2015). "ह्यूमन गैट मोशन मॉडलिंग के लिए मल्टीलेयर जॉइंट गैट-पोज मैनिफोल्ड्स". IEEE Transactions on Cybernetics. 45 (11): 2413–24. doi:10.1109/TCYB.2014.2373393. PMID 25532201. S2CID 15591304.

[27] van der Maaten, L.J.P.; Hinton, G.E. (2008). "t-SNE का उपयोग करके उच्च-आयामी डेटा की कल्पना करना" (PDF). Journal of Machine Learning Research. 9: 2579–2605.

[28] Li, James X. (2004). "संबंधपरक परिप्रेक्ष्य मानचित्र के साथ उच्च-आयामी डेटा की कल्पना करना" (PDF). Information Visualization. 3: 49–59. doi:10.1057/palgrave.ivs.9500051. S2CID 7566939.

[29] Taylor, D.; Klimm, F.; Harrington, H. A.; Kramár, M.; Mischaikow, K.; Porter, M. A.; Mucha, P. J. (2015). "नेटवर्क पर प्रसार प्रक्रियाओं की जांच के लिए संक्रामक मानचित्रों का सामयिक डेटा विश्लेषण". Nature Communications. 6: 7723. arXiv:1408.1168. Bibcode:2015NatCo...6.7723T. doi:10.1038/ncomms8723. PMC 4566922. PMID 26194875.

[Demart-30] 30.0 ^30.1 Demartines, P.; Hérault, J. (1997). "Curvilinear Component Analysis: A Self-Organizing Neural Network for Nonlinear Mapping of Data Sets" (PDF). IEEE Transactions on Neural Networks. 8 (1): 148–154. doi:10.1109/72.554199. PMID 18255618.

[Jigang-31] Sun, Jigang; Crowe, Malcolm; Fyfe, Colin (2010). "Curvilinear component analysis and Bregman divergences" (PDF). कृत्रिम तंत्रिका नेटवर्क पर यूरोपीय संगोष्ठी (Esan). d-side publications. pp. 81–86.

[32] Walder, Christian; Schölkopf, Bernhard (2009). "Diffeomorphic Dimensionality Reduction" (PDF). न्यूरल इन्फर्मेशन प्रोसेसिंग सिस्टम्स में प्रगति. Vol. 22. MIT Press. pp. 1713–20.

[33] Wang, Chang; Mahadevan, Sridhar (July 2008). Procrustes विश्लेषण का उपयोग करते हुए मैनिफोल्ड एलाइनमेंट (PDF). The 25th International Conference on Machine Learning. pp. 1120–7.

[34] Lafon, Stephane (May 2004). डिफ्यूजन मैप्स और जियोमेट्रिक हार्मोनिक्स (PhD). Yale University.

[ReferenceA-35] 35.0 ^35.1 Coifman, Ronald R.; Lafon, Stephane (July 2006). "प्रसार मानचित्र" (PDF). Applied and Computational Harmonic Analysis. 21 (1): 5–30. doi:10.1016/j.acha.2006.04.006. S2CID 17160669.

[36] Bah, B. (2008). Diffusion Maps: Applications and Analysis (Masters). University of Oxford.

[37] Venna, J.; Kaski, S. (2006). "स्थानीय बहुआयामी स्केलिंग". Neural Networks. 19 (6–7): 889–899. doi:10.1016/j.neunet.2006.05.014. PMID 16787737.

[38] Scholz, M.; Kaplan, F.; Guy, C. L.; Kopka, J.; Selbig, J. (2005). "Non-linear PCA: a missing data approach". Bioinformatics. Oxford University Press. 21 (20): 3887–95. doi:10.1093/bioinformatics/bti634. PMID 16109748.

[39] S. Lespinats, M. Verleysen, A. Giron, B. Fertil, DD-HDS: a tool for visualization and exploration of high-dimensional data, IEEE Transactions on Neural Networks 18 (5) (2007) 1265–1279.

[40] Gashler, M. and Ventura, D. and Martinez, T., Iterative Non-linear Dimensionality Reduction with Manifold Sculpting, In Platt, J.C. and Koller, D. and Singer, Y. and Roweis, S., editor, Advances in Neural Information Processing Systems 20, pp. 513–520, MIT Press, Cambridge, MA, 2008

[41] Lespinats S., Fertil B., Villemain P. and Herault J., Rankvisu: Mapping from the neighbourhood network, Neurocomputing, vol. 72 (13–15), pp. 2964–2978, 2009.

[42] Rosman, G.; Bronstein, M.M.; Bronstein, A.M.; Kimmel, R. (2010). "स्थलाकृतिक रूप से बाधित आइसोमेट्रिक एंबेडिंग द्वारा नॉनलाइनियर डायमेंशनलिटी रिडक्शन" (PDF). International Journal of Computer Vision. 89 (1): 56–68. doi:10.1007/s11263-010-0322-1. S2CID 1365750.

[43] McInnes, Leland; Healy, John; Melville, James (2018-12-07). "डायमेंशन रिडक्शन के लिए यूनिफ़ॉर्म मैनिफोल्ड सन्निकटन और प्रोजेक्शन". arXiv:1802.03426.

[44] "UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction — umap 0.3 documentation". umap-learn.readthedocs.io. Retrieved 2019-05-04.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

Anonymous

Search